Room temperature measurements of the 3D orientation of single CdSe quantum dots using polarization microscopy

Abstract

Simple far-field emission polarization microscopy reveals that the emission transition dipole of CdSe colloidal quantum dots (QDs) is twofold degenerate at room temperature. We measure, model, and compare polarization anisotropy statistics of CdSe QDs and DiI (a one-dimensional emitter). We find excellent agreement between experiment and theory if the transition dipole of CdSe QDs is assumed to be twofold degenerate. This implies that the three-dimensional orientation of the unique crystal axis in QDs can be determined at room temperature with polarization microscopy. We describe an optical setup to measure four polarization angles of multiple single QDs simultaneously and in real time (≈16 Hz). We use this setup in a proof-of-concept experiment to demonstrate that the rotational motion of QDs can be monitored in various host matrices.

Optical investigations of transition dipole orientations have uncovered behavior ranging from structural changes in biological systems (1) to fast and slow relaxation dynamics at the molecular level in glassy matrices (2). Most of these studies rely on organic dye molecules that have absorbing and emitting transition dipoles that are linear dipoles (nondegenerate, or linear emitters). In general, conventional far-field microscopy of such species can provide information only about the in-plane orientation of the chromophores through the projection of the transition dipole onto the focal plane. Insight into the full 3D orientation of optical probes should provide further detailed information about complex processes in the condensed phase. Scanning near-field microscopy and aberrated or defocused wide-field microscopy have been used in conjunction with linear emitters, providing information about the 3D orientation of transition dipoles of single molecules (3–6). These methods require especially high spatial resolution resulting in a smaller field of view and greater acquisition times. A theoretical method to determine the 3D orientation of the linear transition dipole of a single molecule by using polarization microscopy was also developed (7). Recently, scanning confocal microscopy has been used to image single absorbing transition dipoles by annular illumination to enhance the longitudinal component of the excitation source (8).

A chromophore with a twofold degenerate dipole (2D or circular emitter) intrinsically contains 3D-orientation information. For a randomly oriented circular emitter, the 2D polarization is projected as an elliptical shape on the sample plane where the ellipticity and direction of the long axis depend on the 3D orientation of the transition dipole relative to the optical axis. Recently, CdSe quantum dots (QDs) were shown to have a 2D transition dipole at cryogenic temperatures (4). Here we demonstrate that a 2D transition dipole is also observed at room temperature, where biological applications can be pursued (9, 10).

Quantum confinement of the exciton in CdSe colloidal QDs results in discrete, atomic-like electronic energy levels. Numerous experimental studies on ensembles of QDs have suggested that the lowest-lying states that participate in the emission process are doubly degenerate in the plane perpendicular to the c axis (9, 11–13). This degeneracy is responsible for the previously observed 2D transition dipole in emission at 10 K. In this article we show that single CdSe QDs also have a 2D transition dipole at room temperature. We use this finding to design an optical setup that can track the rotational motion of multiple single QDs simultaneously in various host matrices and at different temperatures.

Experimental Methods

The emitting transition dipoles of 1D and 2D chromophores were probed by using far-field polarization microscopy at room temperature. The samples were illuminated and the image was collected by using an oil-immersion microscope objective (numerical aperture, 1.25). Single DiI molecules (1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanite perchlorate) were chosen as a well known organic dye molecule with a 1D (linear) transition dipole. The CdSe QDs were prepared by following the method of Murray et al. (14) and overcoated with a few layers of ZnS (15). A dilute solution of QDs (or DiI molecules) was spin-cast in a polymethylmethacrylate (PMMA) matrix onto a glass substrate. The fluorescence signal from individual QDs was split into its parallel and perpendicular polarization components by a polarization-displacement prism.

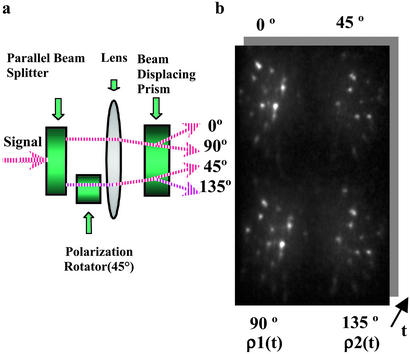
To monitor orientation dynamics in real time, we used a modified optical layout that measures two polarization anisotropy values from four polarization components of the emission from multiple individual QDs simultaneously. First, the emission signal was split into two parallel beams by a set of three prisms. One of the beams was then rotated by 45° with a polarization rotator as shown in Fig. 1a. These parallel beams were then split further according to their polarization by using a polarization-displacement prism to yield the 0, 90, 45, and 135° polarization components of the emission for each QD as seen in Fig. 1b. Two polarization anisotropy values were defined by the 0 and 90° components and the 45 and 135° components, respectively, for each QD. Because every pair of in-plane and out-of plane angles produces a pair of anisotropy values, a data analysis program was written to match the observed anisotropy values to the pair of two angles that defines the QD orientation. The time trace of anisotropy values then translates into a corresponding angular rotational time trace.

Figure 1.

(a) Schematic of the apparatus used to obtain the image in b. The fluorescence signal is split into two parallel beams. One beam is then rotated by 45° with a polarization rotator. The two beams are then passed through a polarization beam-displacing prism to yield the 0, 90, 45, and 135° polarization components of the image. (b) Four polarization components (0, 90, 45, and 135°) of the same QDs obtained simultaneously. Two components (0 and 90°) define one anisotropy value, and the other two (45 and 135°) define the second anisotropy value. A series of these images creates a time series of anisotropy values.

Results and Discussion

To identify the nature of the transition dipole for CdSe QDs, polarization anisotropy (ρ) values, defined as

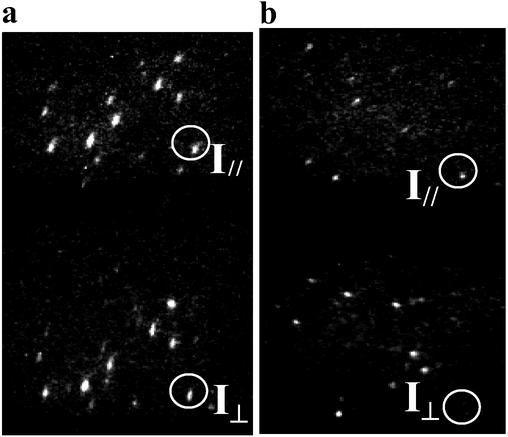
where I_par(per) is the parallel (perpendicular) polarization component of emission intensity, were obtained. Fig. 2 a and b show the orthogonal polarization components of the fluorescence from single QDs and DiI molecules, respectively. Most of the QD images show both polarization components as in Fig. 2a, whereas those from DiI molecules seldom show a complimentary pair in the orthogonal polarization. As an example, in Fig. 2, this is shown in the photoemission images in orthogonal polarization from a QD and a DiI molecule inside two vertical circles, respectively. The different statistical distributions of anisotropy values clearly reveal the different nature of the emitting transition dipoles between QDs and DiI molecules. Care was taken to properly prepare samples where the possibility for any rotational or translational motion of the QDs (or DiIs) was reduced greatly and random distributions of orientations were ensured. Anisotropy values of the QDs and DiI molecules were nearly constant for the entire acquisition time except for when the dots were in their “off” state (not luminescing), where noise then dominated the data. This verified that the particles in the PMMA matrix were frozen at their initial positions and that we were looking at single chromophores. Without careful background subtraction and rejection of QD dark periods, averaged anisotropy values may be reduced to zero, leading to misleadingly small values for the degree of polarization.

Figure 2.

Polarized fluorescence images of single CdSe QDs (2.8 nm in radius) (a) and DiI molecules (b). The emission is split into two images with orthogonal polarization components by using a polarization-displacement prism. These images are used to obtain polarization anisotropy values. The intensity images of orthogonal polarization pairs of photoemission from a QD and a DiI molecule are shown inside two vertical circles in a and b.

Histograms of the theoretical and experimental polarization anisotropy values of DiI molecules and QDs are shown in Fig. 3 (a and c and b and d, respectively). The theoretical distributions were calculated by using transition dipole models based on ref. 9. I_par and I_per functions were defined in terms of the in-plane (φ) and out-of-plane (θ) angles accordingly. Anisotropy values (ρ) were generated assuming a random distribution of chromophore orientations. Care must be taken here to correct for the numerical aperture of the objective in the generation of anisotropy values. The projection of a dipole depends on the captured light cone, which is determined by the numerical aperture of the objective; the anisotropy values were corrected for the collection angle (59.6°) of our microscope objective, modifying previous methods in the case of linear dipoles (16, 17) to the 2D system of this article. Experimental distributions of anisotropy values for QDs and DiI molecules were consistent with theoretical predictions for 1D and 2D transition dipoles, respectively, as shown in Fig. 2 a and b. Experimental and theoretical distributions of the polarization anisotropy values were not statistically different according to a χ² test.

Figure 3.

Theoretical histograms of the probability density, f(ρ), of polarization anisotropy values ρ for 1D (a) and 2D (b) transition dipoles, assuming that the emitters are oriented randomly. These histograms demonstrate good agreement with experimental results for DiI (1D dipole) (c) and CdSe QDs (2D dipole) (d). (e) The anisotropy (ρ) variation of the emission while rotating the detected polarization angle is plotted for four QDs. (f) The experimental distribution of the degree of polarization (DOP) is additional evidence of the 2D character of the transition dipole of a CdSe QD. The distribution was obtained from 21 individual QDs. The shape of this distribution at room temperature is similar to that at low temperature.

Further evidence for a 2D transition dipole in single QDs is shown in Fig. 3 e and f. By sequentially rotating the polarization-displacement prism from 0 to 180°, changes in anisotropy values from the same single QD were plotted to show a sinusoidal pattern over rotated angles as shown in Fig. 3e. Moreover, the degree-of-polarization values for individual QDs, defined as (I_max − I_min)/I_max, were extrapolated out at the maxima of oscillatory plots. Fig. 3f demonstrates that the distribution of degree-of-polarization values for the randomly oriented set of QDs at room temperature is very much consistent with a 2D transition dipole (4), in contrast with previous work (18). The experimental mean value of the degree-of-polarization was measured to be 0.59 with the standard deviation, ±0.28, as compared with the simulated mean value of 0.50 (±0.36) for generic 2D transition dipoles.

We also investigated size-dependent emission properties of QDs with 1.3-, 1.8-, and 2.8-nm radii. All three sizes of QDs showed statistically the same distribution of polarization anisotropy values as the 2D theoretical analogue. According to theory, only the highest energy state among the five band-edge fine structure states is predicted to have a 1D emitting transition dipole (13). The polarization measurements above show that the contribution of the singly defined uppermost state to the emission polarization at room temperature is insignificant in our size range. This is consistent with simple calculations based on the energy spacing between the lowest optically active state and the uppermost state, combined with their oscillator strengths, (19) that predict ≈10% of the population in the uppermost state at room temperature.

The projection of the 2D transition dipole onto the sample plane can provide out-of-plane and in-plane angle information about the QD orientation from measuring the ellipticity of the projection and the direction of the major axis (9). However, to obtain both the in-plane and out-of-plane angle and consequently the full 3D orientation, two anisotropy values are needed. Fig. 3a shows four QDs, each with four different polarization components from our optical setup. Although the fluorescence image is divided into four components, the signal-to-noise ratio is still excellent.

As a proof-of-concept experiment to show that QDs can serve as a local probe of orientational dynamics, dilute concentrations of QDs were embedded in a few polymer/solvent mixtures, and the individual QD rotational dynamics (≈10–20 Hz) were monitored. As an example, Fig. 4a maps the temperature-dependent rotational dynamics of QDs in a hexadecane/PMMA system for 300 s with a 10-Hz acquisition rate. Each mark on the spherical map corresponds to the QD crystalline axis orientation, and the lines connect between two sequential positions. The longitude and latitude correspond to in-plane (φ) and out-of-plane (θ) angles, respectively. At temperatures lower than the melting point (18°C) of hexadecane, we would expect QDs not to fluctuate much from their original position, whereas at temperatures above the melting point, the QDs should show more rotational diffusion. The blue plots demonstrate low-temperature motion (10°C), whereas green and red plots show two sequential segments of the high-temperature motion (27°C). Periods where the dot is in its “off” state (not emitting) have been removed from the plots. As expected, the low-temperature data (blue plots) show little motion compared with the jumps of the green and red plots at the higher temperature. This is well demonstrated in the lag plots of the out-of plane angle and the in-plane angle in Fig. 4 b and c, respectively. The plots [φ(t) vs. φ(t + 1) and θ(t) vs. θ(t + 1), where (t + 1) corresponds to one data point farther in time that at time t] show that the rotational dynamics are correlated in time, because the data points are clustered along the diagonal. At low temperature, the cluster (blue plots) is tightly bound along the diagonal, but as the temperature is raised, two new clusters (green and red) are formed at different positions along the diagonal. The deviation from the diagonal distribution is a measure of the extent of fluctuation. Although the in-plane and out-of-plane angles were not constant at 10°C (blue plots), the extent of the fluctuations was much smaller than at 27°C (green and red). Compared with the lag plot of the out-of-plane angle in Fig. 4c, the in-plane angle in Fig. 4b shows more motion in general, thus indicating different dynamics for each angular motion. This may be explained if this particular QD was not perfectly embedded inside the matrix but resided close to an interface.

Figure 4.

(a) Projection map of the temperature-dependent rotational dynamics of a QD over 300 s with a 10-Hz acquisition rate. Hexadecane (melting point = 18°C) mixed with PMMA was used as a matrix. The temperature was increased and sequentially measured in three traces: blue (10°C), green (27°C), and red (27°C). (b and c) Lag plots [φ(t) vs. φ(t + 1) and θ(t) vs. θ(t + 1)] show that the positions correlate in time, and that the deviations from the center values of in-plane angle (φ) (b) and out-of-plane angle (θ) (c) are larger at temperatures above the melting point than below. The colors correspond to those described for a. (d) Rotational dynamics of a QD in a viscous polymer matrix, poly(phenyl-glycidyl)-ether-co-aldehyde, at room temperature. In sequence, three distinctive dynamics were observed and grouped with different colors (blue, green, and red, sequentially). (e) Rotational dynamics in a polymer that is less viscous than in d shows larger fluctuations. (f) Rotational dynamics in hexadecane/PMMA matrix.

Fig. 4d shows the rotational movement of a QD in a viscous polymer matrix, poly(phenyl-glycidyl)-ether-co-aldehyde, at room temperature. As a function of time, three distinctive dynamics were observed and grouped in different colors. The dynamics in the blue track demonstrate little fluctuation around a single mean, but sudden jumping migration is observed in the green track. Because of the symmetry of the projected transition dipoles, changes of ±θ and f ± π produce the same anisotropy values. This degeneracy can be resolved if the rotational motion is sufficiently slow such that sudden jumps between degenerate areas of angle phase space are unlikely. If the changes in angles are small enough, then the previous angles in the trajectory can be used to extrapolate the next angle and resolve the degeneracy. Fig. 4e demonstrates rather large fluctuations around a single mean value of the rotational motion of a QD in polymer that is less viscous than in Fig. 4d. It is clear that statistical studies from a number of QDs are necessary to appropriately understand these systems because a single QD cannot be representative of the dynamics occurring in the entire host matrix. Fig. 4f shows rotational dynamics in a hexadecane/PMMA matrix. This plot clearly shows the migration from one type of trajectory motion in blue to another in green. From these experiments we can conclude that to understand the physics of dynamical properties of various host matrices fully, the rotational motions of many QDs must be observed simultaneously.

Conclusion

The appeal of CdSe QDs over conventional dye molecules is threefold: (i) the 2D transition dipole of QDs enables the application of simple far-field microscopy to monitor 3D dynamical motion in real time, (ii) QDs are photophysically more stable than organic dyes, and (iii) simultaneous detection of different colored QDs can be performed with one excitation source. The 2D transition dipole property of QDs enables the use of simple far-field microscopy to gain powerful 3D orientation data. By using the emission polarization and optical properties of QDs, the rotational motion of many QDs can be monitored simultaneously in various matrices, coupled to various nano-objects, man-made, or biological, and in real time. These QDs may be useful in better understanding the collective microscopic orientational motions in a variety of systems.

Abbreviations

QD

quantum dot

PMMA

polymethylmethacrylate