Efficient Estimation of Phase-Resetting Curves in Real Neurons and its Significance for Neural-Network Modeling

Abstract

The phase-resetting curve (PRC) of a neural oscillator describes the effect of a perturbation on its periodic motion and is therefore useful to study how the neuron responds to stimuli and whether it phase locks to other neurons in a network. Combining theory, computer simulations and electrophysiological experiments we present a simple method for estimating the PRC of real neurons. This allows us to simplify the complex dynamics of a single neuron to a phase model. We also illustrate how to infer the existence of coherent network activity from the estimated PRC.

Biological systems frequently show periodic activity at different organization levels, from cells to organisms. The mechanisms underlying those rhythms can be complex with hidden variables not accessible to observation. However, useful information about the dynamics of the system can be gained by studying phase-resetting curves (PRCs) [1], which describe the phase shift of the oscillation in response to a perturbing pulse of variable amplitude at each phase of the oscillation. PRCs can reveal the existence of singularities, called “black holes” or “sudden death” phase at which perturbations can stop the periodic motion [1,2]. Furthermore, the PRC allows one to predict entrainment to periodic stimuli and phase locking with other coupled oscillators [1,2].

In physics and chemistry the infinitesimal PRC (or phase-dependent sensitivity), i.e., the oscillator’s response to weak perturbations, usually suffices to understand collective dynamical properties like coherent oscillations, traveling waves, and pattern formation [3]. A perturbation is weak if its effect on the amplitude and intrinsic period is negligible. This approximation is often valid also in firing neurons, where a small current pulse delays or advances the next spike (action potential) without changing its shape or average firing frequency. Any dynamical system of N variables x₁, x₂, …, x_N with an asymptotically stable limit cycle (periodic behavior) that is weakly perturbed can be described by a phase model of the following form [3]

$$\frac{d\varphi }{dt}=\omega +\varepsilon \mathrm{\Pi }(\varphi )Z(\varphi ),$$ (1)

where ϕ is the instantaneous phase, ω is the natural angular frequency, Π(ϕ) represents the infinitesimal perturbation of order ɛ applied along the limit cycle to a dynamical variable, say x₁, and Z(ϕ) is the infinitesimal phase-resetting curve or phase-dependent sensitivity with respect to x₁. If Z(ϕ) is known, the oscillator dynamics are fully determined for any weak perturbation. Thus, in the context of neuroscience, the estimation of infinitesimal phase-resetting curves can provide insight into neural dynamics, as demonstrated in mathematical models [4–8]. In particular, the knowledge of the PRC reveals the bifurcation type underlying the onset of repetitive firing [7,8] and facilitates the study of interactions leading to neural synchrony and coherent network oscillations [5,6]. In addition, neural phase models considerably simplify the complexity of detailed biological models [5–9] when studying synchronization.

The reduction of a dynamical system to phase model (1) is possible explicitly if the dynamical equations for all the N variables x₁, x₂, …, x_N are known [3]. This is useful for theoretical models but not for real neurons where only one variable is recorded (typically the membrane potential) and the rest (gating variables) remain hidden. However, this lack of information about the full dynamical system can be compensated by fitting the instantaneous phase of the neuron to phase model (1), where the external perturbation of the membrane potential Π(ϕ) is known and the infinitesimal (PRC) Z(ϕ) is approximated by a few Fourier components,

$$\frac{d\varphi }{dt}=\omega +\mathrm{\Pi }(\varphi )\sum _{n=0}^3(a_n\mathrm{\hspace{0.17em} }\text{cos}n\varphi +b_n\mathrm{\hspace{0.17em} }\text{sin}n\varphi ).$$ (2)

Thus, the experimental estimation of the PRC reduces to a linear-regression problem where the Fourier coefficients are the unknowns and the data to fit are the instantaneous phase of the neuron (calculated by linear interpolation between 0 and 2π, values that correspond to two consecutive action potentials) and its derivative (which as a result is a piecewise constant function). The choice of Π(ϕ) must be compatible with the approximation of a weakly perturbed limit cycle. In practice, the best choice is to inject a small, brief positive current once per cycle, each time at a different phase. To do so, a train of periodic brief pulses is injected with a period similar (but different, in order to prevent phase locking) to the natural period of the firing neuron. Although the PRC is calculated for convenience in the ideal case in which the neuron fires periodically, once the PRC is determined it describes the neural response above firing threshold to arbitrary weak inputs Π(ϕ), including interactions with other neurons.

We first tested our approach to estimating PRCs in computer simulations of a neuron model of the Morris-Lecar (ML) type [8]. When a steady current of increasing magnitude is injected into the ML neuron the onset of repetitive firing occurs at a bifurcation class that depends on the model parameters. A saddle-node bifurcation leads to type I excitability, i.e., the neuron can fire with arbitrary low frequencies [7,8] and behaves as an input integrator [10]. A Hopf bifurcation leads to type II excitability, i.e., the membrane potential displays small amplitude oscillations before the neuron starts firing at a finite frequency [7,8]. In this case the neuron behaves as a resonator with respect to inputs [10]. Type I neural oscillators possess nonnegative PRCs whereas type II neural oscillators possess PRCs that are partially positive and partially negative [7,8]. That is, an infinitesimal positive perturbation of the membrane potential will never delay the next spike in a type I neuron, whereas such a perturbation may delay or advance the next spike in a type II neuron, depending on the phase at which the pulse is delivered. Beyond type I, II, other types of neural excitability are possible [10]. However they are characteristic of bursting neurons, which are not considered here because they cannot be fully described by a phase model.

Figure 1 summarizes the results of our computational studies on the PRC of the ML model for type I, II excitability. The corresponding parameters were taken from [8]. The theoretical (black line) and the estimated (gray line with circles) PRC for both type I [Fig. 1(a)] and type II [Fig. 1(b)] are very similar, indicating that our method can provide an accurate estimate of the PRC. The theoretical PRCs were calculated numerically from the full dynamical models with xppaut [11].

FIG. 1.

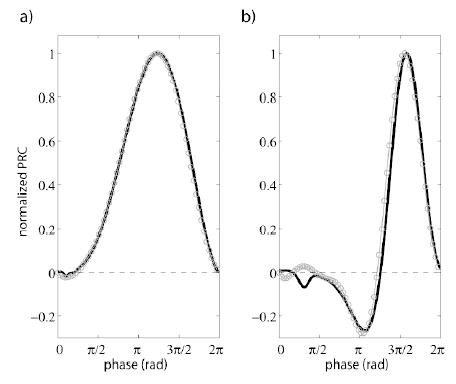
Estimation of phase-resetting curves in a Morris-Lecar neuron model [8]. Black lines represent the actual PRC calculated numerically from the full model. Gray lines with circles represent the estimation of the PRC from the membrane potential with our approach. (a) Type I excitability: The match between the real and the estimated PRCs is perfect. (b) Type II excitability: There is only a small mismatch at the beginning of the cycle.

Having shown that our approach reliably estimates the PRC of simulated neurons we applied it to real neurons as well, in particular, to mitral cells of the mouse olfactory bulb. Mitral cell (MCs) receive input from olfactory sensory neurons in the nose and relay this information to higher processing networks. The mechanisms underlying the olfactory code are still controversial, but one feature of the neural dynamics in the olfactory bulb is the existence of network oscillations in the beta/gamma frequency band (20–80 Hz) most likely due to MC synchrony [12]. We therefore were interested in estimating the PRC of MCs to better understand the mechanisms of this synchrony.

Whole-cell patch-clamp recordings from MCs (n = 3) in vitro were obtained using standard electrophysiological techniques [13]. A constant current was injected into the MC to make it fire at a constant frequency within the beta/gamma frequency band. Then, as in the simulations, a periodic train of brief pulses (duration = 0.5 ms; amplitude = 20 pA) was superimposed on the constant current (300 pA). The interval between pulses was fixed and similar, but different, to the intrinsic period of the neuron (~25 ms). Figure 2(a) shows a recorded segment of the membrane potential of a MC. The effect of the perturbations can be clearly seen. The perturbed membrane potential was recorded during 30 sweeps of 400 ms with interceded pauses of 15 s. The sampling frequency was 10 kHz. This relatively small amount of data (480 gamma cycles) sufficed for the estimation of the PRC as shown in Fig. 2(b) (thick black line). The shape of the membrane potential during one cycle is also shown (gray line). Both curves have been rescaled to their maxima to aid visualization [14].

FIG. 2.

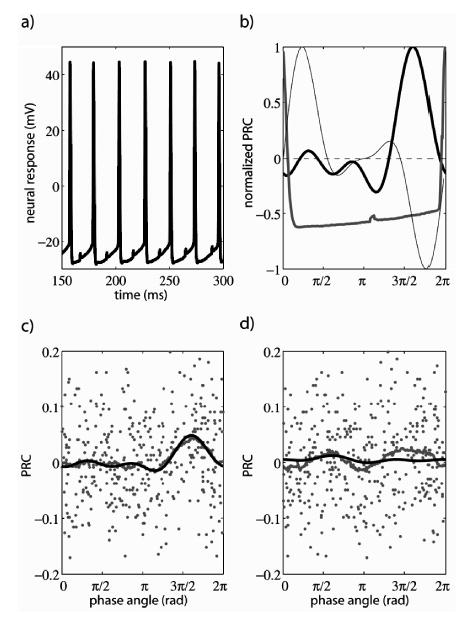
Experimental estimation of phase-resetting curves. (a) Traces of a neuron’s membrane potential. The effect of the perturbing current pulse can be clearly seen in each cycle at a different phase. (b) Estimated PRC (thick black line), membrane-potential cycle with a perturbation at an arbitrary phase (gray line) and odd part of the inhibitory interaction function (see text; thin line). Each curve has been rescaled to improve visualization. (c) Raw estimation of the PRC (dots) and smoothing over a 2π/3 interval (gray line) compared with the estimated PRC with our approach. Both curves match, which indicates that the raw data are consistent with a phase model. (d) Same as (c) but after shuffling the raw PRC data. The PRC is roughly flat and yields inconsistent results with the smoothing; i.e., the shuffled data cannot be described by a phase model.

Contrary to the case of simulated neurons, in real neurons one cannot compare the estimated PRC with a theoretical one. However, it is still possible to asses the validity of the curve obtained. In Fig. 2(c), the black line represents the estimated PRC by fitting the instantaneous phase of the perturbed neuron to formula (2) and the gray line represents the smoothing of the data points (dots). Both curves match each other suggesting that the PRC estimated by (2) retrieves a hidden structure in the noisy data. The comparison between both curves serves as a self-consistency criterion, which is important because linear-regression algorithms, like the fitting to formula (2), always have a mathematical solution. However, by comparing with the smoothed data, one can check whether this solution is meaningful. On the other hand, smoothing of the experimental data alone is not adequate to reconstruct the PRC because of two reasons: (i) smoothing is not parameter free (we used a Savitzky-Golay filter [15] of order 3 over a window of approximately 2π/3), and (ii) the smoothed curve is still noisy compared with the one obtained by fitting the data to phase model (2). As an additional control, the data points are shuffled along the abscissa [Fig. 2(d)]. In this case, as expected, neither the fitting nor the smoothing yields a realistic PRC. The mismatch between them indicates that the random structure of the shuffled data cannot fit a phase model consistently. Furthermore, we ruled out an undersampling effect: when repeating the analysis for two different halves (with ~240 cycles each) of the data set, both analyses yielded similar PRCs which were in turn similar to the PRC obtained from the whole data set (results not shown). Repeating the analyses for thirds and fourths of the data set resulted in dissimilar PRCs, indicating that we had more than a sufficient amount of data for the fitting.

In Fig. 2(b) the estimated PRC shows that a positive perturbation of the membrane potential after a spike delays the next spike, whereas such a perturbation before a spike advances the next spike. As mentioned above, this partially positive, partially negative PRC is a fingerprint of type II excitability, which indicates that MCs behave as resonators with respect to the inputs. This result is consistent with the finding that the membrane potential of MCs exhibits oscillations (period ~50 ms) below the threshold for spike generation [16], which in turn suggests that the onset of regular spiking in MC occurs via a Hopf bifurcation [8,10], as the injected current increases. As a consequence, MCs whose membrane potential is below, but close to, firing threshold are more sensitive to input frequencies similar to the intrinsic period (subthreshold resonance). Above threshold, further from the Hopf bifurcation, for example, when MCs regularly fire in the high-beta or low-gamma band (period ~25 ms), like the neurons studied here, the nature of the bifurcation is still apparent in the partially negative and partially positive PRC, which has important consequences for synchrony between MCs, as discussed below.

The phase model of two coupled oscillators, 1 and 2, is given by the two equations

$$\frac{d{\varphi }_{1,2}}{dt}={\omega }_{1,2}+H_{1,2}({\varphi }_{1,2}-{\varphi }_{2,1}),$$ (3)

where the interaction function H(θ) is the convolution over the limit cycle of the PRC, Z(θ), with the function modeling the coupling [3]. In the case of neural oscillators, the coupling is effected through synaptic interactions that can be modeled by a positive (excitatory synapse) or negative (inhibitory synapse) alpha function, so that H(θ) reads

$$H_{1,2}(\theta )=\frac{\pm \varepsilon }{T}{\int }_0^T{Z}_{1,2}(t-\theta )(t / \tau )\mathrm{\hspace{0.17em} }\text{exp}(-t / \tau )dt,$$ (4)

where the synaptic current is given by the alpha function t/τ exp(−t/τ with time to peak τ ~ 1 ms and amplitude of order ±ɛ. It is easy to prove that two identical neural oscillators will phase lock with a phase difference Δ, if the odd part of function H has a zero at Δ with positive slope [8]. Since Z(θ) can be estimated with our approach, H can also be estimated and one can predict the type of synaptic interaction that leads to synchrony between MC pairs. The result is displayed in Fig. 2(b) for an inhibitory synapse (thin line). For an excitatory synapse just take this curve multiplied by −1. We predict that two mitral cells can phase lock at Δ = 0 (synchrony) and Δ = π (antisynchrony) only through inhibitory synapses but not through excitatory ones. Interestingly, biological studies indicate that MCs coupled through inhibitory local interneurons (granule cells) are able to (transiently) synchronize [17]. The phase model (3) can be generalized for several neurons by including terms with all possible pairwise interaction functions. The equations cannot be solved analytically in the general case but they can be easily solved numerically allowing for fast simulations of large networks.

Recently Rosenblum and Pikovsky have proposed a method to estimate the coupling and coupling direction of two interacting oscillators [18] that are driven by noise. The method consists of a linear regression of phase data to a phase model where the coupling functions are of the general form f_1,2(ϕ₁,ϕ₂). Since these functions reduce to the form H_1,2(ϕ_1,2 – ϕ_2,1) for weakly coupled oscillators our approach is in a mathematical sense, a particular case of theirs, with the important difference that the coupled oscillators we have considered above are not driven by noise but only by mutual perturbations.

Other authors have previously studied the influence of perturbations on the firing period of real neurons. In cat neocortical neurons [19], it has been shown that transient positive pulses always shorten the firing period in a phase-dependent manner (type I oscillators). More recently other authors have estimated spike-time response curves (STRCs) of stellate cells in the entorhinal cortex [20]. The STRC is similar to a PRC where the perturbing pulses are alpha functions. The STRC is calculated by normalizing the difference between the interspike interval of the perturbed cycle with the unperturbed one. Even though this raw estimation of a STRC is quite noisy compared to our method, it allows the authors to assess the significance of negative values of the STRC that reveal type II excitability in those neurons. In a very recent Letter, the authors take advantage of the STRC to induce synchrony in hybrid neural networks (real neurons coupled to virtual neurons in real time) with dynamic patch-clamp techniques [21]. This promising result may be broadly applied if the PRC estimation is improved as with our method. Other authors have also estimated the PRC from the traces of simulated [22] and real [23,24] membrane potentials. To do so, the neuron’s limit cycle is embedded in the phase space reconstructed with delay coordinates. In this space the tangential component of the velocity along the limit cycle is an accurate estimator of the PRC, but only for type I oscillators. As demonstrated by those authors [22], their method fails for type II oscillators because when perturbed, the normal displacement off the limit cycle is not negligible. Here we have presented an alternative method to estimate PRCs that is valid for both type I, II neurons. Our approach requires few recordings with standard electrophysiological techniques. In addition, the algorithm to compute the PRC is simple, reliable and fast, as shown with simulated and real neurons. Following the illustrative study of coupled mitral cells presented here, we expect our method to help elucidate mechanisms for neural synchrony in the olfactory bulb and other biological neural networks.