M-Coffee: combining multiple sequence alignment methods with T-Coffee

Abstract

We introduce M-Coffee, a meta-method for assembling multiple sequence alignments (MSA) by combining the output of several individual methods into one single MSA. M-Coffee is an extension of T-Coffee and uses consistency to estimate a consensus alignment. We show that the procedure is robust to variations in the choice of constituent methods and reasonably tolerant to duplicate MSAs. We also show that performances can be improved by carefully selecting the constituent methods. M-Coffee outperforms all the individual methods on three major reference datasets: HOMSTRAD, Prefab and Balibase. We also show that on a case-by-case basis, M-Coffee is twice as likely to deliver the best alignment than any individual method. Given a collection of pre-computed MSAs, M-Coffee has similar CPU requirements to the original T-Coffee. M-Coffee is a freeware open-source package available from http://www.tcoffee.org/.

INTRODUCTION

The multiple alignment of DNA or protein sequences is one of the most commonly used techniques in sequence analysis. Multiple alignments constitute a necessary pre-requisite in phylogeny, remote homologue detection and structure prediction. Until recently the choice for building multiple sequence alignments (MSAs) was limited to a handful of packages but a recent increase in genomic data has fuelled the development of many novel methods arguably more accurate and faster than the older ones. In practice this widened choice has also made it harder to objectively choose the appropriate method for a specific problem.

Unfortunately the standard multiple sequence alignment problem is NP-hard, which means that it is impossible to solve it for more than a few sequences. This complexity explains why so many different approaches have been developed (1,2), such as progressive alignment (3), iteration (4–6) and genetic algorithms (7). One very useful development has been the design of consistency-based methods whose purpose is to generate an alignment consistent with a set of pairwise alignments. The use of consistency was first described by Gotoh (8) and Kececioglu (9) and independently re-formalized by Vingron and Argos (10) as a dot matrix multiplication procedure that bears much resemblance with T-Coffee. Consistency was later re-discovered by Morgenstern et al. (11) who refers to it as overlapping weights. In 2000, Notredame et al. (12) described a novel algorithm combining the overlapping weights with a progressive alignment strategy. This algorithm was implemented in T-Coffee and resulted in significant accuracy improvement over existing methods. Since then, consistency based objective functions have been used within several new multiple alignment packages, including POA (13), MAFFT 5 (14), Muscle 6 (5), ProbCons (15) and PCMA (16).

More than 50 MSA methods have been described over the last 10 years (Medline, January 08, 2006), with no less than 20 new publications in 2005 alone. The complexity and variety of these algorithms and the fact than none provides a definite answer to the problem makes it almost impossible to tell them apart from a theoretical point of view. In practice however, these methods are compared using empirical evaluations made on structure-based sequence alignments. This popular approach suffers from at least two shortcomings, most notably the fact that MSA methods trained and evaluated this way are biased toward generating structurally rather than evolutionarily correct alignments. Furthermore, although structural information is more resilient than sequence signal over long evolutionary distances, the assembly of a structure-based MSA is in itself a difficult task, which has resulted in the development of several alternative structure-based MSA collections. Some, like BaliBase (17) or Prefab (5), have been designed specifically for the validation of MSA methods while others like HOMSTRAD (18) are more generic. As there is no simple way to evaluate and rank these reference collections, it has become common practice to use them all when benchmarking new packages. The rationale for these analyses is that the average best performing package will constitute the safest choice when computing an MSA of uncharacterized sequences. However, such a choice is no guarantee for success as it is well established that the best performer is only more likely, but not certain, to be the most accurate on any specific dataset. Using this average best is merely an attempt to increase the chances of success, just like betting on the horse with the best odds.

The description of a complex problem partially solved by several more or less different methods calls for comparisons with other similar situations in computational biology like secondary structure and gene predictions. In these contexts, Meta-methods, or Jury-based methods (19,20) have often proven to be superior to the constitutive methods. However, in the case of gene or structure predictions, the output is relatively easy to combine into the intersection or union of individual predictions. Such a combination protocol is harder to define when it comes to MSAs where each pair of aligned residues constitutes an element of prediction. Fortunately, consistency-based objective functions provide an elegant and simple solution to the problem of averaging several alignments into one meaningful consensus. Given a collection of alternative alignments, consistency-based objective functions define the optimal alignment as the one having the highest level of consistency with the collection. It is realistic to consider this optimally consistent alignment as some sort of consensus. This approach, first described by Bucka-Lassen et al. (21) for the combination of alternative DNA alignments, is the core of the T-Coffee algorithm. While any consistency-based packages currently available would probably be equally well suited to the combination of MSAs, T-Coffee bears the advantage of having been specifically designed for that purpose thanks to the concept of a library. T-Coffee does not explicitly align sequences but compiles libraries based on externally produced alignments. During the alignment process, the libraries are combined into the final MSA. Originally generated using ClustalW and Lalign, the libraries can also be produced by structural alignment packages or any sequence alignment program, pairwise or multiple. In this work, we took this concept much further and showed that T-Coffee can easily combine up to 15 alternative MSAs of the same sequences. We call this meta-mode M-Coffee and using several well-known benchmarks, we show that M-Coffee is the most accurate and flexible MSA meta-method described so far.

SYSTEM AND METHODS

The benchmark system

The main benchmark dataset was derived from the February 2005 release of HOMSTRAD (18). HOMSTRAD is a database of protein alignments assembled automatically by the structural alignment program COMPARER from sets of sequences where all members have a known 3D structure. Alignments containing <4 sequences were removed, leaving a set of 233 alignments. Alignment accuracy was calculated with Column Score (CS) using the aln_compare program (12). CS is the proportion of columns of residues correctly aligned between the test and reference alignments (22).

Two other Benchmark datasets were used to further validate the method: Balibase v3.0 (23) and Prefab v4.0 (5). Balibase (17) is a collection of hand-curated alignments. It contains five categories of typical alignment problems, including long internal insertions and terminal deletions. Balibase v3.0 includes two different sets of sequences: realistic full-length protein sequences and artificial short sequences where the homologous regions are extracted from the full-length sequences. The shorter sequence sets are denoted by an S in the Results section. This removes the bias for global alignment programmes in the earlier versions of Balibase (24).

Prefab is based on pairs of structurally aligned sequences with known 3D structures. Each pair is supplemented with up to 50 homologous sequences, used to compute the MSA and removed when the resulting alignment is compared with the structural reference.

Generating MSAs

Fifteen widely used multiple alignment programs from eight different laboratories were selected for this study. They were chosen to cover a wide range algorithms used to align protein sequences.

ClustalW (25,26) version 1.83 is the most widely used multiple alignment program. It uses a progressive alignment scheme where an initial guide tree (calculated from pairwise alignments) is used to guide a full multiple alignment by progressively incorporating all the sequences into the MSA.

T-Coffee (12) version 2.03 uses a consistency-based objective function (27) optimized using progressive alignment. It tries to maximize the score between the final multiple alignment and a library of pairwise residue-by-residue scores derived from a mixture of local and global pairwise alignments.

ProbCons (15) version 1.09 is, like T-Coffee, a consistency-based method. Alignments are generated using a library of paired hidden Markov models. It is currently the most accurate method as benchmarked on the HOMSTRAD dataset (14).

PCMA (16) version 2.0 uses a consistency-based objective function to align distantly related sequences, and a ClustalW like algorithm to align similar sequences.

Muscle (5) version 3.52 and version 6.0. Muscle v3.52 uses a progressive alignment algorithm with a Log Expectation score to align sets of sequences along a guide tree. Muscle v6.0 uses the same objective function as in ProbCons to further refine the alignment from Muscle v3.52.

Dialign2 (28) version 2.2.1 is a local multiple alignment method and is an improvement on the original segment-to-segment based approach of Dialign (11,29).

Dialign-T (30) v0.1.3 is a new version of Dialign, which incorporates the Dialign objective function in a progressive alignment algorithm.

The MAFFT (14) suite version 5.531 is a series of progressive alignment programs (31). The package consists of five alignment programs:

FFT-NS1: A progressive alignment algorithm that uses a fast Fourier transform (FFT) algorithm to calculate the guide tree.

FFT-NS2: Same as FFT-NS1 except, the guide tree is re-calculated after a first alignment and the alignment is repeated.

FFT-NSI: Same as FFT-NSI but includes an iterative alignment refinement step.

F-INSI: Incorporates local pairwise alignment information.

G-INSI: Incorporates global pairwise alignment information.

POA (32) version 2 uses partial order graphs to build an MSA. Two options of POA were used in this study (i) default, and (ii) do-global. The default setting is a local alignment algorithm (called POA-local), while do-global uses a global alignment algorithm (called POA-global).

The method tree

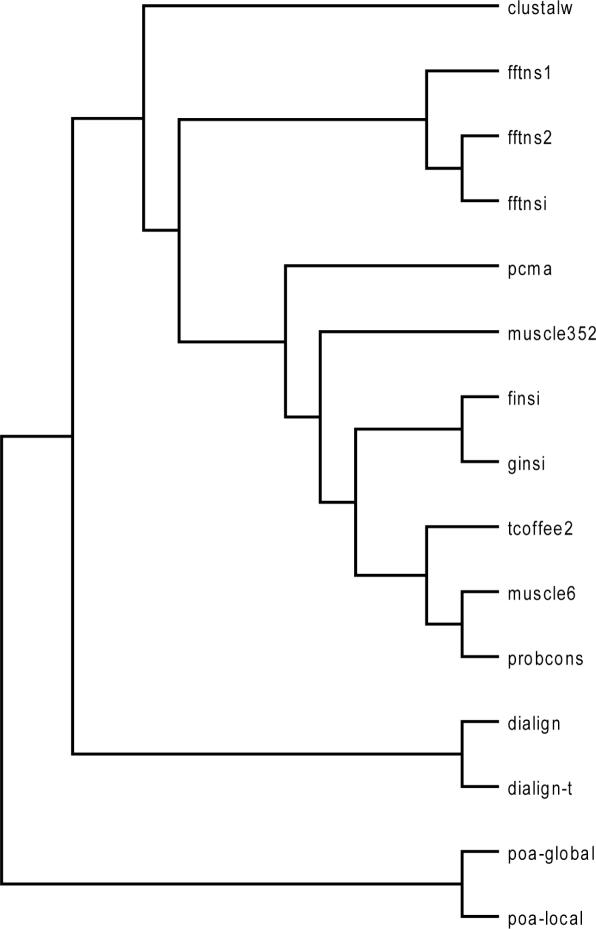
A method tree was calculated to visually display the level of similarity between various methods. The first step is the computation of a distance matrix where each entry is a measure of the average differences between two methods on the entire HOMSTRAD dataset. This value is estimated by aligning each HOMSTRAD dataset with both methods, and by estimating with aln_compare the proportion of residues identically aligned in corresponding alignments. These figures are converted to a distance and averaged to yield the final entry. Note that in this context HOMSTRAD is used as a source of homologous sequences rather than a collection of reference alignments. The tree is calculated by applying the UPGMA algorithm onto the distance matrix. This tree (shown on Figure 1) can also be used to compute the method weights.

Figure 1.

Methods Tree. A UPGMA tree which shows the clustering of all the multiple alignments. Pairwise distances are calculated on the HOMSTRAD benchmark by computing the SP differences of the alignments produced by individual methods.

Combining the alignment methods

T-Coffee (12) was used to combine outputs from different alignment programs into one improved multiple alignment. The ability of T-Coffee to take data in the form of a library was exploited to combine the alignment methods. This functionality has already been used very successfully to incorporate structural information when PDB entries are available for one or more sequences (33). A library is a generated by assigning each pair of aligned residues in a pairwise alignment weight. T-Coffee then tries to find an alignment with the maximum sum of weights. In this case the libraries are generated from alignments created by the different MSA packages. All of the libraries are then input into T-Coffee to produce one alignment. The default weight used in the library is the percent identity of the parent sequences. To apply one of the extra method weighting schemes described below, the original T-Coffee weight is multiplied by the method weight.

Method weighting

Four different schemes were used to generate weights for each of the alignment methods. Two of the schemes are tree-based, and were calculated based on the method tree described earlier.

1. Variance/Covariance (VarCov) weights are calculated from the inverse of a variance/covariance matrix, as described for sequence weights by Altschul et al. (34). For the variance (the diagonal elements of the matrix) of a method we use the number of columns differing between the generated alignment and the corresponding reference alignment in HOMSTRAD. For the covariance between two methods (the off-diagonal elements) we use the number of columns identical between two alignments generated by two different alignment methods, which are wrong when compared with the reference alignment. The row sums of the pseudo inverse of the variance/covariance matrix are the method weights.

2. Altschul Carrillo Lipman (ACL) weights are calculated using a tree connecting the methods. This was described in relation to sequences by Altschul et al. (34), but can be used to weight any data related by a tree. A variance/covariance matrix is calculated from the tree and the row sums from the inverse of this matrix are the method weights. In this case, the variance of a method is the distance from the root of the tree. The rationale is that the nearer an object is to the root, the better an estimate of the root, it provides. Covariances are calculated using the function below.

   $$p_{pq}=\frac{l_{pq}^2}{l_p{l}_q},$$

   where P_pq is the covariance between p and q, l_pq is the shared branch length between p and q, and l_p is the distance of p from the root.

   Using this weighting scheme a method receives a low weight if it is far away from the root of the tree or if it has close neighbours. The underlying assumption is that although a divergent method contains lots of information it is hard to exploit this information without bringing in too much extra noise.

3. Thompson Higgins Gibson (THG) weights are also tree-based (35) and are used by ClustalW. Weights are assigned based on the distance of the method from the root of the tree. Methods, which have a common branch with other methods, share the weight derived from the shared branch. For example if three methods share a branch then each method will receive a third of the weight derived from the common branch.

   Under this scheme a method only gets down weighted for having closely related neighbours. Methods that have a common branch share the weight derived from the shared branch. Groups of related methods receive low weights as they contain a lot of duplicated information. Highly divergent methods receive high weights as these contain unique information.

4. Accuracy (ACC) weights are crude heuristic weights rewarding accuracy. They are set to the score of the alignment method over HOMSTRAD, normalized so that their sum equals the number of methods. Highly accurate methods are up weighted and less accurate methods are down weighted.

Availability

M-Coffee is part of the T-Coffee package. T-Coffee is written in Perl and in C, and will run on any UNIX-type platform. It is a freeware open source distributed under a GNU Public license and available from http://www.tcoffee.org/.

RESULTS

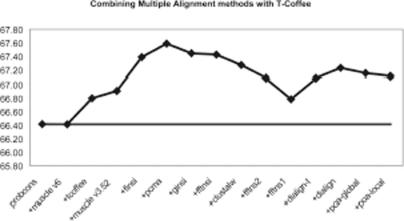
Our first task was to determine how the 15 MSA methods considered here should be combined into one consensus alignment. Given 15 methods, one should consider either defining an optimal subset or devising a weighting scheme that makes it possible to combine all the methods at once. Our first attempt was to use a greedy procedure in order to define an optimal subset of methods. Methods were ranked according to their overall accuracy on the 233 HOMSTRAD reference datasets and the order thus defined was used to define subsets of methods used within M-Coffee. Results are shown on Figure 2, where subset 1 only contains the best method (ProbCons), subset 2 contains the best and the second best (ProbCons + Muscle 6), and so on. The graph clearly shows a peak, which is significantly better than the point before it (Wilcoxon P < 0.001), suggesting that an accumulation of low accuracy methods eventually affects the overall results. On the other hand, the graph also indicates that except for the two first subsets, the accuracy of M-Coffee is clearly higher than any of the constituting methods, thus establishing the efficiency of the combination.

Figure 2.

CS after combining multiple alignment methods with T-Coffee. Alignments are added in order of decreasing performance as single methods (as determined on HOMSTRAD) from left to right. The peak of 67.59 is achieved using a combination of six methods. It is significantly better than ProbCons, the best single method (Wilcoxon signed rank test, P < 0.001), whose performance is materialized by the straight line.

The degradation in accuracy when very similar methods are added, like the MAFFT family of programs (FFTNSI, FFTNS2, FFTNS1 and so on), is not surprising when considering the underlying principle of consistency. Consistency is only useful as an accuracy indicator when methods are unlikely to commit exactly the same error. However, this assumption is no longer true when nearly identical methods are being combined. When this happens, incorrect alignment portions find their way into the final model simply because they appear highly consistent to the T-Coffee algorithm. This intuition that all methods cannot be considered as equally independent is well confirmed by the tree topology on Figure 1. The objective function plays an important role in grouping the methods, with, for example, most consistency-based methods clustered around T-Coffee (ProbCons, Muscle6, finsi, ginsi). The tree also reveals how methods developed by the same laboratory tend to be highly correlated, possibly because of arbitrary code settings.

Estimating the level of independent information contributed by one sequence or method is a recurring problem in biology. It is especially important when dealing with multiple sets of sequences (profiles, alignments) where the sequences are assumed to be independent although they are known to be evolutionarily related (and therefore correlated). Weighting schemes are used to deal with these contradictions, by estimating the amount of independent information contained in each sequence. For instance, given the tree on Figure 1, one would expect outlier methods like POA or ClustalW to have a high weight while methods with lots of close neighbours like T-Coffee, ProbCons and Muscle6 or the MAFFT series are expected to have lower weights, as if it were split between close relatives. We tested this hypothesis by applying two known tree-based weighting schemes on the method tree (THG and ALT) as well as the VarCov weighting scheme on the distance matrix (compare System and Methods). We also designed a fourth scheme, based on accuracy and that is meant to be used as a control. Results on Table 1 show the high level of correlation between the two tree-based weighting schemes that differ mostly by the magnitude of their values (0.24–2.51 for ACL, 0.56–1.87 for THG). The ACC weights are simply correlated to the methods accuracy, and attribute similar high weights to highly similar methods like T-Coffee and ProbCons. Tree-based methods tend to overweight outliers, which may be a shortcoming when the outliers display very low levels of accuracy, like POA. The VarCov weights work on a different principle and give credit to the methods containing the most unique (outliers) and accurate information. For instance, under this scheme, ClustalW receives a high weight (1.77) because it is an outlier and an accurate program. FFTNSI on the other hand is down weighted because it does not provide any useful information aside from what is already in either FFTNS1 or FFTNS2. The ACC weights are used as a control and simply reflect benchmarks results.

Table 1.

The first column lists the individual methods used

Alignment method	Default %CS	VarCov weight	THG weight	ALT weight	ACC weight	No weight
CLUSTALW v1.83*	61.15	1.77	1.41	1.86	1.01	1.00
DIALIGN	55.71	1.31	1.33	1.83	0.92	1.00
DIALIGN-T*	57.92	1.34	1.33	1.83	0.95	1.00
FFTNS1	58.27	0.81	0.74	0.64	0.96	1.00
FFTNS2	60.47	0.40	0.64	0.44	1.00	1.00
FFTNSI	63.07	0.17	0.64	0.44	1.04	1.00
FINSI*	64.22	0.79	0.74	0.38	1.06	1.00
GINSI	63.43	0.50	0.74	0.38	1.04	1.00
Muscle v3.52	64.49	1.02	0.85	0.54	1.06	1.00
Muscle v6.0*	66.04	0.78	0.56	0.24	1.09	1.00
PCMA*	63.73	1.41	0.94	0.75	1.05	1.00
POA-global*	51.90	1.37	1.87	2.51	0.85	1.00
POA-local	49.28	1.42	1.87	2.51	0.81	1.00
ProbCons v1.09*	66.41	0.73	0.56	0.24	1.09	1.00
T-Coffee v2.03*	65.37	1.18	0.78	0.42	1.08	1.00
%CS for M-Coffee15		67.33	66.96	65.79	67.16	67.11
%CS for M-Coffee8		67.32	66.33	64.89	67.85	67.75

Methods in boldface marked with an asterisk are part of the M-Coffee8 selection of methods. Column 2 indicates the average performance of each individual method on HOMSTRAD. Columns 3–7 are the weights for each method as calculated by the indicated weighting schemes. The last two lines show the average score of M-Coffee15 and M-Coffee8, using all the indicted weighting schemes.

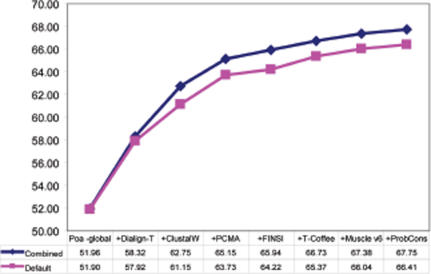
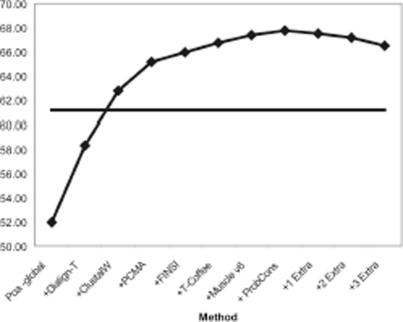
We tested these four sets of weights to combine the 15 methods into M-Coffee (M-Coffee15). The results (second last line, Table 1) indicate that although the VarCov weights deliver the best overall results they fail to significantly outperform a simple combination of all the methods (No weights). These results, combined with the observations made on Figure 2 led us to believe that the weighting schemes do not appear to properly address the problem of method redundancy, while the overall results suggest a need for some crude and discrete filtering. We eventually considered that arbitrary code setting (e.g. choosing between alignments with equal scores) could be one of the reasons for misleading consistency between packages of the same groups. This lead us to hand pick one method per developer (the most accurate) and use the resulting subsets to run our tests. The eight selected methods were POA-global, Dialign-T, ClustalW, PCMA, FINSI, T-Coffee, Muscle v6 and ProbCons. This combination of methods will be called M-Coffee8. Results are shown on the last line of Table 1 and on Figure 3. Interestingly, M-Coffee8 outperforms any of the constitutive method all along the combination process, thus suggesting an always beneficial combination. Figure 3 also shows that M-Coffee8 is more accurate than ProbCons, even before inclusion of that method. Finally, in order to further analyse the effect of method redundancy, we increased the number of occurrences of the ClustalW MSAs, from 1 copy (normal) up to 4. The results indicate that over-representing some MSA methods ends up reducing M-Coffee average accuracy, with a drop correlated with the number of extra copies (Figure 4). Yet this effect is moderate and even with three extra ClustalW MSA copies, the overall accuracy remains significantly higher than that of ClustalW (66% versus 61%).

Figure 3.

M-Coffee8. The top line (closed diamonds) is the CS on the HOMSTRAD benchmark after combining multiple alignments using only one method per developer. The bottom line (closed squares) is the default performance for each method on the benchmark.

Figure 4.

Effect of adding in 1, 2 or 3 extra ClustalW alignments to M-Coffee8. The average accuracy of ClustalW is materialized by the solid line.

Further validation of M-Coffee8 with was carried out by testing this procedure on two other benchmarks: the new BaliBase and Prefab. As suggested by results on Table 1, the tests were carried out by combining for each dataset the eight un-weighted MSAs with M-Coffee. The results (Table 2) show that M-Coffee significantly outperforms individual methods on every category of HOMSTRAD and Prefab (>1400 MSAs altogether) and on 6 out of 10 Balibase categories. Total results confirm M-Coffee to be the average best performer on the three datasets. Further analysis on individual datasets (Table 3) also reveals that on average M-Coffee is about twice more likely to deliver the most accurate MSA than any of the individual methods (1104 versus 614).

Table 2.

The CS accuracy performance of M-Coffee8 and various individual methods on the HOMSTRAD, Prefab and Balibase references

	M-Coffee8	ClustalW	Dialign-T	FINSI	Muscle 6	PCMA	POA	Probcons	T-Coffee
Homstrad	67.75*	61.15	57.92	64.22	66.04	63.73	51.9	66.41	65.37
Prefab <10%	27.19	18.25	15.51	24.86	24.14	25.53	9.09	24.81	23.41
Prefab 10 to <20%	59.80*	43.27	44.11	58.76	54.76	55.96	32.26	56.21	55.28
Prefab 20 to <30%	84.58*	74.79	75.28	83.76	82.09	81.47	64.42	82.85	82.39
Prefab 30 to <40%	92.54*	87.27	85.62	91.81	90.42	89.84	79.96	91.68	91.51
Prefab 40 to <100%	97.05*	94.91	96.07	96.92	96.17	95.03	94.30	96.20	96.68
Prefab total	72.91*	61.68	62.05	72.01	69.56	69.76	52.61	70.54	69.97
BaliBase Set: 11	43.18*	22.68	25.32	38.95	34.37	37.45	11.18	39.55	32.68
BaliBase Set: 12	85.91*	71.43	72.57	82.68	84.80	82.61	51.05	84.80	83.00
BaliBase Set: 20	43.12	21.68	29.20	45.85	36.49	44.83	13.37	37.78	39.68
BaliBase Set: 30	59.19*	25.48	35.19	57.59	41.04	58.15	7.89	47.26	47.48
BaliBase Set: 40	58.17	39.04	44.75	60.02	48.42	53.83	14.42	51.25	55.58
BaliBase Set: 50	59.81	33.69	44.25	57.69	50.56	59.88	21.63	55.25	57.31
BaliBase Set: S11	59.50	40.76	33.34	50.63	59.37	44.76	31.37	58.45	47.61
BaliBase Set: S12	86.59	79.05	76.20	84.02	86.95	82.91	68.14	87.05	83.75
BaliBase Set: S2	56.76	44.37	36.90	53.85	55.78	51.85	35.24	54.46	49.78
BaliBase Set: S3	69.41*	49.69	47.31	63.83	63.14	64.10	36.14	65.03	64.45
BaliBase Set: S5	60.60	43.27	45.47	57.73	60.33	56.73	28.47	59.80	55.67
BaliBase total	62.02	42.83	44.59	59.34	56.47	57.92	29.00	58.24	56.10

HOMSTRAD was evaluated with aln_compare, Prefab with Qscore and BaliBAse with BaliScore. Methods significantly better (P < 0.05) than the next best are marked with an asterisk. The highest score in each benchmark is highlighted in bold.

Table 3.

Individual dataset analysis

	M-Coffee8 better	M-Coffee8 worse	P(Wilcoxon Signed)	Best single method
Homstrad	139	65	0.000	ProbCons
Prefab <10%	49	37	0.16	PCMA
Prefab 10 to <20%	326	226	0.000	Finsi
Prefab 20 to <30%	278	132	0.000	Finsi
Prefab 30 to <40%	64	35	0.003	ProbCons
Prefab 40 to <100%	62	25	0.002	Finsi
Prefab total	779	455	0.000	/
BaliBase Set: 11	19	5	0.002	ProbCons
BaliBase Set: 12	26	7	0.008	ProbCons
BaliBase Set: 20	16	14	0.967	Finsi
BaliBase Set: 30	16	5	0.013	PCMA
BaliBase Set: 40	24	10	0.333	Finsi
BaliBase Set: 50	12	4	0.078	PCMA
BaliBase Set: S11	12	15	0.793	Muscle 6
BaliBase Set: S12	13	11	0.437	ProbCons
BaliBase Set: S2	21	13	0.397	Muscle 6
BaliBase Set: S3	19	6	0.024	ProbCons
BaliBase Set: S5	8	5	0.623	Muscle 6
BaliBase total	186	95	0.002	/
Total	1104	615		/
Total versus ProbCons	1249	615		ProBcons

The data are the same as in Table 2. On each subset, M-Coffee8 is compared with the best performing method. Column 2 indicates the number of times M-Cofee8 is better/worse than the best single method on that subset. The two last lines indicate the total for the table (Total) and the result of a comparison against ProbCons, the best individual method.

In terms of CPU time, M-Coffee is very similar to the standard T-Coffee with the difference that it does not require the estimation of the pairwise library. For instance, if we consider 1bxkA-1he2A, a standard prefab dataset of 50 sequences, 200 amino acid long and 47% average identity, the default T-Coffee requires 270 s to align that dataset on a standard PC (Pentium 2 MHz, 500 MB RAM), while M-Coffee8 requires 180 s on a similar machine and M-Coffee15 requires 220 s (these figures do not include the pre-computation of the alignments with individual methods).

DISCUSSION AND CONCLUSION

In this paper we describe M-Coffee, an extension of the T-Coffee package able to efficiently combine the output of various MSA packages into one final MSA. We show that M-Coffee is on average 1–3 point percent more accurate than the best individual method and nearly twice more likely to deliver the best multiple alignment. Apart from delivering high quality alignments, M-Coffee constitutes a simple and efficient platform for the combination of various MSAs into one unique accurate model. As such it provides a convincing solution to the daunting task of choosing the right method and it should prove quite robust with respect to the evolution of novel individual methods.

M-Coffee relies on consistency and is therefore based on the assumption that incorrect alignments are less likely to be consistent than correct ones. This holds well as long as the combined methods are independent, but it breaks down when correlated methods are introduced. We have shown here that the best results can be obtained when carefully selecting the right combination of methods. The main issue with such a selection is that it may be hard to automate and will always require expert knowledge. We propose two reasonable alternatives, one based on a weighting scheme that makes it possible to include all known methods, without a priori knowledge, and a second simpler (and less efficient recipe) where all methods are included, except the less accurate ones. Both these means of selecting methods can easily be adapted to an increasing number of methods, by setting up some centralized accuracy evaluation, in the style of the EVA server (36), a server used to continuously test the accuracy of protein secondary structure prediction methods. This being said, we also show that the effect of incorporating duplicated methods is not dramatic, and that even with 4 duplicated alignments of 12 MSAs, M-Coffee remains more accurate than most individual methods (including the duplicated one). These results suggest that the combination procedure is a rather robust process able to cope with a significant amount of noise.

The problem with Meta-methods is their tendency to harmonize a field of research by unfairly competing against the individual methods they are made of. In the case of M-Coffee it is interesting to stress the importance of original and independent individual methods, as illustrated by the method tree. It is also worth pointing out that our analysis reveals several method convergences (Figure 1) that may not be entirely obvious for a non-specialist basing his judgement on their technical descriptions. Overall, M-Coffee will perform best and improve, as long as independent methods keep being produced. Such a concept resonates strongly with the notions of ‘crowds’ and ‘mobs’ and how a group of non-expert people can arrive at more accurate decisions than a small number of ‘experts’ (37). Crowds are described as having the potential to be wise but only as long as the crowd members are independent and not forming a mob. Mobs are consistent but easily lead to the wrong decision.