Abstract
The primate visual system is arranged hierarchically, starting from the retina and continuing through a series of extrastriate visual areas. Selectivity for motion is first found in individual neurons in the primate visual cortex (V1), in which many simple cells respond selectively to the direction and speed of moving stimuli. Beyond simple cells, most studies of direction selectivity have focused on either V1 complex cells or neurons in the middle temporal area (MT/V5). To understand how visual information is transferred along this pathway, we have studied all three types of neurons, using a reverse correlation procedure to obtain high spatial and temporal resolution maps of activity for different motion stimuli. Most complex and MT cells showed strong second-order interactions, indicating that they were tuned for particular displacements of an apparent motion stimulus. The spatiotemporal structure of these interactions showed a high degree of similarity between the populations of V1 complex cells and MT cells, in terms of the spatiotemporal limits and preferences for motion and their two-dimensional spatial structure. Much of the structure in the V1 and MT second-order kernels could be accounted for on the basis of the first-order responses of V1 simple cells, under the assumption of a Reichardt or motion-energy type of computation.
Keywords: cortex, MT, striate cortex, vision, visual, computation
Introduction
Neurons in the primary visual cortex (V1) encode many aspects of the visual input, including shape, color, depth, motion, and spatial position. In contrast, neurons in the many extrastriate areas are less tuned for stimulus position and more tuned for other visual features. In particular, neurons in the middle temporal area (MT or V5) are tuned for the direction of stimulus motion, primarily as a consequence of a strong projection from direction-selective V1 neurons (Maunsell and van Essen, 1983; Movshon and Newsome, 1996). As a result, comparisons of motion selectivity between V1 and MT are useful for understanding how the visual cortex, and perhaps the cortex as a whole, processes information.
Neurons in MT have receptive field diameters that are ∼10 times those found in V1 (Gattass and Gross, 1981), raising the possibility that MT neurons can measure motion over a greater spatial range than V1 neurons (Mikami et al., 1986). Alternatively, MT neurons may simply sum the outputs of V1 neurons that have different receptive field locations but common direction preferences. In this case, the spatial aspects of motion selectivity would be determined by V1, and one would not necessarily expect to find substantial differences between the two areas.
One general approach to understanding the processing of visual information is to measure the input–output relationships of individual neurons. For any given stimulus, the input corresponds to the time-varying distribution of luminances reaching the retina, and the output corresponds to the spiking activity of the neuron under study. The luminance distribution comprises the first-order statistics of the input: it can be captured by a composite of individual measurements made at specific points in space and time. In contrast, motion is a second-order feature of the input: it requires a conjunction of measurements at two points separated by some distance in space and time. The ratio of the separations in two dimensions of space and one dimension of time corresponds to the stimulus velocity, and such a second-order measurement is a common feature of motion-processing models (Adelson and Bergen, 1985; van Santen and Sperling, 1985).
In this paper, we report measurements of the second-order kernels of MT neurons and V1 complex cells and compare them with first-order maps from V1 simple cells. The kernels capture the input–output relationship between motion stimuli and spiking activity, for a range of stimulus velocities. Quantification of the kernels suggests a high degree of similarity between the processing of motion in V1 and MT, in terms of both the preferences and limits of spatiotemporal selectivity. In MT, the same basic kernel structure is repeated across individual spatial receptive fields, in a manner that is predictable from a simple summation of V1 complex cell activity. Moreover, many of the spatiotemporal aspects of the observed second-order responses can be predicted from the first-order properties of V1 simple cells, as has been shown previously for V1 complex cells (Rybicki et al., 1972; Movshon et al., 1978b; Baker and Cynader, 1986; Emerson et al., 1987; Livingstone and Conway, 2003).
Materials and Methods
Experimental procedures
Electrophysiology. Monkeys were prepared for chronic recording from V1 and MT, as described previously (Livingstone, 1998; Born et al., 2000). All procedures were approved by the Harvard Medical Area Standing Committee on Animals.
We recorded from single units in V1 and MT of five alert rhesus macaque monkeys while they performed a simple fixation task. The monkeys fixated a small spot and were rewarded for keeping their gaze within a fixation window that was 2° in diameter Each single unit was isolated by spike height and waveform.
Visual stimuli. Neurons were screened with a bar stimulus. The bar luminance was 39 cd/m2 on a gray background (20 cd/m2). Once a neuron was isolated properly, we obtained a direction-tuning curve and, in some cases, a speed-tuning curve. Cells that responded at least twice as strongly in one direction as in the opposite direction were considered direction selective. This criterion included every MT cell that could be well isolated but excluded ∼75% of V1 neurons (De Valois et al., 1982; Foster et al., 1985). The direction-tuning curve was calculated from 5 to 15 1-s sweeps of the stimulus in each of 20 directions spaced evenly around the circle. For MT neurons, tuning curves were obtained with random-dot fields sized to the classical receptive field of the neuron under study. The size of the individual dots was equal to that of the spots used in the noise mapping experiments (side length, 0.20–0.25°). For V1 cells, direction tuning was assessed with either a dot field or a long bar of optimal length and contrast polarity that was swept in a direction perpendicular to its orientation. Direction-tuning curves were obtained by averaging the firing rate over the period of stimulus presentation, which was 1000 ms. The mean bandwidth of direction tuning (measured by fitting a circular Gaussian to the direction-tuning curves) was 94.1 ± 39.5° (SD) in MT. In V1, the mean bandwidth was 99.4 ± 51.5° for cells measured with random-dot fields (n = 54) and 65.9 ± 29.8° for cells measured with long bars (n = 59). Thus, the bandwidth depended in part on the stimulus used to measure direction selectivity (Albright, 1984).
The sparse noise stimuli were identical to those used previously (Livingstone et al., 2001). All cells were studied with two-dimensional whitenoise stimuli, consisting of pairs of spots flashed at 60 Hz. We used white and black stimuli that were 19 cd/m2 above and below the mean background gray luminance of 20 cd/m2. The dots changed position at random from frame to frame, within a square stimulus range that was at least 2.0 × 2.0°. When black and white stimuli overlapped, the resultant stimulus was the same gray as the background. To achieve maximum spatial resolution, we used the smallest black and white spots that elicited reliable spiking activity from the neuron under study. For MT neurons, this was almost always 0.25 × 0.25°, whereas in V1 neurons, we were usually able to use spots that were 0.20 × 0.20°.
Analysis
Measurement of kernels. The correlation analysis used here was identical to the analysis used in previous studies (Livingstone et al., 2001). Briefly, a computer recorded the evoked spike train (1 ms resolution), each stimulus position, and the monkey's eye position (4 ms resolution). For each map, between 5000 and 50,000 spikes were collected over a 20–60 min period. The kernels were then calculated by correlating the spike train with the stimulus sequence. Before the kernel computation, the positions of the stimuli on each frame were corrected to account for small drifts in the monkeys' eye position.
In this paper, we present our results in terms of the “forward correlation” between the stimulus and the spike train. This was computed by smoothing the spike train with a 17 ms boxcar filter and counting the average number of spikes that followed each stimulus at a given correlation delay. Computed in this manner, the forward correlation is equivalent (up to a scaling factor) to the more standard “reverse correlation” procedure (Marmarelis and Marmarelis, 1978; Baker, 2001; Ringach et al., 2003). The advantage of the forward correlation is that it can be interpreted as the average number of spikes per stimulus presentation, which makes it analogous to the standard poststimulus histogram. Second-order kernels were computed for MT cells and complex V1 cells, and first-order kernels were computed for V1 simple cells.
First-order kernels. The first-order portion of the neuronal response to a spatiotemporal stimulus s(x,y,t) is given by the following convolution integral:
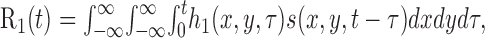 |
where τ is the delay between the stimulus and the response. When the stimulus is random, the kernel h1 (x,y,τ) can be obtained by cross-correlating the response R1(t) with the stimulus sequence s(x,y,t – τ) (Marmarelis and Marmarelis, 1978), where τ is the chosen correlation delay. In our analysis, this was accomplished by computing separate correlations for the white and black stimulus sequences. For a linear system, stimuli that consist of positive and negative deviations from mean luminance evoke opposite responses, so the correlations with the white and black stimuli represent measurements of h1(x,y,τ) and –h1(x,y,τ). The final estimate of the kernel h1(x,y,τ) is obtained by subtracting the correlation with the black stimulus from the correlation with the white stimulus and dividing by two (Emerson et al., 1987).
Second-order kernels. The second-order kernel specifies the response of the neuron to two spot stimuli located at spatial positions (x1,y1) and (x2,y2) and occurring τ1 and τ2 time units before time t. The stimulus-dependent portion of the second-order response to an arbitrary stimulus s(x,y,t) is given by the following convolution integral (Marmarelis and Marmarelis, 1978):
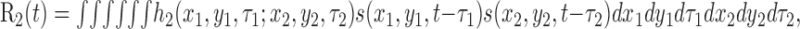 |
where h2 is the second-order kernel. The integration limits have been suppressed for clarity here and in subsequent equations.
As with the first-order kernels, the second-order kernels were estimated by cross-correlation. However, in this case, the relevant stimulus quantity is the contrast polarity of the product of pairs of stimuli separated in space and time. Thus, the displacement of a white spot on one frame to a black spot on the second frame constituted a negative stimulus, and a white-to-white sequence constituted a positive stimulus. In practice the kernel was estimated by correlating the spike train with the four possible sequences that occurred between any two frames (white–white, white–black, black–black, and black–white). The complete kernels were then calculated by summing the same-contrast individual maps (white-to-white and black-to-black) and subtracting the opposite-contrast maps (white-to-black and black-to-white), as described by Livingstone et al. (2001). The resulting kernel is similar to a second-order Wiener-like calculation (Emerson et al., 1987). An important advantage of this procedure is that the subtraction cancels any terms attributable to responses to individual white or black stimuli. This is important, because direction-selective complex cells and MT cells are both driven strongly by flashed stimuli (Mikami et al., 1986), which do not by themselves contain information about velocity. Our second-order measurement is essentially uncontaminated by such on-diagonal and lower-order influences (Emerson et al., 1987).
The result of the second-order kernel computation was a six-dimensional function h2(x1,y1,x2,y2,τ1,τ2) describing the response of the cell to all stimulus displacements. Previous work has shown that such kernels change very little with absolute spatial position in V1 (Movshon et al., 1978b; Baker and Cynader, 1986; Emerson et al., 1987; Livingstone and Conway, 2003) and MT (Livingstone et al., 2001). Consequently, we focused on the responses as a function of the relative positions of the stimuli. This enabled us to simplify the kernel by substituting x2 = x1 + Δx and y2 = y1 +Δy and integrating over space to get the following:
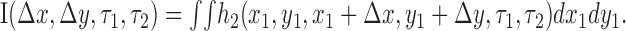 |
Averaging over space in this manner improves the quality of the kernels substantially, without sacrificing information about their structure (Emerson et al., 1987).
We further simplify the terminology by defining the temporal separation between stimuli as τ2 = τ1 + Δτ. This gives us the interaction function (Gaska et al., 1994), as follows:
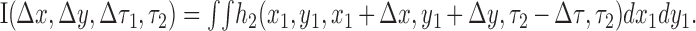 |
The interaction function I describes the second-order kernel as a function of the separation between two stimuli in space (Δx, Δy) and time (Δτ). The time course of the impulse response is measured from the time of occurrence of the second stimulus (τ2).
In this paper, we describe the second-order kernels in terms of displacement maps, each of which corresponds to the response of a neuron to all stimulus displacements (Δx, Δy) at a fixed interstimulus interval (Δτ) and correlation delay (τ2). These maps generally contain both positive and negative regions, which we will refer to as “facilitatory” and “suppressive,” respectively. These terms make sense only in the context of the kernel formulation and are not meant to imply specific synaptic mechanisms. In this way, the analysis is quite similar to the measurement of the first-order kernels of V1 simple cells described above (Movshon et al., 1978a; Jones and Palmer, 1987), in which one relates spiking activity to the sign of contrast of a single stimulus. In those studies, the response to a dark stimulus was subtracted from the response to a bright stimulus to estimate the “inhibition” attributable to the dark stimulus. In the case of the second-order kernel, we are interested in the sign of contrast of the product of two stimuli, so we subtract opposite-contrast sequences from same-contrast sequences.
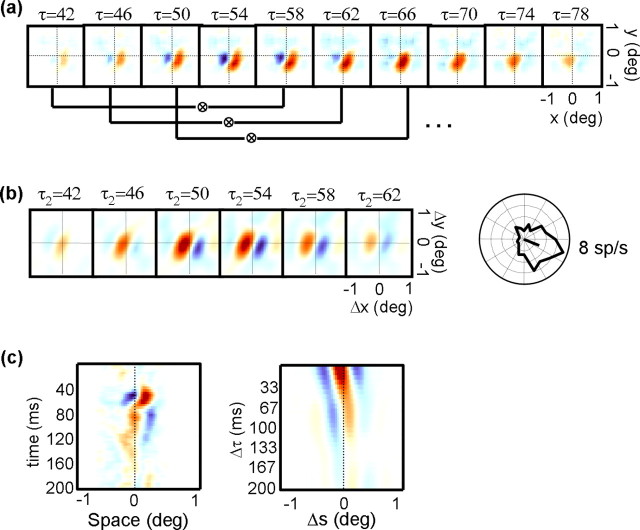
Figure 1a shows an interaction function for a single MT cell. Each panel contains a pseudocolor displacement map depicting the response of the neuron for a particular stimulus displacement (Δx, Δy), with the position of the second spot in any two-spot stimulus sequence being at the origin (0,0). Each column corresponds to successive time points (τ2) after the displacement of the stimulus (i.e., response latency), and each row corresponds to a different temporal separation (Δτ) between stimuli. In all maps, red indicates facilitation and blue indicates suppression. Thus, the red and blue regions in the maps demonstrate that the response of the cell was facilitated by a rightward apparent motion sequence and suppressed by leftward motion. The scale bar on the left of the figure indicates that the depth of this modulation was 0.12 spikes per stimulus presentation. Thus, on average, for every 100 presentations of the noise stimulus, the most effective stimulus led to 12 more spikes for same-contrast sequences than for opposite-contrast sequences. The response was strongest for small temporal separations and peaked at a poststimulus time of ∼65 ms.
Figure 1.
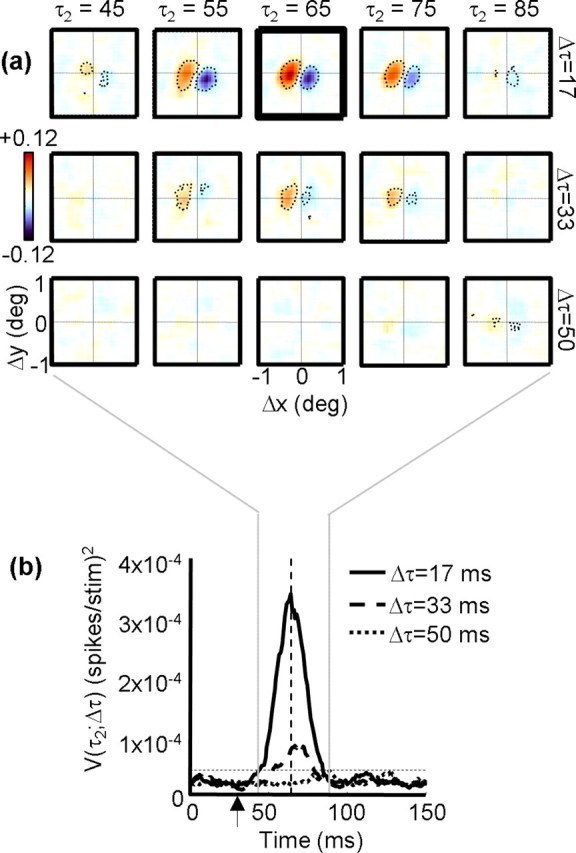
a, Example interaction function I(Δx, Δy, Δτ, τ2). Each square contains a displacement map, which codes the response as a function of the spatial separation between two stimuli (Δx, Δy). The position of the second stimulus in any two-spot sequence is the origin of each map. Positive (facilitatory) responses are coded in orange, and negative (suppressive) responses are coded in blue. The response of the cell in the figure was therefore facilitated by a rightward apparent motion sequence and suppressed by a leftward sequence. Each row indicates a different temporal separation between stimuli (Δτ), and each column indicates a different correlation delay (τ2). The displacement map outlined in thick black is the peak map, which is defined as the map that has the highest variance. Pixels that differ from baseline by±3 SDs (see Materials and Methods) are outlined by the dotted contour. b, Variance as a function of time for the neuron depicted in a. The solid curve indicates the variance in each displacement map as a function of delay (τ2), when Δτ = 17 ms (1 monitor refresh). The dashed curve shows the same time course for the case in which Δτ = 33 ms (2 refreshes), and the dotted curve corresponds to Δτ = 50 ms (3 refreshes). The vertical dashed line indicates the peak response, which corresponds to the highlighted map in a. The horizontal dashed line is the threshold above which a response is considered significantly above the baseline noise. The vertical arrow indicates the interval over which the baseline noise is measured.
To quantify the time course of the responses shown in Figure 1a, we computed the variance of each displacement map at 1 ms intervals. By using the variance, we take into account both positive (facilitatory) and negative (suppressive) deviations from the baseline activity, which is near zero. For each row in Figure 1a, the variance as a function of time is as follows:
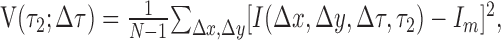 |
where N is the number of pixels in each map, and Im is the mean of all the pixels. Figure 1b shows the time course of the response for the cell in Figure 1a, for Δτ values of one frame (solid line), two frames (dashed line), and three frames (dotted line). When Δτ is equal to one frame (∼17 ms), there is a strong response that begins at ∼45 ms and peaks at 64 ms. Larger values of Δτ lead to smaller responses. This cell was typical in that the response was strongest at the shortest temporal separation Δτ, and the spatial structure was stable across the correlation delay τ2.
For correlation delays (τ2) of <30 ms, the responses of neurons in V1 and MT are unrelated to the stimulus sequence, so we can use this portion of the data to estimate the noise in the recording. The noise was therefore estimated as the mean of V during the first 30 ms of the response, and subsequent responses were considered statistically significant if they exceeded this level by 3 SDs. This significance threshold is shown as the horizontal dashed line in Figure 1b. The individual pixels that exceeded baseline by ±3 SDs are outlined by the dotted contours in Figure 1a.
Curve fitting
For speed-tuning curves, data were averaged over a 1000 ms stimulus presentation. The preferred speed was determined as the peak of a log-Gaussian fit to the tuning curve. The map profiles were fit to Gabor functions of the following form:
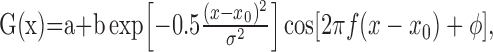 |
where a is the floor, b is the amplitude, x0 is the center, σ is the envelope width, f is the frequency, and ϕ is the phase. Function fits were optimized via a least-squares criterion using the Levenberg–Marquardt algorithm in Matlab (MathWorks, Natick, MA).
Permutation test
To test the significance of the singular values obtained from the Δs/Δτ maps, we performed a permutation test. The order of stimulus frames was shuffled, and the reverse correlation procedure was repeated to generate a new map. The singular value decomposition (SVD) was then performed on this map, and the entire procedure was repeated 100 times. To be considered significantly above the noise, a singular value obtained from the data had to be 2 SDs above the mean of the maps obtained during the shuffling procedure.
Tilt direction index
The degree of tilt in each spatiotemporal map was computed from the discrete Fourier transform of the map. Taking the peak of the transform as the optimal spatial and temporal frequencies (Fs and Ft), the tilt direction index (TDI) was computed as (Rp – Rn)/(Rp + Rn), where Rp and Rn are the response amplitudes at (Fs, Ft) and (Fs, –Ft) (Anzai et al., 2001).
Biphasic index
For each neuron, we computed the facilitatory time course P(τ2; Δx, Δy, Δτ), using the values of Δx, Δy, and Δτ that yielded the peak of the interaction function I(Δx, Δy, Δτ, τ2). Only responses that were significantly above baseline were considered. Some examples of P appear as the red lines in the bottom row of Figure 12a. Similarly, the optimal suppressive response is defined as N(τ2; Δx, Δy, Δτ), where Δx, Δy, and Δτ are the points at which the minimum response is obtained. These are shown as the blue traces in the bottom row of Figure 12a.
Figure 12.
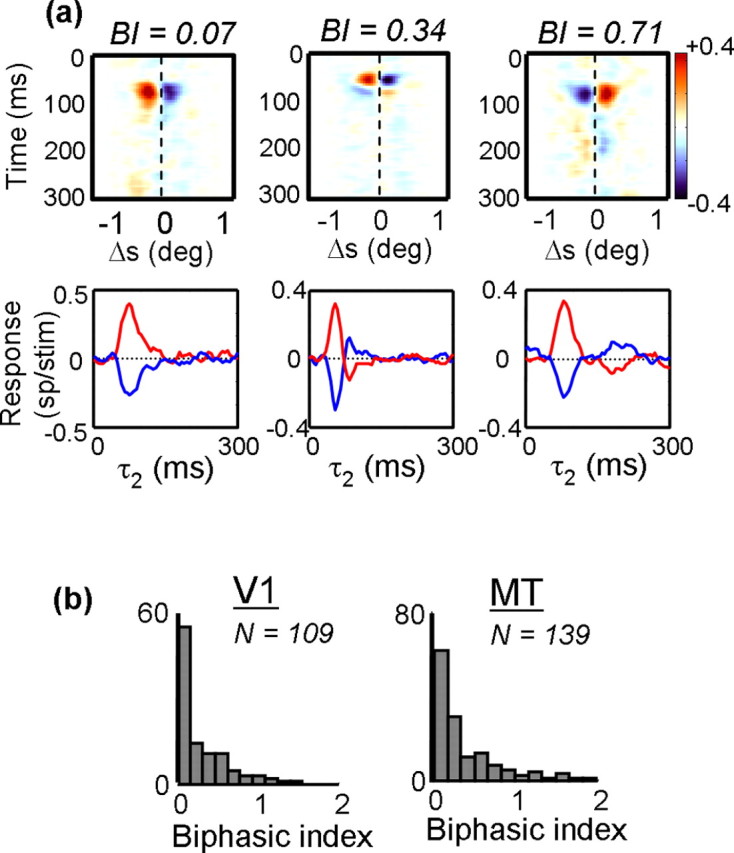
The effect of correlation delay (τ2) on spatial response profiles. The top row shows maps in which the rows indicate response as a function of spatial displacement. The columns show how the responses change as a function of correlation delay. Beneath each map is the impulse response, taken through the peak of each facilitatory (red) or suppressive (blue) response. b, Population histograms of the biphasic index (see Materials and Methods) for V1 (left) and MT (right). Neurons with a biphasic index near 0 maintained their preferred direction throughout the duration of their response, whereas neurons with a biphasic index near 1 showed a reversal in preferred direction at long correlation delays.
As is evident from Figure 12a, the facilitatory and suppressive time courses were generally mirror images of each other, so they were combined in the calculation of the biphasic index. We did this by subtracting the suppressive trace from the facilitatory trace, which is equivalent to flipping the blue traces in Figure 12a about the x-axis and adding them to the red traces. We then integrated the total negative deviations from baseline over time to get a measure of the extent to which the cell reversed direction and normalized this number by the total positive deviations, again obtained by integrating over time. The biphasic index (BI) was thus defined as follows:
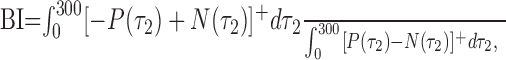 |
where [...]+ is the rectification operation. Thus, a BI of 0 indicates that the response of a neuron never showed suppression in the preferred direction [–P(τ2)] or facilitation in the null direction [+N(τ2)]. A BI near 1 indicated that the neuron fired as many spikes for motion in the null direction as in the preferred direction.
Reichardt/motion energy models
Many models suggest that direction selectivity involves a multiplication or squaring of luminance signals, after linear filtering (Reichardt, 1961; Adelson and Bergen, 1985; van Santen and Sperling, 1985). Both computations can be reduced to a second-order kernel of the type we have computed (Courellis and Marmarelis, 1992), in which the outputs of linear filters are combined in a nonlinear manner and summed over space. Using the notation introduced previously, this is equivalent to the following:
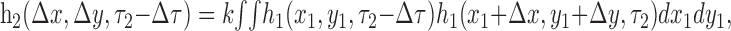 |
where k is a scaling factor. This is equivalent to the spatial autocorrelation of the linear filter h1 (Emerson et al., 1992; Baker, 2001) evaluated for pairs of time points separated by Δτ (see Fig. 13).
Figure 13.
a, The first-order response of a V1 simple cell. Here, each map shows the response of a neuron as a function of spatial position (x,y) at a different correlation delay (τ). The solid lines connect pairs of maps that were cross-correlated to obtain simulated second-order maps. b, Simulated displacement maps showing predicted responses as a function of spatial displacement (Δx, Δy), with correlation delay τ2 increasing from left to right. The maps were calculated from the simple cell responses shown in a. On the right is shown the direction-tuning curve for the same neuron in response to a long bar moving in a direction perpendicular to its orientation. c, Space–time map computed from the maps shown in a (left), along with a simulated Δs–Δτ map computed from the displacement maps shown in b (right).
In our experiments, the linear filters were estimated as described above from the responses to V1 simple cells. The autocorrelation was then computed between slices through h1(x,y,τ) at two delays separated by 16 ms (see Fig. 13), to facilitate comparison between second-order kernels computed with Δτ equal to one frame. The peak of this function was then compared with second-order kernels measured in complex cells and MT cells.
Kernel predictions
Predictions based on the first- and second-order kernels were generated by calculating 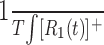 and
and 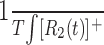 , where T is the total time over which the response was averaged.
, where T is the total time over which the response was averaged.
Results
We computed second-order kernels for 131 V1 complex cells and 166 MT cells recorded from five awake, fixating macaque monkeys. Eighteen of the V1 cells and 21 of the MT cells did not have responses that were significantly above the noise and so were discarded from additional analysis. The remaining cells all had second-order kernels with clear structure.
Our analysis allowed us to express the behavior of the neurons in terms of a two-spot apparent motion sequence. Each sequence involved the displacement of a spot over a distance (Δx, Δy) in some time interval (Δτ). The response of the neuron had a time course that we measure from the time of occurrence of the second stimulus (τ2). The full response is therefore expressed in terms of the interaction function I(Δx, Δy, Δτ, τ2). In the following sections, we describe the characteristics of various two-dimensional slices through this interaction function.
Spatial subunit structure: I(Δx, Δy)
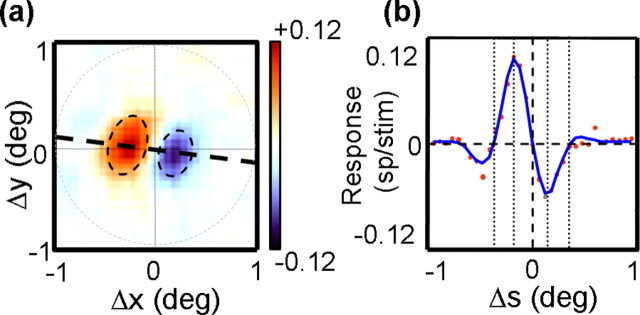
We first examined the spatial structure of the interaction functions by taking all of the responses to spatial displacements (Δx, Δy) at the optimal Δτ and τ2. Figure 2a shows such a displacement map for the MT cell shown in Figure 1a. The peak response occurred at a latency of τ2 = 64 ms and Δτ = 17 ms (one frame), at which point the map exhibited strong facilitatory and suppressive regions in the Δx, Δy space. The red regions indicate facilitatory interactions, in which the response to a single spot was facilitated when the immediately preceding spot was to its left and slightly up. This means that the cell preferred rightward motion. Similarly, the blue regions indicate suppression for leftward apparent motion. In keeping with previous terminology (Movshon et al., 1978a; Emerson et al., 1987), we will refer to the structure of each displacement map as a subunit.
Figure 2.
a, The peak displacement map from the neuron in Figure 1a. The dashed line connects the peak of the facilitatory region to the origin of the map and is used to determine the spatial profile of the response in b. The dashed circle delineates the region over which profiles are measured. The dashed ovals show elliptical Gaussian fits to the facilitatory and suppressive response regions. b, The spatial profile of the map shown in a. Each dot corresponds to the response at one point along the profile. The solid blue curve is the Gabor fit to these points. The dashed vertical line indicates the point at which the spatial displacement (Δs) is 0. Different features of the Gabor fit are shown as dotted vertical lines, which indicate, from left to right, the zero-crossing for facilitation, the peak for facilitation, the peak for suppressive, and the zero-crossing for suppression.
Taking the peak displacement map allows us to examine the spatial structure of the subunits while ignoring the temporal aspects of the kernels. In subsequent sections, we show that the maps are generally separable in space and time, so this procedure captures most of the spatial features of the subunits. The peak map in Figure 2a was typical in that it showed slightly elongated regions of facilitation and suppression, arranged perpendicular to the axis of elongation (Pack et al., 2003a). The dashed line in the figure connects the origin of the map with the peak of the facilitatory region. Plotting the value of the map at each point along this line yields the cross-section shown in Figure 2b. The cross-section was well fit by a one-dimensional Gabor function (blue line), with an R2 of 0.97.
All of the cross-sections were 2° in length, as indicated by the circle in Figure 2b. For all of the neurons in the V1 and MT populations, we fit these profiles with Gabor functions (mean R2 = 0.97). The Gabor function captures key aspects of the displacement map, including the preferences and limits of direction selectivity. One of the main goals of this work was to compare these features between V1 and MT.
Dependence on eccentricity
In comparing the spatial aspects of direction selectivity between V1 and MT, it is important to consider the influence of retinal eccentricity (Mikami et al., 1986). For V1, the receptive fields were typically within 5° of the fovea, although a few had eccentricities >20°. These two clusters of eccentricities corresponded to recordings from the operculum and from the roof of the calcarine sulcus, which were often encountered along the same penetration. For the MT population, eccentricities were sampled more evenly. In all cases, the noise stimulus was centered on the center of the receptive field under study.
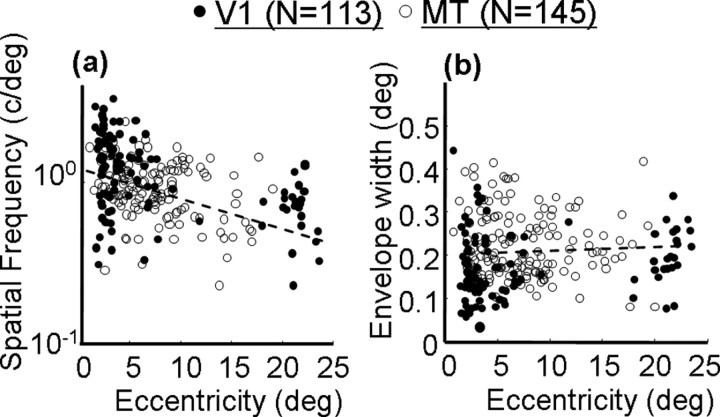
Across both cortical regions, there was a consistent relationship between retinal eccentricity and the frequency of the best-fitting Gabor function: more eccentric cells had broader tuning for stimulus displacement and, hence, lower Gabor frequencies. This relationship is plotted for the population of V1 and MT cells in Figure 3. Although there is a great deal of scatter at any given eccentricity, there is clearly a negative slope in the data, and there is no obvious difference between V1 and MT. The relationship between eccentricity and Gabor frequency was highly significant for MT (linear regression, p < 0.01) and for the combined population from both areas (p < 0.0001). The regression could not reliably be performed on V1 because of the non-normality of the distribution of eccentricities, but the trend appears to be similar. Note that this does not imply that spatial frequency preferences for drifting gratings are identical between V1 and MT [in fact, MT as a population prefers lower spatial frequencies than V1 (Priebe et al., 2003)]. Rather, our stimuli provided a coarse measure of spatial frequency in displacement space and may have missed some of the responses to high spatial frequencies that are known to be present in V1 (Foster et al., 1985).
Figure 3.
Correlations between aspects of the best-fitting Gabor functions and the retinal eccentricities of the neurons. Open circles indicate V1 neurons, and filled circles indicate MT neurons. The dashed lines show the regression lines. a, Correlation between retinal eccentricity and Gabor frequency. b, Correlation between retinal eccentricity and Gabor envelope width.
Somewhat surprisingly, the tendency for the subunits to become coarser at greater eccentricities was not accompanied by an increase in the size of the spatial envelope of the Gabor function fits (Fig. 3b). Although there is a slight upward trend in the data, particularly for V1 neurons, the relationship for the population as a whole did not reach significance (linear regression, p > 0.1). Based on previous work in V1 (Ringach, 2002), such a correlation would have been expected. However, the difference may be attributable to our inability to sample longer-range interactions that may have been present at large eccentricities. For example, we cannot determine whether the more eccentric profile in Figure 4b remains at zero or contains another subregion beyond 1°. Overall, these results suggest that the effect of stimulus displacement on the responses of V1 and MT neurons is determined in part by the retinal eccentricity of the subunit. Cells at greater eccentricities tolerate larger stimulus jumps, just as V1 neurons at larger eccentricities prefer lower spatial frequencies (De Valois et al., 1982) and higher velocities (Orban et al., 1986).
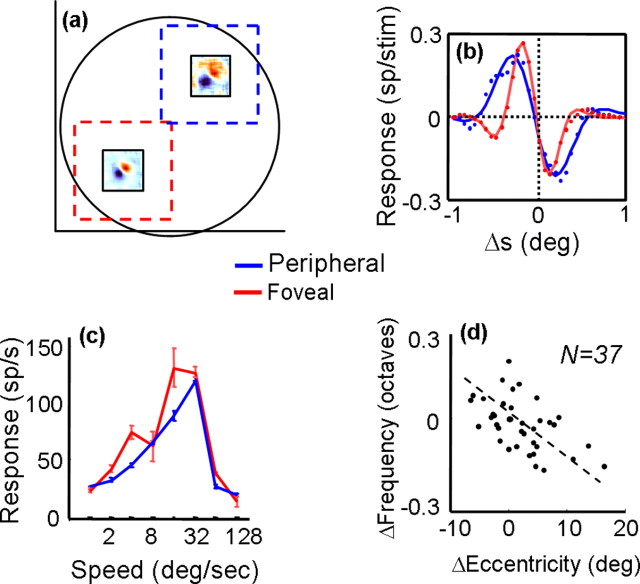
Figure 4.
a, Displacement maps computed at different eccentricities within the same MT receptive field. The dashed squares show the sizes and positions of random-dot patches used to measure speed tuning at the corresponding receptive field locations. b, Spatial profiles for the foveal (red) and peripheral (blue) displacement maps shown in a. Each dot corresponds to the response at a point along a line through the peak of each map. The solid curves are the best-fitting Gabor functions. c, Speed-tuning curves collected with random-dot fields centered on the foveal (red) and peripheral (blue) receptive field locations. Error bars indicate SD of the mean. d, Shift in frequency of the best-fitting Gabor as a function of change in retinal eccentricity for 37 displacement maps computed within the receptive fields of 17 MT neurons. Each dot corresponds to the difference in frequency for a given change in retinal eccentricity, and the dashed line is the result of a linear regression.
The receptive field sizes of most MT neurons were much greater than the longest apparent motion sequence that elicited a response. Consequently, we were in some cases able to study the relationship between eccentricity and subunit structure within the same MT receptive field, by performing multiple noise mappings at different spatial positions. Figure 4a shows an example of one cell for which additional noise maps were obtained at two different positions, each displaced symmetrically from the center by ∼3° (the center map has been omitted for clarity). Although the two maps clearly indicate a preference for the same motion direction (down–left), the map taken at the greater retinal eccentricity is coarser. As such, it responds to a broader range of stimulus displacements, and its absolute peak response is shifted toward larger displacements. This can be seen clearly in the cross-sections of the two maps, along with their Gabor function fits (Fig. 4b). As in the population data in Figure 3, the decrease in Gabor frequency is not accompanied by a change in the size of the spatial envelope. Both profiles decay to zero at approximately the same point, and the extra bumps visible in the profile of the more foveal subunit suggest that the frequency is changing in a manner that is essentially independent of the envelope.
For this cell, we obtained separate speed-tuning curves for the two subunits, using random-dot fields centered on the same positions as the noise maps. The dots fields were larger than the stimuli used to generate the maps, but they did not overlap spatially. The resulting curves, shown in Figure 4c, indicate that speed tuning was very similar at the two locations, although the more foveal curve responded more strongly to slower speeds. Similar results of speed tuning at different spatial locations were obtained with five other MT neurons, suggesting that there may be modest changes in preferred speed across individual MT receptive fields (Treue and Andersen, 1996).
We measured the subunit structure at multiple eccentricities within 17 MT receptive fields. For each cell, we first obtained a map at the center of the receptive field and then obtained one or more maps at other positions within the receptive field. Thus, we had 17 center maps and 37 maps from the receptive field peripheries. For each map, we calculated a corresponding Gabor frequency, defined as Fc for the center maps and Fp(n) for each of the n peripheral maps obtained from a given cell. The value of n ranged from 1 to 4. Thus, a simple way to quantify the effect of eccentricity on Gabor frequency is to compute, for each peripheral map, the ratio ΔF = log(Fc/Fp(n)). This captures the change in Gabor frequency, which can be related to the difference in retinal eccentricities at which the two maps were obtained: ΔE = (Ec – Ep). The values of (ΔE, ΔF) are plotted in Figure 4d.
If the Gabor frequency were constant across the entire receptive field, the frequency difference (y-axis) would be zero, regardless of the eccentricity difference (x-axis). In contrast to this prediction, a linear regression indicates a highly significant correlation between ΔE and ΔF (p < 0.0001), with a slope of –0.014. As in the between-cell data shown in Figure 3a, greater eccentricities are associated with lower frequencies. This means that, even within a single MT receptive field, the range of dot displacements to which a cell responds changes in a predictable manner. Note that the lower signal-to-noise ratio near the edges of the receptive field cannot explain this result, because it would introduce similar effects at all eccentricities, leading to a V-shaped plot in Figure 4d.
The result in Figure 4d means that, on average, a 1° change in eccentricity within an MT receptive field is accompanied by a shift in the subunit frequency of ∼0.014 octaves. By comparison, the slope of the regression line for comparisons made across cells (Fig. 3a) was –0.016. In other words, one encounters a similar change in subunit structure across eccentricities, whether moving across V1 receptive fields, across MT receptive fields, or within MT receptive fields.
Preferred spatial displacement
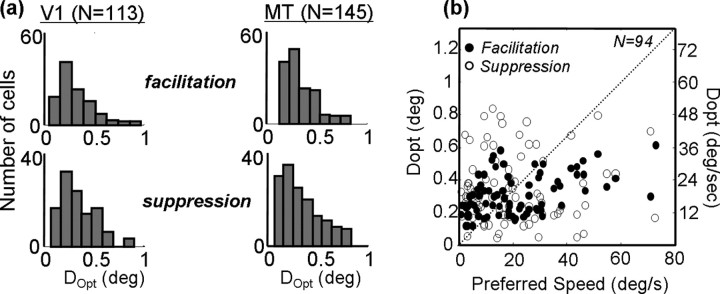
The cross-sections shown in Figures 2 and 4 capture the preferences and limits of neuronal responses to two-spot apparent motion. As such, it is useful to compare these quantities between V1 and MT to determine to what extent the behavior of MT neurons can be accounted for on the basis of their inputs. For each cell, we computed the preferred dot displacement Dopt as the peak of the Gabor fit to the cross-section through I(Δx, Δy). This is shown as the vertical dotted line through the peak in Figure 2b. We also computed the optimal spatial displacement for suppression from the Gabor function (Fig. 2b, vertical line through the trough). Histograms of these values are shown in Figure 5a for both V1 (left) and MT (right). The distributions are clearly quite similar, with the means for facilitation being 0.26° (0.11° SD) for V1 and 0.31° (0.13° SD) for MT. This difference was marginally significant (p < 0.06, t test), but the substantial overlap in the two populations is consistent with a simple explanation in terms of a selective projection from V1 to MT. Similarly, the mean values of Dopt for suppression were 0.33° (0.14° SD) in V1 and 0.26° (0.14° SD) in MT. This difference did not reach significance (p > 0.2, t test).
Figure 5.
a, Measurements of Dopt, which is the spatial displacement yielding the maximal facilitatory or suppressive response for each neuron. The maximum is defined from the peak (or trough) of the Gabor fit to the spatial profile, as shown in Figure 2 b. The population of V1 cells is shown on the left, and MT cells are on the right. Facilitation is on top, and suppression is on the bottom. b, The x-axis shows, for 94 MT neurons, the peak of a log-Gaussian fit to speed-tuning curves like those shown in Figure 4c. The y-axis shows Dopt for facilitation (filled circles) and suppression (open circles).
Figure 5b shows the relationship between preferred speed for random-dot fields and Dopt for facilitation and suppression in 94 MT cells. Although no correlation is apparent for suppression, a significant correlation exists between Dopt for facilitation and preferred speed (Spearman's rank correlation, p < 0.05). The correlation is weak (R2 = 0.31), and Dopt clearly underestimates preferred speed for speeds greater than ∼20°/s. This latter finding can be further appreciated by inspection of Figure 5a (right), which shows very few neurons that prefer values of Dopt beyond ∼0.5°, which corresponds to a speed of 30°/s.
Maximum spatial displacement
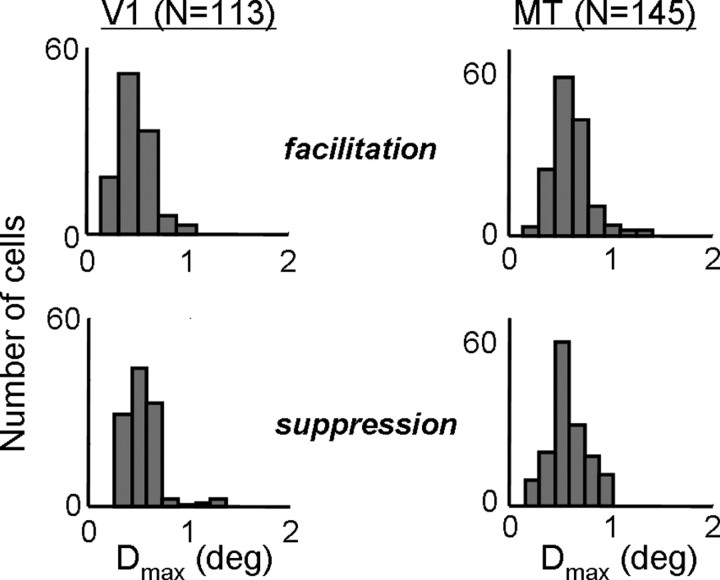
To get an idea of the limits of speed tuning, we also measured the maximum spatial displacement Dmax. This was defined as the first zero-crossing of the Gabor function (Baker and Cynader, 1986) in the preferred direction of each neuron (Fig. 2b, leftmost vertical line).
As with measurements of Dopt, the distributions of Dmax were similar for V1 and MT (Fig. 6). For facilitation, the mean value for V1 was 0.59° (0.28° SD), whereas the mean value for MT was 0.67° (0.31° SD). These differences were again marginally significant (p < 0.05), but the distributions were mostly overlapping. The distributions of Dmax for suppression were nearly identical between V1 (0.49 ± 0.17°) and MT (0.49 ± 0.22°). Together with the measurements of Dopt, these results suggest that there is no systematic difference between the subunit structures found in V1 complex cells and in MT cells. Similar results were obtained with random-dot field stimuli (Churchland et al., 2005).
Figure 6.
Measurements of Dmax, which is the maximal spatial displacement to which a neuron is sensitive. This is defined as the zero-crossing of the Gabor fit to the spatial profile shown in Figure 2b. Population histograms for Dmax are shown for V1 (left) and MT (right), for facilitation (top) and suppression (bottom).
Subunit aspect ratio
In addition to the overall sizes of the subunits, we can examine their two-dimensional shape. Nearly all of the subunits consisted of one facilitatory and one suppressive subregion. From inspection of Figure 2a, it is clear that both the facilitatory and suppressive regions are elliptical in shape, with the axis of elongation being perpendicular to the preferred-null direction axis (Pack et al., 2003a). Because our probe stimuli are not oriented, the elongation of the subunits must reflect the orientation selectivity of the inputs of each neuron.
To study the elongation of the V1 and MT subunits, we fit each displacement map with an elliptical Gaussian function (Fig. 2a, ellipses). For the orientation of the facilitatory region, we truncated the maps at the 1/e contour. Suppressive regions were studied in the same way, after first inverting the positive and negative portions of the map. Gaussian fits were generally excellent, with only 12 MT neurons and 9 V1 neurons being rejected, with R2 values <0.9.
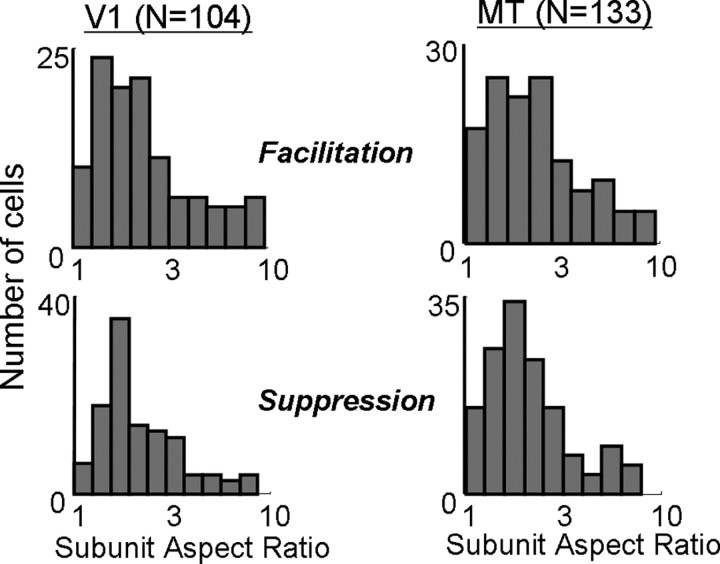
Figure 7 shows the distributions of subunit aspect ratios found in V1 and MT for the facilitation and suppression. The geometric means of the aspect ratios for facilitation were 2.2 in V1 and 2.1 in MT (p > 0.2, t test). For suppression, the corresponding values were 2.1 and 2.0 (p > 0.3, t test). Thus, it appears that the subunits are modestly elongated, suggesting a limited degree of orientation selectivity in the inputs to both V1 and MT cells, although it is possible that our procedure slightly underestimated aspect ratio (Jacobson et al., 1993).
Figure 7.
Measurements of the subunit aspect ratio. Aspect ratio was defined as the ratio of length to width of the best-fitting elliptical Gaussian for facilitatory (top) and suppressive (bottom) fields in V1 (left) and MT (right).
Spatiotemporal interactions: I(Δs, Δτ)
One possible reason for the limited range of spatial displacements indicated in Figure 5 is that peak displacement maps ignore crucial aspects of the interaction function I(Δx, Δy, Δτ, τ2). For example, the neurons might respond to larger spatial displacements at larger values of Δτ. Such a change in preferred spatial displacement with increased temporal separation between stimuli might render MT neurons sensitive to the ratio Δs/Δτ, where s is the magnitude of a two-dimensional spatial displacement. This type of invariant velocity selectivity is often assumed to be one of the primary functional differences between direction selectivity in V1 and MT.
We tested the velocity sensitivity of neurons in V1 and MT by computing profiles like those in Figure 2b at values of Δτ ranging from 16 to 150 ms. To do this, we first computed the profile for the peak displacement map to establish the preferred-null access (Fig. 2a, thick dashed line). We then used the same axis to obtain profiles at the other values of Δτ and stacked the profiles to obtain the Δs–Δτ maps. Using the same axis for each value of Δτ allowed us to measure changes in preferred spatial displacement regardless of changes in preferred direction, which were generally negligible (Perge et al., 2004). For most neurons, we did not measure simultaneous interactions (Δτ = 0), although it would be of some theoretical interest to do so (Jacobson et al., 1993; Baker, 2001; Livingstone et al., 2001; Livingstone and Conway, 2003).
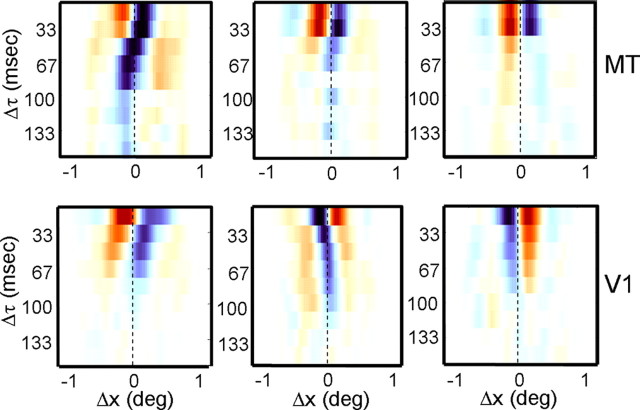
Figure 8 shows example Δs–Δτ maps for three V1 cells and three MT cells. The y-axis indicates the time Δτ between stimuli, and the x-axis indicates the spatial displacement Δs. The colors indicate facilitation and suppression, as in the maps in Figures 1 and 2. Thus, a horizontal row is a color-coded version of the cross-sections shown in Figures 2b and 4b. The slant evident in some of the maps suggests that the preferred spatial displacements for these cells change as a function of the temporal separation between stimuli.
Figure 8.
Examples of maps showing the spatial profile as a function of the temporal separation (Δτ) between stimuli for three MT cells (top) and three V1 cells (bottom). For each map, the rows are color-coded spatial profiles, with orange indicating facilitation and blue indicating suppression. The columns correspond to different values of Δτ, and the vertical dashed lines correspond to zero spatial displacement.
As Δτ is increased, the V1 cell in the bottom left panel of Figure 8 shows an increase in its responses to large stimulus displacements. This is evident in the slant of the reddish regions on the left of the map, and it is exactly what one would expect from a cell that was tuned to the ratio Δs/Δτ. In contrast, the cell in the top left panel of Figure 8 shows a reversal in the spatial profile of its suppressive responses, so that the overall effect of increasing Δτ appears to be a phase shift in the response profile. This latter result is similar to the predictions of motion energy models (Adelson and Bergen, 1985), which do not encode velocity per se, but rather a limited range of spatiotemporal displacements. We will first consider the slant present in the Δs–Δτ maps in V1 and MT and then examine specific predictions of a simple model of velocity tuning.
Separability of I(Δs, Δτ) maps
One way to examine the slant in the (Δs, Δτ) space is to examine separability of responses to spatial and temporal displacements. For a neuron with responses that are separable in space and time, the Δs–Δτ maps in Figure 8a can be described as the product of a spatial profile (like those in Fig. 2b) and a temporal profile. The temporal profile may be biphasic (as the one in the top left panel of Fig. 8a appears to be), but the separability of the response implies that responses to velocity will depend on individual values of Δs and Δτ rather than their ratio. In contrast, a neuron with an inseparable response map will have a response to spatial displacements that varies systematically with the temporal interval between stimuli and so could be tuned to the ratio Δs/Δτ.
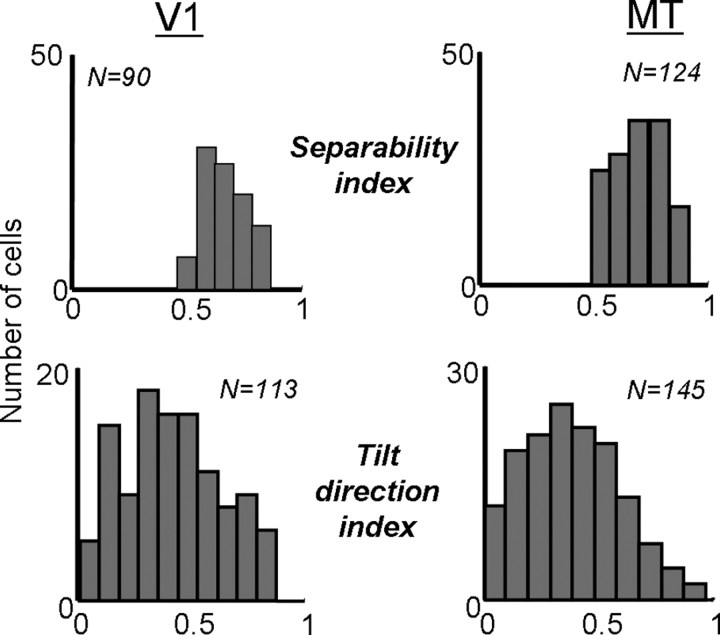
We tested the separability of V1 and MT responses by performing a singular value decomposition on the Δs–Δτ map of each neuron. The SVD calculates a series of orthogonal maps (known as singular vectors), each capturing less of the variance than the preceding one. A completely separable map would be described by one singular vector, whereas inseparable maps would require more singular vectors. The extent to which a singular vector contributes to the map is described by a scalar known as the singular value. The statistical significance of each singular value was tested with a permutation test (p < 0.05), in which the maps were recalculated with the order of the stimulus frames shuffled (see Materials and Methods). The permutation test led us to discard 31 V1 neurons and 20 MT neurons, because none of their singular values reached significance.
Using the singular values for each map, we can describe separability in a continuous manner by calculating a separability index (SI) (Mazer et al., 2002; Grunewald and Skoumbourdis, 2004):
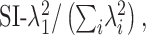 |
where λn is the nth singular value. The SI measures the extent to which the first singular vector is sufficient to account for the variability in each map, with an SI of 1 meaning complete separability and an SI near 0 indicating inseparability. The SIs for the V1 neurons shown in Figure 8 were 0.64, 0.75, and 0.88, from left to right. For the MT neurons in Figure 8, the SIs were 0.58, 0.70, and 0.91. Across the populations, the distributions of SIs for V1 and MT are shown in Figure 9. For V1, the mean SI was 0.71 (0.15 SD), whereas in MT, the mean was 0.70 (0.10 SD). These differences were not significantly different (t test, p > 0.2). If we consider only singular values that were significantly above the noise (permutation test, p < 0.05), then the mean SI becomes 0.80 (0.22 SD) for V1 and 0.86 (0.18 SD) for MT. Similar results on the separability of V1 and MT neurons have been obtained with sinusoidal grating stimuli (Foster et al., 1985; Priebe et al., 2003).
Figure 9.
Measures of separability in V1 (left) and MT (right). The top row shows population histograms of the separability index, calculated from a singular value decomposition of maps like those shown in Figure 8. The bottom row shows the tilt direction index, calculated from the discrete Fourier transform of the maps (see Materials and Methods).
Orientation in I(Δs, Δτ) maps
A second way to examine the separability of the neurons is to examine the orientation of the Δs–Δτ maps. Neurons that change their preferred spatial displacement as a function of the inter-stimulus interval (Δτ) should show a slant in their Δs–Δτ maps. The degree of this slant can be computed with a tilt direction index, which describes the amount of slant from 0 to 1, with 0 indicating no slant and 1 indicating that the map is completely described by one direction of tilt (Anzai et al., 2001; Baker, 2001) (see Materials and Methods). Thus, the TDI should be inversely related to measures of separability, which was indeed the case in both V1 (p < 0.01) and MT (p < 0.002). This suggests that much of the inseparability found in the data were attributable to spatiotemporal slant.
For the V1 cells shown in Figure 8, the TDIs were, from left to right, 0.86, 0.52, and 0.10. The corresponding values for the MT cells were 0.85, 0.51, and 0.04. The distribution of TDIs is shown at the bottom of Figure 9 for V1 (left) and MT (right). The mean TDI for the population of V1 cells was 0.42 (0.22 SD) and that for MT cells was 0.39 (0.21 SD), which did not differ significantly (t test, p > 0.16).
Modeling of velocity tuning
Neither of the previous two analyses tested any particular hypothesis about velocity tuning. Both simply looked for structure in the data that one might expect to find if the neurons were velocity tuned. This is a rather indirect way to examine velocity tuning, because a neuron such as the one shown in the top left panel of Figure 8 can show slant in Δs/Δτ space without being tuned to velocity. Indeed, there are many ways in which a neuron can exhibit inseparability without being tuned for velocity (Baker, 2001). We therefore examined a third way to explore velocity tuning by developing and testing specific models that predict particular space–time structure for velocity-tuned neurons. These models can then be checked against the data to determine which accounts for more of the variance (Levitt et al., 1994; Priebe et al., 2003).
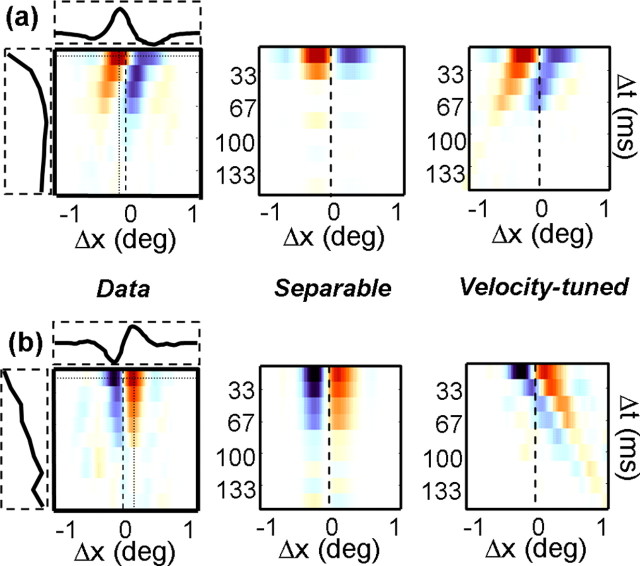
We performed such an analysis for our population of V1 and MT neurons. A separable model was derived from the spatial and temporal profiles (horizontal and vertical slices) through the peak of each map. These are shown for two example cells in Figure 10a. The left column shows the Δs/Δτ maps for two of the cells shown in Figure 8, with the dashed rectangles along the sides of the maps indicating the spatial and temporal profiles taken at the peaks of the maps. The separable prediction was then the outer product of these functions (middle column). The velocity-tuned prediction was computed by shifting each spatial profile by an appropriate amount to obtain a line of constant velocity (right column). To determine which model provided a better fit to the data, we computed the partial correlations between the models and the data (Levitt et al., 1994; Priebe et al., 2003).
Figure 10.
A simple model of velocity tuning (Levitt et al., 1994). a, The leftmost map corresponds to the example shown in Figure 8 (bottom left). The horizontal and vertical dotted lines intersect at the point of peak facilitation, and the curves shown in the horizontal and vertical boxes correspond to response profiles taken along these lines. The middle map indicates the “separable” prediction, defined as the outer product of the horizontal and vertical curves shown next to leftmost map. The rightmost map shows the “velocity-tuned” prediction, obtained by shifting the peak spatial profile by an appropriate amount to maintain the preferred velocity (Δs/Δτ). b, Same as a but for the example neuron shown in the bottom right of Figure 8.
For the neuron in Figure 10a, the correlation between the velocity-tuned prediction and the data were 0.70, whereas the correlation for the separable prediction was 0.44. For the neuron in Figure 10b, the values were 0.29 and 0.83. Thus, the neuron in Figure 10a conforms to a simple model of velocity tuning, whereas the neuron in Figure 10b is tuned for a particular displacement in space and time.
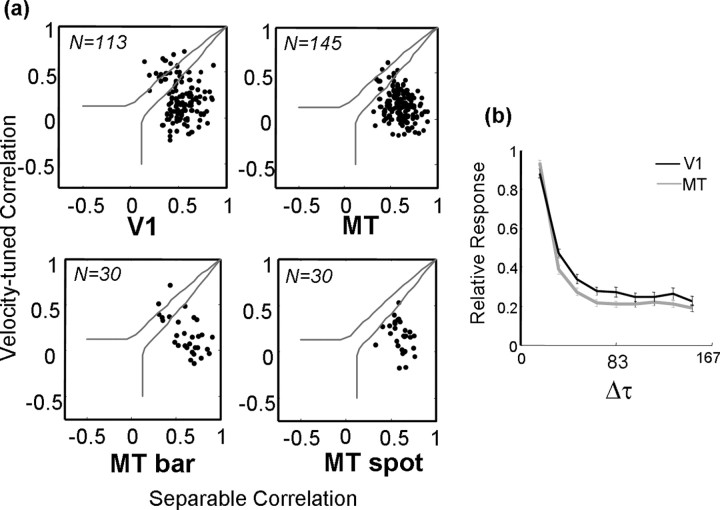
Figure 11a (top row) shows the results for V1 and MT. In both areas, there was a preponderance of separable neurons. In V1, 9 of 113 neurons were significantly velocity tuned, whereas in MT, there were only 2 of 145 that were significantly velocity tuned. The rest were either significantly separable or could not be classified by this technique.
Figure 11.
Distributions of correlation values for the separable and inseparable predictions for V1 (top left) and MT (top right). Each dot corresponds to a neuron, and the solid gray lines show thresholds for significance at the level of p < 0.05. Neurons that fall between the two lines cannot be categorized as being consistent with either prediction. The bottom row shows a comparison of the correlation values for 30 MT neurons for which displacements maps were computed using long bars (left) and small spots (right). b, Normalized response strength as a function of the temporal separation between stimuli (Δτ) for the population of neurons in V1 (black) and MT (gray).
The lack of velocity tuning in MT is somewhat surprising given previous results with sinusoidal gratings (Perrone and Thiele, 2001; Priebe et al., 2003). These studies found that a subpopulation of MT neurons exhibited velocity tuning that was invariant over a range of spatial and temporal stimulus frequencies. One study (Priebe et al., 2003) found that velocity tuning increased with contrast, which may reconcile our findings with theirs. The stimuli in our experiment, although high in luminance contrast (99%), were extremely compact in space and time, so that the total contrast per stimulus was extremely low. Also, relative to receptive field size, the stimuli were much larger in V1 than in MT, which might explain why we find slightly more inseparability in V1.
We examined this issue by collecting additional maps from 30 MT neurons with the spot stimuli replaced with a pair of long bars (2.4°) oriented perpendicular to the preferred direction of each neuron. The stimulus sequence and analysis were otherwise identical, but the total contrast (power) delivered to the receptive field on each stimulus frame was greater by a factor of ∼100. Figure 11a (bottom row) shows a comparison of the nonparametric analysis for the 30 neurons. The panel on the left shows the results for the bar stimuli, which clearly indicate a shift for some neurons toward inseparability. This shift was significant in 10% (3 of 30) of the neurons (Fisher's r–z transformation, p < 0.05). The panel on the right shows the results for the same neurons using the small spot stimuli. As in the larger sample, nearly all were significantly separable. Thus, it appears that MT neurons exhibit more velocity-tuned behavior at higher stimulus contrasts, as reported previously (Priebe et al., 2003).
The difference appears to be genuinely attributable to the higher contrast and not to the difference in the spatial structure of the spot and bar stimuli. When we tested 11 of these neurons with lower-contrast (12%) bars of the same length, the space–time maps were once again separable. There was little difference between these maps and those obtained with spots (data not shown).
One of the primary reasons for the lack of space–time interactions in our data were the strong preference of most neurons for short interstimulus intervals (Δτ). In fact, most of the neurons had very little response to spatial displacements of any magnitude when Δτ was more than two refreshes (33 ms) (Churchland and Lisberger, 2001). Consequently, the Δs–Δτ maps were often quite noisy. Noise tends to increase the TDI and decrease the separability of most neurons, so that our analyses probably overestimated the extent of the interactions. (The TDI increases because random noise has, on average, equal energy at all orientations, so that the position of the peak of the discrete Fourier transform is random. Consequently, the mean TDI for random noise is near 0.5. Similarly, random noise has a relatively flat distribution of singular vectors, leading to low separability.) This becomes clear when one examines the total responsiveness of the neurons as a function of Δτ [the value of the function V(τ2; Δτ) described in Materials and Methods, at the peak of τ2]. The normalized population averages shown in Figure 11b indicate that, on average, by Δτ = 50 ms, the responses had fallen to approximately one-third of their peak. In other words, V1 and MT do not exhibit invariant velocity tuning in Δs/Δτ space in large part because they simply do not respond to large values of Δτ.
Impulse responses: I(Δs, τ)
The analyses thus far have examined the interaction function I(Δx, Δy, Δτ, τ2), with the correlation delay (τ2) fixed at the point that provided the highest signal-to-noise ratio. However, for many cells in V1 and MT, the displacement maps change significantly with correlation delay (τ2). To examine this dynamic response in more detail, we calculated cross-sections through the map at different delays. The crosssections were color coded and stacked vertically to create a Δs–τ2 map.
Examples of Δs–τ2 maps are shown in Figure 12a. The middle cell is a V1 cell, and the other two are MT cells. Within each map, the rows describe the activity as a function of spatial displacement (Δs) along the preferred-null axis, and the columns show the time course of the impulse response from 0 to 300 ms. For the cell on the left, the response begins ∼60 ms, peaks at 80 ms, and has mostly disappeared by 120 ms. For the other two neurons, there is a similar time course to the early part of the response but, at longer correlation delays, both neurons reverse their preferred directions. For the rightmost neuron, the reversal is pronounced and long lasting.
As in Figure 12, the dynamics of facilitation and suppression were generally mirror images of each other, with the exception that the peak amplitude of suppression was often slightly smaller than that of facilitation. Thus, the amplitude of facilitation was highly correlated with the amplitude of suppression, with the best-fitting regression line having a slope of 0.79 in MT and 0.78 in V1 (p < 0.0001).
To quantify the extent of direction reversals, we calculated a biphasic index (see Materials and Methods) from the Δs–τ2 map of each neuron. The biphasic index measures the extent to which neurons reversed preferred direction over time, with a value of 1 indicating a complete reversal and 0 meaning no reversal. The three example neurons in Figure 12a had biphasic indices of 0.07, 0.34, and 0.71, from left to right. For the population of V1 neurons (Fig. 12b, left), the median biphasic index was 0.14, meaning that most of the neurons behaved like the one in the leftmost column of Figure 12a. Results for MT neurons were similar, with the mean biphasic index being 0.22 (Fig. 12b, right). There was no significant difference between the V1 and MT populations (t test, p > 0.12). Thus, most V1 and MT neurons maintained the same preferred direction throughout most of their impulse responses, although a few clearly showed direction reversals. Similar results were obtained with random-dot stimuli (Perge et al., 2004).
V1 simple cells
In previous work, we showed that an apparent motion sequence in which the stimulus contrast reversed led to a reversal of direction selectivity in both V1 and MT (Livingstone et al., 2001; Livingstone and Conway, 2003). Thus, a cell that preferred leftward motion for a white-to-white sequence preferred rightward motion for a white-to-black sequence. Such a reversal of direction selectivity means that the measured subunits are derived from the outputs of neurons that are sensitive to stimulus contrast polarity. This is not a characteristic of either MT neurons or the complex V1 cells that project to MT (Movshon and Newsome, 1996).
V1 simple cells, conversely, are sensitive to contrast polarity (by definition), and many of them are direction selective. This suggests that the second-order subunits that we have described here might originate from V1 simple cells (or their inputs). To test this idea, we recorded from 57 simple cells using the same sparse noise stimulus as in the previous experiments. Simple cell responses can be described primarily by their first-order kernels, which represent the firing probability as a function of the positions and contrast polarities of individual stimulus elements in space and time.
An example is shown in Figure 13a. As in the previous examples, the response unfolds from left to right, and the spatial structure of the subunits is shown in each map. However, rather than showing displacements Δx and Δy, the maps now show the response as a function of spatial position (x,y). Similar to the second-order kernels, the first-order map in Figure 13a shows a clear subunit structure with two elongated positive and negative regions arranged in a parallel manner. Cells with more than two subregions were rare (Ringach, 2002). Over time, the relative positions (or phases) of the positive and negative regions shift, suggesting a preference for stimuli moving perpendicular to the axis of elongation. This type of spatiotemporal structure is characteristic of direction-selective simple cells (McLean and Palmer, 1989; Reid et al., 1991; DeAngelis et al., 1993a).
Theoretically, the type of direction selectivity observed in simple cells could give rise to the second-order kernels found in complex cells and in MT. The minimal requirement is that first-order responses of the kind shown in Figure 13a be multiplied or squared and summed over space (Adelson and Bergen, 1985; van Santen and Sperling, 1985). (Actually, true direction selectivity requires at least two simple cells with differing positions or phases, but because information about spatial phase is absent from the second-order kernels, we have ignored this requirement for the present discussion.) In other words, the motion energy is the product of the first-order responses at two points in space and time. In this sense, it is analogous to the second-order kernels that we have described, and we can use the same methods to predict the response of a neuron that performed this multiplication. Such a neuron would likely be a V1 complex cell or an MT cell, both of which have strong second-order responses. In fact, if these second-order responses are derived from the outputs of simple cells like the one shown in Figure 13a, we might expect a population of predicted second-order responses to match what we have described in our spatiotemporal measurements of actual second-order kernels.
Figure 13b shows the result of this calculation (for details, see Materials and Methods), using the simple cell in Figure 13a as the input to the simulated second-order kernel. Here the axes of each map represent stimulus displacement (Δx, Δy), and the results are qualitatively similar to the second-order maps shown in Figure 1 and in previous work. In this case, the subunit exhibits a preference for motion down and to the right, along with elongated suppressive and facilitatory regions. The subunit structure agrees well with the direction tuning observed when bars were swept through the receptive field (Fig. 13b, right).
Figure 13c (left) shows a space–time map derived from the first-order responses shown in Figure 13a. The slant evident in the map indicates a preference for rightward motion, as is observed in the direction-tuning curve shown in Figure 13b. The right panel of Figure 13c shows the simulated Δs–Δτ map for the same cell.
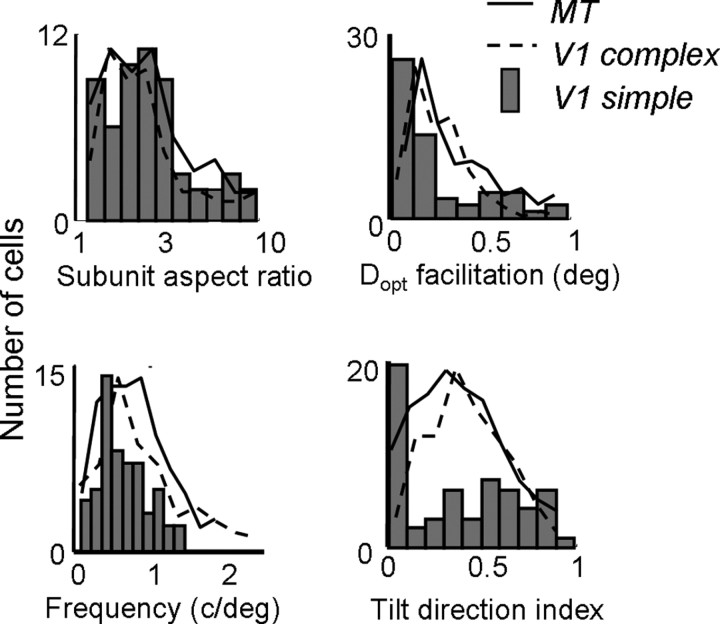
We simulated second-order kernels of this type for each of the 57 simple cells in our population. Measurements of aspect ratio, Gabor frequency, optimal spatial displacement (Dopt), and space–time slant are shown in the histograms in Figure 14. The solid and dashed lines superimposed on each histogram show the corresponding distributions for each measurement in V1 complex cells and MT cells. From the left column of Figure 14, it is clear that the simulated kernels exhibit spatial structure similar that of the observed kernels. That is, second-order kernels derived from the first-order responses of simple cells seem to account for the distributions of aspect ratios, Gabor frequencies, and preferred spatial displacements found in complex cells and MT cells. The mean subunit aspect ratio was 2.51, which was slightly higher than what we observed in complex and MT cells. However, the distributions were clearly very similar across all three cell types, as was also the case for the subunit spatial frequency (Fig. 14, top right). Similarly, the mean preferred spatial displacement (Dopt for facilitation) was 0.30 (0.23 SD), which was comparable with that observed in complex cells and MT cells.
Figure 14.
Population histograms for second-order kernels derived from first-order responses of V1 simple cells. The histograms show subunit aspect ratio (top left), Dopt for facilitation (top right), Gabor frequency (bottom left), and tilt direction index (bottom right) for the simulated interaction kernels. The same values for MT (solid lines) and V1 (dashed lines) are superimposed on each histogram.
Conversely, the simulated kernels do not account even qualitatively for the space–time slant seen in the actual second-order kernels. The bottom right panel of Figure 14 shows the distribution of TDIs for the simulated kernels. In contrast to the actual second-order kernels, there is a preponderance of cells with TDIs near 0, indicating very little slant in the Δs–Δτ space. Many of these cells also exhibited extra suppressive lobes in their simulated Δs–Δτ maps, because the second-order map was similar to the autocorrelation of individual frames of the first-order map.
The lack of space–time slant may be a consequence of additive noise in the simple-to-complex cell projection. As mentioned above, such noise could increase the TDIs of actual cells but would be absent from the simulated maps, which are noiseless. Of course, the discrepancy could also be attributable to a selective projection from the minority of simple cells that show substantial slant to direction-selective complex cells.
Predictions based on the full kernels
For each cell in the V1 and MT population (with the exception of nine simple cells), we had a corresponding direction-tuning curve, measured with dots or bars. As a first pass at determining the predictive power of the kernels, we simulated the responses of the first- and second-order kernels to the stimuli used to generate the direction-tuning curves. The simulated tuning curves were then compared with the actual time-averaged direction-tuning curves. Note that we are not describing results for individual spike trains, which the kernels generally did not predict well (data not shown).
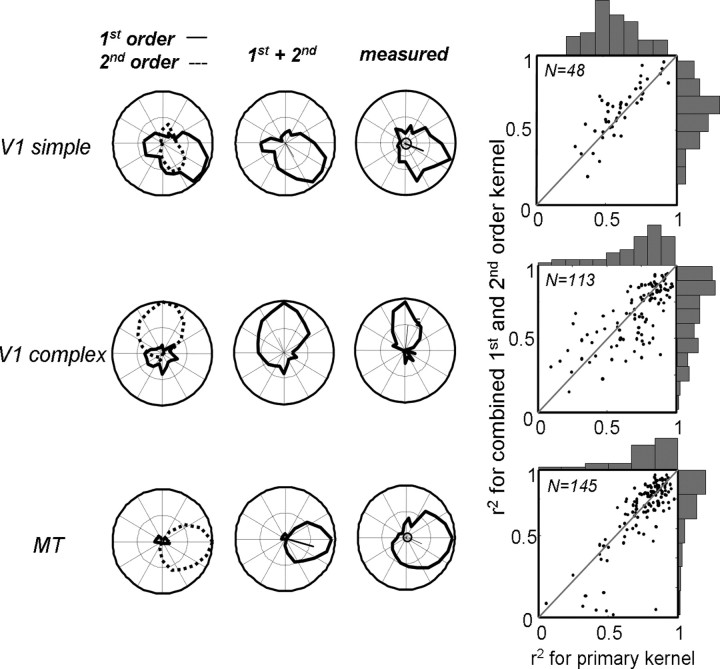
Figure 15 shows the results for a V1 simple cell (the same as the one in Fig. 13), a V1 complex cell, and an MT cell (the same as the one in Fig. 1). The first column shows the individual predictions for the first-order (solid line) and second-order (dotted line) kernels. The middle column shows the prediction for the two kernels combined, and the last column shows the measured tuning curve. A few trends are evident in the data. First, many simple cells had second-order responses that were direction tuned, with preferences that were similar to those of the first-order kernel. (Baker, 2001). These second-order kernels, although generally low in amplitude, often improved the correlation between the prediction and the data, as in the first row of Figure 15. For this cell, the correlation between the first-order kernel and the data was R2 = 0.71, which improved to R2 = 0.86 with the addition of the second-order kernel. Second, the first-order kernels of V1 complex cells, although often high in amplitude, were generally not direction selective and tended to worsen the correlation between the prediction and the data. For the cell in the second row of Figure 15, the correlation between the response of the second-order kernel and the data was R2 = 0.87, which decreased to R2 = 0.82 with the addition of the first-order kernel. Third, the first-order kernels of MT neurons were always negligible in amplitude and nondirectional (Fig. 15, third row).
Figure 15.
Predictions of full first- and second-order kernels. The first row shows an example V1 simple cell, along with its predicted first-order (solid line) and second-order (dotted line) direction-tuning curves. The combined tuning curve is shown in the second column, and the tuning curve measured with drifting random-dot fields is shown in the third column. The extent to which the primary kernel (first-order) and combined first- and second-order kernels capture the measured tuning curve are shown as correlation coefficients in the fourth column. Rows 2 and 3 show similar data for V1 complex cells and MT cells.
The fourth column of Figure 15 compares the predictive power of the primary kernels (first-order for simple cells, second-order for complex cells and MT cells) with that of the combined kernels for each cell type. For the primary kernel, the median R2 values were 0.56, 0.72, and 0.80 in simple, complex, and MT cells. For the combined kernels, these values were 0.66, 0.69, and 0.78. For the secondary kernels, the values were 0.59, 0.08, and 0.05. This suggests that, although the first-order responses in complex and MT cells do not carry information about motion, the second-order responses of simple cells do contribute to the observed direction tuning. This was confirmed in 17 of 45 (38%) simple cells, for which the prediction of the combined kernel was significantly better than that of the first-order kernel (partial correlation, p < 0.05). In contrast, the combined kernel only outperformed the primary kernel in 8 of 113 (7%) of the complex cells and 2 of 145 (1%) of the MT cells.
Discussion
Using sparse noise stimuli, we have mapped the subunit structure of direction-selective receptive fields in V1 and MT. For MT cells and for V1 complex cells, we examined the second-order subunits, which represent selectivity for stimulus displacement in space and time. For V1 simple cells, we studied the first-order subunits, which capture the selectivity for the contrast polarity of individual stimuli. In both V1 and MT, the results show that direction selectivity is computed on a very fine spatial scale, with the maximal spatial displacement being <1° for most neurons. These spatial displacements scale in a predictable way with retinal eccentricity but are essentially unrelated to the temporal aspects of the stimulus, with the exception that nearly all of the neurons studied prefer short (<17 ms) interstimulus intervals. Some basic characteristics of the spatial structure of the second-order subunits can be explained by the first-order characteristics of simple cells in V1, although, as a population, the second-order subunits exhibit greater space–time slant than would be predicted from motion energy models.
These results bear on two important questions in visual neurophysiology. First, how is information about a given stimulus transmitted through the various stages of the visual cortical hierarchy? Second, to what extent can the responses of visual cortical neurons be predicted from first- and second-order descriptions of the stimulus? We address these issues in the following sections.
Hierarchical processing in the visual cortex
Along the primate visual pathway, selectivity for motion direction is first observed in V1 simple cells, which also exhibit some superposition in their responses to first-order (luminance) signals (Hubel and Wiesel, 1962). Most direction-selective simple cells exhibit space–time slant, meaning that the temporal and spatial properties of the receptive fields covary in such a way as to provide limited velocity selectivity (Reid et al., 1987; McLean and Palmer, 1989; DeAngelis et al., 1993b; Conway and Livingstone, 2003). Given that simple cells project to complex cells (Martinez and Alonso, 2001), this type of direction selectivity could account for the subunit structure found in complex cells, assuming a motion energy or Reichardt-style motion model (Adelson and Bergen, 1985; van Santen and Sperling, 1985). Data in support of this idea are shown in Figures 13 and 14.
Our population of MT neurons exhibited second-order spatial structure that was strikingly similar to that of the V1 complex cell population. Both populations showed modestly oriented subunits (Fig. 7), a preference for short spatiotemporal stimulus displacements (Figs. 5, 6), and separability in space and time (Figs. 8, 9, 10, 11, 12). This high degree of similarity suggests that MT receptive fields are derived primarily by summing the outputs of V1 complex cells sharing a common preferred direction. Consistent with this idea is the observation that the subunits become coarser at greater eccentricities, whether the measurements are made across the receptive fields of many different V1 neurons or within the receptive field of a single MT neuron (Figs. 3, 4).
Predictive power of the subunits
Our results suggest that the subunit structure of receptive fields in MT can be traced back to the response properties of V1 simple cells. We have shown that these subunits accurately predict certain features of the responses to conventional stimuli such as dots and bars (Fig. 15). In particular, the preferred direction and retinal disparity appear to be computed by simple cells and preserved through several synapses to the level of MT (Pack et al., 2003a).
In contrast to predictions of motion direction, the second-order kernels do not accurately predict the preferred speed of the MT neurons, which is often underestimated (Fig. 5b). This is also consistent with the idea that the MT subunits are derived from simple cell outputs, because simple cells prefer slower speeds than complex cells (Movshon, 1975), and complex cells prefer slower speeds than MT cells (Mikami et al., 1986; Churchland et al., 2005). Part of this transformation is manifested in the subunits: we observed lower space–time slant (preferred velocity) in simple cells than in complex cells or MT cells (Fig. 14, bottom right). However, previous work suggests that the transformation to greater preferred speeds in MT requires more than two successive stimulus presentations and may require as many as 10 (Mikami et al., 1986). Such higher-order interactions would not be present in our second-order kernels, and we and others have not found fourth-order interactions in our data (Emerson et al., 1987; Livingstone et al., 2001). Similarly, our technique does not to reveal the selectivity for “non-Fourier” motion that is known to exist in both V1 and MT (Albright, 1992; O'Keefe and Movshon, 1998).
Another shortcoming in our subunit measurements is the use of small spot stimuli to map spatial structure. Although useful for obtaining high spatial resolution, this method minimizes the influence of spatial nonlinearities, such as surround suppression, which play an important role in the processing of more complicated stimuli (Hubel and Wiesel, 1965; Sillito et al., 1995; Levitt and Lund, 1997; Kapadia et al., 1999; Sceniak et al., 1999; Pack et al., 2003b). For a few MT neurons, we attempted to measure purely spatial nonlinearities by calculating kernels for Δτ = 0 and found little structure in these simultaneous interactions (data not shown). As with speed computations, these contextual effects appear to depend on the total contrast in the stimulus (Levitt and Lund, 1997; Polat et al., 1998; Kapadia et al., 1999; Sceniak et al., 1999; Pack et al., 2005), which is low for our sparse noise stimuli.
Previous experiments have found substantial differences between responses in V1 and MT to complex stimuli. For instance, selectivity for non-Fourier motion (Albright, 1992; O'Keefe and Movshon, 1998), for transparent motion (Qian and Andersen, 1994), and for two-dimensional motion signals (Movshon and Newsome, 1996) appear to be more prevalent in MT than in V1. The latter finding was hypothesized to be the result of the construction of a velocity space in the projection from V1 to MT (Heeger et al., 1996). Such a transformation would manifest itself at the single-cell level as velocity-tuning in the spatiotemporal responses of MT neurons but not V1 neurons. Contrary to this hypothesis, our results suggest that there is very little velocity tuning in either area (Figs. 9, 10, 11). Previous work using sinusoidal gratings in anesthetized animals has reached a similar conclusion (Foster et al., 1985; Lisberger et al., 2003; Priebe et al., 2003), although velocity tuning in these studies was somewhat more common.
The finding that MT neurons are more selective than V1 neurons to transparent motion suggests a role for MT in suppressing motion noise (Qian and Andersen, 1994). Indeed, our finding (Fig. 15) that the predictive power of the kernels increases from simple cells to complex cells to MT cells suggests that each stage sums over larger numbers of antecedent neurons with similar response properties. This would be useful for suppressing locally conflicting motion directions, uncorrelated noise, or temporal flicker at the level of MT. Also, the progression from simple to complex to MT cells appears to achieve a limited sort of form invariance: MT cells, in contrast to V1 cells, are almost completely insensitive to contrast polarity, as manifested in the absence of first-order kernels in these cells.
Relation to perception and behavior
Psychophysical experiments on humans have examined the perception of motion from sequences of discrete stimuli (apparent motion). As in our physiological data, apparent motion is usually perceived for spatial displacements (Δs) of <1° and temporal displacements (Δτ) of <100 ms (Baker and Braddick, 1985). The spatial limits of this type of perception depend on retinal eccentricity in a manner that is at least qualitatively consistent with our results (Baker and Braddick, 1985). These spatial limits can be extended if multiple stimulus displacements are presented (Nakayama and Silverman, 1984), suggesting that our two-flash apparent motion stimuli may underestimate Dmax for the neuronal populations. Consistent with our second-order kernels is the finding that human observers perceive a reversal of motion direction for stimulus sequences that reverse contrast (Anstis and Rogers, 1975; Livingstone et al., 2001).
Psychophysical observers are less sensitive to the magnitudes of temporal displacements than to spatial displacements, and they are relatively insensitive to velocity (Smith and Edgar, 1990; Priebe and Lisberger, 2004). That is, humans tend to confound the spatial composition of an object with its speed, suggesting that they do not possess a cue-invariant measure of velocity. Similar behavior was seen in our V1 and MT cells, which exhibited separable selectivities to spatial and temporal displacement rather than invariant velocity selectivity.
Conclusions
We have shown how an elementary visual computation, direction selectivity, is transmitted through the earliest stages of cortical processing to extrastriate area MT. Our results suggest that the elementary aspects of the computation of motion are performed by the simple cells, with subsequent areas performing a summation over larger regions of visual space. This simple model is derived from correlations between the spike trains and the statistics of the sparse noise input and thus does not include important higher-order aspects of visual processing. Whether or not the resulting mathematical kernels are predictive of responses to more complicated stimuli is an entirely empirical question, which will be the subject of additional research.
Footnotes
This work was supported by National Science Foundation Grant BCS-0235398 and Canada Research Chair 202444 (C.C.P.) and National Institutes of Health Grants EY13135 (M.S.L.) and EY11379 and EY12196 (R.T.B.). Phillip Hendrickson, Tamara Chuprina, and David Freeman provided excellent technical assistance. We thank Eric Schwartz and Aaron Seitz for helpful comments on a previous version of this manuscript.
Correspondence should be addressed to Christopher Pack, Montreal Neurological Institute, 3801 University Street, Room 896A, Montreal, Quebec, Canada H3A 2B4. E-mail: christopher.pack@mcgill.ca.
DOI:10.1523/JNEUROSCI.3226-05.2006
Copyright © 2006 Society for Neuroscience 0270-6474/06/260893-15$15.00/0
References
- Adelson EH, Bergen JR (1985) Spatiotemporal energy models for the perception of motion. J Opt Soc Am A 2: 284–299. [DOI] [PubMed] [Google Scholar]
- Albright TD (1984) Direction and orientation selectivity of neurons in visual area MT of the macaque. J Neurophysiol 52: 1106–1130. [DOI] [PubMed] [Google Scholar]
- Albright TD (1992) Form-cue invariant motion processing in primate visual cortex. Science 255: 1141–1143. [DOI] [PubMed] [Google Scholar]
- Anstis SM, Rogers BJ (1975) Illusory reversal of visual depth and movement during changes of contrast. Vision Res 15: 957–961. [DOI] [PubMed] [Google Scholar]
- Anzai A, Ohzawa I, Freeman RD (2001) Joint-encoding of motion and depth by visual cortical neurons: neural basis of the Pulfrich effect. Nat Neurosci 4: 513–518. [DOI] [PubMed] [Google Scholar]
- Baker Jr CL (2001) Linear filtering and nonlinear interactions in direction-selective visual cortex neurons: a noise correlation analysis. Vis Neurosci 18: 465–485. [DOI] [PubMed] [Google Scholar]
- Baker Jr CL, Braddick OJ (1985) Eccentricity-dependent scaling of the limits for short-range apparent motion perception. Vision Res 25: 803–812. [DOI] [PubMed] [Google Scholar]
- Baker Jr CL, Cynader MS (1986) Spatial receptive-field properties of direction-selective neurons in cat striate cortex. J Neurophysiol 55: 1136–1152. [DOI] [PubMed] [Google Scholar]
- Born RT, Groh JM, Zhao R, Lukasewycz SJ (2000) Segregation of object and background motion in visual area MT: effects of microstimulation on eye movements. Neuron 26: 725–734. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Lisberger SG (2001) Shifts in the population response in the middle temporal visual area parallel perceptual and motor illusions produced by apparent motion. J Neurosci 21: 9387–9402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Priebe NJ, Lisberger SG (2005) Comparison of the spatial limits on direction selectivity in visual areas MT and V1. J Neurophysiol 93: 1235–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conway BR, Livingstone MS (2003) Space-time maps and two-bar interactions of different classes of direction-selective cells in macaque v-1. J Neurophysiol 89: 2726–2742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courellis SH, Marmarelis VZ (1992) Nonlinear functional representations for motion detection and speed estimation schemes. In: Nonlinear vision (Pinter RB, Nabet B, eds), pp 91–108. Boca Raton, FL: CRC.
- DeAngelis GC, Ohzawa I, Freeman RD (1993a) Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex. I. General characteristics and postnatal development. J Neurophysiol 69: 1091–1117. [DOI] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD (1993b) Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex. II. Linearity of temporal and spatial summation. J Neurophysiol 69: 1118–1135. [DOI] [PubMed] [Google Scholar]
- De Valois RL, Albrecht DG, Thorell LG (1982) Spatial frequency selectivity of cells in macaque visual cortex. Vision Res 22: 545–559. [DOI] [PubMed] [Google Scholar]
- Emerson RC, Citron MC, Vaughn WJ, Klein SA (1987) Nonlinear directionally selective subunits in complex cells of cat striate cortex. J Neurophysiol 58: 33–65. [DOI] [PubMed] [Google Scholar]
- Emerson RC, Bergen JR, Adelson EH (1992) Directionally selective complex cells and the computation of motion energy in cat visual cortex. Vision Res 32: 203–218. [DOI] [PubMed] [Google Scholar]
- Foster KH, Gaska JP, Nagler M, Pollen DA (1985) Spatial and temporal frequency selectivity of neurones in visual cortical areas V1 and V2 of the macaque monkey. J Physiol (Lond) 365: 331–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaska JP, Jacobson LD, Chen HW, Pollen DA (1994) Space-time spectra of complex cell filters in the macaque monkey: a comparison of results obtained with pseudowhite noise and grating stimuli. Vis Neurosci 11: 805–821. [DOI] [PubMed] [Google Scholar]
- Gattass R, Gross CG (1981) Visual topography of striate projection zone (MT) in posterior superior temporal sulcus of the macaque. J Neurophysiol 46: 621–638. [DOI] [PubMed] [Google Scholar]
- Grunewald A, Skoumbourdis EK (2004) The integration of multiple stimulus features by V1 neurons. J Neurosci 24: 9185–9194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ, Simoncelli EP, Movshon JA (1996) Computational models of cortical visual processing. Proc Natl Acad Sci USA 93: 623–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN (1962) Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol (Lond) 160: 106–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN (1965) Receptive fields and functional architecture in two non-striate visual areas (18 and 19) of the cat. J Neurophysiol 28: 229–289. [DOI] [PubMed] [Google Scholar]
- Jacobson LD, Gaska JP, Chen HW, Pollen DA (1993) Structural testing of multi-input linear-nonlinear cascade models for cells in macaque striate cortex. Vision Res 33: 609–626. [DOI] [PubMed] [Google Scholar]
- Jones JP, Palmer LA (1987) The two-dimensional spatial structure of simple receptive fields in cat striate cortex. J Neurophysiol 58: 1187–1211. [DOI] [PubMed] [Google Scholar]
- Kapadia MK, Westheimer G, Gilbert CD (1999) Dynamics of spatial summation in primary visual cortex of alert monkeys. Proc Natl Acad Sci USA 96: 12073–12078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt JB, Lund JS (1997) Contrast dependence of contextual effects in primate visual cortex. Nature 387: 73–76. [DOI] [PubMed] [Google Scholar]
- Levitt JB, Kiper DC, Movshon JA (1994) Receptive fields and functional architecture of macaque V2. J Neurophysiol 71: 2517–2542. [DOI] [PubMed] [Google Scholar]
- Lisberger SG, Priebe NJ, Movshon JA (2003) Spatiotemporal frequency tuning of neurons in macaque V1. Soc Neurosci Abstr 29: 484.483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone MS (1998) Mechanisms of direction selectivity in macaque V1. Neuron 20: 509–526. [DOI] [PubMed] [Google Scholar]
- Livingstone MS, Conway BR (2003) Substructure of direction-selective receptive fields in macaque v1. J Neurophysiol 89: 2743–2759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone MS, Pack CC, Born RT (2001) Two-dimensional substructure of MT receptive fields. Neuron 30: 781–793. [DOI] [PubMed] [Google Scholar]
- Marmarelis PZ, Marmarelis VZ (1978) Analysis of physiological systems: the white noise approach. New York: Plenum.
- Martinez LM, Alonso JM (2001) Construction of complex receptive fields in cat primary visual cortex. Neuron 32: 515–525. [DOI] [PubMed] [Google Scholar]
- Maunsell JH, van Essen DC (1983) The connections of the middle temporal visual area (MT) and their relationship to a cortical hierarchy in the macaque monkey. J Neurosci 3: 2563–2586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazer JA, Vinje WE, McDermott J, Schiller PH, Gallant JL (2002) Spatial frequency and orientation tuning dynamics in area V1. Proc Natl Acad Sci USA 99: 1645–1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean J, Palmer LA (1989) Contribution of linear spatiotemporal receptive field structure to velocity selectivity of simple cells in area 17 of cat. Vision Res 29: 675–679. [DOI] [PubMed] [Google Scholar]
- Mikami A, Newsome WT, Wurtz RH (1986) Motion selectivity in macaque visual cortex. II. Spatiotemporal range of directional interactions in MT and V1. J Neurophysiol 55: 1328–1339. [DOI] [PubMed] [Google Scholar]
- Movshon JA (1975) The velocity tuning of single units in cat striate cortex. J Physiol (Lond) 249: 445–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Newsome WT (1996) Visual response properties of striate cortical neurons projecting to area MT in macaque monkeys. J Neurosci 16: 7733–7741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ (1978a) Spatial summation in the receptive fields of simple cells in the cat's striate cortex. J Physiol (Lond) 283: 53–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Thompson ID, Tolhurst DJ (1978b) Receptive field organization of complex cells in the cat's striate cortex. J Physiol (Lond) 283: 79–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama K, Silverman GH (1984) Temporal and spatial characteristics of the upper displacement limit for motion in random dots. Vision Res 24: 293–299. [DOI] [PubMed] [Google Scholar]
- O'Keefe LP, Movshon JA (1998) Processing of first- and second-order motion signals by neurons in area MT of the macaque monkey. Vis Neurosci 15: 305–317. [DOI] [PubMed] [Google Scholar]
- Orban GA, Kennedy H, Bullier J (1986) Velocity sensitivity and direction selectivity of neurons in areas V1 and V2 of the monkey: influence of eccentricity. J Neurophysiol 56: 462–480. [DOI] [PubMed] [Google Scholar]
- Pack CC, Born RT, Livingstone MS (2003a) Two-dimensional substructure of motion and stereo interactions in primary visual cortex of alert macaque. Neuron 37: 525–535. [DOI] [PubMed] [Google Scholar]
- Pack CC, Livingstone M, Duffy K, Born RT (2003b) End-stopping and the aperture problem: two-dimensional motion signals in macaque V1. Neuron 39: 671–680. [DOI] [PubMed] [Google Scholar]
- Pack CC, Hunter JN, Born RT (2005) Contrast dependence of suppressive influences in cortical area MT of alert macaque. J Neurophysiol 93: 1809–1815. [DOI] [PubMed] [Google Scholar]
- Perge JA, Borghuis BG, Bours RJ, Lankheet MJ, van Wezel RJ (2004) Temporal dynamics of direction tuning in motion sensitive macaque area MT. J Neurophysiol 93: 2104–2116. [DOI] [PubMed] [Google Scholar]
- Perrone JA, Thiele A (2001) Speed skills: measuring the visual speed analyzing properties of primate MT neurons. Nat Neurosci 4: 526–532. [DOI] [PubMed] [Google Scholar]
- Polat U, Mizobe K, Pettet MW, Kasamatsu T, Norcia AM (1998) Collinear stimuli regulate visual responses depending on cell's contrast threshold. Nature 391: 580–584. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG (2004) Estimating target speed from the population response in visual area MT. J Neurosci 24: 1907–1916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Cassanello CR, Lisberger SG (2003) The neural representation of speed in macaque area MT/V5. J Neurosci 23: 5650–5661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N, Andersen RA (1994) Transparent motion perception as detection of unbalanced motion signals. II. Physiology. J Neurosci 14: 7367–7380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reichardt W (1961) Autocorrelation, a principle for the evaluation of sensory information by the central nervous system. In: Sensory communications (Rosenblith WA, ed), pp 303–318. New York: Wiley.
- Reid RC, Soodak RE, Shapley RM (1987) Linear mechanisms of directional selectivity in simple cells of cat striate cortex. Proc Natl Acad Sci USA 84: 8740–8744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid RC, Soodak RE, Shapley RM (1991) Directional selectivity and spatiotemporal structure of receptive fields of simple cells in cat striate cortex. J Neurophysiol 66: 505–529. [DOI] [PubMed] [Google Scholar]
- Ringach DL (2002) Spatial structure and symmetry of simple-cell receptive fields in macaque primary visual cortex. J Neurophysiol 88: 455–463. [DOI] [PubMed] [Google Scholar]
- Ringach DL, Hawken MJ, Shapley R (2003) Dynamics of orientation tuning in macaque V1: the role of global and tuned suppression. J Neurophysiol 90: 342–352. [DOI] [PubMed] [Google Scholar]
- Rybicki GB, Tracy DM, Pollen DA (1972) Complex cell response depends on interslit spacing. Nat New Biol 240: 77–78. [DOI] [PubMed] [Google Scholar]
- Sceniak MP, Ringach DL, Hawken MJ, Shapley R (1999) Contrast's effect on spatial summation by macaque V1 neurons. Nat Neurosci 2: 733–739. [DOI] [PubMed] [Google Scholar]
- Sillito AM, Grieve KL, Jones HE, Cudeiro J, Davis J (1995) Visual cortical mechanisms detecting focal orientation discontinuities. Nature 378: 492–496. [DOI] [PubMed] [Google Scholar]
- Smith AT, Edgar GK (1990) The influence of spatial frequency on perceived temporal frequency and perceived speed. Vision Res 30: 1467–1474. [DOI] [PubMed] [Google Scholar]
- Treue S, Andersen RA (1996) Neural responses to velocity gradients in macaque cortical area MT. Vis Neurosci 13: 797–804. [DOI] [PubMed] [Google Scholar]
- van Santen JP, Sperling G (1985) Elaborated Reichardt detectors. J Opt Soc Am A 2: 300–321. [DOI] [PubMed] [Google Scholar]