A fast response mechanism for insulin storage in crystals may involve kink generation by association of 2D clusters

Abstract

Crystals that are likely rhombohedral of Zn–insulin hexamers form in the islets of Langerhans in the pancreases of many mammals. The suggested functions of crystal formation is to protect the insulin from proteases and increase the degree of conversion of soluble proinsulin. To accomplish these ends, crystal growth should be fast and adaptable to rate fluctuations in the conversion reaction. Zn–insulin crystals grow layer by layer. Each layer spreads by the attachment of molecules to kinks located at the layers’ edges, also called steps. The kinks are thought to be generated either by thermal fluctuations, as postulated by Gibbs, or by 1D nucleation of new crystalline rows. The kink density determines the rate at which steps advance, and these two kink-generation mechanisms lead to weak near-linear responses of the growth rate to concentration variations. We demonstrate for the crystallization of Zn–insulin a mechanism of kink generation whereby 2D clusters of several insulin molecules preformed on the terraces between steps associate to the steps. This mechanism results in several-fold-higher kink density, a faster rate of crystallization, and a high sensitivity of the kinetics to small increases of the solute concentration. If the found mechanism operates during insulin crystallization in vivo, it could be a part of the biological regulation of insulin production and function. For other crystallizing materials in biological and nonbiological systems, this mechanism provides an understanding of the often seen nonlinear acceleration of the kinetics.

Although the equilibrium and thermodynamic aspects of phase transformations, such as crystallization, are reasonably well understood, many open issues related to their kinetics remain (1). Nevertheless, many of the fundamental properties of the new phase, such as size and macroscopic patterns, are kinetically controlled (1). In an important instance, living organisms rely mostly on kinetic control for the selection of the crystalline phases with properties essential to their existence (2). Insulin crystallization is an example where fine-tuning of the kinetics of growth of the new phase may be crucial for the biological function of the crystals. Aside from crystalline biominerals (2), insulin is a unique example of benign crystallization in vivo with important biological function (3–5); crystals of proteins and small molecules in living organisms often cause disease: gout (6), kidney stones (7, 8), anemia (9), and cataract (10).

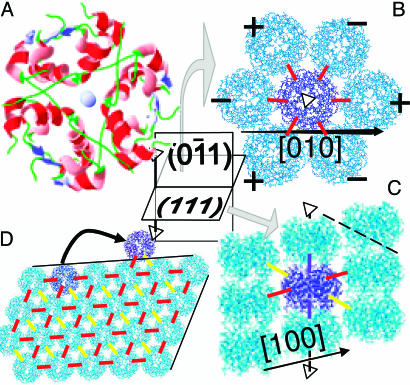
Zn–insulin hexamers in the islets of Langerhans in the pancreatic β-cells form apparently rhombohedral crystals (3–5) whose structure is illustrated in Fig. 1 (11). The likely biological function of insulin crystallization in vivo is to protect the insulin from further proteolysis (after conversion from proinsulin) while it is stored until regulated secretion into the blood serum (4, 5). It has been suggested that crystal formation increases the degree of conversion from soluble proinsulin; however, nearly normal conversion occurs with proinsulin/insulin mutated to prevent crystal formation or in several known mammals, such as the guinea pig, where no crystals form (4, 12). Either of the two functions of crystallization requires that the rate of growth of the crystals be fast and readily responsive to inevitable fluctuations in the rate of conversion. In contrast, like many other faceted crystals, Zn–insulin crystals grow by spreading of layers (13–16). Zn–insulin hexamers join the edges of the growing layers, the steps, at sites of specific configuration, kinks (17). The two known kink-generation mechanisms are by thermal fluctuations (18, 19) or 1D nucleation of new crystalline rows (20–22). Because kink density determines the rate at which steps advance (19, 23), these two kink-generation mechanisms lead to weak linear or sublinear responses of the growth rate to variations of Zn–insulin concentration (19, 21–23). Thus, it appears that the known crystallization mechanisms and the associated linear kinetic dependencies fail to provide an understanding of the expected fast growth rates and nonlinear acceleration of the rates of insulin crystallization (1). Below, we demonstrate a mechanism of kink generation during crystallization of insulin that has not been observed with other materials and that ensures nonlinear acceleration of the crystallization rates in response to increased insulin concentration.

Fig. 1.

The structure of R3 insulin crystals and of steps on their {100}faces. (A) The 2Zn insulin hexamer, which is the dominant species in the solution and the building block of the crystals; with the chosen viewpoint, the two Zn²⁺ ions are shown as exaggerated, nearly overlapping spheres in the center of the image. (B) Structure of (111) crystal plane perpendicular to threefold axis (see schematic). Six surrounding molecules are elevated or depressed with respect to the highlighted central molecule, as indicated by + and − and as seen in C. Marked rhombohedral [010] direction is inclined with respect to the plane of image. (C) Structure of (011) crystal plane parallel to threefold axis. Arrow marks a rhombohedral [100] direction. Dashed line shows orientation of a (100) plane. AFM viewing direction in Fig. 2A is perpendicular to this plane, and molecular rows from the higher layer appear in the crevices between rows from the lower layer. (D) Structure of rhombohedral (100) plane forming the faces of insulin crystals. Solid black lines mark two of the 〈010〉 directions, along which steps are oriented. (B–D) Blue dashes mark two strong bonds with free energy φ₁ along a threefold axis, [111] direction; red dashes mark six strong bonds with free energy φ₂ in (111) plane; and yellow dashes mark six weak bonds with free energy φ₃ along 〈011〉 directions (11). All images were created with swiss-pdbviewer (30).

Results and Discussion

Kink Generation by Thermal Fluctuations at σ ≤ 0.05.

We examined in situ the growth of rhombohedral (R3) crystals of porcine insulin growing from solution, with pH and composition close to those in vivo by tapping mode (13, 24) atomic force microscopy (AFM) (see Methods). Briefly, solution with supersaturation σ ≡ C/C_e − 1 ≈ 0.1 (where C is insulin concentration and C_e is solubility) was pumped into the AFM fluid cell over pregrown insulin crystals. As the crystals grow, the supersaturation drops over several days to near zero.

The crystals grow exclusively by generation of layers on screw dislocations piercing the {100} faces (13, 16). Because the crystals grow by the association of hexamers and they are the dominant species in the solution, we refer to them as molecules. Fig. 2A shows the structure of a step toward the end of an experiment, when supersaturation is very low and the step contains only single-molecule kinks. From Fig. 2A and other similar images at very low supersaturations, the number of molecules between kinks n_k on step segments along the densely packed 〈010〉 directions has a Poissonian-like distribution with a mean n̄_k = 5.6 (Fig. 2B) corresponding to a kink density n̄ k⁻¹ of 0.18. For insight into the kink generation mechanism at low supersaturations, we evaluate the free energy of kink formation from the mean kink density as in ref. 19. When a molecule is moved from position “in step” to position “at step” (Fig. 1D), three strong bonds and one weak bond are broken, i.e., free energy equal to 3φ₂ + φ₃ is lost (see Figs. 1 B and C), and one strong bond and one weak bond are created, gaining φ₂ + φ₃. Because contacts with molecules in underlying layers are identical at both positions, they cancel out in the net 2φ₂. The result is four kinks, i.e., the kink free energy ω = φ₂/2.

Fig. 2.

Structure of steps on {100} faces of insulin crystals at supersaturations σ < 0.05. (A) AFM image of typical structure of steps on a (100) face of insulin crystals at low supersaturations toward the end of an experiment. A step with two kinks (curved arrows) is highlighted with white lines. An insulin hexamer is encircled in black. (B) Distribution of the number of molecules between kinks n_k determined from images similar to A. The mean n̄_k is shown..

By using the relation n̄_k = 1/2exp(ω/k_BT) + 1 (where k_B is the Boltzmann constant and T is temperature) (19), which is derived by assuming that all kinks are created by thermal fluctuations of the step edge, with n̄_k = 5.6, (Fig. 2B), we get a free energy of the kink ω = 5.5 kJ/mol and φ₂ = 11.1 kJ/mol. Next, we define a reduced crystallization free energy ΔG′ = −1/2(2φ₁ + 6φ₂ + 6φ₃), which sums the free energies of all bonds formed during crystallization (shown in Figs. 1 B and C). This ΔG′ differs from the full crystallization free energy ΔG_cryst because it excludes the protein entropy change upon crystallization ΔS_protein (25–27). Following ref. 11, we assume that φ₁ ≈ φ₂ and φ₃ ≈ φ₂/2. Thus, we get ΔG′ = −61.3 kJ·mol⁻¹; variation of the ratios between φ₁, φ₂, and φ₃ within the constrains of the ratios between φ₁, φ₂, and φ₃ postulated in ref. 11 does not affect the main conclusion below (e.g., with φ₁ − 1.5 φ₂ and φ₃ − φ₂/5, ΔG″ = −58 kJ/mol). Because ΔG_cryst = −30 kJ·mol⁻¹ (25), we get ΔS_protein = (ΔG′ − ΔG_cryst)/T ≈ −105 J·mol⁻¹·K⁻¹. ΔS_protein accounts for the loss of six translational and rotational degrees of freedom partially balanced by the newly created vibrational degrees of freedom (28). Estimates of the magnitude of the net effect have a consensus value centered around −(100 − 120) J·mol⁻¹·K⁻¹ (29). A direct experimental determination of ΔS_protein for insulin crystallization at conditions identical to those used here yielded −110 ± 10 J·mol⁻¹·K⁻¹ (25). The similarity of these three data points support the value of ΔS_protein found as (ΔG′ − ΔG_cryst°)/T and the conclusion that the kink density is determined by the φ_i values; i.e., at low supersaturations, the kinks are due to thermal fluctuations of the step edge. For insight into how kink density affects step propagation, we monitored a step with a disabled slow scan axis of the AFM. The acquired pseudoimages depict the step position as a function of time (Fig. 3A) (31, 32). As seen with other systems before (23, 31), with steps whose structures are similar to the one seen in Fig. 2A, we see shifts in step position of one molecular diameter due to attachment or detachment of molecules to the monitored site at the step edge (Fig. 3A). The step velocity from Fig. 3A and other similar images is v ≈ 0.05 − 0.15 nm·s⁻¹.

Fig. 3.

Step dynamics on (100) faces of insulin crystals. (A) Typical step dynamics at σ < 0.05. Image acquired with a disabled slow scan axis of the AFM. In this imaging mode, the AFM tip moves along a single line of chosen length on the crystal’s surface. The AFM controller records a pseudoimage in which the axis, x, which is perpendicular to the fast-scanning direction, is replaced with a time axis, t: x = Δxft (where Δx is the spacing between scan lines in the displayed image and f is the scanning frequency). Positive and transient negative step shifts are marked with white and black arrowheads, respectively. (B) A pseudoimage at supersaturations σ ≈ 0.1 at the beginning of an experiment that shows, in addition to one-molecular-diameter step shifts, jumps of 5 and 11 molecular diameters due to propagation of multiple kinks. Definition of kink depth d_k is illustrated. (C) Statistics of multiple kinks. Single kinks are the most common, and multiple kinks occur less frequently. The 11-molecule-deep kink depicted in B is not reflected in the data because of the shorter range of kink depth axis. (D) Frequency of occurrence of time intervals between two successive step movements of one molecular diameter measured on pseudoimages such as those shown in B. Peak at time = 0 s is due to several events within the time between scan lines, because of, e.g., the passing through the scan line of a multiple kink. The total number of events is 108. The mean time between single-molecule events is shown.

Mounds and Nonlinear Acceleration of Kinetics at σ ≈ 0.1.

Previous studies of insulin crystallization at σ > 0.2 revealed kink density n̄k−₁ ≈ 0.3, which was difficult to quantify exactly because of fast step motion (16, 33). To understand the transition between low values of n̄k−₁ at σ ≤ 0.05 and n̄k−₁ at higher values of σ we monitored the step edge at σ ≈ 0.1 at earlier times of observation. The trace of the step edge in Fig. 3B shows step jumps of several molecular diameters. These jumps are unlikely for steps with single kinks generated by thermal fluctuations or 1D nucleation (22, 23); indeed, Fig. 4 shows that they reflect the propagation of multiple kinks. Single kink propagation is still the most frequent (Fig. 3C), and Fig. 3C shows that kinks of greater depths have decreasing probabilities.

Fig. 4.

Evolution of step morphology at σ ≈ 0.1 at the beginning of an experiment (A) Initial configuration step. (B) Two newly formed mounds, indicated with a black arrowhead and a white square (shown enlarged in Inset). (Inset) Mound depth d is defined. (B and C) The lower mound in B produces multiple kinks indicated with a black arrowhead in C. Multiple kinks generated above the field of view cover molecular rows generated by mounds in B. (D) At 430 s, the step straightens out again. (D–F) The spreading of a multiple kink generated out of the viewfield is monitored between 430 and 608 s. White arrowheads in F point to two defects in the outermost row of molecules. Black arrows indicate scan directions. Times after the first image are marked on the frames; a shift of the viewfield to follow the step took 10 s between D and E. Black lines mark step location on the current image, and white lines mark step location in the preceding image.

From Fig. 3D, the mean time between molecular attachment to a randomly selected step site is Δt̄ = 9.7 s. Because v = a/Δ (molecular diameter, a = 5.5 nm) (34), the corresponding step velocity v ≈ 0.57 nm s⁻¹. Comparing this value to v ≈ 0.1 nm·s⁻¹ from Fig. 3A and other similar images, we see that step propagation by multiple kinks leads to a several-fold increase in the step velocity, v. From these v values, the step kinetic coefficient β, defined as v = βΩn_eσ (27) [where Ω = 6.7 × 10⁻²⁰ cm³ is the crystal volume per hexamer (11) and n_e = C_e N_Avogadro/M_w = 1.34 × 10¹⁵ cm⁻³ is the number density of hexamers in a solution at equilibrium with crystals] is 2.2 × 10⁻³ cm·s⁻¹ at σ ≤ 0.05 and 6.3 × 10⁻³ cm·s⁻¹ at σ ≥ 0.1.

Fig. 4 (for additional examples, see Figs. 7–10, which are published as supporting information on the PNAS web site) shows that the multiple kinks originate as mounds of insulin molecules at the steps, which then grow fast only in the direction parallel to the step. The mounds are two to five molecules deep, and they are rich in kinks. Some of the multiple kinks in Fig. 3B are deeper than the observed mounds, which suggests a mechanism of cooperative creation of multiple mounds. This mechanism is discussed below in relation with the mechanism of mound generation.

The intensity of mound formation is higher at higher supersaturations, which were present in our experiments at earlier times of observation. The mounds affect step propagation in two ways: They lead to higher kink density n̄k−₁, and each mound locally advances the step several molecules at a time. Because overall single-molecule attachment events dominate (Figs. 3 C and D), we conclude that the main contribution of the mounds to the nonlinear acceleration of crystallization kinetics is to generate abundant kinks. Note that the kink density cannot increase indefinitely; it is limited by a geometric ceiling of 0.5 (e.g., in a regular arrangement of two molecules and two voids in a row) and likely less if kink dynamics are accounted for. Thus, the mound mechanism of nonlinear kinetic acceleration is limited, and a constant value of the step kinetic coefficient would ensue at a threshold supersaturation. Comparing β = 6.3 × 10⁻³ cm·s⁻¹ at σ ≈ 0.1 to β = 6.3 × 10⁻³ cm·s⁻¹ at σ > 0.2 from ref. 35, we conclude that the threshold value of σ is 0.10–0.15. The nonlinear acceleration in step kinetics due to mound formation is schematically illustrated in Fig. 5 and compared with experimental v(σ) data in Fig. 5B.

Fig. 5.

A schematic illustration of the effect of mound formation on kink density n̄k−₁, kinetic coefficient β, and step velocity v. (A) As supersaturation σ = C/C_e − 1 increases from the top to bottom cartoons, the intensity of mound formation increases. This increase leads to a higher n̄k−₁ and proportionally higher β and v. Kinks are indicated by a light-colored contour around the molecule that is to the left or right of them. (B) According to the relations shown, ν is the frequency of molecular attempts to attach to step and U_o is the barrier for such attachment. The large x marks kinetics reflected in Fig. 3A, where σ ≈ 0.05 and v ≈ 0.10 nm·s⁻¹; the large plus sign marks kinetics reflected in Fig. 3B, where σ ≈ 0.1 and v ≈ 0.6 nm·s⁻¹; white squares mark data from refs. 16 and 35 for σ > 0.2; and vertical dashed lines delineate σ ranges of three kink generation regimes illustrated in A.

The physiological significance of the nonlinear acceleration of step kinetics is related to the corresponding values of the kinetic coefficient for the face β_f, defined as R = β_fΩn_eσ so that β_f = βp [where R = pv is the crystal growth rate and p ≈ 10⁻² (16) is the vicinal slope of the surface proportional to the density of the steps (1)]. The values for β_f are 2.2 × 10⁻⁵ cm·s⁻¹ at σ ≤ 0.05 and 6.3 × 10⁻⁵ cm·s⁻¹ at σ ≥ 0.1. If these β_f values apply in vivo, crystal growth rates of ≈0.05 nm·s⁻¹ [which would allow an ≈100-nm crystal to grow within 30 min (4)] require σ ≈ 1; i.e., C ≈ 2C_e with the high β_f and significantly higher σ ≈ 3 if kinks are only generated by thermal fluctuations, and the lower β_f operates at all supersaturations.

The low supersaturations related to the higher density of mound-generated kinks indicate that neither of the two steps in the proinsulin conversion/insulin crystallization reaction control its overall rate. If proinsulin conversion were the slow and controlling step, C ≈ C_e and σ ≤ 0.1–0.2 would ensue, whereas a slow crystallization step would result in accumulation of dissolved insulin and high σ values. Thus, proinsulin conversion and insulin crystallization are kinetically coupled.

Another puzzle of insulin biosynthesis to which a solution can be put forth based on the mechanism of mound-generated kinks is related to the fact that insulin crystallization occurs in the presence of high proinsulin concentrations (4, 5). During growth at high supersaturations, proinsulin is readily incorporated in insulin crystals, whereby, besides making them highly imperfect, it delays crystal formation by hours and even days (36). Incorporation of proinsulin in insulin crystals would prevent proinsulin conversion and thus decrease the efficiency of insulin biosynthesis, and the resulting delays would defy the physiological function of insulin crystallization; yet, it is not clear how crystallization in vivo is protected from proinsulin incorporation. We propose that the low supersaturation maintained during crystallization via mound-generated kinks may be the answer to the puzzle. Indeed, high supersaturations during crystal growth are known to cause instabilities, such as step bunching, which in turn often lead to solution occlusions, high defect density, and extraneous trapping of impurities (37). Another consequence of growth at high supersaturations is the formation of metastable dense liquid clusters of several hundred nanometers in size and their association to the growing crystals (38). Both the instabilities and the associating clusters provide pathways for proinsulin incorporation into the insulin crystals. In contrast, at the relatively low supersaturations σ ≈ 1, insulin crystallization occurs in a nearly perfect manner, with all the selectivity inherent in the crystallization process (1).

The Mechanism of Mound Formation: 2D Clusters on the Terraces Between Steps.

To understand the mechanism of mound formation, we note that the lack of correlation with the scan direction and of detectable influence of the tip on the morphology of the steps exclude the possibility of scanning-induced artifacts. Below, we discuss four possible mechanisms: creation of multiple kinks at step intersections, step edge instability, nucleation of mounds at the step edge, and association of 2D clusters preformed on the terraces between steps to the steps’ edges.

The intersections between two steps of different orientations coming from different sources were seen to produce large agglomerations of 20–50 kinks. These rough step segments in the concave angle between the steps propagate fast; the concave edge is filled within a few hundred nanometers and step orientations along the crystallographic orientations illustrated in Fig. 1 is restored. This phenomenon has relatively week effect on the overall kinetics of crystallization. Frequent zoom-in/zoom-out image sequences, illustrated in Fig. 11, which is published as supporting information on the PNAS web site, show that all mounds and multiple kinks observed above are located along straight step segments and lead to faster overall kinetics of crystallization.

Instabilities of the step shape, leading to “kink bunching,” could be caused by, for instance, an asymmetry of attachment of a molecule from the left- and right-hand sides of a kink, called the kink Erlich–Schwoebel effect (39), or by impurities incorporated or adsorbed at the step that make kink propagation nonlinear. Instability-related deviations from the straight step shape evolve, grow, and lead to a persistent wavy step shape (39, 40). In contrast, Fig. 4 (for additional examples, see Figs. 7–9) shows that the step shape deviations are triggered by well defined mounds, which spread out and leave straight step segments. We conclude that step-shape instabilities are not the reason behind the observed step behavior.

The other two mechanisms rely on the existence of a population of adsorbed insulin hexamers on the terraces between steps. In support of this population, we note that the velocity of closely spaced steps, i.e., those closer than 100 nm apart, is significantly slower than the velocity of well separated steps (16, 33). In analogy to the proteins lysozyme, canavalin, and ferritin (37, 41, 42), the strength of this step–step interaction suggests that it is due to competition between the steps for supply of molecules adsorbed on the terraces and that the width of the zone on both sides of a step of lower surface concentration of insulin (known as the denuded zone) is ≈50 nm or ≈10 molecular sizes.

Nucleation of clusters from individual hexamers at a step edge requires the existence of an energy barrier that prevents the integration of the accumulated molecules into the step. Possible sources of such a barrier are impurities, lattice point defects, and lattice strain. No impurities of sizes comparable or larger than that of insulin were detectable in numerous molecular resolution images of the steps. Although it is typically assumed that only impurity species of sizes comparable with that of the protein are of consequence in crystallization of proteins (43, 44), one can still think that molecules smaller than the AFM resolution might attach to a growth site and block it. One would expect such small molecule impurities to have characteristics times of attachment to the steps or kinks shorter by orders of magnitude than the times that the kinks and step are exposed to such adsorption (45). Thus, it is unlikely that any combination of parameters could lead to impurity effects at low supersaturations and their lack at high supersaturations.

Although point defects (mostly, vacancies) in the outermost rows of insulin hexamers were present (see Fig. 4F) their number was small, they healed rapidly, and their locations were not related to locations of mound formation. Lattice strain at the step edge would be manifest in a deviation of outermost insulin hexamers from their equilibrium lattice positions. We carried out cross-correlation analysis of images in grip (Groningen Image Processing Package). With the exception of the vacancies, all molecules at the step edge were found to occupy their equilibrium lattice positions. An area of an image well away from the step was selected and compared with areas of various sizes (from two molecules to four unit cells) that included the step. Strong cross-correlation peaks at the positions of the molecules were invariably observed. Thus, the “nucleation at the step” scenario, although still possible because of the limited resolution of the images in Figs. 2A and 4E, is unlikely.

Two-dimensional clusters on the terraces between steps may be undetectable because of their mobility and hydrodynamic interactions with the scanning tip, as in refs. 46 and 47; for further examples and theory of cluster mobility on surfaces, see refs. 48 and 49. However, in the vicinity of a step, the cluster mobility seems to be reduced, and Fig. 6 (for additional examples, see Fig. 12, which is published as supporting information on the PNAS web site) shows clusters associating to a step and creating a mound. The residual mobility of the clusters in Fig. 6 prevents identification of their structure before their association. The 2D clusters might be ordered or disordered, akin to a 2D liquid formed in the pool of hexamers adsorbed on the terraces: examples of liquid phases in 2D systems (50) have been discussed (51). A 3D analog of this process would be layer generation by the landing of dense liquid droplets on the surface of an existing crystal (52). In further analogy, the stacks of layers formed by 3D nucleation do not grow in height but expand laterally (52), a behavior similar to that of the mounds described above.

Fig. 6.

Attachment of two clusters to a multiple kink formation. (A) Starting configuration of a step with an advancing multiple kink. (B) A 2D cluster indicated with a white arrowhead near a multiple kink. The image of the cluster is fuzzy probably because of cluster mobility and because its size and structure are hard to judge. (C) The cluster joins a step, creating a three- or four-molecule-deep mound. (D) Another cluster indicated with a black arrowhead is seen near a protruding mound. Black arrows indicate scan directions. Black lines mark the step position in the current image, and white lines mark the location of the step in the preceding image.

Fig. 6D shows that a second cluster attaches to the mound created by the cluster seen in Figs. 6 A–C. This sequence illustrates cooperative association of several clusters, which may be due to the mechanism schematically depicted in Fig. 13, which is published as supporting information on the PNAS web site. An associating cluster promotes the step to the area away from the step, where the concentration of molecules and clusters is higher, which facilitates the association of further clusters. This mechanism is one of instability of the step shape similar to the Mullins–Sekerka (53) or the Bales–Zangwill (54) models; however, the instability is due to the supply of clusters to the step, and, correspondingly, the evolution of the instability is stopped by the depletion of the clusters on the terraces. This mechanism explains the occurrences of 7- and 11-fold kinks initiated by mounds that are at most five molecules deep. This mechanism is also supported by the observations in Figs. 4, 7, 8, and 12 that large multiple kinks consist of several groups of double, triple, and quadruple kinks. Fig. 3C shows that kinks deeper than six molecules are very rare. It is likely that such kinks are the result of coalescence of smaller multiple kinks.

Summary and Conclusions

We have demonstrated on the example of insulin crystallization a mechanism of step advancement diffenent from those commonly discussed. We have shown that at moderate and high supersaturation, the kink density increases from the value determined by the intensity of the thermal fluctuations not, as thought before, because of 1D nucleation of new molecular rows along the step edge but because of the association of 2D clusters of several insulin molecules at the step edge. This mechanism could operate for any solution crystallization system for which the thermodynamically determined kink density is low with a single precondition that the molecules adsorb on the terraces between steps before incorporation into the steps. The increasing kink density leads to an increasing kinetic coefficient as supersaturation is increased and to a superlinear increase of the step velocity and crystal growth rate at near-equilibrium conditions. If this mechanism operates for insulin crystals in vivo, it provides for fast response to sudden increases of the rate of insulin production from proinsulin and may be a part of glucose-regulation mechanisms in sick and healthy organisms.

Methods

Rhombohedral (R3) crystals of porcine insulin were grown from solution with pH = 7.0 maintained by citric buffer at a low ionic strength of 0.05 M in the presence of 0.005 M ZnCl₂.

To monitor the dynamics of steps at low supersaturations, crystals were incubated in solutions with insulin concentration C = 0.09 mg·ml⁻¹. The steps continued to grow for several days, although this concentration is below the solubility value of 0.15 ± 0.02 mg·ml⁻¹ from ref. 25. Comparing the crystal sizes at the start of an experiment and after growth cessation [the absence of a “dead zone” for step motion and the reversibility of growth and dissolution at the molecular level (16) indicate that growth cessation is due to equilibration] and accounting for the balance of insulin mass, we estimate the solubility C_e ≈ 0.08 mg·ml⁻¹; the discrepancy with the previous determination is likely due to inconsistencies of the solution composition. Thus, the supersaturation σ = (C/C_e − 1) at the beginning of the experiments discussed here is ≈0.1, and it drops to close to zero during a 4- to 6-day experiment.

We employ tapping mode (13, 24) AFM (16, 41, 55); for details, see ref. 16. The resolution of the AFM images, such as the one in Fig. 2A, is ≈2.0–2.5 nm and allows identification of individual insulin hexamers in the top crystal layer (11). Chernov, and B. M. Pettitt for critical discussion of the manuscript; I. Reviakine for image and data analyses, for active and creative participation in the discussion of the results, and for writing an initial draft of the manuscript; O. Gliko for help with the temperature control set up; and W. Keegstra (University of Groningen, The Netherlands) for help with the installation and use of the grip (Groningen Image Processing) software package. This work was supported by Grant NAG8-1854 from the Office of Biological and Physical Research at the National Aeronautic and Space Administration.

Abbreviation

AMF

atomic force microscopy.