Regulation of blood flow in activated human brain by cytosolic NADH/NAD⁺ ratio

Abstract

It has been known for more than a century that increases in neuronal activity in the brain are reliably accompanied by changes in local blood flow. More recently it has been appreciated that these blood flow increases are accompanied by increases in glycolysis that are much greater than the increases in oxidative phosphorylation. It has been proposed by us and others that this activity-induced increase in glycolysis mediates the increase in blood flow by mechanisms linked through the near-equilibrium relationship between cytosolic NADH/NAD⁺ and the lactate/pyruvate ratios. Here we show in awake human subjects that by transiently raising blood pyruvate concentration during local increases in functional brain activity, a maneuver designed to reduce the cytosolic NADH/NAD⁺ ratio, the expected blood flow response measured with positron-emission tomography is significantly attenuated. This result provides critical additional support for the hypothesis that, like in anesthetized rodents, the cytosolic NADH/NAD⁺ ratio of awake human subjects links activity-induced increases in glycolysis to signaling pathways for the regulation of blood flow.

Local changes in brain blood flow are a well known accompaniment of changes in neural activity, but the reason for these changes in blood flow and the mechanism(s) by which they are achieved remain unclear. Previous studies from our laboratory demonstrated that the increase in cerebral blood flow (CBF) in response to physiological stimulation does not occur to match the delivery of metabolic substrates to momentary changes in their use (1–3). These observations have forced us to think in new ways about these relationships.

Important clues relating changes in neuronal activity to blood flow come from three observations. First, although oxidative phosphorylation is the primary source of brain energy production in the baseline state, glycolysis appears to have an enhanced role in the changes in brain metabolism accompanying changes in neural activity. Second, the increase in glycolysis appears to occur, at least in part, in astrocytes in support of the uptake of glutamate from the synaptic cleft and its conversion to glutamine. And, third, astrocytes have recently been implicated as mediators of the blood flow changes associated with increases in neural activity. Based on these observations we (4) and others (5, 6) have posited that glycolytically evoked increases in the cytosolic free NADH/NAD⁺ ratio provide a means by which the magnitude of the blood flow response to a change in brain cellular activity is regulated.

Experiments testing the above hypothesis (4–6) have been based on the well known near-equilibrium between the cytosolic NADH/NAD⁺ and lactate/pyruvate ratios (7). Consistent with this relationship, it has been demonstrated in anesthetized rats that changes in plasma lactate/pyruvate ratio induced by the i.v. injection of lactate or pyruvate can be used to regulate the blood flow response to increases in physiological activity. As an important extension of this work in anesthetized rats, our previous results demonstrated that lactate injection in awake humans augments the regional CBF response to visual stimulation. In addition, this augmentation is positively correlated with the lactate/pyruvate ratio (4). A remaining test of our hypothesis was to show, using the same experimental design, methods, and analysis, that a reduction in the lactate/pyruvate ratio in awake humans has the opposite effect. In the present experiment we used i.v. pyruvate infusions in awake humans to reduce the lactate/pyruvate ratio transiently while measuring regional brain blood flow with positron-emission tomography (PET) during visual stimulation.

Results

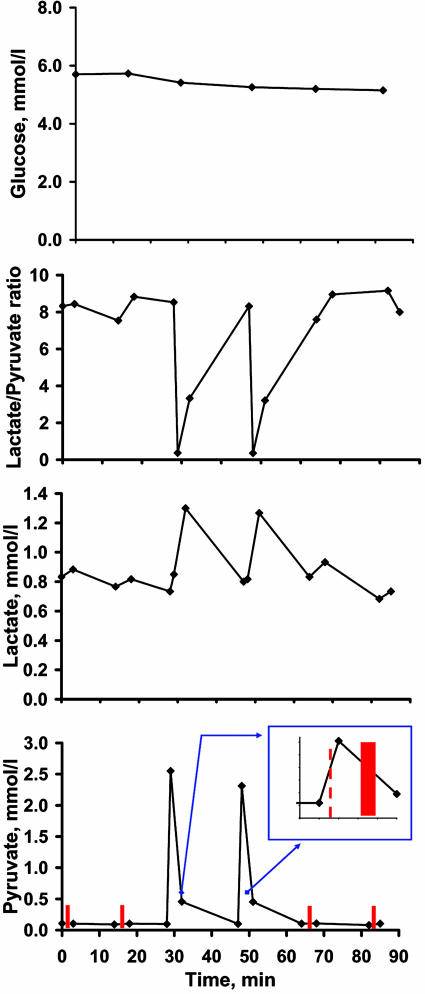
Plasma pyruvate levels were increased ≈24-fold at the end of each pyruvate bolus injection (from ≈0.1 mmol/liter to ≈ 2.4 mmol/liter), then dropped significantly over the next 3 min, remaining 4.5-fold higher at the end of each PET scan compared with baseline (Fig. 1 and Table 1). The lactate/pyruvate ratio declined ≈21-fold after pyruvate injection compared with baseline levels (from ≈8.4 to ≈0.4) and was still reduced by 2-fold by the end of each pyruvate CBF scan. Plasma pyruvate, lactate, and the lactate/pyruvate ratio all returned to baseline levels during the 15-min delay after each pyruvate injection (Fig. 1 and Table 1). There were no significant changes in arterial glucose and blood gas values during the study (Tables 1 and 2).

Fig. 1.

Blood values for glucose, lactate, pyruvate, and lactate/pyruvateratio. Inset illustrates the start time of pyruvate injection (red dashed line) and the PET scan (red bar). The values are means for six subjects. The values and SDs for all measures are presented in Table 2.

Table 1.

Global CBF and blood glucose, lactate, pyruvate, and lactate/pyruvate ratio levels at different stages

Parameters	Saline		Pyruvate		Saline
	Rest	Activation	Rest	Activation	Rest	Activation
Global CBF, ml/100 g per min	60.2 ± 14.5	57.6 ± 13.1	56.6 ± 11.2	59.2 ± 13.8	57.7 ± 16.1	57.3 ± 12.6
Glucose, mmol/liter	5.7 ± 1.0	5.7 ± 0.6	5.4 ± 0.6	5.3 ± 0.6	5.2 ± 0.6	5.2 ± 0.5
Lactate, mmol/liter
Before pyruvate injection			0.7 ± 0.3	0.8 ± 0.3
Before PET scan	0.8 ± 0.3	0.8 ± 0.3	0.9 ± 0.4	0.8 ± 0.2	0.8 ± 0.3	0.7 ± 0.2
After PET scan	0.9 ± 0.3	0.8 ± 0.2	1.3 ± 0.3∗	1.3 ± 0.3∗	0.9 ± 0.3	0.7 ± 0.2
Pyruvate, mmol/liter
Before pyruvate injection			0.10 ± 0.04	0.10 ± 0.03
Before PET scan	0.11 ± 0.05	0.09 ± 0.03	2.55 ± 0.81∗	2.31 ± 0.61∗	0.10 ± 0.03	0.08 ± 0.03
After PET scan	0.10 ± 0.03	0.10 ± 0.04	0.46 ± 0.18∗	0.45 ± 0.20∗	0.11 ± 0.03	0.10 ± 0.03
Lactate/pyruvate ratio
Before pyruvate injection			8.5 ± 2.7	8.3 ± 1.2
Before PET scan	8.3 ± 2.8	7.5 ± 1.7	0.4 ± 0.2∗	0.4 ± 0.2∗	7.6 ± 1.1	9.2 ± 2.5
After PET scan	8.4 ± 1.2	8.8 ± 2.5	3.3 ± 1.7∗	3.2 ± 1.4∗	9.0 ± 1.7	8.0 ± 3.1

Values are means ± SD; n = 6. ∗, Significant change compared with rest baseline before PET scan (two-tailed paired t test; P < 0.05)

Table 2.

Demographic and blood gas data

Subject	Gender	Age, years	pH	PaCO2, mmHg	PaO2, mmHg	Hct	Hb, g/liter	SaO2	CaO2, ml of O2 per liter
1	F	27	7.41 ± 0.07	34 ± 2	96 ± 4	0.37 ± 0.01	120 ± 5	0.98 ± 0.00	163 ± 7
2	F	21	7.40 ± 0.04	37 ± 1	96 ± 3	0.34 ± 0.04	92 ± 2	0.97 ± 0.00	124 ± 2
3	F	24	7.39 ± 0.03	34 ± 2	100 ± 1	0.41 ± 0.01	131 ± 7	0.97 ± 0.00	177 ± 9
4	M	29	7.36 ± 0.01	38 ± 1	101 ± 1	0.36 ± 0.00	110 ± 5	0.98 ± 0.01	152 ± 3
5	M	32	7.35 ± 0.05	40 ± 3	86 ± 6	0.42 ± 0.01	132 ± 3	0.97 ± 0.01	178 ± 2
6	F	25	7.41 ± 0.03	34 ± 1	102 ± 1	0.33 ± 0.01	112 ± 1	0.99 ± 0.02	160 ± 13

Values are means ± SD. SaO₂, arterial oxygen saturation; CaO₂; arterial oxygen content; F, female; M, male.

In the presence of a bolus injection of saline, visual stimulation resulted in a 23.1 ± 4.5% increase in regional CBF (Δ%CBF_S) in the visual cortex. In the presence of a bolus injection of pyruvate, the same visual stimulation resulted in an 18.6 ± 3.4% increase in CBF (Δ%CBF_P). The percent decrease in Δ%CBF, i.e., the percent pyruvate-evoked attenuation of CBF response, was calculated as 100 × (Δ%CBF_P − Δ%CBF_S)/Δ%CBF_S; thus, the bolus injection of pyruvate attenuated the CBF response to the visual stimulation by 19.2 ± 4.5%. This decrement in blood flow response to visual stimulation after an injection of pyruvate was statistically significant (t = 6.78, P = 0.0011; two-tailed paired t test). In the second saline pair of studies, CBF response to visual activation was not significantly different from that in the first saline pair of studies (20.3 ± 1.1%; t = 1.38, P = 0.2275; two-tailed paired t test).

In the resting state, mean visual cortex CBF for the pyruvate scan was 6.1 ± 3.6% higher than that for the first saline scan (t = 4.01, P = 0.0103; two-tailed paired t test) and 2.1 ± 2.4% higher than that for the second saline scan (t = 2.30, P = 0.0696; two-tailed paired t test). However, global CBF values were stable throughout the study (Table 1), including the resting global blood flow in response to pyruvate injection (t = 0.68, P = 0.53; two-tailed paired t test). The unexpected finding of a significant increase in the local resting blood flow in visual cortex after the first pyruvate injection, which has not been observed in previous animal experiments (5, 6), raised for us the possibility that this change in the baseline level of activity contributed to the attenuated blood flow response to visual stimulation after the second pyruvate injection. To evaluate this possibility we examined the relationship between the increases in visual cortex blood flow and resting blood flow across all conditions, and we observed no relationship (r = 0.232, P = 0.354, Pearson correlation). Thus, an elevated baseline level of activity in the visual cortex was not related to a diminished response to stimulation.

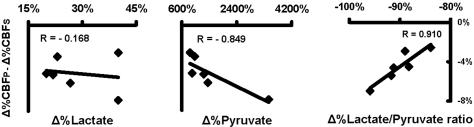
The magnitude of the individual pyruvate-attenuated CBF increases (Δ%CBF_P − Δ%CBF_S) was correlated with the individual changes in plasma lactate/pyruvate ratio (r = 0.910, P = 0.0081, Pearson correlation; Fig. 2). It was also correlated, to a somewhat weaker extent, with changes in plasma pyruvate levels (r = −0.849, P = 0.030, Pearson correlation), but there was no significant correlation with plasma lactate (r = −0.168, P = 0.769, Pearson correlation; Fig. 2).

Fig. 2.

Correlation between pyruvate-attenuated CBF increases and percent changes in plasma lactate, pyruvate, and lactate/pyruvate ratio obtained from averaging the measured values just before and immediately after the PET scan.

Discussion

The opposing effects on CBF from lactate and pyruvate injections and the dependence of the CBF change on the lactate/pyruvate ratio strongly support the hypothesis that changes in the cytosolic free NADH/NAD⁺ ratio, which is in near-equilibrium with the lactate/pyruvate ratio, modulate blood flow responses during physiological stimulation of the human brain.

The amino acid glutamate is the primary excitatory neurotransmitter in the brain. The synaptic action of glutamate is terminated with its uptake into astrocytes, where it is converted to glutamine (8, 9) (Fig. 3). Glutamate uptake into astrocytes is Na⁺-dependent and involves activation of astrocyte Na⁺/K⁺-ATPase, which, in turn, stimulates glycolysis (10, 11). It was proposed that the processes of glutamate uptake plus conversion to glutamine by astrocytes consumes two ATP (11). The advantage of glycolysis over oxidative phosphorylation in this situation may be its more rapid delivery of ATP in a setting where intermittent changes in neuronal activity are occurring in tens of milliseconds.

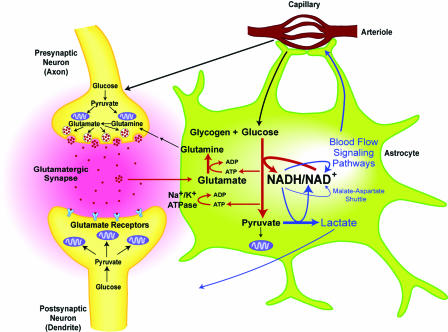
Fig. 3.

Proposed model of regulation of blood flow in physiologicallystimulated human brain. Neuronal firing is associated with intermittent release of glutamate into the synaptic cleft to activate postsynaptic glutamate receptors. There is subsequent rapid glutamate uptake by astrocytes, conversion of glutamate to glutamine, and release of glutamine out of astrocytes. Glutamine is taken up by neurons for conversion back to glutamate. Glutamate uptake involves activation of Na⁺/K⁺-ATPase. Glutamate uptake and cycling in astrocytes is ATP-consuming and stimulates glycolysis. Increased glycolysis leads to increased production of NADH and a rise in the cytosolic NADH/NAD⁺ ratio. Regeneration of NAD⁺ is critical for continuation of glycolysis, and several mechanisms are recruited, including (i) malate–aspartate electron shuttle to mitochondria, (ii) conversion of pyruvate to lactate, and (iii) signaling pathways that promote an increase in brain blood flow. However, astrocytes have fewer mitochondria and lack important components of the malate–aspartate shuttle compared with neurons. Lactate produced from pyruvate will egress from astrocytes and may be taken up by neurons or removed by the increased blood flow. The impact of activated neurons in the regulation of blood flow is likely to be less than that of astrocytes, because neurons may increase ATP production without a large rise in the NADH/NAD⁺ ratio because of simultaneous increase in both glycolysis and oxidative phosphorylation, and they have more effective pathways of NAD⁺ regeneration.

Increased glycolysis, leading to an elevated NADH/NAD⁺ ratio, recruits mechanisms for the regeneration of NAD⁺. These include the transfer of electrons and protons from NADH to mitochondria by means of the malate–aspartate shuttle and the reduction of pyruvate to lactate (Fig. 3). However, astrocytes, in contrast to neurons, are known to lack important components of the malate–aspartate shuttle (12). Under these circumstances lactate may be produced and egress from astrocytes faster than it is used by neurons, raising tissue lactate levels (13, 14). The increased tissue lactate will slow cytosolic pyruvate to lactate conversion, causing a further rise in the NADH/NAD⁺ ratio. It seems eminently reasonable that these events might be linked to signaling pathways that promote an increase in blood flow designed to remove the excess of lactate.

It is very hard to verify lactate removal from the activated brain tissue, because in vitro or with magnetic resonance spectroscopy only local content can be evaluated, and it is not possible to differentiate what is removed from what is locally used. Evaluation of arteriovenous difference is probably the only reliable way of quantitative assessment of lactate removal, but it may be not sensitive enough to catch small changes in plasma lactate levels evoked by local brain stimulation. Nevertheless, Madsen et al. (15) reported that mental activation in humans induced a 31% increase in cerebral arteriovenous difference for lactate (from −0.04 mmol/liter to −0.06 mmol/liter, respectively) because of higher increase in venous lactate (from 0.5 mmol/liter to 0.53 mmol/liter) than in arterial lactate (from 0.46 mmol/liter to 0.47 mmol/liter) in response to brain activation. The removal of lactate remained increased during the first 20 min after cessation of mental activation. It is of note that even during resting state arteriovenous difference was negative, which means that some excess of lactate may be created even on the baseline level of brain metabolism. This finding was earlier reported in humans by Gibbs et al. (16) and Raichle et al. (17). Madsen et al. (18) later presented almost opposite results in rats, but in this experiment activation was not only mental but also physical, and it evoked a substantial increase in arterial lactate due to skeletal muscle activity, which may affect the results. Of note, the resting arteriovenous difference for lactate in rats was negative, as in the above-mentioned study in humans (18). Interesting findings were recently obtained in anesthetized monkeys by combining ¹⁸F-FDG PET and ¹³C-NMR (19). The difference between cerebral metabolic rate of glucose and tricarboxylic acid cycle flux was ≈10%, which may be interpreted as the indirect evidence that some amount (up to 10%) of pyruvate is converted to lactate and removed from the brain cells.

Activation likely increases energy production in neurons as well as in astrocytes. However, there are reasons to believe that the increase in ATP production in neurons will rely predominantly on oxidative phosphorylation rather than on glycolysis, as it does in astrocytes. It is known that neurons have more mitochondria than glial cells (20); the distribution of cytochrome oxidase within neurons is heterogeneous, with most of oxidative activity found in dendrites (20), which are the primary consumers of energy; and, in contrast to astrocytes, neurons have high levels of important carriers for the malate–aspartate shuttle (12). Thus, neurons in the activated state should have more proportional changes in glycolysis and oxidative phosphorylation and more effective pathways of NAD⁺ regeneration compared with astrocytes. In other words, neurons may increase ATP production without a large rise in the NADH/NAD⁺ ratio due to simultaneous increase in both glycolysis and oxidative phosphorylation, and, furthermore, this increase in the NADH/NAD⁺ ratio may be diminished without significant involvement of the blood flow signaling pathways. On the other hand, astrocytes can accommodate the rapidly changing requirements for glutamate uptake and cycling with a rapid increase in glycolysis. In this context it is probably no accident that astrocytes are the only repository of glycogen (21), a ready substrate for glycolysis in the mammalian brain.

Many links between changes in brain activity and blood flow regulation have been explored (22); a role for NADH/NAD⁺ was first postulated and studied by Ido and colleagues (5, 6). They suggested that transfer of excess electrons from NADH to O₂ by NADH-oxidase generates superoxide, which elevates Ca²⁺ to activate nitric oxide production by nitric oxide synthase. They demonstrated in rats in vivo that inhibitor of nitric oxide synthase completely prevents increased blood flow in stimulated somatosensory and visual cortex and that the chemical analog of superoxide dismutase blocks increased blood flow in the stimulated somatosensory but not the visual cortex (5, 6). Recently Zonta et al. (23) proposed that it is the activation of metabotropic glutamate receptors by glutamate which trigger increases in Ca²⁺ in astrocytes, and this in turn activates a vasoactive agent, most likely a cyclooxygenase product (23). However, Mulligan and MacVicar (24) reported vasoconstriction but not a vasodilatation in response to an increase in astrocytic Ca²⁺, with subsequent involvement of arachidonic acid pathway. This observation indicates that generation of nitric oxide by neuronal activity might contribute to vasodilatation by preventing the vasoconstriction induced by arachidonic acid released from astrocytes (24, 25). Both reports support our hypothesis that glutamate and activation of astrocytes are centrally involved in blood flow regulation (23, 24). The particular mechanism by which an increase in the ratio of free cytosolic NADH/NAD⁺ augments blood flows evoked by physiological work remains unclear, and further work is needed to verify mechanisms that are specifically triggered by changes in the NADH/NAD⁺ ratio.

A leading role for astrocytes in blood flow regulation mediated through changes in the cytosolic NADH/NAD⁺ ratio is strongly supported by the results of a study reported recently by Kasischke et al. (26). They demonstrated an increase in NADH fluorescence in the cytosol of astrocytes in response to stimulation of Schaffer collateral neurons in rat hippocampal slices (26). They concluded that increased neuronal firing leads to an increase in glycolysis, resulting in the observed increase in the cytosolic NADH/NAD⁺ ratio in astrocytes. However, the increase in NADH fluorescence occurred temporally later (>10 sec) compared with the well known rapid response of the blood flow to brain stimulation (<5 sec). The reason for this delay may be methodological. The fluorescence method measures predominantly (93%) the fraction of NADH that is bound to proteins (27), and in the cytosol these proteins would be mostly enzymes of the reactions that lead to regeneration of NAD⁺ and restoration of the normal NADH/NAD⁺ ratio. Increase in bound fraction reflects increase in free NADH, but increase in bound fraction will lag behind the increase in free NADH, with the caveat that the precise duration of this lag is not known. The authors also observed an initial decrease in NADH fluorescence in the neuronal mitochondria, and mitochondrial enzymes that bind NADH are those that participate in oxidative phosphorylation to provide ATPs. This observation conforms to our suggestion that during physiological stimulation neurons are more involved in oxidative phosphorylation than are astrocytes.

In conclusion, our hypothesis differs from previous concepts of blood flow regulation in that we do not try to tie blood flow changes in the stimulated brain with potential changes in total energetic requirements or requirement for “fuel.” In general, the energy requirements of the activated brain are likely increased to a very small extent compared with that at baseline (28), and the human brain has an oversupply of necessary substrates (e.g., glucose and oxygen) at almost any level of physiological stimulation (1, 3). We believe the data suggest that the blood flow in the activated brain is regulated by the need to support very specific and vital reactions such as glutamate uptake and cycling by astrocytes. Blood flow change in the physiologically stimulated brain is thus related to changes in glycolysis predominantly in astrocytes and is aimed to balance the cytosolic NADH/NAD⁺ ratio.

Subjects and Methods

Subjects.

Six healthy right-handed subjects (four females and two males, ranging in age from 21 to 32 years old; mean age ± SD was 26.3 ± 3.9 years) were recruited from the Washington University community. The Human Studies Committee and the Radioactive Drug Research Committee of our institution approved the protocol of this study. Written informed consent was obtained.

PET Imaging.

Each subject underwent a single PET session consisting of six CBF scans. Studies were done by using a Siemens/CTI ECAT EXACT HR 47 tomograph (Siemens, Iselin, NJ) (29). This scanner collects 47 simultaneous slices with 3.125-mm spacing encompassing an axial field of view of 15 cm. Transaxial and axial spatial resolution are ≈4.3 mm full-width half-maximum (FWHM) at the slice center. Studies were done in the 2D acquisition mode (interslice septa extended). A transmission scan for attenuation correction of all emission data was obtained. Each subject had a radial artery catheter placed under local anesthesia for blood sampling. A 20-gauge i.v. catheter was placed in the antecubital vein and advanced to the axillary vein. This location prevented any local irritation from the pyruvate infusion.

Each measurement of the CBF was initiated by a bolus i.v. injection of 50 mCi (1 Ci = 37 GBq) of [¹⁵O]water and a concomitant 3-min dynamic scan (50 frames: 35 2-sec frames; eight 5-sec frames; and seven 10-sec frames). Arterial blood sampling was done by continuous arterial blood withdrawal over a shielded scintillator to count blood activity. Twelve minutes were allowed between tracer injections for [¹⁵O] decay; however, 20 min was allowed after each study with pyruvate injection. Measurements of arterial values for pH, PaCO₂, PaO₂, Hct, Hb, oxygen saturation (SaO₂), and oxygen content (CaO₂) were performed at regular intervals during the study (see Table 1).

Six PET scans were performed on each subject after injection of saline or pyruvate in the following sequence: (i) saline–rest (CBF₁); (ii) saline–activation (CBF₂); (iii) pyruvate–rest (CBF₃); (iv) pyruvate–activation (CBF₄); (v) saline–rest (CBF₅); (vi) saline–activation (CBF₆). Sixty seconds before scans 1, 2, 5, and 6 the subjects received an injection of 20 ml of saline. Starting 60 sec before scans 3 and 4 the subjects received a rapid i.v. infusion (over 30 sec) of pyruvate (0.2 mmol or 17.4 mg per kg of body weight) diluted in saline to make a total amount of 20 ml. Subjects were blind to the order of saline and pyruvate.

Arterial glucose, lactate, and pyruvate levels were obtained before and after each PET scan and before and after each pyruvate injection.

Visual Stimulation Paradigm.

Three PET scans in each subject were done during rest with eyes closed, and three scans were done while looking at a visual stimulus. The stimulus was presented by using a computer monitor showing a high spatial frequency black–white sinusoidal vertical grating moving horizontally. The grating moved left or right, alternating slowly to prevent afterimages. A small crosshair was provided in the center for fixation. The subjects were instructed to ignore the grating and keep their gaze fixated on the central crosshair. Visual stimulation was started at the end of pyruvate or saline injection.

MRI.

To guide anatomical localization, MRI scans were obtained in all subjects. MRI scans were performed on a Magnetom Vision 1.5T imaging system (Siemens). A magnetization-prepared rapid-gradient echo acquisition was used to acquire anatomic images that consisted of 128 contiguous 1.25-mm-thick sagittal slices. Scanning parameters were as follows: repetition time = 10 msec, echo time = 4 msec, inversion time = 300 msec, flip angle = 8, matrix = 256 × 256 pixels, voxel size = 1 × 1 × 1.25.

PET Image Reconstruction and Registration.

Two types of images were created from the dynamic PET scan. First, all 180 sec of data were summed. The resulting images underwent coregistration for correction of head movement between scans by using in-house software (30). Then, 40-sec summed images were made from the dynamic data starting ≈6 sec after the [¹⁵O]water bolus began entry into the brain, as judged by the rise in counts. This 40-sec image was corrected for head motion by using the spatial transformation matrix calculated from aligning the 180-sec summed images. Quantitative global CBF values were calculated from the 40-sec data (31) after masking the brain data by using a 42% threshold applied to the summed [¹⁵O]water image. The 40-sec image of [¹⁵O]water was also normalized for whole-brain activity and used to calculate qualitative changes in regional CBF and to make subtraction images for volume of interest (VOI) analysis (31).

VOI Analysis.

For each subject, two images of visual cortex activation after saline injection were created from the subtraction images: CBF₂ − CBF₁ and CBF₆ − CBF₅. An image of visual cortex activation after pyruvate injection was created from the subtraction image: CBF₄ − CBF₃. To create VOI for analysis, these three subtraction images (saline and pyruvate) were averaged and smoothed with a 3D Gaussian filter (0.4 cycles per pixel cutoff). The final subtraction image resolution was ≈13 mm full-width half-maximum.

For each subject’s final subtraction scan a VOI was created by selecting thresholds that result in visual cortex VOI of ≈1,000 voxels, which is equal to 12 ml. In all cases VOI was confirmed to be centered over the primary visual cortex by comparing location to coregistered MRI images. This VOI was applied to each of the six normalized 40-sec scans to obtain the qualitative CBF data for each region.

Statistical Analysis.

The means and SD across subjects (n = 6) of the regional CBF and the global CBF for each of the six states (CBF₁, CBF₂, CBF₃, CBF₄, CBF₅, and CBF₆) were calculated and analyzed by using t tests (two-tailed paired, significance set at P < 0.05; for all tests, degree of freedom was 5). An estimate of mean serum lactate, pyruvate, or lactate/pyruvate ratio during the PET scan was calculated by averaging the prescan and postscan measurements for each substrate. The mean values were used in two-tailed Pearson analysis of correlation between the percent changes in plasma lactate, pyruvate, and lactate/pyruvate ratio and the pyruvate-related decrease in percent CBF response to visual stimulation. The percent changes in plasma lactate, pyruvate, and lactate/pyruvate ratio after pyruvate injection were calculated from the average of mean values corresponding to CBF₁ and CBF₂ (L/P_CBF1–2 for lactate/pyruvate ratio) and the average of the mean values corresponding to the CBF₃ and CBF₄ (L/P_CBF3–4 for lactate/pyruvate ratio) as follows (shown for lactate/pyruvate ratio): Δ%lactate/pyruvate = 100 × (L/P_CBF3–4 − L/P_CBF1–2)/L/P_CBF1–2. The percent changes in CBF during activation with saline or pyruvate injection were calculated as Δ%CBF_S = 100 × (CBF₂ − CBF₁)/CBF₁ and Δ%CBF_P = 100 × (CBF₄ − CBF₃)/CBF₃, respectively.

Abbreviations

CBF

cerebral blood flow

PET

positron-emission tomography

VOI

volume of interest.