Directing electron transfer within Photosystem I by breaking H-bonds in the cofactor branches

Abstract

Photosystem I has two branches of cofactors down which light-driven electron transfer (ET) could potentially proceed, each consisting of a pair of chlorophylls (Chls) and a phylloquinone (PhQ). Forward ET from PhQ to the next ET cofactor (F_X) is described by two kinetic components with decay times of ≈20 and ≈200 ns, which have been proposed to represent ET from PhQ_B and PhQ_A, respectively. Immediately preceding each quinone is a Chl (ec3), which receives a H-bond from a nearby tyrosine. To decrease the reduction potential of each of these Chls, and thus modify the relative yield of ET within the targeted branch, this H-bond was removed by conversion of each Tyr to Phe in the green alga Chlamydomonas reinhardtii. Together, transient optical absorption spectroscopy performed in vivo and transient electron paramagnetic resonance data from thylakoid membranes showed that the mutations affect the relative amplitudes, but not the lifetimes, of the two kinetic components representing ET from PhQ to F_X. The mutation near ec3_A increases the fraction of the faster component at the expense of the slower component, with the opposite effect seen in the ec3_B mutant. We interpret this result as a decrease in the relative use of the targeted branch. This finding suggests that in Photosystem I, unlike type II reaction centers, the relative efficiency of the two branches is extremely sensitive to the energetics of the embedded redox cofactors.

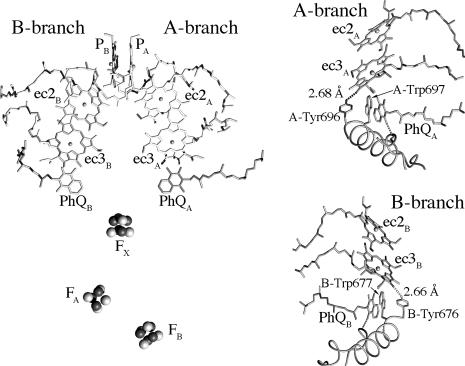
Photosynthetic reaction centers (RCs) are the membrane proteins responsible for the capture and storage of light energy in photosynthetic organisms. As with all of the RCs, Photosystem I (PS1) has a C2 symmetrical structure with two virtually identical branches of redox cofactors extending across the membrane (see Fig. 1). The x-ray crystal structure of PS1 from Thermosynechococcus elongatus (1) has allowed identification of amino acid residues interacting with the electron transfer (ET) cofactors, permitting the use of site-directed mutagenesis to investigate to what extent ET occurs in the two branches. Many of these studies (2–10) point toward the possibility that ET takes place in both branches of cofactors (A-branch and B-branch; see Fig. 1). The data consistently show that the major fraction occurs in the A-branch and that the slow phase of ET from phylloquinone (PhQ) to F_x is associated with this branch. The involvement of the B-branch is less clear, but there is mounting evidence to support the assignment of the fast component of PhQ to F_x ET to this branch. If ET does indeed occur in both branches in PS1, this behavior would be remarkably different from the type II RCs. In purple bacterial RCs, for example, it is well known that initial ET is biased almost exclusively toward the A-branch, probably because the B-branch quinone is a mobile electron and proton carrier in this type of RC. The strong biasing of the ET in the type II RCs makes it difficult to investigate the factors governing the directionality in these systems, because very large perturbations are required to induce a change. In this regard, PS1 may be a better candidate for such studies, but until the recent finding that each PhQ specifically interacts with distinct β-carotenes (11), they have been hampered by the lack of specific spectroscopic markers.

Fig. 1.

Arrangement of ET cofactors in PS1. (Left) Overall arrangement of the cofactors showing the two branches. (Right) Close-up view of the ec3 Chl regions in the A-branch (Upper) and B-branch (Lower), showing the H-bonds donated by the targeted Tyr residues.

Most of the initial point mutation studies of ET in PS1 involved the quinone-binding sites. Attention has now turned to the cofactors immediately upstream of the PhQs, the ec3 chlorophylls (Chls) (Fig. 1). Site-directed mutations of the Met serving as axial ligand to each ec3 Chl have been described in Chlamydomonas (6–8) and Synechocystis (9, 10). Ultrafast pump-probe data from the C. reinhardtii mutants indicate a slowing or blockage of ET from the affected ec3 Chl in mutants of both PsaA–Met-688^§§ and PsaB–Met-668 (8); along with pulsed EPR data from the same mutants (7, 12), these data implied the use of both branches. In contrast, experiments with the Synechocystis mutants implied that ET is strongly biased toward the A-branch. Mutation of the axial ligand to ec3_A altered the spin polarization patterns of the P₇₀₀⁺ PhQ⁻ and P₇₀₀⁺ F_X⁻ radical pairs, as seen by transient EPR (9), indicating an increase in the lifetime of the P₇₀₀⁺ ec3_A⁻ radical pair and a significant population of ³P₇₀₀ formed by radical pair recombination. Mutation of PsaB–Met-668 had no discernible effect on the transient EPR signals. Ultrafast pump-probe data (10) confirmed that forward ET from a Chl intermediate was slowed when PsaA–Met-688, but not when PsaB–Met-668, was altered.

Although altering the axial ligand of the ec3 Chls has strong effects on ET in PS1, the consequences of a change in the ET properties of a given branch on the probability for ET to occur down the other branch has never been characterized to date. This issue, which underlies the more general concern of the partitioning of ET between the two branches, is addressed here. We describe mutants of tyrosine residues, PsaA–Tyr-696 and PsaB–Tyr-676, that donate a H-bond to the 13¹-keto oxygen of the ec3_A and ec3_B Chls, respectively (see Fig. 1). The importance of H-bonds to cofactors in the bacterial RC has been well studied (13). As shown previously in the case of Photosystem II (14), the loss of such a H-bond should shift the Chl’s reduction potential to more negative values, thus altering the rate, and possibly the yield, of ET to the targeted ec3 Chl.

Results

Rationale and Construction of Mutants and Their Initial Characterization.

To predict the effect of the mutations, we constructed models of the ec3_A⁻ radical anion with either PsaA–Tyr-696 or PsaA–Phe-696 (see Methods) and performed density functional theory calculations of the highest occupied molecular orbital energy in ec3_A^•−, in accordance with Koopmans’ theorem (15–17). These calculations predicted an ≈150 mV decrease in the reduction potential of ec3_A.

Plasmids with the PsaA–Y696F and PsaB–Y676F mutations were introduced into C. reinhardtii strains lacking the psaA or psaB genes, respectively. In the WT background, both mutants behaved essentially the same as a strain made by introducing the WT gene (data not shown), and immunoblots with antibodies against PsaA and PsaD indicated that the mutants possessed levels of PS1 polypeptides similar to the WT strain (data not shown). All subsequent work described here made use of strains lacking Photosystem II and most of the LHC complement.

Time-Resolved Absorption Changes in Vivo.

The absorption changes associated with reoxidation of PhQ are described by two exponential decay components (18, 19). The fact that point mutations near PhQ_A or PhQ_B resulted in changes in the rates of either the slower (τ ≈ 200 ns) or faster (τ ≈ 20 ns) components, respectively (3, 5), are most easily interpreted in terms of a bidirectional model, in which ET occurs with a given probability in either the A- or B-branch, resulting in reduction of PhQ_A or PhQ_B, respectively. This model predicts that the amplitudes of the two components are determined by the relative use of each branch, and the observation that mutations in neither PhQ-binding site observably changed these amplitudes argues in favor of this interpretation. Conversely, mutations expected to cause changes in the relative use of the two ET pathways should result in changes in the amplitudes of the two decay components without changes in their rates or associated spectra.

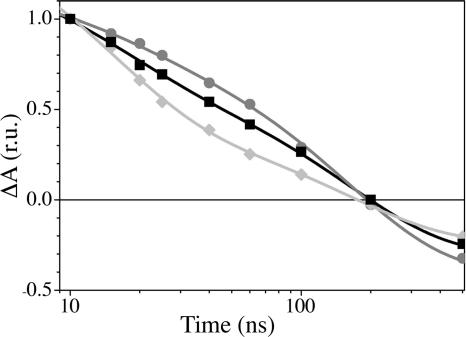
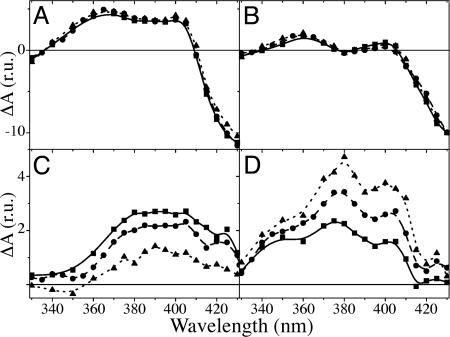
Fig. 2 shows the decay of flash-induced absorbance changes at 380 nm in whole cells of the WT, PsaA–Y696F, and PsaB–Y676F strains. In the mutant affecting ec3_A, the overall decay is faster than in the WT strain, whereas it is slower in the mutant affecting ec3_B. The initial slopes of the decay in the WT strain are steeper than in the PsaB–Y676F mutant and less steep than in the PsaA–Y696F mutant, suggesting that the rate or amplitude of the fast phase differs in the three strains. To address this issue, we measured the kinetics of absorption changes in a broader spectral range (330–430 nm) and independently fitted each data set globally with three exponentials. The calculated decay rates were similar in all three strains (Table 1). The decay-associated spectrum (DAS) of the ≈20-ns phase (Fig. 3C) is larger in amplitude in the PsaA–Y696F mutant than in WT, whereas that of the slower phase is smaller. Conversely, in the PsaB–Y676F mutant, the spectrum of the faster phase (Fig. 3D) is smaller than in WT, and that of the slower phase is larger (Fig. 3C). The general shapes of the spectra associated with these components are conserved, indicating that the YF mutations do not induce any significant additional contributions to the DAS. The initial amplitude of the signal (extrapolation to t = 0 of the absorption changes; Fig. 3A) should be proportional to the amount of charge-separated state ( P₇₀₀⁺PhQ⁻) in the nanosecond time range. The DAS of the ≈6-μs component (Fig. 3B) displays a prominent bleaching peaking at ≈430-nm region and is ascribed to the reduction of P₇₀₀⁺ by plastocyanin. It is thus proportional to the fraction of centers in which P₇₀₀⁺ is still present in the microsecond time range. These two spectra are very similar in all three strains, in shape as well as amplitude.

Fig. 2.

Decay of flash-induced absorption change at 380 nm (PhQ⁻), shown as a semilog plot. The solid lines are a fit of a biexponential decay function to the experimental data. WT, squares and black line; PsaA–Y696F, diamonds and light gray line; PsaB–Y676F, circles and dark gray line. r.u., relative units.

Table 1.

Global fitting parameters for decay components

Strain	Exponential decay times (τ) of the three kinetic components†	Fast decay, % (ratio of fast∕slow)
		Optical‡	EPR§
PsaA–Y696F	22 ± 3 ns	230 ± 23 ns	5.3 ± 0.3 μs	64 (1.78)	70 (2.33)
WT	25 ± 2 ns	250 ± 15 ns	5.8 ± 0.2 μs	40 (0.67)	40 (0.67)
PsaB–Y676F	20 ± 3 ns	220 ± 25 ns	6.2 ± 0.4 μs	17 (0.20)	25 (0.33)

^†Obtained from the global fitting analysis of the optical data.

^‡The ratio of the total submicrosecond decay at 380 nm attributed to the faster (≈20 ns) component, using the decay rates obtained by global analysis.

^§The fraction (X) of ET from PhQ to FeS occurring with rate k₁′ (see text for details).

Fig. 3.

Spectra of the various components obtained by global fit analysis with three exponential decays, plus an offset. Shown are an extrapolation to t = 0 of the flash-induced absorption change (A) and the DAS of the ≈6-μs (B; P₇₀₀⁺), ≈20-ns (C; PhQ_B⁻), and ≈200-ns (D; PhQ_A⁻) components. The spectra were normalized to the amplitude of the ≈6-μs component ( P₇₀₀⁺) at 430 nm. WT, circles and dashed line; PsaA–Y696F, squares and solid line; PsaB–Y676F, triangles and dotted line. r.u., relative units.

Transient EPR Spectroscopy.

Recently, it was shown that the fraction of fast ET can be estimated by simulation of the transient EPR data sets from PS1, although the kinetics of the fast phase are not resolved (20). We performed transient EPR experiments on the mutants to confirm the changes in the relative amplitudes of the fast and slow components. Thylakoid membranes were used to avoid the detergent-induced effects seen in spinach (18) and in cyanobacterial subunit-deletion mutants (20).

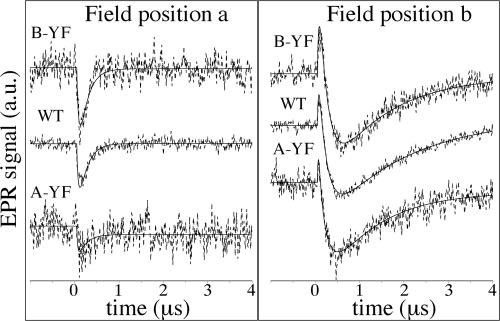
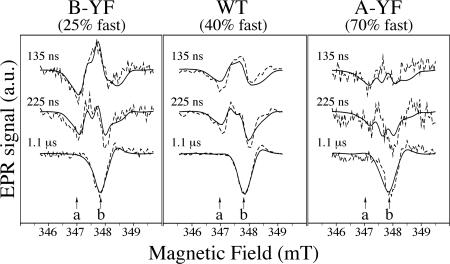
Fig. 4 shows spin-polarized EPR transients taken at two magnetic field positions (a and b in Fig. 5), and transient spin-polarized EPR spectra at two different time ranges are shown in Fig. 5. At position a (Fig. 4 Left), only the PhQ⁻ part of the P₇₀₀⁺PhQ⁻ radical pair is observed as an emissive (negative) signal. At position b (Fig. 4 Right), P₇₀₀⁺PhQ⁻ produces an absorptive (positive) signal at early times, whereas P₇₀₀⁺(FeS)⁻ appears as a negative signal and dominates at late times. The transients in both parts of Fig. 4 have been normalized so that the three samples have the same amplitude for the emissive contribution from P₇₀₀⁺(FeS)⁻ at field position b at late time. With this normalization, the magnitude of the contributions from P₇₀₀⁺PhQ⁻ reflect the fraction of slow ET. As readily seen in the traces at position b, where the signals from P₇₀₀⁺PhQ⁻ and P₇₀₀⁺(FeS)⁻ have opposite signs, the absorptive feature at early times due to P₇₀₀⁺PhQ⁻ is strongest in the B-branch mutant and weakest in the A-branch mutant (Fig. 4 Right). The emissive signal at position a (Fig. 4 Left) exhibits similar behavior.

Fig. 4.

Spin-polarized EPR transients of thylakoid membranes from WT, PsaA–Y696F, and PsaB–Y676F. (See Fig. 5 for magnetic field positions.) Dashed curves are experimental transients, and solid lines are fits (see text). a.u., arbitrary units.

Fig. 5.

Spin-polarized transient EPR spectra of the P₇₀₀⁺PhQ⁻ and P₇₀₀⁺FeS⁻ radical pairs in PsaA–Y696F, PsaB–Y676F, and WT. The dashed and solid lines are experimental and calculated spectra, respectively, obtained by averaging the signal intensity over a 100-ns time window centered at the given times. Arrows labeled a and b indicate the positions at which the transients in Fig. 4 were taken. a.u., arbitrary units.

The effect of the two components is also apparent in the spectra shown in Fig. 5. In the PsaB–Y676F mutant, the early spectrum is mostly the emission∕absorption∕emission pattern due to P₇₀₀⁺PhQ⁻ from the large fraction of slow ET. An important feature of the P₇₀₀⁺PhQ⁻ spectrum is that the total amplitude of the emissive (negative) and absorptive (positive) parts of the spectrum should be of equal strength (i.e., no net polarization). In the PsaA–Y696F mutant, the early spectrum shows only emission, suggesting that the absorptive features of the P₇₀₀⁺PhQ⁻ spectrum are cancelled out by the emission due to P₇₀₀⁺(FeS)⁻ generated by the large fraction of fast component.

The solid traces in Figs. 4 and 5 are fits to the data using the following functions:

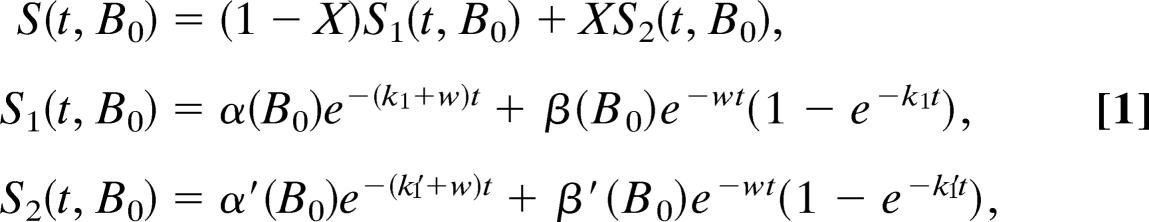where k₁ and k₁′ are the rates of ET from PhQ⁻ to F_X, and X is the fraction of PS1 in which forward ET is fast (k₁′). The rate of spin relaxation (w) is assumed to be the same for all radical pairs. Because k₁′ is faster than the inverse of the EPR response time, S₂(t, B₀) cannot be determined from the kinetic traces alone. We took two approaches to this problem. First, to evaluate the lifetime of the slow component, we fixed the values of X and k₁′ using the optical data and fitted the transients in Fig. 4. For these fits, the EPR signal strengths of the corresponding radical pairs associated with each of the two phases are assumed to be the same, i.e., α(B₀) = α′(B₀) and β(B₀) = β′(B₀). All of the transients shown in Fig. 4 give τ = 245 ± 50 ns for the slow component, confirming that the YF mutations do not alter the kinetics of this phase. In addition, we performed global fits of all time∕field data sets, in which the amplitudes were calculated by using known values of the spectral parameters (see Fig. 5), as described in detail in ref. 20. Because the amplitudes and shapes of the observed polarization patterns at early and late times depend on the fraction of fast ET, the value of X can be determined from these fits. In agreement with the optical data, X is largest in the PsaA–Y696F mutant and smallest in the PsaB–Y676F mutant (Table 1). Together, the transient EPR results confirm the findings from the optical experiments that the two YF mutations affect the relative amounts of the fast and slow ET components but do not have any influence on their rates.

Ultrafast Optical Spectroscopy.

ET from the PhQ(s) to the FeS clusters does not involve cofactors interacting directly with residues PsaA–Tyr-696 or PsaB–Tyr-676, so the effect of the YF mutations can only be inferred from the observed changes in the amplitudes of the two kinetic components. We therefore used ultrafast pump-probe spectroscopy to examine more directly the influence of these mutations on excitation, energy transfer, and the primary ET steps.

Spectra taken 320 fs after excitation at 20 K were used to assess the effects of the mutations upon RC excitation. The main features of this spectrum are a broad negative band between ≈670–700 nm due to photobleaching of Chl absorbance and weaker positive bands at shorter wavelengths ascribed to Chl excited state absorption; both of these features are composed of several bands, due to the excitonic coupling of the Chls (6). Consistent with the expected contribution of both ec3 Chls to the excitonic spectrum, both YF mutations provoked changes in it (see Fig. 7, which is published as supporting information on the PNAS web site). Experiments at room temperature using longer delays permitted observation of primary charge separation and secondary ET. Both YF mutants exhibited trapping times (≈25 ps) and DAS (data not shown) indistinguishable from those of the WT (8), indicating that the rates of energy transfer and initial charge separation are not strongly affected. Thus, neither mutation produced detectable long-range perturbations of core antenna Chls, nor did they inhibit primary charge separation within the RC.

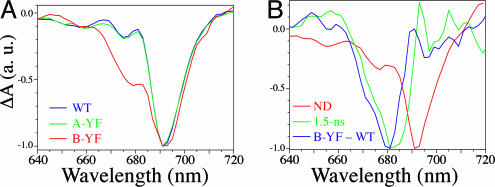
The spectrum taken 200–300 ps after excitation should reflect only the P₇₀₀⁺PhQ⁻ state, because trapping and ET from ec3 to PhQ occurs in less than ≈50 ps (21–23). Because PhQ⁻ has essentially no absorption in the red region, this spectrum should be dominated by contributions from Chls. In both WT and PsaA–Y696F PS1, the main feature is the P₇₀₀⁺ bleaching band (Fig. 6A); there is no significant accumulation of a negative band at ≈680 nm, attributed to the A₀⁻ intermediate Chl (8, 22). However, there are indications of such a band in the PsaB–Y676F mutant. The main feature of the double difference spectrum (PsaB–Y676F − WT) is a negative band peaking at ≈680 nm with a possible shoulder at ≈670 nm. When a longer time scale (4 ns) was used, a new decay component was found with a lifetime of 1.5 ± 0.15 ns and a DAS very similar to the double difference spectrum (Fig. 6B). The assignment of this band is discussed below.

Fig. 6.

Ultrafast pump–probe spectra of PS1 particles from WT, PsaA–Y696F, and PsaB–Y676F. (A) Difference spectra from WT (blue), PsaA–Y696F (green), and PsaB–Y676F (red) PS1 measured at room temperature 200–300 ps after a ≈150-fs excitation pulse at 695 nm under conditions in which P₇₀₀ was reduced (i.e., “open state”). (B) DAS of 1.5-ns component (green) and nondecaying spectrum (red) from experiments on a 4-ns scale, compared with the difference between the spectra shown in A for PsaB–Y676F and WT (blue). a.u., arbitrary units.

Discussion

Efficiency of ET Past the Targeted ec3 Chl.

Before attempting to explain the mutation-induced changes in the amplitudes of the two kinetic components ascribed to PhQ⁻ reoxidation, we must address the issue of the PhQ reduction yield. A decreased PhQ reduction yield in the mutants could result either from a decreased trapping efficiency (i.e., less charge separation) or from a charge recombination process blocking ET to PhQ. A decreased quantum yield of charge separation should be accompanied by an additional kinetic component representing loss of energy by means of excited state decay. Charge recombination occurring before PhQ reduction also would be accompanied by a new kinetic component. In the entire time window studied here (10⁻¹³ to 10⁻⁵ s), we only found one additional kinetic component: a ≈1.5 ns lifetime in the PsaB–Y696F mutant. This lifetime is much shorter than the P₇₀₀⁺ A₀⁻ recombination rate of ≈30 ns seen when ET past ec3 is blocked in WT PS1 (21), but it might represent back reaction from P₇₀₀⁺ ec3_B⁻ if the PsaB–Y676F mutation influenced this rate. In this case, the effective yield of PhQ_B reduction would be lower in this mutant, and the relative amplitude of the fast phase assigned to PhQ_B⁻ reoxidation would be decreased. However, if one compares Fig. 3 A and B, it is clear that all of the initial bleaching at 430 nm ( P₇₀₀⁺) decayed with τ ≈ 6 μs for both YF mutants; there is no evidence for an additional P₇₀₀⁺ decay component. Second, back-reaction from the A₀ cofactor (ec3) is known to produce the ³P₇₀₀ triplet state efficiently, which can be seen by transient EPR and absorbance difference spectroscopy, as demonstrated for mutations of the ec3_A axial ligand (9). Neither YF mutant produced any discernible ³P₇₀₀ signal by either technique (data not shown). Thus, we conclude that the YF mutations do not cause any significant back reaction from P₇₀₀⁺ec3⁻. Consequently, the yield of PhQ reduction per P₇₀₀⁺ is similar in all three strains. This finding is important, because the amplitudes of the two phases of PhQ⁻ reoxidation would not otherwise be reliable indicators of the relative use of the two branches.

Because the ≈1.5-ns component observed in the PsaB–Y676F mutant does not appear to represent back reaction from P₇₀₀⁺ec3⁻, we consider here the possibility that it represents forward ET from P₇₀₀⁺ ec3_B⁻ to P₇₀₀⁺ PhQ_B⁻, which would correspond to an ≈50- to 100-fold increase in lifetime. This scenario can be excluded, because such a long lifetime for the primary radical pair should have a dramatic influence on the spin-polarized EPR spectra of subsequent radical pairs [ P₇₀₀⁺PhQ⁻ and P₇₀₀⁺(FeS)⁻, in this case] (24–26). These effects are well documented experimentally for the chlorobial RC (27) and the PS1 ec3 axial ligand mutants (ref. 9 and reviewed in ref. 28). The spectra in Fig. 5 show no evidence for such effects. Thus, the long-lived Chl bleaching band may not be associated with forward or reverse ET from P₇₀₀⁺ec3⁻ and instead may be due to a long-lived Chl excited state that could be ascribed to uncoupled Chls. Note that, even if formation of this state reduces the quantum yield of charge separation in the PsaB–Y676F mutant, it should not affect the discussion of directionality below, where we deal with the partitioning of ET between the two branches after charge separation has occurred.

Interpretations of the Effects of the Mutations.

The fact that the two YF mutations produce complementary effects, consistent with the assignment of the two kinetic phases to the two branches, clearly indicates bidirectional ET. However, the results can be interpreted in terms of several models, depending on how the biphasic PhQ reoxidation kinetics are explained. Several such models have been proposed to rationalize the biphasic kinetics (see ref. 29 for a review), but they can be divided into two main types: bidirectional models that assign the two phases to ET in the two branches and unidirectional equilibrium models that propose that they are the result of alternate states.

Bidirectional models.

In bidirectional models, the slow and fast kinetic phases are assigned to reoxidation of PhQ_A and PhQ_B, respectively. If this assignment is correct, then each of the two YF mutations leads to a lower relative yield of ET in the branch carrying the mutation. However, the underlying explanation for the changes in directionality depends on how the choice between the two possible pathways takes place. Here we consider two possibilities, referred to as the “branch competition model” and the “donor-side equilibrium model.” In the former, the two branches compete for electrons from the primary donor, and their relative use is determined by the relevant energetic and coupling parameters governing generation of the two possible primary radical pairs. In the latter, the branching ratio is determined by the relative populations of two different conformational states.

The branch competition model explains the changes in the amplitudes of the two kinetic phases as resulting from the predicted mutation-induced shift of the targeted ec3 Chl’s reduction potential. In this interpretation, each YF mutation would render the associated ec3 Chl a poorer electron acceptor, thus destabilizing that specific P₇₀₀⁺ec3⁻ state and decreasing the use of that branch. Thus, the PsaA–Y696F mutation breaks the H-bond to ec3_A, destabilizing the P₇₀₀⁺ ec3_A⁻ state and resulting in less ET down the A-branch, which would be manifested as a decrease in the amplitude of the slower component. Because the two branches are in competition, the decrease of ET in the A-branch would be accompanied by an increase in ET down the B-branch and thus an increase in the faster component. By similar logic, the PsaB–Y676F mutation would decrease the relative amplitude of the faster component.

In the donor-side equilibrium model, the mutations would act by altering the equilibrium between two putative conformational states of PS1. In one state, ET would be predominantly, or exclusively, through the A-side, whereas ET would use the B-side in the other conformation. The PsaA–Y696F or PsaB–Y676F mutations thus would destabilize the former or latter, respectively. However, the lack of any information regarding the existence and the nature of these putative conformational states makes it impossible to predict the direction of any mutation-induced shift in equilibrium.

Unidirectional equilibrium models.

It has been suggested that the biphasic kinetics may arise as the result of an equilibrium between P₇₀₀⁺PhQ⁻ and P₇₀₀⁺ F_X⁻ (30–32), because the difference in reduction potential between either PhQ and F_X is small and the forward and backward ET rates are thus likely to be similar. In addition, the fact that biochemical treatment and∕or loss of stromal subunits can induce changes in the ratio of the two phases (18, 20) suggests another model in which a structural and∕or chemical equilibrium in the vicinity of the PhQ(s) or F_X can influence the biphasic kinetics. Here, we will discuss these models together without specifying the nature of the equilibrium. In this context, the fact that the two YF mutations shift the ratio of the two phases by roughly the same amount but in opposite directions, suggests that the shift in the equilibrium would be caused by a structural change roughly equidistant from PsaA–Tyr-696 and PsaB–Tyr-676. Although such long-range effects are not unknown, the constraints placed on them in the context of this model are formidable. The two mutations would have to shift the equilibrium without noticeably changing either PhQ reoxidation rate. Conversely, mutations of the Trps adjacent to the PhQs, PsaA–Trp-697 and PsaB–Trp-677, would have to affect the rate constants in such a way that only one of the observed rates is altered without changing the relative amplitudes of the two phases (3, 5).

Primary Effects of the YF Mutations and the Charge-Separation Mechanism.

For the reasons summarized above, we favor the branch competition model, because it explains our data in the most straightforward manner. However, if this model holds true, then we must explain how the YF mutations affect the branching ratio. It seems clear that breaking the H-bond to an ec3 Chl would raise the energy of any radical pair involving that cofactor, but for such a change to affect the directionality of ET within PS1, a radical pair involving ec3 must be part of the initial charge-separation mechanism. The most common model for initial charge separation in PS1 is based largely on results from the purple bacterial RC (33) and proposes that charge separation initially generates P₇₀₀⁺ec2⁻, followed by forward ET to generate P₇₀₀⁺ec3⁻ (where ec2 and ec3 are the second and third Chl of the ET branch, respectively). However, unless there were a rapid equilibrium between the P₇₀₀*, P₇₀₀⁺ ec2_A⁻, and P₇₀₀⁺ec2_B⁻ states before secondary ET, which seems unlikely, it is not clear how changes in the energy of a P₇₀₀⁺ec3⁻ state could influence the competition between the branches.

However, one significant difference between PS1 and the type II RCs is that the ec2 and ec3 Chls form a much more strongly coupled pair with partial overlap of their nearly parallel macrocycle rings (see Fig. 1). In contrast, the corresponding cofactors of the purple bacterial RC (B and H) are arranged with their rings at an angle of almost 45° (34). Recent calculations of ET integrals have indicated that the ec2–ec3 pairs are about as well coupled as P_A–P_B in P₇₀₀ (35) (where P_A is Chl a′ on the A-side of P₇₀₀ and P_B is Chl a on the B-side of P₇₀₀), and high-field EPR spectra of the photoaccumulated A₀⁻ anion radical in WT and PsaA–Y696F PS1 are compatible with a model in which the unpaired electron is partially shared between ec2_A and ec3_A (A.P., R. Luthra, J. van Tol, Y.L., L.-C. Brunel, and K.R., unpublished data). Thus, charge separation might initially generate P₇₀₀⁺(e2∕ec3)⁻, with unpaired spin partially shared between the Chls. This hypothesis could explain how loss of a H-bond to a specific ec3 Chl could result in redirection of ET to the other branch.

A second model has recently been suggested (23), in which the primary radical pair is instead ec2⁺ec3⁻, followed by rapid ET from P₇₀₀ to generate P₇₀₀⁺ec3⁻. In effect, there would be two traps (ec2_A∕ec3_A and ec2_B∕ec3_B) competing to form a charge-separated state. This model also would explain the effect of the loss of a H-bond to ec3, because raising the energy of a specific ec2⁺ec3⁻ state would lower the rate of its formation. To account for the compensatory increase in the formation of the primary radical pair in the unaffected branch, excitonic coupling among the RC Chls should be strong enough to allow the two traps, (ec2_A∕ec3_A) and (ec2_B∕ec3_B), to compete for charge separation. This model might also explain why breaking the H-bond to P_A did not affect directionality (36), if P₇₀₀ is not the primary donor.

Concluding Remarks

The results presented here provide further evidence for ET in both branches of PS1, including transient EPR data in which the influence of the fast phase can be seen and correlated with mutations in the two branches, in excellent agreement with the results from the optical studies. Although all of the models discussed above can be used to rationalize the observed effects of the YF mutations, the branch competition model explains their behavior in the most straightforward manner. It is important to note that this model, in concert with well understood principles of how a H-bond would be expected to stabilize a Chl anion radical, was able to make strong predictions about the effect of the YF mutations, which were subsequently realized. In contrast, the models involving the shift of an equilibrium between hypothetical conformational states can only explain these results after the fact, by positing further assumptions. For these reasons, we take the data presented here as making a strong argument in favor of the branch competition model. Lastly, these results not only implicate the ec3 Chls in the initial charge separation event, but they also indicate that directionality within PS1 is quite sensitive to the energetics of the embedded cofactors.

Methods

Estimation of the Mutation’s Effect on the Reduction Potential of ec3.

Theoretical models of the ec3_A⁻ radical anion Chl with either PsaA–Tyr-696 or Phe-696 were constructed, based on the coordinates in Protein Data Bank ID code 1JB0 (1). Hydrogens were added by using modeling facilities of hyperchem 7 (Hypercube, Inc., Gainesville, FL). The phytol ester of ec3_A was replaced with a methanol ester, and the N- and C-terminal peptide bonds of the Tyr residue were converted to an amine and aldehyde, respectively. The −OH group of the Tyr side chain was replaced with −H to make the model complex with Phe. Density functional theory calculations of the vacuum energies of model complexes and individual molecules, using the B3LYP hybrid functional in combination with the 6–31G(d) Gaussian basis set, were performed by using gaussian 98 (Gaussian Inc., Pittsburgh) installed on a Cray SV1.

Construction of Mutants.

Mutations were created by PCR and introduced into C. reinhardtii strains with a normal genetic background or harboring the FUD7 (psbAΔ) and P71 mutations (36), to simplify biochemical purification and spectroscopic analysis.

Time-Resolved Optical Spectroscopy in Vivo.

Spectroscopic measurements in whole cells were performed by using a home-built spectrophotometer exactly as described in ref. 36.

Preparation of Thylakoid Membranes and PS1 Particles.

Cells were grown in Tris-acetate-phosphate (TAP) medium (37) at 25°C. Thylakoid membranes were purified by using sucrose gradients (38), and PS1 particles were prepared by anion exchange chromatography (8).

Transient EPR Spectroscopy.

Transient EPR time∕field data sets were recorded at ambient temperature by using a modified EPR 200D-SRC X-band spectrometer (Bruker Canada, Milton, ON, Canada) as described in refs. 4 and 39.

Ultrafast Optical Spectroscopy.

Ultrafast pump-probe spectroscopy was performed with PS1 particles as described in refs. 8 and 40. Transient spectra in the 630- to 750-nm region were collected on two time scales: from −10 to 400 ps (with 5- and 100-ps step sizes before and after 15 ps, respectively) and from −400 to 4,000 ps (with 80-ps step size). The excitation intensities were kept at <1 photon per RC for all experiments, except the ones employing longer time scale, where 2–3 photons per RC was used. DAS were calculated from global fitting, accounting for deconvolution of the recorded signals with the instrument response function, by using locally written software (asufit).

Glossary

Abbreviations:

ET

electron transfer

Chl

chlorophyll

PhQ

phylloquinone

PS1

Photosystem I

RC

reaction center

ec2

second Chl of ET branch

ec3

third Chl of ET branch

DAS

decay-associated spectrum∕spectra

P_A

Chl a′ on A-side of P₇₀₀

P_B

Chl a on B-side of P₇₀₀.