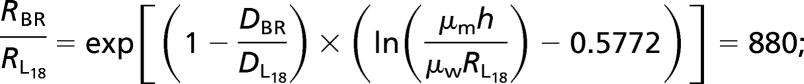Lateral mobility of proteins in liquid membranes revisited

Abstract

The biological function of transmembrane proteins is closely related to their insertion, which has most often been studied through their lateral mobility. For >30 years, it has been thought that hardly any information on the size of the diffusing object can be extracted from such experiments. Indeed, the hydrodynamic model developed by Saffman and Delbrück predicts a weak, logarithmic dependence of the diffusion coefficient D with the radius R of the protein. Despite widespread use, its validity has never been thoroughly investigated. To check this model, we measured the diffusion coefficients of various peptides and transmembrane proteins, incorporated into giant unilamellar vesicles of 1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (SOPC) or in model bilayers of tunable thickness. We show in this work that, for several integral proteins spanning a large range of sizes, the diffusion coefficient is strongly linked to the protein dimensions. A heuristic model results in a Stokes-like expression for D, (D ∝ 1/R), which fits literature data as well as ours. Diffusion measurement is then a fast and fruitful method; it allows determining the oligomerization degree of proteins or studying lipid–protein and protein–protein interactions within bilayers.

In the hydrodynamic model of Saffman and Delbrück (1), transmembrane peptides and proteins are described as diffusing in a perfectly continuous medium, ignoring the finite size of the lipids. This model predicts that the diffusion coefficient D of a simple cylinder embedded in a thin sheet of fluid matching its height (Fig. 1) is given by

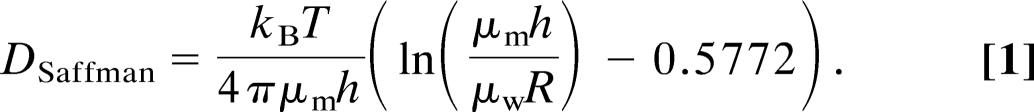In this expression, the adjustable parameters are by order of importance: the thickness h and viscosity μ_m of the liquid membrane, the radius R of the diffusing cylinder, and the viscosity of the surrounding aqueous phase μ_w. This result follows from solving the flow field in the membrane and in the surrounding fluid, assuming no-slip boundary conditions at the surface of the cylinder, which is considered as large compared with the bilayer components (i.e., R > h).

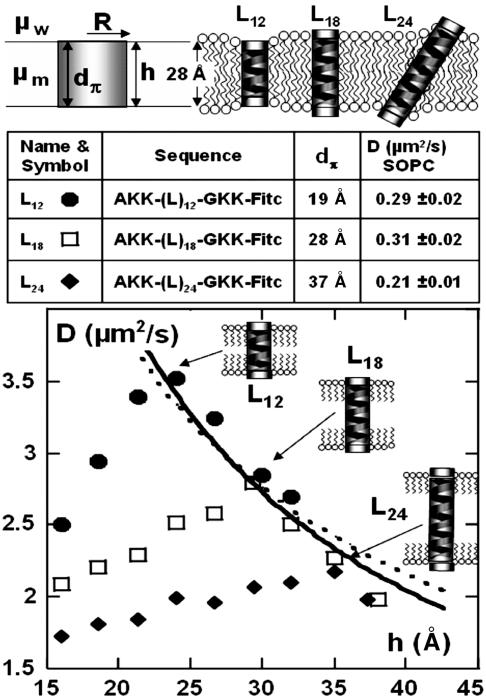
Fig. 1.

Peptides used and their D variations versus bilayer thickness h. (Top) The parameters used in the Saffman–Delbrück model (Eq. 1), in the case of peptides diffusing in a giant unilamellar vesicle (GUV) made of SOPC. (Middle) A summary of the properties of the peptides used, their sequences, and their hydrophobic length d_π. The right-hand column gives the measured diffusion coefficient of these peptides in single GUVs. The diffusion coefficient was determined by using evanescent fluorescence recovery after pattern photobleaching technique. The data are typically averaged >200 vesicles. (Bottom) The variation of the diffusion due to the swelling of the C₁₂E₅ bilayer for the three analog peptides L₁₂ (•), L₁₈ (□), and L₂₄ (♦). For each peptide, five sets of experiments allowed us to obtain average values with a reproducibility of >5% (the symbol size). The dotted line is the fit with the Saffman–Delbrück model (Eq. 1), using only one adjustable parameter, μ_m. The radius was taken as 5.5 Å and the viscosity of water as 0.01 P, leading to μ_m = 2.94 P. The solid line represents a simple 1/h dependence. Note that the relative D variations are the same in C₁₂E₅ bilayers and in SOPC membranes: for h = 28 Å, L₂₄ diffuses 30% slower than L₁₈; L₁₂ and L₁₈ have similar mobilities.

Numerous biological studies, both in model systems (2–4) and living cells (5, 6), refer to this continuum approach (7). Because D depends only weakly on R, the characterization of protein or rafts radii is delicate (8); for example, increasing the radius from 10 to 100 Å changes the mobility by a mere 30% [for h = 30 Å and μ_m = 10 poise (P; 1 P = 0.1 Pa·s)].

To check the applicability of the Saffman–Delbrück formula (Eq. 1), we have used fringe pattern photobleaching under the microscope (9) to measure precisely the self-diffusion of transmembrane peptides and proteins of well characterized dimensions.

Results and Discussion

The weight of the bilayer thickness, h, has never been investigated. Rather than using lipids of various lengths, we opted for a unique system where the bilayer thickness can be continuously tuned, leaving the bilayer viscosity constant.

We use a phase of model bilayers made of nonionic surfactants (penta-monododecylether; C₁₂E₅) diluted by water. These bilayers can be swollen at will by a hydrophobic solvent, which increases h from 16 Å [unswollen bilayer (10)] up to 40 Å, as checked by small-angle x-ray scattering experiments. To simplify the analysis, we wish to keep the viscosity of the membrane unchanged upon swelling. To do so, we choose dodecane, which matches the hydrophobic tails of the surfactant. We tested the properties of each monolayer by labeled surfactants (C₁₂–FITC) and those of the whole bilayer by longer probes: labeled lipids [1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (SOPC)–4-chloro-7-nitrobenz-2-oxa-1,3-diazole (NBD)]. As detailed in Materials and Methods, the fact that the diffusion coefficients of these two different molecules remained constant upon swelling indicates that the viscosity of this “model membrane” was mainly unaltered, with the midplane dodecane displaying the same apparent viscosity as the C₁₂E₅ monolayers.

We have synthesized model peptides of increasing hydrophobic length d_π: L₁₂, L₁₈, and L₂₄ (Fig. 1), and radius of 5.5 Å. Poly-leucine sequences, capped at both ends by polar heads, create stable and well defined α-helices as models of transmembrane “cylinders.”

Upon swelling, the diffusion coefficient varies in a similar manner for all of the peptides studied (Fig. 1). The value of D has a maximum D_max when the hydrophobic membrane thickness, h, matches the peptide hydrophobic length d_π, corresponding to Saffman’s conditions. The variation of D_max with h is best fitted with a simple 1/h law (solid line), whereas the dotted line gives the predicted D_Saffman of Eq. 1.

To investigate the dependence of D on the radius R, a model transmembrane protein, bacteriorhodopsin (BR), was incorporated into giant unilamellar vesicles (GUVs) of SOPC (11). The peptide L₁₈, perfectly adapted to the membrane (h = d_p = 28 Å), calibrates the bilayer’s properties.

BR, made of seven transmembrane α- helices [R_BR = 18 Å (12)], diffuses 3.8-times slower than the single helix L₁₈-peptide. (D_BR = 0.08 and D_L18 = 0.31 μm²/s). Such a difference, according to the Saffman–Delbruck formula (Eq. 1), indicates that the proteins are aggregated in giant clusters of radius R_Saffman = 0.48 μm.^∥ However, confocal microscopy shows no such large objects, but a homogeneous fluorescence distribution in agreement with previous electron-microscopy results (13, 14) that favor a monomeric state (in the dark state of the light-activated protein). Thus, the D_BR value suggests a 1/R behavior because D_BR/D_L18 ≈ R_L18/R_BR.

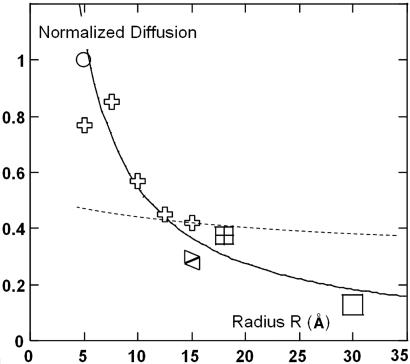
This behavior, in contrast to the Saffman–Delbrück prediction, is supported by literature. In Fig. 2, we gather published diffusion coefficients of transmembrane peptides (15) and various proteins (16). The D variations, normalized by the lipid diffusion, show a continuous decrease of mobility, fitted by a simple 1/R law.

Fig. 2.

Normalized diffusion coefficient (D/D_lipid) vs. peptide radius R in lipid bilayers. Crosses correspond respectively from the left to monomers, dimers, trimers, tetramers, and hexamers of transmembrane peptides (15). The square symbols at R = 15, 18, and 30 Å correspond, respectively, to acetylcholine receptor (AChR), BR, and SR-ATPase (16). The solid line is a 1/R fit, and the dashed line represents the prediction of Saffman’s model, using h = 28 Å, μ_m = 1.75 P, and μ_w = 1 cP as in ref 15.

Furthermore, two recent studies allow the comparison of diffusion coefficients of two large transmembrane objects embedded in the same membrane. In the first (17), the mobilities of MscL [R = 25 Å (18)] and LacS [R = 32 Å (19)] differ by a factor of 1.3 corresponding to the ratio of their radii. In the second (14), a 1/R law fits correctly the data obtained by FCS and freeze-fracture electron microscopy on photo-activated, oligomerized BR.

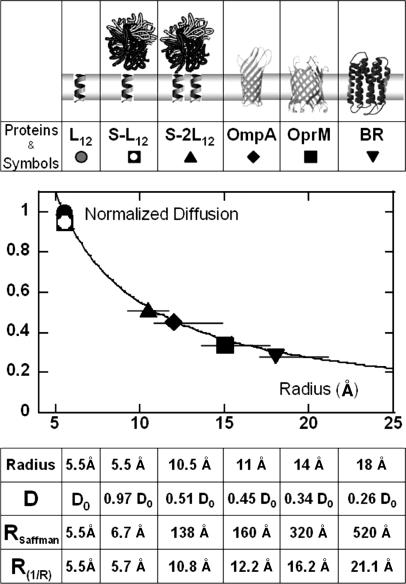
We then switched back to the C₁₂E₅ bilayers, with incorporated proteins, for further investigation (Fig. 3). A simple test was first performed by using biotinated L₁₂ peptides embedded in bilayers adapted to match their length (h = d_π = 21 Å).

Fig. 3.

Normalized diffusion coefficient (D/D_L12) vs. peptide radius R, in C₁₂E₅ bilayers. The formation of streptavidin-peptide assemblies is described in Materials and Methods. To avoid possible denaturation, the transmembrane proteins are embedded in dodecane-free membranes. The hydrophobic mismatch between protein height and bilayer thickness creates a local deformation. As discussed in Materials and Methods, this effect leads to a large uncertainty in the effective radius of the protein, represented by the horizontal bars in the plot. The diffusion coefficients are normalized by the diffusion of the L₁₂ peptide (R_L12 = 5.5 Å ≈ R_SOPC), extrapolated to the thickness of a dry bilayer in Fig. 1 (D₀ = 4.8 ± 0.2 μm²/s). From the measured D values and Eq. 1, one can estimate the corresponding

where h = 16 Å, and μ_m = 2.94 P, μ_w = 10⁻² P, as in Fig. 1. The dashed line is the fit using these parameters. For comparison, we indicate the radii calculated from the 1/R law (solid line, as in Fig. 2):

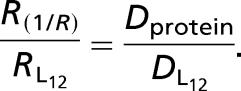When water-soluble streptavidin is grafted onto one transmembrane peptide, the observed decrease of D_L12 is only 3%. However, when the peptide concentration is twice as large as the streptavidin concentration, stable dimers are formed. The diffusion coefficient of such dimers is half that found for monomers. The object created is anisotropic, but the equivalent size calculated using Eq. 1 seems grossly overestimated: the dimer would be equivalent to a cylinder of radius R_Saffman = 138 Å (considering the viscosity of the model bilayers μ_m = 2.94 P, its thickness h = 21 Å, and μ_w = 10⁻² P). On the contrary, as indicated Fig. 3, the variation observed is compatible with a 1/R dependence.**

The above experiments confirm that the diffusion coefficient is rather insensitive to the size R_w of the polar heads, because of the high viscosity contrast (≈μ_m·h/μ_wR_w) between the bilayer and water. However, it varies strongly with the hydrophobic size of the diffusing object.

To further explore the dependence of D on the radius R, two β-barrel proteins, OmpA (20) and OprM (21), along with BR, were inserted in dodecane-free bilayers of C₁₂E₅. Compared with the diffusion of L₁₂, the protein diffusion constant is significantly reduced. We found a factor of 3.5 difference between the peptide and BR diffusion coefficients, as in SOPC membranes. Because h < d_π, the diffusing objects are not in strict Saffman conditions, but estimations can still be made using Eq. 1, leading to radii of R_Saffman ∼ 160, 320, and 520 Å for the above proteins. These values are unrealistic, and greatly exceed the known radii of these proteins (Fig. 3). The data are well fitted by the 1/R dependence (Fig. 3), using radii that are only slightly larger than the published values. The small increase in the effective radii most probably arises because of the mismatch between the protein height and membrane thickness, as discussed in the Fig. 3 legend.

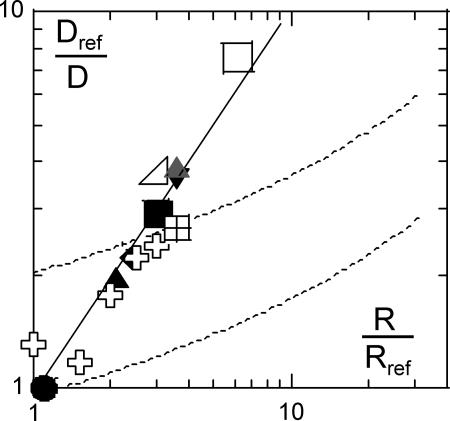
Our experimental results, as well as published data, indicate that the diffusion coefficient is inversely proportional to the radius R of the diffusing object (Fig. 4) and to the thickness h of the membrane (Fig. 1). These observations suggest a heuristic Stokes–Einstein-like expression

where a characteristic length, λ, is introduced for dimensional reasons.

Fig. 4.

Normalized inverse diffusion coefficient D_ref/D vs. object radius R/R_ref, (open symbols are data gathered from the literature, and filled symbols are from this work). For peptide assemblies and proteins in C₁₂E₅ bilayers (filled symbols as in Fig. 3), the peptide L₁₂ serves as reference: D_ref/D = D_L12/D; the BR in SOPC (gray triangle) is compared with the L₁₈ peptide: D_ref/D = D_L18/D. As in Fig. 2, for oligomers of peptides (crosses), acetylcholine receptor (AChR), BR, and SR-ATPase (squares), the lipid diffusion serves as reference. The solid line is a power-law regression leading to D_ref/D ∝ R^1.04; for comparison, the dashed line represents the prediction of the Saffman–Delbrück model (Eq. 1) (upper line, same as in Fig. 3, and lower fit as in Fig. 2).

Saffman–Delbrück’s model and its numerous extensions (22, 23) have developed a hydrodynamic approach for the diffusion of particles much larger than the bilayer molecules. The membrane was treated as a constant-viscosity, Newtonian fluid layer, its surface staying perfectly flat over large distances, creating purely two-dimensional flows.

The data presented here show a strong disagreement with the Saffman–Delbrück formula (Eq. 1). Under experimental conditions, the diffusing proteins are rarely six times larger than the lipid lateral dimension; this fact may lead to a breakdown of the validity of the hydrodynamic calculation.

The characteristic length, λ, accounts for the complex nature of the membrane (24) and should be related to the extent of membrane perturbation induced by the diffusing object. Because the viscosity of model membranes is far from being settled, the λ values can only be roughly estimated. For D = 1 μm²/s, R = 5.5 Å, h = 30 Å, and reported μ_m values ranging from 1 up to 10³ P (2, 25), the corresponding λ values vary between 5 and 5,000 Å.

It should be emphasized that, on molecular length-scales, the membrane is not a featureless continuum, because the lipid chains possess finite sizes and internal degrees of freedom. Molecular dynamics “snapshots” of bilayers show a very heterogeneous medium (26) with defects in the membrane packing. Supporting this view, a recent mesoscopic simulation (27) showed that “the diffusive process occurs through collective and correlated motions of lipids,” with a correlation length scale of ≈10 Å. On larger length scales, thermal fluctuations and undulations also may contribute to the dissipation of velocity gradients.

One can expect, however, that in the limit of macroscopic inclusions, such that R ≫ λ, the analysis of Saffman–Delbruck still applies. At this stage, more theoretical work seems to be the next logical step.

Conclusion

Our data raise physical questions concerning our understanding of the bilayer “fluid.” The heuristic law we propose open perspectives for simple and widespread photobleaching or correlation spectroscopy techniques, which will give information about the peptide conformation or protein oligomerization in model systems of giant vesicles. In living cells, the fact that, even in the absence of physical barriers, clusters of proteins should diffuse much slower than dispersed receptors may be decisive when analyzing single particle tracking experiments.

Materials and Methods

Peptides.

The synthetic peptides mimic the hydrophobic transmembrane α-helical segments of integral membrane proteins (28). They consist of a simple hydrophobic α-helix, capped at one or both ends by polar heads and labeled with a fluorescent group (FITC) or with biotin to enable an association reaction. A sequence of polyleucines of variable length (12, 18, or 24 aa) creates a robust and well characterized transmembrane domain; the anchoring to the surface of the bilayer is ensured by positively charged lysine residues. Fig. 1 illustrates and summarizes their properties.

Synthesis.

Commercial solvents of analytical grade were redistilled before use. Peptides were synthesized and purified as trifluoroacetic acid (TFA) salts, using previously published solid-phase synthesis and reversed-phase high-performance liquid chromatographic procedures (29, 30).

Proteins.

• (i)OprM is a large protein of the outer membrane of Pseudomonas aeruginosa, whose structure is close to that of TolC; its hydrophobic domain is a β-barrel of 12 strands (21).
• (ii)Eight strands constitute the transmembrane domain of OmpA (20); its purification and handling are described in ref. 31.
• (iii)BR (12) is a protein with multitransmembrane segments, purified from purple membranes of Halobacterium salinarium. The BR was kept in its dark-adapted state during all experiments.

These proteins were labeled as described in ref. 11 or using Fluoreporter kits purchased from Molecular Probes and following the manufacturer’s procedures.

Preparation of the GUVs.

The vesicles were made of SOPC as the main component. The phospholipids used in this study were purchased from Avanti Polar Lipids and used without further purification.

Peptides were dissolved with lipids in chloroform, and the mixture (1 peptide for 10³ lipids) was spread and evaporated on rough Teflon substrates. After lipid hydration, giant vesicles were formed in 270 milliosmolar (mOsm) glucose solution (32, 33). The vesicle suspension was added to an aqueous sucrose solution or PBS buffer of a slightly higher osmolarity (290 mOsm) than that of the vesicles. The deflated vesicles can be micromanipulated and present a flat area in contact with the surfaces suitable for evanescent photobleaching. For the BR incorporation, an electroformation procedure was used. See ref. 11 for details.

Lyotropic Phases.

Choosing C₁₂E₅ as a suitable component, we found that the common surfactant used with transmembrane proteins, β-octylglucopyranoside (β-OG), acts as a perfect cosurfactant. Simply added to a mixture of water and C₁₂E₅, β-OG helps the surfactant to create spontaneously a regular network of multiconnected bilayers and controls the properties of these “sponge” or L₃ phases over the wide range of conditions (buffer, temperature, etc.) desired. The phases used in these experiments are mixtures of water:C₁₂E₅:β-OG in a 100:30:1 volume ratio.

The structure of the sponge phases has been extensively studied (34, 35). Small-angle x-ray scattering experiments were performed as a careful check of the phase properties, as described in refs. 36 and 37.

The thickness of such bilayers is perfectly controlled and can be increased up to 3-fold through the precise addition of a hydrophobic solvent (10). To simplify the analysis, we chose the solvent to keep the viscosity of the membrane constant upon swelling.

We tested the properties of the monolayers by labeled surfactants (C₁₂–FITC), and the bilayer by a labeled lipid (SOPC–4-chloro-7-nitrobenz-2-oxa-1,3-diazole). The lipid inserts into one hydrophobic monolayer (8 Å) and tests the viscosity of an extra 6 Å. For dry bilayers [h = 16 Å (38)], the lipid tail contacts the opposite leaflet; upon swelling, midplane solvent progressively replaces that contribution to the friction.

Using dodecane, which matches the hydrophobic tails of the surfactant, the swelling has no apparent effect on the viscosities. D_SOPC remains constant (5 ± 0.2 μm²/s), and D_C12 stays at 8 ± 0.2 μm²/s. Using shorter chains, the viscosity of the monolayer is decreased, whereas branched hydrocarbons cause an increase of the midplane friction.

To avoid insertion defects, the peptides were incorporated into dry bilayers of C₁₂E₅; dodecane then was added in a step-by-step process. To eliminate the possibility of destructive interactions between dodecane and the complex transmembrane domains of the proteins, OmpA, OprM, and BR were embedded in dry bilayers.

In this case, the protein hydrophobic height is larger than the hydrophobic thickness of the bilayer, creating a local deformation. Different studies (26, 39) estimate that this perturbation extends on the length scale of one to two surfactant molecules. Such a surfactant annulus may either diffuse along with the protein as a compact block or be constantly regenerated as surfactant molecules adjacent to or near the protein exchange with those further away. Thus, the pertinent dimension of the diffusing “object” could be either equal to the protein radius or 10 Å larger.

The hypothesis of aggregation of diffusing species, leading to much larger radii, is unlikely at our protein/surfactant ratio of 1:10⁶, and the recovery of fluorescence would not be purely monoexponential as observed.

Streptavidin-peptide assemblies were prepared as follows.

• (i)in the absence of peptides, we checked that the high mobility (15 μm²/s) of streptavidin corresponds to this large soluble protein (50 Å in diameter), confined between the bilayers but without interactions with these bilayers. (Streptavidin labeled with FITC was purchased from Interchim, Montluçon, France.)
• (ii)By adding peptides, we followed the grafting of streptavidin; when one equivalent of peptide is incorporated, we observed a monoexponential recovery of fluorescence, with a characteristic time matching the one obtained with labeled L₁₂ peptides under the same conditions. In that case, the streptavidin molecules are mainly bound to a unique peptide.
• (iii)By adding an excess of peptides (from 2 up to 10 equivalents of peptide), we observed a different diffusion coefficient, showing that streptavidin now associates laterally two peptides. The water spacing between the bilayers is kept at 300 Å for this set of experiments, avoiding interactions between molecules embedded in two different bilayers.

Preparation of the Samples and Concentrations Used.

To focus on effects arising solely from individual behavior, we performed concentration-dependent measurements. As the detection is made over large areas, the peptides and proteins were added at minimal concentrations, removing the effects of protein–protein interaction. Typically, for one peptide, 10⁴ to 10⁶ surfactants were used in the lyotropic phase, and 10³ lipids for the GUVs experiments. A typical sample is only 5 μl in volume, introduced by suction into 200-μm-thick flat microchannnels. The temperature was controlled at 20°C, while the sponge phases are stable over a 10–35°C temperature range. Any phase transition is easily detectable, given its well known defect features observable under the microscope between crossed polarizers; systematic controls were performed between each experiment.

Diffusion Measured by Fluorescence Recovery After Pattern Photobleaching.

The fluorescence recovery after pattern photobleaching technique is described in detail in ref. 40. Briefly, when illuminated by a high-intensity laser flash (200 mW), the fluorescent molecules dispersed within the sample are irreversibly bleached. The recovery of fluorescence intensity with time, I(t), in the bleached areas is governed by the self-diffusion of the unbleached probes and monitored by a low-intensity laser beam. To improve the signal-to-noise ratio, we created a macroscopic gradient of fluorescence following a fringe pattern, using two laser beams intersecting exactly in the focal plane of a light microscope. A piezoelectric crystal made the monitoring beam sweep the bleached fringes at a frequency, ω, and the signal was detected at ω and 2ω using a lock-in amplifier. A nonzero signal at ω would betray convection, while at 2ω the enhanced recovery signal was obtained. In all experiments, monoexponential recoveries of fluorescence were measured: the signal at 2ω is proportional to I₀[1 − exp(−t/τ)]. A typical measure of diffusion consists of five characteristic times τ corresponding to five different fringe sizes i, with each τ being determined from an average of 10 experiments. We checked that all of the diffusive behavior followed Brownian motion, and the diffusion coefficients were deduced by the classical relation D = i²/(4π²τ), where the interfringe values i are in the range 1–300 μm and the typical time values are from 0.1 to 10³ s.

Glossary

Abbreviations:

BR

bacteriorhodopsin

C₁₂E₅

penta-monododecylether

GUV

giant unilamellar vesicle

P

poise

SOPC

1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine.