Early computational processing in binocular vision and depth perception

Abstract

Stereoscopic depth perception is a fascinating ability in its own right and also a useful model of perception. In recent years, considerable progress has been made in understanding the early cortical circuitry underlying this ability. Inputs from left and right eyes are first combined in primary visual cortex (V1), where many cells are tuned for binocular disparity. Although the observation of disparity tuning in V1, combined with psychophysical evidence that stereopsis must occur early in visual processing, led to initial suggestions that V1 was the neural correlate of stereoscopic depth perception, more recent work indicates that this must occur in higher visual areas. The firing of cells in V1 appears to depend relatively simply on the visual stimuli within local receptive fields in each retina, whereas the perception of depth reflects global properties of the stimulus. However, V1 neurons appear to be specialized in a number of respects to encode ecologically relevant binocular disparities. This suggests that they carry out essential preprocessing underlying stereoscopic depth perception in higher areas. This article reviews recent progress in developing accurate models of the computations carried out by these neurons. We seem close to achieving a mathematical description of the initial stages of the brain’s stereo algorithm. This is important in itself––for instance, it may enable improved stereopsis in computer vision––and paves the way for a full understanding of how depth perception arises.

1. Stereopsis as a model of perception

Although we have two eyes, we are not aware of the fact during visual perception: we perceive the world as if through a single “cyclopean eye” in the middle of our forehead. Yet at the same time, we have the remarkable ability to deduce depth from the small differences in left- and right-eye retinal images which occur because our eyes are set apart in our head. This stereoscopic ability and its counterpart, binocular single vision, have fascinated us since their existence was first fully appreciated in the nineteenth century. Recently, binocular vision has come into prominence as a tool for probing one of the fundamental questions of neuroscience: how external stimuli give rise to conscious perception.

There are several reasons why stereopsis is a particularly suitable model system for this goal.

1. The problem to be solved is relatively well-defined, compared to for example face or speech recognition, and its mathematical basis is thoroughly understood (Fig. 1; Hartley and Zisserman, 2000; Longuet-Higgins, 1981).

2. As a consequence of this simplicity, stereopsis can be studied in both animals and humans. Monkeys perceive stereoscopic depth much as humans do, and can be trained to report their perceptions (Bough, 1970). Thus, psychophysical studies of perception can be combined with electrophysiological studies of neuronal activity in the same animal––of critical importance in the attempt to relate perception and neuronal activity.

3. The circuitry specific to this task probably occurs entirely within the cortex, since at lower levels in the visual pathway inputs from the two eyes are processed largely separately. Thus, stereopsis is a good system in which to study specifically cortical processing.

Fig. 1.

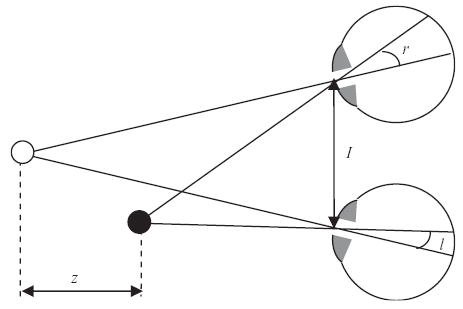
The geometry of stereopsis. The eyes are fixating the white sphere, which therefore falls on the fovea in both retinae. The black sphere is closer to the observer; its images therefore fall at non-corresponding points in the two retinae. Its distance z from the fixation point can be deduced from its retinal disparity δ = r−l and the interocular distance I. To deduce its absolute position in space, we also need to know the positions of the eyes. In principle, these can be deduced from purely retinal information, provided the locations of the retinal images of enough objects are known (Hartley and Zisserman, 2000).

Stereopsis appears to exist in several species, including toads, owls, hawks, rabbits, goats, and horses (Howard and Rogers, 1995). The circuitry supporting this ability may differ substantially between species (Pettigrew, 1991). My interest here is how stereopsis is achieved in humans, and to this end I concentrate on results from the monkey and, to a lesser extent, the cat. These are the two species which have been most extensively studied, and in the case of the monkey, most resemble our own visual system. This review examines our current understanding of the earliest stage of the cortical circuitry supporting stereopsis in these species. This first stage is the combination of left and right-eye inputs which occurs in primary visual cortex (known as V1 in the monkey, roughly corresponding functionally to cat areas 17 and 18 combined). The various claims concerning the role of V1 in stereopsis are discussed and critically evaluated. A key theme which emerges is the valuable contribution which theoretical modeling work has made in illuminating and sharpening our thinking.

2. V1 is not the neural correlate of depth perception

In order to deduce the depth of an object from its retinal disparity, one needs to know where the image of that object falls in both retinae (Fig. 1). Thus, for every object visible in one eye, the visual system needs to find its partner in the other eye, that is, it has to solve the correspondence problem. Until about 40 years ago, a viable theory was that the visual system operates on the two retinal images separately, performing scene segmentation and object recognition, and then finally, for each object in the scene, compares where its images fall in the two retinae. In this picture, stereopsis is viewed as a very high-level process, occurring after other processes such as object recognition. However, in the 1960s, Bela Julesz drew attention to the fact that stereopsis works perfectly well with random-dot patterns resembling the static on an untuned television (Fig. 2). Although monocularly these images do not contain any structure at all, when viewed binocularly, disparate regions are perceived vividly in depth. Julesz described these stimuli as “cyclopean”: they contain features which can only be viewed with our mind’s “cyclopean eye”, when the separate monocular images are put together in the brain.

Fig. 2.

Random-dot stereogram. A: For clarity, only 25 × 25 large pixels are shown. It is then clear that the left and right images are identical except for a central disparate region, here indicated by a gray square. B: here the image consists of 250 × 250 pixels. Again, a square central region is disparate, as can be seen by free-fusing the images. To do this, hold the page at a comfortable distance and study the image. Allow the eyes to cross or diverge until you are seeing double. Then concentrate on aligning the heavy black boxes drawn around the pattern, until you can see three boxes instead of four: left, right and a fused one in the middle. Finally move your attention to the centre of the random-dot pattern and look for the square.

Fig. 2 shows two example cyclopean stimuli. In the upper stereogram, the image consists of just a few large pixels, to enable the structure of the stimulus to be discerned; in the lower stereogram, there are a hundred times as many dots. Such images pose the correspondence problem in its most challenging form, since each dot has hundreds of identical potential matches in the other eye. In order to find the correct match one cannot consider the dots individually, but must also take into account the pattern of the neighboring dots. That is, the correspondence problem must be solved at a “global” rather than a purely local level. Julesz coined the term “global stereopsis” to describe our ability to perceive depth in such stimuli. We distinguish between a “globally correct match”—that is, the correct identification of features in the left and right images which correspond to the same object in space—and “false matches”, features in the left and right images which appear similar, but do not actually correspond to the same object in space. Random-dot patterns contain a multitude of false local matches which must be rejected in order to arrive at a globally consistent solution of the correspondence problem. This will turn out to be a critical test of whether a given brain area is solving the correspondence problem.

Our ability to perceive depth in cyclopean stimuli suggests that stereopsis occurs early in the visual system, prior to object recognition (Julesz, 1971; Poggio and Poggio, 1984). When, just a few years later, it was found that many neurons in striate cortex of the anesthetized cat modulate their firing according to the binocular disparity of a bar stimulus and that some respond best to non-zero disparities (Nikara et al., 1968), this was immediately hailed as a neural mechanism of binocular depth discrimination (Barlow et al., 1967).

2.1. Disparity selectivity is not the same as depth perception

Yet the observation of disparity selectivity does not, in itself, enable us to make this claim. Because neurons respond to stimuli only in a restricted region of the retina known as the receptive field, a binocular neuron will inevitably be sensitive to the disparity of an object, simply because, as the object moves in depth, it must eventually fall off the receptive field in one or both eyes (Fig. 3). Thus, disparity selectivity is an inevitable side-effect of pairing inputs from left and right retinal inputs, even if this pairing has nothing to do with depth discrimination. The retinal topography in V1 means that left and right inputs would tend to have receptive fields at similar locations in the two retinae, so the binocular cell would generally respond best to disparities close to zero. However, any inexactness in the topography, or differences in receptive field structure between left and right eyes, would naturally explain the observed scatter in preferred disparities. A simple model of this process, which has experimental support (Freeman and Ohzawa, 1990; Ohzawa and Freeman, 1986b), is to propose that a binocular neuron receives input (L,R) from both eyes, and fires at a rate proportional to the linear sum of the monocular inputs (L + R) (Fig. 3). If the input is bipolar (i.e. can take both positive and negative values), then the cell must also apply an output threshold, since it cannot encode negative values of (L + R) by firing a negative number of spikes. Thus we can write the cell’s response as

Fig. 3.

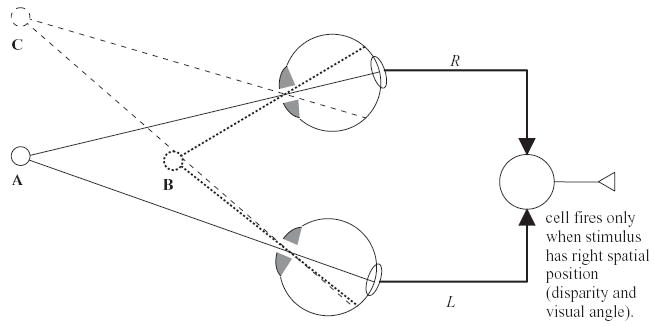
Linear summation of L and R inputs gives a simple kind of disparity tuning. The ovals drawn on each retina indicate the left- and right-eye receptive fields, where stimuli excite the binocular cell under consideration. The output from each receptive field (L, R) is combined at a binocular cell in V1. This cell is sensitive to the three-dimensional position of a stimulus. It responds to the white sphere at position A, since then the image of the sphere falls in the receptive field in each eye and L and R are both positive. It does not respond when the sphere has a different disparity (B), since then the image of the sphere has moved off the receptive field, and L and R are zero. It also does not respond when the sphere has the same disparity but a different angular position (C). Thus, this unit is sensitive to disparity, but also to visual angle.

$$C=\text{Thresh}(L+R).$$ (1)

Units of this type would respond to local matches in the stimuli, irrespective of whether these matches turned out to be true or false on a global scale. Since a prerequisite of depth perception is the solution of the correspondence problem, units of this type cannot implement depth perception. To understand the role of V1 in depth perception, we need to understand whether V1 neurons are described by simple models like Eq. (1) or whether they solve the global correspondence problem.

Evidence that they do seemed forthcoming a few years later, when Gian Poggio and his collaborators, working in the awake monkey, revealed that many V1 neurons are sensitive to disparity in random-dot stereograms (Poggio, 1990; Poggio et al., 1988, 1985). Using random-dot patterns avoids the problem, inevitable with bar stimuli, of confounding changes in disparity with changes in monocular stimulation. With bar stimuli, any change in disparity necessitates a change in the monocular stimulus in at least one eye. In contrast, with dynamic random-dot patterns, there is no monocular information which would allow one even to detect when disparity changes occur. To know the disparity of a random-dot stereogram, one must have solved the correspondence problem. It is tempting, therefore, to argue that the sensitivity of V1 neurons to disparity in random-dot stereograms means that they must encode a solution of the correspondence problem (Ohzawa, 1998; Poggio, 1990).

In fact, this observation suffers from the same problem as the earlier studies: the sensitivity of neurons to disparity in random-dot stereograms does not prove that they are specialized to encode disparity, still less that they have solved the correspondence problem. Even the simple model discussed above (Eq. (1)), which just linearly combines left- and right-eye inputs and then outputs the result if this is positive, will be sensitive to binocular disparity in such stimuli. Fig. 4A shows a simulated disparity tuning curve obtained with this model. In fact, current evidence suggests that the output nonlinearity of real cells is more accurately described by half-wave rectification followed by squaring (Heeger, 1991; Ohzawa et al., 1990). Models of this form are known as energy models (Adelson and Bergen, 1985; Ohzawa et al., 1990). Fig. 4B shows a simulated disparity tuning curve for an energy unit (C = [Thresh(L + R)²]). Clearly both models, with or without the additional squaring non linearity, modulate their firing rate as a function of the disparity in the random-dot stereogram (despite statements to the contrary (Qian, 1994,1997)). Yet they have not solved the correspondence problem; they are simply responding to stimuli within their receptive fields, irrespective of whether these form part of a global match or not.

Fig. 4.

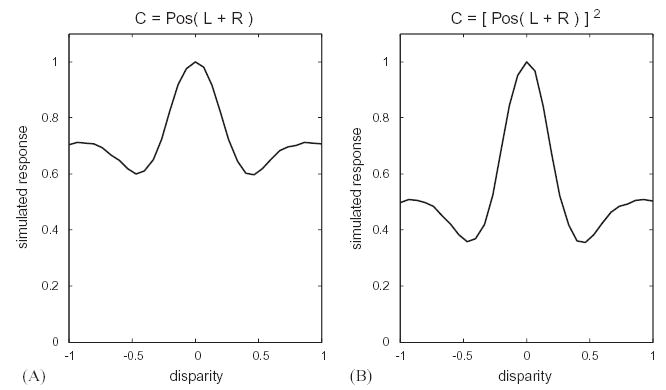
Simple local models are tuned to disparity in random-dot stereograms. A shows results for a model with half-wave rectification only; and B for the energy model (with half-wave rectification followed by squaring). The receptive fields in left and right eyes are identical Gabor functions; the graphs show the mean response averaged over 10,000 different random-dot patterns at each disparity.

How, then, can these models sense disparity in random-dot patterns, if a knowledge of disparity in these stimuli requires solving the correspondence problem? The resolution of the paradox is to note that the simulations in Fig. 4, like experimental disparity tuning curves, show the mean response averaged over several thousand random-dot patterns (experiments use dynamic random-dot stereograms, changing every dozen or so milliseconds, because V1 neurons rapidly adapt to a constant stimulus and cease firing). In any individual stereogram, the model neuron will respond to false matches, precisely because it has not solved the correspondence problem (Fleet et al., 1996). As Fig. 5 shows, a random-dot stereogram at the preferred disparity will always present matching stimuli to the two eyes, whereas stereograms at different disparities will present matching stimuli by chance only some of the time. This is why the mean response varies as a function of disparity, even though the model neuron itself is only considering local matches rather than a global solution of the correspondence problem.

Fig. 5.

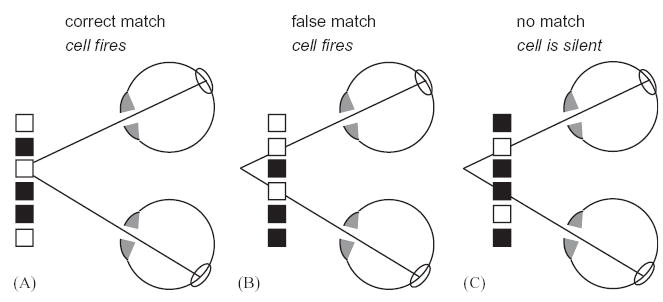
Neurons with localized receptive fields are susceptible to false matches. The ovals drawn on the retina mark the left and right receptive fields of a binocular neuron (cf. Fig. 3). The black and white squares represent a random-dot stereogram at a particular disparity (corresponding to a depth in space). In (A), the random-dot pattern is at the neuron’s preferred disparity; the cell experiences matching stimuli in its receptive fields, and so the cell fires. (B,C) show random-dot patterns at a different disparity. Sometimes, by chance, these present matching stimuli to the two receptive fields (B). These false matches will also drive the cell. However, the false matches are not reliable; stereograms away from the cell’s preferred disparity sometimes present non-matching stimuli (C), which do not drive the cell. In contrast, any random-dot pattern at the cell’s preferred disparity (A) will present matching stimuli to the two receptive fields. This is how even a cell which does not encode a solution of the correspondence problem can nevertheless respond differently on average to random-dot patterns at different disparities.

Formally, a unit whose response is C = (L + R)² computes a local cross-correlation of the left and right images, after these have been passed through a filter specified by the receptive field profiles (Fleet et al., 1996; Qian and Zhu, 1997). For more realistic models which incorporate various additional nonlinearities, such as thresholds, this is not exactly true, but cross-correlation is still a useful approximation of the operation they perform. The size of the receptive field determines the size of the local image patch which is cross-correlated, and the spatial frequency and orientation tuning of the receptive field determines which spectral components of the image are selected. Units which respond strongly to an image are signaling that there is a peak in the local cross-correlation at the disparity to which they are tuned. However, because these units do not distinguish between false and correct matches, this does not necessarily mean that there is an object at the depth corresponding to that disparity. For instance, Fig. 5B shows a false match causing the cell to respond even though there is no object at its preferred disparity.

2.2. V1 neurons are sensitive to local matches, not to global solutions of the correspondence problem

The fact that purely local models can sense disparity in random-dot patterns has important consequences. It demonstrates that the observation that real neurons are tuned to disparity in random-dot patterns does not, after all, prove that they have solved the global correspondence problem. The same model also inspired an ingenious test of whether these neurons have solved the correspondence problem or not. Cumming and Parker (1997) realized that an energy-model unit would continue to respond to disparity in anti-correlated stereograms, in which the contrast polarity in one eye is inverted, so that all the white dots are replaced with black dots and vice versa. These contain no global solution of the correspondence problem, and elicit no sensation of depth (Cumming et al., 1998). Thus, if activity in V1 encodes a solution of the correspondence problem, one would not expect a modulation in firing rate in response to anti-correlated stereograms at different disparities. These are indistinguishable perceptually (none evoking any impression of depth), and so should evoke equivalent activity in the brain area which is the neural correlate of depth perception. However, anti-correlated stimuli contain a multitude of false matches, and so will still stimulate local disparity detectors like the energy unit considered above, since these simply signal the local correlation between left and right images, irrespective of whether a global solution exists. Thus, if V1 neurons are similar to energy units, they should still modulate their firing rate with anti-correlated stereograms. The only difference is that, with anti-correlated stimuli, the energy-model predicts an inversion of the disparity tuning curve: at disparities where the response is maximal for correlated stimuli, it will be minimal for anti-correlated, and vice versa. This occurs because disparity-tuning in the energy model C = (L + R)² arises from the cross-term 2LR, and this becomes −2LR when the polarity in one image is inverted.

Cumming and Parker (1997) found that V1 neurons responded very nearly as predicted by the energy model. Neurons continued to modulate their firing as a function of disparity even in anti-correlated stimuli, where neither humans nor monkeys perceive any depth. Furthermore, the inversion predicted by the energy model was also observed. It is a dramatic success for the model that it so well predicts the response of real neurons to a highly artificial stimulus; anti-correlated stimuli are unknown in natural viewing. This is powerful evidence that V1 neurons are indeed performing relatively straightforward processing of the retinal images, rather than the more sophisticated analysis which must eventually support depth perception.

Initially, there was a loophole in this argument. Although V1 neurons do modulate their firing in response to anti-correlated stereograms, the modulation is weaker than for correlated stimuli. This is not in agreement with the energy model, which predicts that the amplitude of modulation should be the same for both correlated and anti-correlated stimuli. This indicated a failure of existing models of disparity selectivity, which is disturbing in itself since it means that we have not yet understood the computation being carried out by V1. However, in this case the failure of the model had potentially wider implications, perhaps reflecting a fundamental flaw in attempts to understand the mechanisms of disparity selectivity in V1. As we have argued, the neural correlate of depth perception should not respond at all to anti-correlated stereograms, while the energy model predicts an equally strong response to both correlated and anti-correlated stimuli. The behavior of V1 is intermediate between these two: neurons respond to anti-correlated stereograms, but more weakly than predicted by the energy model. This raises the question of whether the reduction in amplitude was directly due to the lack of depth perception. For example, higher visual areas in which the correspondence problem is solved might normally send reinforcing feedback down to V1; the lack of such reinforcement when no solution exists might explain the weaker modulation with anti-correlated stimuli (Ohzawa, 1998). This quantitative discrepancy with the energy model therefore potentially indicated a severe problem with existing models. If disparity selectivity in V1 is substantially affected by feedback from higher areas, then attempts to model it based only on the retinal stimulus within a restricted receptive field would be fundamentally flawed: the response of neurons would depend not only on the stimulus within their own receptive field, but also on global properties of the image such as whether a viable solution of the correspondence problem can be found.

However, it has recently been demonstrated (Read et al., 2002) that the energy model in fact needs only a trivial modification in order to account for the weaker modulation with anti-correlated stimuli. If we postulate that the linear inputs from each eye pass through a threshold before binocular combination,

$$C={[\text{Thresh}(L)+\text{Thresh}(R)]}^2,$$ (2)

then the amplitude of modulation depends on the correlation of the stimuli. If the receptive field profiles in the two eyes are similar, the modulation is weaker with anti-correlated stimuli, as observed in most cells. (If the receptive field profiles are opposite in the two eyes, then model neurons can be built which give stronger modulation for anti-correlated stimuli. A few such cells are observed (Cumming and Parker, 1997).) Example simulations with this model are shown in Fig. 6. The top row shows results for two model cells where the thresholds in Eq. (2) are set at zero (half-wave rectification); this substantially reduces the response to anti-correlated stimuli. The bottom row shows that by raising the threshold, the response to anti-correlated stimuli can be essentially abolished, as occurs in some real cells. Thus, the reduced response to anti-correlated stimuli can in fact be explained perfectly well with a local model whose response is a simple function of the image within the receptive field and which is not influenced by global correspondence.

Fig. 6.

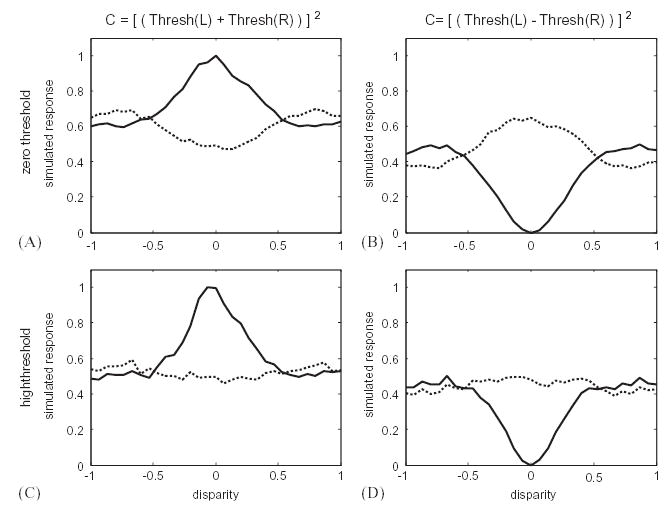
The reduced response to anti-correlated stimuli can be explained if the monocular inputs are thresholded before being combined. Solid lines show the response to ordinary, correlated random-dot patterns, dotted lines to anti-correlated patterns. There is far less modulation for the anti-correlated stimuli. The left-hand column (AC) shows a “tuned-excitatory”-type tuning curve (Poggio and Fischer, 1977), with a peak for a preferred disparity. For these cells, the reduced response to anti-correlated stimuli could also be explained with an output threshold, retaining the linear combination of left and right-eye inputs (Lippert and Wagner, 2001). However, this would not explain the reduced response in “tuned-inhibitory” cells like those on the right (BD), where the tuning curve has a central trough rather than a peak. Thresholds prior to binocular combination explain the reduced response in both types of disparity tuning (Read et al., 2002). In the top row (AB), the threshold is set at zero (half-wave rectification). If higher thresholds are used, the response to anti-correlated stimuli is suppressed further. The bottom row (CD) shows results from a simulation where the threshold was set so high that only 12% of random-dot patterns elicited a response from the monocular subunit (cf. 50% for a threshold at zero). In all simulations, the receptive fields are the same as for Fig. 4, and the curves show the mean response to 10,000 random-dot patterns at each disparity.

Postulating thresholds prior to binocular combination also enables us to explain a number of other observations which were puzzling for the energy model. For example, most V1 cells do not respond to stimuli in which the luminance is the same over a wide area; they are much better driven by stimuli containing both bright and dark regions, such as sinusoidal luminance gratings. It can be shown that the energy model requires such cells to have oscillatory disparity tuning curves, containing several peaks and troughs. In reality, disparity tuning curves are usually dominated by a single peak or trough; they may have side-lobes, but these are usually less than required to fulfill the energy model predictions (Ohzawa et al., 1997; Prince et al., 2002b; Read and Cumming, 2003c). Adding thresholds prior to binocular combination produces model units with less extreme side-lobes, in better agreement with experiment (Read and Cumming, 2003c). Another problem for the energy model is that it predicts a correlation between ocular dominance and strength of disparity tuning which is not observed. Many real cells which are “monocular”, in the sense that they do not respond to stimulation in one eye, are nevertheless tuned to disparity, demonstrating that they are receiving information from both eyes (Ohzawa and Freeman, 1986a; Prince et al., 2002a; Read and Cumming, 2003b). This is easily explained by assuming that the silent eye sends purely inhibitory input; so it is not possible to drive the cell through this eye alone, but when both eyes are stimulated, the inhibitory eye can modulate the response as a function of disparity. This contradicts the original energy model, a key feature of which is linearity up to binocular combination, meaning that both eyes must be capable of supplying either inhibitory or excitatory input, depending on the stimulus. Postulating that one eye sends purely inhibitory input breaks this linearity by applying a threshold prior to binocular combination (in this case an inverted threshold: the silent eye will pass only negative input). Thus, thresholds prior to binocular combination also immediately explain the existence of “monocular” disparity-tuned cells.

With this new model, it is possible to explain the responses of V1 neurons in purely local terms, including the reduced response to anti-correlated stimuli. Of course, this does not rule out global influences. However, other experiments aiming to dissociate local matches from global stereopsis also support the idea that V1 neurons are influenced only by local properties of the stimulus. One example is the response to stimuli which are ambiguous because they are periodic. When a stereogram is constructed from a periodic image, such as a sinusoidal luminance grating (Fig. 7), many different matches are possible. This is sometimes known as the wallpaper illusion, after the unsettling effect which can occur when looking at a wall decorated with vertical stripes: the stripes can be perceived as standing out in front of the wall (Fig. 8B), instead of on its surface (Fig. 8A). The effect occurs because a stripe in one eye can be matched with any of the stripes visible in the other eye. This is similar to the false-matching problem in random-dot patterns, where a dot can be matched with any of the multitude of identical dots in the other eye. In the random-dot case, the matches are disambiguated by considering the agreement with neighboring dots: there is only one globally consistent match in which neighboring matches have similar disparity. For a finite periodic stimulus, the edges of the stimulus define a global disparity, which is then used to disambiguate the central region (Fig. 8). This offers another way of testing whether V1 neurons are sensitive to the global match, using sinusoidal luminance gratings. Consider a receptive field which is entirely covered by the grating. As the disparity of the grating edges changes by multiples of one grating spatial period, the stimulus within the receptive field is unchanged, while the perception of depth changes with the edge disparity (Fig. 9). A neuron which responded purely locally to stimulation within its receptive field would respond equally to all these stimuli; a neuron which encoded the perception of depth would modulate its firing rate. Cumming and Parker (2000) found that the response of V1 neurons remained constant, again suggesting that their response takes no account of the global match.

Fig. 7.

A sinusoidal luminance grating stimulus. The luminance varies sinusoidally as a function of position in one dimension.

Fig. 8.

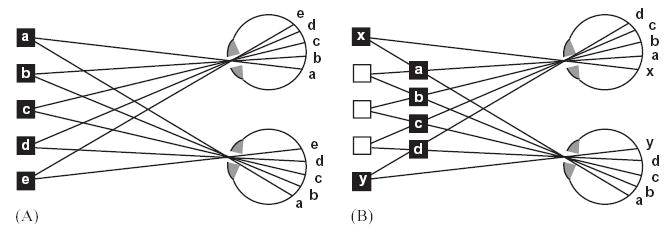
The wallpaper illusion for a periodic stimulus. The alphabetical labels are not part of the stimulus, but indicate the matches made between the identical retinal stimuli. (A): matches are made at anatomically corresponding points on the retina; the stimulus is perceived in the fixation plane. (B): matches are made at non-corresponding retinal points; the stimulus is perceived in front of the fixation plane. If the stimulus were infinite in extent, this match would be equally valid physically. For the five-period stimulus shown, the edges convey the correct disparity. Thus, the match shown in (B) implies a jump in disparity (between x and a, and between d and y). This is why, when there is a sufficiently small number of periods present, the match in (A) is reliably perceived.

Fig. 9.

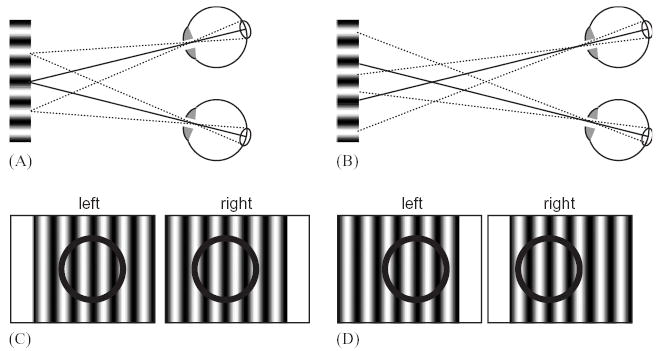
When the disparity of a periodic stimulus changes by a whole spatial period, there is no change in the stimulus within a receptive field. (AB) contain a cross-section showing the arrangement of the stimulus and eye positions in space; (CD) show the stimulus as it appears on the retina. The receptive field location is shown with ellipses on the retinae in (AB), and with a heavy circle in (CD). In (A) and (C), the left and right-eye receptive fields view identical regions of the stimulus. In (B) and (D), the stimulus is further away, so that now the receptive fields view different regions of the stimulus. But since the disparity is exactly one spatial period of the stimulus, the image within each receptive field is identical. Thus, a cell which is sensitive only to the local properties of the image falling within its receptive field, should respond identically to the stimuli shown in (AC) and (BD). In contrast, a neural correlate of depth perception should respond differently, since the perception of stimulus depth in (AC) is different from that in (BD).

Finally, psychophysical studies suggest that stereoscopic depth perception is guided more by relative disparity (differences in disparity between two visual stimuli) than the absolute disparity of each stimulus (Westheimer, 1979). The absolute disparity of any given object in space changes as the eyes move and the images shift on the retina; in contrast, the relative disparity between two objects stays the same. This is illustrated in Fig. 10. Neurons in V1 encode absolute, not relative, disparity (Cumming and Parker, 1999). This, again, suggests that the signals relevant for our depth perception must be constructed outside V1. V1 activity is driven by properties of the retinal image, whereas perception apparently reflects activity in higher areas encoding invariants which reflect properties of the outside world.

Fig. 10.

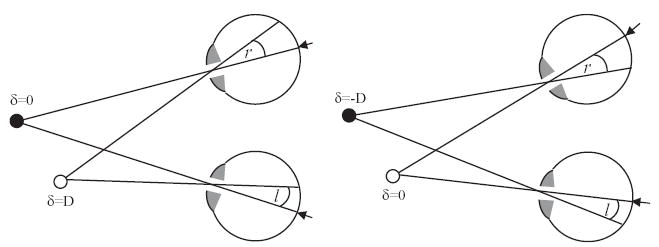
Absolute disparity changes as the eyes move; relative disparity remains constant. The sketches show the same spatial scene viewed with two different eye positions. The little arrows on the retina indicate the fovea. In (A), the eyes are fixating the black object: its absolute disparity is therefore zero, while the white object is nearer to the viewer and therefore has positive absolute disparity, say D. In (B), the eyes are fixating the white object; now, therefore, this has zero absolute disparity, while the black object has negative absolute disparity, -D. However, the relative disparity between the white and black objects, i.e. the difference in their absolute disparities, remains the same at D (=r−l).

3. V1 is specialized for binocular vision and depth perception

Several lines of evidence, then, force us to conclude that activity in V1 is not the neural correlate of depth perception. Indeed, this might have been expected from the fact that V1’s disparity selectivity was first observed in anesthetized animals not capable of discriminating depth or anything else. More seriously, the discussion so far has contained no evidence that V1 is specialized for depth perception at all. We have seen that the activity of V1 neurons can be quantitatively described by local models in which the cell is sensitive only to the stimulus presented to its receptive fields, rather than to global properties which influence depth perception. We have seen that tuning for disparity, even in “cyclopean” stimuli like random-dot patterns, could emerge as a side-effect of randomly combining inputs from left and right eyes within a roughly topographic map (Bishop, 1979). So far, therefore, it may seem as if V1’s sole contribution to depth perception is that it performs an initial, random combination of monocular inputs. However, this is far from the whole story. Recent evidence suggests that, far from simply combining the monocular inputs at random, V1 is adapted to the specific requirements of depth perception, so as to perform essential pre-processing of the signals it receives from the retinae. The output of V1 is then fed to higher visual areas where it results in the conscious percept of stereoscopic depth. In the following sections, we consider the ways in which V1 seems to be specialized for this task.

3.1. V1 neurons are specialized to encode disparity, independent of stimulus position

If disparity tuning arose merely because at large disparities stimuli move outside the receptive field in one or both eyes, then the spatial scale of the disparity tuning curve would be predictable from the receptive field size. In fact, this prediction does not seem to be borne out. Comparisons are problematic, because of difficulty in defining “receptive field size”: different measures produce different estimates, while neurons are known to be sensitive to stimuli outside their classical receptive field (Cavanaugh et al., 2002; Freeman et al., 2001; Walker et al., 1999, 2000, 2002). However, it has been estimated that the sharpness of disparity tuning is a factor of two narrower than expected from the receptive field size (Livingstone and Tsao, 1999; Ohzawa et al., 1997). This suggests that some additional mechanism operates especially to create disparity tuning.

This is apparent if we construct the binocular receptive field for such a unit. Here, we reduce the receptive fields to one dimension by using long bar stimuli at the preferred orientation, and plot the response of the cell as a function of the bar’s position in each eye. Simulated examples are shown in Fig. 11 (top row). The diagonal axis marked “position” in the binocular receptive field plots refers to the position of the object in the visual field, which is the mean of its positions in the two eyes separately. For simple cells (Fig. 11AB), the cell’s response is roughly separable into contributions from left and right eyes, visible as vertical and horizontal stripes of activity in Figure 11AB. The response is greatest when the bar falls on the optimal position in each eye, at the intersection of the vertical and horizontal stripes. Thus, simple cells are tuned for an optimal disparity, but only at the optimal position. The bottom row of Fig. 11 shows how this translates into position in space: the black blob shows the region of space where the cell responds best. For the simple cells (Fig. 11DE), the tuning for position in the visual field is as narrow as for disparity. Ohzawa and collaborators (1990, 1997) showed that, in contrast, many complex cells appear to be tuned to disparity itself. Across a variety of stimulus positions within the receptive field, complex cells display consistent tuning to one preferred disparity. In terms of the binocular receptive field, this means that the region of peak response is diagonally elongated along the position axis (Fig. 11C), so that the response of the cell is no longer separable into a left and right component. In terms of visual space (Fig. 11F), the tuning for depth is now much narrower than for visual position. This suggests a specialization for encoding disparity as an important property of the image; indeed, these cells were described as “ideally suited as disparity detectors” (Ohzawa et al., 1990). Ohzawa and collaborators suggested that complex cells with this behavior may represent the output of several simple cells tuned to different stimulus positions but the same disparity. They showed that combining several model binocular subunits of the form described above produces binocular receptive fields resembling those of real cells. The model cell in Fig. 11C is constructed in this way from the combined outputs of four simple cells. Note that random input of several simple cells into one complex cells would not produce this specialization; to explain the observation, the simple cells feeding into a given complex cell must be matched in their disparity tuning. These models also have the slightly counterintuitive property, again like real complex cells, of being insensitive to the phase of a grating stimulus, and yet tuned to the interocular phase difference between grating stimuli in the two eyes.

Fig. 11.

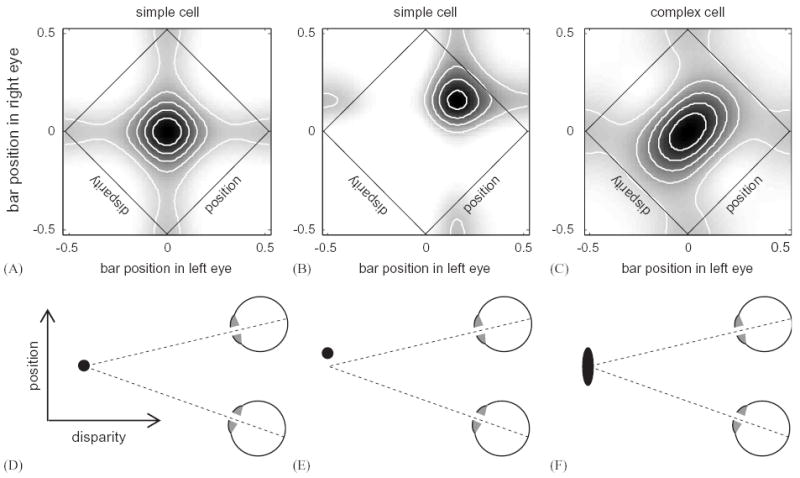
Simple cells encode disparity jointly with position, whereas complex cells are specialised for disparity. The plots show the binocular receptive field for (A,B) two single binocular subunits (simple cells) and (C) the sum of several binocular subunits (complex cell). The grayscale and contours show the response of the cell to a bar aligned with the preferred orientation of the cell, as a function of the bar’s position in left and right eyes (horizontal and vertical axes), or, equivalently, as a function of position in the visual field and disparity (rotated axes). The sketch below each plot indicates how this translates into visual space. The simple cells are energy model subunits (C = Thresh(L + R)²) with identical receptive fields in each eye (in (A), the monocular receptive fields are even-symmetric; in (B) they are odd-symmetric (Ohzawa et al., 1990)). The simple cells respond best to bars at a particular position and disparity, as illustrated in the sketches. The black blob indicates the region of space where the cell responds to stimuli. The complex cell (C) represents the sum of four simple cells (Ohzawa et al., 1990). Its binocular receptive field is elongated along the position axis, meaning that it displays the same tuning for disparity across a range of positions.

3.2. V1 helps to reduce the response to false matches

As discussed above, most V1 neurons respond with weaker modulation to disparity in anti-correlated stereograms. This behavior can be reproduced by a simple model in which inputs from the two eyes are passed through a threshold before being combined in V1 (Read et al., 2002a,b). Mathematically, this model also enables us to construct neurons which modulate more strongly to anti-correlated than to correlated stereograms. Yet such neurons are only rarely observed (Cumming and Parker, 1997). This suggests that there is a bias in the circuitry, tending to produce weaker modulation to anti-correlated stereograms rather than stronger. In effect, V1 is wired up so that it is likely to respond less to local correlations which will ultimately prove false than to correlations which will prove correct at a global level. Although a purely local mechanism cannot tell for sure which correlations are misleading and which correct, it can make a good guess based on local image statistics. In this view, V1 is adapted to respond best to the sort of statistical structure it is usually exposed to, and so is less well driven, on average, by highly unnatural stimuli like anti-correlated stereograms. As in the previous discussion about how local models could be tuned to disparity in random-dot patterns, the arguments are statistical in nature. A model cell may give a very strong response to a particular individual anti-correlated stereogram, but on average the departure from baseline will be smaller than to a correlated stereogram at the optimal disparity. This ameliorates, to some extent, the false matching problem noted by Fleet et al. (1996). Thus, while V1 considers only local information, it seems to be constructed so as to inhibit the response to potential matches which are likely to prove false on a global level. If so, this would be extremely useful pre-processing for whatever brain region ultimately solves the correspondence problem.

3.3. V1 is specialized for ecologically relevant disparities

Because our eyes are displaced horizontally, most disparities we encounter are horizontal. This is not to deny that vertical disparities occur, especially for extrafoveal stimuli viewed at an eccentric angle of gaze; indeed, they may play a critical role in visual perception (Backus et al., 1999; Berends et al., 2002; Brenner et al., 2001; Rogers and Bradshaw, 1993). However, during normal viewing, disparities are overwhelmingly near-horizontal (Read and Cumming, 2004). Previous discussions of this point have recognized two ways in which this anisotropy should manifest itself in an area specialized for binocular vision. First, it was suggested, for reasons which will be discussed in a moment, that disparity-selective cells should show predominantly vertical orientation tuning. Second, the range of tuning to horizontal disparities should be much wider than the range of tuning to vertical disparities, since we can detect much larger horizontal than vertical disparities (Nielsen and Poggio, 1984; Stevenson and Schor, 1997). For many years, it was believed that neither of these anisotropies occurred, casting doubt on whether disparity selectivity in V1 was really specialized for binocular vision at all. Recent evidence suggests that the second of these anisotropies does in fact occur, while the expectation of the first may be based on a over-simplistic understanding of how tuning to orientation and disparity are related.

3.3.1. The expected bias towards vertical orientation tuning is not found

Most previous workers have expected to find that disparity-selective cells are predominantly tuned to vertical orientations. This expectation arises because, in the energy model and its variants, two-dimensional disparity tuning is tightly coupled to orientation tuning. Neurons are sensitive to the orientation of stimuli such as bars and gratings because their receptive fields are elongated along an axis corresponding to the preferred orientation (Hubel and Wiesel, 1962); the preferred orientation is generally the same in both eyes (Bridge and Cumming, 2001; Read and Cumming, 2003c). This means that the cell is expected to respond to changes in disparity over smaller scales when these disparities are applied orthogonal to its preferred orientation than when they are parallel to it; Fig. 12 explains why. If sensitivity is defined in terms of gradient (change in firing rate per degree of disparity), then the cell should be less sensitive to disparity parallel to its preferred orientation. It is important to note that if sensitivity were instead quantified using a measure such as the disparity discrimination index (Prince et al., 2002b), then the cell would be equally sensitive to disparity along both axes.

Fig. 12.

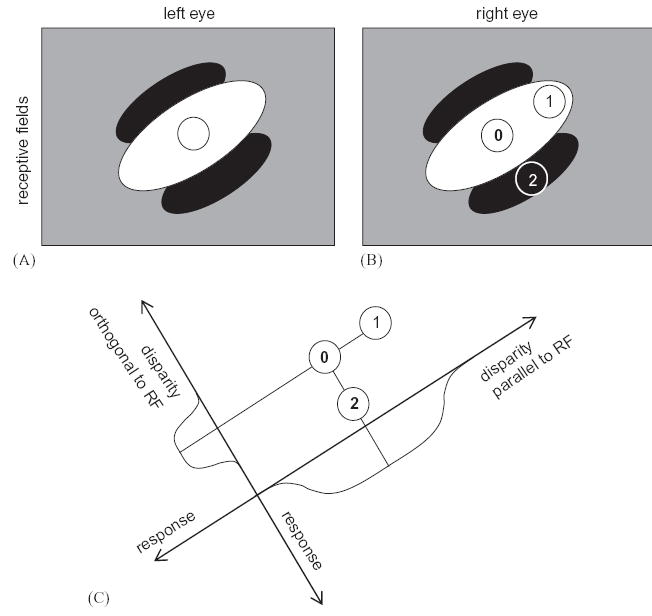
Models predict that neurons should be more sensitive to disparities orthogonal to their preferred orientation. (A,B) shows the receptive fields of a binocular neuron; the left- and right-eyes receptive fields (RFs) are identical, both consisting of a single long ON region oriented at 45° to the horizontal (shown in white) and flanked by OFF regions (black). We consider stimuli with three different disparities. In each case, the left eye’s image falls in the center of the left receptive field (circle in A). The different disparities occur because the right eye’s image falls at different positions for the three stimuli. These are labeled with numbers 0, 1, 2 in (B). In (C), the disparities of the three stimuli are plotted in disparity space. Stimulus 0 has zero disparity; its images fall in the middle of the central ON region of the receptive field in each eye and so it elicits a strong response. Stimulus 1 has disparity parallel to the receptive field orientation. Even though its image is displaced in the right eye, its images still fall within the ON region in both eyes, so the cell still responds strongly to both these stimuli. In consequence, the disparity tuning curve, showing response as a function of disparity parallel to receptive field (C), is broad. Conversely, stimulus 2 has the same magnitude disparity, but in a direction orthogonal to the receptive field orientation. Its image in the right eye falls on the OFF flank of the receptive field (B), so the binocular neuron does not respond. This leads to a much narrower disparity tuning curve (C); the response falls off rapidly as a function of disparity orthogonal to the receptive field. This means that the neuron is more sensitive to disparity orthogonal to its preferred orientation, in the sense that its response falls off more rapidly as a function of disparity in this direction (Read and Cumming, 2004).

The significance of this expected difference in sensitivity has been greatly overplayed, even leading to the erroneous claim that neurons cannot encode binocular disparity parallel to the receptive field orientation (Anzai et al., 1999; Matthews et al., 2003), and thus that neurons tuned to horizontal orientations are incapable of sensing horizontal disparity at all. Since most real disparities are horizontal, this led to an expectation that disparity-selective cells should show predominantly vertical orientation tuning (DeAngelis et al., 1995; Gonzalez and Perez, 1998; LeVay and Voigt, 1988; Maske et al., 1986a; Nelson et al., 1977; Ohzawa and Freeman, 1986b). In fact, it turns out experimentally that disparity-selective cells are as likely to be tuned to horizontal as vertical orientations, nor are vertically-oriented cells especially sensitive to interocular phase differences or position disparities (LeVay and Voigt, 1988; Nelson et al., 1977; Ohzawa and Freeman, 1986b, though see Menz and Freeman, 2004a). The failure to observe the expected bias was regarded as something of a puzzle, possibly suggesting that V1 was not specialized for the particular problems of binocular vision.

3.3.2. There is no reason to expect a bias towards vertical orientations

However, the expectation was based on flawed arguments. It is not true that neurons cannot encode disparity parallel to their preferred orientation. This misconception may stem from the common use of stimuli whose entire spectral power is at the preferred orientation of the cell, for example a one-dimensional grating stimulus aligned with the long axis of the receptive field. In this case, disparities applied parallel to the preferred orientation leave the stimulus unchanged, so the failure to encode such disparities is a consequence of the stimulus rather than a property of the neuron. The concentration on such stimuli may stem from the metaphor that striate neurons perform Fourier analysis of the visual stimuli. If receptive fields really were Fourier components, then they would extend across the entire retina, and they would indeed be unable to encode disparity parallel to their orientation. In fact, however, receptive fields are localized on the retina. With finite receptive fields, an energy-model unit encodes disparity both parallel and orthogonal to its preferred orientation; the encoding simply occurs over longer spatial scales parallel to the preferred orientation than orthogonal to it (Fig. 13).

Fig. 13.

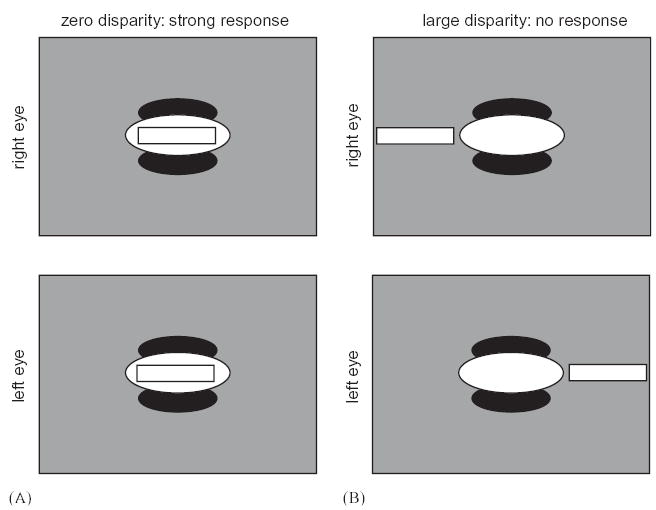
Cells tuned to horizontal-orientation can still encode horizontal disparity. The sketches show a horizontally-oriented receptive field in the left and right retina, with a bar stimulus superimposed. In A, the bar has zero disparity and falls over the ON subregion of the receptive field in both eyes, resulting in a high firing rate. In B, the disparity has been increased until the bar has moved off the receptive field in both eyes, so the cell does not respond. The cell thus encodes horizontal disparity in fundamentally the same way as a vertically oriented cell would, the only difference being that its disparity tuning curve has a larger spatial scale.

If the cells which were most sensitive (in the gradient sense) to horizontal disparity were the most useful for stereopsis, then this would be a valid reason for expecting a bias towards vertical orientations in disparity-selective cells. However, a population of broadly-tuned units can be equally capable of making fine discriminations as a population whose members have narrow tuning (Lehky and Sejnowski, 1990). Also, it has been clear since the earliest theoretical studies of stereopsis that there may well be a need for a population of cells encoding disparity on a range of spatial scales: the most sensitive cells may be important for achieving high stereoacuity, but the less sensitive cells, which encode disparity over long spatial scales, may be essential for disambiguating matches on smaller scales (Marr and Poggio, 1979). Thus, cells tuned to horizontal and vertical orientations may play different but equally useful roles in depth perception. This may be the reason why subjects can perceive slightly larger horizontal disparities in noise stimuli containing the full range of orientations than in “barcode” noise containing only vertical orientations (Read and Eagle, 2000). Simulations based on the energy model suggest that this improvement may be due to the additional contribution of cells tuned to oblique and horizontal orientations, which are activated by the broadband stimulus (Read, 2002b); cells tuned to horizontal orientations encode disparity over longer scales than equivalent cells which are vertically oriented, so that larger disparities can be detected in stimuli which activate these cells. There is psychophysical evidence that stereopsis, like other aspects of vision, proceeds through several different orientation channels, including horizontal (Mansfield and Parker, 1993). Finally, including effects such as end-stopping may further enhance the tuning of horizontally-oriented cells to horizontal disparity. This was suggested by Maske et al. (1986a,b), although their experiment did not control for the monocular effects of moving their bar stimulus.

Thus, it is not at all clear that an anisotropy favoring vertical orientations should ever have been expected, even if the energy model accurately described the relationship between preferred orientation and disparity tuning. Indeed, since vertical disparities in natural viewing are almost all close to zero, most cells should not only be tuned to zero vertical disparity, but also should quickly cease to respond as the stimulus vertical disparity moves away from zero, i.e. they should be highly sensitive to vertical disparity. This is important because, while real stimuli contain very few real vertical disparities, false matches are equally likely to have disparity in any direction. Thus, in order to reduce the response to false matches and ease the solution of the correspondence problem, it is essential to prevent cells from responding to local correlations at nonzero vertical disparities. From this point of view, then, one might have expected a bias towards horizontally-oriented cells, since according to the energy model these should be the most sensitive to vertical disparity.

3.3.3. Disparity tuning is decoupled from orientation tuning

Ironically, new evidence has revealed that these arguments are all based on a false premise. It turns out that V1 neurons are indeed typically more sensitive to vertical than to horizontal disparity, but in contrast with the energy model prediction, this occurs independently of preferred orientation (Cumming, 2002). The expected relationship between receptive field orientation and disparity tuning, which seemed so unassailable based on drawings like Fig. 12, does not hold (Gonzalez et al., 2003).

This is clearly useful for stereo vision. Natural stimuli contain power at all orientations; the decoupling of orientation tuning from disparity tuning means that high sensitivity to vertical disparity, and the consequent rejecting of false vertical-disparity matches, can be achieved for all visual elements, not just those oriented horizontally. However, it flies in the face of all previous models of disparity selectivity, and thus theoreticians face a new challenge in explaining how it is achieved. We have recently suggested two possibilities (Read and Cumming, 2004): (i) pooling inputs from several complex cells tuned to different horizontal disparities, in much the same way as inputs from several simple cells tuned to different stimulus positions are combined in the energy model (Ohzawa et al., 1990), or (ii) a form of end-stopping in which the monocular responses undergo gain control by horizontally-elongated suppressive regions (Freeman and Ohzawa, 1990; Maske et al., 1986a,b).

3.3.4. Disparity tuning has a wider range horizontally than vertically

We now turn to the more straightforward anisotropy: the expectation that V1 should be tuned to a wider range of horizontal disparities than vertical disparities. Suggestive evidence in support of this idea was provided by several receptive field mapping studies showing that interocular differences in the arrangement of receptive field subregions tend to be more pronounced for vertically-oriented cells (Anzai et al., 1999; DeAngelis et al., 1991; DeAngelis et al., 1995). According to the energy model, this observation should translate into a wider scatter in preferred disparities along the horizontal than along the vertical axis. However, disparity tuning was not directly measured in these studies, and as we have seen, the energy model is not always a reliable guide when it comes to predicting disparity tuning from orientation. Thus, to confirm the expected anisotropy, disparity tuning must be measured directly.

An early report that neurons in cat area 17 showed a wider range of tuning to horizontal disparities than to vertical (Barlow et al., 1967) was not backed up by subsequent studies (Joshua and Bishop, 1970; von der Heydt et al., 1978). The conflicting reports probably reflect the difficulty of measuring absolute disparity tuning in the anesthetized animal. Conversely, most studies in the awake monkey have used stimuli with only horizontal disparity, and so have not probed vertical disparity tuning. A recent study in awake macaque (Cumming, 2002), applying both vertical and horizontal disparities, supports the anisotropic distribution of preferred disparity: the spread in the horizontal component of preferred disparity (~ 0.9°) was much greater than the spread in the vertical component (~ 0.3°). This suggests that disparity tuning in V1 is indeed specialized towards extracting the information which will be most useful in depth perception.

3.3.5. V1 is specialized for horizontal disparities

Thus, the most recent studies confirm that V1 is indeed adapted for the horizontal disparities which overwhelmingly predominate in binocular vision. This adaptation occurs both at the population level (the distribution of preferred disparities has a wider range horizontally than vertically) and at the level of individual cells (cells maintain their response for a wider range of horizontal than vertical disparities, and are sensitive to small departures from zero vertical disparity). Here as elsewhere, theoretical models have been central in formulating expectations about how V1 should encode disparity. However, this has also sounded a cautionary note on the importance of testing theoretical intuitions. It seemed so obvious that disparity tuning must reflect the orientation tuning of the receptive fields that this was not experimentally tested for several decades. When it was, the experiment revealed that the “obvious” assumption was incorrect and that V1 neurons were specialized for horizontal disparity in a way not previously suspected.

3.6. V1 combines information across spatial scales

The brain processes visual information, including disparity, in a range of channels tuned to different spatial frequency and orientations (Campbell and Robson, 1968; Julesz and Miller, 1975; Shapley and Lennie, 1985). Soon after the correspondence problem was recognized, it was appreciated that this parallel processing might be especially useful in the case of stereopsis. This is essentially because different channels see different false matches, whereas all channels see the true match (Fleet et al., 1996). Thus, comparing information across channels provides a powerful way to work out which matches are correct. The first model to take account of this (Marr and Poggio, 1979) proposed a “coarse-to-fine” hierarchical algorithm, in which the correspondence problem is initially solved at coarse (low frequency) spatial scales, and the resulting matches are used to constrain finer resolution matches at the next stage. Subsequent psychophysical studies have supported the general idea of coarse-to-fine processing (Mallot et al., 1996b; Parker et al., 1997; Rohaly and Wilson, 1993; Smallman, 1995; Watt, 1987; Wilson et al., 1991), while ruling out the precise form of constraint proposed by early models (Rohaly and Wilson, 1993; Smallman and MacLeod, 1997). Many studies have also provided evidence that information at high frequencies can influence the perception of lower frequencies, suggesting the existence of a fine-to-coarse hierarchy as well (Mallot et al., 1996b; Rohaly and Wilson, 1994; Smallman, 1995). Until very recently, however, there was no evidence addressing how these non-linear cross-channel influences might be implemented in the brain.

While there is wide agreement on the need to combine disparity information across spatial scales, the details of how this is achieved are still unclear. A processing sequence such as coarse-to-fine can be understood either as a logical disambiguation hierarchy or a temporal sequence (Mallot et al., 1996a; Watt, 1987). In a temporal sequence, information from the coarser scales is processed first, and the results of this computation affect the subsequent processing of finer scales. Marr and Poggio’s original model (1979)1 was of this general form, and there is some psychophysical evidence suggesting a specifically temporal coarse-to-fine sequence (Parker et al., 1992, 1997; Watt, 1987). However, the hierarchy could also be purely logical, meaning that information from the coarser scales is used to help disambiguate the finer scales, without necessarily being processed earlier in time. One version of the stereo correspondence algorithm by Prazdny (1985) is of this form.

Very recently, Menz and Freeman (2003; 2004a,b) have suggested that both logical and temporal hierarchies may exist in primary visual cortex. Working in the anesthetized cat, they found that neurons with coarse disparity tuning tended to respond more rapidly to a visual stimulus than neurons with finer tuning. Furthermore, the disparity tuning of individual complex cells tended to evolve from coarser to finer scales during a 40 ms time-window (although the total frequency shift is only about 20% on average, 80% maximum, which is small compared to the estimated 1–2 octaves of a spatial frequency channel). Together, these effects mean that the cortex responds more rapidly to information at coarser spatial scales, with finer scales being processed later, supporting a temporal coarse-to-fine sequence. Menz and Freeman also studied the connectivity between pairs of cells. They found that the presynaptic cell more reliably elicited a spike in the postsynaptic cell when the presynaptic cell had coarser disparity tuning: that is, coarse-to-fine connections tend to be stronger. However, they also found fine-to-coarse connections, and though usually weaker, these were slightly more numerous than the coarse-to-fine connections. The average difference in frequency between the pre- and post-synaptic cells was around 20%, with the maximum around 60%.

Thus, once again, the properties of disparity-selective V1 neurons are well matched with the requirements of stereo perception: further evidence that they are specialized for this task. In agreement with the psychophysics, V1 neurons exhibit information transfer between spatial channels in both the coarse-to-fine and fine-to-coarse directions, while the specifically temporal sequence proceeds from coarse to fine scales. These cross-channel interactions presumably continue further in brain areas beyond V1, explaining why the disparities of spatial frequency components up to 2 octaves apart appear to influence each other perceptually (Rohaly and Wilson, 1993; Rohaly and Wilson, 1994; Wilson et al., 1991), whereas interactions in V1 appear to span less than an octave.

4. Extrastriate cortical areas

Although the computations performed in V1 are adapted in several ways to the requirements of stereo vision, we have seen that depth perception itself must occur outside V1. This section provides a brief overview of what is currently known about disparity processing in extrastriate cortex. Sensitivity to binocular disparity is found in many extrastriate areas, including V2, V3, V3A, VP, MT, MST and IT (Backus et al., 2001; Tsao et al., 2003b; see Gonzalez and Perez (1998) for a review). In recent years, several groups have begun to explore how disparity processing in extrastriate areas differs from that in V1. Evidence is emerging that extrastriate areas elaborate the initial encoding so as to extract ever more complicated and perceptually relevant stimulus properties. For example, whereas we saw above that V1 encodes absolute, not relative, disparity (Cumming and Parker, 1999), by V2, neurons begin to show sensitivity to relative disparity (Thomas et al., 2002). Second, V1 receptive fields appear to be organized so as to detect disparity in frontoparallel planes; the response to more complicated stimuli can be predicted simply by considering the average disparity present across the receptive field (Nienborg et al., 2004). In contrast, there is growing evidence that extrastriate areas are selective for more sophisticated depth structures. V2 neurons seem to respond selectively to disparity-defined edges (von der Heydt et al., 2000), a possible neural substrate for the use of stereo cues in scene segmentation (Julesz, 1971; Zhaoping, 2002). Neurons in V4 (Hinkle and Connor, 2002), in middle temporal cortex (Nguyenkim and DeAngelis, 2003) and the caudal intraparietal sulcus (Taira et al., 2000) are sensitive to the orientation of disparity-defined planes, and neurons in inferior temporal cortex (IT) are sensitive to the shape and curvature of disparity-defined surfaces (Janssen et al., 2001, 1999, 2000a,Janssen et al., b, Tanaka et al., 2001). This fits with the idea that higher brain areas extract more complicated features from the pattern of retinal disparities, and integrate stereo information into different perceptual systems. For example, disparity selectivity in parietal association cortex may support the use of stereo vision in guiding hand movements (Sakata et al., 1997), whereas disparity selectivity in IT may be important for object recognition (Uka et al., 2000).

Several recent studies have indicated a link between depth perception and neuronal activity in middle temporal cortex (MT). For example, microstimulating MT, with small amounts of electrical current, biases reported depth towards the preferred disparity of the stimulation site (DeAngelis et al., 1998). Several studies have used a “rotating cylinder” stimulus (see Parker and Krug (2003) for a description), which is particularly effective for MT neurons. Its interest is that in the absence of disparity the stimulus is bistable, like the Necker cube; it can be perceived as rotating either clockwise or counterclockwise. Adding appropriate disparity cues renders the rotation unambiguous. For the unambiguous stimulus, most MT neurons respond better to one sense of rotation than the other. Remarkably, in the ambiguous case, MT neurons respond according to the sense of rotation which is being perceived at the time (Bradley et al., 1998). That is, a neuron which usually prefers clockwise rotation will tend to fire more when the ambiguous stimulus is being perceived as rotating clockwise than when it is perceived as counterclockwise, even though the visual stimulus in the two cases is identical. Simply by recording a single neuron in MT, an experimenter can predict with around 70% accuracy the direction of rotation currently perceived by the monkey (Dodd et al., 2001). It is as yet unclear whether MT is itself the neural correlate of perception in these stimuli, or whether MT activity is read out by a still higher visual area. However, together these studies indicate a close link between MT activity and the disparity-based perception of depth and structure-from-motion. This contrasts with the situation in V1, where—although several lines of evidence appear to indicate that V1 performs the initial processing supporting depth perception—there is as yet no direct evidence ruling out other possibilities. It remains conceivable that disparity selectivity in V1 makes no contribution to depth perception, existing solely for other purposes such as vergence eye movements or binocular single vision. A microstimulation study like that of DeAngelis et al. (1998) would be hard to carry out in V1, which lacks the clustering of disparity preference found in MT (DeAngelis and Newsome, 1999; Prince et al., 2002b). It would therefore be difficult to ensure that microstimulation activated neurons with similar disparity tuning.

A key piece of evidence suggesting that V1 is not the neural substrate of stereo depth perception was that V1 neurons continue to signal disparity in anti-correlated random-dot patterns, indicating they are responding to false matches. It has recently been reported that neurons in IT do not respond to these false matches (Janssen et al., 2003), indicating that the correspondence problem has been solved at least by this stage of the ventral stream. A major effort of future research will be understanding where and how this occurs.

5. Outstanding questions

Even within V1, there are many aspects which we do not yet understand. For example, the temporal aspects of disparity tuning have only just begun to be addressed (Cumming and Read, 2003; Menz and Freeman, 2003, 2004b; Read and Cumming, 2003a). Furthermore, although the variety of V1 disparity-selective neurons has been extensively documented, we still do not understand what this variety achieves. Poggio and Fischer (1977) initially classified cells into four groups: tuned-excitatory, tuned-inhibitory, near and far, although more recently these have been interpreted as forming a continuum rather than distinct classes (Freeman and Ohzawa, 1990; Ohzawa et al., 1996; Prince et al., 2002a) (see Fig. 14). In one form of the energy model, known as the pure phase-disparity model (DeAngelis et al., 1991; Fleet et al., 1996; Zhu and Qian, 1996), left- and right-eye receptive fields are assumed to have the same retinal position, and tuning to non-zero disparity arises purely from differences in receptive field structure. In this model, the difference in receptive field structure (the phase disparity) determines both the preferred disparity, and the class of disparity tuning. In this view, therefore, the role of the tuned-excitatory and near/far classes is simply to provide tuning to a range of disparities. However, recent physiological evidence (Anzai et al., 1997; Anzai et al., 1999; Prince et al., 2002a; Tsao et al., 2003a) has tended to favor a hybrid model, incorporating both position and phase disparity. In this view, tuning to non-zero disparity could be achieved with position disparity alone, so the different classes are not necessary for this purpose. One possibility is that the different classes have no significance, but simply arise due to random connections between receptive fields with slightly different structures and retinal positions. Phase disparity may arise during development in order to cancel out the inevitable position disparity arising from random jitter within the topographic map, so as to obtain receptive fields whose ON and OFF subregions are in register as much as possible (Erwin and Miller, 1999; Parker, 1991).

Fig. 14.

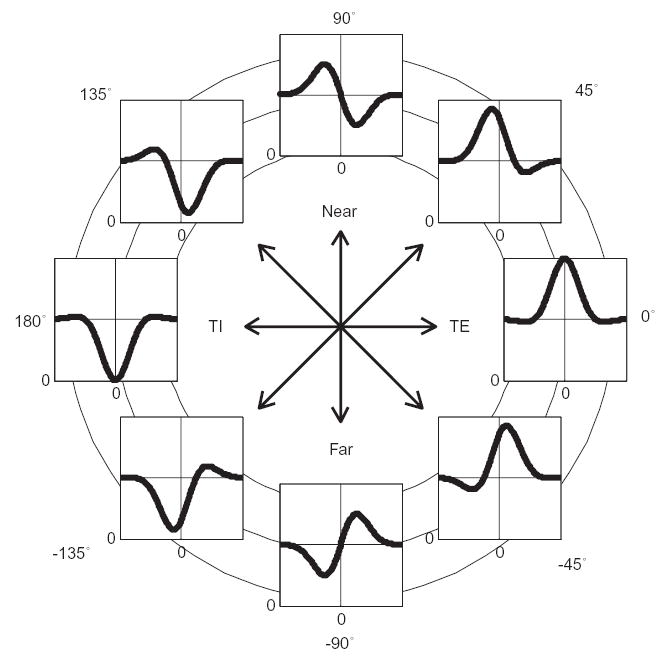
Idealized members of Poggio and Fischer’s (1977) four classes of disparity tuning: tuned-excitatory, near, tuned-inhibitory, and far, showing how they form part of a continuum. In each graph, the horizontal axis is disparity and the vertical axis is response rate. The curves are Gabor functions (the product of a cosine and a Gaussian); the angle represents the phase of the cosine component. Figure reproduced from Read and Cumming (2003b).

However, it is also possible that the different classes are specifically designed to play distinct roles. This is hinted at by the finding that “odd-symmetric” tuning, corresponding to the near/far classes of Poggio and Fischer (1977), is much commoner in MT than in V1 (DeAngelis and Uka, 2003). In the model of Lehky and Sejnowski (1990), near and far neurons, arranged so that the steepest part of their disparity tuning curves occur near zero disparity, play an important role in achieving high stereoacuity near zero disparity. Poggio and Fischer (1977) suggested that the different classes of neurons, as well as supporting depth perception, might also play distinct roles in the control of eye movements, with the far neurons initiating convergence, the near neurons initiating divergence, and the tuned-excitatory neurons helping to keep the target fixed on the fovea. No one, however, has yet suggested a specific role for the tuned-inhibitory neurons, which make up 10–20% of disparity-selective neurons (Poggio and Fischer, 1977; Read and Cumming, 2003b).

The different classes of tuning will certainly have to be taken into account by higher brain areas which “read out” V1 activity. Understanding how input from V1 is interpreted by the different brain areas to which it projects is the major challenge currently facing theories of stereopsis. Although several physiologically-based models have been proposed (Fleet et al., 1996; Grossberg, 1994; Grossberg and Howe, 2003; Lehky and Sejnowski, 1990; Lippert and Wagner, 2002; Matthews et al., 2003; McLoughlin and Grossberg, 1998; Mikaelian and Qian, 2000; Prince and Eagle, 2000; Qian, 1994, 1997; Qian and Andersen, 1997; Read, 2002a,b; Tsai and Victor, 2003; Watanabe and Idesawa, 2003; Zhaoping, 2002), much work remains to be done in tying these theories more closely to the known physiology, and expanding them to provide a complete account of stereoscopic perception.

6. Conclusions

Primary visual cortex, V1, contains a population of neurons specialized for binocular vision. It does not itself solve the global correspondence problem and is not the neural correlate for depth perception. The response of V1 neurons appears to be determined only by the pattern of light within a localized region of the retina (the “receptive field”, interpreted broadly to include any surround regions, as well as the classical receptive field). At least in the disparity domain, there is no evidence that V1 neurons are sensitive to the global context of the stimulus, even though this can have profound effects on perception. However, several features indicate that the convergence of monocular inputs in V1 does not occur randomly, but rather is designed to achieve the specific encoding of horizontal disparity. The most likely interpretation is that V1 performs early preprocessing which is used to support binocular vision in higher visual areas. Just as the retina is not the neural correlate of vision, but performs extensive pre-processing which enables visual perception in higher stages of the visual system, so V1 may contain a kind of “cyclopean retina”. Whereas photoreceptors sense the amount of light falling on the retina, disparity-tuned neurons in V1 may perform an analogous function in sensing the degree of local interocular correlation.

Progress in understanding binocular vision has been greatly aided by the development of quantitative models tightly coupled to the physiology. First, modeling has been important in clarifying logic. For example, it was initially thought that neurons which respond to disparity in random-dot stereograms must have solved the correspondence problem; the construction of a purely local model which shows the same property demonstrates that this reasoning is flawed. Similarly, if it were impossible to build a local model which produced weaker responses to anti-correlated than to correlated random-dot patterns, then this property of V1 neurons would be strong evidence that they are sensitive to global properties of the stimulus, such as whether a solution of the correspondence problem exists. The conclusion that V1 neurons are, in fact, insensitive to the global properties of the stimulus rests partly on the success of local models in capturing their response. It is critical that models should be tightly tied to experiment; the failure to experimentally test predictions relating disparity tuning to orientation led an important aspect of V1 processing to be overlooked for many years. But when models are linked to experiment, the results can be extremely productive; indeed, suggesting critical experiments is one of the most important roles of quantitative modeling. For example, the fact that the energy model responds to disparity in anti-correlated stereograms inspired the use of these stimuli to probe whether the correspondence problem is solved in V1, and the first demonstration that it is not. Quantitative models may be practically useful, if new biologically inspired computer algorithms lead to more reliable extraction of depth, for example in satellite imaging. Finally, quantitative models represent a mathematical description of the pre-processing performed by V1. This is an essential foundation which enables us to begin to explore how higher visual areas may further process the outputs from V1 so as to produce a global solution of the correspondence problem and, ultimately, perception of depth. In summary, stereo vision is a multidisciplinary field in which a combination of physiology, psychophysics and mathematical modeling is fast progressing towards the goal of understanding how neuronal activity gives rise to perception.