Aligning Paramecium caudatum with Static Magnetic Fields

Abstract

As they negotiate their environs, unicellular organisms adjust their swimming in response to various physical fields such as temperature, chemical gradients, and electric fields. Because of the weak magnetic properties of most biological materials, however, they do not respond to the earth's magnetic field (5 × 10⁻⁵ Tesla) except in rare cases. Here, we show that the trajectories of Paramecium caudatum align with intense static magnetic fields >3 Tesla. Otherwise straight trajectories curve in magnetic fields and eventually orient parallel or antiparallel to the applied field direction. Neutrally buoyant immobilized paramecia also align with their long axis in the direction of the field. We model this magneto-orientation as a strictly passive, nonphysiological response to a magnetic torque exerted on the diamagnetically anisotropic components of the paramecia. We have determined the average net anisotropy of the diamagnetic susceptibility, Δχ_p, of a whole Paramecium: We show how the measured Δχ_p compares to the anisotropy of the diamagnetic susceptibilities of the components in the cell. We suggest that magnetic fields can be exploited as a novel, noninvasive, quantitative means to manipulate swimming populations of unicellular organisms.

INTRODUCTION

Swimming unicellular organisms exhibit a variety of “tactic” and “kinetic” behaviors in imposed fields (1). In response to chemical gradients (2–4), variations in illumination (5–7), gravity (8–10), and electric fields (11,12) they may change their swimming direction or speed or modify the rate at which they change direction. Most often, these chemotactic, phototactic, gravitactic, and galvanotactic responses are active responses. They reflect a physiological sensitivity to these fields and depend on an underlying chemomechanical network that controls the reaction. An example of an active response is that displayed by a Paramecium in a DC electric field. It orients with the field and swims toward the cathode due to a change in its membrane potential. This phenomenon is not observed in nonswimming Paramecium (11). On the other hand, there also exist passive responses for which a physical field such as gravity may directly orient an organism without eliciting a physiological change (13–15). Although these responses are simpler, they can still provide survival advantages. Also, the passive responses of cells can be exploited for the benign manipulation and/or trapping of cells as has been done with magnetic and optical tweezers (16–18). Thus, cells can be studied without modifying their physiology.

Here, we demonstrate that static magnetic fields exert torques on elongated mobile and immobile cells (paramecia) without eliciting an active response. Because these torques can be calibrated and adjusted, they have potential as a noninvasive tool to measure the “tactic” active responses of cells to other external stimuli. Specifically, we present investigations of the response of Paramecium caudatum to intense, homogeneous, DC magnetic fields (the response of Paramecium to alternating magnetic fields has been studied before (19,20)). We show that the trajectories of motile paramecia curve and nonswimming paramecia turn to become aligned with intense static magnetic fields in excess of ∼3 Tesla (T). We successfully model these phenomena as a passive rotational response to the net torque that the magnetic field exerts on rigid, diamagnetically anisotropic structures in the cell cortex. The magnetic fields do not induce swimming speed changes that one could associate with a physiological response.

MATERIALS AND METHODS

Paramecium and experimental chambers

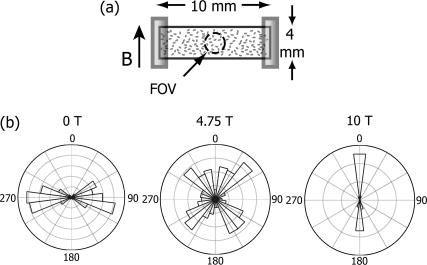
Paramecium caudatum was cultured on Hey medium and collected for experiments during their stationary phase of growth. They were collected using their gravitactic property and suspended in test solution (1 mM CaCl₂, 1 mM KCl, 0.1 mM MgSO₄, 1.5 mM MOPS, pH 7.2) 1–2 h before experimentation to adapt. Two different types of experimental chambers were employed. Both had a depth (2 mm) that was much smaller than the width and the length to provide a nearly two-dimensional environment. The first type was chosen to be square to eliminate asymmetries arising in the swimming track distributions due to the geometry of the chamber (21). These chambers, depicted in the inset of Fig.1 e, were made of an acrylic frame of 2 mm depth and 20 × 20 mm area. Both sides of the frame were covered with a microscope slide and sealed with 5-min epoxy glue. The chambers were flushed a few times with water and tested to be harmless to paramecia. Solution containing paramecia was injected with a syringe through holes on one side of the frame. These holes were later sealed with VALAP (1:1:1 vaseline, lanolin, and paraffin). The second type of chamber had a rectangular geometry. These were made from a borosilicate rectangular tube (VitroCom, Mountain Lakes, NJ) (2 × 4 × 10 mm) with ends sealed with acrylic caps (Fig. 5 a).

FIGURE 1.

Orientation of the trajectories of paramecia in a magnetic field. Panels a and b are the tracks at B = 0 T and B = 9 T, respectively. Each track consists of a series of displacement vectors recorded at 5 frames per second. Panels c and d are circular histograms of the track orientation for panels a and b, respectively; the bin size is 15°. (e) Order parameter 〈m〉 as a function of the magnetic field; 〈m〉 = 1 indicates perfect alignment. The curve is to guide the eye. (Inset) A sketch of a square sample chamber and its orientation with respect to the magnetic field. The field of view is depicted as a dashed circle.

FIGURE 5.

Orientation histograms of trajectories in a rectangular chamber. (a) Sketch of a rectangular chamber observed from the side. The dashed circle depicts the field of view. (b) Orientation histograms at three different fields.

Paramecium tetraurelia, kindly provided by Professor Judith Van Houten, were cultured on wheat grass and collected in the stationary phase. We performed two sets of behavioral experiments on them using the above-mentioned test solution and a test solution low in K⁺ (1 mM CaCl₂, 0.5 mM MgSO₄, 2 mM Tris-HCl, pH 7.2 (22)).

Paramecia were immobilized by being suspended in a 0.5-mM solution of NiCl₂ for 10–15 min (8). After immobilization, individual cells were transferred with a micropipette into the experimental chamber. Ficoll (Ficoll 400, Sigma-Aldrich, St. Louis, MO) solution with 11% w/v concentration was used to provide a neutrally buoyant solution for the paramecia. The viscosity of Ficoll solution was estimated to be at (20±2)°C (23) (the temperature during the experiment).

Apparatus

The experiments were performed using two magnets: a 50-mm bore, 25-T maximum field, resistive magnet at the National High Magnetic Field Laboratory and a superconducting solenoid (American Magnetics, Oak Ridge, TN) with an 11-mm room temperature bore and a maximum field of 9 T.

Paramecia were observed through a 6-mm diameter, side view, borescope (Instrument Technology, Westfield, MA). Their motions were recorded using a VCR and a charge-coupled device camera (Sony XC-333). Green light (565 nm, Luxeon V star LED, Lumileds Lighting, LLC, San Jose, CA) along with 3 × 1 mm optical fibers were used for illumination (a similar setup is described elsewhere (24)). A frame grabber (EPIX, Buffalo Grove, IL) was used to digitize the movies at five frames per second for 3-min intervals. Associated software (XCAP, EPIX, Buffalo Grove, IL) was used to calculate the trajectories of swimming paramecia. Further analysis was done using custom Matlab (The Mathworks, Natick, MA) codes.

The orientation of a Paramecium's trajectory was defined to be the direction of the axis of its helical motion (26,27). After a couple of helical periods, this orientation closely coincides with the orientation of the displacement vector of the total trajectory. Only trajectories that extended a couple of periods or more were analyzed. The angles of individual trajectories, θ_i, were measured relative to the magnetic field direction. Because some paramecia reverse their direction or make abrupt turns due to avoiding reactions, a filtering procedure was used to eliminate those tracks (on average, ∼15% of the total tracks).

RESULTS AND ANALYSIS

The magnetic field induced modification of the trajectories of motile paramecia is demonstrated in Fig. 1. Swimming tracks in 0 T (Fig. 1 a) are randomly oriented and form straight helical trajectories. In 9 T (Fig. 1 b) the tracks remain helical and straight but largely align parallel or antiparallel to the magnetic field direction. The histograms of the orientations reinforce these observations showing that the tracks in 0 T are oriented at all angles whereas the tracks in 9 T align to within 7.5° of the magnetic field axis. The asymmetry in the number of upward and downward swimmers in the histograms can be attributed to the fact that the average downward swimming speed exceeds the average upward swimming speed because of sedimentation. In order for the downward flux of paramecia to equal the upward flux the number of downward swimmers must be smaller than the number of upward swimmers.

We characterize the degree of alignment in different magnetic fields by using a two-dimensional, uniaxial order parameter (28) 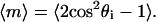The angular brackets denote an average over the track distribution. For a set of tracks that are perfectly aligned parallel or antiparallel with the field, Perpendicular and random alignments yiel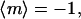d and 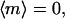respectively. It is important to emphasize that describes orientation along an axis and, thus, differs from the orientation coefficient employed in gravitaxis studies, which describes orientation along a specific direction (8). The dependence of on B in Fig. 1 e shows that the tracks are substantially aligned near 4.5 T and completely aligned at 9 T.

To help determine whether the magnetic field induced alignment is a passive (purely physical) or an active (physiological) response we investigated the effect of magnetic fields on immobilized Paramecium. Fig. 2 a shows a time series of images of an immobilized, neutrally buoyant Paramecium in a Ficoll solution in a 4-T magnetic field. Before being placed in the magnet, this cell was oriented horizontally (perpendicular to the magnetic field) by the use of a thin rod. Once in the magnet it rotated to vertical over the course of ∼4 min (the viscosity of the Ficoll solution was 6.5 times the viscosity of water). The time dependence of this rotation and those observed at other magnetic field strengths for the same cell are shown in Fig. 2 b. At higher fields the rotation occurs more rapidly and the rate of rotation is largest near 45°. Thus, even nonswimming Paramecium align with a magnetic field in the Tesla range in a manner that depends on field strength. This result suggests that the magnetic alignment of motile paramecia is passive.

FIGURE 2.

Orientation of immobilized Paramecium by a magnetic field. (a) Image sequence of a nonswimming neutrally buoyant Paramecium in a 4-T magnetic field in Ficoll solution. (b) Orientation rate as a function of time; t = 0 is set for θ = 45°, θ is defined by the inset. (c) ln (tanθ) versus scaled time, where B₀ = 6.4 T. Δχ_p is measured from the slope of the fitted dashed line (see Eq. 1).

Experiments on blood cells and other nonmagnetic biomaterials indicate that the magnetic torque acting on the immobilized Paramecium could result from the interaction of the magnetic field with its diamagnetically anisotropic components (29–32). In principle, magnetic fields can also exert a torque on cells with a completely isotropic magnetic susceptibility provided their shape is anisotropic. We neglect this effect as Roberts has estimated that fields near 100 T would be required to turn paramecia using just the shape torque (33). Thus, presuming a cylindrically symmetric cell, the magnetic torque is where Δχ_p is the net anisotropy of the diamagnetic susceptibility of a Paramecium cell (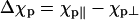), θ is the angle between its long axis and the magnetic field (see Fig. 2), and μ₀ is the magnetic permeability (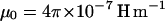). Because the rotations occur at low Reynolds numbers, the orientation rate is linearly proportional to the torque, that is 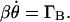β is the drag coefficient for rotation about a minor axis. Integration yields:

(1)

We compare the data to this prediction in Fig. 2 c by plotting ln(tanθ) versus a rescaled time axis where the scaled time is defined as For the set of experiments in Fig. 2 b, we chose B₀ = 6.4 T as the basis for scaling. With this scaling, the data collapse on a single line, suggesting that the model applies. The slope of the fitted line in Fig. 2 c is used to estimate Δχ_p. The drag coefficient for rotation around the minor axis of a solid ellipsoid of revolution is given by: (34) (for Paramecium the semiminor axis, a = 20 × 10⁻⁶ m and semimajor axis, b = 100 × 10⁻⁶ m). The results of trials performed on three different paramecia were (5.9 ± 0.6) × 10⁻²³ m³, (7.1 ± 1.4) × 10⁻²³ m³ and (6.9 ± 1.5) × 10⁻²³ m³, respectively, with the resulting mean value of In a 4-T magnetic field, this value of diamagnetic anisotropy yields a magnetic potential energy or 10⁵×k_BT indicating that the orientation is completely athermal.

To investigate the origin of the alignment of motile paramecia we analyzed the trajectories of individuals upon their takeoff from the boundary of a chamber. Normally, paramecia take off at random angles and execute straight trajectories. In magnetic fields, however, their trajectories curve toward the axis defined by the magnetic field. This phenomenon is shown in the inset of Fig. 3 a. Notice that the curvature appears for both upward and downward swimmers. Qualitatively, this behavior is expected for a passive response to the magnetic torque described above. The torque superimposes a rotation on the normal translation of the Paramecium. We have tested this effect quantitatively.

FIGURE 3.

Swimming trajectories in magnetic field. (a) A set of trajectories with the same initial angles in the magnetic fields indicated. The dashed lines are fits of Eq. 3 to the data. (Inset) A downward and an upward trajectory in a 4.6-T field. The dashed line depicts the boundaries of the chamber (scale bar, 500 μm). (b) Δχ_p values obtained from fits to trajectories as a function of magnetic field; the dashed line is a linear fit to Δχ_p vs. B.

In our model, a motile Paramecium of density ρ experiences a total forc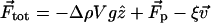e where ρ₀ is the density of the liquid, g is the acceleration due to gravity, is the propulsion force, ξ is the linear drag coefficient, and v and V are the swimming speed and the volume of the Paramecium, respectively. We presume that F_p is directed along the long axis of the Paramecium. This approximation neglects the torques and resulting angular velocities (26,35) that give rise to the helical motion that is superimposed on their normal, relatively straight trajectories. It reduces the number of fitting parameters and is justified by the quality of the fits. Because at low Reynolds number the total force is zero, the equation of motion is:

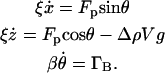(2)

Integration of the equations gives:

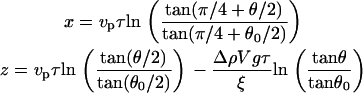(3a)

(3b)

where ξ = 6πη/5(4a + b) for an ellipsoid (36), 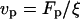is the propulsion speed (37), 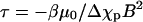and θ₀ is the initial angle.

Fig. 3 a shows examples of a set of tracks with similar takeoff angles (symbols) and their respective fits (dashed lines) using the three free parameters, v_p, θ₀, and Δχ_p. Fig. 3 b shows the values obtained for Δχ_p for a number of tracks as a function of magnetic field. The results of averaged values of Δχ_p and v_p are summarized in Table 1. Notice that Δχ_p varies little as the field increases from 3 to 10 T (a 10-fold increase in torque). At 17.6 T, however, Δχ_p is significantly lower. This field turns paramecia in less than a helical period, which may render our simplified equations of motion invalid. Excluding the result for 17.6 T, the average Δχ_p for swimming paramecia is (8.3 ± 0.9) × 10⁻²³ m³, which is comparable to the values obtained for the immobilized paramecia.

TABLE 1.

Trajectory data

B (T)	Number analyzed	〈Δχp〉* × (10−23) m3	σ** × (10−23) m3	〈vp〉 (μm/s)
3	39	9.4 ± 0.9	5.3	908 ± 17
4.8	55	8.0 ± 0.3	2.7	920 ± 15
7.2	43	8.5 ± 0.3	2.2	920 ± 13
10.1	43	7.5 ± 0.2	1.5	940 ± 15
17.6	15	5.4 ± 0.6	2.2	874 ± 12

^*The error is the standard deviation of the mean.

^**σ is the standard deviation.

Finally, this passive model suggests how the orientation distributions presented in Fig. 1 arise. Without a magnetic field, the tracks have all orientations implying that there are collisions that randomize their swimming directions. At the low Paramecium densities used in these experiments, these collisions most likely occur with the walls rather than with other paramecia. In a magnetic field, these randomly oriented trajectories turn to align with the magnetic field as they swim toward the field of view. The longer they swim or the stronger the field, the more aligned they become. Using this idea, we have simulated the evolution of the distribution in magnetic field. We start with a random distribution of orientations and let each orientation change with time according to Eq. 1. By iteration we obtain a characteristic time τ_c, at which the calculated and measured values of 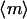are comparable (Fig. 4). For the data shown in Fig. 1 e, τ_c ≈ 10 s. This characteristic time corresponds to a characteristic length l_c, traveled by the organism that is estimated by 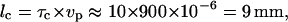where v_p is the ∼900 μs⁻¹. This length is nearly identical to the distance that a Paramecium swims to reach the field of view (center of the chamber) coming from the wall.

FIGURE 4.

Order parameter of the square and the rectangular chambers. The crosses are the measured values of and the open symbols are from the simulation described in the text.

We have performed a similar analysis on data obtained using a rectangular shaped container (Fig. 5 a). The associated orientation histograms at different magnetic fields are shown in Fig. 5 b. Notice that at 0 T the distribution is no longer random but oriented along the long dimension of the chamber. Such geometrical effects have been observed previously but their origin is not well understood (21). Fig. 4 shows measured and simulated values of for the rectangular chamber. The simulation employed the 0-T orientation distributions as the initial distribution and evolved it in time using Eq. 1. Two characteristic times were necessary for fitting the data. We found that for < 0 ( T), which corresponds to more horizontal than vertical swimmers, τ_c ≈ 6 s provided a good fit (open triangles in Fig. 4). On the other hand, for which corresponds to more vertical than horizontal swimmers, τ_c ≈ 2 s provided a good fit (open diamonds in Fig. 4). Accordingly, the characteristic length over which the horizontal swimmers can turn in B is l_h = 5.4 mm, which is substantially longer than the length over which vertical swimmers can turn l_v = 1.8 mm. These two lengths correspond to the halfwidth and halfheight of the experimental chamber (where our field of view was located). This simple approach provides an explanation for the orientation of a distribution based on magnetic torque model and reinforces that the swimming trajectories are oriented through a passive mechanism.

DISCUSSION

This work shows that the trajectories of motile Paramecium caudatum align with intense static magnetic fields exceeding ∼3 T. Since immobilized paramecia also align and the time dependence of their alignment is comparable to that of motile paramecia, the latter appears to be a passive response to the magnetic torque. That is, the torque acts on the whole Paramecium and not on some sensing organelle that dictates changes in the direction of swimming. The details of the time dependence of the rotation are consistent with a magnetic torque that is proportional to B²sin2θ, where θ is the angle between the long axis of the Paramecium and the magnetic field. This dependence intimates that the torque originates in an interaction between the magnetic field and a net anisotropy of the diamagnetic susceptibilities of the constituents of the paramecia.

The result that paramecia respond passively to magnetic fields of the intensity used in our experiments was not predictable. It was at odds with the suggestions made by Rosen and Rosen based on their experiments on Paramecium bursaria in moderate static magnetic fields (0.13 T) (38). They observed the magnetic field to induce changes in swimming speed and thus, to exert a physiological influence. They speculated that the magnetic fields change the cilia beating pattern by affecting the ion fluxes across the membrane. This alteration could occur if the magnetic field were to distort the membrane shape (39,40). Speed changes might also result from magnetic torques exerted directly upon the beating cilia. We saw no clear evidence of speed changes in our substantially larger data set (Table 1) or of altered swimming mechanics. Perhaps, the effect of the high magnetic fields employed in our experiments outweighs these lower field influences considered earlier.

The passive alignment of motile paramecia with magnetic fields differs from that exhibited by magnetotactic bacteria (15). The bacteria swim parallel to much weaker magnetic fields that are of order 10⁻⁴ T or less. The magnetic torque acts directly on internal chains of permanently magnetic magnetite particles or “magnetosomes” that are rigidly fixed to the bacterium. Also, they only swim toward a specific magnetic pole because the torque on a permanent magnetic dipole has a sinθ dependence. By contrast, the induced magnetic moment in paramecia orient them toward both poles because their torque has a sin2θ dependence.

In our model of the magnetic reorientation of motile Paramecium, we have been able to neglect the influence of gravitational torques. Gravitational torques can arise because of shape asymmetry (14) and/or internal density inhomogeneities and tend to orient the Paramecium parallel with the gravity vector. In our experiments, the gravity vector and magnetic field vector are parallel. The gravitational torque is of the general form: 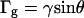(41). Mogami et al. (41) experimentally determined γ =0.09 rad s⁻¹ for Paramecium caudatum, but point out that this value depends on the age of the cells, which affects their shape and internal density variation. This value for γ would give rise to a considerable alignment (order parameter 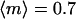) at 0 T for the characteristic time τ_c = 10 s of our experiments. However, our data show a close to random distribution at B = 0 T (Fig. 1 e). We conclude that for our paramecia, γ ≪ 0.09 rad s⁻¹ and thus, ignoring gravitational torques is justified.

Given that the alignment appears to be a passive, diamagnetic response, we consider whether the measured anisotropy in the diamagnetic susceptibility, Δχ_p, is reasonable. We start by identifying the structures that are most likely to couple to the magnetic field. Such structures must be rigidly set relative to the Paramecium. Their superposition must possess an axis of symmetry coincident with the long axis of the Paramecium. The structures in the cytoplasm, including the nuclei and contractile vacuoles do not exhibit much symmetry or rigidity and thus, seem unlikely targets. The most obvious candidates are structures associated with the cortex of the Paramecium. The cortex, which envelops the cell, is 4-μm thick, constitutes 40% of the total cell volume and is responsible for its rigidity (42). The overall structure of the cortex is quite uniform except in the region near the oral groove. Thus, it has the required overall symmetry. Electron micrographs have revealed that the cortex is composed of nearly identical units ∼1 μm² in area that are connected to each other in a mosaic pattern in plane with the surface of the Paramecium. Each “cortical unit” includes cilia, trychocysts, plasma membrane, cortical microtubules, and fibrils (43), all of which have anisotropies in their diamagnetic susceptibilities. It is therefore plausible that a cortical unit has a net anisotropy in its diamagnetic susceptibility, Δχ_cu (assuming the units are cylindrically symmetric). If Δχ_cu < 0, then the superposition of all units produces Δχ_p > 0 so that paramecia align with a magnetic field.

How large is Δχ_cu and is its value reasonable? To address this question, we model the cortex of a Paramecium as a cylindrical tube with a 20-μm outer radius and 200-μm length with hemispherical endcaps (see Fig. 6). The energy difference between parallel and perpendicular alignments with the magnetic field is proportional to Δχ_cuN_cu/2, where N_cu is the number of cortical units in the cylinder. Estimating N_cu = 25,000 and equating this to 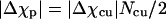yields Δχ_cu = −5.4 × 10⁻²⁷ m³ (we have used Δχ_p = 6.7 × 10⁻²³ m³). To determine whether this value is realistic, we compare it to the anisotropy of the diamagnetic susceptibility of microtubules. The total anisotropy of the diamagnetic susceptibility of perfectly aligned microtubules filling a volume equivalent to the volume of a cortical unit is 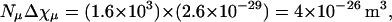where N_μ is the number of microtubules filling a cortical unit and Δχ_μ is the anisotropy of the diamagnetic susceptibility of a 5-μm-long microtubule (44). This result suggests that if all the material in the cortical unit has approximately the same anisotropy of the diamagnetic susceptibility as a microtubule then 14% of the total material would have to be aligned to give rise to the observed Δχ_cu. Consequently, we conclude that the measured Δχ_p is reasonable.

FIGURE 6.

Schematic of simplified cortex and a cortical unit. (a) The outer radius is 20 μm and the inner one is 16 μm. A cortical unit is shown with its long axis perpendicular to the cell surface. (b) Orientation energy of the cell is the difference between the two depicted orientations.

One might expect many other swimming elongated, unicellular organisms to orient in a static magnetic field on the basis of the analysis above and measurements on other cell types (31). Indeed, we have observed that the trajectories of Paramecium multimicronucleatum and Paramecium tetraurelia align along magnetic field lines at similar field strengths. Others (22) reported that P. tetraurelia align perpendicular to weak magnetic fields (0.68 T) in test solutions low in K⁺, but we could not reproduce that result. In our model, the cell walls of the organisms only need to be homogeneous and composed of diamagnetically anisotropic material. A simple scaling argument based on Eq. 1 suggests that even very small organisms could be observed to align. The characteristic time for alignment scales as the rotational drag over the magnetic torque. Because the magnetic torque scales with the cell volume, then this characteristic time depends linearly on the ratio of the long axis to the short axis of a cell (i.e., b/a). Within this picture, only random thermal fluctuations would prevent the smallest cells from aligning. Scaling down from Paramecium, cells as short as 4 μm with a 0.8-μm diameter have an estimated magnetic energy equivalent to the thermal randomizing energy, k_BT, at 5 T. Interestingly, there is evidence that the bacteria, Escherichia coli (length = 1 μm and diameter = 0.5 μm), align completely within tens of seconds in fields of ∼12 T (45).

The capability to exert a calibrated, noninvasive torque on a population of swimming organisms has potential as a tool to aid investigations of their responses to other fields or perturbations. For instance, the galvanotactic response of paramecia involves a reorientation, whenever the applied electric field changes direction. This reorientation necessarily requires paramecia to exert a turning torque. The strength of this turning torque can be measured directly by balancing it with a magnetic torque. Thus, an active response can be measured using the passive response to a magnetic torque.

Moreover, magneto-orientation can be used to direct a population of swimming paramecia. This can be extremely helpful in studying the “kinetic” responses of paramecia to other fields such as gravity or chemical gradients, because it can yield a large population of directed swimmers. For example, Paramecium caudatum exhibits a small negative gravikinesis. Upward swimmers propel themselves forward harder than downward swimmers (8,46–48). This behavior has received a great deal of attention as it is an example of gravisensitivity at the single cell level (49–51). It can be difficult to measure, however, because it requires statistical vector analysis of a large number of swimming tracks that are oriented in random directions. To simplify matters, Machemer came up with the elegant idea of applying a second physical field to align the swimming along the gravity vector (8). He exploited the galvanotactic response of the paramecia to create populations of either upward or downward swimmers. Unfortunately, the active response to the electric fields, which includes speed changes, complicated the analysis of the active gravitational response. By using magneto-orientation in gravikinesis experiments one can enjoy the benefits of Machemer's approach without the complications introduced by the superposition of two active responses.

CONCLUSIONS

We have shown that with intense static magnetic fields of over 3 T we can manipulate the swimming direction of microorganisms. The orientation of motile paramecia by magnetic field was modeled successfully as a passive reaction to a magnetic torque exerted on diamagnetically anisotropic, structurally rigid components of the cells. The quality of the fits to this model indicates that the influence of other possible orienting mechanisms is negligible. The orientation of immobilized Paramecium with the field confirms that the orientation is a passive response and thus, no physiological networks are involved in this reaction. We have attributed the required net anisotropy of the diamagnetic anisotropy, Δχ_p, to structures rigidly fixed within the cell cortex. The shape asymmetry of the cell and hence, its cortex and the sign of the anisotropy of each of the cortical units combine so that paramecia experience a net torque aligning their long axis with a magnetic field. We envision using this noninvasive physical field in conjunction with other fields such as chemical gradients or gravity in quantitative studies of the sensitivity of Paramecium to their stimuli.