Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2006 Feb 3;90(8):2718–2730. doi: 10.1529/biophysj.105.073304

Size, Motion, and Function of the SecY Translocon Revealed by Molecular Dynamics Simulations with Virtual Probes

Pu Tian 1, Ioan Andricioaei 1
PMCID: PMC1414555  PMID: 16461399

Abstract

We report a hybrid, coarse-grained and atomistic, molecular dynamics simulation study of the size, motion, and function of the SecY protein-conducting channel. Growing and pushing virtual soft ball constructs through the pore of SecY, we mimic the push-through of polypeptides, performed cotranslationally by the ribosome and posttranslationally by the SecA ATPase. Forced lateral opening of a “front gate” between transmembrane helices is also induced by the passage of the virtual probes, with implications for the membrane insertion of peptides. We conclude that the SecY channel can stretch to allow passage of peptides with transversal sizes of ∼16 Å. The observed motion of a transmembrane helical “plug” controlling the closed and open states of the channel is consistent with experimental results and confirms previous hypotheses. Additionally, the “hinge” region for front gate opening is observed to be highly mobile as postulated. Both the forced dilation of a “ring” of residues at the middle of the pore and the lateral opening of the front gate are shown to induce plug displacement, but neither accomplish a full-extent motion of the plug to the back of the channel. For probes whose passage does not destroy the resilience of the SecY, both lateral exit and full translocation are observed, despite the fact that applied forces were always in the direction along the pore axis. Lateral exit is accompanied by front gate opening and slight plug displacement, whereas full translocation is accompanied by large plug displacement but no apparent lateral opening. Simulations also reveal that dilating the pore ring is a more effective way to destabilize the plug than intercalation of a cylinder-like probe at the front gate. Based on the simulations, the existence of a family of diverse open states is proposed.

INTRODUCTION

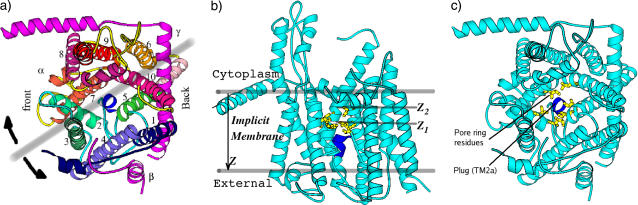
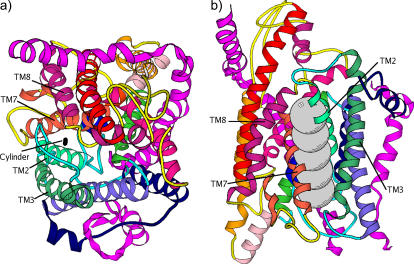
Secretion proteins are synthesized in the cytoplasm and translocated across lipid membranes to the external side through protein-conducting channels (1). Integrated membrane proteins also utilize such channels as a means of transfer from the cytoplasm into the lipid bilayer (2). The details concerning the mechanisms by which translocation and membrane-protein integration occur have been close to mysteries until the recent breakthrough crystal structure of the Methanococcus jannaschii SecY complex (3). As shown in Fig. 1 a, the SecY complex has three subunits. The α-subunit consists of 10 transmembrane (TM) α-helices that span the membrane and run roughly parallel to each other in a direction perpendicular to the membrane plane. Among them, TM1–5 form one half and TM6–10 form the other half of the channel wall. The β-subunit is a simple helix with a rather disordered cytoplasmic region; this subunit does not interact significantly with other parts of the protein and is not essential for function. Lastly, the γ-subunit is composed of two helices with an “L”-shaped geometry and clamps the two halves of the α-subunit together. The pore formed by the α-subunit has a funnel-like shape at both the cytoplasmic (upper) and external (lower) sides. In a sectional plane perpendicular to the membrane and passing through the center of the pore, these two funnels create an hourglass-like space for the channel, with a bottleneck (i.e., the narrowest internal region) that tapers the pore in the middle. This bottleneck is formed by six bulky hydrophobic residues (Ile-75, Val-79, Ile-170, Ile-174, Ile-260, and Leu-460). Following the crystal structure nomenclature in van den Berg et al. (3), we refer to it as the “pore ring” (see Fig. 1, b and c). Just below the pore ring (i.e., toward the external side of the membrane) sits a particular segment (helix TM2a) that seems to “clog” the pore and is therefore called the “plug”. Although the protein channel has to sample open states to perform its function of protein translocation and membrane-protein integration, only a closed state (i.e., with the plug obturating passage through the pore) was crystallized.

FIGURE 1.

FIGURE 1

Open in a new tab

(a) Top view (from cytoplasmic side) of the SecY pore complex. The β-subunit and the γ-subunit are in magenta. The α-subunit has 10 TMs as denoted by the numbers in the figure. The plug (TM2a) is the short helix in blue, located at the center of the figure. The pink part of the TM5 and the loop connecting TM5 and TM6 constitute the hinge region. The thick gray line is a pseudosymmetry axis. Two black arrows indicate a lateral opening of the pore complex hinges on the loop between TM5 and TM6. (b) The approximate position of the SecY in membrane and the two positions z1 and z2 where we grow soft balls in a front side view, note the position of the pore ring (yellow residues) and the plug (blue residues). For clarity (i.e., for the pore ring to be seen), TM2 and TM3 were deleted in the middle panel. (c) A top view showing the positions of the pore ring and the plug.

In addition to the crystal structure, biochemical results (4–6) on SecY and its homologs bring further insight into the functional role in protein translocation and membrane integration. In particular, the disulphide mutants of the Escherichia coli protein channel (7) (in E. coli, the pore is formed by SecY and SecE) have provided evidence in favor of the following hypotheses:

  1. Cross-linking between residue 67 of the E. coli α-subunit (SecY; corresponding to Thr-61 of M. jannaschii) and residue 120 of the E. coli γ-subunit (SecE; corresponding to residue 64 of M. jannaschii) could occur. This was remarkable because these two residues are more than 20 Å away from each other in the crystal structure. Disulphide bridging resulted in a dominant-negative phenotype, and we interpreted this as a consequence of a permanently open channel locked in by the cross-link. This indicated the existence of an “open” state of the channel in vivo in which the plug flexes to a backward position, with at least one residue (Thr-61) of the plug in close proximity to residue 64 of the γ-subunit.

  2. Whereas formation of a disulphide bridge between E. coli residue 64 of the α-subunit (SecY) and residue 120 of the γ-subunit is also lethal, cross-linking between neighbor residues (64–67) does not influence channel function. This suggested that the plug preserves its helical structure in both the open and closed states.

Based on the aforementioned crystallographic and biochemical data, Rapoport and co-workers (3,8) proposed a model involving a series of distinct major motions that the protein pore must undergo to accomplish either protein translocation to the outside of a cell or integration into the lipid bilayer membrane. According to this model, translocations were hypothesized to involve the displacement of the plug (TM2a) from its closed state position to the back and external side of the protein channel, with the final position in the space formed between TM1, TM5, and the γ-subunit. On the other hand, integration of membrane proteins would involve the lateral opening of a groove at the protein channel edge, in between TM2/3 and TM7/8. Looked at from above, i.e., from the cytoplasmic side, in a plane parallel to the membrane, this motion would open apart the two halves of the α-subunit by hinging on a loop region (see Fig. 1 a) in between TM5 and TM6. This hinge would coordinate both lateral opening and plug motion. We are particularly interested in this study in constructing these hypothesized open states and in generating possible dynamical pathways toward these states. In performing this, we aim to understand the interplay between structural dynamics and the function apparent in this remarkable protein complex. In addition, we set to also gauge the size of the pore and the extent of pore opening.

Firstly, to probe the size of the SecY pore, we grow soft balls of various sizes at two different positions within the pore and observe the expansion of the pore in response to this virtual probing. Secondly, soft balls of various sizes are pushed through the pore (with both constant forces and constant velocities) to obtain putative open state structures of the SecY complex. Thirdly, to assess the mechanism of lateral peptide signal-sequence insertion in the membrane, we also grow a cylindrical construct of five vertically stacked soft balls in the groove between TM2 and TM7. This procedure mimics an α–helical like signal sequence, with the goal to observe the effects of forced front opening on the pore structure and with implications to membrane protein insertion. Finally, we discuss the role of dimerization and propose that a family of diversely open states might exist.

METHODS

Effective energy functions for both water (9) and lipids (10) (as implemented in the CHARMM package (11)) are utilized in this study. In this implicit water and lipid-slab model, which has been successfully used to study membrane protein stability and membrane-binding proteins (12,13), both media are represented as a continuum with different solvent-exclusion parameters and with smooth transitions at the interfaces. A recent study (14) also demonstrated that implicit membrane models can predict static properties accurately. The undulations of lipids (15) are neglected by assuming a planar slab; this approximation should be reasonable since undulation is negligible within the lateral area covered by the channel protein. Although the hydrophobic-hydrophilic pattern of the SecY complex suggests the basic position for its placement in the membrane, it is not detailed enough to describe the actual orientation of SecY relative to the membrane. Fortunately, it was found that the β-subunit is very close to a position normal to the lipid plane (3). To set up the initial conditions of the simulation, we first rotate the protein so that the β-subunit adopts a normal orientation (along the z axis) with respect to the model membrane (which is parallel to the x-y plane and has its center plane at z = 0) and take the centroid (x0, y0, z0) of backbone atoms of the β-subunit TM residues (30–49) to be the origin of the coordinate axes. The z axis points from the cytoplasmic side to the external side (see Fig. 1 b). In this setup, different protein position and membrane thickness combinations were then tried, and molecular dynamics equilibration runs in each corresponding model membrane slabs were performed for 2 ns. Out of these simulations, we selected for the production runs the position-thickness combination that gave the least overall backbone root mean-square deviation (RMSD) from the crystal structure during 2 ns of equilibration. (An RMSD plot is available in the Supplementary Material.)

The main structural features observed during equilibration are as follows: the N-terminal helix of the γ-subunit experiences the largest deviation (up to 5 Å), the β-subunit has an intermediate deviation of ∼3.5 Å, and the α-subunit, which forms the SecY pore, preserves the crystal structure reasonably well (within a deviation of 2 Å). Additionally, excellent agreement is observed for the calculated and experimental B-factors for the α-subunit, indicating that not only the average structure but also the average fluctuations are well reproduced using the implicit solvent. (A comparison plot is available in the Supplementary Material.) Although it is not possible to obtain quantitatively accurate dynamical behavior with the simple model we use, qualitatively correct dynamical description is achievable (16).

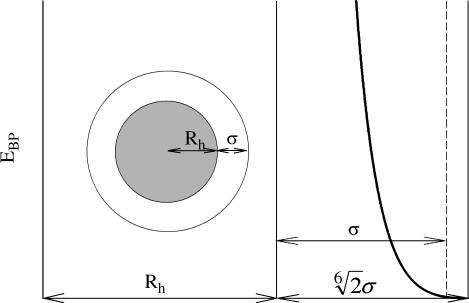
The soft balls, used to probe the size and associated motions of the SecY complex, interact with the protein according to a ball-protein repulsive potential energy, EBP, modeled as

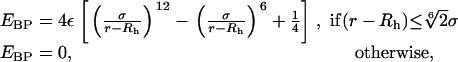graphic file with name M1.gif (1)

where σ controls the softness of the ball and is taken to be 2 Å in this study. The distance r is measured between the center of mass of the ball and the center of mass of each protein atom; Rh, the hard-core radius of the ball, is tuning the ball size to take on desired values. This virtual probe interaction is schematically shown in Fig. 2. Rh + σ is taken to be the effective radius of the soft ball and is denoted by R subsequently.

FIGURE 2.

FIGURE 2

Open in a new tab

Schematics of the soft balls used to probe the SecY complex. Although protein atoms will start to feel a ball at center-of-mass distance 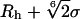Inline graphic, at a center-of-mass distance Rh + σ, EBP is ε, which is specified to be 1 kcal/mol in our simulations, where the outmost part of such a ball is fairly soft, that volume should be easily accessible to protein atoms. We use Rh + σ as the effective ball radius (denoted R in the text).

RESULTS

The size and resilience of the SecY pore from virtual ball growing

With inspiration drawn from experimental studies in which gold nanoparticles of various sizes are utilized to measure the size of mitochondrial protein import pores (17), we have used the above-described virtual balls to measure the size of the SecY pore and to gauge the extent of stretching (i.e., the resilience limit) of the channel. To avoid overlapping protein atoms with an arbitrarily sized ball, we obtain the desired ball sizes by growing them from a zero-size point. Specifically, Rh in Eq. 1 is initially set to 0.0 and σ is slowly increased to the desired value (2 Å). Thereafter, σ is kept constant and Rh is gradually increased to 10 Å in 10 ns. We grew such soft balls at two different points, hereafter referred to as positions z1 and z2 (see Fig. 1 b). For both, their x and y coordinates were those of the geometric center of the plug backbone atoms. Their z coordinates were z1 = −1.5 Å and z2 = −7 Å, with z1 determined by the backbone atom geometrical center of the pore ring residues and z2 selected as a position close to the cytoplasm side but still within the pore. In other words, the two points, z1 and z2, from which balls were pushed down through the pore are stacked, in this order, on the vertical above the plug. This positioning is certainly arbitrary. It simply reflects our intent toward a merely qualitative probing of the likely SecY motions induced by translocation of a peptide chain from the cytoplasmic side. In the next section, we shall move the balls downward (referred to that as pushing procedures), and in this section we present results for growing procedures for which the center of mass of the growing ball is fixed in space.

By devise, the size of the ball is not large enough initially to interact with the inner side of the pore. As the ball grows sufficiently to dilate the protein pore, TM2 and TM7 start to separate, in accord with a hypothesis in previous structural analysis (3). A series of snapshots of the ball-growth process at position z1 is shown in Fig. 3. Dilation starts to develop as the ball achieves a radial size of 7 Å (Fig. 3 b). By the time the ball reaches 10 Å (Fig. 3 e) in radius, a large space of ∼10 Å develops. Under the physiological conditions of a real lipid environment, this dilation would induce a lipid influx. At position z2, the inner channel size is larger and no considerable dilation is observed until R reaches 10 Å, although bending of helices at the cytoplasmic side is induced for balls as small as 8 Å in radius. (Similar snapshots at position z2 are available in the Supplementary Material.) These observations indicate that, without a significant increase (≥2 Å) of the interhelical distance between TM2 and TM7 when compared with the crystal structure, the SecY pore can be expanded to ∼14 Å in diameter at position z1 (i.e., close to the center of the pore ring) and 18 Å in diameter at position z2 (close to the membrane-cytoplasm interface).

FIGURE 3.

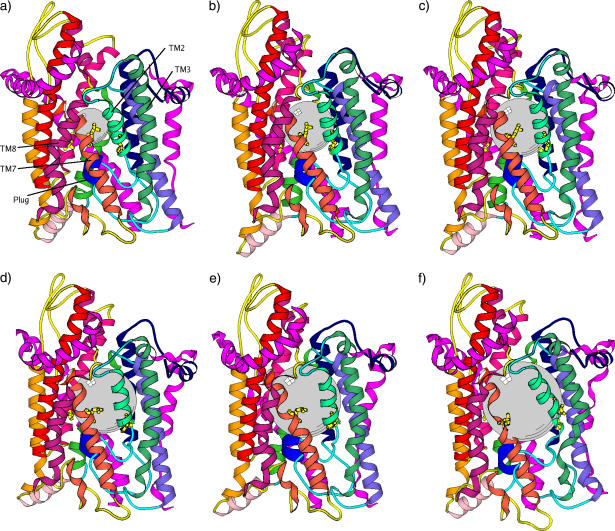
FIGURE 3

Open in a new tab

A series of snapshots from a ball growth trajectory. Coloring scheme is the same as in Fig. 1 a. This demonstrates that the front side is the lateral opening place, as speculated. (a) R = 6 Å, (b) R = 7 Å, (c) R = 8 Å, (d) R = 9 Å, (e) R = 10 Å, and (f) R = 12 Å.

It is imaginable that, for flawless cyclical performance, the SecY pore needs to expand to a transient state that can handle secretion protein passage and then return to its stationary state (the closed, obturated state observed in the crystal structure) upon accomplishing translocation. The return to the closed state should proceed relatively rapidly. Otherwise, a large influx/outflux of ions, metabolites, or water could unbalance the proper chemical gradient between the cytoplasm and the external environment and therefore result in malfunction or even cell death. Although it is conceivable that the six pore-ring residues, displaced during translocation, can return quickly to the closed state (as this involves only local side-chain motion), if the backbone is in a dilated position (e.g., by bending helices, see above), the ring cannot fully seal the pore. Diffusion of ions (18) and water (19) across open membrane pores can occur on timescales not much longer than nanoseconds. Therefore, it is essential for the entire SecY complex to “fold” back to a nearly closed state on a submicrosecond timescale to retain its resistance to permeation. Our relaxation simulations, described next, demonstrated its capability to fold back on the nanosecond timescale when expanded by various sized balls.

To test the effects of the ball-induced expansion on the resilience of the SecY pore (i.e., on its ability to return to the initial shape on the nanosecond timescale), a series of snapshots with various ball sizes (radii from 4 to 12 Å with 1 Å increments) were taken from the ball-growth trajectories started at position z2. Subsequently, for each snapshot, the constraint that fixed the ball was switched off and the system was allowed to relax. We observed that when the ball is small (diameter <10 Å), it undergoes only thermal motion, thereby having to escape only translational-entropy barriers (20) as it eventually diffuses out of the pore. This behavior is expected because a small ball does not undergo significant repulsion from the protein.

Mid-sized balls (diameter 12–14 Å) were rapidly (within 100 ps) pushed out of the pore to the cytoplasmic side. (A representative figure of such a push-back event is available in the Supplementary Material.) This is due to the funnel shape of the channel, which makes the net force experienced by a soft ball at this position point up toward the cytoplasmic side (see Fig. 1 b). The resilience of the channel was surprisingly strong: even when, instead of relaxation without applied forces, we pushed the balls in with small forces (10 pN) pointed toward the external side, the balls were still pushed back by the pore to the cytoplasmic side.

However, large balls (diameter ≥16 Å) tended to get stuck on the nanoscale timescale, despite the fact that the ball was very close to the cytoplasm; this is likely because a large deformation of helices imposes an energy barrier for ball escape. This, however, did not necessarily indicate loss of protein resilience. We removed the inserted large balls and performed simulations of such dilated SecY pores. The results show that, within 4 ns, dilation caused by balls with diameter ≤22 Å were able to partially recover. (A representative figure of such a partial relaxation event is available in the Supplementary Material.) These observations suggest that the SecY pore at position z2 can stretch to at least 22 Å in diameter, with its resilience on the nanosecond timescale being preserved. The ability of this upper funnel part to expand is of great importance. A recent study (21) suggests that this part of the pore needs to provide space not only for a single TM helix to pass but also for it to allow 180° turns for some TM helices. This is needed to satisfy the topology requirement for the membrane insertion of a tertiary structure composed of several concatenated helices.

The open state and the dynamical transition between the open and closed states from virtual pushing

As mentioned above, based upon the structural characteristics of the closed SecY pore and the putative position of the plug in the open state (inferred from mutation studies (7)), it was suggested that, relative to the closed state, the plug has to displace ∼22 Å to the back and ∼12 Å to the external side of the membrane (see Fig. 1 a) to achieve an open structure (3). To generate an open state in our simulations given only the closed state (i.e., the crystal structure), we tried to push soft balls of various sizes through the pore to observe any resulting plug displacement or lateral opening. In single molecule manipulation experiments, both constant velocity loading (22) and constant force (23) are utilized to interrogate biomolecules in terms of their structural dynamics. Inspired by such manipulations, we tried both approaches in our ball-translocation virtual experiments. We found that for balls >10 Å in radius, the large magnitude of the outward motion of the helices resulted in wide lateral opening, which would cause lipid influx into the channel in a real membrane environment. Therefore only balls with R ≤ 10 Å were used.

Pushing procedures were carried out as follows. Snapshots with various ball sizes were taken from the ball-growing trajectories described in the section “The size and resilience of the SecY pore from virtual ball growing”, and 2 ns of relaxation simulation were performed with the ball fixed. Then either constant forces or constant velocities were imparted to the ball in a direction normal to the model lipid slab and pointing toward the external side. For constant-force pushing, the soft balls start from position z2 with R = 4, 5, 6, and 7 Å, whereas for the constant velocity simulations, the start position is z1 with R = 4, 5, 6, 7, 8, 9, and 10 Å. Since the interaction of a protein atom with the implicit lipid slab is determined by the atom's vertical position, it was important, during the push, that SecY remained fixed in the z direction. For this purpose, we used a harmonic constraint on the pore's center of mass with force constant k = 20 kcal/mol/Å2. This ensured that fluctuations of SecY's center of mass along the z direction were <1 Å.

Constant velocity pushing from z1

To accomplish a constant velocity push with a specified velocity value, we simply reset the ball's z-component velocity to that value at each time step, whereas the velocity components of the ball within a slab plane were allowed to change, as dictated by the interaction between the ball and the SecY complex. Various velocities were specified so that a ball will be pushed to the external side of the pore within 1.2, 3, 6, and 12 ns, respectively (for balls with R ≤ 5 Å only 1.2 ns of pushing were simulated). Four independent trajectories were generated for each given velocity and ball size.

Balls with R ≤ 4 Å experienced relatively small resistance forces (<100 pN) when pushed through the pore ring within the nanosecond timescale. All soft balls in this size range passed the pore ring and exited laterally without displacing the plug, despite the fact that the biasing forces were pointing downward, i.e., toward the external side of the channel. Although not directly relevant to the physiology of the SecY pore (the size of these small balls is about that of single residues, but in reality peptides are translocated presumably with intact secondary structures), these observations demonstrate that the plug has significant stability in the closed state position.

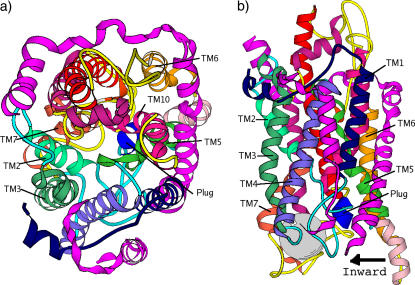
For balls with R from 6 to 8 Å we have observed two distinct scenarios after they pass the pore ring. These medium-sized balls either translocate to the external side or they exit laterally in between TM2 and TM7. To translocate to the external side, a ball has to first displace the plug down to the external side and then laterally displace it toward the back to some extent (see Figs. 4 and 5). To exit laterally, balls need to considerably displace the plug to the back but not to the external side. They then find their way out in between TM2/3 and TM7. For the relatively smaller balls in this category (6–7 Å in radius), TM2/3 and TM7 preserved their helical structure very well, whereas lateral exit of larger balls (8 Å or larger in radius) severely distorted the helical structure of these TM helices. (Representative figures of various extents of front gate structure preservation, notably for TM2/3 and TM7, are available in the Supplementary Material.) Displacement of the plug was always accompanied by the motion of the “hinge” (see Fig. 1 a for hinge location). When the plug was pushed all the way to the external side, its backward motion was accompanied by an “outward” motion of the hinge (i.e., a movement of the hinge region away from the pore axis, as sketched in Fig. 4 b). Otherwise, the lateral motion of the plug was associated with an “inward” motion of the hinge (i.e., a movement of the hinge region closer to the pore axis, sketched in Fig. 5 b). In all lateral exit events, because the plug is not pushed all the way down to the external side, its displacement was always associated with inward hinge motion.

FIGURE 4.

FIGURE 4

Open in a new tab

Top and side view of a ball with radius 8 Å at just above the pore ring position and after being pushed to the external side of the channel (followed by full translocation). Coloring scheme is the same as in Fig. 1 a. (a) Side view of a ball just above the pore ring position. (b) Side view of a ball at the external side of the channel. (c) Top view of the channel when a ball is above the pore ring position (ball not shown). (d) Top view of the channel when a ball is at the external side of the channel (ball not shown).

FIGURE 5.

FIGURE 5

Open in a new tab

Top and side view of a SecY complex after a ball with radius 6 Å was pushed to the external side of the channel (followed by lateral exit). Coloring scheme is the same as in Fig. 1 a. (a) Side view of the SecY complex with a ball at the external side of the channel. (b) Top view of the channel when a ball is at the external side of the channel (ball not shown).

Balls with R ≥ 9 Å all exited laterally in between TM2 and TM7. This is because for such large balls, the lateral resilience of the SecY channel has been destroyed (see the section titled “The size and resilience of the SecY pore from virtual ball growing”). This indicates that the largest expansion accessible to a functional (i.e., resilient) pore is ∼16 Å in diameter. To further open the gate laterally is much easier than to significantly displace the plug to make space for translocation to the external side.

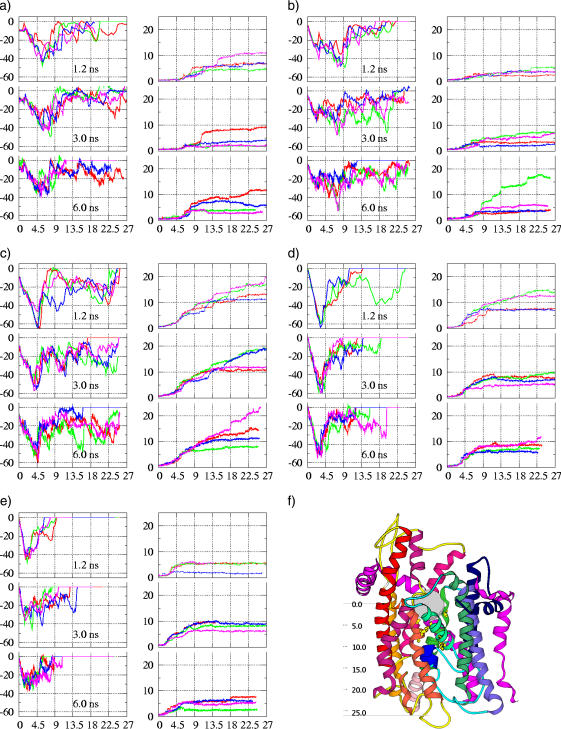
Fig. 6 shows the force opposing the push (indicated by the (−) sign relative to the velocity of the ball) and the RMSD of the plug backbone for various ball sizes and velocities. We point to two major features of the plots:

  1. The maximum force experienced by the balls is largest for R = 8 Å and starts to decrease for balls with R = 9 and 10 Å. However, the peak force is not solely determined by the plug displacement for balls with R = 8, 9, and 10 Å. Instead, it is partially due also to the opening of the pore ring. (Because of the size of these balls, they can simultaneously make contacts with both pore ring residues and the plug.) Again, this is in agreement with the previous argument of lateral resilience. This indicates that the largest expansion accessible to a functional (i.e., resilient) pore is ∼16–18 Å in diameter.

  2. The position of the force peak for balls with R ≤ 7 Å corresponds to the displacement of the plug, despite the fact that the plug is displaced much less than for balls with R ≥ 8 Å. This is, in fact, in accordance with the observation that for balls with R ≥ 8 Å, passing the pore ring is associated with considerable displacement of the plug (∼5 Å, see Fig. 6, d and e), whereas balls with R ≤ 7 pass the pore ring with only a trivial plug displacement (∼2 Å, see Fig. 6, a and b). Therefore, by the time the ball is in contact with the plug, which has been significantly destabilized for balls with R ≥ 8 Å, it remains almost “unperturbed” for balls with R ≤ 7 Å. If we compare the force associated with passing the pore ring, one can observe that it jumps from ∼30 to ∼60 (kcal/(mol Å)) at a ball size of R = 8 Å, levels off for R = 9 Å, then starts to decrease for R = 10 Å. Accordingly, the force associated with displacement of the plug due to direct ball contact is actually smaller for balls with R ≥ 8 Å than for balls with R ≤ 7 Å.

FIGURE 6.

FIGURE 6

Open in a new tab

(a–e) Left panel for each figure: force experienced in four independent runs (in green, red, blue, and magenta lines) by balls of various sizes being pushed through the SecY complex within different times (1.2 ns, 3 ns, and 6 ns). The horizontal axis is the position of a ball (in angstroms) relative to the initial ball position (shown in f), the vertical axis is the force (kcal/(mol·Å)). (a–e) Right panel for each figure: RMSD (Å) of the plug backbone atoms as a function of the ball position. During calculation of the RMSD, the backbone of the TM6 and TM9 are translated and rotated to fit the start configuration. (a) R = 6 Å, (b) R = 7 Å, (c) R = 8 Å, (d) R = 9 Å, (e) R = 10 Å, and (f) relative position.

Notably, for all the trajectories, regardless of the magnitude of plug displacement, the direction for the plug displacement is toward the back of the channel, as speculated previously (3). The largest plug displacement observed is ∼25 Å, with the final position at the back close to the C-terminal of the γ-subunit and in between the hinge and TM1. This matches the proposed fully open state (3) and agrees with the cross-linking results (see Fig. 4).

Constant force pushing from z2

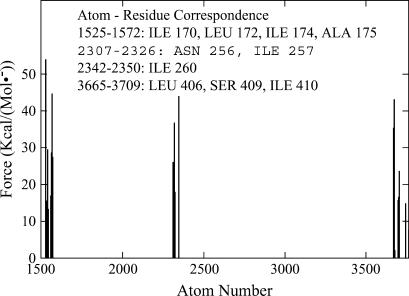
This strategy has revealed a similar probe-size dependence as that for constant velocity pushing from z1. Smaller balls (R ≤ 5 Å) tended to exit laterally after passing the pore ring, whereas larger balls tended to accomplish full translocation with large plug displacement. (Representative figures for translocation and lateral exit are available in the Supplementary Material.) Therefore, passing the pore ring and displacing the plug were separate events. As expected, the resistance arose mainly from the bulky hydrophobic residues at the bottleneck and from residues very close to them, as shown in Fig. 7. The forces needed to push a ball through the SecY pore (laterally or to the trans side) on the nanosecond timescale range from 100 pN to 1500 pN depending upon ball size.

FIGURE 7.

FIGURE 7

Open in a new tab

Force experienced by various atoms forming the pore ring due to the push of a ball with a radius of 6 Å; data are collected during 2000 time steps before the ball passes the pore ring. Note that large force peaks are around four of the six pore ring residues suggested by the crystal structure. In the equilibrated structure, the plug moved toward the external side for ∼2 Å, resulting in Ile-75 and Val-79 being off the top of the plug whereas test balls are placed right above the plug. Therefore, these two residues do not experience large forces like the other four pore ring residues.

In summary, virtual pushing with soft balls to probe the behavior of SecY has revealed two distinct mechanisms. To exit to the external side, the translocation probes need to push the plug toward the external side first and then all the way to the back but with very small lateral opening. To exit laterally into the lipid environments, the insertion substrate needs to push the plug toward the back only partially (i.e., there is no need for the plug to reach the γ-subunit) and to laterally open the pore in between TM2/3 and TM 7.

Signal sequence specificity revealed by virtual-cylinder intercalation at the “front gate”

Under physiological conditions, there are no driving forces of the magnitude felt by the virtual probes descried hitherto (be they ball growing, pushing, or otherwise). It is hard to justify the large input of energy that could possibly push the virtual probes on the timescale we have. What our simulations are, however, providing (by generating the response to the probes) are the likely minimum-resistance conformational pathways that the protein will undertake to accomplish translocation in a cellular environment. Although no formal proof can be given, it is likely that the conformational changes occurring during in vivo translocations are a subset of (or very similar to) the pathways discovered by virtual probing. Similar arguments are used to demonstrate that qualitatively correct pathways are obtained from steered molecular dynamics studies with large applied forces (24).

Up to this point, our computational findings demonstrated that major motions related to the channel opening/expansion are i), pore ring expansion, with the dilation of the pore mainly due to the separation of TM2 and TM7; ii), plug displacement toward the back of the channel; and iii), the associated hinge (loop region connecting TM5 and TM6) motion, highly in agreement with suggestions provided in the original crystal structure article (3).

Since all these conformational change motions are coupled to different extents, a natural question would be which of them is the active motion (the drive) and which are the passive ones (the response)? The biological counterpart of this “mechanical” question is how are various events arranged temporally and spatially to achieve protein secretion to the exterior or peptide integration into the membrane?

Translocation cannot be achieved by the SecY pore alone. Instead, association of a channel partner is necessary. This is achieved by binding, from the cytosolic side, with either the ribosome (to translocate peptides cotranslationally) or with the SecA ATPase (for posttranslation translocation) (25). Although such binding might engender some conformational change in the pore complex that would destabilize the closed state, it is believed that translocation does not fully occur without the molecular motor-like push of either of the two binding partners (3).

The similarity between the results from constant force and constant velocity pushing implicates that the details by which the ribosome or the SecA ATPase load the polypeptide into the channel are not likely to be decisive for the key motions of the SecY TM helices (although the timescales involved will differ). The agreement between our predicted open state and the cross-linked-mutant open structure (7) also supports this point of view, as does the discussion in the section titled “Constant force versus constant velocity on the relative role of backbone disruption and loss of nonbonded side-chain contacts”.

Furthermore, experiments on the SecY binding partners indicate that either the ribosome (26,27) or SecA (25) would bind, from the cytoplasmic side, at the C-terminal loop (between TM6 and TM7 and between TM8 and TM9). Intercalation of signal sequences in between TM2 and TM7/8, i.e., in the groove between the two halves of the α-subunit, would follow after binding (4). These two consecutive events will initiate the translocation process by destabilizing the plug and opening the channel.

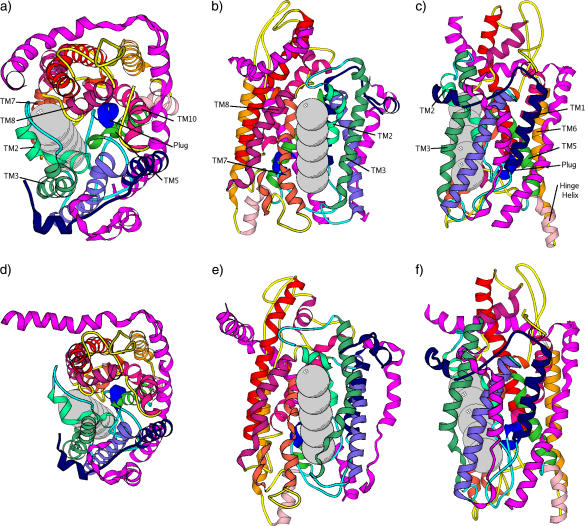
To test these speculations, we grow a cylindrical construct formed from five consecutive balls stacked vertically on a line to approximate a cylinder within the groove-like space formed among TM2, TM7, and TM8 (see Fig. 8). This construct is therefore intended to better mimic the signal sequence at its putative insertion site than did the previously described growing of balls within the central channel.

FIGURE 8.

FIGURE 8

Open in a new tab

Position of the cylinder for lateral opening the SecY complex. Coloring scheme is the same as in Fig. 1 a. (a) A slightly tilted top view shows that the cylinder will be grown in between TM2 and TM7/8, where indicated by the black dot. (b) A side view of a hypothetical situation where a cylinder with radius 5 Å and length 19.7 Å is placed at the position shown in a. Apparently, this causes significant overlap with TM2 and TM7. By growing this ball slowly, TM2 and TM7 will be pushed away from each other and the front gate will open as a result.

Similarly to the previous procedures of growing a ball in the channel, here we first place five points with zero volume and slowly increase σ to 2 Å. Then Rh is gradually increased to 5 Å. In the previous procedures, both growing balls and pushing balls through the channel are performed on timescales of ∼10 ns, and the secondary structure of helices are reasonably well preserved (except for very large balls, i.e., with R ≥ 9 Å). We have attempted to grow the cylinder on timescales from a few nanoseconds to ∼100 ns. Surprisingly, we found that the helical structure of TM2 and TM7 are better preserved during faster growth (i.e., ≤20 ns, see Fig. 9, a–c) than during a slower process (≥50 ns, see Fig. 9, d–f). Accordingly, the induced plug displacement is larger (∼5 Å) for the faster cylinder growth (Fig. 10). Additionally, the induced plug displacement is purely lateral to the back of the channel, accompanied by inward motion (Fig. 9, c and f) of the hinge. No considerable movement of the plug toward the external side is observed in any of the cylinder growth trajectories. This observation, when compared with that from the previous ball-pushing simulations, suggests that the pore ring dilation is a more effective way to destabilize the plug than intercalation of a cylindrical helix in between TM2 and TM7. Therefore, we speculated that mutations of pore ring residues can destabilize the closed plug state. Interestingly, recent experimental studies (28) confirm that many signal sequence suppressor (prl) mutations are in the pore ring, and the channel can be opened without a signal sequence.

FIGURE 9.

FIGURE 9

Open in a new tab

Final configuration of a SecY complex after a cylinder consisting of five balls with radius of 5 Å is intercalated between TM2 and TM7 by growing these balls at two different speeds. a–c are for 5 ns ball growth; d–f are for 50 ns ball growth; a and d are top views, which show that the plug is displaced to the back of the channel; b and e are front views, which show the deformation of TM2 and TM7 by the cylinder. c and f are side views, which show the bending of the hinge toward the pore axis (inward motion).

FIGURE 10.

FIGURE 10

Open in a new tab

Backbone RMSD of the plug during the growth of a cylinder intercalated in between TM2/3 and TM7/8.

Apparently, for the longer cylinder growth processes, the work done effectively melted the local TM2 and TM7 whereas during the fast cylinder growth, the work done is at least partially transformed into the global motion of the protein. However, in biological systems, if the intercalation of a helix would occur, that would certainly take more than 10 ns. There are two possibilities to explain such contradictions. One is that the intercalation of a signal sequence merely anchors the polypeptide to SecY but does not actually destabilize the plug in favor of the open state. The other possibility would be that the complex secondary-structure geometry of a signal polypeptide is quite important and our representation is too coarse to capture these subtleties. The second explanation is conducive to undertaking more realistic representations of the inserted polypeptide. Meanwhile, we believe that our detection of the plug motion and pore size using virtual soft balls is effective in generating the qualitative SecY response for a general polypeptide sequence.

The above discussion vividly embodies the difference between the specific and nonspecific interactions involved during translocation. The residues of the signal sequences and the corresponding residues forming the binding site in the SecY channel are conserved mainly in terms of hydrophobicity and charge patterns (3). Such interactions cannot be captured by our coarse cylindrical model. On the other hand, a wide variety of proteins can be translocated through the pore. Given the diversity of their sequences, no specific interactions are expected to be involved: the majority of the effects that matter are likely to have to do with the size of the pore opening. Therefore, although we could effectively detect the size and the motion of the plug with a soft ball, the intercalation of signal sequences and its effects, mainly determined by the interactions stemming from well-defined hydrophobicity and charge patterns, cannot be studied in detail by this simple method.

DISCUSSION

Constant force versus constant velocity

Constant force (23,29) and constant velocity (22) manipulations of biomolecules are two extreme idealizations of the realistic way proteins (or nucleic acids) are pulled or pushed by molecular motors. The former procedure utilizes magnetic or optical bead trapping to detect the behavior of attached biomolecules under specific tensions. In the latter case, atomic force microscopy is often used to unfold proteins by moving their tip at a constant velocity and observing the position and magnitude of force peaks. Such pulling is usually far away from equilibrium. However, in both cases, applied forces are usually transmitted through the backbone of the biomolecules, and significant disruption of both van der Waals and backbone dihedral interactions are involved. The time-ordered sequence of these two sets of events, and consequently the response of the biomolecules, will be strongly dependent on the way external loads are applied. In our virtual ball translocations, the ball-protein interactions mainly involved side chains of proteins and disruption of the van der Waals interactions. For the backbone of the SecY complex, significant dihedrals change only occurred at the hinge region and at the few residues connecting the plug to TM1 and TM2b. Therefore, our forced translocation of balls through the channel should be less sensitive to how loading is applied to the ball than in the case of pulling biomolecules to unfold them. This consequently explains further the good agreement observed between these two scenarios in our virtual probing of the SecY pore.

Simple probes versus realistic peptides

Peptides can presumably translocate with intact secondary structure (e.g., with α-helices), which certainly have more complex interactions with the SecY pore than our simple repulsive balls do. Moreover, due to the limit of the accessible timescale for our simulations, large forces (∼1000 pN) had to be utilized to push a ball through the pore. If α-helices of comparable size were to be subjected to such large forces, they would certainly unfold before translocating. One way to solve the problem would be to constrain the helical structure, which will make it rather rigid. This would amount, ultimately, to not much more that rendering the helix to be effectively similar to a rigid ball/cylinder in terms of probing the size dependence of the transition between a closed and an open pore.

Regardless of whether a translocating peptide is destined for membrane or secretion, it is essential for the SecY pore to undergo a sufficiently large opening that allows peptide passage. Additionally, as discussed above, the diversity of such sequences is likely to make the specific interactions less important (except for the signal sequences). Therefore, we deem that our choice of simple soft balls as a way of probing the size and the major motional correlation is, given the described limitations, reasonable and tractable. It is true that precise atomistic details of the tripartite interaction between the nascent protein, the SecY complex, and the lipids (30) are lost in the coarse graining of our computational modeling. However, the model does capture overall features of this interaction. This is because the SecY pore has to be expanded and the plug has to be displaced to accomplish a successful translocation. Consequently, the interaction between a SecY pore and a translocating protein will be a predominantly repulsive one.

On the role of dimerization

Although the crystal structure demonstrated, with no ambiguity, that a single copy of SecY complex is sufficient to act as a translocation pore, experimental observations (31–33) suggest that oligomers, rather than monomers, are the dominating form for SecY (with dimers having the strongest evidence (34)).

Hydrophobicity patterns are usually very different for secretion and membrane proteins. It has been demonstrated (30) that this is utilized to differentiate between the two categories of proteins via direct interaction between a nascent chain and lipids. Based on the crystal structure and our simulations the front gate would be a region of choice for such interactions to occur. However, a front-to-front dimer would block such an interaction for the translocating peptide and consequently suppress membrane protein integration. Therefore, dimerization might play a role in differentiating membrane and secretion proteins. Although both back-to-back (35) and front-to-front (36) dimerization were reported by cryo-electron microscopy imaging, the detailed conformational change of the monomer due to dimerization could not be deduced. Therefore, interpretation of the specific role of dimerization has to wait for high-resolution structures.

Possible existence of a diverse family of open states

Out of the many simulated soft ball translocation events, only a few forced translocations experienced full displacement of the plug to the back of the channel (two out of eight in constant velocity translocations for balls with R = 7(8)Å). The others were accompanied by only partial plug movement toward the channel back. In reality, the SecY channel presumably translocates a wide variety of secretion proteins with different secondary structures and sizes. Translocations might occur in such ways that the plug is displaced only by the necessary amount to accommodate the translocating peptide. The benefit of only a partial displacement of the plug is that it can rapidly return to the closed state. In the previously mentioned mutational studies (7), in E. coli both residue 64 and 67 of the α-subunit (SecY) can form (when replaced by Cys) disulphide bridges with residue 120 of the γ-subunit (SecE) in vivo. This indicates that in the open state, the position of the plug can vary at least by a few angstroms. This could be indicative of a nearly isoenergetic population of open states, rather than a uniquely defined open structure. The members of the open state family are expected to have diverse positions of the plug.

CONCLUSIONS

We have presented a molecular dynamics simulation study of the size, motion, and function of a SecY complex, a protein-conducting channel with an implicit solvent (water and membrane) model, and a coarse-grained, soft ball representation of the translocated moieties. By growing in different arrangements and pushing various sized repulsive balls through the pore of the SecY channel, we have determined that the diameter of the pore can be expanded to ∼16 Å without significant loss of its resilience. We have provided the atomic details of the major motions associated with the function of the SecY, making connections to hypotheses proposed based on the structure: i), pore ring opening; ii), lateral dilation of the pore (front gate opening) mainly due to the separation of TM2 and TM7; and iii), displacement of the plug toward the back of the channel. All these major motions were observed to be coordinated by the hinge region. We also demonstrated that dilating the pore ring is a more effective way to destabilize the plug (toward an open state) than intercalation of a cylinder-like structure in between TM2 and TM7. The puzzle regarding the role of dimerization was discussed in light of the latest data. Based on our simulations, we have also proposed the theoretical possibility that a family of diverse open states exists.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental]
biophysj_105.073304_index.html (779B, html)

Acknowledgments

While our work was in progress, we became aware of simulations of realistic peptides translocating through an atomically explicit membrane carried out in Professor Klaus Schulten's laboratory (K. Schulten, University of Illinois, Urbana-Champaign, 2005, personal communication). Readers interested in the atomistic-detail interaction between the nascent protein, the SecY complex, and the lipid membrane atoms are encouraged to follow that work.

We thank Professor Tom Rapoport for advice and encouragement. We also thank the referees for their constructive comments.

This work was supported by funds from the University of Michigan.

References

  • 1.Matlack, K. E. S., W. Mothes, and T. A. Rapoport. 1998. Protein translocation: tunnel vision. Cell. 92:381–390. [DOI] [PubMed] [Google Scholar]
  • 2.White, S. H., and G. von Heijne. 2004. The machinery of membrane protein assembly. Curr. Opin. Struct. Biol. 14:397–404. [DOI] [PubMed] [Google Scholar]
  • 3.van den Berg, B., W. C. Jr., I. Collinson, Y. Modis, E. Hartmann, S. Harrison, and T. Rapoport. 2004. X-ray structure of a protein-conducting channel. Nature. 427:36–44. [DOI] [PubMed] [Google Scholar]
  • 4.Plath, K., W. Mothes, B. Wilkinson, C. Stirling, and T. Rapoport. 1998. Signal sequence recognition in posttranslational protein transport across the yeast ER membrane. Cell. 94:795–807. [DOI] [PubMed] [Google Scholar]
  • 5.Heinrich, S., W. Mothes, J. Brunner, and T. Rapoport. 2000. The Sec61p complex mediates the integration of a membrane protein by allowing lipid partition of the transmembrane domain. Cell. 102:233–244. [DOI] [PubMed] [Google Scholar]
  • 6.Tziatzios, C., D. Schubert, M. Lotz, D. Gundogan, H. Betz, H. Schagger, W. Haase, F. Duong, and I. Collinson. 2004. The bacterial protein-translocation complex: SecYEG dimers associate with one or two SecA molecules. J. Mol. Biol. 340:513–524. [DOI] [PubMed] [Google Scholar]
  • 7.Harris, C., and T. Silhavy. 1999. Mapping an interface of SecY (PrlA) and SecE (PrlG) by using synthetic phenotypes and in vivo cross-linking. J. Bacteriol. 181:3438–3444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Clemons, W. Jr., J.-F. Menetret, C. Akey, and T. Rapoport. 2004. Structural insight into the protein translocation channel. Curr. Opin. Struct. Biol. 14:390–396. [DOI] [PubMed] [Google Scholar]
  • 9.Lazaridis, T., and M. Karplus. 1999. Effective energy function for proteins in solution. Proteins. 35:133–152. [DOI] [PubMed] [Google Scholar]
  • 10.Lazaridis, T. 2003. Effective energy function for proteins in lipid membranes. Proteins. 52:176–192. [DOI] [PubMed] [Google Scholar]
  • 11.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics. J. Comput. Chem. 4:187–217. [Google Scholar]
  • 12.Madhusoodanan, M., and T. Lazaridis. 2005. The contribution of Cα-H···O hydrogen bonds to membrane protein stability depends on the position of the amide. Biochemistry. 44:1607–1613. [DOI] [PubMed] [Google Scholar]
  • 13.Lazaridis, T. 2005. Implicit solvent simulations of peptide interactions with anionic lipid membranes. Proteins. 58:518–527. [DOI] [PubMed] [Google Scholar]
  • 14.Im, W., and C. Brooks III. 2005. Interfacial folding and membrane insertion of designed peptides studied by molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 102:6777–6782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Lipowsky, R., and E. Sackmann, editors. 1995. Structure and Dynamics of Membranes, Handbook of Biological Physics, Vol. 1. Elsevier, Amsterdam.
  • 16.Shen, M., and K. Freed. 2002. Long time dynamics of Met-Enkephalin: comparison of explicit and implicit solvent models. Biophys. J. 82:1791–1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Schwartz, M. P., and A. Matouschek. 1999. The dimensions of the protein import channels in the outer and inner mitochondrial membranes. Proc. Natl. Acad. Sci. USA. 96:13086–13090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Berneche, S., and B. Roux. 2001. Energetics of ion conduction through the K+ channel. Nature. 414:73–77. [DOI] [PubMed] [Google Scholar]
  • 19.Zhu, F., E. Tajkhorshid, and K. Schulten. 2004. Theory and simulations of water permeation in aquaporin-1. Biophys. J. 86:50–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Bicout, D. J., and A. Szabo. 2000. Entropic barriers, transition states, funnels, and exponential protein folding kinetics: a simple model. Protein Sci. 9:452–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Sadlish, H., D. Pitonzo, A. Johnson, and W. Skach. 2005. Sequential triage of transmembrane segments by Sec61α during biogenesis of a native multispanning membrane protein. Nat. Struct. Mol. Biol. 12:870–878. [DOI] [PubMed] [Google Scholar]
  • 22.Best, R. B., D. J. Brockwell, J. L. Toca-Herrera, A. W. Blake, D. A. Smith, S. E. Radford, and J. Clarke. 2003. Force mode atomic microscopy as a tool for protein folding studies. Anal. Chim. Acta. 479:87–105. [Google Scholar]
  • 23.Bustamante, C., Z. Bryant, and S. Smith. 2003. Ten years of tension: single-molecules DNA mechanics. Nature. 421:423–427. [DOI] [PubMed] [Google Scholar]
  • 24.Lu, H., B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten. 1998. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulations. Biophys. J. 75:662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Mori, H., and K. Ito. 2001. The Sec protein-translocation pathway. Trends Microbiol. 9:494–500. [DOI] [PubMed] [Google Scholar]
  • 26.Raden, D., W. Song, and R. Gilmore. 2000. Role of the cytoplasmic segments of Sec61α in the ribosome-binding and translocation-promoting activities of the Sec61 complex. J. Cell Biol. 150:53–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Prinz, A., C. Behrens, T. Rapoport, E. Hartmann, and K. Kalies. 2000. Evolutionarily conserved binding of ribosomes to the translocation channel via the large ribosome RNA. EMBO J. 19:1900–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Tam, P., A. Maillard, K. Chan, and F. Duong. 2005. Investigating the SecY plug movement at the SecYEG translocation channel. EMBO J. 24:3380–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Bustamante, C., Y. Chemla, N. Forde, and D. Izhaky. 2004. Mechanical processes in biochemistry. Annu. Rev. Biochem. 73:705–748. [DOI] [PubMed] [Google Scholar]
  • 30.Hessa, T., H. Kim, K. Bihlmaier, C. Lundin, J. Boekel, H. Andersson, I. Nilsson, S. H. White, and G. von Heijne. 2005. Recognition of transmembrane helices by the endoplasmic reticulum translocon. Nature. 433:377–381. [DOI] [PubMed] [Google Scholar]
  • 31.Beckmann, R., D. Bubeck, R. Grassucci, P. Penczek, A. Verschoor, G. Blobel, and J. Frank. 1997. Alignment of conduits for the nascent polypeptide chain in the ribosome-Sec61 complex. Science. 278:2123–2126. [DOI] [PubMed] [Google Scholar]
  • 32.Beckmann, R., C. Spahn, N. Eswar, J. Helmers, P. Penczek, A. Sali, J. Frank, and G. Blobel. 2001. Architecture of the protein-conducting channel associated with the translating 80s ribosome. Cell. 107:361–372. [DOI] [PubMed] [Google Scholar]
  • 33.Mori, H., T. Tsukazaki, R. Masui, S. Kuramitsu, S. Yokoyama, A. E. Johnson, Y. Kimura, Y. Akiyama, and K. Ito. 2003. Fluorescence resonance energy transfer analysis of protein translocase: SecYE from Thermis thermophilus HB8 forms a constitutive oligomer in membranes. J. Biol. Chem. 278:14257–14264. [DOI] [PubMed] [Google Scholar]
  • 34.Duong, F. 2003. Binding, activation and dissociation of the dimeric SecA ATPase at the dimeric SecYEG translocase. EMBO J. 22:4375–4384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Breyton, C., W. Hasse, T. Rapoport, W. Kuhlbrandt, and I. Collinson. 2002. Three-dimensional structure of the bacterial protein-translocation complex SecYEG. Nature. 418:662–665. [DOI] [PubMed] [Google Scholar]
  • 36.Mitra, K., C. Schaffitzel, T. Shaikh, F. Tama, S. Jenni, C. L. Brooks III, N. Ban, and J. Frank. 2005. Structure of the E. coli protein-conducting channel bound to a translocating ribosome. Nature. 438:318–324. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental]
biophysj_105.073304_index.html (779B, html)
biophysj_105.073304_1.pdf (1.5MB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES