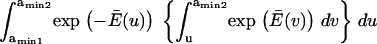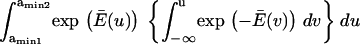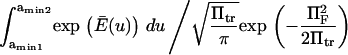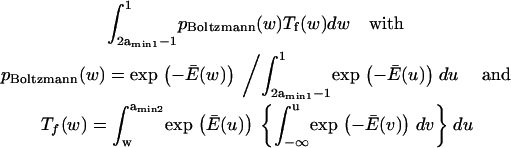A Coarse-Grained Model for Force-Induced Protein Deformation and Kinetics

Abstract

Force-induced changes in protein conformation are thought to be responsible for certain cellular responses to mechanical force. Changes in conformation subsequently initiate a biochemical response by alterations in, for example, binding affinity to another protein or enzymatic activity. Here, a model of protein extension under external forcing is created inspired by Kramers' theory for reaction rate kinetics in liquids. The protein is assumed to have two distinct conformational states: a relaxed state, C₁, preferred in the absence of external force, and an extended state, C₂, favored under force application. In the context of mechanotransduction, the extended state is a conformation from which the protein can initiate signaling. Appearance and persistence of C₂ are assumed to lead to transduction of the mechanical signal into a chemical one. The protein energy landscape is represented by two harmonic wells of stiffness κ₁ and κ₂, whose minima correspond to conformations C₁ and C₂. First passage time t_f from C₁ to C₂ is determined from the Fokker-Plank equation employing several different approaches found in the literature. These various approaches exhibit significant differences in behavior as force increases. Although the level of applied force and the energy difference between states largely determine equilibrium, the dominant influence on t_f is the height of the transition state. Distortions in the energy landscape due to force can also have a significant influence, however, exhibiting a weaker force dependence than exponential as previously reported, approaching a nearly constant value at a level of force that depends on the ratio κ₁/κ₂. Two model systems are used to demonstrate the utility of this approach: a short α-helix undergoing a transition between two well-defined states and a simple molecular motor.

INTRODUCTION

Cells sense mechanical stimuli and respond by varying their biological behavior accordingly. Although the mechanisms for sensation and transduction of mechanical forces into biological signals are still largely unknown, the hypothesis of mechanotransduction through force-induced changes in molecular conformation has been gaining broad support (1–3). Alternatively, either membrane-associated or intracellular proteins might change conformation under force, undergoing a transition to a state with enhanced binding affinity or altered enzymatic activity, thereby initiating a signaling cascade. In particular, force transmission from the extracellular matrix to the cell interior occurs through a chain of proteins, e.g., the fibronectin/integrin bond, integrin-associated proteins on the intracellular side (paxillin, talin, vinculin, etc.), and proteins linking the focal adhesion complex to the cytoskeleton (4), any of which would be a candidate for conformational change and force transduction into a biochemical signal.

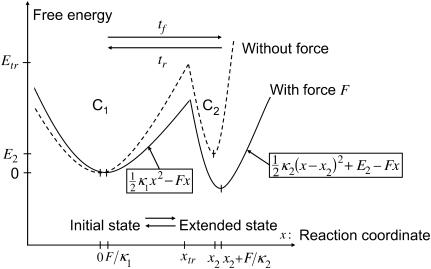
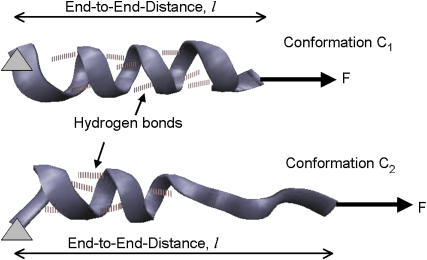
Here we present a generic coarse-grained model linking force to protein conformational change, analyzed in terms of the mechanical properties of the protein states. Assuming that binding is a force-independent event and occurs preferentially in one conformation (relaxed or extended), our model links force applied to a protein to its propensity to initiate a signal. We consider a simplifying case of a protein having just two conformational states: C₁, dominating without force application, and C₂, an extended state favored by force. Our analysis is based on the simplest possible energy landscape corresponding to this situation: two harmonic wells whose minima represent the two states (see Fig. 1), connected via a one-dimensional trajectory. Even though most proteins are likely to sample several intermediary conformations (local minima between the wells) while traversing a complex reaction trajectory (5), our model accounts only for the highest energy peak, or the last one encountered before the reactive state is attained. Both the equilibrium distribution of states as well as the kinetics of reaction are considered.

FIGURE 1.

Idealized protein energy landscape when extended in the direction x. The y axis is the Gibbs free energy G. The boxes contain the landscape equations used to calculate the times t_f and t_r, the first passage times to travel the distance depicted by the associated arrow. C₁ is an initial, relaxed state; C₂ a final, extended state.

Few studies of force-induced alterations between two protein conformations leading to signaling have been reported, and these largely focus on mechanosensitive ion channels. For example, force is thought to induce the change in conductance seen in hair cells (e.g., Gillespie and Walker (6) and Howard and Hudspeth (7)) and in the MscL stretch-activated ion channel (e.g., Wiggins and Phillips (8)). The need for kinetic or transition rate analysis stems from two observations: i), mechanical stimulation of cells or proteins in vivo, in experiments and in simulations spans a wide range of time scales from picoseconds (molecular dynamics simulations) to hours (cell remodeling); hence regimes likely exist for which kinetics dominates over thermodynamic equilibrium, and ii), some proteins are likely to function out of equilibrium (e.g., molecular motors cannot function at equilibrium (cf. Fisher and Kolomeisky (9)).

Here we adopt a widely used microscopic approach based on the Smoluchowski equation to deduce mean first-passage times. Four different approaches (described and labeled i–iv in Methods) are used to derive kinetic information on diffusion-controlled reactions (10) and their predictions compared. This general approach has been successfully applied to nonforced reactions (e.g., Kramers (11) and Schulten and co-workers (12,13)) in the case of a two-state, double-well landscape), as well as forced reactions of bond rupture by escape from a single energy well (14–16). Another method to account for force dependence of kinetic constants is to apply Bell's phenomenological exponential dependence on force for the rate of bond dissociation (17). This approach has been extended to time-dependent applied forces to find statistics on the rupture forces in atomic force microscopy (AFM) experiments (15).

Several methods have been proposed to extract kinetic information from single-molecule pulling experiments leading to unbinding from a substrate or unfolding. AFM results have been analyzed in the context of mean first passage-times (16) on one-dimensional energy landscapes to investigate rupture of the avidin-biotin bond. Whereas unbinding was then modeled as escape from a single energy well, here we introduce a two-well landscape to model the transition between two stable, native conformational states of a single molecule. Izrailev et al. (16) distinguish several regimes depending on the level of force applied to the biotin molecule, and found that the conditions relevant to AFM experiments correspond to what they termed the “activated regime”. This regime corresponds to the limit of large energy barriers (large 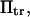as defined in Methods) in the kinetic studies of conformational changes presented here. Hummer and Szabo (15) present another method to extract rate kinetics from pulling experiments, also based on escape from a single energy well.

Most kinetic models for protein deformation or unbinding consider only the energy barrier between states, whereas we propose a model that takes into account the shape of the landscape along the entire reaction path. Molecular dynamics offers ways to link conformational changes of specific proteins under forces applied at specified protein locations. However, such simulations require knowledge of the full atomic structure specific to the particular protein, and typically are confined, due to computational constraints, to forces large compared to those experienced in vivo. Our approach is complementary in that it only considers a single degree of freedom or trajectory and a single transition between states. All intraprotein force interactions are therefore represented by the two parabolic wells to produce a simplified model for the purpose of the examining both equilibrium states and kinetics.

METHODS

General approach

Protein deformation typically occurs in a viscous-dominated regime (18), where motion along the reaction coordinate exhibits randomness and appears Brownian. To account for both these fluctuations and the landscape shape (not merely the transition peak energy), we use an approach based on statistical mechanics theory similar to Kramers (11) in the presence of an external force. Movement of the protein extremity is described using the Smoluchowski equation (see, e.g., Hänggi et al. (19), a force balance on a microcanonical ensemble of particles). Similar methods have been successfully applied to a single parabolic well to describe bond rupture rates under force (14–16). Several methods are used and compared to determine mean first-passage times along the energy landscape, which, in some instances, can then be used to deduce kinetic rate constants for forced conformational changes as a function of the protein mechanical characteristics.

The energy landscape for protein extension

Consider a protein having two conformational states: C₁, preferentially populated when no force is applied, and C₂, an extended state, and acted upon by a contact force (see Fig. 1). A simple energy landscape E(x) describing this situation consists of two parabolic wells:

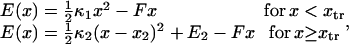(1)

with κ₁ and κ₂ stiffness values of the first and second well, respectively, x_tr the position of the transition state, x₂ the position of the extended state C₂ when no force is applied, E₂ the zero-force free-energy difference between C₁ and C₂, and F the force applied to the protein.

A single reaction coordinate, x, is chosen, corresponding to the direction of protein deformation and force application. Energy minima (describing C₁ and C₂ states, respectively) are located initially at 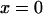and 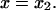The two parabolas intersect at a transition state 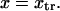With increasing force, the transition state remains at the same reaction coordinate 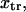but the minima shift to 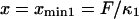and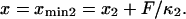

Parameter constraints

Although the parameters are free to vary, the simple landscape geometry adopted imposes several constraints on the range of values:

1. To ensure that C₁ is the preferred state at zero force, it is required that 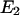be >0.

2. The minimum of the first well (when distorted by force) should not pass the transition point; i.e., 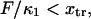leading to the constraint 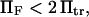with 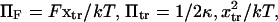and k the Boltzmann constant.

3. Similarly, the transition point should not pass the minimum of the second well; i.e., 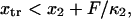leading to the constraint 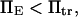with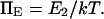

Influence of force on equilibrium

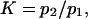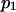A potentially measurable quantity is the equilibrium constant for protein extension, i.e., the ratio of conformational probabilities where and 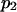are the probabilities corresponding to the relaxed (C₁) or extended (C₂) states, respectively. The equilibrium constant K depends only on the difference in energy 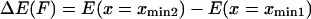between extended and relaxed states and not on the details of the landscape, as described by Boltzmann's law (20):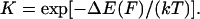

Force consequently leads to a reduction in the thermodynamic cost in passing from state C₁ to C₂, and the ratio of conformational probabilities is therefore (21)

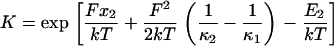(2)

First-passage time calculation

Mean first-passage time 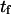associated with the transition from C₁ to C₂ is calculated as the main kinetic information on protein extension. The quantity 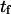has been extensively used as a measure of reaction times (11,12,14,21), and in this study represents the average time necessary for the protein extremity to diffuse from its equilibrium state C₁ (minimum of the first well) to the elongated state C₂ (minimum of the second well) (Fig. 1). Similarly, the reverse mean first-passage time 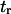for the protein to change conformation from C₂ to C₁ is calculated as a kinetic constant characteristic of the protein conformational in the reverse direction (Fig. 1).

The mean first-passage time 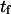can be evaluated in different ways depending on assumptions chosen to solve the Fokker-Plank equation governing the protein conformational change (see Appendix). Previous methods (11,12,14,21) begin by integrating the Fokker-Plank equation between a reaction coordinate 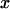and the reaction coordinate of the final state (i.e., 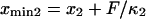in our case), and make the assumption that the probability of the final state remains close to zero. This latter assumption, i.e., C₂ is not yet populated, is relevant for our model of mechanotransduction where signaling would be initiated as soon as the extended state becomes populated.

Kramers (11) and Evans and Ritchie (11,14) assume a stationary current across the energy barrier and that the barrier itself is much larger than the thermal energy; consequently, they only need to consider the landscape shape near the initial state and in the vicinity of the barrier. They then deduce the forward kinetic rate as being ∼ As an alternative to this last step, Schulten and co-workers (12,13) and Howard (21) integrate the Fokker-Plank equation a second time using one of the following two assumptions: i), at all times, the molecular conformation resides between the starting and the final reaction coordinate (21), i.e.,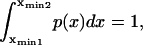 with 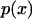the probability of finding the protein in conformation x; or ii), the flux of probability approaches zero as 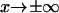(Eq. 2.1 in Schulten et al. (12)). Howard's assumption is less realistic for our case where the protein also samples conformations 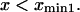In our case, we follow Schulten and co-workers' approach (zero flux at infinity), as it seems most realistic and appropriate for conformational change and compare predictions obtained from all methods.

We calculated the normalized passage time 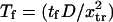for each method (Kramers (11) and Evans and Ritchie (14), Schulten and co-workers (12,13), or Howard (21) applied to our two-well landscape (Eq. 16, see Appendix). For example Schulten and co-workers' method gives

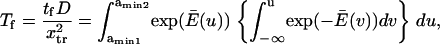(3)

where the normalized reaction coordinate is 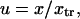the integral boundaries are 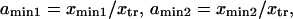and the normalized energy landscape

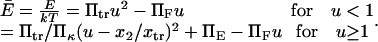(4)

Therefore, T_f depends upon only four parameters:

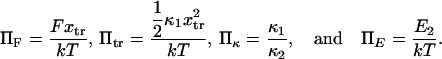(5)

The expression for 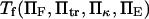is not algebraically tractable, and was evaluated numerically using Maple 9 (Maplesoft, Waterloo, Ontario, Canada) for a range of values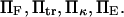

Similarly, the normalized reverse passage time 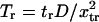is

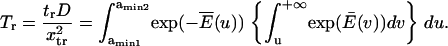(6)

Finally, calculating a passage time starting from the single coordinate 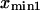fails to account for the distribution of initial states within the first energy well. To do so, we modified the expression of the extension time:

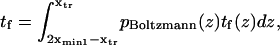(7)

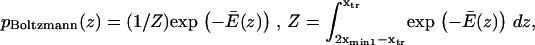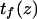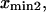with and = the first passage time from to obtained replacing 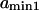by 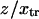in Eq. 3. Equation 7 was evaluated numerically using discrete Riemann integrals with both 15 and 20 terms.

To summarize, we calculated the extension time for a double-well energy landscape using four different methods (see Table 1):

1. Double integration of the Fokker-Plank equation with the condition 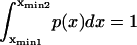(drawn from Howard (21)).

2. Double integration of the Fokker-Plank equation with the flux of probability going to zero at 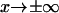(based on Howard (12) and Schulten and co-workers (13)).

3. Simple integration with assumptions on the landscape shape (based on Kramer (11) and Evans and Ritchie (14).

4. Average of passage times obtained with method ii, weighted to take into account the Boltzmann distribution of initial conformations within the first well (see Eq. 7). Whereas method iv is perhaps the most rigorous, it is also the most computationally intensive. As discussed below, based on a comparison of the four approaches, we chose to use method ii for the bulk of the results presented here.

TABLE 1.

Equations used to obtain the dimensionless extension time to go from conformation C₁ to conformation C₂

Method	Equation used to evaluate the dimensionless extension time	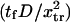References
i		(21)
ii		(12,13)
iii		(11,14)
iv		(12,13)

Results from these different methods are compared in Results and in Fig. 6.

Smoothed landscape

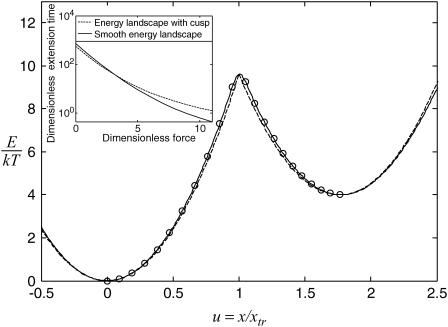
The double-well energy landscape we consider has a cusp at the transition state 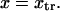This could artificially influence our results since the landscape along the entire reaction path is used to calculate extension times and, as we show below, the transition state is a primary determinant of t_f. To study the effect of this cusp on our results, the energy landscape was smoothed using Thiele's continued fraction interpolation (22) by fitting points on the landscape to a rational fraction using Maple 9 (Maplesoft). The 18 or 22 points used for fitting were equally spaced in each well, but avoided the cusp at ±0.05 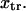We then compared the smoothed landscape with the one containing the cusp by slightly modifying 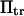so that both landscapes had precisely the same energy barrier (Fig. 2).

FIGURE 2.

Example of energy landscape smoothing when 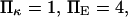and 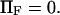Smooth landscape (solid line) is obtained by the Thiele interpolation of 22 points (○) on a landscape with an energy barrier 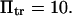It is then compared with the cusp landscape having the same energy barrier (dashed line). (Inset) Extension times obtained with the two landscape types (smooth or with cusp) as a function of force. Parameters are the same except for 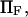which is allowed to vary.

Extension times 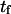calculated using the smoothed potential differed from those of the cusp potential in proportion to the quality of the fit (see inset in Fig. 2). In addition, the agreement was better when the barrier height was large (small dimensionless force 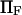), i.e., when the cusp is the dominant feature of the landscape. We also verified that the agreement between the extension times for the smooth and cusp potentials improved with the quality of the fit. Therefore, we concluded that the cusp in our landscape per se did not have a significant impact on the extension time results, and only present results using the simple cusp potential.

Characteristic time for protein extension

Consider a constant force F applied to the protein at time t = 0 (with a loading rate ≫k_f, k_r). The first-order kinetic equation describing the conversion from initial state to extended state is

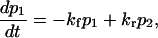(8)

with p₁ and p₂ the probability of conformations C₁ and C₂, respectively, and k_f and k_r the forward and reverse rate constants for the protein to change conformation from C₁ to C₂. In some instances (see Discussion), k_f and k_r can be approximated as the inverse of the mean first-passage time associated with the transition, i.e.,

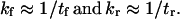(9)

Behind such an evaluation for k_f and k_r is a partitioning of all microstates into two classes, e.g., by designating all the states by either shorter than or more extended than the transition state. Consequently, 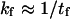and 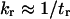(Eq. 9) is only valid when 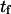and 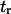are similar to the passage times just to the barrier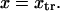

Solving Eq. 8 using the initial condition 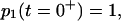the time course of the probability of both conformations is

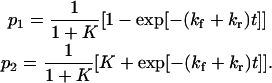(10)

Therefore, the characteristic time to obtain the new equilibrium is 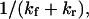directly calculable from the passage times 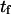and 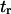when the approximations of Eq. 9 are valid.

Steered molecular dynamics simulations on a simplified protein model

For the purpose of comparison to our coarse-grained simulations, we constructed a simple α-helix (a 15 mer of polyalanine) and analyzed it using steered molecular dynamics (SMD) (23). One advantage of an α-helix is that the helical axis uniquely defines a unidirectional reaction coordinate, along which the external force is applied. An extensive free-energy calculation using constant velocity SMD and Jarzynski's equality has recently been reported by Park et al. (24) on a very similar deca-alanine α-helix. Here however, rather than attempting to evaluate the potential of mean force, we applied a constant force and used distance constraints on the 15 mer of polyalanine to compare our SMD results with those from the coarse-grained model. The number of alanine residues in the polypeptide and the distance constraints selection has been selected so as to yield a stable and simple model that exhibits two distinct conformations. Many parameters extracted from the constant force SMD of this specifically designed model can be better related to our coarse-grained model, as seen in the Results section.

The polyalanine α-helix was constructed by creating a linear polyalanine sequence and specifying all the φ-dihedral angles to −57° and all the ψ-dihedral angles to −47°, which is characteristic dihedral angles for an α-helix. The N- and C-termini were capped with an amino group and a carboxylate group, respectively, with ionic states representative of the physiological pH level. The CHARMM (26) script for creating an α-helix is available online (25). The commercially available molecular dynamics software CHARMM (26) was used to carry out the SMD simulations with the ACE2 implicit water module (27) and SHAKE constraints (28) for efficiency. Energy of the α-helix structure was minimized in 15,000 steps, heated to 300 K in 40 ps, and the system was equilibrated for 120 ps using a time step of 2 fs. After equilibration, the helix was repositioned placing the N-terminus at the origin and the C-terminus along the x axis. Holding the helix fixed by a harmonic constraint at the N-terminus, the C-terminus was pulled with constant force along the x axis. After a sequence of simulations in which several polypeptides arrangements were tried, we chose an α-helical system with 11 potential H-bonds, with six forced to remain intact under force and the other five allowed to form or break due to the combined effects of electrostatic attraction and van der Waals repulsion. The criterion for this choice was that the system exhibits two distinct states, with no apparent intermediate states. We imposed nuclear Overhauser effect constraints to the six H-bonding pairs, out of 11 possible, starting from the N-terminus carbonyl group, by specifying a limit distance of 4.25 Å between ith carbonyl carbon and (i + 4)th amide nitrogen with a force constant of 10.0 kcal/mol Ų. This model leaves five H-bonding pairs near the C-terminus to simultaneously either all break or all form to yield two distinct conformations (C₁ and C₂). The polyalanine α-helix was constructed by creating a linear polyalanine sequence and specifying all the φ-dihedral angles to −57° and all the ψ-dihedral angles to −47°, which is the characteristic dihedral angle for an α-helix. The N- and C-termini were capped with an amino group and a carboxylate group, respectively, with ionic states representative of the physiological pH level. The CHARMM (29) script for creating an α-helix is available online (25). Simulations were performed for 100 ns per simulation at forces of 30 pN, 65 pN, 70 pN, 75 pN, 80 pN, 85 pN, and 100 pN.

Thermal fluctuations caused the forced end to exhibit relatively large displacements perpendicular to the direction of force application (see Fig. 3; left end is fixed and right end fluctuates). To compare with our single-dimensional coarse-grained model, we therefore present results in terms of the time-averaged component of force acting along the axis of the α-helix.

FIGURE 3.

Two distinct conformations, C₁ (top) and C₂ (bottom), of the simplified protein model used in SMD example. Left end of the helix is held fixed, whereas the right end is pulled with a constant force in the direction shown by the arrow. Six hydrogen-bonding pairs near the fixed end are constrained not to break.

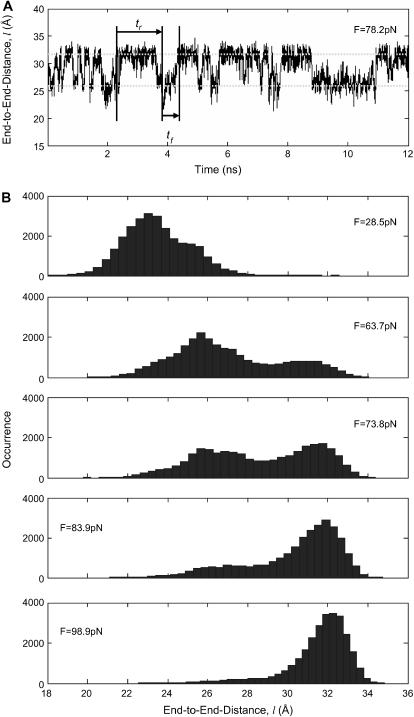
Parameters were extracted from SMD simulations for comparison with our coarse-grained model. End-to-end distances, defined as the distance between the two termini (Fig. 3), were recorded every 4 ps and used to generate histograms (Fig. 4 B) to identify the most frequently sampled configurations.

FIGURE 4.

(A) Time trace of the end-to-end distance of the helix at F = 78.2 pN (corrected from F =80 pN). A forward passage time and a reverse passage time are shown. Mean passage times are obtained by averaging throughout the simulation. (B) Histograms showing single and double peaks at various force magnitudes. Linear shift on the peaks are evident with varying forces.

Forward mean first-passage time from the coiled to extended conformation (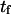) was determined, assuming ergodicity, as the average time the molecule resides in state C₁ before undergoing a transition to C₂, whereas reverse mean passage time (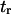) was determined as the time residing in the extended conformation (C₂) before returning to the coiled conformation (C₁) (Fig. 4 A). We introduced these SMD-determined parameters into our coarse-grained model, and compared the forward and reverse mean passage times obtained by both methods (SMD and coarse-grained model).

RESULTS

Selected parameter ranges

To represent a protein with two distinct conformational states, we chose 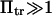(baseline value of 10, with variations between 5 and 25). To assure that, in the unforced condition, C₁ was the preferred state, we further specified that 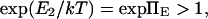hence was selected as our baseline value, with variations considered between 0 and 10. No restrictions were imposed on the relative values of well stiffness 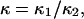so we chose a baseline value of 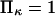with variations in the range 0.2–5.

Forces ∼100 pN have been shown to rupture molecular bonds (30), and conformational changes are likely to involve lower forces of at most a few tens of piconewtons (for comparison, myosin motors produce 3–4 pN force (cf. (30,31)). Typical distances between protein conformational states x₂ ∼ 0.1–10 nm—yielding 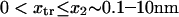—and kT ∼ 4 pN.nm at body temperature led us to vary 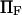from 0 to 20 (corresponding, for example, to F=40 pN and x_tr=2 nm).

Equilibrium states

The probability of each conformational state at equilibrium is described by Eq. 2, as obtained previously by Howard (21). The second term in the argument of the exponential suggests nonmonotonic behavior in the special case of 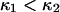and large F²: cases in which 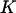increases, then decreases as applied force is increased (consistent with the hypothesis put forward by Howard (21)). However, the parameter constraints (see Methods) preclude this from happening. One could argue that constraint 2 (the transition point should not cross over the reaction coordinate of the extended state, see the “Parameter constraints” paragraph in Methods) is only necessary for our kinetic study, and could be relaxed in this thermodynamic approach. Even so, we found that this corresponds to cases where the force is so large that the first well minimum is at a more extended coordinate than the second well minimum, clearly an unrealistic situation.

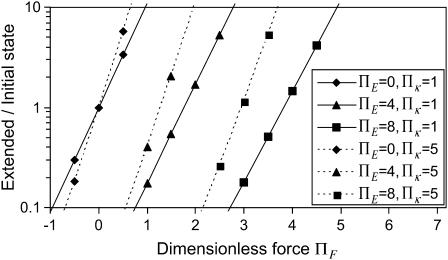
Another important consequence of Eq. 2 is that for typical values of the parameters, conversion of the protein from 10% to 90% in the extended state C₂, occurs over a very narrow range of only a few 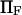(see Fig. 5). Large values of 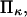i.e., a relaxed state C₁ stiffer than C₂, make this transition even sharper (see Fig. 5).

FIGURE 5.

Equilibrium ratio of probabilities 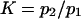of finding the protein in extended/initial state as a function of force applied 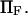The parameters are 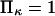(dotted lines) or 5 (solid lines), 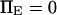(♦), 2 (▴), or 4 (▪), and 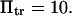Negative forces 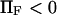oppose protein extension.

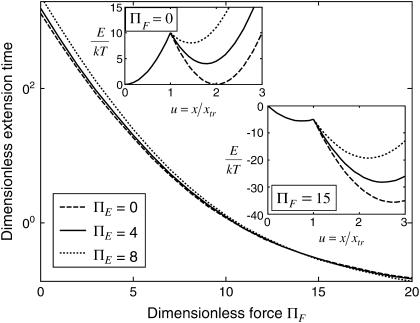
Comparison of extension time predictions

Of the four approximate methods described above, method iv is the most accurate but also the most computationally demanding. Extension times obtained with this method differed by no more than 5% (for 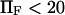) from those obtained with method ii, which does not include the last averaging of method iv (see Eq. 7 and Fig. 6). Therefore we concluded that we could use method ii as an accurate estimate for the extension time.

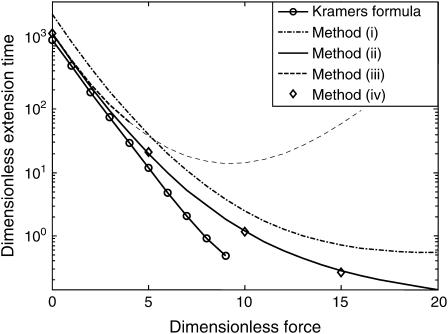
FIGURE 6.

Dimensionless protein extension time 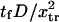versus dimensionless force applied 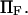The other dimensionless parameters are held constant: 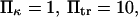and 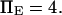Kramers' analytical formula for the dimensionless time in the specific case of a potential with a cusp at the energy barrier (inverse of the dimensionless kinetic rate of Kramers (11) is expressed in our notation as 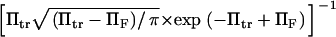. Its validity is restricted to low 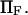Method i is based on Howard (21), method ii on Schulten et al. (12), method iii on Kramers (11) and Evans and Ritchie (14), and method iv is a finer estimate of the extension time based on method ii (see text for details). Method iii is also only valid for low 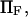therefore results for large forces (beyond the range of validity) are represented by a thinner, dotted line.

Somewhat surprisingly, method i matched closely with that of method ii up to 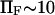(see Fig. 6), despite what might at first appear to be a rather simplistic and restrictive assumption in the former—that the probability of conformations between the two energy minima equals 1 at all times, i.e.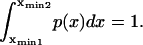

Finally, as expected, results from method iii, similar to Evans and Ritchie (14) and Kramers (11), agree with results from the other methods for low force, but the departure for 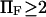was quite dramatic (see Fig. 6). This suggests that the assumption that the energy barrier is much greater that the thermal energy used by these authors and in method iii breaks down, for 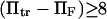or, for the parameters used in Fig. 6, 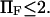We drew the same conclusion from comparison of results from methods i and ii with the analytical solution provided by Kramers (11) in the specific case of a potential with a cusp and a high-energy barrier, i.e., 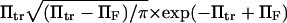in our notation. All results presented from this point onward were obtained using method ii.

Variations of forward and reverse first passage times

Force significantly enhances transition from the initial to extended state for all cases in the chosen range of parameter values (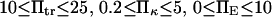). In all cases, a larger force applied to the protein induced a shorter extension time t_f (Figs. 7–9). For example, at the baseline values 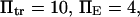and 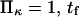decreases from ∼1.54 10³ 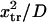at 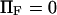to ∼0.29 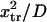at 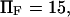enabling the protein to change conformation ∼5500 times faster when forced. Note that the C₁ to C₂ transition time under force is then at least 3.5 times shorter than the pure diffusion time 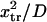, corresponding to C₁ to C₂ conversion for a protein with zero stiffness (i.e., a flat energy landscape).

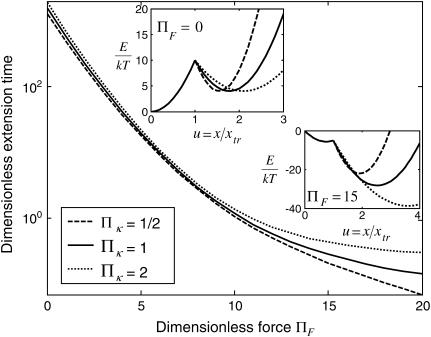
FIGURE 7.

Dimensionless extension time 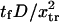versus dimensionless force applied 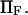The other dimensionless parameters are held constant: 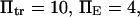and 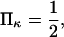1, or 2. (Insets) Normalized energy landscape used to calculate the extension time (same parameters).

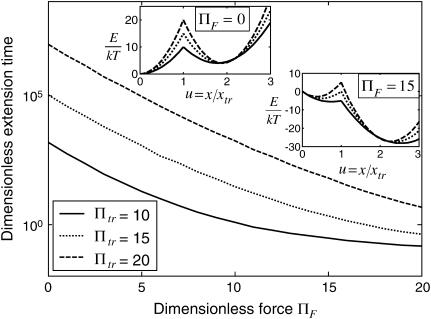
FIGURE 8.

Dimensionless extension time 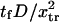versus dimensionless force applied 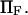The other dimensionless parameters are held constant: 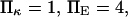and 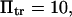15, or 20. (Insets) Normalized energy landscape used to calculate the extension time (same parameters).

FIGURE 9.

Dimensionless extension time 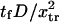versus dimensionless force applied 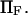The other dimensionless parameters are held constant: 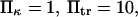and 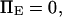4, or 8. (Insets) Normalized energy landscape used to calculate the extension time (same parameters).

At low forces (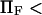5–10, depending on the other dimensionless parameters), the decrease in 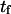is exponential (consistent with the law proposed for bond dissociation by Bell (17)), but the transition is less rapid at larger forces (Figs. 7–9).

At constant 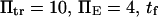decreases with 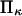(Fig. 7) approaching a plateau of 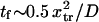for 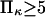(data not shown). At these given values for 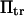and 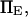the transition cannot occur in a time <500 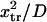without force (data not shown). Lowering the transition energy 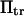has the expected effect of hastening transition to the extended state (Fig. 8). However, the exponential dependence of 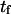on force breaks down at lower forces for small transition energies 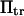(Fig. 8). Varying 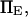the dimensionless zero-force energy difference between C₁ and C₂ does not significantly influence the variations of the extension time with force (Fig. 9). In general terms, whereas equilibrium is largely determined by 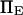and 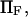extension times are relatively insensitive to 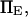and depend primarily on 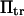and 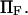The effects of 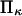are generally small, except for higher values of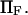

Variations in the reverse mean first-passage time t_r as computed from Eq. 6 generally vary as 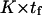, so that the model is self-consistent (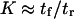) as well as being in agreement with equilibrium thermodynamics.

As a limiting case, the first-passage time to diffuse up the first well (from C₁ to the transition state) was calculated with our method i and compared with the analytical formula available for F = 0 (11,21) and 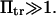Reasonable agreement (maximum difference of nearly 10%) was observed in the chosen parameter range (see first paragraph of Results).

Characteristic time for conformational change

The characteristic (relaxation) time to reach equilibrium probabilities of extended and initial conformational states upon application of a stepwise force is 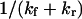(see Eq. 10). Application of a small force (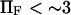) tends to increase the relaxation time to reach equilibrium and obtain a large probability of extended state (data not shown), i.e., the forward constant is not increasing fast enough to exceed the drop of the reverse constant under small forces. Large forces, in contrast, favor the extended state at equilibrium while increasing the kinetic of conversion to the extended state (data not shown). Typical values for these times are 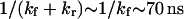(for our baseline values with 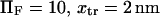and D ∼ 67 μm²/s (21)). The time to ramp the force from zero to its constant value must therefore be much greater than 70 ns for our analysis to be valid. Even though the characteristic relaxation time 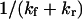may decrease with force, the probability of the extended state at any point in time p₂(t) (see Eq. 10) always increases with force (data not shown), as the final equilibrium probability p₂(t = ∞) is increased by force.

Comparison of coarse-grained model to SMD simulation

The end-to-end distance (l) was extracted at each time frame (4 ps per frame) from all of the SMD simulations (e.g., F = 78.2 pN shown in Fig. 4 A). Plotting the histogram of l, the molecule is seen to sample two predominant conformations (end-to-end distances with the most occurrences on Fig. 4, A and B). Assuming ergodicity, these conformations correspond to energy minima of our idealized energy landscape: 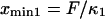and 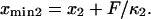Plotting the end-to-end distance with the most occurrences ( 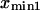and 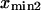) as a function of force (data not shown) yields the zero-force end-to-end distance of C₁ and C₂ ( 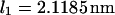and 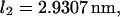respectively; hence the reaction coordinate 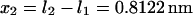). The locations of x_min1 and x_min2 determined from the peaks of the histograms follow a linear trend with applied force 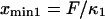and 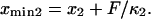The slope ratio of 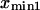and 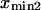from the same plot gives 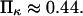Thermal fluctuations are greater at small forces (C₁) than at large forces (C₂) (see Fig. 4 A), hence 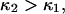roughly by a factor of 2. At F = 74 pN, the SMD simulations show that the molecule spends an equal amount of time in states C₁ and C₂. This, as well as the geometric constraints described in Methods, lead to the parameter values 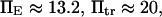and a transition state 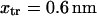(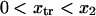). Finally, it follows that 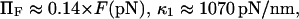and .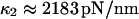

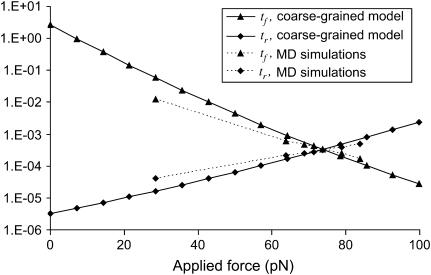
The passage time t_f decreased with applied force, and t_r increased with applied force both with lower and upper limits of zero and infinity, respectively (see Fig. 10). Hence, the coarse-grained model and SMD simulations yielded similar trends, though extension times exhibited a stronger dependence on force with the coarse-grained model. Since the extension times are dependent upon the shape of the energy landscape, one explanation for the difference in extension rates could be that the actual shape of the wells is different from the assumed parabolic wells.

FIGURE 10.

Protein extension times from coarse-grained model as a function of applied force along the helix axis direction. (Dotted line) SMD results from pulling on 15 mer of polyalanine forming an α-helix. Extension times are extracted as explained in Methods and in Fig. 5. (Solid line) Results from coarse-grained model with 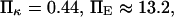and 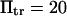(see text for parameter extraction). Both the coarse-grained model and SMD simulations exhibit similar trends for the first-passage times transforming the initial into the extended state (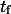) or the reverse ().

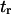DISCUSSION

A generic model is developed for protein extension employing the physics of diffusion under force inspired by Kramers' theory. The protein is assumed to have two distinct conformational states: a relaxed state, C₁, preferred in the absence of external force, and an extended state, C₂, populated under force application. Our model takes into account the mechanical features of the protein, as influenced by the weak interactions within a single protein. Its main purpose is to mechanically characterize the behavior of a protein's force-induced deformations and kinetics using a coarse-grained, approximate method. For now, we focus on the simplest system, and present an approach that incorporates a two-potential well energy landscape. Equilibrium results show that transitions to an activated state can occur over a narrow range of applied force. Extension times initially follow the anticipated exponential dependence on force, but the behavior deviates as the energy landscape becomes increasingly distorted. When cast in dimensionless form, all these results can be expressed in terms of four dimensionless parameters. Extension times are predominantly influenced by conditions at the transition state, although the stiffness of the potential well can become significant under higher applied forces.

Simulations of complete unfolding of a protein (e.g., titin in Rief et al. (32), fibronectin domain in Gao et al. (33)), or unbinding from a substrate (e.g., avidin-biotin in Izrailev et al. (16)) have typically used large forces (on the order of nanonewtons) to be computationally feasible with (SMD, and hence fall within a drift motion regime (16). As this probes a different regime from the thermally activated one used in our coarse-grained model (16,34), we performed new simulations with smaller, steady forces (30–90 pN), inducing small deformations (<1 nm, compared to ∼28 nm for unfolding of a single titin domain (32)) and slow kinetics (timescales on the order of nanoseconds rather than picoseconds). These slower transitions with smaller displacements are perhaps of more interest in the context of mechanotransduction. Using parameter values taken from equilibrium conditions, reasonable agreement was obtained for the variation in time constants with applied force (Fig. 10). Values of 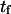and 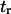extracted from SMD do not vary as rapidly with force as those computed with the coarse-grained model. A reason for this discrepancy could be that more energy dimensions are sampled in SMD than in our one-dimensional coarse-grained model, or that these differences reflect the more complicated shape of the true energy landscape.

Equilibrium analysis

Thermodynamic analysis shows that conversion of the protein from 10% to 90% in the extended state usually occurs over a very narrow force change of a few 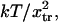i.e., a few piconewtons for states separated by distances x₂ ∼ x_tr on the order of nanometers. This can be viewed in the context of forced-induced conformational changes in intracellular proteins, leading to changes in binding affinities or enzymatic activities, as has been proposed as a mechanism for mechanotransduction (30). The methodology presented here might therefore be useful in the creation of coarse-grained models of mechanosensing. Typical forces needed to rupture bonds are on the order of tens to hundreds of piconewtons, e.g., 20 pN for fibronectin-integrin (35), up to 170 pN for biotin-avidin (36). Our study shows that with reasonable parameter values, nanometer-scale conformational changes require only a few tens of piconewton force (see Fig. 5).

Variations of forward and reverse passage times

Increasing force has the anticipated effect of enhancing the transition from initial to extended state for all cases considered. However, the decrease in reaction time t_f with increased force is relatively minor under certain conditions, in particular when the second well stiffness is small (large 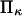) making the extended state very compliant and sensitive to distortion by force. This behavior can be explained by the large distortion of the softer extended state under applied force. At large 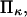a softer extended state experiences a relatively large distortion (Δx = F/κ₂) under applied force, whereas the initial state C₁ only displaces by Δx = F/κ₁. This lengthens the path to travel down the second well, so that the time to travel from the energy barrier down to C₂ becomes significant compared to the time it takes to travel up the first well from C₁ to the energy barrier. Incidentally, this invalidates the concept of reaction (or extension) rate (e.g., used in Eqs. 8 and 10), which neglects relaxation in the second well as a prerequisite (11). Only in cases where the time to travel down the second well is negligible (low forces applied), does 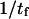represent the extension rate 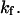A protein's propensity to rapidly transform from one conformational state to another state under force is hence directly dependent on the relative stiffnesses of these conformations, characterized by the dimensionless parameter,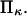

Comparison with other models

Evans and Ritchie (14) first described bond rupture adding external force to the Fokker-Plank equation and using a single harmonic well appropriate for bond dissociation. Here, we have added a second harmonic well with its own characteristics and location to model a second extended conformational state to link the applied force to conformational changes. Our predictions for the force-dependence of protein extension time can be compared with existing models for the force-dependent bond rupture rate, as both phenomena include a force-aided escape from an energy well over an energy barrier. Bell's analysis (17) states that the rate of bond rupture is proportional to 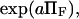with a a scaling factor close to unity. 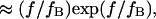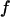Evans and Ritchie's experimentally validated model for bond rupture under force predicts a dependence on force for the rupture rate where and 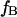correspond to 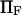and 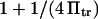in our notation, respectively (14). This corresponds to a slightly stronger dependence on force than the Bell model with the dissociation rate increasing more rapidly with force when 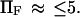Our results for the inverse of the time of C₁ to C₂ extension exhibit a weaker dependence on force than either Evans and Ritchie (14) or Bell (17) (see, e.g., Figs. 7–9), especially visible at higher forces where we find a plateau, whereas none was predicted for bond dissociation (14,17). We believe that the weaker dependence at high force arises from the distortion of the extended conformation, which lengthens the time to reach C₂ (see Results). Note that the inverse of the extension time approaches Evans and Ritchie's dissociation rate at large forces, as it should, when 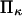becomes small (very stiff extended state), so that movement down the second well is rapid.

Ritort and others (37) describe molecular conformational changes under force using dissipated work, and offer a means of deducing equilibrium landscape characteristics from multiple pulling experiments on the molecule in cases when the energy barrier is small. Landscape obtained in such a manner could be combined with our studies to examine the effect on kinetics of different landscapes. We find, like Fischer and Kolomeisky (9), that even with a simple two-state model, the velocity versus load plots exhibit different shapes depending on the values chosen for the parameters.

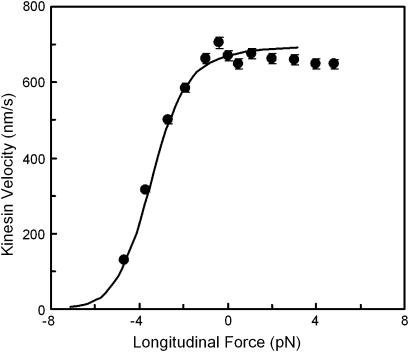
Application of the theory to a simple processive motor

Our protein deformation model can be used to reproduce some of the features of a processive molecular motor being forced in the direction opposing its movement. A well-studied example is the movement of kinesin along a microtubule. According to recent experiments (38), the power stroke in the kinesin reaction cycle should be well aligned with the microtubule axis. We therefore consider the power stroke to be a single longitudinal load-dependent conformational change of x₂ = 8.2 nm (kinesin step size) along the microtubule axis, which can be slowed by reverse force application, and that the forward progression time 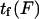can be determined by our analysis. Attributing a global characteristic time 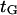to all other (longitudinal load-independent) rate-limiting conformational changes in the kinesin reaction cycle, the rate of the kinesin cycle can be written 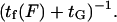Kinesin velocity 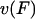along the microtubule is then computed as the step size divided by the kinesin cycle time

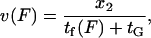(11)

where 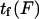is a function of D, x_tr, and 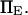Based on experimental results (38,39), we selected 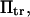D, and 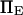so that 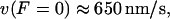i), ii), 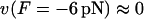(stalling force), and iii), the position of the energy maximum is at 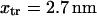of the initial, prestroke kinesin state. 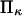was arbitrarily set to unity as it had little effect on 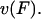Adjusting the characteristic time 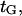we were able to capture the trend of kinesin velocity variations with force (see Fig. 11).

FIGURE 11.

Model prediction for kinesin velocity (solid curve) as a function of force for a single longitudinal force-dependent conformational change in the kinesin cycle (see text for expression and calculation of the velocity). Solid circles correspond to optical force clamp measurements from Block and others ((38), Fig.4 A) under saturating ATP conditions (1.6 mM ATP).

As expected, the load-independent conformational changes (characterized by 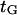) are responsible for the velocity plateau at positive forces (see Fig. 11). This would imply that the force-dependent “power stroke” is not rate-limiting for these force values, as has been suggested by others (e.g., Block et al. (38)).

Note that a diffusivity of 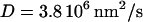was found to best satisfy the constraints mentioned above. This value is ∼20 times smaller than the diffusivity of a free-floating 100 kDa globular protein domain (15). This is consistent with the 360 kDa kinesin being attached to the microtubule during the whole reaction cycle, and hence restrained in its diffusion.

Application to mechanotransduction

Interest in the fundamental mechanisms of mechanotransduction has led to an increased focus on force-induced conformational change, producing subsequent alterations in binding affinity or enzymatic activity. Progress has been slow, however, since numerous proteins are involved in the transmission of force into and throughout the cell, and only a small fraction of these are sufficiently well characterized to permit detailed analysis, either by molecular dynamics simulation or experimentally. Alternative, more approximate methods are therefore needed if progress is to be made in the near term. Here, a simple, coarse-grained model of protein conformational change is presented, capable of simulating some of the basic characteristics of protein kinetics and conformational change. Numerous simplifications are made, representing the true energy landscape by a single degree of freedom in the direction of forcing, and assuming harmonic potential wells with just two well-defined minima. Despite its simplicity, however, the current model can serve as a useful starting point for more detailed models. Since the solutions are obtained numerically, other, nonharmonic potential wells with multiple minima could be simulated, and deformations could be allowed in two or even three dimensions, if information were available to support such extensions. Similarly, simulation of multiple proteins, such as those comprising a focal adhesion, becomes computationally feasible.

APPENDIX: GENERAL PRINCIPLE OF PASSAGE TIME CALCULATION

To determine t₀, mean first-passage time over a distance x₀, consider an ensemble of identical particles in a one-dimensional box bounded by a reflecting wall at x = 0 and an absorbing wall at x = x₀. As soon as a particle hits the absorbing wall it is placed back at x = 0 so that the total number of particles is conserved. The first-passage time is given at steady state by

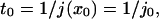(12)

where 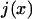the normalized flux of particles at position x in the +x direction, constant and equal to 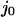throughout the box due to conservation of particles. If each particle is subjected to both diffusion and a “drift” due to an external force F(x), the flux is

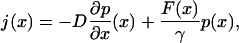(13)

where 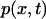is the probability of a particle to be at position x, D the diffusivity of the particle, 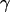the drag coefficient, and F(x) the external force applied on the particle in the x direction.

Finally taking the derivative of Eq. 13, one obtains the Fokker-Plank equation at steady state:

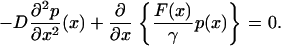(14)

Finding the passage time t₀ requires solving Eq. 14 for 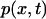with two boundary conditions, one of them being

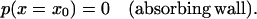(15)

In the simplest method, we present (method i, based on Howard (21)) an integral condition: 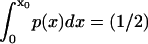is specified. Consequently F(x), the external force acting on the particle (or protein domain), is a combination of a harmonic spring force (exerted by the rest of the molecule on the pulled domain), and a constant external force F, corresponding to a total energy 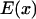described in Eq. 1. Considering diffusion between two arbitrary points 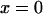to 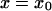and using these boundaries to integrate Eq. 14, we obtain the following passage time (method i):

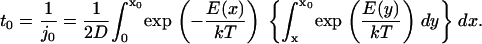(16)

Details on evaluation of passage times using methods ii–iv are provided in Table 1.