Simulation-Based Methods for Interpreting X-Ray Data from Lipid Bilayers

Abstract

The fully hydrated liquid crystalline phase of the dimyristoylphosphatidycholine lipid bilayer at 30°C was simulated using molecular dynamics with the CHARMM potential for five surface areas per lipid (A) in the range 55–65 Ų that brackets the previously determined experimental area 60.6 Ų. The results of these simulations are used to develop a new hybrid zero-baseline structural model, denoted H2, for the electron density profile, ρ(z), for the purpose of interpreting x-ray diffraction data. H2 and also the older hybrid baseline model were tested by fitting to partial information from the simulation and various constraints, both of which correspond to those available experimentally. The A, ρ(z), and F(q) obtained from the models agree with those calculated directly from simulation at each of the five areas, thereby validating this use of the models. The new H2 was then applied to experimental dimyristoylphosphatidycholine data; it yields A = 60.6 ± 0.5 Ų, in agreement with the earlier estimate obtained using the hybrid baseline model. The electron density profiles also compare well, despite considerable differences in the functional forms of the two models. Overall, the simulated ρ(z) at A = 60.7 Ų agrees well with experiment, demonstrating the accuracy of the CHARMM lipid force field; small discrepancies indicate targets for improvements. Lastly, a simulation-based model-free approach for obtaining A is proposed. It is based on interpolating the area that minimizes the difference between the experimental F(q) and simulated F(q) evaluated for a range of surface areas. This approach is independent of structural models and could be used to determine structural properties of bilayers with different lipids, cholesterol, and peptides.

INTRODUCTION

Numerous studies over many years have focused on refining the structure of lipid bilayers (1–5). However, quantitatively accurate structures of even pure bilayers have been difficult to obtain, especially in the most biologically relevant liquid crystalline (L_α) phase consisting of disordered and fully hydrated lipids. Such bilayers are not crystalline with atomic positions determined at the Ångström level, but have atomic distribution functions with widths spread over 5 Å. This precludes an atomic-level structural description and substantially limits the quality and quantity of structural data that can be obtained. Consequently, structural models are required to elucidate structural quantities in real space (e.g., electron density profiles, surface areas/lipid, component densities) from experimental observations in reciprocal space, i.e., the scattering form factors, F(q) (6,7). Broadly stated, a structural model specifies the form of the electron density profile, ρ(z), and the specific values of the parameters are determined by fitting to experiment.

A variety of structural models have been applied to membranes. Wilkins et al. (5) employed constant electron densities for different regions to obtain the electron density of the L_α phase, but the physically unrealistic discontinuities at the edges of regions lead to spurious large amplitude high q oscillations in F(q) (5,7,8). The structural model of Wiener and White (4) consisting exclusively of Gaussians is not confounded by discontinuities, but the large number of free parameters restricts applications to systems at low hydration. The structural model developed by Nagle and co-workers (8), here denoted the hybrid baseline model (HB), falls between the previous two. Specifically it consists of two functional types: Gaussians representing the lipid headgroups and the terminal methyls; and a baseline function consisting of strips representing water and the methylene plateau joined by a smooth bridging function. With additional assumptions and data, HB also yields the surface area per lipid, A. Given that most molecular simulation or modeling studies require A for at least the initial condition, the importance of this feature in a structural model is clear.

An awkward aspect of HB involves the baseline function: the electron density in the superposition region is due not only to the water and the hydrocarbon chain methylenes, but also to the headgroup components. A more transparent model has no baseline function and more simply represents both the methylenes and the water by separate functions; such a model has been advocated for reflectometry studies of monolayers (9). The first part of this article develops a hybrid zero-baseline model, denoted H2, for analyzing and interpreting diffraction data from bilayers.

The approach employed here is simulation based. Results from molecular dynamics (MD) simulations have been fruitfully compared with those from diffraction experiments. For example, Feller et al. (10) demonstrated that the distributions of certain lipid component groups were not Gaussian. More recently, Sachs et al. (11) and Benz et al. (12) compared the simulations with experiment for various molecular properties in real and Fourier space. Here the application uses simulations to help motivate the functional form of H2, and to provide test cases for comparing HB and H2. The obvious advantage of testing models with simulations is that much more detailed structural information is available from a simulation than from experiments on real systems. Even if mistuned force fields or incomplete equilibration quantitatively distort the simulated structure, e.g., giving incorrect volume of water or lipid molecules, the ensuing well-defined structure is still a valid test case of the same generic type as typical bilayers.

The simulations used in this article were performed for dimyristoylphosphatidycholine (DMPC) at five different fixed A, which bracket the previously determined value of 60.6 Ų (6). Our primary test for models of ρ(z) is whether they can determine A from the equivalent information available from x-ray experiments, which consists foremost of the electronic scattering form factor F(q). Another important goal of a structural model is to locate the component pieces of the lipid molecule within the bilayer and to determine the hydrophobic thickness. The determination of A is a difficult test, one that neither HB nor H2 can pass, unless information in addition to F(q) is provided to constrain the many parameters required in any realistic electron density model. It should be emphasized that this is not a criticism of the model method; indeed, the advantage of the model method for ρ(z) is that information from other experiments can be imposed on the model. This advantage is not offered by representing the electron density profile by a Fourier series or Fourier transform. In addition, structural models can also be extended to include information from simulations, and this article develops guidelines regarding the kind of information that may be included.

The program that emerges from the preceding part of the introduction is to use simulations to produce and test a generic model, which is then used to analyze the experimental data of Kučerka et al. (6). A second aspect of this article involves the direct comparison of simulation and experiment. By performing this comparison in q space, no model is required, but the discrepancies are difficult to interpret. Because the structural models represent the F(q) data very well, they can be used to carry out a comparison in real space. Nevertheless, the question arises, at which value of A should one compare a simulation to experiment? Our answer to this question leads to a simulation-based, model-free method for estimating the surface area.

By way of outline, the following section describes the methods used in the molecular dynamics simulations, and discusses a common approximation related to the use of atomic form factors to obtain F(q). The Results section is divided into the following six subsections: i), “Component volumes from simulations” (an important first step for providing constraints for the model); ii), “Simulated ρ(z) and F(q)” (a comparison of these quantities from simulations of five areas, 55, 59.7, 60.7, 61.7, and 65 Ų); iii), “Structural models” (development of H2 guided by the simulation results and comparison with HB); iv), “Test of structural models” (fitting the simulated F(q) to determine what constraints are required and to estimate the level of confidence in obtaining A); v), “Application to experimental x-ray data” (comparison of density profiles obtained by H2 and HB from the experimental F(q)); and vi), “Comparison of DMPC simulations to experiment and a model-free method” (simulated results for F(q) and ρ(z) are compared to experiment, targets are identified for CHARMM potential development, and a simulation-based, model-free method for estimating A is proposed). Both force-field evaluation and the model-free method require consideration of the best statistical ensemble for performing simulations. This is addressed in the Discussion and Conclusion section. It is argued that the constant surface area rather than constant isotropic pressure ensembles are more appropriate for the applications in this article because of the possibility of finite size effects and small deficiencies in the force field or methodology.

METHODOLOGY

Molecular dynamics simulations were performed with the CHARMM program (13) using the revised CHARMM27 (C27r) force field (14) and the modified TIP3P water model (15,16). The leapfrog Verlet algorithm was used with tetragonal periodic boundary conditions and a time step of 1 fs. The Lennard-Jones interactions were smoothed by a switching function over 8–10 Å (13). Constant particle number, pressure, surface area, and temperature ensemble (NPAT) simulations were run using the pressure-based nonelectrostatic long-range correction (17) with a long-range cutoff of 30 Å. The particle mesh Ewald (18) method was used for the long-range (beyond 10 Å) electrostatic contribution to the total energy with κ = 0.34 Å⁻¹ and a fast-Fourier grid density of ∼1 Å⁻¹. All hydrogen atoms were constrained using the SHAKE algorithm (19). The extended system formalism was used to maintain the temperature via the Hoover thermostat (20) with a thermostat coupling constant of 20,000 kcal mol⁻¹ ps⁻², and pressure was maintained with a barostat (21,22) with a piston mass of 2000 amu.

The DMPC bilayer consisted of 36 lipids per monolayer (72 total) with 1848 water molecules with periodic boundary conditions in all directions with a fixed A, i.e., the box lengths in the x and y direction are fixed. This system size has been shown to result in equivalent electron densities and other structural properties for systems larger than 72 lipids (23). Five trajectories with different cross-sectional areas (55, 59.7, 60.7, 61.7, and 65 Ų per lipid) were generated. The velocities were initialized at 203.15 K with a temperature increment of 10 K every 1 ps until the target temperature of 303.15 K was obtained, and the systems were then equilibrated for 3 ns. All averages were evaluated for production runs of 10 ns with coordinates saved at 1 ps intervals.

The electron density profile ρ(z) along the bilayer normal z was obtained as an average of the 10,000 snapshots following Feller et al. (24). To account for temporal displacements of the entire bilayer along z, the center of the bilayer for each snapshot was taken to be z_M, the mass weighted projection of the lipids along the z axis, and adjusted atomic positions z_i were then obtained from the raw atomic positions by subtracting z_M. The small system size suppressed undulations, so z_M did not vary significantly with lateral position in each snapshot. Based on the z_i, the number of electrons in each atom of lipid and water was then added to a histogram with a bin size of 0.1 Å in the z direction, Δz. Division by the bin volume and the number of snapshots provided the electron density ρ(z_j) for 660 values of z_j, which includes water images to ±33 Å.

The continuous form factors, F(q), for symmetric bilayers (ρ(−z) = ρ(z)), are defined as

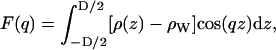(1)

where 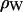is the electron density of pure water. The discrete form factor from simulation is determined at each value of q_k,

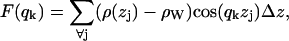(2)

where the electron density of water in simulations is 0.34 e Å⁻³ for TIP3P waters. The integrand in Eq. 1 at the upper and lower limits is zero because ρ(z) is equal to 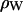, and similarly for Eq. 2 at ρ(z_j) ≅ ρ_W. Values of F(q_k) were obtained from the ρ(z_j) for 800 values of q_k evenly spaced from q = 0 to q_max = 0.8 Å⁻¹; q_max is the upper experimental limit for DMPC (6). This procedure (11) assumes that the electrons are localized at the atomic nucleus, which is equivalent to assuming that the atomic form factors f_i(q) are constants equal to f_i(0).

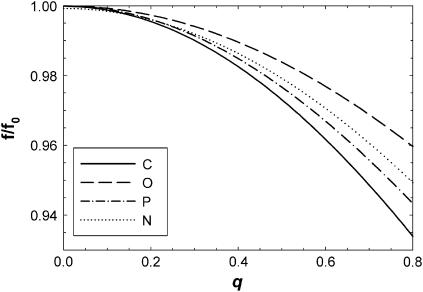
Benz et al. (12) have recently emphasized that the atomic form factors are not constants so that one should calculate which is only the same as the preceding procedure when f_i(q) are constants. However, Fig. 1 shows that the relevant f_i(q)/f_i(0) (25) deviate by only ∼2% from 1.0 at the upper experimental range of q-values in reference (11). The deviation for our upper experimental range is only 5% because the distribution of electrons around nuclei is highly concentrated within a radial distance of order σ_el ∼ 0.3 Å. This distribution would require a spatial convolution of the electron density in the z direction, but only over the distance σ_el which is typically five times smaller than the van der Waals radii of atoms. This correction makes little difference to ρ(z) or F(q) in the experimental range of q, because the intrinsic disorder in the bilayer already broadens the distribution functions for the locations of the nuclei by σ_in > 2 Å and the total broadening σ = (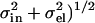 is negligibly different from the broadening σ_in of the nuclei alone. Indeed, the A and ρ(z) obtained using the atomic form factor correction to F(q) were nearly identical (within 0.1%) to values obtained without the correction. It should be noted that the use of atomic form factors is only exact for atoms. Because lipids are molecules, their valence electrons are displaced from atomic orbitals. Consequently, the use of atomic form factors is not exact. One needs molecular orbitals and orientation dependence of chemical bonds. However, this complication makes as little difference to F(q) as the use or nonuse of atomic form factors described above.

FIGURE 1.

Normalized atomic form factors f_i(q)/f_i(0) for carbon, oxygen, phosphorus, and nitrogen atoms within the experimental q-range (0 < q < 0.8 Å⁻¹).

Electron density weighted histograms 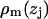were obtained for each of the m = 1,…,7 groups: water, choline, phosphate, glycerol, carbonyl, methylenes on the tails, and the terminal methyls on the tails. Following the method of Petrache et al. (26), these ρ_m(z_j) were converted into probability distributions, i.e., 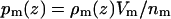. The sum of all probabilities, 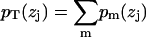, should ideally be unity for each z_j bin, and this method obtains the component volumes V_m by minimizing 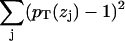. The deviations from unity test the assumption that the component volumes are independent of z. Petrache et al. (26) obtained component volumes for the seven components listed above, as well as for a four-component model with choline, phosphate, glycerol, and carbonyl combined into a single headgroup distribution. In addition to these, we have obtained volumes for a six-component model that combines the glycerol and carbonyl groups into one component, and a five-component model that additionally combines the phosphate and choline into a single group.

Deviations from a Gaussian distribution for the probability distributions p_m(z) of the component groups and combined distributions were quantified by kurtosis, 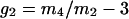, and skew, , where m_i is the i^th sample moment about the mean. If a distribution is Gaussian, then g₁ and g₂ are equal to zero.

RESULTS

Component volumes from simulations

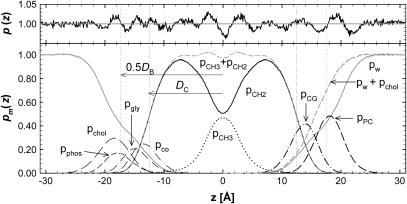
Spatial distributions of the component groups are shown by p_m(z) in Fig. 2. The average deviations from unity of the sum of all the component probabilities are of the order of ±1%. The region with the largest deviations occurred near the bilayer center where the average deviations were ±2.4%. It may also be noted that, although the values of the volumes V_m modulate the maximal values of the individual p_m(z_i) in Fig. 2, the locations of the maxima (which locate the mean positions of the component groups along z) are independent of the volumetric analysis.

FIGURE 2.

The bottom panel shows the component probabilities for the A = 60.7 Ų simulation, p_m(z) along the bilayer normal z for water (w), choline (chol), phosphate (phos), glycerol (gly), and carbonyls (co) on the left, and on the right for combinations of some of these components, phosphate + choline (PC), carbonyl + glycerol (CG), and water + choline, with chain methylenes (CH2) and terminal methyls (CH3) and their sum in the middle. The Gibbs dividing surfaces are indicated by vertical dashed lines labeled D_C for the hydrocarbon boundary and 0.5D_B for the Luzzati water boundary. The top panel shows deviations of p_tot(z_i) from unity with the right half from the six-component analysis and the left half from the seven-component analysis.

Table 1 lists the lipid component volumes for the five surface areas simulated using a six-component volumetric analysis. Four-, five-, and seven-component analyses were also performed. Standard deviations obtained by comparing the four volumetric analyses were ∼1.0 ų (±0.09%) in the total volume V_L. Consistent with reference (27), standard deviations in the sum of the volumes of the phosphate and choline were smaller than the deviations in the individual components. The total headgroup volume V_H is nearly independent of simulated area A. The constancy of V_H is expected because the headgroup is largely immersed in water. This simulation result supports the assumption used in structural modeling that the value of V_H determined experimentally for the gel phase can be used for determination of the fluid phase structure. The total chain volume V_C shows a small systematic increase as A is increased; this is consistent with more disordered chains requiring greater volume. The water volume V_W is independent of A with the volume of water essentially equal to that in the bulk.

TABLE 1.

Volumetric results from simulations using the six-parameter volumetric analysis for total lipid volume (V_L) and component volumes for water (V_W), chain methylene (V_CH2), terminal methyl (V_CH3), phosphate (V_phos), choline (V_chol), carbonyl + glycerol (V_CG), total head (V_H), total chains (V_C), and r = V_CH3 / V_CH2

	Simulated					Experiment 60.6
A (Å2)	55	59.7	60.7	61.7	65
VL (Å3)	1061.3	1072.0	1072.3	1070.4	1074.6	1101
VW	29.5	29.5	29.5	29.5	29.5	30.0
Vchol	109.4	109.7	105.5	109.7	108.1	–
Vphos	69.7	68.5	72.85	68.0	69.2	–
VCG	142.6	145.3	145.6	145.6	147.3	–
VCH2	26.3	26.7	26.8	26.7	26.9	27.7
VCH3	54.0	53.7	53.0	52.9	52.8	52.6
VH	321.6	323.5	323.9	323.4	324.5	331
VC	739.7	748.5	748.4	747.1	750.1	770
r	2.05	2.01	1.98	1.98	1.97	1.9

Experimental column from Kučerka et al. (6).

Simulated ρ(z) and F(q)

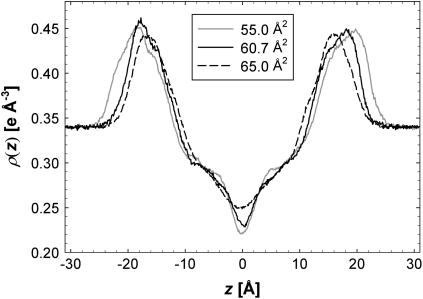
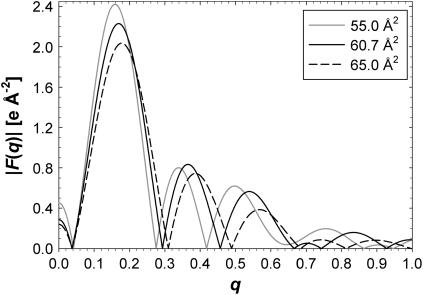
Fig. 3 shows total electron density profiles ρ(z) for three of the simulated areas. The simulation at A = 65 Ų is nearly symmetric and fairly smooth, which is consistent with this simulation having reached equilibrium. As the simulated area is reduced, the simulated electron densities become less smooth and more asymmetric, suggesting that equilibration takes longer, possibly due to stronger excluded volume constraints in the headgroup region. However, the “high-frequency” roughness of these electron density profiles has a negligible effect on the calculated form factors F(q) within the experimental range 0 < q < 0.8 Å⁻¹. Fig. 4 shows the corresponding F(q). The F(q) curves vary significantly, which demonstrates that experimental measurements of F(q) should be important for determining A and bilayer structure.

FIGURE 3.

The electron density profiles, ρ(z), as a function of z along the bilayer normal for simulated areas 55 (solid gray), 60.7 (solid black), and 65 Ų (dashed black).

FIGURE 4.

Form factors, F(q), from three of the five simulated areas, 55 (solid gray), 60.7 (solid black), and 65 Ų (dashed black).

Structural models

A major issue in structural modeling is the number of adjustable parameters. It is desirable that a model be able to represent all interesting features of lipid bilayers. On the other hand, a model with too many parameters can fit the data by different combinations of the parametric values; i.e., the parameters are underdetermined. In general, simple functional forms with few parameters that still provide a good representation of the data and physical features are preferable to more general forms with more parameters. Here a new structural model is developed with a robust number of parameters based upon our simulation results.

The most realistic structural models currently use the Gaussian functional form to represent the distributions of some of the lipid component groups in the bilayer (4,8). Nevertheless, the distribution functions for any component group need not be purely Gaussian and indeed, deviations were observed in earlier simulations (10). A comparison is shown in Fig. 5 for various lipid components at 60.7 Ų. The values of kurtosis g₂ in the distributions for choline, phosphate, glycerol, and carbonyl for the simulation at 60.7 Ų are small −0.07, −0.19, −0.14, and −0.06, respectively, and similar small values are calculated for other A. In general, the distributions are more Gaussian for the phosphate + choline (PC) and carbonyl + glycerol (CG) combined components, with g₂ = +0.06 and −0.07, respectively. Similarly, g₁ in the individual group distributions is reduced from about −0.2 to +0.1 when the headgroups are combined. In contrast, a substantially larger kurtosis, g₂ = +1.03, is obtained for the distribution of methyls from both monolayers (Fig. 5, bottom panel). The skew is zero to within statistical error by symmetry. The distribution of terminal methyls from only one monolayer (not shown) is strongly skewed toward the headgroups of that monolayer (g₁ = 0.3).

FIGURE 5.

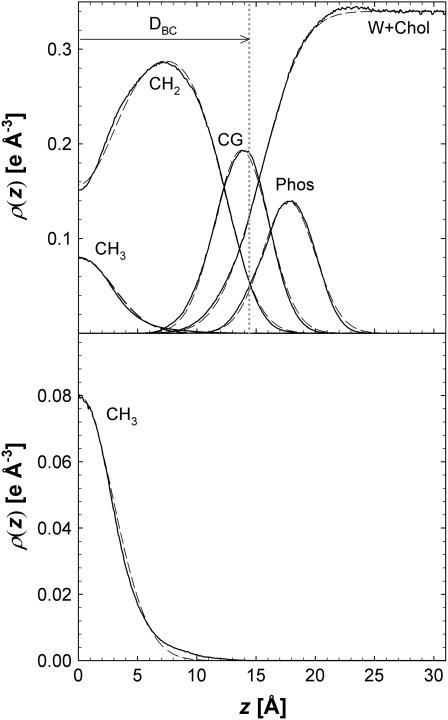
Results of independently fitting Gaussians to the phosphate, terminal methyl, and CG distributions and the other functional forms in H2 to the water + choline and methylene distributions for the A = 60.7 Ų simulation. The solid lines are results from MD and the dashed H2. The bottom panel shows the terminal methyl distribution on an expanded scale.

The new structural model, H2, consists of functional forms that provide excellent representations of the electron densities for the five components shown in Fig. 5,

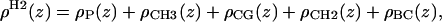(3)

where the notation for the densities is ρ_P(z) for the phosphate groups, ρ_CH3(z) for the terminal methyls, ρ_CG(z) for the carbonyl + glycerol, 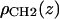for the methylenes on the hydrocarbon chains, and ρ_BC(z) for the water + choline (BC). The functional forms are described next.

One Gaussian represents the contribution of the phosphate group in the upper leaflet to the electron density profile,

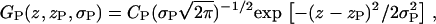(4a)

and a similar G_P Gaussian with parameter −z_P represents the phosphate in the lower leaflet, so

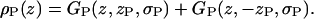(4b)

A single Gaussian models the terminal methyls from both leaflets,

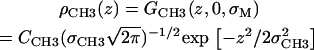(5)

By symmetry, combining the methyl distribution from both leaflets results in a skew of zero, though there remains a substantial positive kurtosis (Fig. 5). A second Gaussian for the methyl density does not significantly improve the overall fit of the model to F(q), and is not included in ρ_CH3(z) to avoid additional adjustable parameters.

H2 uses just one Gaussian for the carbonyl and glycerol groups in each leaflet,

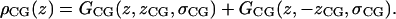(6)

Combining the carbonyl and glycerol groups in each monolayer in a single Gaussian reduces the number of parameters. This simplification arises because the distributions of these two groups overlap considerably (Fig. 2). Each Gaussian has parameters for its width σ, and integrated size, C. G_P and G_CG also each have a parameter for the position z along the bilayer normal; G_CH3 is constrained by symmetry to z_CH3 = 0.

There are a total of eight parameters for the first three terms on the right side of Eq. 3. However, the number of electrons, 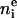, is known for each component group and equals the molecular area A multiplied by the integral of the Gaussian over z. Therefore, C_P × A = 47 for each of the two phosphate group Gaussians, C_CH3 × A = 36 for the single methyl Gaussian, and C_CG × A = 67 for each of the two carbonyl-glycerol Gaussians. These physical constraints reduce the number of independent Gaussian parameters to five.

Although Gaussians provide good approximations for small, localized groups, they are clearly inappropriate for representing the many methylene groups on the hydrocarbon tails of the lipids (Fig. 5). As illustrated by the p_CH3 + p_CH2 curve in Fig. 2, these methylenes and the terminal methyls together comprise the entire hydrophobic core of the bilayer. The composite probability distribution is well represented by the sum of two classical error functions (also used in Schalke et al. (9) to model monolayers)

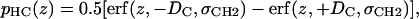(7a)

where the error function (erf) is defined by

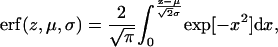(7b)

with location μ and width σ. One parameter is required in H2 for the average locations D_C and −D_C of the boundaries of the hydrocarbon interfaces, otherwise identified as the Gibbs dividing surfaces between the hydrocarbon region and the headgroup region. Another parameter 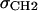gives the widths of these surfaces (68% of the change from total hydrocarbon to no hydrocarbon occurs within D_C ± 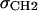). However, to obtain the contribution of just the methylenes to the electron density, it is necessary to subtract the terminal methyl distribution from p_HC, taking into account that the number of electrons ( 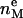= 9) and the volume V_CH3 of the terminal methyls are different from the methylenes (28). For the contribution of the methylenes to the electron density profile,

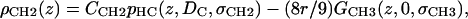(8)

where the parameter 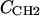is the electron density of the methylene region. 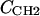is proportional to 8/V_CH2, and the parameter defined by r = V_CH3/V_CH2 is employed in the terminal methyl subtraction. Furthermore, the integral of 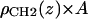should be constrained to be the total number of chain methylene electrons (192 for DMPC). This constraint reduces the number of independent parameters required for the methylenes from four to three.

The final term in Eq. 3 is the water + choline distribution. The water distribution shown in Fig. 2 is not well described by a simple form. One error function does not provide a good fit and two error functions proliferate the number of parameters. However, Fig. 2 suggests that the composite distribution function consisting of water + choline component of the headgroup can be well represented by error functions

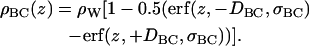(9)

H2 exploits this by using an electron density contribution, ρ_BC(z), consisting of two parameters (D_BC and σ_BC), multiplied by the known electron density of pure water, ρ_W. If the feature represented by ρ_BC(z) corresponded only to water, then D_BC would be the Luzzati thickness defined as D_B and shown in Fig. 2. This is not the case because the D_BC in Eq. 9 includes the choline component. The integral of ρ_BC(z) × A is the total number of electrons of choline plus the number of electrons corresponding to n_W water molecules per lipid in the simulation cell. However, this relationship does not immediately reduce the number of independent parameters because n_W is a parameter that cannot be measured experimentally for fully hydrated samples (3). Therefore, n_W should not be taken from the simulations for the purpose of testing models.

The total electron density profile in H2 is obtained by summing the components of Eq. 3, specified in Eqs. 4–9. The first column of Table 2 shows how the separate components yield a total of 16 parameters. Thus far, a total of five constraints have been noted for the number of electrons, reducing the number of independent parameters to 11.

TABLE 2.

Parameter count for H2 and HB models

	H2			HB
	P	C	I	P	C	I
P or PC head	3		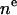2	3	R	2
CG head	3		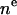2	3	VL	2
CH3	2		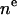1	2	r	1
CH2	4		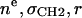1	1	–	1
BC or water	3	ρW,VL,σBC	0	1	ρW	0
Baseline function	–	–	–	2	wb, zb	0
Area	1	VC	0	1	VC	0
DH1	–	DH1	−1	–	DH1	−1
Totals	16	11	5	13	8	5

Constraints
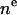	No. of electrons
r	Ratio of methyl to methylene volume
ρW	Known water electron density
VL	Total lipid volume (only lipid)
VC	Chain volume (lipid volume minus headgroup)
σCH2	Width of methylene error function
σBC	Width of BC error function
R	Ratio of headgroup peak areas
wb	Width of bridge in baseline function
zb	Position of bridge in baseline function

P is the number of parameters for each feature, column C abbreviates the names of the constraints, and I is the number of independent degrees of freedom in the fitting.

Now the next type of constraints that involve volumes is introduced. Experimentally, the volume V_L of the lipid molecule is the most accurate datum. This allows the elimination of n_W as a free parameter because the volume AD/2 of half the experimental or simulation unit cell is just V_L + n_W V_W. As shown by Nagle and Wiener (28), this constraint is equivalent to the relation

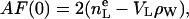(10)

where 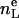is the number of electrons in the lipid molecule and F(0) is the integral of (ρ(z) − ρ_W). Because H2 combines the water + choline into a single distribution, the total volume constraint used in H2 is

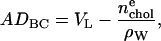(11)

which is derived under the assumption that the electron density of choline region equals that of water.

The simplest and most powerful volumetric relation for H2 is

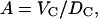(12)

which immediately yields A from the fitted D_C in Eq. 8 and from V_C, which is obtained by subtracting the headgroup volume V_H (29) from the total lipid volume V_L.

Experiment obtains estimates for the volumetric r ratio (4,28), so this is constrained in H2. These three volumetric constraints (V_L, V_C, and r) therefore reduce the number of independent parameters in H2 from 11 to 8. Three additional constraints are needed to maintain robustness in the model fits. The widths of the error functions of the BC and CH2 distributions, σ_i, were too flexible in the unconstrained fits. Therefore, these values were constrained to within ±0.1Å from the simulated value by soft Bayesian constraints. A final constraint for H2 refers to the distance D_H1 obtained from gel phase studies; D_H1 is the distance between the location D_HH/2 of the maximum in the electron density and the location D_C of the hydrocarbon Gibbs dividing surface. The use of these constraints reduces the number of independent parameters to five.

HB has been amply described in previous applications (6,29), so the focus is on the differences with H2. HB consists of four terms,

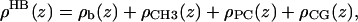(13)

which are the electron densities for the baseline, ρ_b(z), methyl, ρ_CH3(z), phosphate + choline, ρ_PC(z), and carbonyl + glycerol, ρ_CG(z). The major difference is that HB reduces the number of model parameters with a baseline function ρ_b(z) to represent both the methylenes and the water. This baseline function employs a smoothly varying bridge between the known electron density of bulk water, ρ_W, and a methylene plateau, . The bridge has two independent parameters, one for the location of the center z_b of the bridge and one for its width w_b. For gel phases the difference in the electron densities of the methylene plateau and water is small (∼5%), so structure determination is rather insensitive to the bridge parameters. The difference is larger for fluid phases (∼20%), but simulations have enabled the location of the bridge to be constrained relative to the headgroup peaks (6). The width of the bridge has also been constrained to be the width of the region that simulated ρ(z) contains both hydrocarbon and water, ∼8 Å as seen in Fig. 2. These constraints play a similar role as the 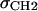and σ_BC constraints used in H2, but are considerably different in detail. H2 requires four parameters, D_C, 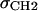, D_BC, and σ_BC to describe the baseline features that are incorporated by only two parameters for the bridge in the HB baseline function. The fit to the F(q) data is more sensitive to the H2 parameters D_C and D_BC, which vary strongly depending upon the lipid.

In HB the headgroup and terminal methyls are also represented by Gaussians with the difference that they are superimposed on the baseline function. Therefore the methyl Gaussian is a negative trough (like the last term in Eq. 8 for H2), and represents the deficit in electron density compared to the more electron dense methylenes. Similarly, the headgroup Gaussians, G_PC and G_CG, are scaled to represent only the electron density in these components in excess of the baseline function. The constraints r, V_C, and D_H1 are the same as those applied to H2, as indicated in Table 2. The constraints in H2 on 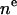for the component groups have two counterparts in HB. The first is the R constraint on the ratio of the integrated sizes of the two Gaussian headgroup peaks and the second is a V_L constraint in Eq. 10. Table 2 lists the total number of independent parameters as five when A is counted as a parameter and the bridge in the baseline function is constrained as described above (6).

Although the baseline function reduces the number of parameters in HB, its primary description does not include a most important feature, namely, the hydrophobic boundary D_C that is included explicitly in H2. Therefore, the A cannot be directly determined from Eq. 12 for HB. Instead, D_C for HB is obtained from the headgroup peak location D_HH/2, using D_C = D_HH/2 − D_H1, where D_H1 is obtained from the gel phase (29); this is equivalent to the bootstrap method of McIntosh and Simon (30).

Test of structural models

As a first test, H2 was fit to the simulated F(q) without constraining D_H1 or the widths of the error functions. Only form factors at q < 0.8 were used in all fits because that is the experimentally accessible range. The A obtained from this eight-parameter fit deviated significantly from the actual simulated surface area, e.g., for the simulation at 60.7 Ų the predicted area was 66.0 Ų. In addition, the two fitted Gibbs dividing surfaces, D_BC and D_C, were >1 Å too close to the bilayer center and their widths were too large. Constraining the σ_i-values, but not D_H1, improved the value of A, but only to 64.0 Ų. Despite the disagreement with A, both of these fits provided excellent agreement with F(q) and the total ρ(z). This demonstrates that the unconstrained H2 with eight or six fitted parameters is underdetermined and parameter flexibility results in poor component determination. Consequently, all the constraints for H2 listed in Table 2 are required.

Even with only five parameters, the fits of the model to the simulated F(q) data have such small deviations that they cannot be distinguished graphically from the simulated data shown in Fig. 4. This indicates that the model is more than adequate to account for primary F(q) data from x-ray diffraction. The predicted A obtained from H2 with all constraints are compared to the simulated A in Table 3. There is excellent agreement with the simulated A, where the H2 determined A has negligible bias and an average root mean square deviation of 0.1 Ų.

TABLE 3.

Area A in Ų for the H2 and HB structural models when fit to F(q) obtained from simulations performed at the exact A shown in the top row

Simulation	55.0	59.7	60.7	61.7	65	RMSD	Bias
H2	54.8	59.9	61.0	61.7	64.6	0.1	+0.02
HB	54.7	60.0	60.6	61.8	65.3	0.1	+0.06

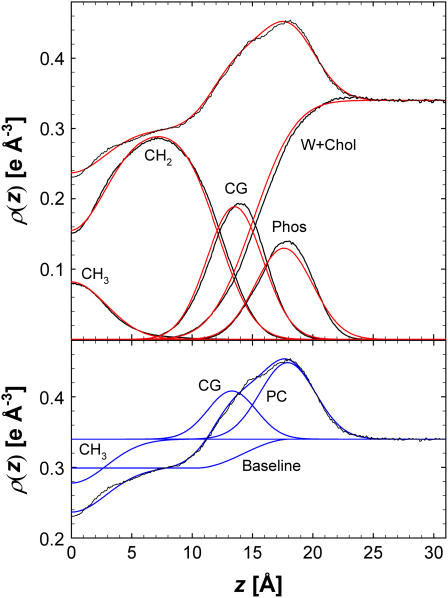
Fig. 6 shows that the H2 parameter fit yields good representations of the electron densities of the individual components, although there are small, but noticeable, deviations in the carbonyl + glycerol and phosphate peaks. The methyl trough tends to be slightly higher than simulations because kurtosis is absent in G_CH3. However, the model results agree well overall with the simulated ρ(z). The parameters for the constrained H2 fit to the simulated F(q) with A = 60.7 Ų are listed in Table 4.

FIGURE 6.

Results of fitting H2 (top panel in red) and HB (bottom panel in blue) for A = 60.7 Ų with the total ρ(z) and the component ρ(z) (simulation results in black). The CG, PC, and CH₃ component contributions for the HB model are shown as differences from the water level ρ_W and the total electron density is the sum of the baseline and the component contributions.

TABLE 4.

Values of the H2 parameters fit to the simulated and the experimental form factors

	Asim = 60.7 Å2	Fit to x-ray
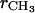	1.98*	1.9*
CP	0.77	0.78
zP	17.72	17.83
σP	2.37	2.18
CCG	1.10	1.11
zCG	13.64	13.88
σCG	2.32	2.28
CBC	0.34	0.33
DBC	15.17	15.68
σBC	2.77†	2.96†
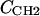	0.30	0.29
DC	12.27	12.70
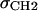	2.31†	2.32†
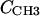	0.59	0.59
σCH3	2.89	2.22
A (VC/DC)	61.0	60.6
DH1	5.28*	4.95*
∂A/∂r (Å2/0.1Å)	0.32	0.19
∂A/∂DH1 (Å2/0.1Å)	0.53	0.45
RMSD	0.013	0.022

^*Hard constrained values.

^†Soft constrained values.

HB was fit with five independent parameters and the constraints listed in Table 2. It fits the simulated F(q) in the experimental range 0 < q < 0.8 so well that, like H2, one cannot discern any deviations from the simulated F(q) curves on the scale of Fig. 4. The bottom panel of Fig. 6 shows that ρ^HB(z) from the fitted model agrees well with the simulated ρ(z). Fig. 6 also shows the individual terms of HB and allows comparison with the simulated contributions from the molecular components. G_PC is located very close to the phosphate distribution and G_CG is located near the carbonyl distribution. The size of the G_CG is considerably smaller than the sum of the carbonyl and glycerol contributions because the baseline function contains a fraction of the carbonyl and glycerol electrons. G_PC is larger than G_CG by the constrained factor R = 1.76 because the electron density of the phosphate is much larger and a smaller proportion of its electrons are included in the baseline function. The results for A are listed in Table 3.

Application of the models to experimental x-ray data

The HB model has previously been applied to DMPC experimental F(q) and volumetric data (6). This section applies H2 to the same data. The constrained parameters V_L, r, and D_H1 were set to values obtained from experiment rather than the simulated values shown in Tables 1 and 4. The experimental uncertainties for r are estimated to be of order ±0.1 and for D_H1 of the order of ±0.1 Å. Table 4 examines the sensitivity of the fitting results on these parameters, i.e., 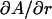and 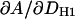. Clearly, the value of A depends strongly on D_H1 with a change in A of 0.45 Ų for every 0.1 Å change in D_H1. The H2 fits are less sensitive to a change in r, where 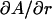= 0.19 Ų per 0.1 Å change in r. The resulting A for these H2 fits is 60.6 ± 0.5 Ų with a confidence based on the uncertainties in r and D_H1.

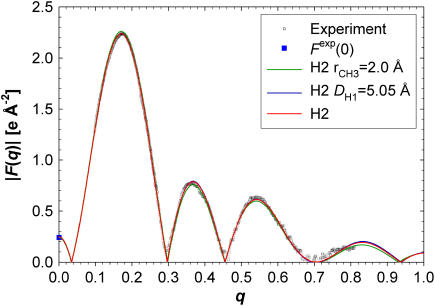
The fits to the experimental F(q) data are very good as shown in Fig. 7 and Table 4 for H2 and by Kučerka et al. (6) for HB. Because the fits to the simulated F(q) have negligible RMSD, the H2 RMSD in Table 4 contains mostly experimental error in F(q). The fits to the F(q) are equally good when r and D_H1 are varied within their estimated uncertainty. Therefore, the accuracy of the values used in these constraints cannot be deduced from the F(q) data and their uncertainties propagate uncertainty in the determination of A. However, the model form factors for different values of the constraints begin to differ for q-values that exceed the current experimental range, as seen in Fig. 7; this emphasizes the desirability for obtaining data to the highest possible q-value. None of the preceding model fits change the sign of F(q) near q = 0.7, and the locations of the maxima in the lobes and the crossing points where F(q) = 0 are nearly identical.

FIGURE 7.

H2 form factors fit to the experimental F(q). The red H2 curve shows the result for the parameters in Table 4 and the other two H2 plots are for the altered values of D_H1 and r given in the legend.

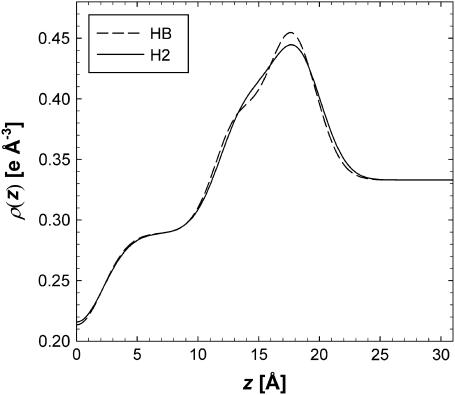
The ρ(z) of the HB and H2 models are compared in Fig. 8. Overall agreement is satisfactory, although there are distinct differences in the electron densities for various positions within the bilayer. HB has a higher phosphate peak than H2 and a lower carbonyl-glycerol shoulder. Kučerka et al. (6) reported A = 60.6 ± 0.5 Ų using the HB model, in agreement with H2.

FIGURE 8.

Comparison of the ρ(z) obtained from HB and H2 (from Table 4) fit to experimental form factors.

Comparison of DMPC simulations to experiment and a model-free method

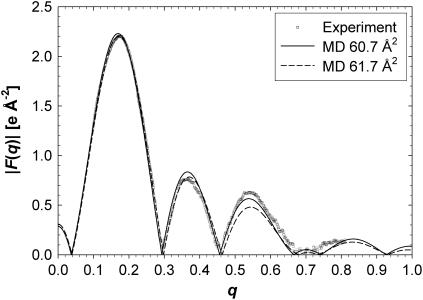
The simulated form factors are compared with experiment in Fig. 9 for two simulated surface areas, and the deviations from experiment are listed in Table 5. The absolute scale of the experimental F(q) is unknown and simulations can help to obtain it (11). There were two scaling factors embedded in the experimental F(q) data from Kučerka et al. (6), one for the unilamellar samples and one for the oriented samples. If it is assumed that these two relative scaling factors were obtained correctly, then this permits only one scaling factor to compare to simulations; this gives the total root mean square deviation (RMSD) listed in the “One factor” column of Table 5. If two separate scaling factors for each sample type are employed, the RMSD in the last column of Table 5 is obtained. Only a small decrease in RMSD is obtained by employing both scaling factors, which is consistent with the relative scaling factor having been chosen correctly by Kučerka et al. (6).

FIGURE 9.

A comparison of the experimental form factors (6) with those from simulations at two areas. The experimental F(q) was scaled to MD 60.7 Ų and MD 61.7 Ų was artificially rescaled to the experimental F(q) to better view the residuals for that simulation.

TABLE 5.

Comparison of experimental (6) and simulated F(q)

	F(q) scaling
A (Å2)	One factor	Two factors
55.0	0.22 (0.007)	0.19 (0.009)
59.7	0.072 (0.006)	0.066 (0.006)
60.7	0.044 (0.003)	0.042 (0.003)
61.7	0.047 (0.002)	0.047 (0.002)
65.0	0.12 (0.001)	0.12 (0.002)

The RMSD was obtained from the difference of the F(q) from simulations at different areas and the experimental F(q). The standard error of the RMSD for the simulations, given in parentheses, were calculated from 2.5-ns blocks. The experimental F(q) were scaled to best fit the simulated F(q) either with a single factor for both experimental samples (labeled as “One factor”) or with “Two factors”, one for each sample type.

The results in Table 5 show that the simulations fit the experimental data best for A between 60.7 and 61.7 Ų within a standard error of the model-based value (60.6 ± 0.5 Ų). Assuming that the RMSD is parabolic with respect to A, the minimum RMSD occurs at 61.1 Ų. This simulation-based estimate for the area from the experimental data is independent of the structural models and is referred to here as the model-free method.

The simulated F(q) in Fig. 9 cross zero for a short range of q-values near q = 0.7 where the experimental F(q) are very small. In contrast, neither H2 nor HB cross zero in that region. Although this is a clear difference, the experimental data alone do not afford a clear indication that the simulations are incorrect. The more important comparison is that the root mean square residuals for the entire q range are larger for the simulations (0.042) than for the models (0.022).

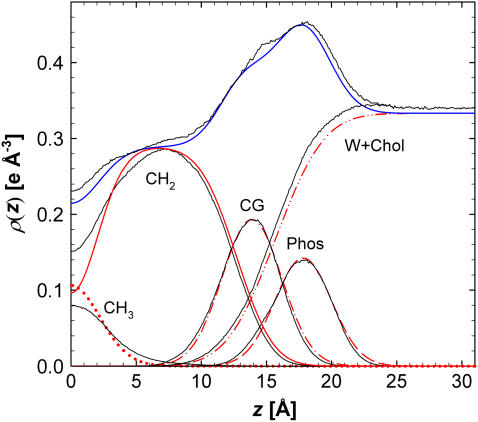
The F(q) do not lend substantial insight into the origin of the differences between simulation and experiment and to where one might look to improve the simulation. For this, the electron densities of the simulation and experiment are compared in Fig. 10. The small differences between HB and H2 due to different functional forms are averaged as a composite experimental result. The comparison of simulation and experiment in Fig. 10 illustrates three regions with differences. The first is the water region, where the simulated electron density for the bulk water region is higher than real water due to the known inaccuracies of the TIP3P water model (31). This also is evident in the lower water volumes in Table 1. At 303 K and 1 bar it was found that the density of water with TIP3P is 1.6% higher than experiment and is the cause for the higher electron density away from the bilayer center. The second region of discrepancy is the higher and more prominent shoulder on the headgroup peak at z = 14 Å near the location of the CG group. Third, the simulated methyl density at the bilayer center and the chain methylene plateau density near z = 8 Å is consistently higher than the experimental results. This discrepancy is consistent with the under prediction of the chain volume V_C in Table 1. Fig. 10 indicates that these differences in the overall electron density profile are fairly minor; in particular, it is encouraging that the locations of the headgroup component distributions are nearly identical for experiment and simulation.

FIGURE 10.

The ρ(z) obtained from the structural models fit to the experimental F(q); average of H2 and HB (blue) and components of H2 (red). The black curves show the simulations for A = 60.7 Ų.

DISCUSSION AND CONCLUSIONS

The primary goal of this article is to use simulations to improve modeling of experimental structural data, especially x-ray F(q), to provide better values of structural parameters for lipid bilayers. The results of DMPC simulations reported here have guided the development of a new structural model, H2, which includes additional structural features in a more transparent way than the previously employed model, HB. The tests with simulations were designed to mimic the way experimental data are analyzed, with a nonlinear least squares fitting to the F(q) data constrained by additional data, such as the volume of the lipid, and outside information, such as the number of electrons in component groups.

Because H2 includes the hydrocarbon thickness D_C explicitly, in principle it is not necessary to use the D_H1 constraint obtained from the gel phase. Such a feature would provide a substantial advantage to H2 over HB. In practice, however, without constraint D_H1 H2 does not obtain satisfactory values of area A as shown by fits to simulated data. H2 obtains accurate values of A with the D_H1 constraint, accurately fits the F(q) data in the experimental q range, and reproduces the simulated total and component ρ(z) (Fig. 6). HB was tested on the simulated data and it performed about as well as H2. Although both models have many parameters to provide realistic representations of bilayer structure, both have five independent degrees of freedom when the necessary number of constraints are applied.

Having passed the simulation test, H2 was applied to experimental data for DMPC (Fig. 7). The overall model results were in excellent agreement with the earlier results obtained with the HB model. The predicted surface area per lipid for both models is 60.6 ± 0.5Å. Although Fig. 8 shows small differences in ρ(z) in the carbonyl + glycerol shoulder and the height, though not the position, of the maximum, there is near-perfect agreement for the other regions. It appears that neither structural model is clearly superior to the other. We believe that both models, with their rather different functional forms, are valuable because their combined use provides an estimate of uncertainties in ρ(z).

An equally important purpose of this article is to demonstrate how to use experimental data to improve simulations. As has been emphasized recently (6,11,12), the primary comparison of simulations to experimental diffraction data should be between the F(q) obtained from simulations and the experiment because this is a direct test that does not involve structural modeling. The first significant result of this test was that the simulations agree fairly well with the experimental F(q) when the simulated area was close to the value obtained by modeling (Fig. 9). Indeed, finding the A that best fits the experimental F(q) is a model-free simulation-based method for obtaining A. If the potentials used in simulation are accurate, then this model-free method will be applicable to other systems such as lipid mixtures and bilayers with incorporated peptides. This method would be superior to structural modeling, because it avoids the need for more structural model parameters than can be successfully fitted to the available experimental data. The model-free method for DMPC results in A = 61.1 Ų, which is within the confidence of the structural modeling value, A = 60.6 ± 0.5Ų. This suggests that the current potentials are already reliable for many purposes. Nevertheless, the statistically significant differences between the simulated and experimental F(q) (Table 5 and Fig. 9) do indicate deficiencies in the CHARMM potential.

Because discrepancies in reciprocal space are difficult to interpret for improving real space potentials, the use of real space modeling of the experimental data provides a more insightful comparison to the simulations. As shown in the previous subsection, the comparison highlights the well-known deficiency in the density of TIP3P water (31), and confirms the volumetric analysis of the simulations that the hydrocarbon chain volume is smaller than experiment (Table 1). A new but small discrepancy is also observed in the carbonyl region of the headgroup, and the methyl trough is insufficiently deep. These all provide clear targets for ongoing development of CHARMM potentials.

The preceding discussion pivots on what ensemble and values of thermodynamic parameters should be employed in simulations. There are two distinct approaches. The approach employed here is to carry out simulations in the NPAT ensemble at or near the experimentally derived surface area. A parameter set is considered well tuned if simulated and experimental properties agree at this surface area. Equivalent results would be expected from simulations carried out in the NPγT ensemble, where γ is the surface tension evaluated at the experimental surface area (32–34). However, there is one property that is poorly obtained in this approach. The bilayer surface tension, γ, which is identically zero experimentally for flaccid bilayers (35), is 19.8 ± 2.9 dyn/cm/monolayer for the present DMPC system at our best A = 60.7 Ų. Finite size effects have been proposed (36) as the reason why the surface tension should differ from zero in simulations, even if the potentials were perfectly tuned. Subsequent theoretical work (37) supports this notion, though it leads to somewhat smaller surface tensions than presently obtained in CHARMM-based simulations. System size dependence of the area has been observed in some recent simulation studies (38) but not in others (39). Another approach is to carry out simulations in the constant isotropic pressure ensemble (NPT). This is equivalent to the NPγT ensemble with imposition of the requirement that γ = 0. Under most conditions the area of bilayers contracts and the bilayer becomes correspondingly thicker when simulated at NPT with the present CHARMM potentials (12,33). This thickening has a strong effect on F(q). The agreement of the simulated and the experimental F(q) will therefore become poor, primarily because the simulated area A is less than the experimental area. For this reason in part, the conclusion of Benz et al. (12) using NPT is considerably more critical of the CHARMM potentials than the conclusions we draw in this article, which uses the NPAT approach and locates the best value of the simulated surface area.

Although the potential for finite size effects is a good reason not to impose the γ = 0 constraint on simulations a priori, it is still prudent to consider that shortcomings in the simulation potentials could contribute to a nonzero value of γ. For example, the surface tension for pure liquids such as water is highly sensitive to the potentials, their cutoffs, and the lack of polarizability (40,41). Such shortcomings would also distort the surface tension of bilayers but would not necessarily have a large effect on the structure, provided that it is simulated at the correct value of A. In contrast, simulations in the NPT ensemble allow these small differences in surface tension to distort A (42) and thereby produce poor agreement with F(q). While obtaining agreement of experiment and large simulation systems constrained to γ = 0 is an ultimate goal, simulating only at NPT appears unduly restrictive and limiting because it magnifies small flaws in the potentials. This point has also been convincingly made by Anézo et al. (42), which emphasizes that obtaining the correct area per lipid is a poor measure of the force-field quality or methodology.

In conclusion, we propose that simulations be performed at several areas in the NPAT ensemble (or at several surface tensions in the NPγT ensemble) as part of a broad-based analysis of a bilayer or biomembrane. The best fit to experimental data provides a simulation-based model-free value for A. When the model F(q) fits the experimental data as well as it does for DMPC in this article, and the electron density profiles from different models agree, then comparison of the simulated electron density with the models provides insight both into deficiencies of the simulation and into the structure of the bilayer.