Force Microscopy of Nonadherent Cells: A Comparison of Leukemia Cell Deformability

Abstract

Atomic force microscopy (AFM) has become an important tool for quantifying mechanical properties of biological materials ranging from single molecules to cells and tissues. Current AFM techniques for measuring elastic and viscoelastic properties of whole cells are based on indentation of cells firmly adhered to a substrate, but these techniques are not appropriate for probing nonadherent cells, such as passive human leukocytes, due to a lateral instability of the cells under load. Here we present a method for characterizing nonadherent cells with AFM by mechanically immobilizing them in microfabricated wells. We apply this technique to compare the deformability of human myeloid and lymphoid leukemia cells and neutrophils at low deformation rates, and we find that the cells are well described by an elastic model based on Hertzian mechanics. Myeloid (HL60) cells were measured to be a factor of 18 times stiffer than lymphoid (Jurkat) cells and six times stiffer than human neutrophils on average (E_∞ = 855 ± 670 Pa for HL60 cells, E_∞ = 48 ± 35 Pa for Jurkat cells, E_∞ = 156 ± 87 for neutrophils, mean ± SD). This work demonstrates a simple method for extending AFM mechanical property measurements to nonadherent cells and characterizes properties of human leukemia cells that may contribute to leukostasis, a complication associated with acute leukemia.

INTRODUCTION

In some diseases, the mechanical properties of individual cells are altered. For example, osteoarthritic chondrocytes (cartilage-producing cells) have been shown to be less stiff than normal chondrocytes, and malignant hepatocytes (liver cells) have been shown to be stiffer than normal hepatocytes (1–3). In diseases of the blood, changes in cell mechanical properties can have profound effects on the cells' ability to flow normally through the vasculature, since increased stiffness impedes progress of cells through small capillaries (4). The reduced deformability of erythrocytes infected with Plasmodium falciparum, the parasite that causes malaria, has been shown to hinder the cells' ability to flow through microfabricated channels (5). Recent research on diabetes mellitus suggests that some complications of the condition can be attributed to increased lymphocyte stiffness (6). In acute leukemia, immature blood cells of the myeloid or lymphoid lineages, called myeloblasts and lymphoblasts, respectively, proliferate uncontrollably. Decreased deformability of these cells, as well as increased adhesion and transmigration, is thought to be linked to leukostasis, a poorly understood condition in which cells aggregate in the vasculature (7). This condition often results in intracranial hemorrhage and respiratory failure that rapidly leads to death, and current therapies based on removal of leukemia cells from the circulation have not proven to decrease mortality (8). Better knowledge of biophysical changes in leukemia cells such as deformability is necessary for improved understanding of the disease, but no widely accepted method or model exists for quantifying the mechanical properties of leukemia cells relevant to leukostasis.

Atomic force microscopy (AFM), first developed as a surface imaging tool (9), can also be used to measure the stiffness of cells firmly adhered to a substrate (10). The primary method of measuring stiffness is indenting the cell with a flexible cantilever driven at a constant extension rate (piezo extension rate) with respect to the sample. The deflection of the cantilever as it indents the cell, which is linearly related to loading force for small deflections, is recorded by reflecting a laser off the cantilever into a split photodiode. A linear elastic model of the cell based on Hertzian mechanics (11) is commonly used with AFM deflection data to determine cell elasticity (12). In addition to constant piezo extension rate measurements, elastic and viscoelastic properties of cells can be obtained from creep experiments (13) and oscillating indentations (14,15) based on similar elastic models.

Nonadhesive cells, such as normal and malignant leukocytes before activation of the inflammatory response, pose a challenge for AFM because they tend to slip from under the cantilever tip under an applied load. Although nonadhesive cells can occasionally be probed using AFM without slippage (13), the experimental throughput is low and may favor those cells which have some level of adherence to the surface. One solution is to coat the substrate surface with polypeptides, making it sticky to the cell. Attaching a nonadherent cell to a surface coated with fibronectin or poly-lysine will prohibit it from moving while probed but can change its morphology and mechanical properties, similar to the changes in cell properties seen upon neutrophil activation (16). Nonadherent cells trapped within Millipore filters have been used for AFM imaging (17), but the pressure used to trap the cells is likely to significantly deform the cells and may change their elastic response.

Micropipette aspiration has been used extensively to determine mechanical properties of fully differentiated leukocytes such as neutrophils (18–23). During micropipette aspiration, a section of membrane and cytoplasm of the cell are drawn into the pipette by a pressure differential. This technique can be used to describe an apparent membrane tension and cytoplasmic viscosity using the liquid droplet model, in which the cell is assumed to be a viscous fluid-filled bag with a constant surface tension. Since aspiration of a cell draws in cytoplasm more readily than nucleus, application of this technique to leukemia cells may overestimate their deformability due to a characteristically high nucleus/cytoplasm ratio (24). Whole cell aspiration is potentially more appropriate for leukemia cell deformation and has been used to describe HL60 mechanical behavior (25,26). However, previous analysis makes use of a power-law fluid model, which is not able to describe a static deformation such as when a cell plugs a capillary, as is believed to occur in leukostasis. A simple method for characterizing and comparing the deformability of leukemia cells at low deformation rates is needed.

We used microfabricated wells (Fig. 1) to mechanically immobilize and study the deformability of HL60 and Jurkat cells, prominent acute myeloid leukemia (AML) and acute lymphoid leukemia (ALL) cell lines, and human neutrophils. AML has been associated with leukostasis at a significantly lower cell concentration than ALL, but the reason for this clinical observation is not known. Comparative measurements of deformability will help in understanding the pathophysiology of the disease. We analyzed our experimental data with two models—a Hertzian mechanics and a liquid droplet model—and determined that the Hertz model is a more appropriate description of these cell lines at low deformation rates. HL60s were found to be significantly stiffer than Jurkat cells and neutrophils, consistent with a model of leukostasis in which stiffness contributes to vessel blockage.

FIGURE 1.

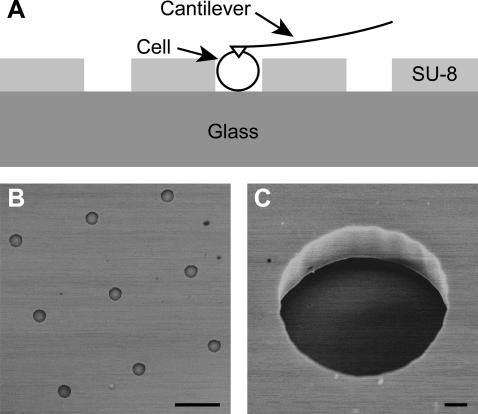
Microfabricated wells for force microscopy of nonadherent cells. (A) Schematic diagram of the microwells showing SU-8 photoresist structures on a glass wafer in which nonadherent cells sit. Cells resting inside the microwells are mechanically immobilized for force microscopy with an AFM cantilever. (B) Scanning electron micrograph of microwells fabricated in 8 × 8 arrays. Scalebar is 50 μm. (C) Scanning electron micrograph of a single microwell showing the vertical sidewalls of the SU-8. Scalebar is 2 μm.

MATERIALS AND METHODS

Cell culture

In this study, the HL60 and Jurkat cell lines (American Type Culture Collection, Manassas, VA, ATCC numbers TIB-152 and CCL-240, respectively) were used as models for AML and ALL, respectively. Cells were cultured in RPMI 1640 containing 10% fetal bovine serum (Gibco, Carlsbad, CA) and maintained in a 5% CO₂ humidified atmosphere at 37°C. Before force microscopy measurements were made, cells were incubated in RPMI 1640 without fetal bovine serum for 24 h at 37°C and 5% CO₂ to synchronize cells in the G0 phase of the cell cycle (27,28).

To isolate neutrophils, whole blood was drawn from healthy donors and collected in heparin. Histopaque 1077 (Sigma-Aldrich, St. Louis, MO) was layered atop Histopaque 1119 to create a dual density gradient. Whole blood was then layered atop the upper gradient and the solution was centrifuged at 700 × g for 30 min, which isolated the neutrophil layer between the two histopaque layers. All layers above the neutrophils were discarded, and the neutrophils were collected and pelleted. The cell pellet was then resuspended in sterile distilled water to lyse any red blood cell contaminants within the solution. After 10 s, 1 part of 10× Hanks buffered salt solution was added. Cells were pelleted and resuspended twice in RPMI to eliminate red blood cell ghosts.

For cell diameter and nucleus/cytoplasm ratio measurements, a Zeiss Axiovert 200 microscope (Carl Zeiss, Thornwood, NY) with a Zeiss 100× 1.3 numerical aperture (NA) oil immersion phase objective was used. Nuclei were fluorescently stained with Hoechst 33342 (Molecular Probes, Eugene, OR) for visualization, and cell morphology was imaged with phase microscopy. Metamorph software (Molecular Devices, Downingtown, PA) was used to quantify the cross-sectional areas of the nuclei and whole cells.

HL60, Jurkat, and neutrophils cells were labeled with Alexa Fluor 546 phalloidin (Molecular Probes) following the standard protocol to image the actin cytoskeleton. Images were taken with a Zeiss LSM 510 Meta confocal microscope (Carl Zeiss).

Microwells

To create microfabricated wells, or microwells, for mechanical immobilization of the cells (Fig. 1), the photocurable epoxy SU-8 5 (Microchem, Newton, MA) was spun onto piranha-cleaned Borofloat glass wafers (Precision Glass and Optics, Santa Ana, CA) and prebaked (2 min at 65°C and 5 min at 95°C). The wafer was then exposed through a mask with a mercury arc lamp (175 mJ/cm²), postexposure baked (1 min at 65°C and 2 min at 95°C), and developed in SU-8 developer (Microchem) for 3 min. Well depth was controlled by spin speed during SU-8 application and measured to be 11.0 μm with an Alpha-Step IQ Surface Profiler (KLA-Tencor, San Jose, CA). Wells were patterned in arrays with diameters ranging from 8 to 20 μm, though for the experiments in this work microwells with diameters of 13.6 ± 0.3 μm (mean ± SD, n = 10) were used for HL60 and Jurkat indentation and microwells with diameters of 10.8 μm ± 0.6 μm (mean ± SD, n = 18) were used for neutrophil indentation. No differences in cell morphology or viability were observed between cells incubated on SU-8 and glass surfaces.

AFM experiments

All force microscopy measurements were obtained on a modified commercial AFM. A Bioscope AFM (Veeco, Santa Barbara, CA) mounted onto a Zeiss Axiovert 25 held the fluid-cell-mounted cantilever (Microlevers, Veeco). For deformability measurements, we used a closed-loop single-axis 50 μm range, 0.7 nm accuracy piezoelectric positioning platform (“piezo”, Mad City Labs, Madison, WI) instead of the piezoelectric tube on the Bioscope AFM head. The piezo platform and photodiode signal were controlled by an RHK SPM 7 controller and RHK SPM32 software (RHK Technology, Troy, MI). V-shaped gold-coated silicon nitride cantilevers (Veeco) with a spring constant of 9–11 pN/nm (calibrated by the thermal noise method (29)) were used in all experiments.

Cells were pipetted onto the wafer and allowed to settle into the microwells. Some cells were moved into wells for force microscopy by gently herding them with the cantilever tip. This movement did not cause any measurable change in cell modulus when analyzed with a two-way ANOVA with cell-type (HL60 versus Jurkat) and microwell status (cells moved into microwells versus cells already in microwells) as the independent variables and cell stiffness as the dependent variable (n_HL60 = 15, n_Jurkat = 16). Cells pushed into the microwells with the AFM cantilever and cells that had fallen into the microwells on their own did not differ in stiffness (p = 0.93). Also, there was no cell-type versus microwell status interaction (p = 0.63), indicating that the difference in stiffness between HL60s and Jurkats was the same for cells that were moved into the microwells as for cells that had fallen into the microwells.

All data were taken at 25°C. Though temperature likely affects the material properties of the cells studied (30), this study is primarily comparative. Experiments were performed within 1 h after cells were removed from the incubator. HL60 apparent stiffness increased slightly over that 1 h period (R² = 0.10, p = 0.01). Jurkat and neutrophil apparent stiffness showed no significant increase over time (R² < 0.001, p = 0.92 and R² = 0.06, p = 0.24, respectively), indicating that the null hypothesis of no correlation cannot be rejected.

A microwell-trapped cell was moved underneath the cantilever tip with a two-axis translation stage. Mechanical properties were determined by extending the piezo platform at a constant rate, deflecting the cantilever upon contact with the cell until ∼800 pN of force was applied or the cell was indented 3 μm (∼25% of cell diameter). Substrate effects may influence stiffness values at indentations more than 10% of cell diameter for the Hertz model (31), though we observed no deviation in the model fit over the entire indentation range. Furthermore, substrate effects would not be expected to affect comparative studies of leukemia cell properties. Only the loading curve was used in analysis of the data.

To determine the role of deformation rate and cell viscosity on deformation response, the piezo extension rate was varied between 24 nm/s and 8643 nm/s. The viscosity of the media had negligible effects on cantilever deflection during probing. This was determined by acquiring indentation data on a hard glass surface at all rates and finding no difference in the loading curves. The cells were probed in a random order of rates to avoid measurement bias. A population of HL60 (n = 60), Jurkat (n = 37), and neutrophil (n = 26) cells was indented to determine the average elasticity of the cells in the limit of low deformation rates (apparent equilibrium Young's modulus, E_∞). For this experiment, the platform moved at 415 nm/s and cells were indented five times each. Student's t-test was used to determine if deformability of the cell types statistically differed.

Experiments were conducted with both the pyramid AFM tip and a 10-μm-diameter sphere indenter. The pyramid silicon nitride tip is 3 μm in height with a 35° half-angle. To attach a sphere to the cantilever tip, cantilever chips were mounted on a manual three-axis micromanipulator and visualized with light microscopy. The cantilever of interest was lowered onto a glass slide containing 5-min epoxy (Devcon, Danvers, MA), and the end of the cantilever was wet with the adhesive. The cantilever tip was then lowered onto a glass slide with dried 10-μm polystyrene beads and adhered to an individual bead. Bonding between the cantilever and the bead was confirmed with light microscopy.

Modeling and analysis

Numerous mechanical models have been used to characterize cell deformability, including the liquid droplet (19), Hertzian mechanics (linear elastic) (10), Maxwell fluid with constant surface tension (18), standard linear solid (32), power-law fluid (26), compound drop (33), and variations of these (34,35). In this work we consider two representative models in the limit of low deformation rate: the liquid droplet and Hertzian mechanics models. The Hertzian mechanics model was selected because it accounts for probe geometry and has been extensively used with AFM (10,12,36). Furthermore, at low deformation rates, the standard linear solid model reduces to a linear elastic model. The liquid droplet model was selected because of its extensive use with leukocytes (37). For low deformation rates, the Maxwell fluid with constant surface tension model reduces to the liquid droplet model.

Hertzian mechanics model

Most AFM mechanical property measurements are made by acquiring cantilever deflection versus sample height with a constant piezo extension rate. These curves can be analyzed by a Hertzian mechanics equation, first derived for two spherical lenses in contact by Hertz (11). For a pyramid punch (38), indentation δ is related to punch load F by

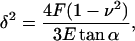(1)

and piezo position z is related to cantilever deflection d by

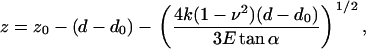(2)

where z is platform position (with negative movement being in the upwards direction), z₀ and d₀ are the contact point, k is the cantilever spring constant, ν is the Poisson ratio (assumed to be 0.5), E is the apparent Young's modulus, and α is the cantilever tip half-angle. This form of the Hertzian mechanics model rests on several assumptions: i), the material is homogeneous, isotropic, and semiinfinite; ii), the material is a linear-elastic solid; and iii), the material undergoes infinitesimally small strains. The validity of these assumptions is examined in the Results section. For further discussions of AFM and Hertzian mechanics see Costa et al. (39), Dimitriadis et al. (31), and Radmacher (12). Custom Matlab (Mathworks, Natick, MA) and Igor (Wavemetrics, Lake Oswego, OR) scripts were used to fit the Hertzian mechanics model to experimental data. The contact point (z₀, d₀) and E were fit to the data using a nonlinear least squares optimization method.

Liquid droplet model

The liquid droplet model with a constant cortical tension has been used extensively to describe neutrophils (19,37). This model has been used predominantly with micropipette experiments where membrane tension is determined by aspirating part of the cell into the pipette. Lomakina et al. (40) derived the liquid droplet model for the indentation of a cell with a sphere, and we extend the derivation for a pyramid indenter appropriate for our AFM measurements.

This model is derived for the static case in which the cell is in static equilibrium with the indenter (Fig. 2). First, an arbitrary section of the cell is considered to satisfy a force balance between the ambient fluid pressure, P₀, and the internal cell pressure, P_c:

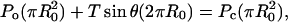(3)

where R₀ is the radius of the projected cross-sectional area, T is the cortical tension, and θ is the half-angle of the section arc. By relating R₀ to cell radius R_c and θ, Eq. 3 simplifies to

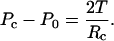(4)

FIGURE 2.

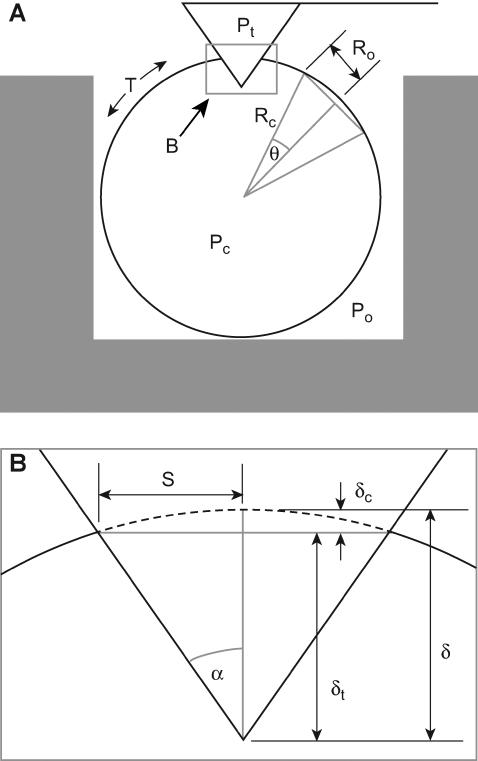
Geometry of a pyramid-tipped cantilever indenting a cell. (A) Schematic diagram of a cell sitting in a microwell. P_c, P_o, and P_t are the pressures of the cell, surrounding fluid, and cantilever tip, respectively. T is cortical tension. The projected contact area between the cell and the cantilever tip is the square defined by S. R_c is the cell radius. R₀ is the radius of the projected cross-sectional area of an arbitrary cell section taken away from the microwell walls and the cantilever tip. θ is the half-angle of the arc of this arbitrary cell shell section. (B) Expanded view of the tip-cell interaction showing that δ, the penetration depth of the pyramidal tip into the cell, is the sum of δ_t, the indentation of the tip beyond the plane described by S, and δ_c, the indentation described by the distance between the sphere shell and the projected contact area; α is the cantilever tip half-angle.

Next the force balance between the pyramid indenter and the cell is examined. The pressure applied by the tip and the ambient fluid, P_t + P₀, over the projected contact area described by the half-length of the contact edge, S, is related to T and P_c by the force balance

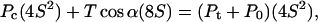(5)

where α is the cantilever tip half-angle. P_t can then be related to R_c, S, and α by combining Eqs. 4 and 5:

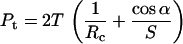(6)

This pressure difference can then be linked to cantilever deflection, d – d₀, using Hooke's law:

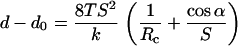(7)

Tip, or cantilever, indentation δ is equal to the sum of δ_t, the indentation of the tip beyond the plane described by S, and δ_c, the indentation described by the distance between the sphere shell and the projected contact area:

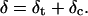(8)

S can be related to δ by

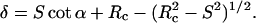(9)

Lastly, z is related to d and δ by

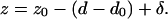(10)

The liquid droplet model described here rests on several assumptions: i), the internal contents of the cell are a homogeneous viscous liquid, ii), the cortical tension is constant around the cell, iii), the indenter is moving at a rate slow enough so the viscosity of the contents and the membrane are inconsequential, iv), the cortical shell conformally deforms around the tip during indentation, and v), the radius of the cell remains constant during indentation. The validity of these assumptions is examined in the Discussion section. A custom Igor script was written to determine cortical tension and contact point using a nonlinear least squares optimization method. Recently, Sen et al. (41) developed a theoretical model for indenting a red blood cell adhered to a surface with a cone-shaped AFM tip. This model could be modified for a spherical cell not adhered to a surface to avoid some of the assumptions used here, but there is no simple analytical solution for it.

RESULTS

We considered three questions. First, at what deformation rates are any viscous contributions from the cytoplasm to the apparent cell elasticity minimized? Second, which model (Hertzian mechanics versus liquid droplet) more accurately describes the deformability of the cells? Third, how different are the mechanical properties of leukemia cells from myeloid and lymphoid lines when compared to each other and to normal neutrophils? Answers to the first two questions are described here in detail for the myeloid (HL60) cell line but were also obtained for the lymphoid (Jurkat) cell line and neutrophils (see Table 1 for a summary of these data, and Supplementary Material for more details on these data). The three cell types are quantitatively compared to answer the third question and provide biophysical insight into clinical complications associated with acute leukemia.

TABLE 1.

Summary of parameters determined for each cell type

	HL60	Jurkat	Neutrophil
Stiffness (Pa)	855 ± 670	48 ± 35	156 ± 87
Hertzian fit MSE (nm2)	2.8 ± 1.6	1.2 ± 0.6	1.7 ± 0.7
Cortical tension (pN/μm)	155 ± 81	21 ± 13	48 ± 20
Liquid droplet fit MSE (nm2)	8.0 ± 4.4	1.6 ± 1.2	2.6 ± 1.7
Cell diameter (μm)	12.4 ± 1.2	11.5 ± 1.5	8.3 ± 0.6
Nucleus:cell ratio (%)	49 ± 6	55 ± 8	39 ± 11

Values are mean ± SD. Hertzian fit MSE and liquid droplet fit MSE refer to the MSE of the Hertzian mechanics model and the liquid droplet model to the data. Sample sizes for determining stiffness and tension and the respective MSEs are 60, 37, and 26 for HL60, Jurkat, and neutrophil cells, respectively. Sample sizes for cell diameter measurements are 51, 44, and 49 for HL60, Jurkat, and neutrophils cells, respectively. Sample sizes for nucleus/whole cell ratio measurements are 40, 47, and 49 for HL60, Jurkat, and neutrophil cells, respectively.

Cell deformability measurements

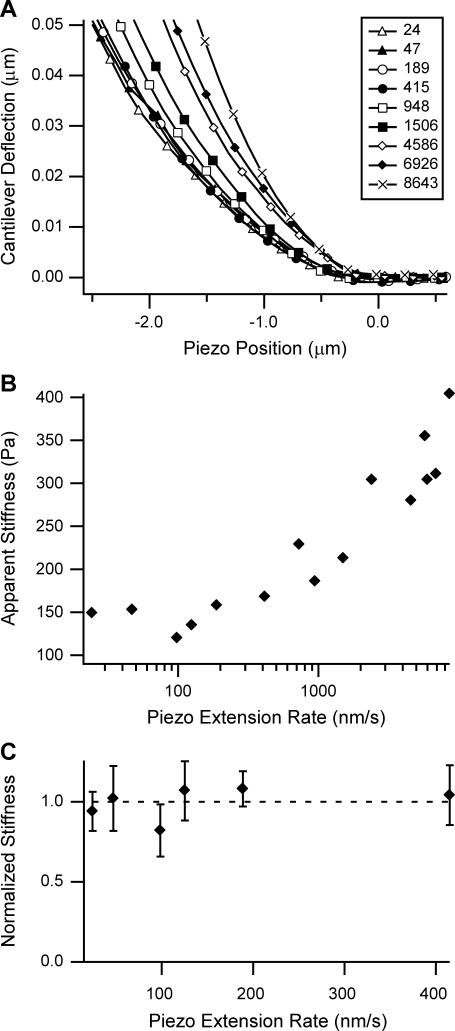
A sample curve from an indentation experiment into a HL60 cell is shown in Fig. 3. When the piezo position is positive, the cantilever tip has not yet come into contact with the cell. As the tip contacts the cell, the cantilever begins to deflect and the curve increases nonlinearly. The influence of deformation rate, and hence cell viscosity, on mechanical property measurements obtained with the AFM was evaluated by conducting experiments at piezo extension rates from 24 to 8643 nm/s. An examination of one specific HL60 cell shows a viscous response at increasing piezo extension rates, since deflection curves increase in slope as rate increases (Fig. 4 A). This trend is seen clearly when using a Hertzian mechanics model to determine apparent stiffness (Fig. 4 B). Apparent stiffness remains relatively constant at and below 415 nm/s but increases monotonically at higher piezo extension rates. The constant apparent stiffness at low deformation rates is seen more clearly in Fig. 4 C, where HL60 cells show no increase in apparent stiffness when piezo extension rate is increased from 24 to 415 nm/s (n = 8), indicating that deformability measurements in this range of piezo extension rates are not significantly influenced by viscosity. For this analysis, apparent stiffness for each cell within the sample was normalized due to the variance of stiffness across cells. This domain of low deformation rates, in which we denote the apparent stiffness E_∞, simplifies the models to which the experimental data are compared and are likely most relevant for the case of a cell plugging a capillary in leukostasis.

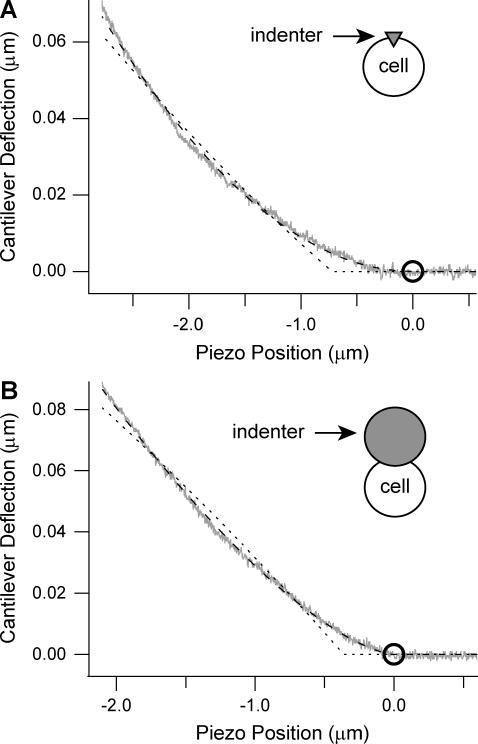
FIGURE 3.

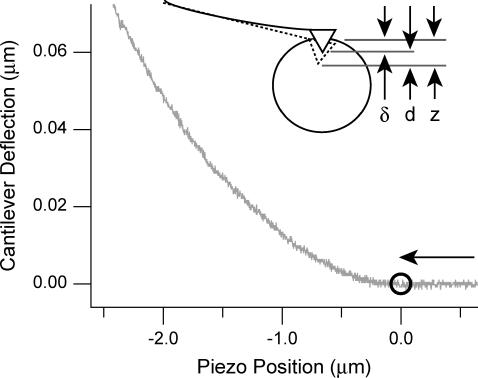
A typical deflection-position curve of a cantilever indenting a HL60 cell in a microwell. Indentation is in the direction of the arrow, and negative piezo position indicates extension after contact with the cell. The contact point is denoted by the circle. The piezo extension rate in this experiment was 1506 nm/s. Deflection of the cantilever is small compared to the indentation of the cell due to the greater stiffness of the cantilever when compared to the cell. Inset: illustration of the relationship between piezo movement z, indentation δ, and deflection d. The deflected cantilever is solid, and the undeflected cantilever is dashed.

FIGURE 4.

Effect of piezo extension rate on apparent stiffness of HL60 cells. (A) At increasing piezo extension rates, the viscosity of the HL60 causes increased cantilever deflection for the same piezo position. All legend values are in nanometers/second. At rates up to 415 nm/s, the deflection curves overlay each other. This indicates that the indentation rate was slow enough for viscosity not to be a factor. (B) HL60 apparent stiffness determined by Hertzian mechanics remains constant at low rates. Data in panel B are from the same cell as panel A. (C) The apparent stiffnesses of eight HL60 cells at low piezo extension rates were normalized and averaged. Normalization was performed by averaging the stiffness of each cell across the experimental extension rates and then dividing the stiffness at each rate by this average. At rates of 415 nm/s and below, apparent stiffness remained constant. Error bars represent the standard deviation.

This same viscous response at higher piezo extension rates was seen in an identical rate analysis performed on Jurkat cells and neutrophils. Both cell types had similar plateaus of apparent stiffness at low piezo extension rates with apparent stiffness increasing monotonically with increasing piezo extension rate. The apparent stiffness of neutrophils was level at 501 nm/s and below, whereas that for Jurkat cells was level at 948 nm/s and below. (Please refer to the Supplementary Material for more details of these experiments.)

The microwell walls are not expected to constrain cells during mechanical property measurements, due to size differences between the well and cell diameter. HL60 cell diameter was 12.4 ± 1.2 μm (n = 51) and Jurkat cell diameter was 11.5 ± 1.5 μm (n = 44), whereas microwell diameter was 13.6 ± 0.3 μm (n = 10). Smaller wells (10.8 ± 0.6 μm, n = 18) held the similarly smaller neutrophils (8.3 ± 0.6 μm, n = 49) for indentation experiments. Cells were selected to be smaller than the wells in which they fell or were placed. For a sample of Jurkat and HL60 cells (n_HL60 = 13, n_Jurkat = 8), there was a near significant correlation between cell diameter and modulus (R² = 0.16, p = 0.06). However, this finding should be interpreted in light of the demonstrated effect of cell type on stiffness. HL60 cells, which are shown to be significantly stiffer than Jurkat cells, also in general are larger. A partial correlation between cell size and stiffness, controlling for cell type, revealed no significant relationship (p = 0.83). This indicates that once the hypothesized relationship between cell type and stiffness is accounted for, cell size is no longer related to stiffness.

Comparison of Hertzian mechanics and liquid droplet models

The Hertzian mechanics and liquid droplet models described previously were fit to the experimental indentation curves for each cell type. An example fit for a HL60 cell indentation is seen in Fig. 5 A. Example fits for Jurkat and neutrophil data can be seen in Supplemental Fig. 3 in Supplementary Material. The Hertz model was used to determine apparent stiffness (E_∞) and contact point (z₀, d₀), and the liquid droplet model was fit for membrane tension (T) and the contact point (z₀, d₀). For each cell type, the Hertz model had a lower mean squared error (MSE) than the liquid droplet model (Table 1). Paired Student's t-test comparing the MSE showed this difference was statistically significant for each cell type (α = 0.05, p_HL60 < 0.001, p_Jurkat = 0.01, p_neutrophil = 0.003). Much of the observed error in the liquid droplet model arose from nonnormally distributed residuals near the contact point, which may be due in part to assumptions of the liquid droplet model used here. Based on these fits, we decided to use the Hertzian mechanics model to compare the stiffness of the different cell types.

FIGURE 5.

Comparison of mechanical models with cell deformation data. (A) An HL60 cell was indented at 24 nm/s. The Hertzian mechanics model (dashed line) fits the data (gray line) better than the liquid droplet model (dotted line). Contact point is denoted by the circle. (B) A sphere shaped indenter with a diameter of 10 μm was attached to the end of the cantilever and pushed into a different cell at 415 nm/s. The Hertzian mechanics (dashed line) and liquid droplet (dotted line) models were modified for a spherical punch and were fit to the data (gray line). Again, the Hertz model was a better fit to the data.

Comparison of HL60, Jurkat, and neutrophil cell deformability

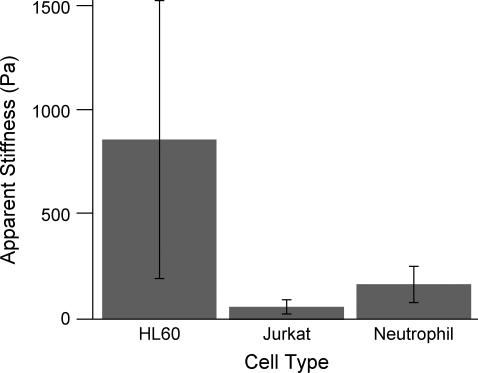
Myeloid and lymphoid leukemia cells as well as human neutrophils were indented under low deformation rates to determine E_∞. Indenting at a piezo rate of 415 nm/s was determined to be in the equilibrium regime, where apparent stiffness is not affected by changes in rate, for all cells indented. We report HL60, Jurkat, and neutrophil cells to have an apparent stiffness of 855 ± 670 Pa, 48 ± 35 Pa, and 156 ± 87 Pa (mean ± SD, n = 60, 37, and 26 respectively) (Fig. 6, Table 1). Effect of cell type on stiffness is significant (α = 0.05, p < 0.001) when using a one-way ANOVA analysis. Using Bonferroni t-tests for post hoc pairwise analyses, we found HL60 cells to be significantly stiffer than Jurkat and neutrophil cells (p < 0.001) and neutrophil cells to be significantly stiffer than Jurkat cells (p < 0.001).

FIGURE 6.

Comparison of myeloid and lymphoid cell line and neutrophil stiffness at low piezo extension rates. With a piezo rate of 415 nm/s, HL60 cells have an average apparent stiffness of 855 Pa with a standard deviation of 670 Pa (n = 60), whereas Jurkat cells are significantly softer (p < 0.001) with an average apparent stiffness of 48 Pa and a standard deviation of 35 Pa (n = 37). Neutrophils have an average apparent stiffness of 156 ± 87 Pa (n = 26, mean ± SD), significantly softer than HL60 cells and significantly stiffer than Jurkat cells (p < 0.001 for both).

DISCUSSION

Modeling

For the three cell types tested, the Hertz model was found to fit the data significantly better than the liquid droplet model, based on paired t-tests described in Results. The mechanical models used here rest on assumptions that affect the determined parameters for stiffness and tension. We examined how the pyramidal indenter model pushing into a liquid droplet could contribute to the observed inaccuracy. First, the model assumes that the cell deforms conformally around the pyramid during indentation. This assumption might not be correct, given previous data which showed that for aspiration experiments with micropipettes with smaller than 1 μm radius, the simple liquid droplet model was not valid due to the bending modulus of the membrane and cortex (42). To test this hypothesis, we indented HL60 cells with a 10-μm-diameter spherical indenter to reduce the effect of the bending modulus. We fit the Hertzian mechanics model for two spheres in contact and fit the liquid droplet model for a spherical punch to the data (Fig. 5 B) and found that the MSEs of the fits were similar to the pyramid punch (MSE_Hertz = 1.1 nm² vs. MSE_droplet = 11.3 nm²), indicating that cell deformation around the indenter tip is not the primary reason the liquid droplet model does not fit the data as well as the Hertzian mechanics model.

Second, the liquid droplet model assumes the indenter and cell are in static equilibrium at all points during indentation. The repeatability of indentation curves shown in Fig. 4 A as well as the constant apparent stiffness at slow deformation rates in Fig. 4 C supports this assumption. Time constants reported by Lomakina et al. (40) are also consistent with the assumption of static equilibrium.

Although the Hertzian mechanics model fits well to the data, errors in the absolute value of elasticity are expected when using this model to estimate the apparent stiffness at low deformation rates, E_∞. The assumption that a cell is homogeneous and isotropic is clearly incorrect—leukocytes, like other cells, have a cytoskeleton, organelles, and nucleus that make them inhomogeneous (43). To quantify the influence of local inhomogeneities on our measurements, we compared the standard deviation of E_∞ of a population of HL60 cells indented with the 10-μm-diameter sphere versus the pyramid tip. We expected the standard deviation for E_∞ to be reduced because any inhomogeneities would be averaged out over the larger contact area, and indeed it was. The standard deviation for E_∞ was reduced from 78% of the mean to 53% of the mean (data not shown). Using such a large indenter, however, caused the semiinfinite solid assumption for Hertzian mechanics to be less valid—a model from Dimitriadis et al. (31) showed increased deviation for the Hertz model as indenter tip radius increases for a sample with finite thickness. For example, when indenting a sample with a modulus of 855 Pa with a 4-μm-diameter tip, the apparent modulus is overestimated by 12%. For a 10-μm-diameter tip, the apparent modulus is overestimated by 85%. Usage of the sphere indenter requires the contact radius to be no more than 10% of the indenter radius for the results to be reliable (44). However, this is difficult when probing soft leukocytes with commercial AFM cantilevers since the cantilevers do not deflect enough when compared to noise in the system to extract adequate data.

The pyramid tip also has limitations when used with the Hertzian mechanics model if the tip (35° half-angle) creates local strains that exceed the linear-elastic assumption. Dimitriadis et al. (31) found this geometry overestimated Young's modulus when compared to that found with a sphere indenter by 60%. The smaller tip does allow for smaller total strain, reducing the effect of the hard glass surface below the cell, which would tend to overestimate the Young's modulus. Nonideal tip geometry could also create errors in estimation of stiffness, for instance, using a blunter tip (one with 5° larger half-angle), whereas still modeling with the expected 35° tip half-angle would result in an overestimation of the apparent stiffness by 20%. Similarly, using a 5° half-angle sharper tip would result in an underestimation of apparent stiffness by 18%.

All simple analytical models have limitations when used to describe constitutive mechanical behavior of cells. Although the Hertzian mechanics model is no exception, it is able to quantify differences in deformability between cell types in a simple and effective manner, which is of interest in the application of cell mechanics to clinical problems where comparisons among cell types are necessary.

Deformability comparison

Cell deformability is thought to play a role in the pathophysiology of leukostasis, as stiffer cells have a higher tendency to mechanically obstruct the vasculature (8,45). Leukostasis has been found to occur at a much higher frequency in AML than ALL at the same cell concentration (8). Clinicians commonly accept that AML cells are more rigid than ALL cells and normal neutrophils (46,47). However, there is scant data that support this assertion. We found HL60 myeloblasts to have a mean E_∞ of 855 Pa and Jurkat lymphoblasts to have an E_∞ of 48 Pa (Fig. 6). This difference is significantly greater than found in filtration experiments, which found ALL cells and AML cells equally deformable (7,30), and implies that leukemic cell deformability may play a larger role in leukostasis than previously thought. As described in Results, Jurkat lymphoblasts and neutrophils were found to be significantly less stiff than HL60 myeloblasts. This is consistent with clinical findings that ALL and chronic myeloid leukemia (a leukemia of more mature myeloid cells) rarely go into leukostasis.

Comparisons of leukemia cell deformability were initially performed in the 1970s. With nucleopore filtration experiments, it was reported that ALL cells were more likely to pass through 8 μm pores than AML cells (30). When accounting for cell diameter, however, these cells were reported to be equally filterable. Micropipette experiments showed that myeloblasts were less deformable than leukemic lymphocytes from patients with chronic, or mature, lymphoid leukemia (7). However, because nonblastic lymphocytes rarely cause leukostasis, these findings are not very revealing. Although our measurements directly compared myeloblast and lymphoblast properties, the cells used were from leukemic cell lines and may not reflect the properties of leukemia cells in vivo. Primary leukemia cell measurements must be performed before any definitive conclusions can be made.

Our data are in the same range for Jurkat E_∞ determined previously with micropipette aspiration using a standard linear solid model (48). Although E_∞ of HL60 cells has not been measured previously (to our knowledge), we can compare these measurements to stiffness measurements of other cell types. Wojcikiewicz et al. (49) reported that the 3A9 cell, a T-cell hybridoma, has an elasticity of 1.4 kPa when indented at 5000 nm/s, on the order of our findings. Domke et al. (50) found stiffness of adherent osteoblasts away from the stress fibers to be ∼500 Pa.

Our values for deformability of neutrophils are also in the range found previously by others. When using the liquid droplet model, we found neutrophils to have a cortical tension of 48 ± 20 pN/μm (mean ± SD). This is comparable to the findings from micropipette aspiration experiments of Evans and Yeung (35 pN/μm (19)), Needham and Hochmuth (24 pN/μm (51)), and Tsai et al. (27 pN/μm (23)). Our value is slightly higher than the cortical tension found by Lomakina et al. (16–24 pN/μm) when they collided neutrophils into spheres via fluid flow (40).

Biophysical mechanism for stiffness difference

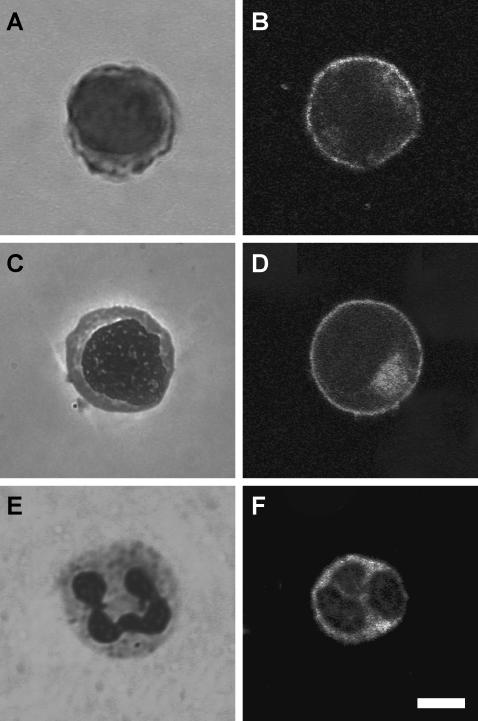
Nuclei have been documented to be substantially larger in most types of leukemias and leukemia cell lines when compared to normal leukocytes (Fig. 7) (52) and have been previously thought to dominate leukemia cell deformability behavior (7). We found that the HL60 cell nucleus is 49 ± 6% (mean ± SD, n = 40) of the total cross section, the Jurkat cell nucleus is 55 ± 8% (mean ± SD, n = 47) of the total cross section, and the neutrophil nucleus is 39 ± 11% of the total cross section (mean ± SD, n = 49), agreeing with previous measurements for AML, ALL, and neutrophils (43,53). When analyzed with a one-way ANOVA, there was a significant effect of cell type on nucleus/whole cell ratio, with significant differences between all ratios in a Newman-Keuls post hoc pairwise analysis (p_HL60-Jurkat = 0.002, p_{HL60-neutrophil} < 0.001, p_{Jurkat-neutrophil} < 0.001). Although nuclei of some cells have been shown to be significantly stiffer than the whole cell (54,55), our data show that simply having a larger nucleus does not mean that a cell is stiffer, as Jurkat cells were found to be of similar stiffness to the neutrophils even though their nuclei are significantly larger.

FIGURE 7.

As seen with Wright-stained cells, the nucleus/cytoplasm ratio in HL60 cells (A) and Jurkat cells (C) is larger than it is for normal neutrophils (E). The cortical actin cytoskeleton density of HL60 (B), Jurkat (D), and neutrophil (F) cells does not appear significantly different. Scale bar is 5 μm.

To determine if the actin cortex was substantially thicker or denser in the HL60 cells than in the Jurkat or neutrophil cells, we fluorescently labeled the actin cytoskeleton and imaged the cells with confocal microscopy (Fig. 7). Based on those images, we could not conclude that there were any differences in the actin cortex of the leukemia cells that would lead to the difference in stiffness. This raises the interesting question of what governs the mechanical properties of these diseased cells. Whether the stiffness difference observed in our measurements lies in cytoskeletal filament networks (actin, microtubules, or lamins), cytoplasm, nuclear or cell membranes, or a combination of these remains unclear. AFM is an ideal tool for further work on this question.

CONCLUSIONS

In this work, we developed microwells to immobilize nonadherent cells for force microscopy and applied this technique to myeloid and lymphoid leukemia cell lines as well as neutrophils. We determined that the Hertzian mechanics model fits the data well and yielded an apparent equilibrium stiffness for the HL60 that is 18 times higher than that of Jurkat cells and six times higher than that of neutrophils. These findings are consistent with the finding that myeloid leukemias are involved in leukostasis at a higher rate than lymphoid leukemias. Comparing leukemia cell deformability will improve the understanding of leukostasis in acute leukemia. Further studies will be needed to investigate the role of deformability with other hypothesized factors involved in leukostasis, including adhesion and transmigration.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.