Messages diffuse faster than messengers

Abstract

In many cell-signaling pathways, information is transmitted by the diffusion of messenger molecules. Diffusion coefficients characterize the messenger's spatial range and the characteristic times of signal propagation. Inside cells, particles usually diffuse in the presence of immobile binding sites (or traps). It is well known that binding to traps results in an effective diffusion coefficient that is smaller than the free coefficient in media free of traps. To measure effective diffusion coefficients in cells, “tagged” particles are often used. Radioactive calcium was used in a giant squid axon and in cytosolic extracts of Xenopus laevis oocytes. Fluorescence recovery after photobleaching yields diffusion coefficients from observations of the distribution of fluorescently labeled proteins. In the absence of traps, free diffusion coefficients give both the rate at which single-particle mean square displacements increase and the rate at which information in the form of inhomogeneities in particle concentration spread out with time. We show here that, in the presence of traps, information diffuses faster than single particles. Thus, messages diffuse faster than messengers. Tagged-particle experiments give the single-particle diffusion coefficients and, thus, can underestimate the rate of diffusive signal propagation.

It is well known that binding to traps results in an effective diffusion coefficient that is smaller than the free coefficient in media free of traps (1). To measure effective diffusion coefficients in cells, “tagged” particles are often used. Radioactive calcium was used in a giant squid axon (2) and in cytosolic extracts of Xenopus laevis oocytes (3). Fluorescence recovery after photobleaching (FRAP) yields diffusion coefficients from observations of the distribution of fluorescently labeled proteins (4–10). In the absence of traps, free diffusion coefficients give both the rate at which single-particle mean square displacements increase and the rate at which information in the form of inhomogeneities in particle concentration spread out with time. We show here that, in the presence of traps, information diffuses faster than single particles and that messages diffuse faster than messengers. Tagged-particle experiments give the single-particle diffusion coefficients and, thus, can underestimate the rate of diffusive signal propagation.

To illustrate these effects, we consider the simplest model that incorporates traps and freely diffusing particles. The free particles, P_f, bind to an immobile substrate, S, resulting in bound particles, P_b, according to the simple reaction scheme

with dissociation constant, K_D = k_off/k_on.

We illustrate the differences between single-particle diffusion and diffusion of inhomogeneities with a sequence of numerical simulations of the appropriate reaction–diffusion equations for all four classes of particles: tagged and untagged bound (P_b^t and P_b^u, respectively) and free (P_f^t and P_f^u, respectively).

Results

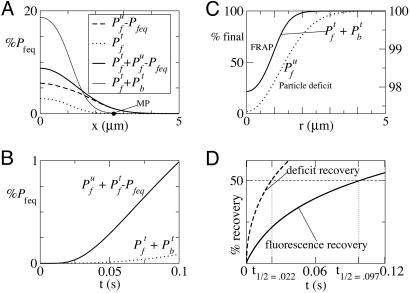
For specificity we use pseudo-on (k_on S_eq) and off rates and diffusion coefficient for GFP-tagged glucocorticoid receptors in the nuclei of mouse adenocarcinoma cells (10). The first simulation (see Methods) (Fig. 1A) mimics experiments (2, 3) in which radioactive calcium (⁴⁵Ca²⁺) is added to an essentially one-dimensional medium. In the simulation, a bolus of tagged particles is added to the leftmost 1.1 μm of the medium in which identical but untagged particles are already in equilibrium with the traps. The equilibrium concentration of free (bound) particles prior to the addition of the bolus is denoted P_beq. Fig. 1 shows the concentration profiles at t = 0.1 s after evolution from initial concentrations (P_f^u, P_b^u, P_f^t, P_b^t) = (P_feq, P_beq, 0.2P_feq, 0) for x ≤ 1.1 μm and (P_f^u, P_b^u, P_f^t, P_b^t) = (P_feq, P_beq, 0, 0) for x > 1.1 μm. The deviation of the particle concentrations from P_feq of total free (thick solid line), total tagged (light solid line), tagged free (dotted line), and untagged free particles (dashed line) are plotted as fractions of P_feq. The spread of the untagged particles is clearly greater than that of the tagged particles. In Fig. 1B, the deviation from background of free particles (P_f^t + P_f^u − P_feq) is shown as a solid line representing what a calcium-sensitive electrode would record at the MP, a measurement point some distance away from the point at which the bolus is added (IP). In the same graph, the total tagged particle concentration, P_f^t + P_b^t is also plotted as a dotted line representing the radioactivity observed at the MP. Clearly, the total free-particle concentration is growing much faster there than the tagged particle concentration (the radioactivity). As proven in Methods and illustrated in Fig. 1B, the time it takes for the total free particle concentration at the MP to reach the same threshold value above P_feq is shorter. The reason is that, as tagged particles diffuse, they compete with the untagged ones for traps. The net effect is that there is a preferential unbinding of untagged particles and binding of tagged ones, because the tagged ones are diffusing into a region with no tagged particles. These additional untagged particles that are released throughout the medium result in the threshold value being reached faster at the MP. The fact that all tagged particles observed at the MP travel the entire distance from IP to MP, in contrast, implies that the effective diffusion coefficient for the population of tagged particles is given by the single-particle effective diffusion coefficient. It follows that the time it takes for inhomogeneities to diffuse throughout the medium is much shorter than the single-particle diffusion time. The experimental observable is the total tagged-particle concentration P_f^t + P_b^t, whereas the quantity of interest for cell signaling is the free-particle deviation from background: P_f^t + P_f^u − P_feq. As illustrated in Fig. 1A, the total tagged population spreads at the same rate as the free tagged particles, much slower than the spread of inhomogeneities.

Fig. 1.

Simulated diffusion of particles in the presence of traps. (A) One-dimensional simulation of the spread of tagged and untagged particles, denoted by superscripts t and u, respectively, in an experiment in which a bolus of tagged particles (such as radioactive calcium) is released at t = 0, raising the concentration of free particles by 20% in the leftmost 1.1 μm. The four curves are P_f^u − P_feq (dashed), P_f^t (dotted), P_f^u + P_f^t − P_feq (thick solid), and P_b^t + P_f^t (thin solid) at t = 0.1 s. MP is the measurement point from which the signals shown in B were obtained. (B) Time course of particle concentrations at MP. The dotted line denotes the total tagged-particle concentration, P_b^t + P_f^t, and the solid line denotes total free particle concentration above background, P_f^t + P_f^u − P_feq. (C) Two three-dimensional simulations in a 5-μm sphere. First, a FRAP-like simulation is shown in which all particles in a sphere of radius 1.1 μm were untagged at t = 0, whereas the particles in the rest of the 5-μm sphere remained tagged. The plot shows the recovery of tagged particles, P_f^t + P_b^t at t = 0.1 s (solid line, left scale). A “particle deficit experiment” is also shown in which the free particle concentration was reduced to P_f = 0.8P_feq in the 1.1-μm sphere at t = 0. The plot shows the free particle recovery at t = 0.1 s (dotted line, right scale). Note that the concentration is almost fully recovered in the particle deficit case but not in the FRAP-like case. (D) Percent recovery as a function of time for the FRAP-like (solid line) and particle deficit (dashed line) simulation (see Methods).

In Fig. 1C, we plot the results of two three-dimensional simulations (see Methods). The first represents a FRAP-like simulation (solid line, left axis), and the second represents a particle-deficit simulation (dotted line, right axis). Both simulations were performed in a sphere of radius 5 μm. In the FRAP-like experiment, the initial conditions were (P_f^t, P_b^t, P_f^u, P_b^u) = (0, 0, P_feq, P_beq) for r ≤ 1.1 μm and (P_f^t, P_b^t, P_f^u, P_b^u) = (P_feq, P_beq, 0, 0) for r > 1.1 μm. In the particle-deficit simulation, there were no tagged particles and the initial conditions were (P_f, P_b) = (0.8P_feq, P_beq) for r ≤ 1.1 μm and (P_f, P_b) = (P_feq, P_beq) for r > 1.1 μm. The plots show the concentrations as a percentage of the final equilibrium concentrations at t = 0.1 s. At this time, P_f in the particle-deficit simulation is spatially uniform to within 3% of its final value, whereas the FRAP-like simulation still shows deviations of 80% from its final equilibrium value. Fig. 1D shows the integrated recovery curves for the particle-deficit (dashed line) and FRAP-like (solid line) simulations. The t_½ is 0.022 s for the particle-recovery simulation and 0.097 s for the fluorescence recovery in the FRAP-like simulation. For this geometry, the measured diffusion coefficients (D_meas) can be obtained from t_½ by D_meas = R_o²/(9.98t_½), where R_o = 1.1 μm is the radius of the perturbed region. The coefficients thus obtained compare well with the ones deduced in Methods (see Eqs. 2 and 3).

Visual comparison of the widths of the concentration peaks and troughs in Fig. 1 A and B reveals that the effective diffusion coefficient obtained in the FRAP-like simulation is identical to the tagged-particle effective diffusion coefficient obtained before, which is proven in Methods and illustrated in Fig. 2. Fluorescence in FRAP experiments spreads at the same rate as a bolus of tagged particles that is added to a background of untagged particles and traps in equilibrium. Therefore, it spreads at a slower rate than a local inhomogeneity of the unlabeled particle concentration, P_f^u. Furthermore, our simulations show that the difference in the rate of spread occurs even before the spreading becomes diffusive (which always occurs in the long time limit in an infinite domain).

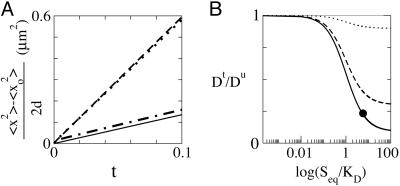
Fig. 2.

Effective diffusion coefficients. (A) (〈 x² 〉 − 〈 x₀² 〉)/(2d)vst (where d is the space dimension: d = 1 in the tagged-particle bolus simulation discussed in Fig. 1A, and d = 3 in the FRAP and particle deficit experiments discussed in Fig. 1C). The four lines shown are for P_f^u + P_f^t (dashed) and P_f^t (dashed–dotted) in the tagged particle bolus simulation, P_f^u in the particle-deficit simulation (dotted), and P_f^t in the FRAP simulation (solid). The slopes of these lines give the effective diffusion coefficients. (B) D^t/D^u as a function of S_eq/K_D. The dotted line corresponds to S_eq/S_T = 0.9, the dashed line corresponds to S_eq/S_T = 0.3, and the solid line corresponds to S_eq/S_T = 0.1. For large S_eq/K_D, the ratio approaches its asymptotic value: S_eq/S_T. The black dot corresponds to the parameters used in all simulations in this report.

In Fig. 2, the mean square displacement (divided by twice the space dimension) is plotted as a function of t for various quantities in the three simulations discussed. The slopes of these curves are the effective diffusion coefficients, and they agree with Eqs. 2 and 3.

We repeated the simulations of Fig. 1 A and B changing k_off and k_on but keeping K_D and all other parameters constant. We observe similar results, but for later times as k_off decreases. In particular, for values of k_off and k_on that are 100 times smaller than those used in Fig. 1 A and B, P_f^t + P_f^u − P_feq is 1.4 times larger than P_b^t + P_f^t at MP, and t = 3 s. The ratio of mean square displacements is 1.75 already at t = 1 s.

As shown in Methods, the spread of tagged particles is determined by the same effective diffusion coefficient

in all the experiments discussed here. S_eq/K_D is the ratio between the mean time a particle stays bound and the mean time between successive trappings (11). D^t is also the effective diffusion coefficient of a single particle in the medium. The spread of a bolus of untagged particles, however, is determined by the coefficient

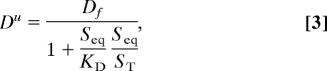which coincides with the one obtained in the rapid buffering approximation (12). In this case, the ratio of bound to free times, S_eq/K_D, is rescaled by a factor that includes all the particles that can become unbound during the diffusive process. The solid, dashed, and dotted lines in Fig. 2B show the ratio of D^t/D^u as a function of S_eq/K_D for S_eq/S_T = 0.1, 0.3, and 0.9, respectively. The difference is largest for large S_eq/K_D and small S_eq/S_T.

Discussion

These results have ramifications for the interpretation of data taken by using FRAP (4–10); other related methods, such as fluorescence loss in photobleaching (FLIP) or fluorescence correlation spectroscopy (FCS); and methods that monitor the spread of radioactivity (2, 3). Assuming that the spread of tagged and untagged particles proceeds at the same rate can result in potentially incorrect inferences about in vivo biological processes. In the case of messengers, diffusion coefficient measurements serve to estimate how long it takes for a local increment of the messenger concentration at point A to reach another at point B. If there are already trapped messenger molecules between A and B, the time it takes for the signal to arrive at B can be much shorter than the time it takes for the input molecules to traverse the intervening distance. If the traps are nearly unoccupied (S_eq ≈ S_T as represented by the dotted curve in Fig. 2B) or if they are almost completely occupied (S_eq = {P_beq/P_feq} K_D ≪ K_D as represented by the curves near the left side of Fig. 2B), the difference disappears and D^t ≈ D^u. In these cases, the tagged particle measurement gives an accurate assessment of the rate at which inhomogeneities smear out (D^t ≈ D^u ≪ D_f in the former case and D^t ≈ D^u ≈ D_f in the latter case). The distinction between collective (D^u) and single-particle (D^t) diffusion is especially important in the case for which, at equilibrium, most of the particles are bound to traps and for which most of the traps are full. In this case, tagged particles will compete with untagged ones for the traps. The net preferential unbinding of untagged particles then results in D^t ≪ D^u. This effect pertains whenever S_eq/K_D > 1 and S_eq/S_T ≪ 1 and the spatial spread of the particles can be measured in experiment, as in the “full model” and “effective-diffusion” regimes defined in ref. 10. There are two other limiting regimes defined in ref. 10 that correspond to different relations between the reactive and diffusive times. In the so-called “reaction-dominant” regime, diffusion coefficients can not be obtained from experimentation. In the “pure-diffusion” regime, D^t ≈ D^u ≈ D_f. Nevertheless, there are differences in the dynamics of FRAP-like experiments and the evolution of perturbations of untagged particles in these two cases as well. As may be concluded from Eqs. 12–15, because of the net preferential unbinding of untagged particles, the time scales with which small perturbations to equilibrium evolve and the time scales of FRAP experiments are different when S_T/S_eq is large, regardless of the spatial extent of the perturbation.

The condition S_T/S_eq ≫ 1 is encountered in the case of calcium signals, because large amounts of calcium ions get bound to buffers inside cells upon their entry in the cytosol. Effective diffusion coefficients can be used in theoretical estimates of the speed of intercellular and intracellular calcium waves (13). They can also be used more generally to determine the spatial range over which local calcium signals spread (14, 15). Inferences based on D^t rather than D^u can lead to erroneous conclusions. Whether D^t and D^u coincide or differ for proteins that are studied by using FRAP or related techniques needs to be assessed on a case-by-case basis. In any case, FRAP experiments provide information on k_off, k_on S_eq, and D^t, from which D_f can be inferred. However, unless k_on and S_eq can be measured independently, it is not possible to infer D^u or the time scale on which perturbations of the native system evolve when S_T/S_eq ≫ 1. This time scale and D^u are the quantities that characterize the dynamics of signal propagation, as opposed to D^t, k_off, and k_on S_eq, which describe the behavior of single or tagged molecules. The dynamics of inhomogeneities, rather than of single molecules, will determine statistical quantities, such as mean response times.

In the past few years, direct observation of single molecules has begun to provide another window into the cell and single-molecule diffusion coefficients have been constructed from what is tantamount to direct observation of the molecules (16, 17). In principle, measurements that resolve trajectories of (many) single molecules can provide complete information and thus yield k_on, k_off, S_T, S_eq, D_f, D^t, and D^u. When there are differences between diffusion coefficients of inhomogeneities and single molecules, we expect them to appear as differences between the rates of diffusion of inhomogeneities in statistical quantities, such as correlations, and of single particles. With current technology, only a few particles can be tracked at a time. Thus, such complete statistics are currently not available (18).

Methods

We use the same letters to represent the species and the concentration of that species (e.g., P_f = [P_f]). We assume that the traps are immobile and distributed uniformly in space. These assumptions are typical of FRAP analyses (10). We denote the total substrate (or trap) concentration by S_T, and the equilibrium concentrations of S, P_b, and P_f by S_eq, P_beq, and P_feq. We used the pseudo-on and off rates reported in ref. 10 for the glucocorticoid receptor: S_eqk_on = 500/s and k_off = 86.4/s. For comparison between the various simulations, we use these same binding rates and diffusion coefficients in the simulations reported in Fig. 1A rather than parameter values that would be appropriate for the binding of calcium. The total binding site concentration S_T and equilibrium concentration of unoccupied sites S_eq were not reported. We used S_eq = 1 mM and S_T = 10 mM, which is not a priori unreasonable for nonspecific binding to DNA for example. We chose the ratio S_eq/S_T = 0.1 to illustrate the difference between diffusion of tagged and untagged particles. The illustrative examples in this manuscript were obtained via numerical simulations of Eq. 4 in one space dimension (tagged particle bolus simulation shown in Fig. 1A) and three space dimensions (FRAP and free-particle deficit simulations shown in Fig. 1B) domain, using first order explicit time-stepping, second order centered differencing for the Laplacian and Neumann boundary conditions. The domain in the three-dimensional simulations was a sphere of radius R = 5 μm and in the one-dimensional simulations a line segment of length 5 μm. The space grid spacing was 0.01 μm, and the time step was 1 μs. The results were quantitatively robust under space and time mesh refinement. The free particle diffusion coefficient used was D_f = 9.2 μm²/s and the other parameters were P_beq = 9 mM, S_T = 10 mM, S_eq = 1 mM, K_D = 0.1728 mM, and P_feq = 1.5552 mM.

Analytical Derivation of Effective Diffusion Coefficients.

Under the assumption that the total concentration of traps, S_T, is uniform, the time evolution of the concentrations is given by

where the superscript i refers to whether the species is tagged (i = t) or untagged (i = u). For the case in which a small bolus of tagged particles is initially added to a background of untagged particles and traps in equilibrium, we consider the initial condition: P_f^u(x, 0) = P_feq, P_b^u(x, 0) = S_TP_feq/(P_feq + K_D), P_b^t(x, 0) = 0, and P_f^t(x, 0) = Φ(x), where Φ(x) is a function of compact support to represent the fact that the bolus is added locally in space. If the added bolus is small or if the spatial domain is large enough, the asymptotic state will be approximately equal to the initial equilibrium configuration. It is then reasonable to describe the dynamics in terms of an expansion around the equilibrium configuration. To this end, we define the variables:

where ε is a small quantity that represents the deviation with respect to equilibrium. We define the vectors u^† = (u^u; u^t)^† = (f_u b_u f_t b_t) and φ^† = (φ^u; φ^t)^† = (0 0 φ 0) and write the evolution equations as

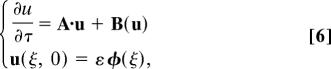where Bis quadratic in u and A is a linear operator, $\mathbf{A}\equiv \left[\begin{array}{cc}{\mathbf{A}}^u& \mathbf{W}\\ 0& {\mathbf{A}}^t\end{array}\right]$, with

We can solve Eq. 6 expanding the solution in powers of ε, u = Σ_i=0^∞ εⁱuⁱ. For the ε⁰ order we obtain u₀ = 0. For the ε¹ order we obtain the system

the solution of which can be expressed in Fourier space as: û₁(q,τ) = e^Â(q)τ. φ̂(q), where q is the conjugate variable to ξ and we have used hats to denote Fourier transforms. Given that the block form of  translates into a similar form for the exponential, the solution of Eq. 9 can be written as

where Ẑ(τ) is a 2 × 2 matrix (19). Our conclusions are independent of the particular form of Ẑ: the matrices A^u(q) and A^t(q) encode the asymptotic spatiotemporal dynamics of the untagged and tagged concentrations, respectively. From Eq. 7 we deduce that these matrices can be written as

from which we obtain that their slowest eigenvalues (ruling the asymptotic dynamics) correspond to small q and satisfy λ ≈ −q²hⁱ/(aⁱ + hⁱ). Thus, the dimensionless effective diffusion coefficients are

Restoring the units and replacing the corresponding values of aⁱ and hⁱ according to Eq. 8 we find the results presented in Eqs. 2 and 3.

The above analysis was for experiments in which a bolus of tagged particles was added as done in refs. 2 and 3. The case of FRAP (10), although conceptually quite different, can be treated similarly by writing down all five evolution equations (tagged and untagged particles and complexes and substrate concentration) and noting that, at t = 0 P_f^u + P_f^t, P_b^u + P_b^t and S = S_T− P_b^u − P_b^t are spatially uniform and at equilibrium. So that from Eq. 4 we deduce that P_f^u + P_f^t = P_feq, P_b^u + P_b^t = P_beq, and S = S_T − P_beq = S_eq for all time. Thus, the solution of the five nonlinear coupled equations can be obtained from

which can be written in dimensionless form as ∂u/∂t = A^tu with A^t defined as before. Thus, the effective diffusion coefficient obtained in this case coincides with that of the tagged particles in the case of the added bolus.

Eqs. 12 and 13 are similar to those that describe the evolution of a small perturbation [(δP_f, δP_b) = (P_f − P_feq, P_b − P_beq)] from equilibrium in the case for which there are no tags. The linearized evolution equations in this case are

Note that the only differences between Eqs. 12 and 13 and Eqs. 14 and 15 are that k_off is rescaled by S_T/S_eq in the latter. Thus, when S_T/S_eq ≫ 1, perturbations of the native system evolve differently from FRAP. Not only are the effective diffusion coefficients different in the two cases, but also in the time scale on which equilibrium is approached if S_T/S_eq is large. Note that Eqs. 14 and 15 can be written in dimensionless form as ∂u/∂t = A^uu, with A^u defined as before. Thus, the effective diffusion coefficient obtained in this case coincides with that of the untagged particles in the case of the added bolus.

Recovery Curves.

The recovery curves shown in Fig. 1D are given by the integral over the perturbed sphere of the difference between the current and initial total particle concentrations divided by the integral of the difference between the final and initial total particle concentrations: 1/V ∫((P_f + P_b)(r, t) − (P_f + P_b)_t=0)dV/((P_f + P_b)_t=∞ − (P_f + P_b)_t=0), where V is the volume of the perturbed sphere.

Abbreviations

MP

measurement point

IP

point at which the bolus is added

FRAP

fluorescence recovery after photobleaching.