Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2006 Mar;16(3):428–435. doi: 10.1101/gr.4526006

Systematic identification of functional orthologs based on protein network comparison

Sourav Bandyopadhyay 1,2, Roded Sharan 3,4, Trey Ideker 1,2,4
PMCID: PMC1415213  PMID: 16510899

Abstract

Annotating protein function across species is an important task that is often complicated by the presence of large paralogous gene families. Here, we report a novel strategy for identifying functionally related proteins that supplements sequence-based comparisons with information on conserved protein–protein interactions. First, the protein interaction networks of two species are aligned by assigning proteins to sequence homology clusters using the Inparanoid algorithm. Next, probabilistic inference is performed on the aligned networks to identify pairs of proteins, one from each species, that are likely to retain the same function based on conservation of their interacting partners. Applying this method to Drosophila melanogaster and Saccharomyces cerevisiae, we analyze 121 cases for which functional orthology assignment is ambiguous when sequence similarity is used alone. In 61 of these cases, the network supports a different protein pair than that favored by sequence comparisons. These results suggest that network analysis can be used to provide a key source of information for refining sequence-based homology searches.

The idea that similar protein sequences imply similar protein functions has long been a central concept in molecular biology. With each new completed genome, an increasingly complex array of sequence alignment and comparative modeling tools are used to annotate functions for the typically thousands of encoded proteins, based largely on similarity to proteins that are well characterized in other species (Brenner 1999; Reese et al. 2000). Ambiguities in the functional annotation process arise when the protein in question has similarity to not one but many paralogous proteins (Sjolander 2004), making it harder to distinguish which of these is the true ortholog—that is, the protein that is directly inherited from a common ancestor. Especially in the genomes of mammals and other higher eukaryotes, large protein families are typically not the exception but the rule.

The difficulty of assigning protein orthology depends largely on the evolutionary history. Protein families for which speciation predates gene duplication are particularly challenging; in these cases, every cross-species protein pair is technically orthologous but it is still necessary to distinguish which protein pairs play functionally equivalent roles, that is, which are functional orthologs (Remm et al. 2001). Conversely, when gene duplication predates speciation, the family can often be subdivided into orthologous pairs that have higher sequence similarity to each other than to other members. However, evolutionary processes such as gene conversion serve to homogenize paralogous sequences over time, making these cases problematic as well (Li et al. 2003). To complicate matters even further, protein function may be lost between distant organisms or conserved across multiple proteins within a single species.

A variety of sequence-based approaches have been proposed to address these challenges. The COGs (Clusters of Orthologous Groups) approach (Tatusov et al. 2000) defines orthologs by using sets of proteins that contain reciprocal best BLAST matches (Altschul et al. 1997) across a minimum of three species. Also available are phylogenetic methods that explicitly address an evolutionary tree, as reviewed in Eisen and Wu (2002). Recent approaches such as Inparanoid (Remm et al. 2001) and OrthoMCL (Li et al. 2003) try to achieve higher sensitivity through sequence clustering techniques that consider a range of BLAST scores beyond the absolute best hits. For Inparanoid, BLAST E-values from the proteins of two species are grouped according to a fixed set of rules that divide proteins into ortholog clusters, each of which contains similar-sequence proteins drawn from both species. Within each group, pairs of proteins (cross-species only) can be assigned an overall score reflecting the likelihood they are functional orthologs.

Other than gene and protein sequences, several large-scale data types have recently become available that provide complementary information on functional conservation. For instance, several groups have used correlated patterns of gene expression across species as evidence for functional relatedness (Stuart et al. 2003; van Noort et al. 2003). Networks of protein–protein interactions are also being generated for a variety of species, through technologies such as the two-hybrid assay (Fields and Song 1989) or coimmunoprecipitation followed by mass spectrometry (Aebersold and Mann 2003). Such networks can be compared to identify “interologs,” that is, interactions that are conserved across species (Matthews et al. 2001). Beyond comparison of interactions individually, methods such as PathBLAST (Kelley et al. 2003, 2004) and that of Sharan et al. (2005) create a global alignment between networks to identify conserved network regions. These approaches can successfully infer conserved components of the cellular machinery and use those components to predict new protein functions and interactions. In addition, interactions that are conserved across species are less likely to represent false positives.

Here, we investigate whether it is possible to use protein network information to predict functionally orthologous proteins across species. While previous tools such as Interolog mapping and PathBLAST have used orthology to identify conserved protein interactions, our approach aims to reverse this logic and use conserved protein interactions to predict functional orthology. It is built on the concept that a protein and its functional ortholog are likely to interact with proteins in their respective networks that are themselves functional orthologs. This type of network-based approach is related to methods for predicting other protein properties based on the interaction network, such as functional annotation of a protein based on the annotations of its neighbors (Letovsky and Kasif 2003; Vazquez et al. 2003; Espadaler et al. 2005; Leone and Pagnani 2005). In our case, the orthology relation between each pair of proteins is modeled as a probabilistic function of the orthology relations of their immediate network neighbors, and orthology relationships are inferred by using Gibbs sampling. We apply this approach to refine the set of functional orthologs between the budding yeast Saccharomyces cerevisiae and the fruit fly Drosophila melanogaster: Not only are these species among the most important model eukaryotes, they are also associated with the largest numbers of experimentally measured protein interactions to date.

Results

Motivation: Interaction conservation is related to orthology

Protein–protein interaction networks for yeast and fly were obtained from the Database of Interacting Proteins (December 2004 download) (Xenarios et al. 2002). These contained 14,319 interactions among 4389 proteins in yeast and 20,720 interactions among 7038 proteins in fly. First, we applied the Inparanoid (Remm et al. 2001) algorithm to the complete sets of proteins from S. cerevisiae and D. melanogaster to define sequence-similar clusters. A total of 2244 clusters were generated, covering 2834 yeast and 3881 fly proteins overall. Of these, 1552 clusters contained only a single yeast/fly protein pair and were assumed to represent unambiguous or “definite” functional orthologs (orthologs we take to be functionally equivalent because of direct ancestry). The remaining 692 clusters contained multiple proteins from yeast and/or fly, leaving the functional orthologs ambiguous.

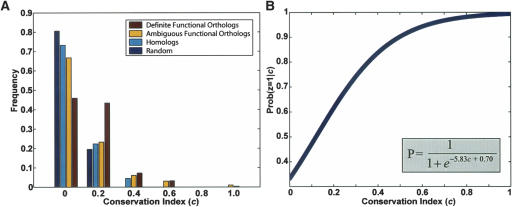
To determine the extent to which proteins and their functional orthologs had conserved protein interactions, we examined the network neighborhoods of definite functional orthologs and compared them to the neighborhoods of less related protein pairs (Fig. 1). As a measure of local network conservation, we computed the conservation index of each protein pair as proportional to the fraction of interactions that were conserved across the two species. For example, in Figure 2b the orthologous pairing B/B′ has a higher conservation index (4/9) than the alternative pairing B/B″ (2/9).

Figure 1.

Figure 1.

Open in a new tab

(A) Network neighborhood conservation for definite orthologs vs. other yeast/fly protein pairs. The distribution of the conservation index “c” is shown for definite functional orthologs (sole members of an Inparanoid cluster), ambiguous functional orthologs (in a cluster with multiple members), homologs (different clusters but similar sequences), and random protein pairs. Definite functional orthologs show a shift toward higher conservation of protein interactions between the yeast and fly protein networks. Mean c = 0.1512, 0.1171, 0.0870, 0.0615 for definite functional orthologs, ambiguous functional orthologs, homologs, and random pairs, respectively. (B) Logistic function relating conservation index to probability of functional orthology. Logistic regression was performed by using the “definite functional ortholog” and “homolog” pairs as positive vs. negative training data, respectively. The resulting function is shown.

Figure 2.

Figure 2.

Open in a new tab

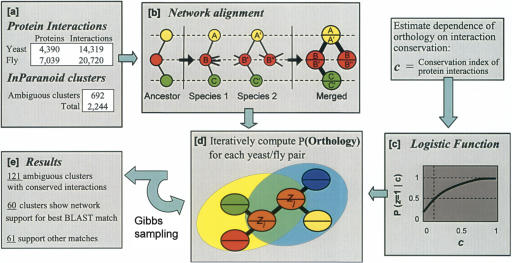
Overview of the method. (a) Protein–protein interaction networks for yeast and fly are combined with clusters of orthologous yeast and fly protein sequences as determined by the Inparanoid algorithm. (b) Networks are aligned into a merged graph representation. In this example, a gene duplication results in two proteins B′ and B″ in species 2 that are orthologous to protein B in species 1. One of these proteins may experience a gain and/or loss of interactions to enable new functional roles (Wagner 2003); however, only conserved interactions are represented in the alignment graph. (c) The logistic function shown in Figure 1B is used to compute the probability of functional orthology for a protein pair given the states of functional orthology for its network neighbors. (d) This probability is updated for each pair over successive iterations of Gibbs sampling. (e) The final probabilities confirm 60 of the best BLAST match pairings. The network supports a different hypothesis for 61 pairings.

Figure 1A shows the set of conservation indices for definite functional orthologs versus those of ambiguous functional orthologs, nonorthologous homologs (best cross-species BLAST matches not assigned to the same Inparanoid cluster), and random pairs of proteins chosen independently of sequence similarity. As expected, the set of definite functional orthologs had the highest occurrence of conserved interactions. Moreover, the mean conservation index was related to the stringency of the pairing: Definite functional orthologs tended to have higher conservation indices than did ambiguous functional orthologs, ambiguous functional orthologs had higher indices than did homologs, and homologs had higher indices than did random protein pairs. Beyond the mean conservation index, there were also significant differences among the four distributions (Supplemental Table 1). These findings confirm that yeast/fly proteins classified as definite functional orthologs are more likely to have equivalent functional roles in the protein network and, conversely, that conserved network context could be used to help discriminate functional orthology from general sequence similarity.

Network-based identification of functional orthologs

To capture these trends to identify functional orthologs, we formulated a procedure to estimate the likelihood of functional orthology for each ambiguous functional ortholog given its conservation index. By this method, the probability of functional orthology for a pair of proteins is influenced by the probabilities of functional orthology for their network neighbors, which in turn depend on their network neighbors, and so on. This type of probabilistic model is known as a Markov random field (Besag 1974). Exact inference in this model is not tractable because of the complex interrelationships between network nodes. Rather, approaches such as clustering, conditioning, and stochastic simulation have been used to derive estimates for the posterior probabilities of node properties. Here, we implemented a method based on Gibbs sampling for its computational tractability and accuracy in densely connected networks (Pearl 1988). An overview of the approach is given in Figure 2, with full details provided in the Methods.

Application to yeast and fly identifies new putative functionally orthologous pairs

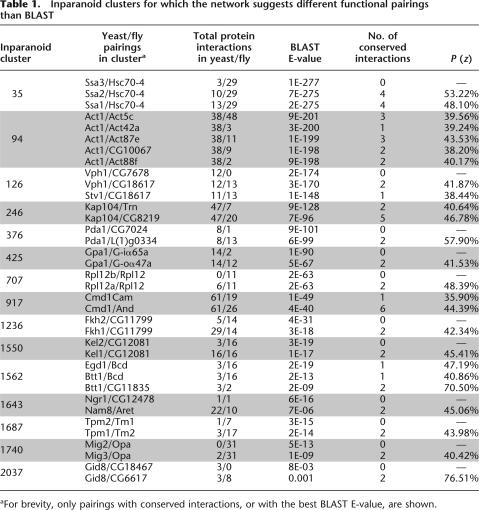
We applied this approach to resolve ambiguous functional orthology relationships in the yeast and fly protein networks. Of the 692 ambiguous Inparanoid clusters, 121 contained protein pairs for which at least one pair had conserved interactions between networks. Application of our Gibbs sampling procedure yielded estimates of probability of functional orthology for each protein pair in these 121 ambiguous clusters. In 60 of these clusters, the highest probability was assigned to the protein pair that was also the most sequence-similar via BLAST. These cases reinforced the intuition that the best sequence matches are also the most functionally similar. The remaining 61 clusters showed the opposite behavior; that is, the highest probability pair was not the most sequence similar pair. Of these 61 cases, 15 were supported by two or more conserved interactions (Table 1). Because the yeast and fly networks are incomplete (i.e., they contain false negatives), in some of these cases we cannot rule out the possibility that conserved interactions with the best BLAST matches have been missed (see Discussion). A complete listing of the results can be found on the Supplemental Web site (http://www.cellcircuits.org/Bandyopadhyay2006/).

Table 1.

Inparanoid clusters for which the network suggests different functional pairings than BLAST

a For brevity, only pairings with conserved interactions, or with the best BLAST E-value, are shown.

graphic file with name 428tab1.jpg

Open in a new tab

Validation

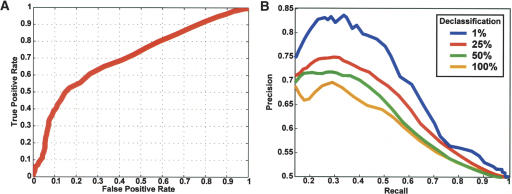
A straightforward validation of the approach would be to analyze its accuracy in recapitulating a gold standard set of protein functional annotations. However, databases of functional annotations are based directly on sequence similarity, and they typically lack the specificity to discriminate among subtle functional differences across large gene families. As an alternative, we used the technique of cross-validation to test the ability of the approach to reclassify protein pairs in the definite functional ortholog set (positive test data) versus the nonorthologous homolog set (negative test data). In each cross-validation trial, 1% of these assignments were hidden (declassified) and monitored during Gibbs sampling to obtain probabilities of functional orthology for positive and negative examples. Reclassification was judged successful if the probability of functional orthology exceeded a particular cutoff value. These statistics were compiled over 100 trials. Figure 3A charts cross-validation performance over a range of probability cutoffs. At a probability cutoff of 0.5, we observed a 50% true-positive rate and a 15% false-positive rate. This shows marked improvement over a random predictor, where we would expect to see the same true-positive rate as false-positive rate.

Figure 3.

Figure 3.

Open in a new tab

(A) Estimated accuracy of the method. The Receiver Operating Characteristic (ROC) curve shows the true-positive rate (percentage of true data predicted correctly as positive) vs. the false-positive rate (percentage of false data predicted incorrectly, i.e., positive) of the method. (B) Dependence of predictions on number of available training examples. Percentage precision (percentage of positive predictions that were correct) vs. recall (true-positive rate) is plotted as the probability cutoff ranges from [0–1]. Different color plots correspond to different percents of declassification of training examples.

Declassifying 1% of the known functional orthologous and nonorthologous pairs reduces the amount of information available to the algorithm and, thus, can reduce its predictive ability. To assess the severity of this effect, we repeated the cross-validation analysis at varying percentages of declassification of positive and negative data (ranging from 1%–100%) (Fig. 3B). For instance, changing the amount of declassification of available training data from 1% to 25% reduced the maximum precision from 83% to 75%. Further declassification yielded more marked reductions in precision and recall.

Discussion

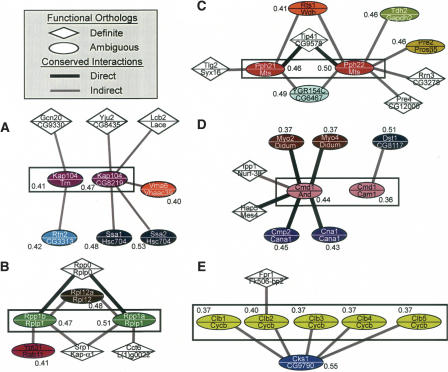
Specific examples of yeast/fly functional orthologs resolved by the network-based approach are shown graphically in Figure 4. In Figure 4A, yeast transportin (Kap104) is orthologous to both Trn and CG8219 in fly with highly significant sequence homology (BLAST E-values 9 × 10–128 and 7 × 10–96, respectively). Transportin is a member of a complex responsible for the nuclear import of mRNA binding proteins and is known to be highly conserved among diverse organisms (Aitchison et al. 1996). Drosophila Trn was identified by using sequence homology based on human transportin1 (Siomi et al. 1998). Both Trn and CG8219 in fly interact with orthologs of members of the Kap104-associated complex in yeast (Ho et al. 2002) suggesting that both of these fly proteins may participate in the functionally similar complex in fly. Our analysis suggests that CG8219 retains more of the original functions of Kap104 (probability of functional orthology of 47% vs. 41% for the Kap104/Trn pairing) due to their conserved interactions with members of the spliceosome complex (Yju2, Ssa1, and Ssa2 in yeast). This result is a case in which the most sequence-similar protein does not appear to be the most functionally related protein in an orthologous cluster given the current network data.

Figure 4.

Figure 4.

Open in a new tab

Example orthologs resolved by network conservation. Each node represents a putative functional match between a yeast/fly protein pair (with names shown above/below the line, respectively). Links between nodes denote conserved interactions (thick black, direct interactions in both species; thin gray, indirect interaction in one of the species; see Methods). Diamond- vs. oval-shaped nodes represent definite vs. ambiguous functional orthologs. Oval nodes of the same color represent ambiguous protein pairs belonging to the same Inparanoid cluster. The mean probability of functional orthology is given next to each ambiguous pair. Cluster 246 (A), 1439 (B), 211 (C), 917 (D), and 1104 (E) show examples of clusters that were disambiguated by conserved network information; the cluster resolved in each panel is outlined by a black rectangle.

The cluster in Figure 4C contains two alternative catalytic α subunits of the protein phosphatase type 2A family (yeast Pph21 and Pph22). Both alternatives interact with a member of the β subunit (Rts1) and have high sequence similarity to the fly Mts protein (75% identity for Pph21, 76% for Pph22). Since Pph21 and Pph22 are at least partially redundant (disruption of both genes in combination is synthetic lethal) (Ronne et al. 1991), it appears that the array of interactions carried out by Mts is conserved across the two yeast orthologs. Nonetheless, based on the available protein interaction data, Pph22 alone has conserved interactions with the proteasome (Pre2/Prosβ5 and Pre4/CG12000), which has been shown to be important for the role of the Pph21/22 complex in degradation of Swe1p (Yang et al. 2000).

As a final example, Figure 4D shows evidence that the yeast Calmodulin (Cmd1) protein is functionally orthologous to fly Androcam (And) rather than to the more sequence-similar fly Calmodulin (Cam1; 60% identity vs. 51% for And). The existence of many conserved interactions for the Cmd1/And pair, compared with only one for Cmd1/Cam1, does not appear to be a result of incomplete coverage: Cmd1 has a total of 61 interactions in the yeast network, and Cam1 and And have 19 and 26 interactions, respectively, in the fly network (most of these do not appear in Fig. 4 because the network alignment only shows interactions that are conserved). Furthermore, multiple sequence alignment and phylogenetic analysis of these genes over a larger number of organisms, including worms and mammals, indicates a closer phylogenetic relationship for yeast Cmd1 and fly And, supporting our hypothesis that they are the true functional orthologs (Supplemental Fig. 1). This apparent discrepancy between functional and sequence similarity is probably a result of the large amount of sequence variability among the calmodulin family of proteins (Tombes et al. 2003) and would have been difficult to probe without protein network information.

In future work, it is possible that incorporating yet other types of conserved linkages, such as transcriptional interactions (Harbison et al. 2004), synthetic–lethal interactions (Guarente 1993), and coexpression relations (Stuart et al. 2003) will allow for a more complete and multifaceted view of protein function. The proposed method would also benefit from a more accurate understanding of network evolution. At the core of our approach is a model for measuring the divergence of orthologous proteins by means of a network “conservation index.” It encapsulates the notion that shorter evolutionary distances correspond to greater relative numbers of conserved interactions. However, a more sophisticated metric might represent explicit evolutionary mechanisms, such as formation of new interactions through gene mutation or duplication (Wagner 2003). It should also be noted that comparative methods rely on the conservation of function between evolutionarily related proteins, and that this functional similarity may be lost among orthologs due to large evolutionary distance; thus, network-based methods that search for the absence of a functional ortholog may also be useful. Finally, further work is needed to analyze the impact of data quality, that is, numbers of false-positive and false-negative interactions (Sprinzak et al. 2003). False positives are largely mitigated by the focus on only those interactions that are conserved across species, because spurious interactions are typically not reproducible (Sharan et al. 2005). False negatives are a larger concern, because they might cause a functionally orthologous pair to be wrongly rejected due to lack of conserved interactions. Certainly, a preponderance of conserved interactions for one particular pair of proteins versus others provides evidence that these proteins are indeed functional orthologs. Although the expected number of false-negative interactions will decrease with forthcoming interaction data sets, future approaches may explicitly incorporate the false-negative rate into the probabilistic model.

In summary, we have presented an algorithm that uses protein interaction measurements to achieve more specific discrimination of functional orthologs than is possible with sequence-based methods alone. It is built on the concept that conserved proteins typically do not function independently but rely on interactions with other proteins to form conserved pathways, and that the specific patterns of conservation of these pathways are informative for determining which cross-species protein pairs have similar functional roles. As these methods mature and as ever greater numbers of protein interactions become available across species, comparative network analysis is likely to play an increasingly central role as a bridge among protein sequence, evolution, and function.

Methods

Inparanoid clusters generation

The complete sets of 5878 yeast and 18,746 fly protein sequences were downloaded from the Saccharomyces Genome Database (Christie et al. 2004) and Flybase (Drysdale et al. 2005), respectively. Protein sequences for both species were grouped together into orthology clusters by using the Inparanoid algorithm (Remm et al. 2001) with default parameters (overlap threshold = 0.5; confidence = 0.05). Inparanoid optionally allows a third genome to be used as an outgroup, which can detect missing sequences and thus improve ortholog detection. However, use of Escherichia coli as an outgroup had a negligible impact on our analysis.

Network alignment

A global network alignment between yeast and fly was constructed as described in Kelley et al. (2004), with the difference that Inparanoid clusters were used instead of BLAST E-values for pairing proteins between the two networks. Briefly, the network alignment is represented as a graph of nodes and links (Fig. 2b). Each node denotes a pair of putatively orthologous proteins a and a′. Each link between a pair of nodes a/a′ and b/b′ denotes a conserved protein interaction, that is, an interaction observed for both (a, b) and (a′, b′). To tolerate a certain amount of missing interaction data, “indirect” links are also defined if a pair of proteins interacts in one species (e.g., a and b interact) and the other pair of proteins (e.g., a′ and b′) is at most distance two in their corresponding interaction maps. Links involving network distances greater than two, or for which the proteins of both species are at distance two, are not allowed (Kelley et al. 2003). The yeast/fly network alignment contains 388 nodes (spanning 348 yeast and 256 fly proteins) linked by 308 conserved interactions (110 direct and 198 indirect).

Each node in the alignment graph is associated with a state z, indicating whether that protein pair represents true functional orthology (z = 1) or not (z = 0). Links between nodes that are each associated with true functional orthology are said to be “strongly conserved.” To compute the frequencies shown in Figure 1A, the protein pair in each Inparanoid cluster having the lowest BLAST E-value is set to z = 1; all others are set to z =0.

Conservation index

We define the conservation index c of node i (representing protein pair a/a′) as twice its number of strongly conserved interactions divided by its total number of interactions over both species:

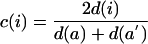graphic file with name M1.gif

where d(i) denotes the number of strongly conserved links involving node i, while d(a) and d(a′) denote the degrees (numbers of interactions) of proteins a and a′ in their respective single-species networks.

Probabilistic model

We model the orthology relations for two species by using a Markov random field (Besag 1974). This model is specified by an undirected graph G =(V, E) corresponding to a network alignment, and conditional probability distributions that relate the event that a given node represents a functionally orthologous pair with those events for its neighbors. A Markov random field model is specified in terms of potential functions on the cliques in the graph

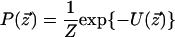graphic file with name M2.gif

where z Inline graphic is some assignment to the states of all nodes in the graph, U(·) is an “energy” function that integrates the potentials over all cliques in the graph, and Z is a normalizing constant. It is not necessary to compute the normalization constant, since all that is required are the conditional probabilities for each node given its neighbors (rather than the joint distribution). For computational efficiency, we used the common auto-logistic model (Besag 1974), which assigns zero potential to cliques of size greater than two. Under this model, the energy takes the form

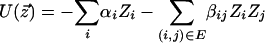graphic file with name M4.gif

which, when substituted into the equation for 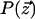Inline graphic above, reduces to a logistic function. Based on our initial observation that the functional orthology of a node is a function of its conservation index (well approximated by a logistic function) (see Fig. 1A; Results), we set αi = α and βij = βi =2β/[d(ai)+ d(ai′)] to obtain the following:

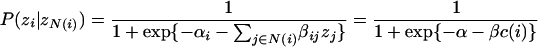graphic file with name M6.gif

where N(i) is the set of neighbors of node i, and zN(i) denotes the set of all zj such that jεN(i). Note that αi and βij could be set to accommodate other equations for conservation index, as long as they are linear in the number of strongly conserved neighbors d(i).

Fitting the logistic function

To provide a set of training data for fitting the parameters α and β of the logistic function, 100 of the 212 definite functional orthologs having at least one conserved interaction were randomly chosen as positive examples, and their states were set to z = 1. Negative examples of “nonorthologs” were generated by randomly selecting 100 yeast proteins and pairing each with its best BLAST matching fly protein not in the same cluster; their states were set to z = 0 (ideally, the negative training data would consist of orthologs that are not functional orthologs, but few such examples exist). Parameters α and β were optimized by maximizing the product of P(zi | zN(i)) over all positive and [1 – P(zi | zN(i))] over all negative training data using the method of conjugate gradients (Press 1992). The optimal logistic function is shown in Figure 1B. Note that the equal numbers of positive and negative training data assume a prior probability of 0.5 of observing a true functional ortholog. Although the actual prior is unknown and may differ from this value, P(zi | zN(i)) remains monotonically related to the true probability of functional orthology.

Orthology inference

We used the above model to estimate the final posterior probabilities P(zi) by using the method of Gibbs sampling (Smith and Roberts 1993). In this approach, nodes representing ambiguous functional orthologs are each assigned a temporary state, z, of zero or one, initially at random. At each iteration, a node i is sampled (with replacement) and its value of zi is updated given the states of its neighbors, zN(i). The new value of zi is set to one with probability P(zi | zN(i)), else zero. Over all iterations, the nodes designated as definite functional orthologs and “nonorthologs” are forced to states of one and zero, respectively. This process is illustrated in Figure 2, c and d.

The Gibbs sampling procedure was carried out for an initial period of 2 × 106 “burn-in” iterations. From this point onward, 2 × 107 additional iterations were performed and statistics computed on the fraction of iterations in which each node acquires a “functionally orthologous” z = 1 state. The final probabilities of functional orthology for each node, P(zi), were estimated as this fraction. The above numbers of iterations were chosen to ensure that results were stable across multiple runs of random initialization configurations (standard deviations for each P(zi) are available in the Supplemental material). Compiled results were aggregated over 100 separate runs of the algorithm and mean probabilities reported.

Acknowledgments

We thank Tomer Shlomi and Ryan Kelley for critical reading of the manuscript, as well as Silpa Suthram for providing interaction data. We gratefully acknowledge the following sources of funding for this project: award R01-GM070743-01 from the NIGMS (T.I.), an Alon fellowship (R.S.), and a Quantitative Systems Biology grant from the NSF (S.B.). T.I. is a fellow of the David and Lucille Packard Foundation.

[Supplemental material is available online at www.genome.org and http://www.cellcircuits.org/Bandyopadhyay2006/.]

Article published online ahead of print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.4526006.

References

  1. Aebersold, R. and Mann, M. 2003. Mass spectrometry-based proteomics. Nature 422: 198–207. [DOI] [PubMed] [Google Scholar]
  2. Aitchison, J.D., Blobel, G., and Rout, M.P. 1996. Kap104p: A karyopherin involved in the nuclear transport of messenger RNA binding proteins. Science 274: 624–627. [DOI] [PubMed] [Google Scholar]
  3. Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25: 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Besag, J. 1974. Spatial interaction and the statistical analysis of lattice systems. J. Roy. Statist. Soc. B: 192–236. [Google Scholar]
  5. Brenner, S.E. 1999. Errors in genome annotation. Trends Genet. 15: 132–133. [DOI] [PubMed] [Google Scholar]
  6. Christie, K.R., Weng, S., Balakrishnan, R., Costanzo, M.C., Dolinski, K., Dwight, S.S., Engel, S.R., Feierbach, B., Fisk, D.G., Hirschman, J.E., et al. 2004. Saccharomyces Genome Database (SGD) provides tools to identify and analyze sequences from Saccharomyces cerevisiae and related sequences from other organisms. Nucleic Acids Res. 32: D311–D314. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Drysdale, R.A., Crosby, M.A., Gelbart, W., Campbell, K., Emmert, D., Matthews, B., Russo, S., Schroeder, A., Smutniak, F., Zhang, P., et al. 2005. FlyBase: Genes and gene models. Nucleic Acids Res. 33: D390–D395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Eisen, J.A. and Wu, M. 2002. Phylogenetic analysis and gene functional predictions: Phylogenomics in action. Theor. Popul. Biol. 61: 481–487. [DOI] [PubMed] [Google Scholar]
  9. Espadaler, J., Aragues, R., Eswar, N., Marti-Renom, M.A., Querol, E., Aviles, F.X., Sali, A., and Oliva, B. 2005. Detecting remotely related proteins by their interactions and sequence similarity. Proc. Natl. Acad. Sci. 102: 7151–7156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fields, S. and Song, O. 1989. A novel genetic system to detect protein–protein interactions. Nature 340: 245–246. [DOI] [PubMed] [Google Scholar]
  11. Guarente, L. 1993. Synthetic enhancement in gene interaction: A genetic tool come of age. Trends Genet. 9: 362–366. [DOI] [PubMed] [Google Scholar]
  12. Harbison, C.T., Gordon, D.B., Lee, T.I., Rinaldi, N.J., Macisaac, K.D., Danford, T.W., Hannett, N.M., Tagne, J.B., Reynolds, D.B., Yoo, J., et al. 2004. Transcriptional regulatory code of a eukaryotic genome. Nature 431: 99–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ho, Y., Gruhler, A., Heilbut, A., Bader, G.D., Moore, L., Adams, S.L., Millar, A., Taylor, P., Bennett, K., Boutilier, K., et al. 2002. Systematic identification of protein complexes in Saccharomyces cerevisiae by mass spectrometry. Nature 415: 180–183. [DOI] [PubMed] [Google Scholar]
  14. Kelley, B.P., Sharan, R., Karp, R.M., Sittler, T., Root, D.E., Stockwell, B.R., and Ideker, T. 2003. Conserved pathways within bacteria and yeast as revealed by global protein network alignment. Proc. Natl. Acad. Sci. 100: 11394–11399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kelley, B.P., Yuan, B., Lewitter, F., Sharan, R., Stockwell, B.R., and Ideker, T. 2004. PathBLAST: A tool for alignment of protein interaction networks. Nucleic Acids Res. 32: W83–W88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Leone, M. and Pagnani, A. 2005. Predicting protein functions with message passing algorithms. Bioinformatics 21: 239–247. [DOI] [PubMed] [Google Scholar]
  17. Letovsky, S. and Kasif, S. 2003. Predicting protein function from protein/protein interaction data: A probabilistic approach. Bioinformatics 19(Suppl 1): I197–I204. [DOI] [PubMed] [Google Scholar]
  18. Li, L., Stoeckert Jr., C.J., and Roos, D.S. 2003. OrthoMCL: Identification of ortholog groups for eukaryotic genomes. Genome Res. 13: 2178–2189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Matthews, L.R., Vaglio, P., Reboul, J., Ge, H., Davis, B.P., Garrels, J., Vincent, S., and Vidal, M. 2001. Identification of potential interaction networks using sequence-based searches for conserved protein–protein interactions or “interologs.” Genome Res. 11: 2120–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pearl, J. 1988. Probabalistic reasoning in intelligent systems: Networks of plausible inference. Morgan Kaufmann Publishers, San Mateo, CA.
  21. Press, W.H. 1992. Numerical recipes in FORTRAN: The art of scientific computing. Cambridge University Press, Cambridge.
  22. Reese, M.G., Hartzell, G., Harris, N.L., Ohler, U., Abril, J.F., and Lewis, S.E. 2000. Genome annotation assessment in Drosophila melanogaster. Genome Res. 10: 483–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Remm, M., Storm, C.E., and Sonnhammer, E.L. 2001. Automatic clustering of orthologs and in-paralogs from pairwise species comparisons. J. Mol. Biol. 314: 1041–1052. [DOI] [PubMed] [Google Scholar]
  24. Ronne, H., Carlberg, M., Hu, G.Z., and Nehlin, J.O. 1991. Protein phosphatase 2A in Saccharomyces cerevisiae: Effects on cell growth and bud morphogenesis. Mol. Cell Biol. 11: 4876–4884. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sharan, R., Suthram, S., Kelley, R.M., Kuhn, T., McCuine, S., Uetz, P., Sittler, T., Karp, R.M., and Ideker, T. 2005. Conserved patterns of protein interaction in multiple species. Proc. Natl. Acad. Sci. 102: 1974–1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Siomi, M.C., Fromont, M., Rain, J.C., Wan, L., Wang, F., Legrain, P., and Dreyfuss, G. 1998. Functional conservation of the transportin nuclear import pathway in divergent organisms. Mol. Cell Biol. 18: 4141–4148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Sjolander, K. 2004. Phylogenomic inference of protein molecular function: Advances and challenges. Bioinformatics 20: 170–179. [DOI] [PubMed] [Google Scholar]
  28. Smith, A. and Roberts, G. 1993. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods J. Roy. Statist. Soc. B 55: 3–23. [Google Scholar]
  29. Sprinzak, E., Sattath, S., and Margalit, H. 2003. How reliable are experimental protein–protein interaction data? J. Mol. Biol. 327: 919–923. [DOI] [PubMed] [Google Scholar]
  30. Stuart, J.M., Segal, E., Koller, D., and Kim, S.K. 2003. A gene-coexpression network for global discovery of conserved genetic modules. Science 302: 249–255. [DOI] [PubMed] [Google Scholar]
  31. Tatusov, R.L., Galperin, M.Y., Natale, D.A., and Koonin, E.V. 2000. The COG database: A tool for genome-scale analysis of protein functions and evolution. Nucleic Acids Res. 28: 33–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Tombes, R.M., Faison, M.O., and Turbeville, J.M. 2003. Organization and evolution of multifunctional Ca2+/CaM-dependent protein kinase genes. Gene 322: 17–31. [DOI] [PubMed] [Google Scholar]
  33. van Noort, V., Snel, B., and Huynen, M.A. 2003. Predicting gene function by conserved co-expression. Trends Genet. 19: 238–242. [DOI] [PubMed] [Google Scholar]
  34. Vazquez, A., Flammini, A., Maritan, A., and Vespignani, A. 2003. Global protein function prediction from protein–protein interaction networks. Nat. Biotechnol. 21: 697–700. [DOI] [PubMed] [Google Scholar]
  35. Wagner, A. 2003. How the global structure of protein interaction networks evolves. Proc. Roy. Soc. Lond. B Biol. Sci. 270: 457–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Xenarios, I., Salwinski, L., Duan, X.J., Higney, P., Kim, S.M., and Eisenberg, D. 2002. DIP, the Database of Interacting Proteins: A research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 30: 303–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Yang, H., Jiang, W., Gentry, M., and Hallberg, R.L. 2000. Loss of a protein phosphatase 2A regulatory subunit (Cdc55p) elicits improper regulation of Swe1p degradation. Mol. Cell Biol. 20: 8143–8156. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES