Statistical Validation of Brain Tumor Shape Approximation via Spherical Harmonics for Image-Guided Neurosurgery

Abstract

Rationale and Objectives

Surgical planning now routinely uses both two-dimensional (2D) and three-dimensional (3D) models that integrate data from multiple imaging modalities, each highlighting one or more aspects of morphology or function. We performed a preliminary evaluation of the use of spherical harmonics (SH) in approximating the 3D shape and estimating the volume of brain tumors of varying characteristics.

Materials and Methods

Magnetic resonance (MR) images from five patients with brain tumors were selected randomly from our MR-guided neurosurgical practice. Standardized mean square reconstruction errors (SMSRE) by tumor volume were measured. Validation metrics for comparing performances of the SH method against segmented contours (SC) were the dice similarity coefficient (DSC) and standardized Euclidean distance (SED) measure.

Results

Tumor volume range was 22413–85189 mm³, and range of number of vertices in triangulated models was 3674–6544. At SH approximations with degree of at least 30, SMSRE were within 1.66 × 10⁻⁵ mm⁻¹. Summary measures yielded a DSC range of 0.89–0.99 (pooled median, 0.97 and significantly >0.7; P < .001) and an SED range of 0.0002–0.0028 (pooled median, 0.0005).

Conclusion

3D shapes of tumors may be approximated by using SH for neurosurgical applications.

Magnetic resonance (MR) imaging (MRI), in conjunction with computerized stereotactic systems, has become an indispensable tool for guiding brain tumor resections. During the last decade, image guidance has led to improvement in both lesion localization and definition of tumor margins, thus increasing the precision and reducing the invasiveness of brain tumor surgery. Data obtained by means of newly developed MRI techniques, such as diffusion tensor MRI and functional MRI, allow for visualization of white-matter fiber tracts and cortical activity, respectively.

Along with the exponential spread of intraoperative navigational tools, the role of computer-assisted surgical planning has expanded. Surgical planning takes advantage of both two-dimensional (2D) and three-dimensional (3D) models, which integrate data from multiple imaging modalities, each highlighting one or more aspects of morphology or function. Thus, multimodality fusion-based models are used increasingly for optimizing lesion targeting and simulating different surgical approaches (1).

It is well known that intrinsic brain tumors tend to spread along the path of adjacent white-matter tracts. Recent studies have shown that these tumors may alter white-matter structure in complex ways (infiltration, displacement, and disruption). Studies attempting to correlate tumor shape with the underlying anatomic substrate (eg, white-matter fiber tract configuration defined by means of diffusion tensor MRI) may provide new insights into the patterns of brain tumor growth and invasion. However, shape analysis of brain tumors is a relatively unexplored field. Different segments of the same tumor may behave differently, with some infiltrating and others displacing fiber tracts. In the absence of anatomic constraints, a tumor likely would grow equally in all directions; hence, it would develop into a sphere-like structure. However, most intra-axial neoplasms show a more irregular shape, reflecting the anisotropic structure of the underlying white-matter. It can be theorized that shape analysis, derived from anatomic MRI, may provide additional clues in respect to the tumor’s biological behavior and help predict the likelihood of therapeutic success.

Shape analysis using spherical harmonics (SH) may help define different patterns of tumor invasion and solve the question of preferential tumor spread along particular fiber tracts. SH are an orthonormal basis of functions defined on the unit sphere. SH expansion defines a 3D surface in a spherical coordinate system (θ, ϕ) in terms of the coefficients of the corresponding SH basis functions. The resulting analytically defined surface closely approximates the desired target surface as the number of coefficients is increased. SH have been used to quantitatively define and approximate 3D geometric features in various fields, including multiple sclerosis lesions (2–4), and complicated anatomic shapes, such as cerebral ventricles (5–7).

MATERIALS AND METHODS

MRI Acquisition

Five sets of MR images were randomly selected from retrospective neurosurgical patients who underwent surgery under intraoperative MRI guidance at our institution through 2002 after obtaining institutional review board approval (#2003-P-001606). Patient and tumor characteristics of this series of cases are listed in Table 1. All MR images were acquired on a 0.5 T open interventional MRI system (Signa SP; GE Medical Systems, Milwaukee, WI). For the present analysis, we used axial fast spin echo T2-weighted acquisitions, repetition time, 5000 milliseconds; echo time, 99 milliseconds; field of view, 220 mm; slice thickness, 5 mm; gap, 1 mm. MR images were transferred onto a UNIX network through Ethernet. Brain tumors were manually segmented in each case by using the 3D Slicer (www.slicer.org) software package. 2D tumor contours defined by segmentation are referred to here as segmented contours (SC).

Table 1.

Tumor Characteristics of Cases in this Study

Case No.	Age (y)	Location	Type	World Health Organization Grade
1	49	Right frontotemporal	Oligodendroglioma	II/IV
2	49	Right frontal	Oligodendroglioma	II/IV
3	40	Left frontoparietal	Oligodendroglioma	II/IV
4	48	Left frontal	Oligodendroglioma	II/IV
5	23	Left frontal	Anaplastic astrocytoma	III/IV

SH

SH, defined in equation (1), are an orthonormal basis of functions defined on the unit sphere that can be used to describe complicated surfaces in 3D.

$$Y_1^m\left(\theta ,\varphi \right)=\sqrt{\frac{2l+1(l-m)!}{4\pi \mathrm{\hspace{0.17em} }(l+m)!}}{P}_1^m\left(\text{cos}\theta \right)\text{exp}(im\varphi )$$ (1)

where Y₁^m (θ, ϕ) is the corresponding SH function, P₁^m (cos θ) is the associated Legendre polynomial, the function’s degree l is a non-negative integer, and the function’s order m can have only the values −l, − (l − 1)…, 0, …, (l − 1), l.

Characterization of 3D Tumor Shape by SH

After a trained expert (I.-F.T.) manually segmented the tumor region on each image of the MRI scan, these segmentations were saved as binary images. The segmented tumor was used as the 3D target to be approximated by SH. The marching cubes algorithm (8) was applied to the binary images to create a 3D triangulated mesh of the tumor’s surface.

To apply SH approximation to the tumor surface, a spherical parameterization of the surface was defined by mapping the tumor surface bijectively to the surface of the unit sphere by using the conformal mapping method described in (9,10). An anatomic surface was modeled as a thin elastic sheet. Regardless of the convoluted nature of such a surface or variations in its convexity and concavity, this method yielded a one-to-one mapping of the tumor surface to the sphere. The solution to two sparse linear systems of equations was obtained. We chose to map the two points farthest away from each other on the tumor surface to the two poles of the unit sphere. Intertumor registration was not required for our purposes.

After spherical mapping was completed, we associated each point on the segmented tumor surface with the spherical coordinates (θ, ϕ) of the point on the sphere to which it was mapped. These spherical coordinates were used in the final approximation by the SH method. Degree of approximation, L > 0, was selected, then corresponding SH functions were estimated. The latter were used to express the approximated surface S (θ, ϕ) as:

$$S(\theta ,\mathrm{\hspace{0.17em} }\varphi )=\sum _{l=0}^L\sum _{m=-l}^l{C}_l^m{Y}_l^m\left(\theta ,\mathrm{\hspace{0.17em} }\varphi \right)$$ (2)

where the coefficients C₁^m are 3D vectors because S(θ, ϕ) = (x(θ, ϕ), y(θ, ϕ), z(θ, ϕ))^T and were solved through least-squares optimization.

Shape Representation of SH Against SC

First, the reconstructed surface lying close to the SC in the same coordinate system was recut along the axial plane into discrete slices. A shape comparison between the SC and its corresponding contours from the recut SH surface was performed.

Subsequently, for each tumor, the shape representation of the SH method was assessed against SC contour-wise. The Euclidian distance between the corresponding points of the contours was computed within each 2D image, where the distance was defined as:

$$d(S_{SH},S_{SC})=\sqrt{{\left(X_{SH}-X_{SC}\right)}^2+{(Y_{SH}-Y_{SC})}^2}$$ (3)

To achieve point correspondences between contours, two steps were taken: First, all traced contours were interpolated and resampled using a smooth-curve fitting method (11) to obtain an equal number of points per contour. Second, these points were ordered along the contour. We further computed the standardized Euclidian distance (SED) by dividing by the corresponding area of S_SC.

Finally, because traditional distance-based metrics might be influenced by tumor volumes, the dice similarity coefficient (DSC) also was used as a validation metric of spatial shape representation. Denoting the area of S_SH by A_SH and the area of S_SC by A_SC, DSC is defined as:

$$D\left(S_{SH},S_{SC}\right)=\frac{2\left(A_{SH\cap SC}\right)}{A_{SH}+A_{SC}}$$ (4)

where A_SH∩SC is the area of the intersection of the SH and SC areas. DSC ranges from 0 to 1, indicating no overlap or complete overlap, respectively. A DSC of 70% was interpreted as satisfactory spatial overlap (12,13).

Statistical Methods

For each case, we derived the satisfactory degree L of the SH model by computing the mean square reconstruction error (MSRE; square millimeters), standardized by the corresponding 3D volume (Vol in cubic millimeters), yielding the standardized MSRE (SMSRE = MSRE/Vol in mm⁻¹) for each L ∈ {5, 10, 20, 30, 40}. We further showed the result of the SH approximation by increasing the degree in the SH model.

To validate the overall agreement of the SH method against SC, Spearman’s rank correlation coefficient ρ was calculated between the area of the derived SH contours and the area of the SC for each case. In addition, tumor-specific minimum, median, and maximum of the DSC values were summarized, along with those of the SEDs by their corresponding areas by SC. Box plots of DSC and distance measures were created.

Surface extraction and SH reconstruction codes were written in Matlab 6.1 (www.mathworks.com) and C language.

RESULTS

Tumor size range was 22413–85189 mm³. For cases in our study, range of number of vertices on the tumor surfaces was 3674–6544. SMSRE (mm⁻¹) are listed in Table 2 as functions of the SH approximation degree (L). We observed that SMSRE was less than 1.66 × 10⁻⁵ mm for L ≥ 30.

Table 2.

SMSRE using SH by Total Volume in an Increasing Degree of Approximation

		SMSRE by Volume (×10−4)(mm−1)
Case No.	Volume (mm3)	L = 5	L = 10	L = 20	L = 30	L = 40
1	22413	0.875	0.254	0.075	0.032	0.015
2	63955	0.972	0.415	0.221	0.166	0.139
3	85189	0.172	0.052	0.016	0.009	0.005
4	41263	0.253	0.095	0.029	0.015	0.008
5	37589	1.840	0.601	0.184	0.097	0.058

One representative slice for case 4 (left frontal oligodendroglioma) and its corresponding segmentation are shown in Figure 1a–b, respectively. Figure 2a shows the original SC used as the 3D target, whereas Figure 2b–d presents the reconstructed shapes for case 4 in increasing value for L (L = 5, L = 10, and L = 40, respectively). Based on these reconstructions and results listed in Table 2, subsequent analyses adopted L = 40, shown in Figure 2d, when applying the SH method for shape approximation.

Figure 1.

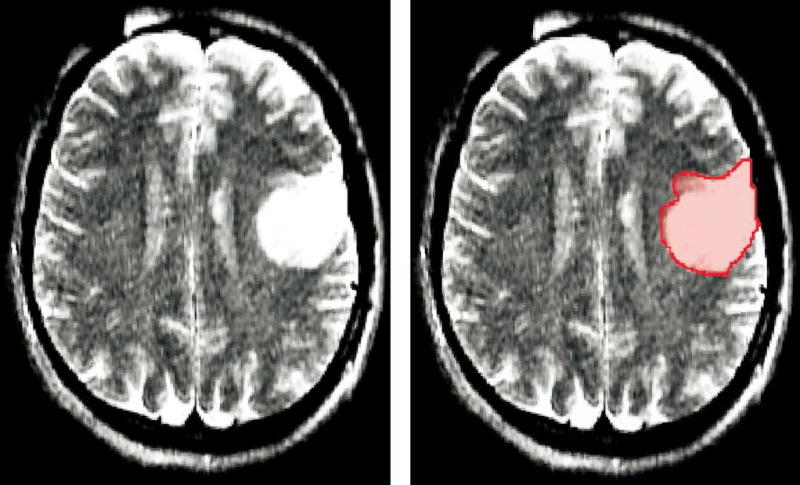
(a) One representative slice for case 4 tumor (left frontal oligodendroglioma) and (b) its corresponding segmentation.

Figure 2.

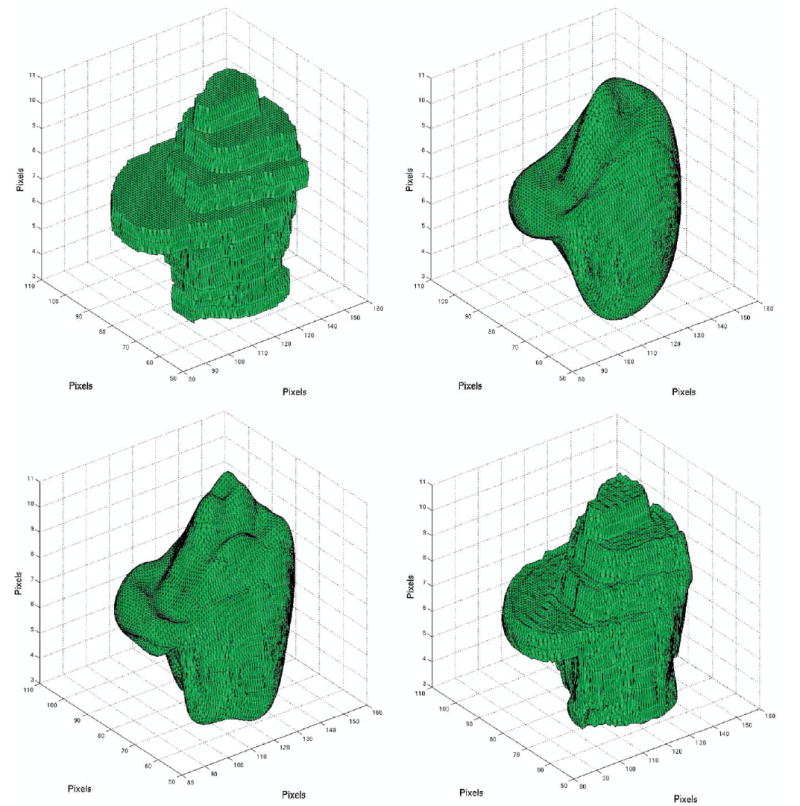
(a) Original segmented tumor (case 4) used as the 3D target for the SH approximation. The tumor’s 3D surfaces reconstructed by SH using varying degrees (L): (b) L = 5, (c) L = 10, (d) L = 40.

Nonparametric Spearman’s rank correlation coefficient ρ indicated a high correlation coefficient between the SH and SC, with perfect correlation other than that for case 2 (ρ ≥ 0.952). DSC values range was 0.890–0.990, with a pooled median DSC of 0.973, also suggesting high spatial similarity. All SEDs were ≤ 2.759 × 10⁻³ (Table 3).

Table 3.

Spearman’s Rank Correlation Coefficient of the Areas, DSC, and SED Between the SH-Approximated and SC

			DSC			SED (×10−3)
Case No.	No. of Contours	Spearman’s ρ	Minimum	Median	Maximum	Minimum	Median	Maximum
1	10	1.000	0.968	0.978	0.987	0.440	0.686	1.104
2	10	0.952	0.911	0.968	0.980	0.265	0.451	1.041
3	9	1.000	0.944	0.977	0.990	0.160	0.238	1.156
4	7	1.000	0.964	0.976	0.986	0.198	0.376	1.137
5	8	1.000	0.890	0.961	0.977	0.286	0.510	2.759
Pooled	44	0.998	0.890	0.973	0.990	0.160	0.456	2.759

Figure 3 shows a scatter plot of the areas derived by SH (on the x-axis) and SC (on the y-axis) for all 44 contours. Box plots of the DSC, which are close to 1, and the SED, which are negligible, also are shown for all cases.

Figure 3.

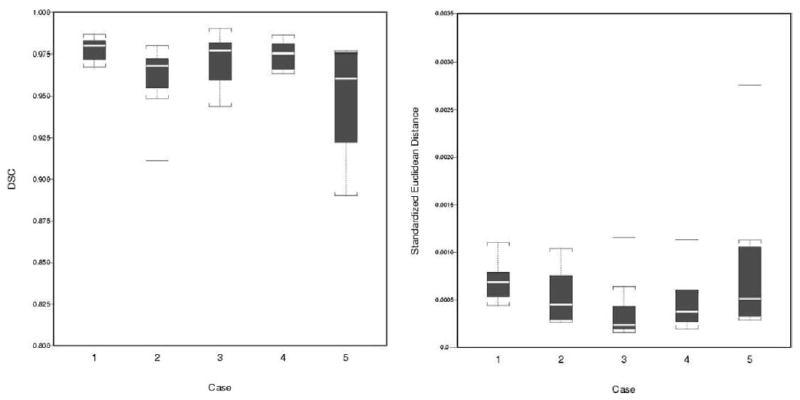
Box plots of agreement between the SH method and SC: (a) DSC and (b) SED by case. In each box, the center line represents the median for the respective sample. The 25% and 75% ordered percentiles (first and third quartiles) are the bottom and top edges. The difference is the interquartile range (IQR). Outliers are horizontal bars outside the boxes, defined as those beyond 1.5 times IQR from these two quartiles.

As an illustration, in Figure 4, we show the difference between SH and SC for the 7 contours belonging to case 4 at L = 40. The close approximation achieved can be visually verified.

Figure 4.

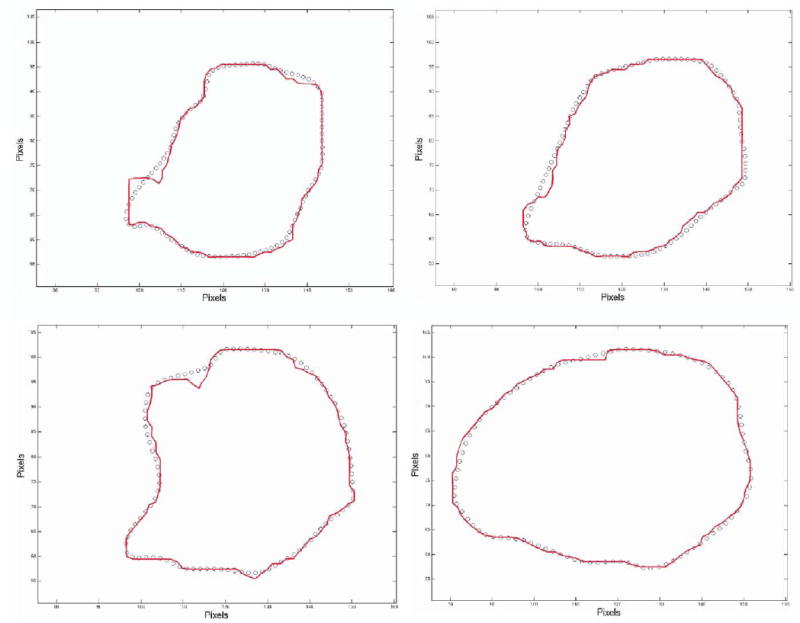
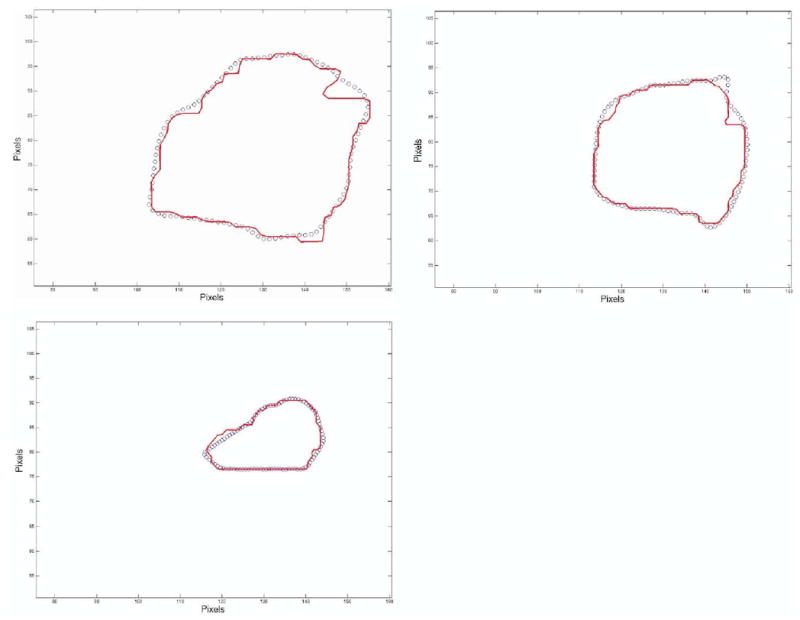
Contour comparison between segmented tumor case 4 (solid line) versus recut SH contours (circles).

DISCUSSION

In our present study, after a manual segmentation procedure for tumor identification, we investigated the potential use of SH for improving brain tumor shape approximation and 3D visualization for surgical planning and assessing tumor invasion. Satisfactory agreement between the SH and SC methods was observed, suggested by a high DSC, low SMSRE, and low SED.

However, we encountered case-to-case variability. For example, tumor shape approximation in case 2 appeared to be more difficult, mainly because of the perysilvian location of the lesion. Hence, tumor location and thus its shape may affect agreement between the two methods. For example, if cortical involvement is present, the lesion’s shape will follow that of the cortical surface. The resulting highly convoluted shape is more difficult to approximate by SH, even when a higher degree (L) is used.

In this retrospective study, we used intraoperative T2-weighted MR images obtained with an open midfield (0.5 T) interventional scanner. We found image quality to be sufficient for the purposes of the present study. Because one of our main goals is to implement the SH method for intraoperative visualization, use of intraoperative images appeared appropriate. Integrated intraoperative MRI systems show greater sensitivity in detecting intracranial tumors compared with direct visual inspection. In the future, SH visualization may serve as a convenient means for enhancing near–real-time lesion identification capabilities of these systems.

Because low-grade gliomas are intrinsically linked with white-matter fiber tracts, knowledge of their location and topographic relationship with the tumor is of paramount importance to avoid postoperative neurological deficits. Therefore, in the future, analyses to establish the optimal degree of approximation and correlate such shape representation with the underlying anatomic substrate (ie, white-matter fiber tract anatomy, described by diffusion tensor MRI) will be considered.

Finally, our method potentially could be useful for comparison of tumors with different histopathologic characteristics, but similar anatomic location and thus anatomic substrate, in an attempt to distinguish patterns of tumor invasion as they relate to biological tumor tissue characteristics. Given the increased need for multimodality imaging for surgical planning and intraoperative guidance, such approximation ultimately may be adapted to accommodate multimodal imaging data.