Abstract
Normalization of cDNA and oligonucleotide microarray data has become a standard procedure to offset non-biological differences between two samples for accurate identification of differentially expressed genes. Although there are many normalization techniques available, their ability to accurately remove systematic variation has not been sufficiently evaluated. In this study, we performed experimental validation of various normalization methods in order to assess their ability to accurately offset non-biological differences (systematic variation). The limitations of many existing normalization methods become apparent when there are unbalanced shifts in transcript levels. To overcome this limitation, we have proposed a novel normalization method that uses a matching algorithm for the distribution peaks of the expression log ratio. The robustness and effectiveness of this method was evaluated using both experimental and simulated data.
INTRODUCTION
The draw of gene expression profiling using microarray is in its ability to study complex interactions of thousands of genes simultaneously. Differential gene expression profiles can provide valuable insights into physiological processes or disease etiology that arise from coordinated action of sets of genes (1). Owing to the inherent noise and systematic variation present in such high-throughput experiments, accurate determination of differential gene expression requires normalization of microarray data. Normalization serves to offset non-biological differences such as dye bias, starting amount of mRNA, spotting or surface characteristics (2), so that the underlying biological variation can be accurately determined.
Normalization of microarray data involves two steps: (i) selection of genes to be used as normalization features and (ii) application of a mathematical operator or metric to calculate the normalization factor using the data from the selected genes. Gene selection can contain the entire gene set (global), housekeeping genes, rank-invariant genes or genes spotted with the same print-tip. Mathematical operators or metrics include expression-intensity mean/median, expression-ratio mean/median, mean/median logarithm expression-ratio, expression-ratio probability density and non-linear/piece-wise linear regression.
A basic assumption for global normalization is that first, the array contains a large enough assortment of random genes that a majority of the genes are not differentially expressed between any two samples (2) and second, the numbers of up- and down-regulated genes on the array are roughly equal. Thus, in situations where there are unbalanced or global shifts in the mRNA population, these global normalization strategies become inappropriate. Housekeeping genes were thought to be a useful guide for normalization owing to the general perception that expression levels of housekeeping genes remain constant even with large expression level changes in endogenous genes. However, many housekeeping genes have been reported to exhibit considerable variability under different experimental conditions (3) and their expression levels are often on the high side, making them unsuitable and unrepresentative of the whole expression intensity range. External spikes have been developed as a replacement for housekeeping genes (4). By controlling the amount of spiked mRNA, a set of genes can be made constant regardless of experimental condition. In this approach mRNA transcripts at different intensities are spiked in equal amounts into both samples hence creating a set of non-differentially expressed genes which are ideal as normalization features. This technique is however not widely used largely because of the extensive preparation work that is required to create this collection of genes.
Owing to possible occurrence of non-linearity in systematic variation, non-linear or piece-wise linear normalization protocols are normally preferred to constant normalization protocols (5–7). The most well-received method, LOWESS, provides a normalization factor by robust local regression of expression log ratio (M) against logarithmic mean expression intensity (A). LOWESS normalization with rank-invariant (5), global (6) or print-tip (6) genes has been proven a powerful non-linear normalization method. However, the limitation and robustness of LOWESS or other normalization methods to handle situations where there is an unbalanced or global shift in mRNA levels have never been systematically evaluated.
In this paper, we have presented a novel normalization technique named Cross-correlation normalization which is able to handle unbalanced shifts in mRNA levels of a large amount of genes. Using a set of spike-in validation data, Cross-correlation method has been compared against well-accepted normalization methods such global LOWESS, global Median, print-tip LOWESS and rank-invariant LOWESS. The ability to handle situations where there is an unbalanced or global shift in mRNA levels was also tested by using data from our mouse cell culture with glutamine deficient versus fully enriched media experiments as well as using yeast stationary versus exponential phase experiments (4). Furthermore, simulated microarray data were used to confirm the effectiveness of this normalization method. The advantage of our proposed normalization method over external controls lies in that it does not require extensive experimental preparation of external spikes nevertheless it delivers much more reliable normalization results compared with other well-accepted methods.
MATERIALS AND METHODS
Microarray setup
Microarray was printed using PCR products prepared from plasmid clones of the NIA 7.4 K clone set (8) plus other ∼400 mouse oligos. PCR products were generated as described in Tanaka et al. (8). The PCR products were purified using NucleoFast PCR purification kit from Macherey Nagel (Duren, Germany), concentrated by vacuum centrifugation and redissolved in printing buffer (1 M Betaine, 10% Glycerol, 50 mM NaPO4, pH 7.5) at a concentration of 100 ng/µl. The PCR products were spotted in duplicates on polylysine coated slides using a Virtek SDDC-3 (Bio-Rad Laboratories, CA) equipped with quill-type steel pins (Telechem, Sunnyvale, CA). Spots were printed at a nominal centre-to-centre spacing of 200 µm. Printed slides were baked at 80°C for 2 h and blocked in succinic anhydride and 1,2 dichloroethane as described by Diehl et al. (9). The number of the print-tips used was 48. Details of the array design can be found on http://www.ncbi.nlm.nih.gov/projects/geo/base platform GPL1961.
Spike-in microarray experiments
The spike-in experiment (10) was used for generating validation datasets by spiking in 200 transcripts to mRNA isolated from mouse hybridoma CRL1606 cells, in order to artificially generate a set of 100 up- and down-regulated genes. The spike-in was done at 11 different concentrations (ranging from 0 to 2 pmol for each gene) with three array replicates for each of 0.025, 0.15, 0.2, 1 and 2 pmol, and six array replicates for each of 0 (self-hybridization), 0.05, 0.1, 0.25, 0.5 and 0.75 pmol and the samples were hybridized onto the cDNA microarrays described above. For details refer to http://www.bii.a-star.edu.sg/microarray.
Glutamine deficient microarray experiments
Mouse hybridoma cell line CRL1606 was grown in serum-free enriched media (BITTE) containing all the essential nutrients and also in glutamine deficient media separately. The cells were maintained as suspension cultures in shaker flasks in a humidified incubator (95% relative humidity) at 37°C, 8% CO2. The viability of the culture was determined by trypan blue exclusion using an Improved Neubauer haemocytometer. When the viability of cells grown in glutamine deficient media reached ∼60%, 10–15 million cells were harvested by centrifugation from both the deficient media and the enriched media for mRNA isolation. This viability corresponds to 7 h after inoculation of the cells grown in glutamine deficient media. Three replicates with hybridization of cDNA generated from cells grown in glutamine deficient media were made including one dye swap. For the control, mRNA was pooled in equal amounts from the corresponding time points in the enriched media. The same in-house developed microarray chips as described above were used.
Cross-correlation normalization
Cross-correlation of one signal with a template is widely used for pattern recognition. Let the template be the distribution t(M) of normalized log ratio in a self-hybridization microarray experiment. Using this idea, we can match the distribution s(M,A) of the log ratio for all genes in an intensity interval (window) with the template. By varying the matching parameter m, the Cross-correlation of s(M,A) with t(M) can be maximized. The optimal matching parameter, which is the optimal m in maximizing the following objective
is assigned as the normalization factor k(A), where M1 and M2 are the lower and upper boundary of M.
In order to cope with non-linearity, all data points in a MA plot are first divided into n number of intensity windows based on their A values. In each (e.g. window i) of the n windows, s(M,Ai) and k(Ai) will then be calculated. The final normalization factor (curve) k(A) is obtained by fitting a spline function to all k(Ai) values.
Selection of templates for Cross-correlation normalization
As mentioned above, the template is the distribution t(M) of the normalized log ratio in a self-hybridization microarray experiment. In order to avoid any bias, the template should be symmetrical around the log ratio zero. Thus, the template should be the average of t(M) and t(−M). Since it is very likely that the span of log ratio in a sample–control experiment is different from that in a self-hybridization experiment [−Mm, Mm], a factor γ = (M2 − M1)/(2Mm) is required to make this two spans comparable. The actual template t*(M) used in the above equation should then be as follows:
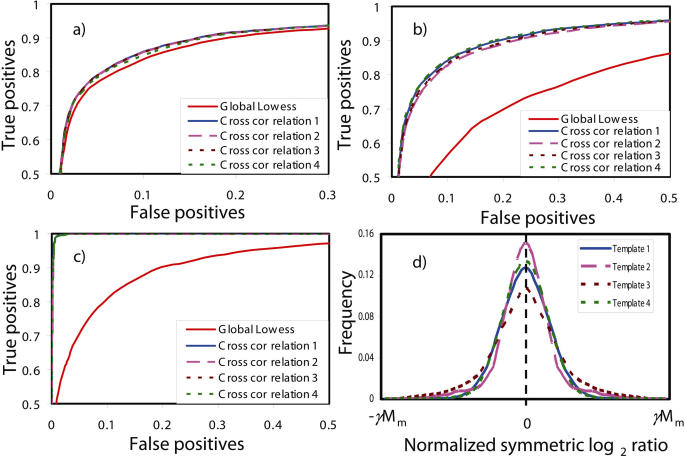
Ideally, the template should originate from a self-hybridization experiment of the same microarray platform. In reality, even the distribution of the normalized log ratio can differ from one replicate to another replicate. Thus, the performance of Cross-correlation normalization should be rather robust when using different templates. Figure 1 compares the performance of Cross-correlation normalization using four different templates. Template 1 is obtained from a simulated self-hybridization, Template 2 from simulated data with 10% down-regulated genes, Template 3 from a self-hybridization in the spike-in microarray experiment (discussed earlier) and Template 4 from a Gaussian distribution. It can be seen from Figure 1 that Cross-correlation normalization delivers consistent results when using different templates.
Figure 1.
Performance of Cross-correlation normalization using different templates: ROC curves of simulated data with a smaller shift in mRNA levels of (a) 10% and (b) 30% genes and with (c) a stronger shift of 30% genes and (d) distributions of different templates. Cross-correlation 1–4 means Cross-correlation normalization using Templates 1–4, respectively. Mm is the maximum value of normalized symmetric log2 ratio.
The modules for Cross-correlation normalization were implemented in Matlab. Along with the templates, these modules are available for download at http://www.bii.a-star.edu.sg/microarray.
Discovery of differentially expressed genes
For discovery of differentially expressed genes, a simple threshold rule was used. In the spike-in data, the median log ratio of a gene over the replicates was used for ranking the gene, while the log ratio of a gene was used to rank the gene in the simulated data.
RESULTS
Spike-in experiments
Different normalization methods (global LOWESS, global Median, print-tip LOWESS, rank-invariant LOWESS and Cross-correlation normalization) were compared using the spike-in validation data in which a set of 200 differentially expressed genes were artificially created (10).
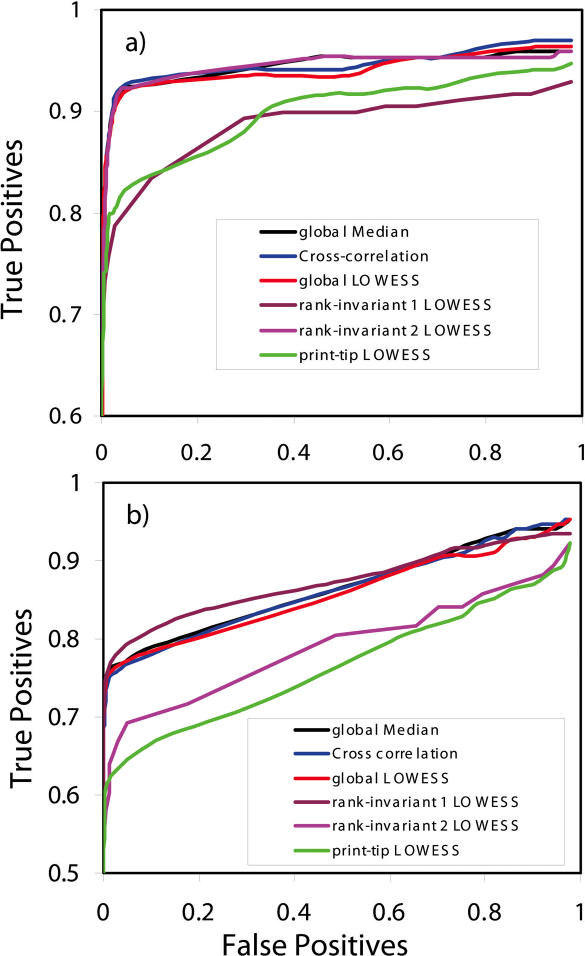
Figure 2 shows the ROC curves for the spike-in concentrations of 0.1 and 0.75 pmol. For these two concentrations six replicates were obtained. Although in this set of validation experiments, only a small percentage of the genes are differentially expressed and the differential expression is balanced, it is clear that some normalization methods give better results than the others. From this set of experiments, global LOWESS, Cross-correlation and global Median normalization methods consistently returned very good results. Print-tip LOWESS normalization, however, was surprisingly inconsistent. Print-tip LOWESS has been regarded as more effective than global LOWESS because of its ability to adjust for systematic differences between different print-tips (5,11). Our experimental results however show that correcting for this systematic variation may not always improve prediction errors. This is shown by Figure 2a and more obviously in Figure 2b where print-tip LOWESS normalization resulted in a much lower prediction rate. The inconsistency is likely because a smaller set of genes is used in normalization. In this microarray setup, 48 print-tips were used for spotting, resulting in approximately only 300 spots per print-tip. Also, global median normalization was able to give as good results as global LOWESS mainly because there is minimal non-linear correlation in the MA values in this set of experiments. The effectiveness of global LOWESS and Cross-correlation normalization over global Median is apparent when there is significant non-linearity between the M and A values. The performance of rank-invariant LOWESS is largely dependent on the criterion for selection of rank-invariant genes. In the spike-in concentration of 0.1 pmol (Figure 2a), the performance of rank-invariant LOWESS deteriorates as the number of rank-invariant genes becomes larger, while rank-invariant normalization delivers the opposite trend for the spike-in concentration of 0.75 pmol (Figure 2b), suggesting a possible robustness problem of this method when applied to two-color arrays.
Figure 2.
ROC curves of spike-in data with (a) 0.1 pmol spike-in concentration and (b) 0.75 pmol spike-in concentration. The following different normalization methods were compared: global LOWESS, global Median, print-tip LOWESS, rank-invariant LOWESS and Cross-correlation. Rank-invariant 1 or 2 means application of a looser or stricter criterion for selection of rank-invariant genes, respectively.
Glutamine deficient experiments
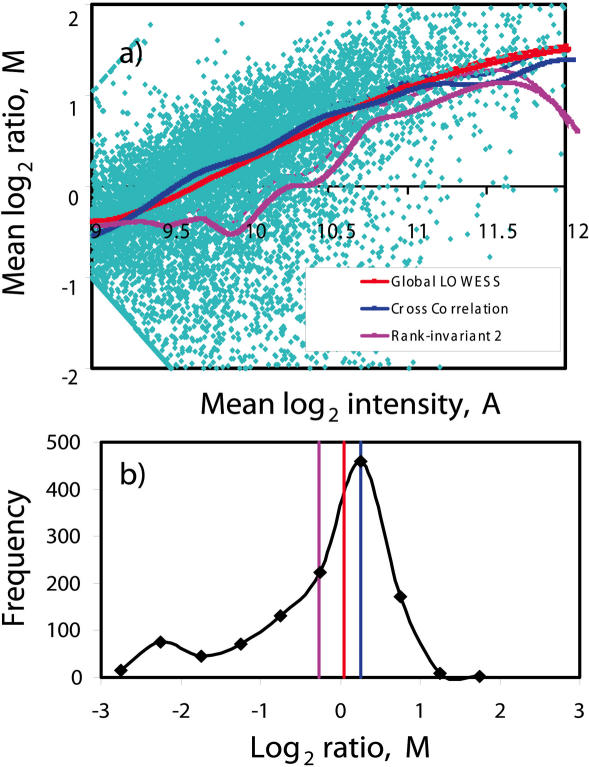
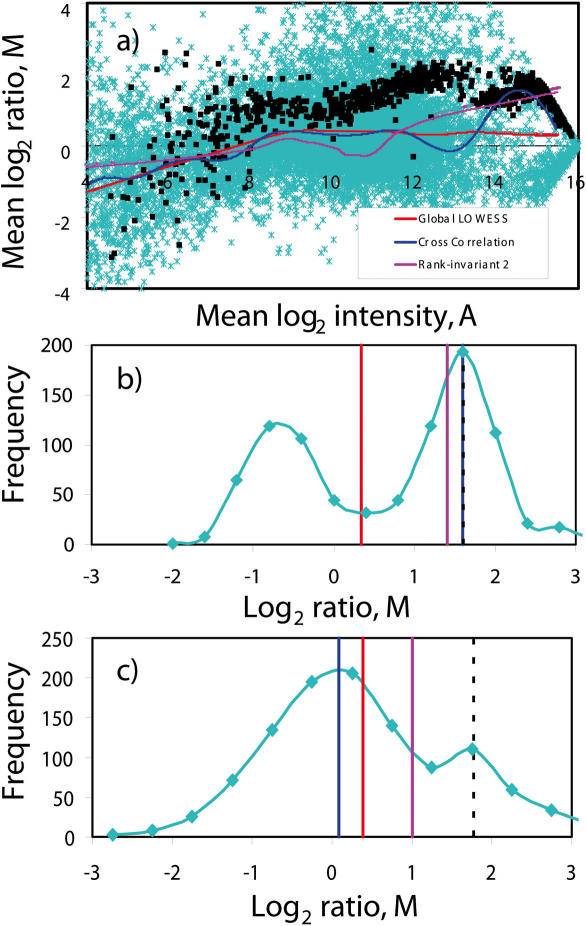
A typical MA plot for this set of experiments is depicted in Figure 3a. From the plot, it is clear that there is significant non-linearity in the data. As such, it is obvious from Figure 3a that normalizing with global Median will give inferior results. It is also observable that a significant proportion of genes were down-regulated when the cells were starved. Owing to this unbalanced shift in mRNA levels, there are differences in global LOWESS normalization and Cross-correlation normalization methods. This is especially observable in the intensity region of 9.6 ≤ A ≤ 9.8. This difference can be explained in Figure 3b which shows the M value histogram of the genes within this intensity interval. The difference in the normalization curves is due to a significant number of down-regulated genes in this intensity range resulting in a bimodal distribution as shown in Figure 3b. The Cross-correlation method is apparently more robust than LOWESS and Rank-invariant normalization as the normalization curve remains at the central mode of the distribution where the non-differentially expressed genes lie.
Figure 3.
(a) MA plot showing unbalanced changes in expression levels when mouse hybridoma CRL 1606 cells are grown in full medium versus glutamine deficiency. Results of LOWESS normalization and Cross-correlation normalization are shown. (b) Histogram of M value for spots within the intensity region of 9.6 ≤ A ≤ 9.8. The vertical red, blue and pink lines represent the respective global LOWESS, Cross-correlation and Rank-invariant normalization values. Rank-invariant 2 means application of a stricter criterion for selection of rank-invariant genes. Rank-invariant normalization with a looser criterion delivers similar results (not shown in the figure) as LOWESS.
Simulated data
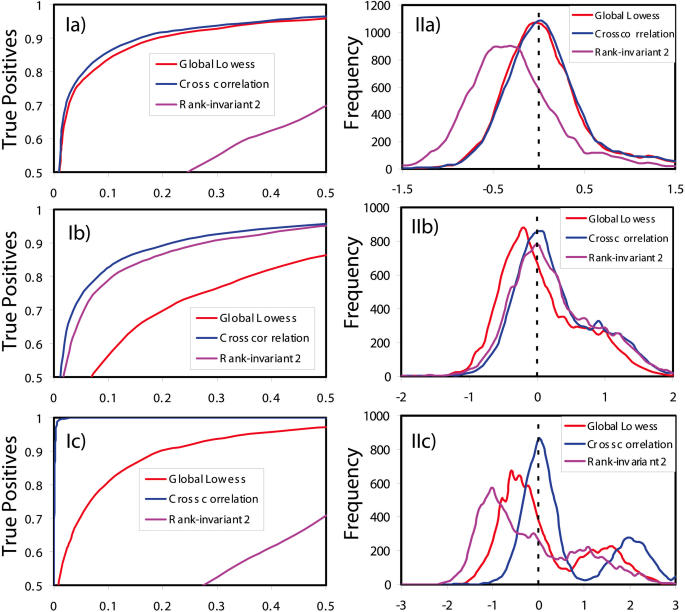
In order to confirm the robustness of Cross-correlation normalization, we compared Cross-correlation and global LOWESS normalization methods using simulated data. Applying the model from Rocke and Durbin (12), we simulated 10 000 data points including 10 and 30% of the data points down-regulated, respectively. Figure 4, Ia and Ib compares the ROC curves of global LOWESS, rank-invariant LOWESS and Cross-correlation normalization for shifts of 10 (smaller) and 30% (larger) of genes in similar mRNA levels. Better normalization should have the distribution peak of normalized log ratio closer to zero. The M value histogram shown in Figure 4, IIa and IIb depicts the normalized log ratio by the Cross-correlation method perfectly distributed around zero regardless of the number of unevenly shifted genes. Thus, in both cases, Cross-correlation normalization outperforms global LOWESS and rank-invariant normalization. With increasing mRNA levels for 30% shifted genes, the superiority of Cross-correlation normalization to other two methods is even more pronounced (Figure 4, Ic and IIc).
Figure 4.
Comparison of different normalization methods using (I) ROC curves and (II) distributions of normalized log ratio based on simulated data with the same shifts in mRNA levels of (a) smaller (10%) and (b) larger (30%) fractions of genes and with (c) a larger shift in mRNA levels of 30% genes. Rank-invariant 2 means application of a stricter criterion for selection of rank-invariant genes. Rank-invariant normalization with a looser criterion delivers similar results (not shown in the figure) as LOWESS.
Yeast stationary versus exponential growth phase
To further confirm the effectiveness of Cross-correlation normalization method and ascertain its limitations, experimental data with global changes in expression levels obtained from Peppel et al. (4) were used. In this study, total RNA were spiked as external controls over three orders of magnitude in intensity. These external controls were spiked to have no difference in fold change. As such, the effectiveness of normalization methods can be compared by how close it lies to these external spikes (Figure 5). Most significantly, Cross-correlation normalization was able to correctly identify down-regulated genes in the intensity region of 14 ≤ A ≤ 15. Figure 5b shows the M value histogram of the genes in the region of 14 ≤ A ≤ 15. In this region, a bimodal M value distribution is observed. LOWESS normalization interpolates between the two modes and returns a midway value. Cross-correlation normalization however, uses a peak matching algorithm to identify the larger of the two modes and normalize the data assuming that the larger mode consists of genes that are non-differentially expressed. Thus, the method is particularly useful when there is a significant shift in mRNA expression level that results in an unbalanced distribution of M value. Since the cross-correlation method assumes that the largest mode contains the non-differentially expressed genes and normalizes the data accordingly (see Materials and Methods), the smaller modes or unbalanced shifts have minimal effect on the normalization procedure unlike in other methods.
Figure 5.
(a) MA plot showing Cross-correlation and global LOWESS normalization of yeast data obtained from cells grown at stationary versus mid log phase from Peppel et al (4). External controls (dark dots) are used as a guide to benchmark normalization methods. Histograms of M value are depicted for spots within the intensity ranges of (b) 14 ≤ A ≤ 15 and (c) 12 ≤ A ≤ 13. The vertical dark (dashed), red, blue and pink lines in (b and c) represent the central of the external controls, the global LOWESS normalization value, the Cross-correlation normalization value and the Rank-invariant normalization value, respectively. Rank-invariant 2 means application of a stricter criterion for selection of rank-invariant genes. Rank-invariant normalization with a looser criterion delivers similar results (not shown in the figure) as LOWESS.
The obvious limitation, however, is that the method will not return the correct normalization value when non-differentially expressed genes do not form the largest mode. This is illustrated in the M value frequency density of the region 12 ≤ A ≤ 13 as shown in Figure 5c. The external spikes lie in the smaller mode, indicating that the correct normalization curve should pass through this value. However as expression of most genes was shifted to down-regulation, Cross-correlation normalization identifies the peak of down-regulated genes and returns a wrong normalization factor.
DISCUSSION
In order for a normalization method to be effective, some theoretical criteria should be obeyed. First, genes selected for normalization should be restricted to non-differentially expressed genes. Differentially expressed genes intrinsically possess three unknown variables (systematic, random and biological variations) whereas non-differentially expressed genes have only two (systematic and random). As the aim of normalization is to predict systematic variation, it is naturally easier to estimate this quantity using non-differentially expressed genes as two variables are confounded instead of three. Second, the normalization operator/metric should be effective in coping with random errors. Because of the nature of microarray experiments, predicting systematic variation inevitably requires appropriate handling of random noise. As such, the number of genes used for normalization should also be statistically representative (large). Normalization based on a small subset of all genes, such as traditional housekeeping genes, may lead to less accurate results. This is probably the reason that print-tip LOWESS and LOWESS with a small set of rank-invariant genes could be less effective compared with the rest of the normalization methods.
Normalization can be described as a catch 22 situation. This procedure requires selection of non-differentially expressed genes (equivalent to identification of differentially expressed genes), but identification of differentially expressed genes is in turn dependent on normalized data. This deadlock makes it difficult to identify all non-differentially expressed genes accurately. As such, global normalization still remains as one of the favorite gene selection methods. To compensate the inaccuracy in gene selection, the normalization operator/metric used should be robust against the effect of differentially expressed genes. The proposed novel normalization method (Cross-correlation normalization) uses peak matching to minimize the effects of differentially expressed genes located in the distribution tails. It has been shown to be highly robust against unbalanced shifts in mRNA levels and superior to existing normalization methods. It should however be noted that there are situations, albeit rare, in which >50% of the genes are differentially expressed. In these rare situations, the peak matching algorithm used by Cross-correlation normalization will yield inaccurate results. The only viable normalization procedure might be to use a large amount of external controls. It should be noted that the data presented in this paper were obtained from two-color (channel) arrays. Since the proposed normalization method is based on a MA plot which can also be produced with two single-channel arrays, this method can be successfully applied to normalization of single-channel arrays such as Affymetrix Genechips and Illumina Beadchips.
Acknowledgments
This work and the Open Access publication charges were generously funded by Agency for Science, Technology and Research, Singapore (A*Star). We thank Jessna Yeo, Angie Chang and Tan Kher Shing, Bioprocessing Technology Institute, for their excellent technical support.
Conflict of interest statement. None declared.
REFERENCES
- 1.Kerr M.K., Martin M., Churchill G.A. Analysis of variance for gene expression microarray data. J. Comput. Biol. 2000;7:819–837. doi: 10.1089/10665270050514954. [DOI] [PubMed] [Google Scholar]
- 2.Quackenbush J. Microarray data normalization and transformation. Nat. Genet. 2002;2:496–501. doi: 10.1038/ng1032. [DOI] [PubMed] [Google Scholar]
- 3.Lee P.D., Sladek R., Greenwood C.M., Hudson T.J. Control genes and variability: absence of ubiquitous reference transcripts in diverse mammalian expression studies. Genome Res. 2002;12:292–297. doi: 10.1101/gr.217802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Peppel J., Kemmeren P., Bakel H., Radonjic M., Leenen D., Holstege F. Monitoring global messenger RNA changes in externally controlled microarray experiments. EMBO Rep. 2003;4:387–393. doi: 10.1038/sj.embor.embor798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tseng G.C., Oh M.K., Rohlin L., Liao J.C., Wong W.H. Issues in cDNA microarray analysis: quality filtering, channel normalization, models of variations and assessment of gene effects. Nucleic Acids Res. 2001;29:2549–2557. doi: 10.1093/nar/29.12.2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yang Y.H., Dudoit S., Luu P., Lin D.M., Peng V., Ngai J., Speed T.P. Normalization for cDNA microarray data: a robust composite method addressing single and multiple slide systematic variation. Nucleic Acids Res. 2002;30:e15. doi: 10.1093/nar/30.4.e15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yang H., Haddad H., Tomas C., Alsaker K., Papoutsakis E.T. A segmental nearest neighbor normalization and gene identification method gives superior results for DNA-array analysis. Proc. Natl Acad. Sci. USA. 2003;100:1122–1127. doi: 10.1073/pnas.0237337100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tanaka T.S., Jaradat S.A., Lim M.K., Kargul G.J., Wang X., Grahovac M.J., Pantano S., Sano Y., Piao Y., Nagaraja R., et al. Genome-wide expression profiling of mid-gestation placenta and embryo using 15k mouse developmental cDNA microarray. Proc. Natl Acad. Sci. USA. 2000;97:9127–9132. doi: 10.1073/pnas.97.16.9127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Diehl F., Grahlmann S., Beier M., Hoheisel J.D. Manufacturing DNA microarrays of high spot homogeneity and reduced background signal. Nucleic Acids Res. 2001;29:e38. doi: 10.1093/nar/29.7.e38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang H. On the search of better validation and statistical methods in microarray data analysis. In: Bajic V.B., Tan T.W., editors. Information Processing and Living Systems. London: Imperial College Press; 2005. pp. 729–740. [Google Scholar]
- 11.Park T., Yi S.G., Kang S.H., Lee S.Y., Lee Y.S., Simon R. Evaluation of normalization methods for microarray data. BMC Bioinformatics. 2003;4:33. doi: 10.1186/1471-2105-4-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rocke D.M., Durbin B. A model for measurement error for gene expression arrays. J. Comput. Biol. 2001;8:557–569. doi: 10.1089/106652701753307485. [DOI] [PubMed] [Google Scholar]