Dynamic matrix composition in engineered cartilage with stochastic supplementation of growth factors

Abstract

Dynamic extracellular matrix (ECM) synthesis is explored in a hypothesized engineered cartilage construct. Growth (α) and decay (β) rate parameters are developed from a previous engineered cartilage model. The presented mathematical model was constructed from the parameterized experimental data using a deterministic and stochastic examination of ECM synthesis based on a negative feedback control mechanism. A growth factor supplementation is incorporated in a probabilistic mathematical approach. The growth factor component modified an initial deterministic model through a Gaussian white noise fluctuation. As the primary constituents of ECM, the mathematical tool is intended to characterize the probable steady state distribution of glycosaminoglycan (GAG) and collagen molecules as well as mean mass accumulation at homeostasis. Computer simulation of the models is applied to reported data from four similar chondrocyte-polymer construct culture systems. The range in rate ratios reflect the differing nature of GAG and collagen synthesis (α_GAG/β_GAG = 4.2 to 148.6; α_collagen/β_collagen = 8.1 to 2590.4). This technique reduced the influencing synthesis factors to a few key descriptive parameters. Additional anabolic and catabolic factors may further be built into the models.

Introduction

Functional characteristics of articular cartilage involve the response of active load bearing (compressive and shear forces) within diarthrodial joints. Damage to the articulating surface can occur due to adverse mechanical and biological perturbations. Despite being a living tissue it has a limited capacity for healing. Damage to the articular surface may spread, resulting in pain and loss of joint movement. With minimal regenerative potential, degenerative damage can lead to osteoarthritis. This joint disease is the most common form of arthritis in Australia where 5 to 10% of the total population is affected.¹ In the United States, more than one million people require treatment per year for damaged articular cartilage.²

Native articular cartilage is a composite of cartilage cells (chondrocytes), extracellular matrix (ECM), and water. The three main biomolecular components of ECM are structural proteins, specialized proteins, and proteoglycans. Structural proteins consist of type II collagen and elastin, specialized proteins consist of fibrillin, fibronectin, and laminin, and lastly, proteoglycans are core proteins to which are attached long chains of repeating disaccharide units known as glycosaminoglycans (GAG). The mechanical behaviour of cartilage is strongly influenced by constituent content and the electrostatic forces between matrix charge groups.³ Quantifying collagen and GAG content over time provides an indicator of the state of ECM and the chondrocyte regenerative or degenerative potential.

Existing techniques to repair damaged articular cartilage with autograft/allograft transplants have had limited success. Tissue engineered cartilage offers a possible alternative. Cartilage tissue engineering typically utilizes the seeding of chondrogenic cells into biodegradable polymeric scaffolds.^4–8 In this arrangement, ECM concentration in cell-polymer constructs is designed to gradually increase and form neo-tissue while scaffold concentration decreases with time.⁹ However, the role of ECM in maintaining and modulating cell function is not fully understood although recent reports have described the role of receptor molecules such as integrins in regulating chondrocytes.^10–11

A relatively strong negative correlation has been observed between GAG molecule deposition within ECM and its synthesis rate in the study of native¹² and engineered⁴ cartilage. This result is consistent with that reported from in vitro modulation of chondrocyte metabolism by extracellular proteoglycan.¹³ Based on this product inhibition mechanism, a mathematical formulation for GAG deposition was described by Hascall et al.^12,14 and adapted for use in cartilage tissue engineering by Wilson et al.⁹ for a characterization of ECM mass or concentration:

$$\frac{d(ECM)}{dt}=k_{ECM}\left\{{(ECM)}_{SS}-(ECM)\right\}$$ (1)

where k_ECM is an ECM synthesis rate constant and the steady-state (ss) condition occurs at t → ∞ and d(ECM)/dt = 0. Thus ECM mass or concentration as a function of time follows the form:

$${(ECM)}_t={(ECM)}_{SS}\left[1-e^{-k_{ECM}t}\right].$$ (2)

Degradation of scaffold mass or concentration is also assumed to follow a first order decay equation:⁹

$$\frac{d(scaffold)}{dt}=-k_S(scaffold)$$ (3)

where k_s is the scaffold decay rate constant. Again, this implies at time-dependent characterization as:

$${(scaffold)}_t={(scaffold)}_{initial}{e}^{-k_{S}t}.$$ (4)

By combining the mathematical formulations (2) and (4), along with the cellular mass content, a total construct mass model is proposed and experimentally validated as a function of culture time.⁹ In the above approach, dependencies between chondrocyte function and ECM molecule production rates as well as the effect of local biomechanical or biochemical factors are not explicitly taken into account.

It is well established that growth factors and cytokines modulate cell function and cartilage development.^15–18 The effects depend on specific combinations of factors, time sequences of their application, and interactions with the mechanical environment (hydrodynamic shear and compression). It has been observed experimentally by several investigators that growth factors play an important role in matrix production and inhibition, but there is limited knowledge about the functional mechanisms associated with these effects.^16–22 This leads to the present objective which is to explore the influence of growth factors within engineered cartilage by modelling hypothetical characteristics of ECM synthesis.

In previous approaches, we presented predictive models which examined deterministic and stochastic mechanisms of engineered cartilage composition. These works examined cellular proliferation effects,²³ a randomised influence of growth factors on synthesis rate,²⁴ a deterministic approach with exponential synthesis terms,²⁵ and a randomised influence of growth factors limited by a carrying capacity parameter with an initial growth factor state.²⁵ Here, dynamic compositional models are again formulated albeit with concomitant growth and decay rate terms. These modelling iterations investigate possible influences in the modulation of ECM synthesis which could be manipulated to enhance the regenerative potential in cartilage therapies. Therefore, the specific aims of this study are to: a) develop a deterministic mathematical model based on published experimental results that describe the accumulation of matrix molecules using distinct rate terms; b) quantify a ‘growth factor effect’ on matrix molecule deposition through a stochastic influence on the synthesis rate term. Both of these modelling approaches are based on current cell-polymer constructs developed for tissue engineered cartilage.

Methods and materials

Deterministic control model

An alternative deterministic model is presented to describe the accumulation of ECM molecules in a cell-polymer construct based on a negative feedback control mechanism. This approach applies distinct growth and decay rate terms originally reported for GAG molecules.^4,13 Here, the model is introduced to describe ECM mass or concentration:

$$\frac{d(ECM)}{dt}=\frac{{\alpha }_0}{1+(ECM)}-{\beta }_0(ECM)$$ (5)

where α₀ and β₀ are, respectively, the natural growth and decay rates of ECM molecules in a cell-polymer construct. The first term in equation (5) incorporates the feedback mechanism for the system. During variable manipulation, ECM is replaced by X and restated as:

$$\frac{dX}{dt}=\frac{{\alpha }_0}{1+X}-{\beta }_{0}X$$ (6)

of which the general solution is:

$$\frac{{(Z+\Omega )}^{\frac{1}{2}-\Omega }}{{(Z-\Omega )}^{\frac{1}{2}+\Omega }}=C{e}^{2\Omega {\beta }_{0}t}$$ (7)

where:

$$Z=X+\frac{1}{2}\mathrm{\hspace{0.17em} }\text{and\hspace{0.28em}}\Omega =\sqrt{\frac{{\alpha }_0}{{\beta }_0}+\frac{1}{4}}.$$ (8)

At the initial condition, t = 0, when chondrocytes are seeded into a polymeric scaffold, the ECM concentration is zero and:

$$C=2^{2\Omega }\frac{{(1+2\Omega )}^{\frac{1}{2}-\Omega }}{{(1-2\Omega )}^{\frac{1}{2}+\Omega }}.$$ (9)

In the steady state condition (t → ∞), Z → Ω and:

$$X\to X_{SS}=-\frac{1}{2}+\sqrt{\frac{{\alpha }_0}{{\beta }_0}+\frac{1}{4}}$$ (10)

By assuming that both GAG and collagen molecules follow the same growth kinetics within ECM, the Deterministic Control Model describes steady state (ss) content:

$$GA{G}_{SS}^{control}=-\frac{1}{2}+\sqrt{\frac{{\alpha }_{GAG}}{{\beta }_{GAG}}+\frac{1}{4}}$$ (11)

where, α_GAG and β_GAG are the natural growth and decay rates, respectively, of GAG molecules and:

$$collage{n}_{SS}^{control}=-\frac{1}{2}+\sqrt{\frac{{\alpha }_{collagen}}{{\beta }_{collagen}}+\frac{1}{4}}$$ (12)

where, α_collagen and β_collagen are the natural growth and decay rates, respectively, of collagen molecules. By combining equations (11), (12), scaffold degradation of (4), and the cellular mass content, $M_{SS}^{cell}$, the mean mass of the total engineered cartilage construct, $M_{SS}^{control}$, in the steady state can then be described:

$$\begin{array}{l}{M}_{SS}^{control}=M_{ss}^{cell}+\left(-\frac{1}{2}+\sqrt{\frac{{\alpha }_{GAG}}{{\beta }_{GAG}}+\frac{1}{4}}\right)+\\ \left(-\frac{1}{2}+\sqrt{\frac{{\alpha }_{collagen}}{{\beta }_{collagen}}+\frac{1}{4}}\right)+\underset{t\to \infty }{lim}{(scaffold)}_{initial}{e}^{-k_{S}t}\end{array}$$ (13)

Stochastic growth hormone treated model

ECM molecule dynamics are further explored through the inclusion of hypothetical growth factor effects. As the functional characteristics of the growth factors are not exactly known, their influence is treated here as random fluctuations. This influence is incorporated into the modelled system as Gaussian white noise. The presence of growth factor is assumed to manipulate the growth rate constant such that:

$$\frac{d(ECM)}{dt}=\frac{{\alpha }_0+{\rho }_0\xi (t)}{1+(ECM)}-{\beta }_0(ECM)$$ (14)

where, ρ₀ξ(t) is the time-dependent, randomised contribution to the synthesis rate. Equation (14) can be rewritten as:

$$\begin{array}{l}d(ECM)=\left\{\frac{{\alpha }_0}{1+(ECM)}-{\beta }_0(ECM)\right\}dt+\\ \frac{{\rho }_0}{1+(ECM)}\xi (t)dt\end{array}$$ (15)

where the random noise function, ξ(t), has the following mean and covariance conditions:

$$\begin{array}{l}E[\xi (t)]=0\\ Cov[\xi (t),\xi (s)]=\delta (t-s)\end{array}$$ (16)

A replacement term can be utilized, based on the interpretation of the integral of ξ(t) :^26–27

$$dW(t)=W(t+dt)-W(t)=\xi (t)dt$$ (17)

and dW (t) ~ N(0, dt)

where N(μ, σ) is a normal distribution with mean, μ, and standard deviation, σ. Equation (15) then becomes:

$$\begin{array}{l}d(ECM)=\left\{\frac{{\alpha }_0}{1+(ECM)}-{\beta }_0(ECM)\right\}dt+\\ \frac{{\rho }_0}{1+(ECM)}dW(t)\end{array}$$ (18)

The corresponding Fokker-Planck equation can be applied with the intent of describing the probabilistic distribution of the matrix molecules:^26–28

$$\begin{array}{l}\frac{\partial P(ECM,t)}{\partial t}=-\frac{\partial }{\partial (ECM)}\\ \left[\left\{\frac{{\alpha }_0}{1+(ECM)}-{\beta }_0(ECM)\right\}P(ECM,t)\right]+\\ \frac{1}{2}\frac{{\partial }^2}{\partial {(ECM)}^2}\left[{\left\{\frac{{\rho }_0}{1+(ECM)}\right\}}^{2}P(ECM,t)\right]\end{array}$$ (19)

where, P(ECM ,t) is the probability density function (PDF) of ECM deposition at time t. In the steady state, as t → ∞ and d(ECM)/dt = 0, the PDF of P(ECM, ∞) or P_∞(ECM) satisfies:

$$\begin{array}{l}\frac{d^2}{d{(ECM)}^2}\left[{\left\{\frac{{\rho }_0}{1+(ECM)}\right\}}^2{P}_{\infty }(ECM)\right]-\\ 2\frac{d}{d(ECM)}\left[\left\{\frac{{\alpha }_0}{1+(ECM)}-{\beta }_0(ECM)\right\}{P}_{\infty }(ECM)\right]=0\end{array}$$ (20)

Therefore, the steady state PDF of ECM deposition, P_ss(ECM) , is proportional to:

$$\begin{array}{l}{(1+ECM)}^2\text{exp}[\frac{(ECM)}{{\rho }_0^2}\{2{\alpha }_0+({\alpha }_0-{\beta }_0)(ECM)-\\ \frac{4{\beta }_0}{3}{(ECM)}^2-\frac{{\beta }_0}{2}{(ECM)}^3\}]\end{array}$$ (21)

and thus,

$$\begin{array}{l}{P}_{SS}(ECM)=C_0{(1+ECM)}^2\\ e^{\frac{(ECM)}{{\rho }_0^2}\left\{2{\alpha }_0+({\alpha }_0-{\beta }_0)(ECM)-\frac{4{\beta }_0}{3}{(ECM)}^2-\frac{{\beta }_0}{2}{(ECM)}^3\right\}}\end{array}$$ (22)

where the constant of proportionality,C₀, can be obtained by solving:

$$\underset{-\infty }{\overset{+\infty }{\int }}{P}_{SS}(ECM)d(ECM)=1$$ (23)

Thus, equation (22) represents the generalized PDF for the matrix molecules. The steady state PDF for the primary ECM molecules are assumed to be independent of each other and controlled by their own growth and decay rates.

Thus the PDF of GAG molecule deposition is given by:

$$\begin{array}{l}{P}_{\infty }(GAG)=C_{GAG}{(1+GAG)}^2\\ e^{\frac{GAG}{{\rho }_{GAG}^2}\left\{2{\alpha }_{GAG}+({\alpha }_{GAG}-{\beta }_{GAG})(GAG)-\frac{4{\beta }_{GAG}}{3}{(GAG)}^2-\frac{{\beta }_{GAG}}{2}{(GAG)}^3\right\}}\end{array}$$ (24)

and the PDF for collagen molecule deposition:

$$\begin{array}{l}{P}_{\infty }(collagen)=C_{collagen}{(1+collagen)}^2\\ e^{\frac{collagen}{{\rho }_{collagen}^2}\left\{2{\alpha }_{collagen}+({\alpha }_{collagen}-{\beta }_{collagen})(collagen)-\frac{4{\beta }_{collagen}}{3}{(collagen)}^2-\frac{{\beta }_{collagen}}{2}{(collagen)}^3\right\}}\end{array}$$ (25)

For the overall mass of the engineered construct, it is assumed that growth factor stimulation and accumulated ECM have no effect on scaffold degradation. The scaffold concentration follows a simple first order decay.⁹ It is also assumed that cellular mass, $M_{SS}^{cell}$, reaches a constant level after proliferating to a concentration level specific to the culture environment.²⁹ Here, this cellular concentration is assumed to be independent of the growth factor-influenced ECM synthesis rates. The mean total engineered cartilage construct mass in the steady state, $M_{SS}^{treated}$, can thus be described as:

$$\begin{array}{l}{M}_{SS}^{treated}=M_{SS}^{cell}+\underset{-\infty }{\overset{+\infty }{\int }}(GAG)P_{\infty }(GAG)d(GAG)+\\ \underset{-\infty }{\overset{+\infty }{\int }}(collagen)P_{\infty }(collagen)d(collagen)+\underset{t\to \infty }{lim}{(scaffold)}_{initial}{e}^{-k_{S}t}\end{array}$$ (26)

where the integral terms define the ECM mass associated with mean distribution, ${\overline{P}}_{\infty }(ECM)$.

Computational analysis

Application of the Deterministic Control Model and the Stochastic Treated Model require quantified parameters which characterize engineered cartilage content. Reports of direct and indirect assays for cell, ECM, and scaffold content through periods of culture are available for parameterization.⁹ In addition, the intrinsic synthesis rate, k, or one over the characteristic time constant, τ, as defined in the initial model,⁹ is applied here as a second equation to determine the two unknown rates of growth and decay for model input:

$$k=\frac{1}{\tau }={\alpha }_0-{\beta }_0$$ (27)

Thus, the steady state values of ECM molecules, GAG_ss and collagen_ss, as well as the characteristic time constants which have been previously determined from experimental data are incorporated into the presented models.^9,29–31 Solutions from equations (11) and (12) combined with relationship (27) defined the rate parameters for each biomolecule: α_GAG, β_GAG, α_collagen, and β_collagen (Table 1). Representative experimentally derived characteristic time constants and kinetic rates of scaffold degradation have been included for comparison (Table 2). All variable manipulation and computational analysis were completed on commercially available software (MathCAD v12, Mathsoft Engineering and Education, Inc., Cambridge, MA).

Table 1.

Representative ECM synthesis parameters previously derived from a cartilage tissue engineering model applied to published experimental data.⁹ Growth (α) and decay (β) rates are further extracted in this work from the Deterministic Control Model. Note: PGA = polyglycolic acid scaffold; BAC = bovine articular cartilage;τ_ECM = matrix molecule characteristic time constants; dw = dry weight; ww = wet weight.

							Growth (α), Decay (β) Rates
Scaffold	Cell type	Ref	GAGss	τGAG	Collagenss	τcollagen	αGAG βGAG	αcollagen βcollagen
PGA	BAC	29	6.8% ww	31.3 days	3.7% ww	15.9 days	3.256 x 10−2 6.139 x 10−4	6.672 x 10−2 3.837 x 10−3
PGA	BAC	30	11.7% dw	18.6 days	50.4% dw	131.5 days	5.441 x 10−2 3.662 x 10−4	7.607 x 10−3 2.937 x 10−6
PGA	BAC	9	6.1% dw	187.0 days	6.5% dw	18.9 days	5.474 x 10−3 1.264 x 10−4	5.400 x 10−2 1.108 x 10−3
PGA	BAC	31	1.6% ww	22.2 days	2.4% ww	16.7 days	5.900 x 10−2 1.400 x 10−2	6.800 x 10−2 8.363 x 10−3

Table 2.

Representative polymeric scaffold degradation parameters derived from a previous cartilage tissue engineering model applied to published experimental data.⁹ Note: τ_Scaffold = scaffold degradation characteristic time constant.

Scaffold material	Initial scaffold porosity	Reference	τScaffold	Scaffold decay rate
PGA	97%	32	56.1 days	1.70 x 10−2
PGA	97%	29	24.3 days	4.11 x 10−2

Results

The specific aims of this work were satisfied through t h e formulation and application of two mathematical models characterizing ECM synthesis within generalized engineered cartilage constructs. Previously parameterized data from four published reports were used to define the growth and decay rates for application in the current models (Table 1). The computer simulations using the Deterministic Control Model reflect the variety of GAG and collagen accumulation growth patterns found in engineered cartilage studies (Figure 1). The curves describe matrix molecule synthesis based on the numerical analysis of experimentally observed engineered cartilage steady state values and intrinsic growth rates as input. The resulting curves were not ‘fitted’ to the previous data but utilize parameters previously defined from that data. The mathematical model was based on two input variables and therefore does not consider the multitude of constituent interactions within ECM which may or may not account for differences between constituents.

Figure 1.

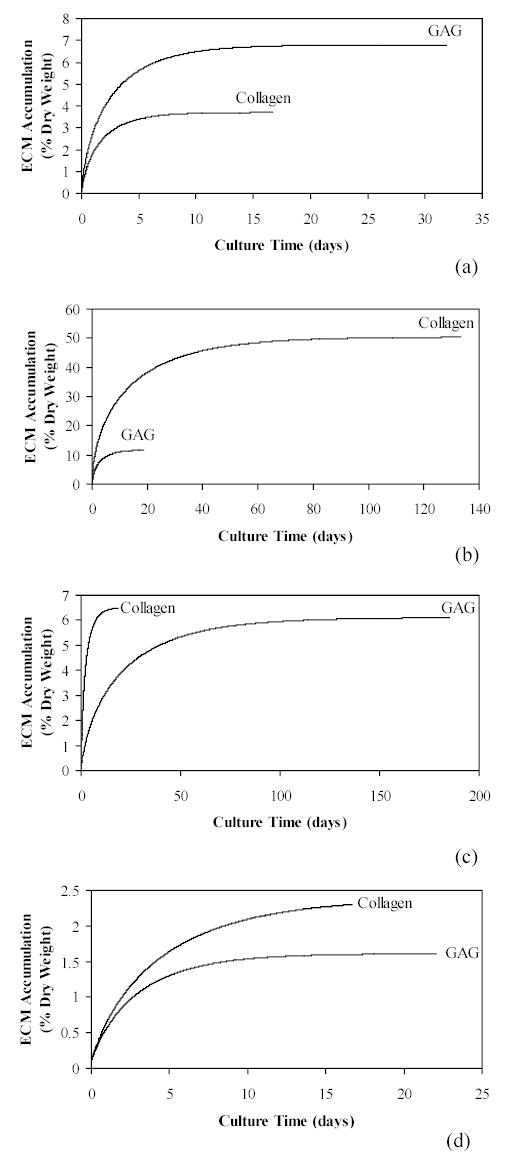
Simulated time-dependent ECM accumulation leading to steady state levels using the Deterministic Control Model, equations (7) through (12). Input parameter values were chosen from reported cartilage engineering experimental data (Table 1): a) Freed et al.²⁹; b) Vunjak-Novakovic et al.³⁰; c) Wilson et al.⁹; and d) Vunjak-Novakovic et al.³¹.

The Stochastic Growth Hormone Treated Model resulted in distribution frequencies of ECM accumulation based on the PDF for each molecule. The randomised growth hormone affect on synthesis rate again produced a variety of accumulation patterns (Figure 2). These distribution patterns for each of the four studies describe probabilistic accumulation as influenced from a single initial relative growth hormone level (ρ_GAG = ρ_collagen = 2.0). Again, the model does not account for a myriad of possible influences in accumulation which could be causing the dramatic differences between GAG and collagen content. Finally, mean steady state accumulations were compared between Control and Treated Models as simulated for both GAG and collagen (Figure 3). Although the expected increase in accumulation due to a stimulated growth rate is apparent, the diverse effect within the four sets of parameters is noticeable.

Figure 2.

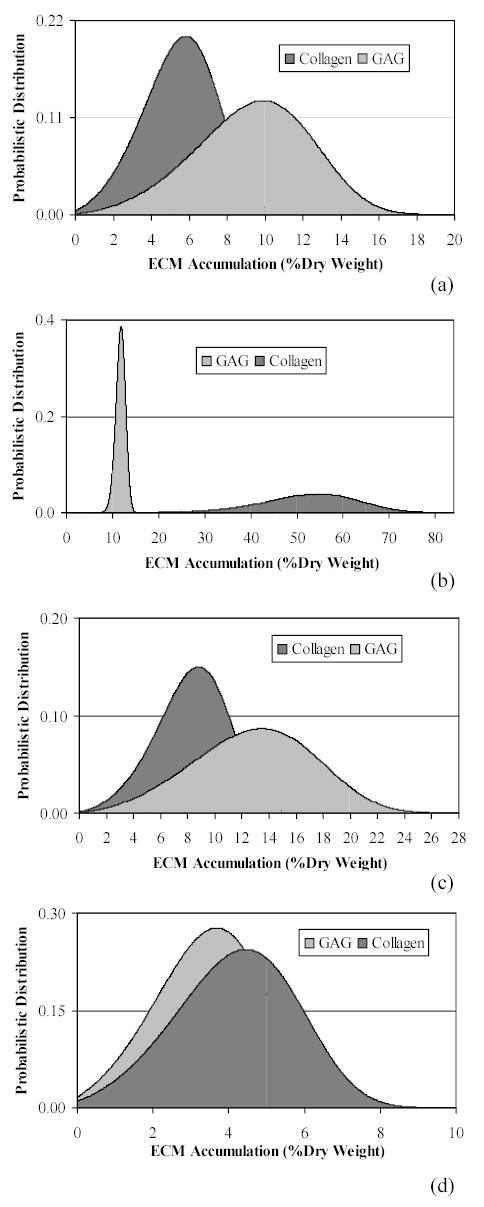
Distribution plots produced from the Probability Density Function describing mean ECM accumulation at the steady state condition for each of the modelled constituents, equations (24) and (25). Here, the growth and density rates for both GAG and collagen were incorporated from representative published cartilage engineering experiments (Table 1): a) Freed et al.²⁹; b) Vunjak – Novakovic et al.³⁰; c) Wilson et al.⁹; and d) Vunjak - Novakovic et al.³¹. For all distributions, the relative growth factor effect is the same, ρ_GAG = ρ_collagen = 2.0.

Figure 3.

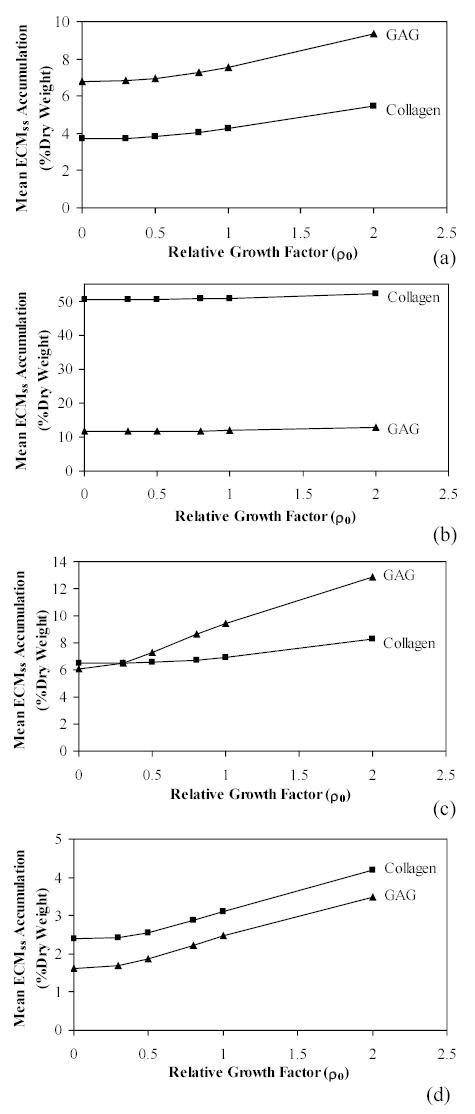
A comparison of the mean steady state ECM accumulation with supplemented growth factor effects. Steady state values of growth factor-influenced accumulation are calculated from the means of the probability functions, ${\overline{P}}_{\infty }(ECM)$, applied to equations (24) and (25) and shown for each constituent in equation (26). ECM growth and density rates were incorporated from representative published cartilage engineering experiments (Table 1): A) Freed et al.²⁹; B) Vunjak-Novakovic et al.³⁰; C) Wilson et al.⁹; and D) Vunjak-Novakovic et al.³¹. For each ECM constituent, mean accumulation values are determined at distinct relative growth factor levels within the Stochastic Treated Model, ρ_GAG = ρ_collagen = 0.3, 0.5, 0.8, 1.0, and 2.0. Accumulation at ρ₀ = 0 represents the mean steady state level from the Deterministic Control Model.

Discussion

In this work, generalized mathematical models of cartilage matrix molecule accumulation in engineered cell-polymer constructs have been constructed based on parameters derived from previous experimental results. The models incorporated a product inhibition mechanism via a negative feedback control network where the rate of synthesis decreases during matrix production.

The presented models provide an analytical tool from which to identify synthesis-influencing variables and parametrically compare empirical data. A new technique is formulated to explicitly determine growth and decay rates of matrix molecules at the steady state condition. In the deterministic model, these two rate parameters characterize the time-dependency of growth leading to the steady state condition. The generalized mathematical model is further studied in an environment where growth factors hypothetically influence the dynamics of matrix molecule accumulation within the cell-polymer construct. The biophysical knowledge of growth factors in cell-polymer constructs is generally insufficient for full analytical prediction. Researchers are investigating the modulatory mechanisms of these growth factors through computational³³ and experimental³⁴ efforts to define explicit physical laws. The presented approach represents a modelling continuation which explores ECM synthesis through deterministic descriptions and stochastic fluctuations within the system dynamics in order to identify the action potentials of anabolic and catabolic factors within the engineered constructs.^23–25 In each of the previous models, published data describing ECM was used to construct models which, in turn attempted to characterize the results based on: cellular proliferation effects,²³ deterministic steady state boundaries,²⁵ and stochastic contributions of growth factors on mathematical synthesis terms.^24,25

The presented deterministic model is again built from parameters defined by cultured experimental constructs. The stochastic modification proposes that the ‘growth factor effect’ acts only on the growth rates of the ECM molecules as distinguished from a decay rate. As a basis for comparison with other growth factor studies, the model shows that an increase in the relative level of growth factor will create more random fluctuations within the system and thus the overall (mean) production of a matrix molecule will be higher. This result is similar to what has been observed experimentally by several researchers describing anabolic manipulation.^{10,18,35–37} These investigations reported on positive response in synthesis due to sequential application of various factors. Specifically, recombinant osteogenic protein-1 (OP-1), also known as bone morphogenetic protein-7 (BMP-7), stimulates ECM production. It has been reported that type II collagen and proteoglycan synthesis increases in bovine and human articular chondrocytes. It has also been reported that insulin-like growth factor (IGF-1) and transforming growth factor (TGF-2) influence proteoglycan synthesis and accumulation in the cell associated matrix.³⁷ These growth factors increase the concentration of proteoglycans although rate effects are not clear.

The models represent a new method to estimate the homeostasis of each matrix molecule species within the construct through incorporation of growth and decay rates. As with any model, limitations exist. Here interactions between molecules or between ECM and the scaffold material are not explored. Although the parameterization process reduces the many possible synthesis influencing factors or variables into a few terms, it does not provide the subtle modification with known active or inactive states of ECM, growth factors, chrondrocytes, etc. which comprise the overall composite. These additional influences may be the cause of the variety of differences shown between GAG and collagen synthesis states (Figures 1 to 3). The reduction of influencing terms and a clear mathematical model does, however, provide a starting point for comparison between the various studies. Additionally, the functional nature of the resulting constructs, although often analysed, are not incorporated into a mechanical result here. Interactions between constituents and the mechanical implications are being explored in ongoing modelling efforts.³⁸

The models use a simplified approach to investigate matrix molecule biosynthesis under the influence of growth factors. Model outcomes can be used to parametrically compare experimental results as well as to explore matrix concentration in the steady state due to additional anabolic and catabolic factors. As a predictive tool, the models may be able to assess culture times necessary to produce a functionally viable construct. This potential application will require a transient analysis of the proposed model, which is currently underway.