Abstract
We present a statistical model for patterns of genetic variation in samples of unrelated individuals from natural populations. This model is based on the idea that, over short regions, haplotypes in a population tend to cluster into groups of similar haplotypes. To capture the fact that, because of recombination, this clustering tends to be local in nature, our model allows cluster memberships to change continuously along the chromosome according to a hidden Markov model. This approach is flexible, allowing for both “block-like” patterns of linkage disequilibrium (LD) and gradual decline in LD with distance. The resulting model is also fast and, as a result, is practicable for large data sets (e.g., thousands of individuals typed at hundreds of thousands of markers). We illustrate the utility of the model by applying it to dense single-nucleotide–polymorphism genotype data for the tasks of imputing missing genotypes and estimating haplotypic phase. For imputing missing genotypes, methods based on this model are as accurate or more accurate than existing methods. For haplotype estimation, the point estimates are slightly less accurate than those from the best existing methods (e.g., for unrelated Centre d'Etude du Polymorphisme Humain individuals from the HapMap project, switch error was 0.055 for our method vs. 0.051 for PHASE) but require a small fraction of the computational cost. In addition, we demonstrate that the model accurately reflects uncertainty in its estimates, in that probabilities computed using the model are approximately well calibrated. The methods described in this article are implemented in a software package, fastPHASE, which is available from the Stephens Lab Web site.
With the advent of cheap, quick, and accurate genotyping technologies, there is a need for statistical models that both are capable of capturing the complex patterns of correlation (i.e., linkage disequilibrium [LD]) that exist among dense markers in samples from natural populations and are computationally tractable for large data sets. Here, we present such a model and assess its ability to accurately capture patterns of variation by applying it to estimate missing genotypes and to infer haplotypic phase from unphased genotype data.
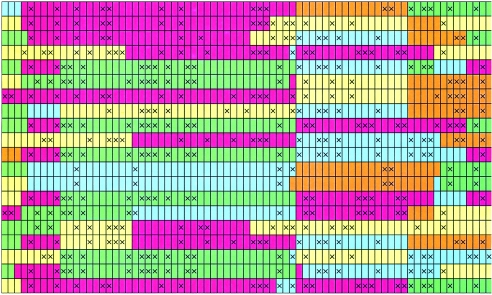
The model is motivated by the observation that, over short regions (say, a few kilobases in human genomes), haplotypes tend to cluster into groups of similar haplotypes. This clustering tends to be local in nature because, as a result of recombination, those haplotypes that are closely related to one another and therefore similar will vary as one moves along a chromosome. To capture this, we allow the cluster membership of observed haplotypes to change continuously along the genome according to a hidden Markov model (HMM). (This idea has been proposed, independently of our work, by others, including Sun et al. [2004], Rastas et al. [2005], and Kimmel and Shamir [2005a]; see the “Discussion” section.) Each cluster can be thought of as (locally) representing a common haplotype, or combination of alleles, and the HMM assumption for cluster membership results in each observed haplotype being modeled as a mosaic of a limited number of common haplotypes (fig. 1). This approach seems more flexible than “block-based” cluster models, which divide the genome into blocks (segments of high LD) and allow cluster membership to change only across block boundaries (e.g., Greenspan and Geiger 2004; Kimmel and Shamir 2005b). The hope is that this more flexible assumption will allow the model to capture complex patterns of LD that are not well captured by block-based alternatives while continuing to capture any “block-like” patterns that are present.
Figure 1.
Illustration of how our model allows cluster membership to change continuously along a chromosome. Each column represents a SNP, with the two alleles indicated by open and crossed squares. Successive pairs of rows represent the estimated pair of haplotypes for successive individuals. Colors represent estimated cluster membership of each allele, which changes as one moves along each haplotype. Locally, each cluster can be thought of as representing a (common) combination of alleles at tightly linked SNPs, and the figure illustrates how each haplotype is modeled as a mosaic of these common combinations. The figure was produced by fitting our model to the HapMap data from 60 unrelated CEPH individuals (see the “Results” section) and then taking a single sample of cluster memberships and haplotypes from their conditional distribution, given the genotype data and parameter estimates (appendix B). For brevity, haplotypes from only 10 individuals are shown.
Another model that also aims to flexibly capture patterns of LD is the PAC model of Li and Stephens (2003), which partially underlies the PHASE software for haplotype inference and estimation of recombination rates (Stephens et al. 2001; Stephens and Donnelly 2003; Stephens and Scheet 2005). One way to view the model we present here is as an attempt to combine the computational convenience of cluster-based models with the flexibility of the PAC model. Indeed, in terms of computational convenience, our model is substantially more attractive than the PAC model, both in that computation increases only linearly with the number of individuals (vs. quadratically for the PAC) and in that the model can be applied directly to unphased genotype data, with unknown haplotypic phases integrated out analytically rather than via a time-consuming and tedious-to-implement Markov chain–Monte Carlo scheme, such as that used by PHASE.
The price we pay for this computational convenience is that our model is purely predictive; in common with the block-based models mentioned above but in contrast to the PAC model, our model does not attempt to directly relate observed genetic variation to underlying demographic or evolutionary processes, such as population size or recombination. As such, it is not directly suited to drawing inferences about these processes. However, it is suited to two other applications that we consider here: inferring unknown (“missing”) genotypes and inferring haplotypes from unphased genotype data. These two applications are important for at least two reasons. First, many methods for analyzing population data (e.g., methods that aim to draw inferences regarding demographic and evolutionary processes) struggle to deal with missing genotypes or unphased data. This may be because dealing with these factors can create an impractical computational burden or simply because necessary additional computer programming has not been done. Therefore, applying those methods in practice often involves initially estimating missing genotypes and haplotypes by some other method. Second (as we expand on in the discussion), the ability to accurately impute missing genotypes and infer haplotypes has implications for the development of methods for association-based mapping of variants involved in common complex diseases. Comparisons with existing approaches for these applications suggest that our model has something to offer, in terms of both speed and accuracy.
Material and Methods
Models
To introduce notation and the basic concepts underlying our model, we begin by describing a simple cluster-based model for haplotypes sampled from a population, in which each haplotype is assumed to have arisen from a single cluster. We then describe a modification to this model that allows cluster membership to change along each haplotype, to capture the fact that, although sampled haplotypes exhibit clusterlike patterns, these patterns tend to be local in nature. Finally, we describe the extension of this model for haplotype data to unphased genotype data through the assumption of Hardy-Weinberg equilibrium (HWE) and a further extension that allows for certain types of deviation from HWE.
Cluster model for haplotypes
Suppose we observe n haplotypes, h=(h1,…,hn), each comprised of data at M markers. Let him denote the allele in the ith haplotype at marker m, so that hi=(hi1,…,hiM). Throughout, we assume the markers are biallelic SNPs, with alleles labeled 0 and 1 (arbitrarily) at each site, although the model is easily extended to multiallelic markers.
A simple cluster model for haplotypes can be developed as follows. Assume that each sampled haplotype originates from one of K clusters (labeled 1,…,K). For simplicity, we initially assume K is known, but we will relax this assumption later. Let zi denote the (unknown) cluster of origin for hi, and let αk denote the relative frequency of cluster k, so that p(zi=k|α)=αk, where α=(α1,…,αK).
We assume that, given the cluster of origin of each haplotype, alleles observed at each marker are independent draws from cluster-specific (and marker-specific) allele frequencies. Thus, if θkm denotes the frequency of allele 1 in cluster k at marker m, and θ denotes the matrix of these values, then
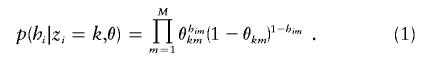 |
Since the clusters of origin are actually unknown, the probability of hi is obtained by summing equation (1) over all possible values of zi and weighting by their probabilities:
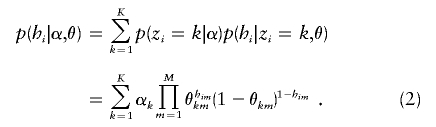 |
Finally, specification of the model for h=(h1,…,hn) is completed by assuming that h1,…,hn are independent and identically distributed from equation (2).
This simple model is essentially a haploid version of a model that has been widely used to capture the clustering that can occur among individuals typed at unlinked (or loosely linked) markers because of population structure in natural populations (Smouse et al. 1990; Rannala and Mountain 1997; Pritchard et al. 2000). However, in those applications, the clusters represent “populations,” whereas here the clusters represent groups of closely related haplotypes. The idea of using this model to capture clustering of haplotypes at tightly linked markers seems to originate with Koivisto et al. (2003), who used it to model data at tightly linked SNPs within a haplotype block (see also Kimmel and Shamir 2005b).
The assumption of independence across markers within clusters may seem slightly counterintuitive in this setting, where one expects to observe strong dependence among markers. The following observations may aid intuition. Each cluster corresponds to a single row of the θ matrix, which is a vector of numbers in the range [0,1], with one number per marker. (In fact, we imposed the constraint 0.01⩽θkm⩽0.99 on the elements of θ, motivated by the idea that this might make the model more robust to factors such as genotyping error.) For estimates of θ obtained from real data sets that we have examined, a moderate proportion (approximately two-thirds for the HapMap data considered below) are very close to either 0 or 1. As a result, each row of θ tends to look like a haplotype (a string of zeros and ones), but with occasional “fuzziness” indicating uncertainty about the alleles at some positions. That is, each cluster can be thought of as representing a particular combination of alleles at a subset of the markers, thus capturing strong dependence among these positions, and the assumption of independence can be thought of as relating to deviations from this base combination.
Local clustering of haplotypes
Although sampled haplotypes certainly exhibit cluster-like patterns, these patterns tend to be local in nature (fig. 1). To capture this, we replace the assumption that each haplotype originates from one of K clusters with the assumption that each allele originates from one of the clusters, and we use an HMM to model the fact that alleles at nearby markers are likely to arise from the same cluster. Specifically, if zim denotes the cluster of origin for him, we assume zi=(zi1,…,ziM) forms a Markov chain on {1,…,K}, with initial-state probabilities
and transition probabilities pm(k→k′) given by
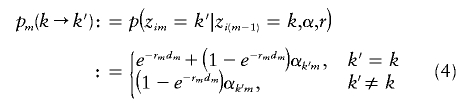 |
for m=2,…,M, where dm is the physical distance between markers m-1 and m (assumed to be known) and where r=(r2,…,rM) and α=(αkm) are parameters to be estimated. This Markov chain is a discretized version of a continuous Markov jump process, with jump rate rm per bp between markers m-1 and m and with transition probabilities
Informally, we think of rm as being related to the recombination rate between m-1 and m, although simulation results (not shown) suggest that generally there may be little correspondence between actual recombination rate and estimates of r. If the physical distances between markers were not known, then the compound parameter rmdm in equation (4) could be replaced by a single parameter without loss of information. Indeed, this is true even if the physical distances are known, unless some constraint is placed on r (e.g., constraining all rm to be equal). All results presented here were based on the unconstrained model and thus do not actually use the physical distances between markers. However, the algorithmic derivations in the appendixes can be used for both the constrained and the unconstrained models.
Given the cluster of origin of each allele, we assume, as before, that the alleles are independent draws from the relevant cluster allele frequencies, so
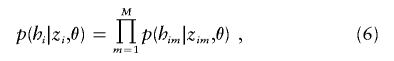 |
where
Since zi is unknown, the probability of hi is obtained by summing equation (6) over all possible values of zi and weighting by their probabilities:
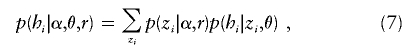 |
where p(zi|α,r) is determined by equations (3) and (4). Naive computation of this sum would require a sum over KM possible values for zi, but the Markov assumption for zi allows the sum to be computed much more efficiently (with computational cost increasing linearly with KM) using standard methods for HMMs (e.g., Rabiner 1989).
Extension to genotype data
Now suppose that, instead of observing haplotypes, we observe unphased genotype data g=(g1,…,gn) on n diploid individuals. Let gim denote the genotype at marker m in individual i, which we will code as the sum of its alleles, so gim has the value 0, 1, or 2. One approach to extending the haplotype-based model above to unphased genotype data is to assume that the two haplotypes that make up each multilocus genotype are independent and identically distributed from equation (7)—that is, to assume HWE. Under this assumption, if z·im denotes the (unordered) pair of clusters from which genotype gim originates, then z·i=(z·i1,…,z·iM) form a Markov chain with initial-state probabilities
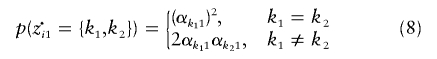 |
and transition probabilities
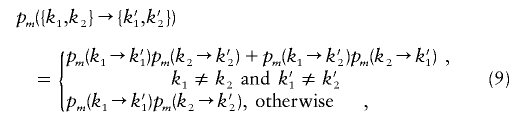 |
where pm(k→k′) is defined in equation (4). These expressions come from pairing two independent Markov chains with transition probabilities given in equation (4).
Given the clusters of origin, z·i, we again assume that the alleles are independent draws from the relevant cluster allele frequencies, so
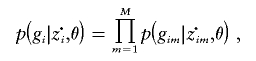 |
where
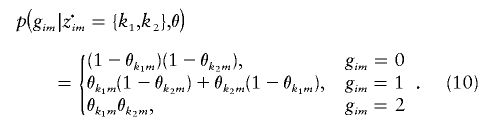 |
Note that, if some gim are missing, this is easily dealt with by replacing the corresponding p(gim|z·im={k1,k2},θ) with any positive constant (e.g., 1.0); this corresponds to the assumption that the genotypes are missing at random.
Since z·i is unknown, the probability of gi is obtained by summing over all possible values:
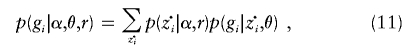 |
where p(z·i|α,r) is determined by equations (8) and (9). As before, methods for HMMs allow this sum to be computed efficiently (with computational cost increasing linearly with K2M) (see appendix A).
This model (11) is reminiscent of the “linkage” model of Falush et al. (2003), who modeled genotype data at loosely linked markers in structured populations. One difference between their model and ours is that they allowed α (q in their notation) to vary among individuals but fixed α across markers, whereas we allow α to vary across markers but assume it to be fixed across individuals. The reason for this difference is that the interpretation of these parameters is very different in the two applications. In the model of Falush et al. (2003), this parameter controls each individual’s proportion of ancestry in each subpopulation (which would be expected to differ across individuals), whereas here it controls the relative frequency of the common haplotypes (which would be expected to differ in different genomic regions). Falush et al. (2003) also restricted r to be constant, whereas we allow it to vary in each marker interval.
Modeling deviations from HWE and incorporation of subpopulation labels
Although the assumption of HWE will not hold exactly for real populations, previous studies have consistently suggested that models based on HWE can perform well at haplotype inference and missing-data imputation, even when there are clear and substantial deviations from HWE (e.g., Fallin and Schork 2000; Stephens and Scheet 2005). Nevertheless, we examined the potential benefits of modifying the above model to deal with a certain type of deviation from HWE. Specifically, we consider the situation in which the sampled individuals might be considered to be sampled from S distinct subpopulations. (For example, the SeattleSNPs data considered below consist of samples from 24 African Americans and 23 individuals of European descent, and we treat these as separate subpopulations.) Let si∈1,…,S denote the subpopulation of origin for individual i (which is assumed to be known here, although extension to the case where si is unknown may also be interesting). Because of shared ancestry, different subpopulations may share some of their haplotype structure, although haplotype frequencies and levels of LD would be expected to differ. To capture this, we let the θ parameters be shared across subpopulations but allowed the α and r parameters to vary among the subpopulations. Thus, α=(α(1),…,α(S)) and r=(r(1),…,r(S)), where (α(j),r(j)) denote the parameters relating to subpopulation j, and
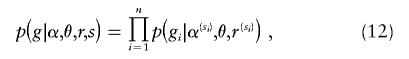 |
where s=(s1,…,sn) and p(gi|α(si),θ,r(si)) is as defined in equation (11).
Computation and Parameter Estimation
In this section, we outline the methods used to fit the models (11) and (12) and to perform two applications: missinggenotype imputation and haplotype inference.
Parameter estimation
We use an expectation-maximization (EM) algorithm (Dempster et al. 1977) to estimate the parameters ν=(θ,α,r) of our model (see appendix C for details). The computational complexity of the algorithm is 𝒪(nMK2) and, in particular, is linear in the number of sampled individuals and markers, which allows it to be fitted to large data sets.
As with any EM algorithm, our algorithm will typically find a local maximum of the likelihood function ℒ(ν;g)=p(g|ν). For realistic data sets, this likelihood surface will have many different local maxima, and thus different starting points for the EM algorithm will typically lead to different parameter estimates. A standard approach to dealing with this problem is to first apply the algorithm T times from T different starting points, obtaining T estimates 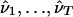 , and then select whichever of these estimates gives the highest value for the likelihood. However, because our focus here is on using the model for prediction and not on parameter estimation itself, it is not necessary to settle on a single estimate for the parameters, and, in our tests, we found that we were able to obtain more accurate predictions by combining results across T estimates, as described below. We also found that, using this strategy of combining across estimates, reliable performance can be obtained with relatively few iterations of the EM algorithm per starting point—probably far fewer than would be required by most methods of monitoring convergence. For the results presented here, we typically used T=20 starts of the EM algorithm, with up to 25 iterations per start, although results of experiments suggest that these values could be reduced without sacrificing accuracy (results not shown). For each initialization of the EM algorithm, we set r=0.00001, chose θkm to be independent and identically distributed uniform on [0.01,0.99], and let α·m∼Dirichlet(1,…,1). Our methods appeared somewhat robust to deviations from these choices (e.g., setting αkm=1/K, for all m and k, produced similar mean accuracy), although we did not undertake a detailed study.
, and then select whichever of these estimates gives the highest value for the likelihood. However, because our focus here is on using the model for prediction and not on parameter estimation itself, it is not necessary to settle on a single estimate for the parameters, and, in our tests, we found that we were able to obtain more accurate predictions by combining results across T estimates, as described below. We also found that, using this strategy of combining across estimates, reliable performance can be obtained with relatively few iterations of the EM algorithm per starting point—probably far fewer than would be required by most methods of monitoring convergence. For the results presented here, we typically used T=20 starts of the EM algorithm, with up to 25 iterations per start, although results of experiments suggest that these values could be reduced without sacrificing accuracy (results not shown). For each initialization of the EM algorithm, we set r=0.00001, chose θkm to be independent and identically distributed uniform on [0.01,0.99], and let α·m∼Dirichlet(1,…,1). Our methods appeared somewhat robust to deviations from these choices (e.g., setting αkm=1/K, for all m and k, produced similar mean accuracy), although we did not undertake a detailed study.
Missing-genotype imputation
For any genotype gim that is unobserved (“missing”), it is straightforward to compute the probability that gim=x (x=0,1,2), given all observed genotypes g and parameter values ν, by use of
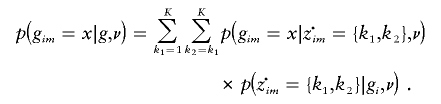 |
The first term in this sum is given by equation (10), and the second term is the conditional distribution of the hidden variables in the HMM, which can be obtained using standard methods for HMMs (appendix A).
A natural point estimate for gim is then obtained by choosing the value of x that maximizes this expression. As noted above, we have found it helpful to combine results over several sets of parameter estimates 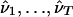 , obtained from T different applications of the EM algorithm using different starting points. Specifically, we used the estimate
, obtained from T different applications of the EM algorithm using different starting points. Specifically, we used the estimate
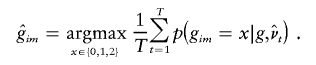 |
This method imputes genotypes marginally and provides a “best guess” for each genotype. It is also straightforward to sample from the joint distribution of the missing genotypes given observed data—for example, by sampling from the conditional distribution of the haplotypes for all individuals, as described below.
Haplotype inference
We consider two aspects of the haplotype inference problem: (1) sampling the pairs of haplotypes of all individuals from their joint distribution given the unphased genotype data—this provides a useful way to assess or account for uncertainty in haplotype estimates—and (2) constructing point estimates of the haplotypes carried by each individual—this is how many haplotype-reconstruction methods are used in practice (as a prelude to subsequent analysis of the estimated haplotypes). It also provides a convenient basis for comparison with other haplotype reconstruction methods.
Sampling haplotypes from their joint distribution
We will use the term “diplotype” to refer to a pair of haplotypes that comprise the genetic data for an individual. Let di denote the diplotype for individual i, and d=(d1,…,dn). Conditional on a particular parameter value ν, the diplotypes of different individuals are independent (i.e., p(d|g,ν)=ip(di|gi,ν)), and thus one can sample from p(d|g,ν) by sampling independently from p(di|gi,ν) for each i. A method for doing this is described in appendix B.
To combine results from T initiations of the EM algorithm, we obtain a sample 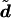 of size T×B as the union of B independent samples from each of
of size T×B as the union of B independent samples from each of 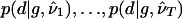 . When constructing
. When constructing 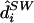 below, we used T=20 and B=50; for
below, we used T=20 and B=50; for 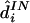 , we used T=20 and B=200.
, we used T=20 and B=200.
Point estimation
We have implemented two different methods for producing point estimates, 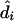 , of the diplotypes of individual i. Both are obtained by first creating a sample
, of the diplotypes of individual i. Both are obtained by first creating a sample 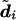 of diplotypes for individual i, as described above. From this sample, we define the following estimates.
of diplotypes for individual i, as described above. From this sample, we define the following estimates.
-
1.
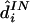 , which is the diplotype that appears most often in
, which is the diplotype that appears most often in 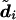 . This estimate is motivated by an attempt to maximize the probability that the whole diplotype is correct or, equivalently, to minimize the “individual error rate”—that is, the proportion of individuals whose haplotypes are not determined by their genotype data (Stephens et al. 2001).
. This estimate is motivated by an attempt to maximize the probability that the whole diplotype is correct or, equivalently, to minimize the “individual error rate”—that is, the proportion of individuals whose haplotypes are not determined by their genotype data (Stephens et al. 2001). -
2.
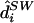 , which is constructed as follows. Starting at one end of the genetic region, we move through the heterozygous sites, phasing each site relative to the previous heterozygous site by selecting the two-site diplotype that occurs most frequently (at that pair of sites) in
, which is constructed as follows. Starting at one end of the genetic region, we move through the heterozygous sites, phasing each site relative to the previous heterozygous site by selecting the two-site diplotype that occurs most frequently (at that pair of sites) in 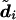 . This estimate is motivated by an attempt to minimize the “switch error”—that is, the proportion of heterozygous sites that are phased incorrectly relative to the previous heterozygous site (this is 1 minus the switch accuracy of Lin et al. [2002]).
. This estimate is motivated by an attempt to minimize the “switch error”—that is, the proportion of heterozygous sites that are phased incorrectly relative to the previous heterozygous site (this is 1 minus the switch accuracy of Lin et al. [2002]).
Note that, for data sets containing a large number of markers, individuals may have a very large number of plausible diplotype configurations, none of which are overwhelmingly more probable than the others. In such cases, the most probable diplotype configuration is both difficult to reliably identify (requiring a very large sample 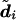 ) and not especially interesting (in that it is very unlikely to be correct). Therefore, for large-scale studies, we would tend to favor the use of
) and not especially interesting (in that it is very unlikely to be correct). Therefore, for large-scale studies, we would tend to favor the use of 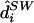 over
over 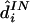 .
.
Selecting K
Selection of K is essentially a model-selection problem, which is, in general, a tricky statistical problem. We found that standard approaches to model selection, such as Akaike information criterion (Akaike 1973) and Bayesian information criterion (Schwarz 1978), do not work well here (selecting a K that is too small), probably because the asymptotics on which they are based do not apply. We therefore used the following cross-validation approach to select K. For each data set, we masked (i.e., made missing) ∼15% of the genotypes at random (note that, in our tests of imputation accuracy below, the data set to be analyzed would already have had some genotypes masked; we did not use these masked genotypes when selecting K). Then, for a range of values of K (we considered K=4, 6, 8, 10, and 12; the upper limit reflects our desire to keep the computational burden low), we used our model to estimate the masked genotypes, as described above, comparing these estimates with the true genotypes. We selected the K that maximized the number of correctly estimated genotypes.
This procedure is relatively computationally intensive, since it involves fitting the model for several values of K, and the computational cost increases with K2. To reduce the computational burden, we used only a small number of starts (as few as three) for the EM algorithm when performing the cross-validation. In addition, in the results we present here, we sometimes chose a single K for several data sets on a common set of individuals. For example, for the SeattleSNPs data considered later, when analyzing data on a particular set of individuals, we selected a single K for all genes, on the basis of applying the cross-validation approach to a subset of the genes. Preliminary comparisons suggested that this approach gave similar average accuracy to the more computationally intensive approach of choosing K separately for each gene (data not shown). For missing-genotype estimation results from the HapMap project, we selected K by using only a small portion of the data, since the data sets were so large.
Because we found performance to be relatively robust to a range of values of K, in cases where the computational cost of this strategy becomes inconvenient an alternative approach would be to simply select a fixed value of K (K=8 seemed to perform reasonably well across a range of scenarios in our tests). It would also be possible, and perhaps fruitful, to combine results across parameter estimates obtained using different values of K rather than selecting a single K value.
Results
The methods described above for imputing missinggenotype data and estimating haplotypes are implemented in a software package called “fastPHASE,” which is available for download from the Stephens Lab Web site. Here, we compare performance of these methods with several other available methods, including PHASE version 2.1.1 (Stephens et al. 2001; Stephens and Donnelly 2003; Stephens and Scheet 2005), GERBIL versions 1.0 and 1.1 (Kimmel and Shamir 2005b), and HaploBlock version 1.2 (Greenspan and Geiger 2004). The models underlying both GERBIL and HaploBlock bear some similarity to our model, being based on the idea of clusters of haplotypes, but in these models, cluster membership is allowed to change only at certain points in the genome (“block-boundaries”), which are estimated from the data. The model underlying PHASE is based on the PAC model of Li and Stephens (2003), which shares the flexibility of the model we present here but is considerably more costly to compute. In comparisons elsewhere (Stephens and Scheet 2005), we found that PHASE outperformed several other methods in accuracy of both missing-data imputation and haplotype estimation, but GERBIL and HaploBlock were not included in those comparisons. For haplotype estimation, Kimmel and Shamir (2005b) found that GERBIL performed better than HaploBlock but slightly less well than PHASE. However, they did not examine accuracy in missing-data imputation, and, as far as we are aware, our comparisons provide the first published assessment of GERBIL and HaploBlock for this task. PHASE and GERBIL were run with their default settings, and HaploBlock was run with the −W option (which produces estimates by combining over multiple solutions, similar to our strategy of combining estimates from multiple runs of the EM algorithm; this option seemed to give more accurate results but took longer to run than the alternative −F option).
Missing-Data Imputation
We examined accuracy of methods for missing-data imputation with both complete sequence data in multiple candidate genes (from the SeattleSNPs Variation Discovery Resource) and genomewide dense SNP data (1 SNP every 2–3 kb across entire chromosomes) from the International HapMap Project (International HapMap Consortium 2005).
SeattleSNPs
We analyzed the same data from the SeattleSNPs resequencing project as were analyzed elsewhere (Stephens and Scheet 2005); we considered sequence data on 50 autosomal genes, containing 15–230 SNPs, from 24 African Americans and 23 individuals of European descent. For each gene, we masked ∼5% of the individual genotypes at random. We then used various methods to estimate the masked genotypes and assessed performance by computing the error rate as the proportion of masked genotypes that were not estimated correctly.
As elsewhere (Stephens and Scheet 2005), we used each method to analyze the data in two ways: (1) analyzing the African American and European-descent samples separately and (2) analyzing the combined sample of 47 individuals together. For both of these approaches, we computed both the overall (total) error rates and error rates stratified by subpopulation (table 1). All four methods performed well—better than most of the methods considered elsewhere [Stephens and Scheet 2005])—with fastPHASE yielding the lowest error rate (although differences among fastPHASE, PHASE, and HaploBlock were not statistically significant). As in a previous study (Stephens and Scheet 2005), our analysis of data from the African American and European-descent samples combined seemed to give a small decrease in error rate compared with analysis of the samples separately, which illustrates the relative robustness of the methods to deviations from HWE.
Table 1.
Error Rates for Estimation of Missing Genotypes for SeattleSNPs[Note]
|
Analyzed Separately |
Analyzed Combined |
||||||
| Method | AA Error |
ED Error |
Totala | AA Error |
ED Error |
Totala | Total (Separate α,r)a |
| fastPHASE | .053 | .024 | .039 | .051 | .022 | .037 | .035 |
| PHASE version 2.1.1 | .058 | .030 | .044 | .052 | .024 | .038 | NA |
| GERBIL version 1.1 | .067 | .030 | .048 | .063 | .026 | .045 | NA |
| HaploBlock | .053 | .026 | .040 | .051 | .026 | .039 | NA |
| fastPHASE with fixed K: | |||||||
| K=4 | .066 | .029 | .048 | .072 | .032 | .052 | .046 |
| K=6 | .059 | .024 | .042 | .061 | .027 | .045 | .039 |
| K=8 | .058 | .026 | .042 | .054 | .024 | .039 | .036 |
| K=10 | .054 | .027 | .041 | .051 | .023 | .037 | .036 |
| K=12 | .053 | .026 | .039 | .051 | .022 | .037 | .035 |
Note.— Error rates are based on estimation of 9,479 missing genotypes. The best-performing method in each column is in bold italics. The differences among fastPHASE, PHASE, and HaploBlock are not statistically significant; the differences between these three methods and GERBIL are significant (P<.007) on the basis of bootstrap resampling of the 50 genes. AA = African American sample; ED = European-descent sample.
Total error rate for combined sample. The “Separate α,r” total gives results from use of the model in section 2.1.4.
We also assessed robustness of the results from fastPHASE to the number of clusters, K (table 1). For these data, results are relatively robust across the range of K considered here, at least provided that K is sufficiently large (say, at least 6). Error rates generally tended to decrease as K increased from 4 to 12, although, for sufficiently large K, we would expect the error rates to increase, and the rather small differences between K=8, 10, and 12 suggest that larger values of K would not produce a substantial improvement in performance.
To examine whether accuracy could be improved by taking account of the subpopulation of each sample, we also analyzed the combined-sample data by using the “separate α, r” model from (12). This model produced a very small improvement in error rate and also appeared to make results more robust to the choice of K (last column of table 1).
The results for fastPHASE in table 1 were all obtained by averaging over parameter estimates from T=20 starts of the EM algorithm. We found that estimates based on only the parameter value (among these 20 estimates) that maximized the likelihood were consistently less accurate. For example, in the combined analysis with K=6, this latter (maximization) strategy gave an error rate of 0.051, compared with 0.045 for the averaging strategy.
CEPH HapMap data
We obtained HapMap data for chromosomes 7 (41,018 SNPs across 159 Mb) and 22 (15,532 SNPs across 35 Mb) from parents in 30 CEPH trios (60 unrelated individuals) from a phase I data freeze (March 2005; International HapMap Project). We produced data sets with missing genotypes by masking 10% and 25% of genotypes at random and computed error rates for different methods of estimating these genotypes. Using fastPHASE, we were able to analyze the complete data for each chromosome. However, other methods struggled computationally; thus, to allow comparisons with these methods, we also split the data sets into nonoverlapping segments, each containing 150 consecutive SNPs, and analyzed each segment separately. Even so, HaploBlock failed to finish computing results for several data sets after weeks of running on multiple machines and thus was omitted from the comparisons. Because of the amount of computation required, we applied PHASE to only the chromosome 22 data sets.
Results are given in table 2. For these data, fastPHASE again produced a lower error rate than those of the other methods, with very slightly better accuracy when all data were analyzed simultaneously instead of in 150-SNP segments. PHASE performs about as well as fastPHASE, and the improvement of these methods over GERBIL was more substantial for these data than for the SeattleSNPs data. The main differences between the data sets are that (i) the HapMap SNPs tend to have a higher minor-allele frequency, because of the way in which these SNPs are ascertained, and (ii) the HapMap SNPs are more widely spaced and thus would be expected to exhibit less LD. Both these factors presumably contribute to the slightly worse performance of all methods for the HapMap data compared with the European-descent sample of the SeattleSNPs data.
Table 2.
Error Rates for Estimation of Missing Genotypes for CEPH HapMap Data[Note]
|
Error Rate for Chromosome |
||||
| 7 |
22 |
|||
|
Data Analyzed and Method |
10% Masked |
25% Masked |
10% Masked |
25% Masked |
| Whole chromosome: | ||||
| fastPHASE | .034 | .041 | .033 | .039 |
| fastPHASE, 1 start | .046 | .057 | .045 | .056 |
| Separate 150-SNP data sets: | ||||
| fastPHASE | .036 | .044 | .035 | .042 |
| PHASE version 2 | … | … | .038 | .049 |
| GERBIL version 1.1 | .056 | .077 | .054 | .073 |
Note.— For each chromosome, 10% and 25% of the data were masked, resulting in 242,481 and 606,985 missing genotypes for chromosome 7 and 93,476 and 232,731 missing genotypes for chromosome 22. Results for fastPHASE were obtained from 20 random starts of the EM algorithm, except for the “1 start” case, for which results were obtained from a single random start.
The high accuracy with which genotypes could be estimated with even 25% missing data prompted us to examine in more detail the relationship between accuracy and rates of missingness (table 3). Although this missing-at-random pattern is not a realistic assumption for missing data observed in real studies, the fact that accuracy remains high (>93%) even with 50% of the genotypes deleted illustrates both the effectiveness of the methodology and the strong correlations that exist among SNPs at this density.
Table 3.
Error Rates for Estimation of Missing Genotypes with fastPHASE for CEPH HapMap Data, Chromosome 22[Note]
| Missing Data (%) |
fastPHASE Error |
| 10 | .033 |
| 20 | .037 |
| 30 | .042 |
| 40 | .051 |
| 50 | .064 |
| 60 | .089 |
| 70 | .137 |
| 80 | .227 |
| 90 | .358 |
Note.— We masked 10%–90% of the data at random, which resulted in 93,476–837,853 missing genotypes, and applied fastPHASE to the entire chromosome 22.
Haplotype Inference
X-chromosome data
We assessed the accuracy of haplotype estimates by using the X-chromosome data from Lin et al. (2002), also analyzed elsewhere by Stephens and Donnelly (2003) and by us (Stephens and Scheet 2005). The data consist of X-chromosome haplotypes derived from 40 unrelated males. The haplotypes comprise eight regions, which range in length from 87 to 327 kb and contain 45–165 SNPs. For each of the eight genes, we used the same 100 data sets as elsewhere (Stephens and Scheet 2005), each consisting of 20 pseudo-individuals, created by randomly pairing the 40 chromosomes.
As in previous comparisons of this type, haplotype estimates obtained using different methods were scored using two error rates: the individual error (the proportion of ambiguous individuals whose haplotypes are not completely correct) and the switch error (the proportion of heterozygote genotypes that are not correctly phased relative to the previous heterozygote genotype). In computing these proportions, we summed both numerator and denominator over all 8×100 data sets (which is slightly different from computing an error rate for each of the eight genes and then averaging these rates, as in table 2 in an earlier publication [Stephens and Scheet 2005]). In computing these scores for each individual, we ignored sites where one or both alleles were missing.
Results are given in table 4. For data sets like these, which contain at least a moderate number of SNPs, estimating any individual’s haplotypes completely correctly is difficult. As a result, individual error rates of all methods are high, and it could be argued that the switch error is a more meaningful measure of performance. However, the qualitative conclusions are the same based on either error rate. Consistent with the results of Kimmel and Shamir (2005b), PHASE slightly outperformed GERBIL, which slightly outperformed HaploBlock; fastPHASE produced an individual error rate between that of PHASE and that of GERBIL and produced the lowest switch error rate (although the difference from the switch error rate of PHASE is small and not statistically significant). As one might hope, the point estimate  from fastPHASE, which aims to minimize the switch error, produces a lower switch error than does
from fastPHASE, which aims to minimize the switch error, produces a lower switch error than does 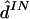 , which aims to minimize the individual error. Conversely,
, which aims to minimize the individual error. Conversely, 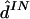 produces a lower individual error rate. Results from fastPHASE are again robust to a range of values of K.
produces a lower individual error rate. Results from fastPHASE are again robust to a range of values of K.
Table 4.
Individual and Switch Error Rates for Haplotype Estimates Produced by Different Methods for the X-Chromosome Data[Note]
| Method | Individual Error |
Switch Error |
fastPHASE (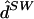 ) ) |
.654 | .111 |
fastPHASE (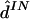 ) ) |
.641 | .116 |
| PHASE version 2.1.1 | .624 | .113 |
| GERBIL version 1.0 | .660 | .118 |
| HaploBlock | .702 | .122 |
fastPHASE (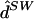 ) with fixed K: ) with fixed K: |
||
| K=4 | .654 | .111 |
| K=6 | .642 | .109 |
| K=8 | .645 | .110 |
| K=10 | .650 | .111 |
| K=12 | .657 | .113 |
Note.— The best-performing method in each error-rate column is in bold italics.
For these data, averaging results over multiple parameter estimates obtained from multiple starts of the EM algorithm turned out to be particularly important for obtaining good performance. For example, for K=4, the point estimate 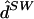 obtained using only the single set of parameter estimates that give the largest likelihood yielded error rates that were worse than those of any of the other methods considered here (individual error 0.716; switch error 0.134).
obtained using only the single set of parameter estimates that give the largest likelihood yielded error rates that were worse than those of any of the other methods considered here (individual error 0.716; switch error 0.134).
It is also notable that, for these data, even the simple-cluster model (which can be obtained as a special case of our model by setting rm=0 for all m) performs similarly to GERBIL, with an individual error rate of 0.648 and a switch error rate of 0.119. This is perhaps because of lower levels of historical recombination for these X-chromosome genes; thus, these data may not provide the best guide to performance of haplotype-inference methods on autosomal data.
HapMap data
Marchini et al. (2006) compared several methods for haplotype inference on samples of both unrelated and related individuals (trios of parents and child). We consider here the data they used from unrelated individuals, which consist of three simulated data sets and one real data set. The simulated data consist of three “trials” (SU1, SU2, and SU4 of Marchini et al. [2006]), which were simulated using coalescent methods with the following conditions: for trial 1, constant-sized population and constant recombination; for trial 2, constant-sized population with variable recombination; and for trial 4, population demography approximating that of a European population and variable recombination, with 2% of genotypes masked. The real data consist of unrelated CEPH samples (60 parents from 30 trios) from the HapMap project (International HapMap Consortium 2005), for which the real haplotypes were determined using the trio data under the assumption of no recombination from parents to offspring. (Under this assumption, the trio data determine phase at a large proportion of sites; the remaining ambiguous sites were ignored in scoring methods.)
We applied fastPHASE to the unphased genotypes from these data and sent the estimated haplotypes (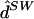 ) to J. Marchini, who independently scored the results. Table 5 compares the results from fastPHASE with those of other methods in the original comparison. The results from fastPHASE were consistently worse than those of PHASE (and those of wphase, for the simulated data) and were consistently better than those of the other methods, HAP and HAP2. Encouragingly for our model, the performance difference between fastPHASE and PHASE was the smallest for the real data, with switch errors of 0.055 and 0.051, respectively.
) to J. Marchini, who independently scored the results. Table 5 compares the results from fastPHASE with those of other methods in the original comparison. The results from fastPHASE were consistently worse than those of PHASE (and those of wphase, for the simulated data) and were consistently better than those of the other methods, HAP and HAP2. Encouragingly for our model, the performance difference between fastPHASE and PHASE was the smallest for the real data, with switch errors of 0.055 and 0.051, respectively.
Table 5.
Accuracy of Haplotype-Inference Methods for Simulated Data (Trials 1, 2, and 4) and Real Data from HapMap[Note]
|
Trial 1 |
Trial 2 |
Trial 4 |
Real Data |
||||||
| Method | Individual Error |
Switch Error |
Individual Error |
Switch Error |
Individual Error |
Switch Error |
Missinga | Individual Error |
Switch Error |
fastPHASE (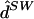 ) ) |
.653 | .045 | .887 | .069 | .760 | .058 | .091 | .879 | .055 |
| PHASE version 2 | .355 | .024 | .404 | .022 | .620 | .053 | .075 | .815 | .051 |
| wphase | .480 | .037 | .521 | .037 | .680 | .066 | .090 | … | … |
| HAP | .886 | .065 | .971 | .098 | .906 | .074 | .116 | .919 | .066 |
| HAP2 | .735 | .069 | .990 | .151 | .871 | .087 | .150 | .901 | .078 |
Calibration of Probability Calculations
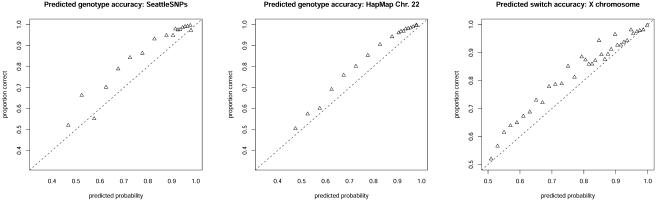
All the comparisons above are based on assessing the accuracy of point estimates of estimated genotypes or inferred haplotypes. However, by use of our model, it is also quick and easy to compute probabilities for each missing genotype and to produce samples from the conditional distribution of haplotypes, given the unphased genotypes. These can be used to take account of uncertainty in estimated genotypes and/or haplotypes in downstream analysis—for example, by performing the subsequent analysis on multiple sampled haplotype reconstructions to check for robustness of conclusions or, more formally, by using Bayesian statistical methods. However, to justify this strategy, the model should ideally produce approximately calibrated predictions. For example, of genotypes assessed to have a probability of 0.9 of being correct, ∼90% should actually be correct.
We therefore assessed the calibration of predictions from our model, for both genotype imputation and haplotype inference. For each imputed genotype, we computed the probability, p, under our model, that the imputed genotype was correct. We then grouped imputed genotypes into bins, according to their value for p, and, for each bin, we compared the average value of p with the proportion of genotypes that were actually correct. For haplotype reconstruction, we examined the calibration of a sample of diplotype configurations, 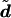 , by looking at potential switch errors—that is, by examining, in each individual, the phase of each heterozygous site relative to the previous heterozygous site. For each such pair of heterozygous sites, we computed the proportion, q, of the configurations in
, by looking at potential switch errors—that is, by examining, in each individual, the phase of each heterozygous site relative to the previous heterozygous site. For each such pair of heterozygous sites, we computed the proportion, q, of the configurations in 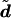 that contained the more common of the two possible phasings. We then grouped these site pairs into bins, according to their value for q, and, for each bin, we compared the average value of q with the proportion of phasings that were actually correct.
that contained the more common of the two possible phasings. We then grouped these site pairs into bins, according to their value for q, and, for each bin, we compared the average value of q with the proportion of phasings that were actually correct.
The results (fig. 2) show that our model is reasonably well calibrated, but slightly conservative, for both tasks. For example, of genotypes assessed a 90% chance of being correct, roughly 96% were actually correct in both the SeattleSNPs and HapMap data sets. One curious feature of the results is the slight drop in accuracy for the highest confidence bin (corresponding to 98% predicted probability of being correct, a value that results from the limits of 0.99 and 0.01 we imposed on elements of θ) in the SeattleSNPs data. Closer inspection reveals that this is because of errors in imputing genotypes of masked heterozygotes at singleton SNPs (i.e., SNPs where only one copy of the minor allele is present). When such genotypes are masked, our model very confidently but wrongly assesses them to be homozygous for the only observed allele. This could be viewed as an artifact due to the fact that the data contain only polymorphic SNPs and that our model does not condition on the markers being polymorphic.
Figure 2.
Calibration of our model for predicting uncertainty in inferred genotypes and haplotypes. Points (triangles) represent probabilities obtained by averaging over the 20 runs of the EM algorithm, as described in the text.
Differences in Computational Requirements
The relative computation times of the different methods we consider here vary across data sets and depend on the way in which the methods were applied (e.g., how many iterations were used). As we applied the methods here, fastPHASE and GERBIL require similar amounts of computational resources, and both are considerably faster than PHASE and HaploBlock. Computation times for all results are summarized in table 6. The increased speed of fastPHASE, compared with PHASE, would be greater for samples with a larger number of individuals.
Table 6.
Comparison of Computation Times (in Hours) for Different Methods[Note]
|
Missing-Genotype Estimation |
||||||
| HapMapChromosome 7 |
HapMapChromosome 22 |
|||||
| Method | SeattleSNPs (10%) |
10% | 25% | 10% | 25% |
Haplotype Inference for X Chromosome (7%) |
| fastPHASE | 1.3 | 9 | 8 | 5 | 5 | 2 |
| PHASE version 2 | 29.3 | NA | NA | 323 | 720 | 151 |
| GERBIL | .6 | 29 | 32 | 10 | 8 | 2 |
| HaploBlock | 160.1 | NA | NA | NA | NA | 265 |
Note.— Each method was applied on a 3-GHz Xeon processor with 1 GB of memory. The SeattleSNPs column is for analyses of all 47 individuals together. For missing-genotype estimation, fastPHASE was applied to the data without inference of haplotypes. Calculation times for HaploBlock with the SeattleSNPs data and for PHASE version 2 with HapMap chromosome 22 data are based on extrapolation from a subset of the data sets. Approximate percentages of missing data are in parentheses. Bold italics indicate the fastest method(s) for each data set.
Discussion
We have presented a model for genetic variation among unrelated individuals, which is computationally tractable for large-scale sets of unphased SNP genotype data. Each data set considered here, including whole-chromosome data from phase I of the HapMap project, took <10 h to analyze (table 6). To test the feasibility of applying our model to even larger data sets, we created a data set containing 3,150 individuals typed at 290,630 SNPs by concatenating 15 copies of the chromosome 2 genotypes of 210 unrelated individuals from phase II of the HapMap project. Our software required 97 h (on a single 3-GHz Xeon processor with 8 GB of RAM) to fit the model once to these data. In addition to its computational convenience, the model is also flexible and can capture both the sudden decline of LD that might be expected across a recombination hotspot and the more gradual decline of LD with distance. Indeed, for the task of imputing missing genotypes, our model performed better than any other method we considered. For inference of haplotypes, it performed slightly less well (on the real-data comparisons) than the best of the methods we considered, PHASE version 2, but at a fraction of the computational cost. It seems slightly puzzling that, at least for CEPH HapMap data, fastPHASE appears to outperform PHASE for missing-genotype imputation (table 2) but to perform less well than PHASE for haplotype inference (last column of table 5). We have no good explanation for why this should be (the differences, though small, appear statistically significant because the data sets are large).
There are at least two factors that may contribute to the improved performance of our model compared with the block-based model underlying GERBIL (which is perhaps the most similar to our model among those considered here). The first is the increased flexibility of our model, in that cluster membership can change continuously along the genome and not only across block boundaries. The second is the fact that we average results over multiple fits of our model to improve accuracy, whereas, as far as we are aware, GERBIL does not. Since a similar averaging strategy also seems to improve performance of HaploBlock, it may be interesting to examine whether averaging could be used to improve performance of GERBIL and, indeed, of other methods.
Our strategy of averaging results across applications of the EM algorithm is slightly unusual. However, averaging results across models has often been observed to produce improved predictive performance, dating back at least to Bates and Granger (1969) and becoming particularly popular recently with the increased use of Bayesian methods and the development of methods such as bagging (Breiman 1996) and boosting (Freund and Schapire 1996). Indeed, there are good theoretical reasons to expect averaging across multiple runs to produce better performance than using results from a single run of the EM algorithm; the averaging reduces the variance of predictions while leaving any bias unchanged. Of course, this alone does not fully explain our empirical finding that averaging across multiple runs produces better performance than making predictions based on the run with the highest likelihood. However, it is worth noting that this latter, more standard approach is also theoretically dubious in this setting, because the asymptotic theory that underlies maximum-likelihood estimation may not be applicable to most data sets, because of the large number of parameters in the model.
The averaging scheme that we use involves formation of equally weighted averages across multiple model fits. One might expect that a more sophisticated averaging scheme might further improve performance. We tried weighting results according to the likelihood of the corresponding parameter estimates, but this typically produced a worse performance, very similar to that of selecting the single parameter values with the largest likelihood, because one or two of the likelihoods are typically much greater than all the others, and so the average is dominated by these parameter values. A Bayesian version of our model would certainly be possible and would provide a more coherent way to average over parameter values. However, a fully Bayesian implementation would presumably greatly increase computational cost and seems unlikely to lead to substantial improvements in prediction accuracies.
Another novel aspect of our work is the extension of our model to deal with samples from multiple subpopulations. For the data we considered here, involving 24 African Americans and 23 individuals of European descent, we found that a slight but consistent improvement in performance could be obtained by taking account of the subpopulation of origin of each individual. We have also found a similar slight improvement when analyzing data from the four analysis panels of the HapMap project (results not shown). It seems likely that the gains of using this model will depend on sample size and the amount of divergence among the subpopulations, although we have not studied this dependence. Given the similarities between our model and those of Pritchard et al. (2000) and Falush et al. (2003), it seems natural to consider extending our model to the case in which the subpopulation(s) of origin of each individual is unknown, effectively producing a method for clustering individuals that can deal with sets of tightly linked markers. This might be especially helpful for investigating population structure in organisms with small genomes and/or little recombination, for which finding large sets of unlinked (or loosely linked) markers will be more problematic than in humans.
Our model has a very large number of parameters, and, for realistic data sets, we would not expect all parameters to be well estimated. It is possible to decrease the number of parameters by imposing constraints on α, θ, and/or r. For example, we tried constraining r and α to be constant across the genome. We also experimented with ad hoc smoothing schemes to encourage α and r to vary smoothly across the genome. However, in comparisons (not shown), these strategies did not lead to an improved performance in our applications, suggesting, perhaps surprisingly, that the large number of parameters does not greatly diminish the predictive power of the model.
While preparing this article, we became aware of independent work by Rastas et al. (2005) and Kimmel and Shamir (2005a) on models similar to the one we present here. In particular, these authors also pursue the strategy of modeling cluster membership along the chromosome by using an HMM. The main difference between their models and ours is that, in our model, when a jump in cluster membership occurs, the distribution of the new cluster does not depend on the current state (that is, the right-hand side of eq. [5] does not depend on k), whereas, in their models, it does. This results in our model being less computationally complex (the procedures we describe here have computational complexity 𝒪(K2) compared with 𝒪(K3) for the EM algorithm of Rastas et al. [2005]). A less important difference is that we allow for the possibility of allowing the jump probability between markers in the HMM to depend on the physical distances between markers—for example, by constraining the rm to be equal in equation (4). However, as noted earlier, we did not find that this improved performance over the unconstrained model, in which jump probabilities do not depend on marker spacing.
In addition to this difference between the models, there are also several further differences, both in the applications considered (Rastas et al. [2005] apply their model to haplotype inference, and Kimmel and Shamir [2005a] consider disease mapping) and in the way these applications are tackled. For example, Rastas et al. (2005) estimate haplotypes for each individual by first using the Viterbi algorithm to find the most-probable cluster memberships and then obtaining the most probable diplotype, given these cluster memberships (see also Kimmel and Shamir 2005b). Note that this will not, in general, find the most probable diplotype for each individual, but the empirical results suggest that it is a reasonable procedure. In contrast, we use Monte Carlo simulation to find haplotype estimates that attempt to minimize two different error measures. In addition, Rastas et al. (2005) and Kimmel and Shamir (2005a) use much more complex initialization strategies for their EM algorithms than we do here. It seems possible that our approach of averaging across runs of the EM algorithm obviates the need for more-complex initialization procedures, and so it is unclear whether combining these approaches would improve performance.
The two applications we considered here—namely, missing-data imputation and haplotype inference—are of direct interest in themselves, particularly as a prelude to subsequent analyses using methods that cannot deal with missing or unphased genotypes. We believe that they are also of indirect interest for the role they may eventually play in the development of powerful association-based methods for mapping disease genes (see also Kimmel and Shamir 2005a). Moreover, although the use of haplotypes in such methods has received more attention, we would argue that, in the longer term, methods to accurately estimate missing and untyped genotypes may prove to be more important. One of the primary motivations for haplotype-based mapping methods is that, if an untyped variant is responsible for affecting phenotype and if this untyped variant (and therefore the phenotype) is strongly associated with a particular haplotype but not with any individual SNP, then haplotype-based tests might succeed in detecting a significant effect where tests based on individual SNPs fail. That is, they are based on the idea that haplotypes may be better predictors of untyped genotypes than are individual SNPs. Indeed, some existing methods are explicitly based on the idea of using haplotypes to predict genotypes at one or more causal SNPs (e.g., Zöllner and Pritchard 2005). However, in these methods, the use of haplotypes is merely a convenient intermediate step in predicting the untyped variants; if one had a “black box” that could predict genotypes of untyped variants directly from unphased genotype data, then this could similarly form the basis of methods for association mapping, bypassing the need for haplotype estimates (see also the work of Chapman et al. [2003], for relevant discussion and the caveat that haplotype estimation methods may still be useful for studying certain types of interactions among closely linked causal SNPs). For this application, a limitation of our model is that, because it has a parameter vector (the columns of θ) that must be estimated for each SNP, it is suited to the imputation of genotypes only at SNPs where several (and preferably many) individuals have been genotyped and not at sites where no individuals have been genotyped. Although the HapMap and large-scale resequencing studies, such as the SeattleSNPs project, helpfully provide reference panels of individuals typed at large numbers of SNPs, many SNPs potentially involved in human disease are currently untyped in such panels, and we are working to extend our model to allow it to impute genotypes at such SNPs. Ultimately, our hope is that the kinds of models and methods examined here will form the foundation for new and more-effective statistical methods for analyzing whole-genome association studies.
Acknowledgments
We thank C. Geyer, for helpful discussions, and two anonymous referees, for comments on the submitted version. This research was supported by National Institutes of Health grant 1RO1HG/LM02585-01.
Appendix A : Forward and Backward Algorithms
Two fundamental quantities associated with HMM computations are the so-called forward and backward probabilities:
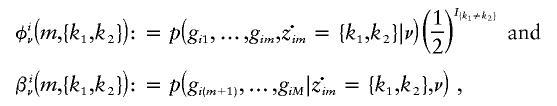 |
where I{A} is equal to 1, if A is true, and zero otherwise. (The factor 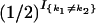 is not usually included in the definition of φ, but we include it here for later notational convenience.) Although computation of these quantities for HMMs via recursive formulas is standard, we give these formulas here because some care is needed to ensure these computations have complexity 𝒪(K2), rather than 𝒪(K4).
is not usually included in the definition of φ, but we include it here for later notational convenience.) Although computation of these quantities for HMMs via recursive formulas is standard, we give these formulas here because some care is needed to ensure these computations have complexity 𝒪(K2), rather than 𝒪(K4).
The forward calculation is given by
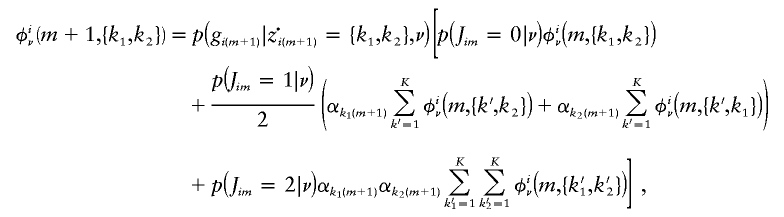 |
for m=1,…,M-1, where φiν(1,{k1,k2}):=p(gi1|z·i1={k1,k2})αk11αk21 and Jim is defined in appendix C. Then, p(gi|ν) may be calculated as 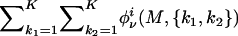 .
.
The corresponding backward recursion is
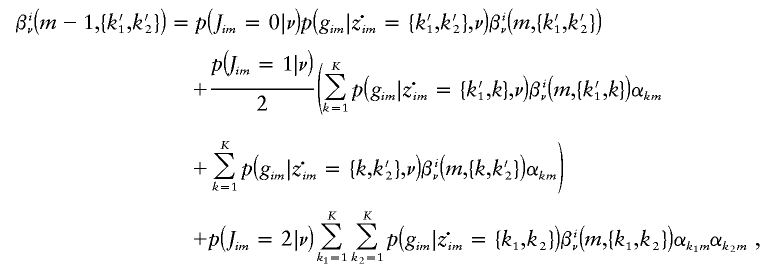 |
for m=2,…,M-1, and with βiν(M,{k1,k2}):=1 for all k1,k2.
To obtain p(z·im={k1,k2}|gi,ν), we use
with the constraint that 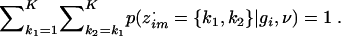
Appendix B : Sampling from p(di|gi,ν)
Recall that di denotes the pair of haplotypes (hai,hbi) for individual i. Additionally, let wi denote the ordered pair of cluster-of-origin indicators that correspond to the haplotypes (hai,hbi). Thus, di and wi may be thought of as “phased versions” of gi and zi, respectively. To sample from p(di|gi,ν), perform the following.
-
1. Sample
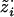 from p(z·i|gi,ν). This involves sampling the hidden state z·i, conditional on the data gi and parameters ν, which is a standard procedure for HMMs. First, sample
from p(z·i|gi,ν). This involves sampling the hidden state z·i, conditional on the data gi and parameters ν, which is a standard procedure for HMMs. First, sample 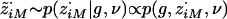 . Then, recursively for m=M-1,…,1, sample
. Then, recursively for m=M-1,…,1, sample 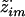 from
from
where pm+1(z·im→z·i(m+1)) is given by equation (9).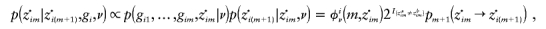
-
2. Sample
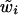 from
from 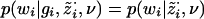 . Since
. Since
each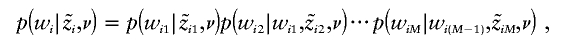
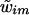 may be sampled sequentially (for m=2,…,M), given
may be sampled sequentially (for m=2,…,M), given 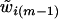 and
and 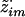 . Given
. Given 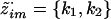 , there are, at most, two possibilities for wim: (k1,k2) and (k2,k1). Thus, probabilities of these outcomes are
, there are, at most, two possibilities for wim: (k1,k2) and (k2,k1). Thus, probabilities of these outcomes are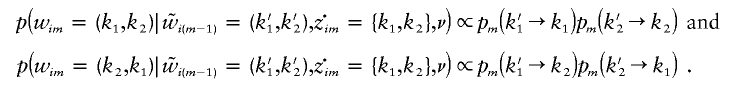
-
3. Sample
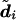 from
from  . This is nontrivial only for heterozygous sites—that is, when gim=1. Then,
. This is nontrivial only for heterozygous sites—that is, when gim=1. Then,
for (haim,hbim)=(0,1),(1,0).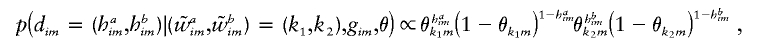
Appendix C : EM Algorithm
Here, we describe an EM algorithm for the estimation of ν=(α,θ,r). To do this, we introduce latent variables relating to “jumps” that occur in the continuous Markov jump process underlying z·i (see “Local clustering of haplotypes” in the “Material and Methods” section). Specifically, let Jim denote the number of jumps between markers m-1 and m for individual i, and let Jimk denote the number of these that jump to cluster k. Thus 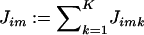 and
and
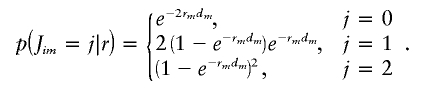 |
Now, let Q(ν|ν*) be the expected complete-data loglikelihood, Eν[logp(g,z,J|ν*)|g]. The algorithm is first initiated with a random guess ν(0). Then, the following is repeated for c=1,…,C:
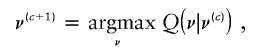 |
for sufficiently large C. The maximization above is accomplished by finding solutions to [∂Q(ν|ν*)]/[∂θkm]=0, [∂Q(ν|ν*)]/[∂αkm]=0, and [∂Q(ν|ν*)]/[∂rm]=0, for all k=1,…,K and m=1,…,M (r1 is not defined). This leads to the following estimators for ν:
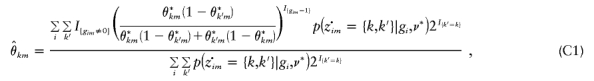 |
 |
and
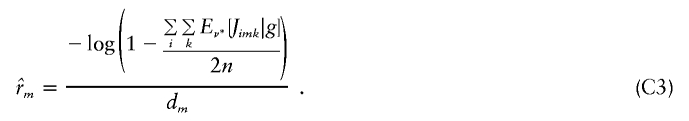 |
In practice, it would be inefficient to calculate 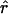 using equation (C3) only to exponentiate it as in equation (4). In fact, when using the model of (7) or (11) in which rm is estimated separately in each marker interval, (1-e-rmdm) could be replaced by a single parameter and estimated with
using equation (C3) only to exponentiate it as in equation (4). In fact, when using the model of (7) or (11) in which rm is estimated separately in each marker interval, (1-e-rmdm) could be replaced by a single parameter and estimated with
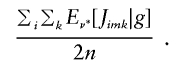 |
However, writing it as above (eq. [C3]) facilitates construction of EM algorithms for the constrained model in which all rm are equal.
Finally, we give expressions for terms necessary in calculating equations (C1–C3). Note that p(z·im|g,ν) depends only on the data for individual i:
with 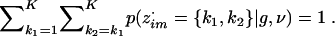
To calculate 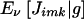 , we use
, we use 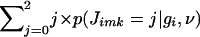 , which reduces to
, which reduces to
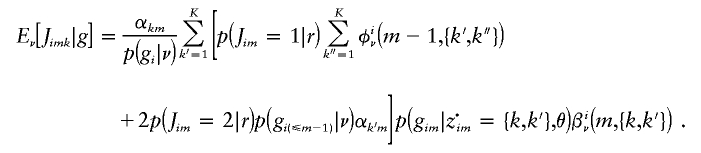 |
Web Resources
The URLs for data presented herein are as follows:
- GERBIL, http://www.cs.tau.ac.il/~rshamir/gerbil/
- HAP Web site, http://research.calit2.net/hap/
- HaploBlock, http://bioinfo.cs.technion.ac.il/haploblock/
- International HapMap Project, http://www.hapmap.org/
- SeattleSNPs, http://pga.gs.washington.edu
- Stephens Lab Web site, http://www.stat.washington.edu/stephens/software.html (for PHASE and fastPHASE software)
References
- Akaike H (1974) A new look at the statistical model identification. IEEE Trans Automatic Control AC 19:719–723 [Google Scholar]
- Bates JM, Granger CWJ (1969) The combination of forecasts. Oper Res Q 20:451–468 [Google Scholar]
- Breiman L (1996) Bagging predictors. Mach Learn 24:123–140 [Google Scholar]
- Chapman J, Cooper J, Todd J, Clayton D (2003) Detecting disease associations due to linkage disequilibrium using haplotype tags: a class of tests and the determinants of statistical power. Hum Hered 56:18–31 10.1159/000073729 [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B 39:1–38 [Google Scholar]
- Fallin D, Schork NJ (2000) Accuracy of haplotype frequency estimation for biallelic loci, via the expectation-maximization algorithm for unphased diploid genotype data. Am J Hum Genet 67:947–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK (2003) Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164:1567–1587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund Y, Schapire R (1996) Experiments with a new boosting algorithm. In: Proceedings of the Thirteenth International Conference of Machine Learning. Morgan Kaufmann, San Francisco, pp 148–156 [Google Scholar]
- Greenspan G, Geiger D (2004) Model-based inference of haplotype block variation. J Comput Biol 11:493–504 10.1089/1066527041410300 [DOI] [PubMed] [Google Scholar]
- Halperin E, Eskin E (2004) Haplotype reconstruction from genotype data using imperfect phylogeny. Bioinformatics 20:1842–1849 10.1093/bioinformatics/bth149 [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium (2005) The International HapMap Project. Nature 437:1299–1320 10.1038/nature04226 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimmel G, Shamir R (2005a) A block-free hidden Markov model for genotypes and its application to disease association. J Comput Biol 12:1243–1260 10.1089/cmb.2005.12.1243 [DOI] [PubMed] [Google Scholar]
- ——— (2005b) GERBIL: genotype resolution and block identification using likelihood. Proc Natl Acad Sci USA 102:158–162 10.1073/pnas.0404730102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koivisto M, Perola M, Varilo T, Hennah W, Ekelund J, Lukk M, Peltonen L, Ukkonen E, Mannila H (2003) An MDL method for finding haplotype blocks and for estimating the strength of haplotype block boundaries. In: Altman RB, Dunker AK, Hunter L, Jung TA, Kline TE (eds) Proceedings of the Pacific Symposium on Biocomputing. Vol 8. World Scientific, Teaneck, NJ, pp 502–513 [DOI] [PubMed] [Google Scholar]
- Li N, Stephens M (2003) Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165:2213–2233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin S, Cutler D, Zwick M, Chakravarti A (2002) Haplotype inference in random population samples. Am J Hum Genet 71:1129–1137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Cutler D, Patterson N, Stephens M, Eskin E, Halperin E, Lin S, Qin ZS, Munro HM, Abecasis GR, Donnelly P, for the International HapMap Consortium (2006) A comparison of phasing algorithms for trios and unrelated individuals. Am J Hum Genet 78:437–450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P (2000) Inference of population structure using multilocus genotype data. Genetics 155:945–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner LR (1989) A tutorial on HMM and selected applications in speech recognition. Proc IEEE 77:257–286 10.1109/5.18626 [DOI] [Google Scholar]
- Rannala B, Mountain JL (1997) Detecting immigration by using multilocus genotypes. Proc Natl Acad Sci USA 94:9197–9201 10.1073/pnas.94.17.9197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rastas P, Koivisto M, Mannila H, Ukkonen E (2005) A hidden Markov technique for haplotype reconstruction. Lect Notes Comput Sci 3692:140–151 [Google Scholar]
- Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6:461–464 [Google Scholar]
- Smouse PE, Waples RS, Tworek JA (1990) A genetic mixture analysis for use with incomplete source population data. Can J Fisheries Aquatic Sci 47:620–634 [Google Scholar]
- Stephens M, Donnelly P (2003) A comparison of Bayesian methods for haplotype reconstruction from population genotype data. Am J Hum Genet 73:1162–1169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens M, Scheet P (2005) Accounting for decay of linkage disequilibrium in haplotype inference and missing-data imputation. Am J Hum Genet 76:449–462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens M, Smith NJ, Donnelly P (2001) A new statistical method for haplotype reconstruction from population data. Am J Hum Genet 68:978–989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun S, Greenwood CTM, Neal RM (2004) Haplotype inference using a hidden Markov model with efficient Markov chain sampling [abstract 2934]. In: Proceedings and abstracts of the American Society of Human Genetics 2004 Annual Meeting, Toronto, October 26–30 [Google Scholar]
- Zöllner S, Pritchard JK (2005) Coalescent-based association mapping and fine mapping of complex trait loci. Genetics 169:1071–1092 10.1534/genetics.104.031799 [DOI] [PMC free article] [PubMed] [Google Scholar]