Abstract
High-throughput genotyping technologies for SNPs have enabled the recent completion of the International HapMap Project (phase I), which has stimulated much interest in studying genomewide linkage-disequilibrium (LD) patterns. Conventional LD measures, such as D′ and r2, are two-point measurements, and their relationship with physical distance is highly noisy. We propose a new LD measure, Δ, defined in terms of the correlation coefficient for shared haplotype lengths around two loci, thereby borrowing information from multiple loci. A U-statistic–based estimator of Δ, which takes into consideration the dependence structure of the observed data, is developed and compared with an estimator based on the usual empirical correlation coefficient. Furthermore, we propose methods for inferring LD-decay rates and recombination hotspots on the basis of Δ. The results from coalescent-simulation studies and analysis of HapMap SNP data demonstrate that the proposed estimators of Δ are superior to the two most popular conventional LD measures, in terms of their close relationship with physical distance and recombination rate, their small variability, and their strong robustness to marker-allele frequencies. These merits may offer new opportunities for mapping complex disease genes and for investigating recombination mechanisms on the basis of better-quantified LD.
Linkage disequilibrium (LD) refers to the association of alleles at different loci on the same chromosome (Lewontin and Kojima 1960). Such allelic associations are mostly due to physical proximity but could be affected by mutation, recombination, gene conversion, selection, genetic drift, or demographic factors such as inbreeding, migration, and population structure (Xiong and Guo [1997] and their references). Investigating LD patterns has profound implications for understanding the architecture of the human genome, for mapping complex disease loci on a fine scale, for studying population genetics, and for elucidating mechanisms of meiotic recombination. High-throughput genotyping technologies for SNPs have stimulated much interest in studying fine-scale genomewide patterns of common DNA variations with the use of >1 million SNPs from a number of human populations (International HapMap Consortium 2003; Hinds et al. 2005).
Although LD is well defined at a conceptual level, existing approaches for quantifying LD suffer from a number of limitations. Conventional LD measures are typically two-point measures—that is, they quantify LD between two loci, A and B, on the basis of only the allele distributions at these two loci, without exploiting information about the allele distributions of and physical distances from neighboring loci. Despite their popularity, D′ and r2 are both sensitive to allele frequencies (Devlin and Risch 1995) and highly variable in their relationship with the physical distance, d, between A and B. The substantial variability of D′ and r2 makes interpretation of individual LD values challenging. Since average values of D′ and r2 are generally monotonically related to physical distance d, LD patterns based on these conventional measures have been summarized by their average values (Dawson et al. 2002) or by the fraction of common SNPs that are in high LD (e.g., r2>0.8) (Hinds et al. 2005) in a region of empirically chosen size.
With the aim of better quantifying LD, several new measures based on population genetics models have been proposed. Morton et al. (2001) proposed an association probability between a pair of loci, under population genetics assumptions regarding recombination, mutation, migration, etc. Other measures do not directly quantify LD in the usual two-locus manner. Instead, LD is assessed in terms of one (reference) locus, by an estimate of the expected genetic distance from the reference locus to either edge of an ancestral segment (McPeek and Strahs 1999) or by an estimate of the population rate of crossing over (theoretically, a function of expected r2) for a given region (Pritchard and Przeworski 2001). For these model-based measures, robustness to any violation of model assumptions is unknown.
Recognizing the increasing interest in assessing genomewide LD patterns and the limitations of existing measures, we propose a new LD measure, Δ, that borrows information from multiple neighboring loci and does not require restrictive modeling assumptions. For a reference locus on any chromosome, an ancestral segment refers to the haplotype preserved from an ancestral chromosome. The ancestral segment extends in both directions from the reference locus to breakpoints, which are the closest loci where events such as crossover or gene conversion occurred during meiosis processes intervening between the ancestral and current chromosomes. Given a dense set of markers in a large region, the lengths of common ancestral segments between chromosomes can be well approximated by the lengths of shared haplotypes and can lead to a sensible and stable measure of allelic association between two loci.
In the “Methods” section, we first define Δ as a function of the correlation coefficient between the lengths of common ancestral segments around two loci of interest. Next, we develop a U-statistic–based estimator of Δ, 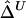 , that takes into account the dependence structure of the observed lengths of shared haplotypes for pairs of chromosomes. An alternative estimator,
, that takes into account the dependence structure of the observed lengths of shared haplotypes for pairs of chromosomes. An alternative estimator, 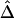 , that naively ignores this dependence structure is also proposed as a simplified and computationally more efficient version. In the “Results” section, simulation studies show that the two estimators,
, that naively ignores this dependence structure is also proposed as a simplified and computationally more efficient version. In the “Results” section, simulation studies show that the two estimators, 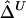 and
and 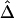 , are strikingly similar. Thus, the remaining simulations and applications to HapMap data focus on properties of the simpler and computationally more tractable estimator,
, are strikingly similar. Thus, the remaining simulations and applications to HapMap data focus on properties of the simpler and computationally more tractable estimator, 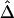 . A method is proposed for estimating LD-decay rates on the basis of the tight relationship between
. A method is proposed for estimating LD-decay rates on the basis of the tight relationship between 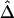 and physical distance d. Then, merits of Δ are demonstrated by analyzing human X-chromosome SNP data from the HapMap Project. We close with a discussion of issues regarding evaluation of the lengths of common ancestral segments.
and physical distance d. Then, merits of Δ are demonstrated by analyzing human X-chromosome SNP data from the HapMap Project. We close with a discussion of issues regarding evaluation of the lengths of common ancestral segments.
Methods
A New LD Measure, Δ
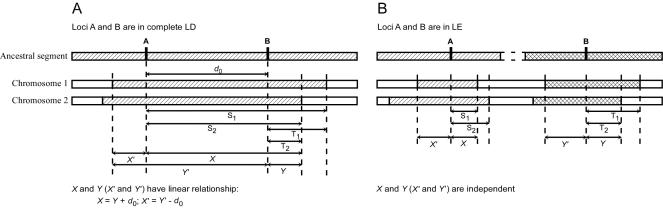
Figure 1 shows the conceptual model that motivates the definition of the LD parameter Δ. For a pair of chromosomes that share a common ancestor around locus A, denote the lengths of the ancestral segments from locus A to their respective breakpoints on one side (e.g., right side) by random variables S1 and S2. Given a locus B located to the right of A at distance d0, random variables T1 and T2 can be defined in the same way. In practice, neither the ancestral haplotypes nor the breakpoints are observable; thus, neither are S1, S2, T1, and T2. Given a dense set of markers, one may observe the lengths of haplotypes shared by the chromosome pair that approximate the lengths of the shared common ancestral segments. These shared haplotype lengths, denoted by X≈min(S1,S2) and Y≈min(T1,T2), may be measured either by physical distance—that is, the number of base pairs (in bp or kb)—or by genetic distance (in cM). However, the former distance is more precise and more relevant because the most appropriate type of data for our proposed methods is that of dense sets of markers (see the “Results” and “Discussion” sections regarding marker density).
Figure 1.
Conceptual model for motivating the LD measure Δ. When loci A and B are in complete LD, the lengths of haplotype sharing around loci A and B are linearly dependent for all chromosome pairs (A). When loci A and B are in LE, the lengths of haplotype sharing around A and B are independent for all chromosome pairs (B).
Two main assumptions are involved in approximating the lengths of shared common ancestral segments by the lengths of shared haplotypes. One is that mutation on the common ancestral segment is ignorable, which is reasonable given the extremely low mutation rate for SNPs. The other is that all alleles identical by state (IBS) are identical by descent (IBD). This second assumption may appear strong, yet the “Discussion” section shows that the new LD measure is robust to violations of the assumption.
Two extreme cases are illustrated in figure 1. When chromosomal segments around loci A and B are co-inherited from the same ancestor, all alleles between loci A and B are IBD (under the assumption of no mutation). In this case, A and B are in complete LD, and the linear relationship X=Y+d0 holds for all chromosome pairs in the population. This perfect linear dependence between X and Y is characterized by a Pearson correlation coefficient of ρxy=1 (fig. 1A). On the other hand, when chromosomal segments around loci A and B are inherited from two independent (unrelated) ancestors, A and B are in complete linkage equilibrium (LE). In this case, the above linear relationship does not hold, and X and Y are independent, corresponding to ρxy=0 (fig. 1B). Therefore, ρxy quantifies the magnitude of LD between A and B.
The same situation applies to the lengths of shared haplotypes on the other side of the reference loci—that is, X′ and Y′ in figure 1. However, the relationship between X+X′ and Y+Y′ is more complex. Therefore, we treat separately the lengths of haplotype sharing to the right and left sides of the reference loci. The new LD measure, Δ, is defined as the arithmetic mean of ρxy and ρx′y′.
There is a statistical challenge in estimating Δ because of the dependence structure of the observed lengths of shared haplotypes between pairs of chromosomes. In the following subsections, an estimator of Δ is developed on the basis of unbiased U-statistics (Lee 1990). We first consider the simplest scenario, in which the sampled haplotypes are distinct by state, which is the case in practice when the population or number of markers is large enough. Then, we extend the method to the general situation where haplotypes are not necessarily distinct.
An Estimator of Δ Based on U-Statistics: 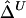 for Distinct Haplotypes
for Distinct Haplotypes
Suppose that one observes n distinct haplotypes, {hi:i=1,…,n}, for a random sample of n chromosomes from a population of interest. It is assumed that the unobservable ancestral segment lengths {(Si,Ti):i=1,…,n} are independently and identically distributed (iid), with joint cumulative distribution function F(S,T),S⩾0,T⩾0. From {hi:i=1,…,n}, one observes X={Xij:i,j=1,…,n,i<j} and Y={Yij:i,j=1,…,n,i<j}, the pairwise lengths of one-sided shared haplotypes for loci A and B, respectively, where (i,j) indexes the 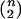 distinct pairs of haplotypes. On the basis of the aforementioned assumptions, Xij≈min(Si,Sj) and Yij≈min(Ti,Tj).
distinct pairs of haplotypes. On the basis of the aforementioned assumptions, Xij≈min(Si,Sj) and Yij≈min(Ti,Tj).
As mentioned before, one of the statistical challenges in estimating the correlation of X and Y is that neither the X nor the Y is a set of independent random variables. To develop a reasonable estimator for the correlation of X and Y, we use U-statistics. As shown in the following proposition, the variances and covariance of X and Y are statistical functionals of degree 4, with kernels that are symmetric functions of four iid random variables. Here, a function is said to be symmetric if it is invariant under permutations of its arguments. As a result, according to Lee (1990, p. 7), the variances and covariance of X and Y can be estimated by the average kernels, termed “U-statistics” because of their unbiasedness. The correlation coefficient of X and Y is then estimated by the estimated covariance standardized by the estimated SDs of X and Y.
Proposition
Let σxy be a statistical functional of degree 4 with kernel function ψ. That is, define σxy as
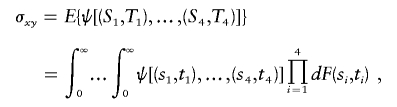 |
where the kernel function is
 |
and {(Si,Ti):i=1,…,n} are iid with cumulative distribution function F(S,T). Then, for X=min(S1,S2) and Y=min(T1,T2), σxy is the covariance of X and Y. The proof is provided in appendix A.
As a result of the proposition, the unique unbiased estimator of the covariance σxy has the form of a U-statistic,
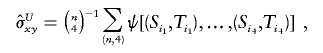 |
where the sum 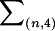 is taken over all distinct four-element subsets {i1,i2,i3,i4} from {1,…,n}. The unobservable random variables min(Si,Sj) and min(Ti,Tj) in the kernel function ψ are then approximated by the corresponding observable random variables Xij and Yij. Hence, the kernel function can be approximated as
is taken over all distinct four-element subsets {i1,i2,i3,i4} from {1,…,n}. The unobservable random variables min(Si,Sj) and min(Ti,Tj) in the kernel function ψ are then approximated by the corresponding observable random variables Xij and Yij. Hence, the kernel function can be approximated as
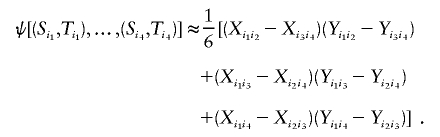 |
Denote the variances of X and Y by σx and σy, respectively. These are also statistical functionals of degree 4:
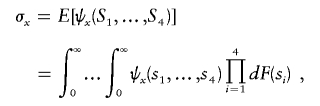 |
where
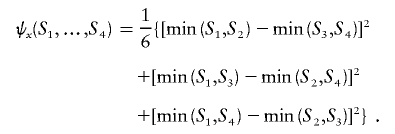 |
One may likewise express σy and ψy for the variance of Y.
Then, the unique unbiased estimators for σx and σy are both U-statistics
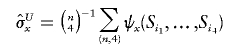 |
and
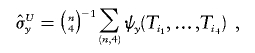 |
where the kernel functions ψx and ψy are approximated by
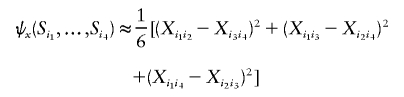 |
and
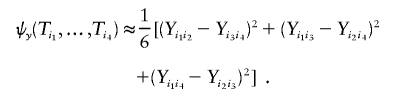 |
A reasonable estimator of the correlation ρxy is then
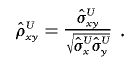 |
Up to this point, we have considered the length of haplotype sharing to one side of a reference locus. Another correlation coefficient, 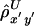 , can be computed likewise for the length of haplotype sharing to the other sides of a pair of loci. An estimator of Δ, denoted by
, can be computed likewise for the length of haplotype sharing to the other sides of a pair of loci. An estimator of Δ, denoted by 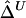 , is then the arithmetic mean of
, is then the arithmetic mean of 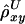 and
and 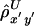 . This measure has reduced variance compared with the two individual correlation coefficients (Y. Wang, unpublished results).
. This measure has reduced variance compared with the two individual correlation coefficients (Y. Wang, unpublished results).
Although, theoretically, correlation coefficients range from −1 to 1, 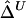 values are seldom negative in our numerical studies. Negative values may occur because of stochastic variation around the true value of zero. In practice, those negative values can be converted to zero.
values are seldom negative in our numerical studies. Negative values may occur because of stochastic variation around the true value of zero. In practice, those negative values can be converted to zero.
An Estimator of Δ Based on Weighted U-Statistics: 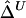 for Nondistinct Haplotypes
for Nondistinct Haplotypes
Next, consider the case in which the n observed haplotypes are not necessarily distinct. Suppose there are m distinct haplotypes {hi:i=1,…,m} that follow a multinomial distribution with parameters (n,θ), where θ={θii=1,…,m} are haplotype frequencies. The haplotype frequencies are the empirical frequencies for phase-known genotype data or may be inferred in the case of unphased data. Among all the distinct four-element subsets of {1,…,m}, the probability for a given subset (i1,i2,i3,i4) is wU(i1,i2,i3,i4)=4!θi1θi2θi3θi4/WU, where the denominator WU is chosen so that 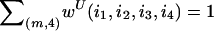 .
.
Then, Lee (1990, p. 64) implies that unbiased estimators for the variances and covariance of X and Y can be obtained from U-statistics weighted by wU:
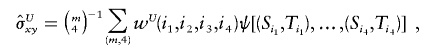 |
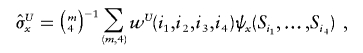 |
and
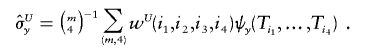 |
For n distinct haplotypes, the weighted U-statistics reduce to the unweighted U-statistics. The correlation coefficient based on weighted U-statistics can be readily applied to unphased genotype data, after haplotype frequencies {θi} are inferred through, for instance, the expectation-maximization (EM) algorithm (Excoffier and Slatkin 1995; Hawley and Kidd 1995; Long et al. 1995).
An Alternative Naive Estimator of Δ, 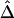
The computation of 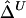 as defined above involves enumerating all
as defined above involves enumerating all 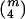 distinct four-element subsets {i1,i2,i3,i4} of {1,…,m} and can be burdensome when the number of distinct haplotypes m is large. When the dependence structure within X and within Y is ignored, intensive computation can be avoided by using a naive estimator
distinct four-element subsets {i1,i2,i3,i4} of {1,…,m} and can be burdensome when the number of distinct haplotypes m is large. When the dependence structure within X and within Y is ignored, intensive computation can be avoided by using a naive estimator 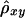 of ρxy.
of ρxy.
In the case of n distinct haplotypes,
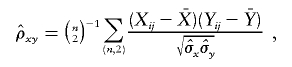 |
where 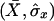 and
and 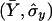 are the usual sample means and variances for the
are the usual sample means and variances for the 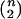 elements of X and Y, respectively.
elements of X and Y, respectively.
In the case of nondistinct haplotypes, each term within the summation above can be weighted by the probability of observing the subset (i,j) from {1,…,m}:
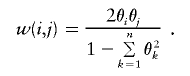 |
Hence,
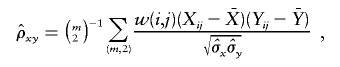 |
where 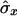 and
and 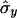 are also weighted by w(i,j),
are also weighted by w(i,j),
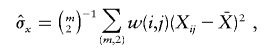 |
and
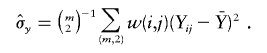 |
Therefore, we propose, as a computationally simpler estimator 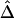 , the average of
, the average of 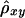 and
and 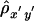 . Simulation studies show that
. Simulation studies show that 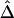 serves as a good approximation of
serves as a good approximation of 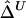 (see the “Results” section). The two estimators are summarized in appendix B. An R package, haploshare, was developed and used to implement computation of the two estimators.
(see the “Results” section). The two estimators are summarized in appendix B. An R package, haploshare, was developed and used to implement computation of the two estimators.
Estimation of Δ for Unphased Data
For estimation of Δ from unphased data, a straightforward two-stage scheme can be adopted. In the first stage, either haplotypes and their frequencies are inferred for the whole data set or phases are inferred for each individual chromosome. We prefer the first approach through the EM algorithm, because it produces unbiased estimates of haplotype frequencies, which can then be used in the second stage to calculate 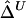 , or
, or 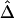 as in the setting of nondistinct haplotypes. The second approach usually results in many ambiguous phases for individual chromosomes, which may compromise the accuracy and stability of
as in the setting of nondistinct haplotypes. The second approach usually results in many ambiguous phases for individual chromosomes, which may compromise the accuracy and stability of 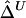 and
and 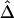 .
.
Results
To investigate properties of Δ and its estimators 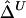 and
and 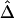 , we performed a series of simulation studies based on genotype data generated by the ms program (Hudson 2002) using the finite-site uniform recombination model. Under this model, the recombination rate for a fixed physical distance should be constant in a given sample, leading to our expectation that LD decays at a constant rate. The crossover probability was chosen to be 10-8 bp−1 for adjacent base pairs, to approximate the average recombination rate for the human genome (i.e., 1 cM per Mb). We then applied our new method to HapMap data, to study human fine-scale genomewide LD patterns.
, we performed a series of simulation studies based on genotype data generated by the ms program (Hudson 2002) using the finite-site uniform recombination model. Under this model, the recombination rate for a fixed physical distance should be constant in a given sample, leading to our expectation that LD decays at a constant rate. The crossover probability was chosen to be 10-8 bp−1 for adjacent base pairs, to approximate the average recombination rate for the human genome (i.e., 1 cM per Mb). We then applied our new method to HapMap data, to study human fine-scale genomewide LD patterns.
Comparison of 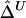 to Its Approximation
to Its Approximation 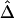 and Impact of Sample Size
and Impact of Sample Size
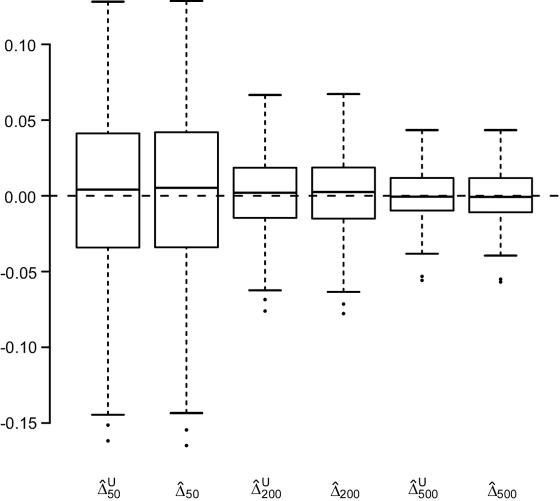
We first focused, for simplicity, on fully phased data, to assess our two main estimators of the LD parameter Δ. Since the underlying parameter value Δ cannot be explicitly specified in the simulations with ms, we generated a large population of haplotypes (N=4,000) for 666 markers covering 300 kb and set 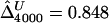 as the true Δ for a given marker pair located 5 kb apart. Then, 300 samples were drawn from the simulated population for sample sizes n=50, 200, and 500. For each sample, both
as the true Δ for a given marker pair located 5 kb apart. Then, 300 samples were drawn from the simulated population for sample sizes n=50, 200, and 500. For each sample, both 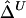 and
and 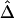 were calculated. In figure 2, boxplots of the biases
were calculated. In figure 2, boxplots of the biases 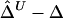 and
and 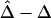 for these 300 samples suggest that, as sample size n increases, both estimators converge to the true Δ. The same analysis was performed for marker pairs located 50 kb and 100 kb apart, and similar results for the biases and variances of
for these 300 samples suggest that, as sample size n increases, both estimators converge to the true Δ. The same analysis was performed for marker pairs located 50 kb and 100 kb apart, and similar results for the biases and variances of 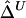 and
and 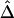 were produced. For all three marker pairs, the SDs for
were produced. For all three marker pairs, the SDs for 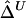 are slightly smaller than those for
are slightly smaller than those for 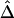 (table 1). Overall, however, the dependence structures within X and within Y do not seem to have much impact on the estimation of the correlation coefficient of X and Y, and, in practice, the two estimators,
(table 1). Overall, however, the dependence structures within X and within Y do not seem to have much impact on the estimation of the correlation coefficient of X and Y, and, in practice, the two estimators, 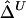 and
and 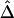 , can be considered equivalent.
, can be considered equivalent.
Figure 2.
Boxplots of biases for the two estimators 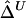 and
and 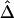 . From a simulated population of N=4,000 haplotypes, 300 random samples of n haplotypes were drawn for n=50, 200, and 500.
. From a simulated population of N=4,000 haplotypes, 300 random samples of n haplotypes were drawn for n=50, 200, and 500. 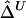 and
and 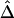 were calculated for a particular marker pair located 5 kb apart. The six boxplots (from left to right) are for
were calculated for a particular marker pair located 5 kb apart. The six boxplots (from left to right) are for 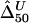 ,
, 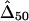 ,
, 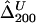 ,
, 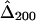 ,
, 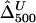 , and
, and 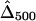 , where the numbers in the subscript denote the sample size, n.
, where the numbers in the subscript denote the sample size, n.
Table 1.
SDs of 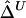 and
and 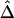 in a Simulation Study[Note]
in a Simulation Study[Note]
| SD |
||||||
|
d=5 kb |
d=50 kb |
d=100 kb |
||||
|
Sample Size (n) |
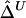 |
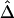 |
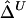 |
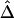 |
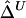 |
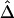 |
| 50 | .0572 | .0579 | .0814 | .0835 | .0532 | .0540 |
| 200 | .0239 | .0245 | .0387 | .0397 | .0228 | .0231 |
| 500 | .0154 | .0158 | .0226 | .0232 | .0132 | .0135 |
Note.— SDs were calculated for 300 random samples of n haplotypes for three marker pairs arbitrarily chosen with physical distance d=5, 50, and 100 kb.
On the basis of these results and because of its simplicity and computational efficiency, we used the naive estimator 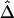 for the remainder of the simulation studies and for the HapMap data analysis.
for the remainder of the simulation studies and for the HapMap data analysis.
Relationship of 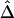 with Physical Distance
with Physical Distance
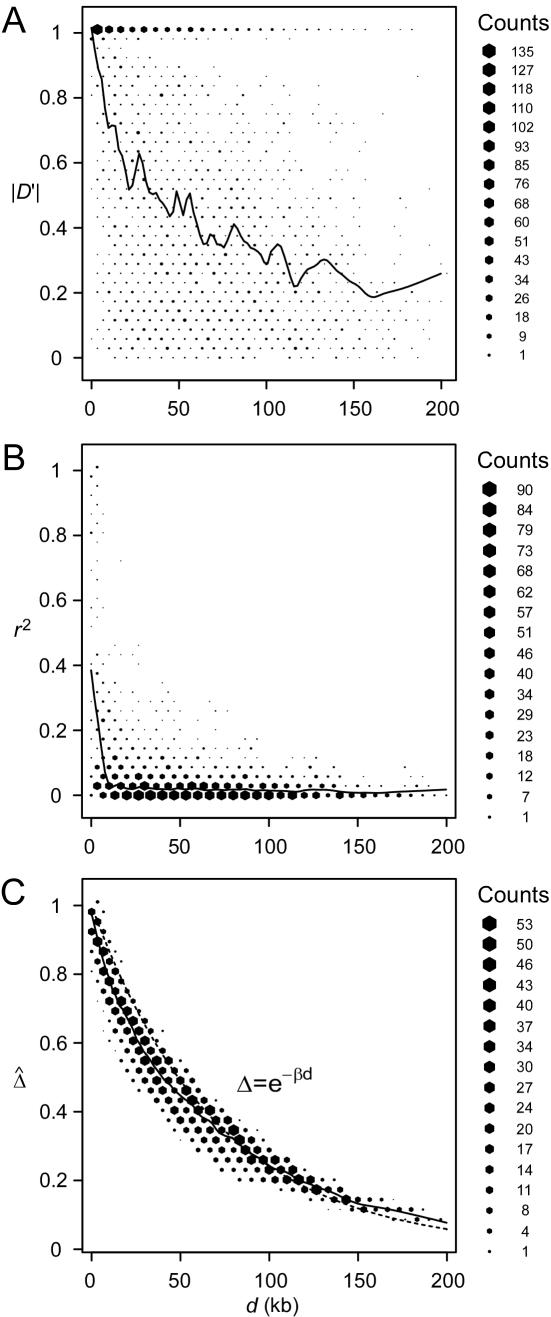
A data set of 245 SNPs, with minor-allele frequencies (MAFs) >5%, was simulated in a region of 500 kb for 200 chromosomes. We focused on 81 SNPs spanning the 200-kb region of interest. Other markers on the flanking regions of the 200-kb region provide information about the length of haplotype sharing for a reference locus at the edge of the region of interest. We computed and displayed the three pairwise LD measures D′ (fig. 3A), r2 (fig. 3B), and 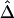 (fig. 3C) for each of the
(fig. 3C) for each of the 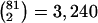 SNP pairs in the region of interest. Visualization tools from the Bioconductor R hexbin package were applied to produce “2D histograms,” which represent the density of data points in a scatterplot by using hexagonal bins of varying areas. Both |D′| and r2 tend to decrease as physical distance d increases, as shown by the locally weighted scatterplot-smoothing (lowess) curves. However, |D′| and r2 are highly variable at any given d. In contrast,
SNP pairs in the region of interest. Visualization tools from the Bioconductor R hexbin package were applied to produce “2D histograms,” which represent the density of data points in a scatterplot by using hexagonal bins of varying areas. Both |D′| and r2 tend to decrease as physical distance d increases, as shown by the locally weighted scatterplot-smoothing (lowess) curves. However, |D′| and r2 are highly variable at any given d. In contrast, 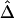 has a nearly deterministic relationship with d.
has a nearly deterministic relationship with d.
Figure 3.
Pairwise LD measured as a function of physical distance d. A, |D′|; B, r2; C, 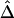 . Hexagonal bins of different areas are used to represent counts (Bioconductor R package hexbin). Locally weighted scatterplot-smoothing (lowess) curves are plotted in black, with the smooth (the Y-axis value) at each value influenced by 5% data points. For SNP data simulated under the uniform recombination model, LD decays exponentially at a constant rate, which can be estimated on the basis of the linear regression model
. Hexagonal bins of different areas are used to represent counts (Bioconductor R package hexbin). Locally weighted scatterplot-smoothing (lowess) curves are plotted in black, with the smooth (the Y-axis value) at each value influenced by 5% data points. For SNP data simulated under the uniform recombination model, LD decays exponentially at a constant rate, which can be estimated on the basis of the linear regression model 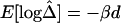 . This relationship is plotted with the dotted line.
. This relationship is plotted with the dotted line.
Moreover, the lowess curve for 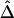 nearly overlaps the exponential function
nearly overlaps the exponential function 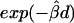 (fig. 3C, dotted line), implying that the relationship between
(fig. 3C, dotted line), implying that the relationship between 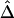 and d fits the expectation that LD decays exponentially with increasing genetic distance, which is equivalent to physical distance d on a fine scale under the uniform-recombination model. Specifically,
and d fits the expectation that LD decays exponentially with increasing genetic distance, which is equivalent to physical distance d on a fine scale under the uniform-recombination model. Specifically, 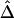 is nearly 1 for any pair of closely located SNPs and decreases at a constant rate. By fitting the linear model
is nearly 1 for any pair of closely located SNPs and decreases at a constant rate. By fitting the linear model 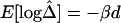 , the LD-decay rate may be estimated as
, the LD-decay rate may be estimated as 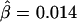 , meaning that
, meaning that  decays exponentially at a rate of 0.014 per kb in the region of interest.
decays exponentially at a rate of 0.014 per kb in the region of interest.
Impact of Phase-Information Loss on 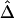
Estimation of Δ, given phase-unknown genotype data, relies on the inference of haplotypes and their frequencies. For a large number of markers, haplotype inference can be very computationally challenging, and many existing programs adopt partition-ligation techniques in which the sequence of markers is partitioned into blocks. However, this strategy may compromise the accuracy of inferred haplotypes for the entire marker sequence. In the following simulation study, we studied how well 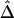 performs for unphased data with different numbers of markers used for haplotype estimation. It was expected that the more accurate the inferred haplotypes, the more robust the estimated Δ. Here, haplotypes were estimated using the software package HPlus, which applies estimating equation theory to implement efficient maximum-likelihood estimation of haplotype frequencies and their variances (Li et al. 2003).
performs for unphased data with different numbers of markers used for haplotype estimation. It was expected that the more accurate the inferred haplotypes, the more robust the estimated Δ. Here, haplotypes were estimated using the software package HPlus, which applies estimating equation theory to implement efficient maximum-likelihood estimation of haplotype frequencies and their variances (Li et al. 2003).
We randomly paired the above 200 haplotypes to create 100 diploid individuals with unphased genotypes. The region of interest was still the 200 kb containing the 81 SNPs. First, haplotypes were estimated for the entire set of 245 SNPs. On the basis of inferred haplotypes with estimated frequencies >0.02%, the naive estimator 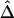 was then computed for the 3,240 SNP pairs and was plotted against physical distances d (fig. 4A). Next, we reduced the number of markers to be haplotyped to 141 and 101, corresponding to 30 and 10, respectively, SNPs in each flanking region, in addition to the 81 SNPs in the region of interest. Figure 4B and 4C show that smaller variations of
was then computed for the 3,240 SNP pairs and was plotted against physical distances d (fig. 4A). Next, we reduced the number of markers to be haplotyped to 141 and 101, corresponding to 30 and 10, respectively, SNPs in each flanking region, in addition to the 81 SNPs in the region of interest. Figure 4B and 4C show that smaller variations of 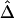 , at any given distance d, are observed for the smaller numbers of markers. These results suggest that
, at any given distance d, are observed for the smaller numbers of markers. These results suggest that 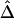 performs well for unphased data and has a similar relationship with physical distance d (fig. 3C), especially when markers are chosen in such a way that haplotypes are inferred reliably.
performs well for unphased data and has a similar relationship with physical distance d (fig. 3C), especially when markers are chosen in such a way that haplotypes are inferred reliably.
Figure 4.
Application of 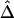 to unphased genotype data. All 245 SNPs (A), 30 SNPs in each of the two flanking regions in addition to the 81 SNPs in the region of interest (B), and 10 SNPs in each of the two flanking regions, in addition to the 81 SNPs in the region of interest (C), are used for haplotype estimation before pairwise
to unphased genotype data. All 245 SNPs (A), 30 SNPs in each of the two flanking regions in addition to the 81 SNPs in the region of interest (B), and 10 SNPs in each of the two flanking regions, in addition to the 81 SNPs in the region of interest (C), are used for haplotype estimation before pairwise 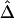 is calculated for the 81 SNPs and plotted against physical distance in each situation.
is calculated for the 81 SNPs and plotted against physical distance in each situation.
However, it is not true that the fewer the markers the better. Comparing figures 4B and 4C, we observe that Δ is underestimated when only 10 SNPs instead of 30 are used in the flanking regions to evaluate the length of haplotype sharing. As a result, the LD-decay rates in the two analyses are different, with 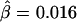 in figure 4B and
in figure 4B and 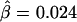 in figure 4C, the former being much closer to that estimated with phased data (
in figure 4C, the former being much closer to that estimated with phased data (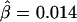 ) using all 245 SNPs.
) using all 245 SNPs.
Therefore, there appears to be the following trade-off. With reduction of the number of markers to be haplotyped and used to evaluate the lengths of haplotype sharing, haplotype inference is more reliable, leading to more robust estimation of Δ. However, the lengths of haplotype sharing might be more censored (see the “Discussion” section) or evaluated on the basis of sparser sets of SNPs (see the “Impact of Marker Density on 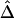 ” subsection), which would lead to biased estimation of Δ. Note that, even though estimation of Δ is biased (as in fig. 4C), the strong relationship of
” subsection), which would lead to biased estimation of Δ. Note that, even though estimation of Δ is biased (as in fig. 4C), the strong relationship of 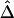 with physical distance is still present, which implies the potential usefulness of
with physical distance is still present, which implies the potential usefulness of 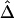 in this situation.
in this situation.
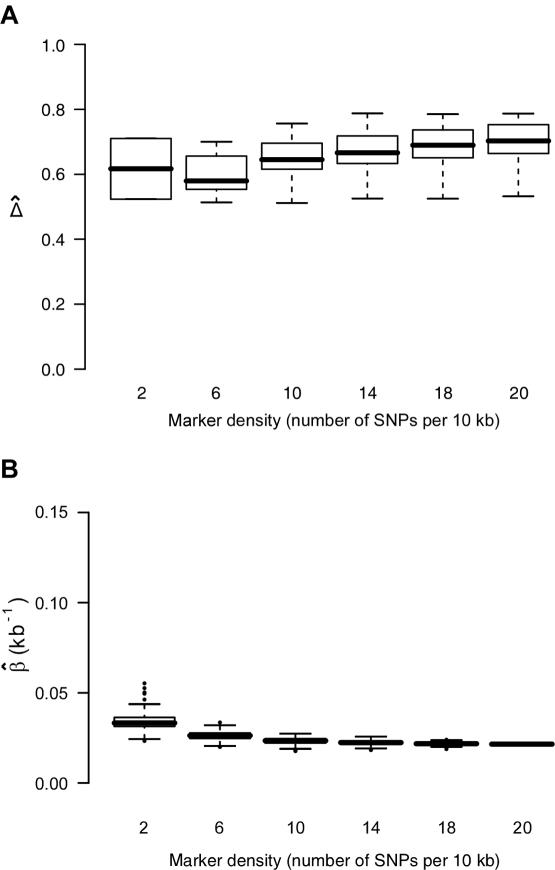
Impact of Marker Density on 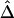
Marker density can have a significant impact on how well the length of haplotype sharing approximates the length of the common ancestral segment. Generally speaking, the denser the marker map, the better the approximation. To study the effect of marker density on 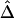 , we simulated a data set of 200 haplotypes in a region of size 180 kb. From the 196 SNPs with MAFs >1% in the middle 100-kb region of interest, we randomly selected subsets of SNPs according to the following percentages: 90%, 70%, 50%, 30%, and 10%. These percentages allowed us to monitor the stability of
, we simulated a data set of 200 haplotypes in a region of size 180 kb. From the 196 SNPs with MAFs >1% in the middle 100-kb region of interest, we randomly selected subsets of SNPs according to the following percentages: 90%, 70%, 50%, 30%, and 10%. These percentages allowed us to monitor the stability of 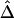 for a fixed physical distance d, since the marker density decreases from 20 to 2 SNPs per 10 kb. This random selection of markers produced similar distributions of MAFs across different subsets, so that the effects of marker density and marker-allele frequency (a potentially influential factor in the behavior of an LD measure) are not confounded. Figure 5A shows the distributions of
for a fixed physical distance d, since the marker density decreases from 20 to 2 SNPs per 10 kb. This random selection of markers produced similar distributions of MAFs across different subsets, so that the effects of marker density and marker-allele frequency (a potentially influential factor in the behavior of an LD measure) are not confounded. Figure 5A shows the distributions of 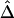 for pairs of markers located 15–16 kb apart for different marker densities. Although
for pairs of markers located 15–16 kb apart for different marker densities. Although 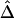 tends to decrease slightly as marker density decreases,
tends to decrease slightly as marker density decreases, 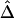 is generally robust to marker density. Similar patterns of robustness were observed for other values of the physical distance d.
is generally robust to marker density. Similar patterns of robustness were observed for other values of the physical distance d.
Figure 5.
Robustness of 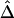 and its estimated decay rate
and its estimated decay rate 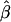 to marker density. A, Distributions of
to marker density. A, Distributions of 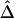 for pairs of SNPs that are located 15–16 kb apart for different marker densities. B, Distributions of estimated LD-decay rates
for pairs of SNPs that are located 15–16 kb apart for different marker densities. B, Distributions of estimated LD-decay rates 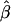 for 200 SNP subsets randomly selected for each marker density. The scale of the vertical axis was chosen to match that in figure 7.
for 200 SNP subsets randomly selected for each marker density. The scale of the vertical axis was chosen to match that in figure 7.
The impact of marker density on the estimated rate of LD decay was also investigated. The process for selecting random subsets of the original markers was repeated 200 times for each marker density, and the LD-decay rate β was estimated each time (fig. 5B). In general, 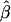 appears to be fairly stable for marker densities of ⩾6 SNPs per 10 kb but not for the low density of 2 SNPs per 10 kb, because of the loss of precision for measuring the length of haplotype sharing. Note that, as the marker density decreases, the number of marker pairs decreases, so that
appears to be fairly stable for marker densities of ⩾6 SNPs per 10 kb but not for the low density of 2 SNPs per 10 kb, because of the loss of precision for measuring the length of haplotype sharing. Note that, as the marker density decreases, the number of marker pairs decreases, so that 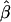 is estimated with larger variance.
is estimated with larger variance.
Impact of Marker-Allele Frequency on 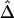
Conventional two-point LD measures are very sensitive to marker-allele frequency. To investigate the sensitivity of 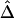 to marker-allele frequency, we used subsets of SNPs with different MAFs from one simulated data set to calculate
to marker-allele frequency, we used subsets of SNPs with different MAFs from one simulated data set to calculate 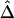 for pairs of markers in each SNP subset. The minimum MAFs in each subset were 0%, 1%, 5%, 10%, and 20%. The corresponding marker densities for each subset were approximately 23, 19, 12, 10, and 6 SNPs per 10 kb. In this range of marker densities, on the basis of the above results, Δ and its decay rate β can be robustly and reliably estimated. Clearly, the exponential relationship between
for pairs of markers in each SNP subset. The minimum MAFs in each subset were 0%, 1%, 5%, 10%, and 20%. The corresponding marker densities for each subset were approximately 23, 19, 12, 10, and 6 SNPs per 10 kb. In this range of marker densities, on the basis of the above results, Δ and its decay rate β can be robustly and reliably estimated. Clearly, the exponential relationship between 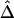 and d and the low variability of
and d and the low variability of 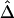 at any given d are both maintained across the five SNP subsets. For pairs of SNPs located a certain distance away from each other—say, 10–11 kb—
at any given d are both maintained across the five SNP subsets. For pairs of SNPs located a certain distance away from each other—say, 10–11 kb—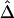 is fairly stable in terms of its median and interquartile range across subsets of SNPs with different MAFs (fig. 6). In contrast, |D′| is more likely to be 1 and r2 is more likely to be close to 0 when SNPs with lower MAFs are included in the analysis. Thus, both |D′| and r2 are highly sensitive to allele frequencies. Furthermore, the estimated rate of LD decay
is fairly stable in terms of its median and interquartile range across subsets of SNPs with different MAFs (fig. 6). In contrast, |D′| is more likely to be 1 and r2 is more likely to be close to 0 when SNPs with lower MAFs are included in the analysis. Thus, both |D′| and r2 are highly sensitive to allele frequencies. Furthermore, the estimated rate of LD decay 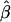 is also very robust to SNP allele frequency, ranging from 0.009 to 0.011 across subsets of SNPs.
is also very robust to SNP allele frequency, ranging from 0.009 to 0.011 across subsets of SNPs.
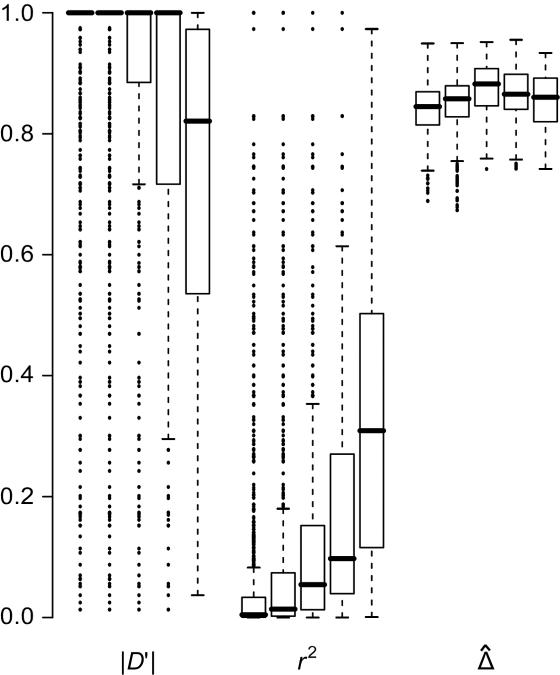
Figure 6.
Robustness of LD measures to marker-allele frequency. Distributions of |D′|, r2, and 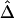 for SNP pairs that are located 10–11 kb apart, with use of subsets of SNPs with MAFs (from left to right) of at least 0%, 1%, 5%, 10%, and 20%, for each measure.
for SNP pairs that are located 10–11 kb apart, with use of subsets of SNPs with MAFs (from left to right) of at least 0%, 1%, 5%, 10%, and 20%, for each measure.
Relationship of 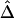 with Recombination Rate
with Recombination Rate
In the ms program, recombination rates for the simulated data can be controlled by crossover probabilities for adjacent base pairs. The following four values for the crossover probability were considered: 10-9, 10-8, 10-7, and 10-6 per kb. For a fixed physical distance—say, d=15–16 kb—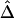 decreases as the recombination rate increases (fig. 7A). Furthermore, LD-decay rates, estimated for 200 independently simulated data sets in each setting, were strongly related to recombination rates (fig. 7B).
decreases as the recombination rate increases (fig. 7A). Furthermore, LD-decay rates, estimated for 200 independently simulated data sets in each setting, were strongly related to recombination rates (fig. 7B).
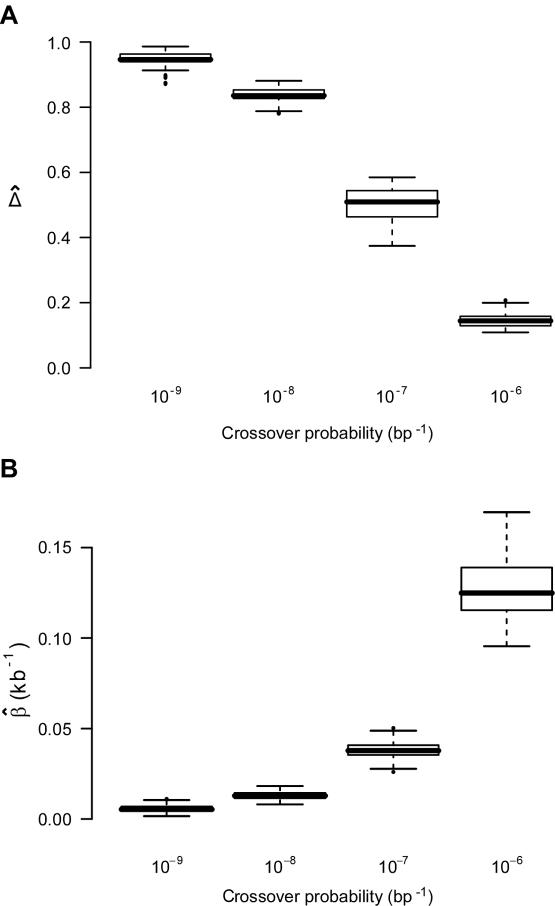
Figure 7.
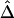 and its estimated decay rate
and its estimated decay rate 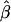 as a function of recombination rate. A, Distributions of
as a function of recombination rate. A, Distributions of 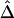 for pairs of SNPs that are located 15–16 kb apart, for different crossover probabilities for adjacent base pairs. B, Distributions of estimated LD-decay rates
for pairs of SNPs that are located 15–16 kb apart, for different crossover probabilities for adjacent base pairs. B, Distributions of estimated LD-decay rates 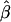 , for 200 simulations at different crossover probabilities.
, for 200 simulations at different crossover probabilities.
Analysis of HapMap SNP Data for the X Chromosome
We applied Δ to HapMap data (phase I) for the X chromosomes of 30 mothers in the CEPH population (Utah residents with ancestry from northern and western Europe). Genotypes were fully phased at 56,001 SNPs, among which there were 19,127 monomorphic SNPs. LD-decay rates β were estimated at every polymorphic SNP locus by applying the method of least squares to the exponential-decay model for 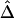 . Specifically, pairwise
. Specifically, pairwise 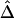 was computed from neighboring polymorphic SNPs within 100-kb windows, as long as there were ⩾7 polymorphic SNPs, so that the number of marker pairs used to estimate β was at least 21 (fig. 8A). The lengths of haplotype sharing were evaluated in 1.1-Mb regions surrounding every polymorphic SNP. The marker density was adequately high in 99% of these regions (>2 per 10 kb) to support reliable estimation of Δ and its decay rate β. The results show that LD on the X chromosome decays exponentially at an average rate of 0.0073 per kb within 100-kb windows, whereas, at certain loci, the rate can reach 0.054 per kb. Figure 8B provides a higher-resolution display for 100 polymorphic SNPs in the 12.89–13.17-Mb region. Pseudocolor images of pairwise |D′|, r2, and
was computed from neighboring polymorphic SNPs within 100-kb windows, as long as there were ⩾7 polymorphic SNPs, so that the number of marker pairs used to estimate β was at least 21 (fig. 8A). The lengths of haplotype sharing were evaluated in 1.1-Mb regions surrounding every polymorphic SNP. The marker density was adequately high in 99% of these regions (>2 per 10 kb) to support reliable estimation of Δ and its decay rate β. The results show that LD on the X chromosome decays exponentially at an average rate of 0.0073 per kb within 100-kb windows, whereas, at certain loci, the rate can reach 0.054 per kb. Figure 8B provides a higher-resolution display for 100 polymorphic SNPs in the 12.89–13.17-Mb region. Pseudocolor images of pairwise |D′|, r2, and 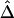 matrices in this region are displayed in figure 8D–8F. Note the much “smoother” appearance of the pseudocolor image for
matrices in this region are displayed in figure 8D–8F. Note the much “smoother” appearance of the pseudocolor image for 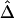 , which clearly suggests blocks of markers with high LD.
, which clearly suggests blocks of markers with high LD.
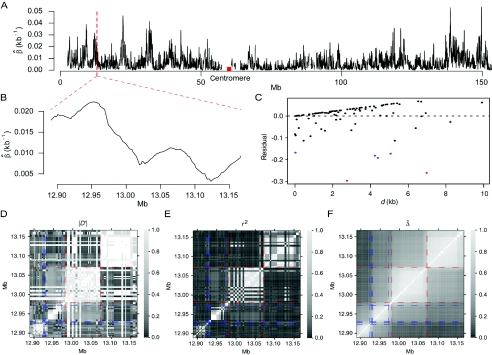
Figure 8.
LD measures for HapMap data for 56,001 SNPs on the X chromosomes of 30 women in the CEPH population. A, LD-decay rates at every SNP locus, estimated from polymorphic SNPs in the neighboring 100-kb region. B, Display with higher resolution for an arbitrarily selected region of 275 kb. C, Residual plot from fitting the linear-regression model 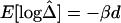 with data from the 275-kb region. Adjacent marker pairs with large negative residuals are heuristically considered recombination hotspots and are plotted using colored dots, with red representing even more extreme residuals than blue. D–F, Pseudocolor images of pairwise |D′|, r2, and
with data from the 275-kb region. Adjacent marker pairs with large negative residuals are heuristically considered recombination hotspots and are plotted using colored dots, with red representing even more extreme residuals than blue. D–F, Pseudocolor images of pairwise |D′|, r2, and 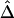 matrices. The red and blue dashed lines correspond to the marker pairs plotted using red and blue dots in panel C.
matrices. The red and blue dashed lines correspond to the marker pairs plotted using red and blue dots in panel C.
Actual genomic data are different from simulated data in one important aspect. The recombination rate can be fixed in the simulated data, whereas it varies greatly in the real data. Since recombination causes LD decay, the recombination rate is directly related to the LD-decay rate, as shown in the simulation studies above. Thus, we do not expect LD to decay at a homogeneous rate in the human genome. However, in the linear-regression model used to estimate the LD-decay rate, LD is assumed to decay at a constant rate within the region of interest. The result therefore reflects the rate at which LD decays, on average, over the region. We have chosen to estimate LD-decay rates on the basis of regions of only 100 kb, with the hope that the LD-decay rate does not change dramatically within such relatively small regions. However, this assumption could still be violated because of recombination hotspots. A recombination hotspot is a site prone to recombination and is experimentally identified as a region as narrow as 1–2 kb, where recombination rates are higher than in neighboring regions (Jeffreys et al. 2001). Therefore, LD decays faster across such a hotspot. If a smaller window size is used, the reduced number of markers may be insufficient for stable parameter estimation in the regression model. More methodological work concerning the development of indices for the investigation of fine-scale LD is needed. We anticipate that the new LD measure Δ will make valuable contributions to this endeavor.
As an example of the usefulness of our new LD measure, a heuristic analysis of data for the 275-kb region in figure 8B suggests that recombination hotspots may be identified as follows on the basis of 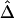 . We focus on all adjacent marker pairs in the region of interest, as long as
. We focus on all adjacent marker pairs in the region of interest, as long as 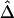 can be calculated on the basis of markers with density higher than 2 SNPs per 10 kb. The tight relationship between
can be calculated on the basis of markers with density higher than 2 SNPs per 10 kb. The tight relationship between 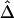 and physical distance d is expected to be maintained for these marker pairs. Under the assumption that LD decays at the same rate across all adjacent marker pairs, the regression model
and physical distance d is expected to be maintained for these marker pairs. Under the assumption that LD decays at the same rate across all adjacent marker pairs, the regression model 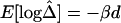 was fit. Outlier adjacent marker pairs, with unexpectedly small residuals (i.e., large negative values), can be considered as recombination hotspots and identified through model diagnostic techniques. However, usual model diagnostic techniques are not applicable here because of the dependence of
was fit. Outlier adjacent marker pairs, with unexpectedly small residuals (i.e., large negative values), can be considered as recombination hotspots and identified through model diagnostic techniques. However, usual model diagnostic techniques are not applicable here because of the dependence of 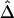 between adjacent marker pairs (as shown by the residual plot in fig. 8C). In this article, we do not intend to address in depth the issue of outlier detection. Instead, we graphically illustrate that adjacent marker pairs with extreme negative residuals (plotted by the red and blue dots in fig. 8C) correspond to potential recombination hotspots (indicated by the red and blue lines, respectively, in fig. 8D–8F).
between adjacent marker pairs (as shown by the residual plot in fig. 8C). In this article, we do not intend to address in depth the issue of outlier detection. Instead, we graphically illustrate that adjacent marker pairs with extreme negative residuals (plotted by the red and blue dots in fig. 8C) correspond to potential recombination hotspots (indicated by the red and blue lines, respectively, in fig. 8D–8F).
Discussion
The proposed LD measure Δ is based on the unobservable lengths of common ancestral segments, which are approximated by shared haplotype lengths. The degree of precision for this approximation, influenced by several factors, directly affects estimation of Δ. Here, we examine the following factors one by one: distinction between IBD and IBS status, marker density, and censoring of shared haplotype lengths.
First, the length of a common ancestral segment is best measured on the basis of alleles IBD for a chromosome pair. However, in practice, it is often impossible to distinguish between IBD and IBS. Here, we argue that 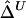 and
and 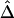 remain robust to discrepancies between IBD and IBS. In the presence of alleles IBS for a long sequence of contiguous loci, the probability of IBD at each locus is greatly elevated and so is the probability that these loci belong to a common ancestral segment. The larger the length of haplotype sharing by state, the higher the probability of IBD. On the other hand, for chromosome pairs that do not share common ancestral segments, the probability of sharing alleles IBS at a long sequence of contiguous loci is very small. We do not expect the background level of haplotype sharing due to IBS to have a significant effect on
remain robust to discrepancies between IBD and IBS. In the presence of alleles IBS for a long sequence of contiguous loci, the probability of IBD at each locus is greatly elevated and so is the probability that these loci belong to a common ancestral segment. The larger the length of haplotype sharing by state, the higher the probability of IBD. On the other hand, for chromosome pairs that do not share common ancestral segments, the probability of sharing alleles IBS at a long sequence of contiguous loci is very small. We do not expect the background level of haplotype sharing due to IBS to have a significant effect on 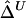 and
and 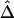 , because these estimators are mostly determined by large shared haplotype lengths at both loci, which are more likely to be due to IBD. Therefore,
, because these estimators are mostly determined by large shared haplotype lengths at both loci, which are more likely to be due to IBD. Therefore, 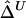 and
and 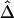 should be robust to the approximation of IBD by IBS.
should be robust to the approximation of IBD by IBS.
Second, higher marker densities lead to better approximation of the lengths of common ancestral segments by the lengths of shared haplotypes. On the basis of our simulation studies, the impact of marker density on estimation of Δ is very limited once this density is above a certain threshold—namely, 2 SNPs per 10 kb—which is feasible given the imminent availability of ultra-high-volume genotyping platforms. Note that one need not identify tagging SNPs when markers are used for the purpose of tracking the length of haplotype sharing. In fact, subsetting SNPs does not enhance but impairs accurate evaluation of the length of haplotype sharing because of reduced marker density.
Third, censoring at the edge of the genotyped region is an important practical issue to be considered. For a region of relatively small size, the length of haplotype sharing may not be observed to its full extent for some chromosome pairs that share extensively long common haplotypes. For genome-scan data, the same problem is present when evaluating the length of haplotype sharing for a reference locus close to a telomere or when dealing with phase-unknown data with a moderate number of markers used for haplotype inference. This phenomenon is very similar to censoring for survival time and may bias 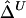 and
and 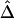 . Further research is needed to adjust these estimators if censoring is involved at one or both markers. For the time being, we recommend that caution be taken for small genotyped regions and that
. Further research is needed to adjust these estimators if censoring is involved at one or both markers. For the time being, we recommend that caution be taken for small genotyped regions and that 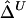 or
or 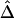 be calculated only if flanking regions of decent sizes are also genotyped. Just as there exists a threshold for marker density above which
be calculated only if flanking regions of decent sizes are also genotyped. Just as there exists a threshold for marker density above which 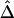 stabilizes, there is such a threshold for the size of flanking regions. Adequate flanking region sizes are usually determined by how fast LD decays in these regions. For instance, when LD decays fast, smaller flanking regions are considered adequate. For HapMap X-chromosome data, the lengths of haplotype sharing were calculated using 500-kb flanking regions on both sides of the reference locus. In addition, to avoid censoring around telomeres, we used only the correlation coefficient for the right-sided or left-sided lengths of haplotype sharing for markers around the left or right, respectively, telomere.
stabilizes, there is such a threshold for the size of flanking regions. Adequate flanking region sizes are usually determined by how fast LD decays in these regions. For instance, when LD decays fast, smaller flanking regions are considered adequate. For HapMap X-chromosome data, the lengths of haplotype sharing were calculated using 500-kb flanking regions on both sides of the reference locus. In addition, to avoid censoring around telomeres, we used only the correlation coefficient for the right-sided or left-sided lengths of haplotype sharing for markers around the left or right, respectively, telomere.
Finally, we address the connections and differences between recombination hotspots and boundaries for haplotype blocks, since the latter have become accepted as a general model for LD patterns throughout the genome. Both terms describe patterns of LD and were often used interchangeably in the past. For instance, Anderson and Novembre (2003) evaluated their method for identifying block boundaries by simulation studies in which recombination hotspots were generated as block boundaries. From the example in the “Results” section, the identified hotspots seemingly are good candidates for block boundaries. However, the two terms refer to different phenomena, and different methods may be required in practice to detect them. For recombination hotspots at which LD decays faster than in other regions, LD decay rate is an important aspect because physical distance plays an essential role. In the HapMap data analysis, hotspots were identified on the basis of residuals for a fitted exponential-decay model for 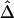 and d instead of on the basis of
and d instead of on the basis of 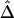 only. In contrast, block boundaries are traditionally chosen to achieve low haplotype diversity within each block, on the basis of significantly low LD values, without taking physical distance into consideration.
only. In contrast, block boundaries are traditionally chosen to achieve low haplotype diversity within each block, on the basis of significantly low LD values, without taking physical distance into consideration.
In conclusion, simulation studies and analysis of HapMap data demonstrate that our proposed LD measure Δ and its estimators 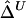 and
and 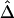 are superior to two of the most popular two-point LD measures, in terms of their relationship with physical distance, their small variability at any given distance, and their robustness to SNP allele frequencies. In contrast to alternative LD measures that are based on population genetics models, Δ is a robust empirical measure and should be applicable regardless of population structure. A definition of LD-decay rate and a regression-based method for estimating such rates were proposed, and simulation studies demonstrated that the LD-decay rate was a function of the recombination rate. The new LD measure Δ is a promising tool for studying population genetics and for mapping complex disease genes. Our proposed methods can also be readily applied to data for more polymorphic DNA markers (e.g., microsatellites) or amino acid sequence data without further extension.
are superior to two of the most popular two-point LD measures, in terms of their relationship with physical distance, their small variability at any given distance, and their robustness to SNP allele frequencies. In contrast to alternative LD measures that are based on population genetics models, Δ is a robust empirical measure and should be applicable regardless of population structure. A definition of LD-decay rate and a regression-based method for estimating such rates were proposed, and simulation studies demonstrated that the LD-decay rate was a function of the recombination rate. The new LD measure Δ is a promising tool for studying population genetics and for mapping complex disease genes. Our proposed methods can also be readily applied to data for more polymorphic DNA markers (e.g., microsatellites) or amino acid sequence data without further extension.
Acknowledgments
This work was partially supported by National Institutes of Health (NIH) training grant 5 T32 HG00047, NIH grant RO1 LM07609, and NIH grant 5RO1 CA106320-05. We thank Ying Qing Chen, Sue Li, and Najma Khalid, for helpful discussions.
Appendix A : Proof of the Proposition
Define Xij=min(Si,Sj) and Yij=min(Ti,Tj). Since (S1,T1),…,(S4,T4) are iid, we have E(X12Y12)=E(X34Y34) and E(X12Y34)=E(X34Y12)=E(X12)E(Y12). Then,
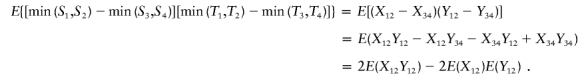 |
Similarly,
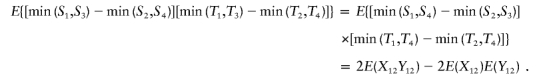 |
Therefore, E{ψ[(S1,T1),…,(S4,T4)]}=E(X12Y12)-E(X12)E(Y12) is the covariance of X and Y.
Appendix B: Two Estimators of Δ
Suppose that, among a random sample of n chromosomes, there are m distinct haplotypes {hi:i=1,…,m} for a region that covers two loci of interest, A and B. The haplotypes {hi} follow a multinomial distribution with parameters (n,θ), where θ={θi:i=1,…,m} are either empirical or inferred haplotype frequencies. Let X={Xij:i,j=1,…,m,i<j} and Y={Yij:i,j=1,…,m,i<j} denote the pairwise lengths of one-sided shared haplotypes for loci A and B, respectively. Similarly, let X′ and Y′ denote the lengths of shared haplotypes on the other sides of loci A and B. The following two estimators of Δ are both arithmetic means of correlation-coefficient estimators  and
and 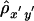 , based on two different estimation approaches.
, based on two different estimation approaches.
-
1. For the U-statistic–based estimator
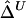 , define functions
, define functions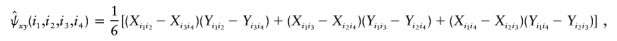
and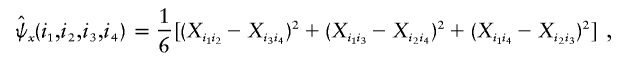
Then,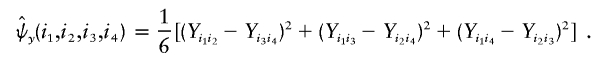
where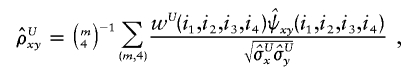
and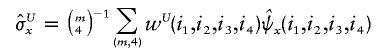
with the weight function wU(i1,i2,i3,i4) proportional to θi1θi2θi3θi4.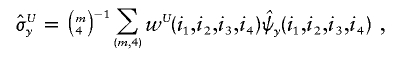
-
2. For the naive estimator
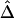 ,
,
where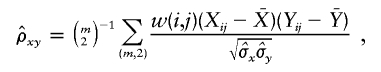
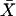 and
and 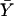 denote the sample means for X and Y, and
denote the sample means for X and Y, and
and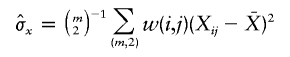
with the weight function w(i,j) proportional to θiθj.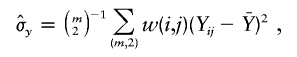
References
- Anderson EC, Novembre J (2003) Finding haplotype block boundaries by using the minimum-description-length principle. Am J Hum Genet 73:336–354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson E, Abecasis GR, Bumpstead S, Chen Y, Hunt S, Beare DM, Pabial J, et al (2002) A first-generation linkage disequilibrium map of human chromosome 22. Nature 418:544–548 10.1038/nature00864 [DOI] [PubMed] [Google Scholar]
- Devlin B, Risch N (1995) A comparison of linkage disequilibrium measures for fine-scale mapping. Genomics 29:311–322 10.1006/geno.1995.9003 [DOI] [PubMed] [Google Scholar]
- Excoffier L, Slatkin M (1995) Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol Biol Evol 12:921–927 [DOI] [PubMed] [Google Scholar]
- Hawley ME, Kidd KK (1995) HAPLO: a program using the EM algorithm to estimate the frequencies of multi-site haplotypes. J Hered 86:409–411 [DOI] [PubMed] [Google Scholar]
- Hinds DA, Stuve LL, Nilsen GB, Halperin E, Eskin E, Ballinger DG, Frazer KA, Cox DR (2005) Whole-genome patterns of common DNA variation in three human populations. Science 307:1072–1079 10.1126/science.1105436 [DOI] [PubMed] [Google Scholar]
- Hudson RR (2002) Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18:337–338 10.1093/bioinformatics/18.2.337 [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium (2003) The International HapMap Project. Nature 426:789–796 10.1038/nature02168 [DOI] [PubMed] [Google Scholar]
- Jeffreys AJ, Kauppi L, Neumann R (2001) Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat Genet 29:217–222 10.1038/ng1001-217 [DOI] [PubMed] [Google Scholar]
- Lee AJ (1990) U-statistics: theory and practice. Marcel Dekker, New York [Google Scholar]
- Lewontin RC, Kojima K (1960) The evolutionary dynamics of complex polymorphisms. Evolution 14:458–472 [Google Scholar]
- Li SS, Khalid N, Carlson C, Zhao LP (2003) Estimating haplotype frequencies and standard errors for multiple single nucleotide polymorphisms. Biostatistics 4:513–522 10.1093/biostatistics/4.4.513 [DOI] [PubMed] [Google Scholar]
- Long JC, Williams RC, Urbanek M (1995) An EM algorithm and testing strategy for multiple-locus haplotypes. Am J Hum Genet 56:799–810 [PMC free article] [PubMed] [Google Scholar]
- McPeek MS, Strahs A (1999) Assessment of linkage disequilibrium by the decay of haplotype sharing, with application to fine-scale genetic mapping. Am J Hum Genet 65:858–875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton NE, Zhang W, Taillon-Miller P, Ennis S, Kwok PY, Collins A (2001) The optimal measure of allelic association. Proc Natl Acad Sci USA 98:5217–5221 10.1073/pnas.091062198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Przeworski M (2001) Linkage disequilibrium in humans: models and data. Am J Hum Genet 69:1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong M, Guo SW (1997) Fine-scale mapping based on linkage disequilibrium: theory and applications. Am J Hum Genet 60:1513–1531 [DOI] [PMC free article] [PubMed] [Google Scholar]