Biases and Reconciliation in Estimates of Linkage Disequilibrium in the Human Genome

Abstract

Genetic association studies of common disease often rely on linkage disequilibrium (LD) along the human genome and in the population under study. Although understanding the characteristics of this correlation has been the focus of many large-scale surveys (culminating in genomewide haplotype maps), the results of different studies have yielded wide-ranging estimates. Since understanding these differences (and whether they can be reconciled) has important implications for whole-genome association studies, in this article we dissect biases in these estimations that are due to known aspects of study design and analytic methodology. In particular, we document in the empirical data that the long-known complicating effects of allele frequency, marker density, and sample size largely reconcile all large-scale surveys. Two exceptions are an underappraisal of redundancy among single-nucleotide polymorphisms (SNPs) when evaluation is limited to short regions (as in candidate-gene resequencing studies) and an inflation in the extent of LD in HapMap phase I, which is likely due to oversampling of specific haplotypes in the creation of the public SNP map. Understanding these factors can guide the understanding of empirical LD surveys and has implications for genetic association studies.

Genetic association studies offer a powerful strategy for dissecting the contribution of common alleles to complex diseases (Risch and Merikangas 1996). Because whole-genome resequencing is not yet practical, widely used study designs rely extensively (either explicitly or implicitly) on linkage disequilibrium (LD), with researchers counting on associations to be detected by correlations between causal variants and neighboring genotyped markers (and not always being fortunate enough to have discovered and genotyped the causal marker in the patient samples). Thus, the extent and structure of LD acutely affect the economics, performance, design, and analysis of genetic association studies (Kruglyak 1999; Reich et al. 2001; de Bakker et al. 2005; Hirschhorn and Daly 2005; Wang et al. 2005).

The design of such studies requires a thorough and robust understanding of LD patterns in the human genome. Many recent studies have independently attempted to quantify these patterns by large-scale examination of SNP alleles in representative human populations (Johnson et al. 2001; Patil et al. 2001; Reich et al. 2001; Gabriel et al. 2002; Carlson et al. 2004; Ke et al. 2004; Hinds et al. 2005), culminating in two genomewide surveys by Perlegen, with 1.6 million SNPs in 71 samples (Hinds et al. 2005), and by the International HapMap Project, with 1 million SNPs (phase I [Altshuler et al. 2005]) going up to >3 million SNPs (phase II [International HapMap Project Web site) in 269 samples.

Since it has not been practical to exhaustively examine each base pair in very large and diverse populations, efforts to characterize variation have, by necessity, required a variety of trade-offs: sequencing a small set of chromosomes over long regions (Patil et al. 2001), sequencing a larger set of samples for a selected set of candidate genes (Crawford et al. 2004), or typing subsets of SNPs from public maps in larger samples and longer genomic spans (Gabriel et al. 2002; Ke et al. 2004; Altshuler et al. 2005; Hinds et al. 2005; International HapMap Project).

The use of incomplete data sets introduces biases in principle, including overrepresentation of high-allele frequencies, artifacts of small samples, and analysis of short genomic regions that underestimates long-range LD. Moreover, particular regions examined may not be representative of genomewide LD patterns, potentially because of extreme natural selection at these regions. It is, therefore, unsurprising that the different choices made in the design of the above studies result in inappreciably different estimates of allelic correlation in the genome (Ke et al. 2004) (see below). Moreover, although the influences of known biases on LD have individually been predicted theoretically and observed empirically (Hedrick 1987; Devlin and Risch 1995; Ardlie et al. 2002; Teare et al. 2002; Ke et al. 2004), a systematic comparison of the available large-scale empirical data after adjustment for biases—uncovering what differences, if any, are not explained by known aspects of study design—has not, to our knowledge, been published elsewhere.

In this article, we examine a variety of large-scale, publicly available data sets through an identical analysis process, and we iteratively examine the impact of biases in study design on a variety of LD measures. The results reveal that most, but not all, differences among surveys can straightforwardly be reconciled and can offer insight into the limitations and interpretations of available genomewide data sets. Finally, they reassure us with regard to the objectiveness of upcoming final HapMap data, only a glimpse of which was available at the time of this article's submission.

Methods

We analyze the following data sets (see table 1): (1) 166 genes resequenced across 47 individuals from two population panels, as part of the SeattleSNPs project (Carlson et al. 2004; SeattleSNPs Variation Discovery Resource Web site); (2) five 500-kb regions from the HapMap ENCODE project, resequenced in 16 individuals and genotyped for every known or discovered marker in the corresponding HapMap 90 individuals (Altshuler et. al 2005; HapMap ENCODE Web site); (3) one 10-Mb region of chromosome 20 typed by the Sanger Center for almost all public SNPs across at least 42 individuals per population panel (Ke et al. 2004; Wellcome Trust Sanger Institute, Human Chromosome 20 Web site); (4) 62 autosomal regions typed for >2,500 public, most of which are now double-hit, SNPs in a pilot study of haplotype structure (Gabriel et al. 2002; Structure of Haplotype Blocks in the Human Genome Web site); (5) genomewide SNP data with 1 million public, mostly double-hit (Reich et al. 2003), SNPs typed in 90 individuals per population panel (Altshuler et al. 2005); and (6) genomewide SNP data released by Perlegen with 1.6 million SNPs typed in 71 individuals from three population panels (Hinds et al. 2005; Perlegen Genotype Browser). All of our data sets are publicly available at their respective Web sites. Although we realize that some of these data sets are continually updated and that other data sets exist, we examined specific data freezes that usually follow one of the designs we already examined.

Table 1.

Public Data Sets Have Different Designs

Data Set and Population	Sample Sizea	Densityb	SNPs in Studyc	Total Lengthd	Region Lengthd	Reference and Web Site
SeattleSNPs:		3	Resequencing	4	.025e	Crawford et al. 2004; SeattleSNPs Variation Discovery Resource
CEPH European (Utah)	48
African American	46
ENCODE:		2.5	Resequencing and public	5	.5	Altshuler et. al 2005; HapMap ENCODE
CEPH European (Utah)	120f
Yoruban (Nigeria)	120f
Han (China) and Japanese	178
Chromosome 20:		.5	Public	10	10	Ke et al. 2004; Wellcome Trust Sanger Institute Chromosome 20
CEPH European (Utah)	96
Beni (Nigeria)	96
Han (China)	96
Gabriel:		.12	Public	13	.2e	Gabriel et al. 2002; Structure of Haplotype Blocks in the Human Genome
CEPH European (Utah)	96
Yoruban	96
Han (China)	96
HapMap:		.2	Public	2,800g	100e,h	Altshuler et. al 2005; International HapMap Project
CEPH European (Utah)	120f
Yoruban	120f
Han (China) and Japanese	178
Perlegen:		.6	Resequencing and public	2,800g	100e,h	Hinds et al. 2005; Perlegen Genotype Browser
CEPH European (Utah)	48
African American	46
Han (China)	48

^aNo. of chromosomes per population.

^bIn SNPs/kb.

^cAscertainment in resequencing/public databases.

^dIn Mb.

^eAverage.

^fIn trios.

^gEntire genome.

^hEntire chromosome.

All SNPs not polymorphic in each panel were deleted when we analyzed that panel. Initially, all polymorphic SNPs (without any frequency cutoff) were used for analysis. In subsequent analysis, SNPs were used per the specific random thinning of data sets. Pairwise statistics of LD (absolute D′ and r²) were computed by Haploview (Barrett et al. 2005). For markers A/a and B/b with allele frequencies P_A⩾P_a and P_B⩾P_b and allele-combination frequencies P_AB, P_Ab, P_aB, and P_ab, such that D=P_AB-P_AP_B⩾0, these pairwise LD statistics are defined as and r²= D2/PAPBPaPb. Allele-combination frequencies were computed by the expectation-maximization algorithm, constrained by family-based obligate-phasing data (Barrett et al. 2005). Data sets were thinned for equating minor-allele frequency spectra, region lengths, marker density, and sample size (see appendix A).

The main tool for analysis, Haploview (Barrett et al. 2005), is open-source, freely available software. All source code used for the analysis in this article is available from the authors' Web site.

Results

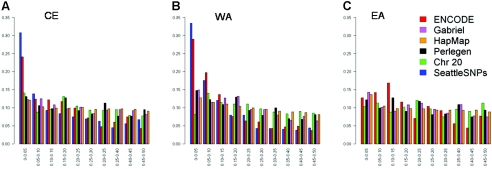
We analyzed six large-scale, publicly available genotype data sets (see table 1 for nomenclature). These data sets represent different trade-offs of data set design, with regard to parameters known to affect measurements of LD, including marker density, proportion of variation ascertained, number of chromosomes genotyped, physical lengths of individual regions, and total physical length spanned (see table 1). Notably, the analyzed data sets differently represent rare versus common alleles and have different allele-frequency spectra (see fig. 1). Since LD patterns vary among populations studied (Gabriel et al. 2002; Evans and Cardon 2005), we limit comparison of LD across data sets to individuals of similar continental origin (Rosenberg et al. 2002) (see fig. 1).

Figure 1.

Different allele-frequency spectra of public data sets. The fraction (Y-axis) of SNPs in each MAF bin (X-axis) is presented for each data set. Hereafter, we group available data by continent of predominant population origin. CE = CEPH European, WA = West African, and EA = East Asian. Whereas this grouping system pools together different populations, it has been observed (Rosenberg et al. 2002) that this approximation explains the lion’s share of the genetic differences between populations and, for our analysis, is actually overconservative (potentially attempting to reconcile populations with different LD). A, Samples from individuals of northern European origin living in Utah, collected by the CEPH. B, Samples from the Yoruba people collected at Ibadan or Nigeria, from the Beni people from Nigeria, or from African Americans of predominantly WA origin (McKeigue et al. 2000). C, Han Chinese individuals living in Beijing, Japanese living in Tokyo, or individuals of Chinese ancestry living in Los Angeles (in all but the SeattleSNPs data set).

There are various ways to quantify LD—on the basis of pairs (Devlin and Risch 1995) or haplotypes consisting of larger sets of markers (Daly et al. 2001; Gabriel et al. 2002; Phillips et al. 2003) and by other methods (Hill and Weir 1994; Morton et al. 2001; Nothnagel and Ott 2002; Sabatti and Risch 2002). For simplicity, we compared three straightforward and widely used measures of LD applied to the available data sets.

• 1. Pairwise relative disequilibrium, known as Lewontin’s D′ (Lewontin 1964), as a function of distance. This metric is proportional to the extent of recombination across the pair of alleles in the history of the sample.
• 2. The pairwise correlation coefficient between a pair of SNPs (r²), which is related to study power under a multiplicative model.
• 3. The fraction of all SNPs that are highly redundant (exceeding a pairwise r² threshold) with one or more others (Carlson et al. 2004)—such that another could proxy for the SNP in a genotyping experiment—which we refer to as the “proxy rate” (Altshuler et. al 2005).

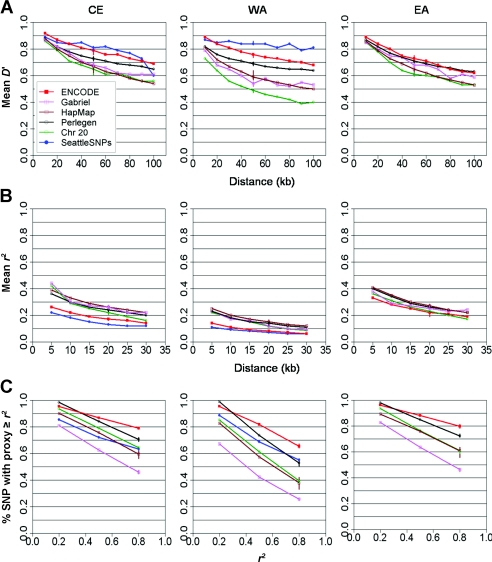
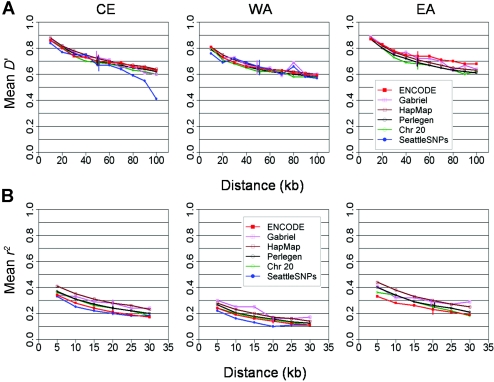
Figure 2 shows the distributions of these three statistics across the six data sets, revealing wide variability among estimates, even within samples drawn from the same continental origin. From these analyses, it is not possible to be sure whether or not the different surveys present a consistent and robust set of estimates of the true results.

Figure 2.

Differences in LD across all data sets, as measured by four measures. A, Mean absolute D′ between marker pairs as a function of distance between the two markers. B, Mean r² between marker pairs as a function of distance. C, Fraction of marker pairs having a proxy with r² greater than or equal to the threshold, as a function of that threshold. All SNPs are included without any filtering on the basis of frequencies. Error bars represent empirical 95% CIs estimated by the bootstrap resampling of 90% of the SNPs.

We next attempted to correct for a set of the known biases detailed in table 1. Each difference in experimental design was evaluated by data reduction: two data sets were aligned with respect to each parameter by reduction of the one that was more complete.

Pairwise LD, MAF, and Sample Size

It is well understood that SNPs of different MAFs, on average, have different LD properties (Pritchard and Przeworski 2001) due both to population genetic effects (common alleles are, on average, older than less common alleles) and to effects of sampling, in that rare SNPs tend to have higher pairwise D′ values and lower pairwise r² values than do common SNPs (fig. B1). Similarly, sample size affects estimation of D′, with smaller samples failing to sample rare fourth gametes and, therefore, inflating estimated D′ (Jorde 2000) (fig. A3).

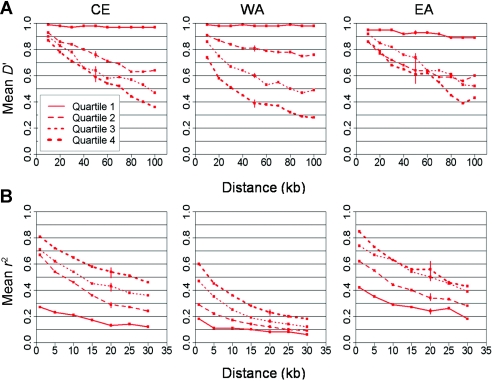
Figure B1.

Effect of MAF on pairwise LD with ENCODE. The average pairwise LD (Y-axis) is shown as a function of distance (X-axis), measured by D′ (A) and r² (B) with ENCODE data in the three populations, CE, WA, and EA. Each curve averages a quartile of SNPs ranked by MAF.

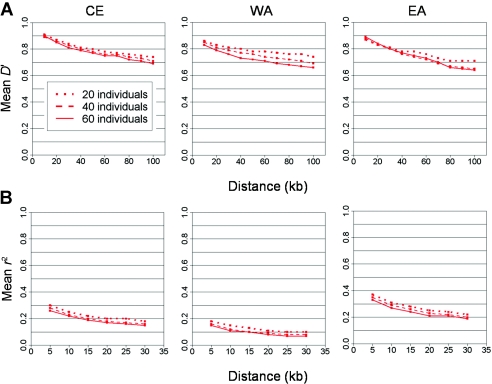
Figure A3.

Effect of sample size on pairwise LD with ENCODE. The average pairwise LD (Y-axis) is shown as a function of distance (X-axis), measured by D′ (A) and r² (B) with ENCODE data in the three populations, CE, WA, and EA. Each curve represents a different number of unrelated individuals resampled from the full ENCODE data.

Figure 1 illustrates how the depth of resequencing determines which MAF strata are represented in each study. The SeattleSNPs and ENCODE data sets, each based on extensive sequencing, are most enriched in rare alleles and have the highest average D′ and the lowest average r² values; data sets based on dbSNP underrepresent low-frequency alleles and show the inverse pattern.

We examined whether the observed differences in pairwise LD are solely the result of these well-understood differences in frequency spectrum and in the number of chromosomes sampled. Specifically, by randomly selecting individuals and ascertaining subsets of markers, we reduced the data sets to achieve the same sample size and allele-frequency spectrum in each (see the “Methods” section and appendix A). Whereas the common ground for sample size was naturally chosen to be the smallest data set sample size—23 unrelated subjects—choosing a standard MAF spectrum is somewhat arbitrary, since there is no single “correct” spectrum. Since there is, in fact, different LD around alleles of different frequencies, the question is best examined as a function of allele frequency. If data were more abundant, it would be ideal to establish the true distribution of pairwise LD for each pair of allele frequencies. Another option is to observe LD only within specific slices of the frequency spectrum (see fig. B1). However, for a baseline that could be evaluated in all studies and still use most of the data, we examined a uniform-frequency distribution, which is also the contribution of each frequency bin to the heterozygosity in theoretical predictions under neutral model assumptions (Kimura and Crow 1964) and in empirical data (Cargill et al. 1999).

Figure 3 demonstrates that these adjustments largely reconcile the different estimates of D′ and r², thus giving reassurance that the largest component of the observed differences in these measures (fig. 2) is simply the different proportions of high-frequency and low-frequency SNPs typed across a range of sample sizes.

Figure 3.

Pairwise LD and correlation reconciled by matching allele frequencies and sample size. Mean absolute D′ (A) and r² (B) across data sets is shown as a function of distance for CE, WA, and EA populations, normalizing allele frequency to a uniform distribution and sample size to 46 chromosomes of unrelated individuals. This normalization reconciles LD and largely reconciles pairwise correlation, with the possible exception that ENCODE and HapMap are noticeably different, especially considering the fact that these data sets examined the same individuals.

Redundancies and Marker Density

In contrast to average values of D′ and r², redundancy in the different data sets (measured using the proxy rate) remained quite variable, despite reconciliation of sample size and allele-frequency distribution. The most obvious explanation is simply marker density (Ke et al. 2004), since increasing marker density increases the likelihood of encountering a proxy SNP (fig. B2). This evaluation may guide decisions regarding SNP density for association studies in the populations examined, since it speaks to the chances of the causal variant having a proxy at different densities. It further motivates us, having controlled for sample size and MAF as above, to also randomly thin each data set to a range of target densities (fig. 4). This serves to reconcile most data sets, with the exception of SeattleSNPs, which is less redundant than the rest even when density and MAF are controlled.

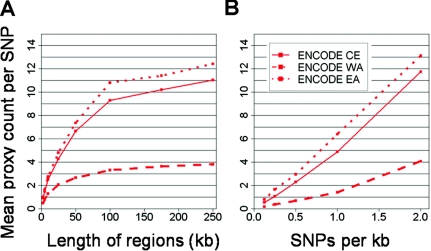
Figure B2.

Effects of density and region length on proxy count with ENCODE. Proxy count (Y-axis) is shown as a function of region length (A, X-axis) and density (B, X-axis).

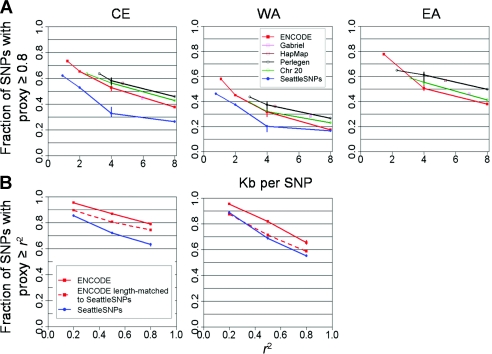
Figure 4.

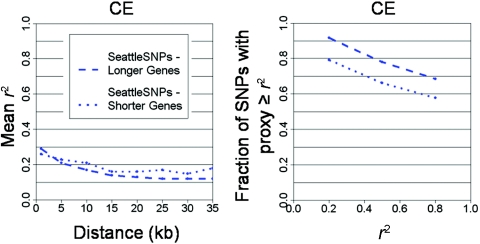
Proxy rate reconciled by controlling for SNP density and region length. A, Fraction of SNPs with another SNP correlated at r²⩾0.8, as a function of SNP density for CE, WA, and EA populations. Proxy rate is shown across data sets with allele frequency normalized to be uniformly distributed and sample size set to 46 chromosomes of unrelated individuals. Proxy count is largely reconciled by controlling for these factors, with the exception of SeattleSNPs. B, Proxy rate compared among SeattleSNPs, with uncontrolled ENCODE for reference (solid red line) and ENCODE controlled for region length and sample size to match SeattleSNPs (dashed red line). These two data sets are similar in allele-frequency spectra and in SNP density but require normalization of region length for reconciliation, demonstrating the importance of this confounder (fig. B2).

To understand the lower estimate of proxy rate in SeattleSNPs (controlled for MAF, sample size, and density), we first verified that, on average, these regions were typical of the rest of the genome in genomewide data sets (fig. A2). However, the length of regions studied by SeattleSNPs was shorter than those in other studies (table 1), which could reduce proxy count: proxies that happen to fall outside the region sequenced are missed. Indeed, comparison of long and short regions within SeattleSNPs supports region length as a confounder of proxy rate but not of pairwise r² (fig. B3). When we trimmed the longer ENCODE regions to match the length distribution of SeattleSNPs, moreover, a very similar proxy count was obtained (fig. 4). These data indicate that proxy count is underestimated in SeattleSNPs because of the size of the region studied, in contrast to a prior consideration of the issue (Crawford et al. 2004).

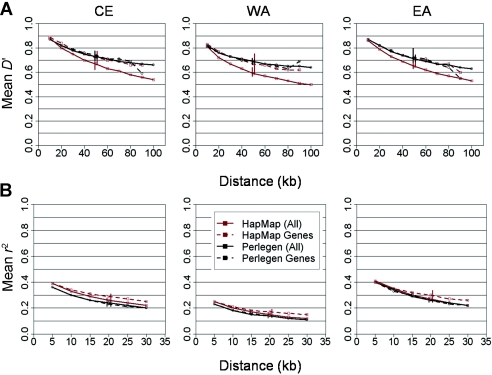
Figure A2.

Analysis of D′ and r² in genes with Perlegen and HapMap. The decay of average pairwise LD (Y-axis) is shown with distance (X-axis), measured by D′ (A) and r² (B) with HapMap and Perlegen data in the three populations, CE, WA, and EA.

Figure B3.

LD in long versus short SeattleSNPs regions. SeattleSNPs regions were sorted by region length and were partitioned into subsets containing the longer and shorter regions, each containing half the SNPs. Mean r² versus genomic distance (A) and proxy rate (B) are shown for longer and shorter region sets.

Longer LD in SNPs from Public Databases

Whereas the above adjustments largely resolve discrepancies between data sets, a closer examination displays a modest (but statistically significant) elevation in the extent of LD in HapMap phase I data (measured using r²) and Gabriel et al. (2002) data (whenever the distance category includes sufficiently many marker pairs) when compared with ENCODE data, even after controlling for the above known concerns (fig. 3). Since ENCODE and HapMap phase I data examine exactly the same individuals, the difference could be explained if ENCODE loci are not representative of the genome as a whole. However, this seems unlikely, given the observed concordance among ENCODE, the whole-genome Perlegen data, and other large surveys.

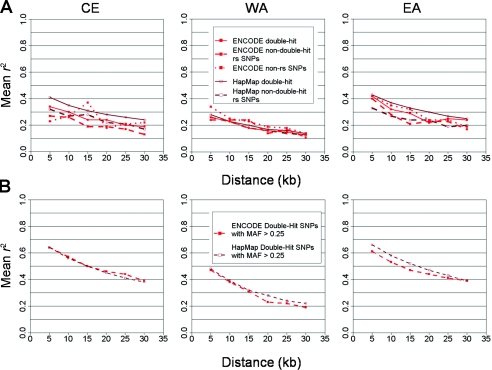
An alternative possibility is that SNP ascertainment for phase I of HapMap influenced the LD properties (Clark et al. 2003; Nielsen and Signorovitch 2003). The HapMap phase I ascertainment scheme prioritized double-hit SNPs, or SNPs in which both alleles have been validated (Altshuler et al. 2005), and, indeed, such SNPs are observed to be more correlated than single-hit SNPs—those that were previously undiscovered—even when controlled for allele frequencies (fig. B4A). Whereas rare alleles are seldom double-hit, the common half (MAF >25%) of the frequency spectrum usually satisfies this criterion, since much of the genome has been sequenced in ⩾8× coverage (Lander et al. 2001; Sachidanandam et al. 2001; Venter et al. 2001; Reich et al. 2003). This leads to the hypothesis that restricting ENCODE and HapMap to double-hit SNPs with MAF >25% (see the “Methods” section and appendix A) would expose reconciled decay of r², a prediction confirmed by the data (fig. B4B).

Figure B4.

Effect of ascertainment on r² with ENCODE and HapMap. A, Effect of dbSNP double-hit status on the decay of average pairwise correlation (r², Y-axis) with distance (X-axis) in ENCODE and HapMap data in the three populations, CE, WA, and EA. Data are stratified by the consideration of only single-hit or double-hit dbSNP SNPs at a time. All data sets are equalized to have the same (uniform) MAF spectrum. B, Pairwise correlation computed in ENCODE and HapMap (all individuals) only for double-hit SNPs with MAF ⩾0.25. These ascertainment and frequency restrictions reconcile these data sets, suggesting that the discrepancy described above results from the differing ascertainment strategies between these data sets (see appendix B).

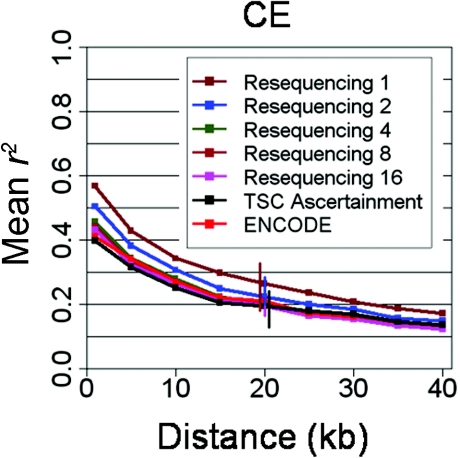
We hypothesized that this inflation of correlation in previously discovered SNPs is expected on the basis of aspects of ascertainment for the public SNP map. Specifically, most HapMap SNPs were discovered by public SNP discovery efforts off sequencing reads with a limited number of chromosomes, usually fewer than a dozen at each SNP site. In contrast, ENCODE SNP discovery involved resequencing an additional 96 chromosomes, with one order of magnitude more variation sampled at each site. Moreover, whereas some of the chromosomes sequenced at any site are locally represented by a single sequence read (e.g., as performed by the SNP Consortium [Sachidanandam et al. 2001]), many other SNPs were discovered by alignment and comparison of long segments of contiguous sequence from single haplotypes; these range from single BACs (150 kb) to flow-sorted chromosomes to, in the most extreme case, 3× genomewide coverage of “donor B” by Celera (Venter et al. 2001). Oversampling of specific haplotypes can result in exaggerated long-range correlation, because repeated sampling of the same lineages leads to preferential discovery of mutations on these lineages, as compared with other alleles of the same frequency (Reich et al. 2002), and mutations on the same lineage give rise to highly correlated alleles. Consistent with this model, we were able to demonstrate this effect in the ENCODE data set by mimicking these ascertainment schemes (see fig. 5).

Figure 5.

r² in ENCODE, as a function of resequencing depth. Effect of resequencing depth on ascertainment bias, as observed by the decay of average pairwise correlation (r², Y-axis) with distance (X-axis) in ENCODE CE data. Ascertainment of SNPs by the resequencing of a certain number of individuals is mimicked by discarding SNPs that are monomorphic in these individuals and controlling for allele-frequency spectrum differences.

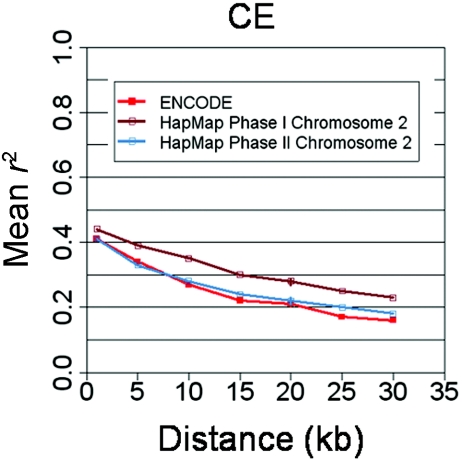
This preferential sampling of lineages—and, therefore, discovery of SNPs that are more correlated than average—is a transient effect of incomplete public SNP databases. Most notably, during the period between selections of SNPs for HapMap phase I and phase II, the public SNP repository grew significantly larger and, therefore, became not only more complete but also more broadly representative of different individuals. The availability of the first chromosome arm of phase II data shows that phase II data are much more similar to ENCODE in the extent of LD (see fig. 6). This indicates that many of the concerns regarding the bias due to ascertainment considerations and compromises made for SNP selection in HapMap should, in fact, be directed only at the phase I data. Final, phase II data is more uniformly and completely ascertained and renders these concerns obsolete.

Figure 6.

HapMap phase II predicted to agree with other data sets in r². Although the HapMap phase I data set does not agree with ENCODE in r² when the latter is adjusted to the uniform MAF distribution, the recent completion of chromosome 2 in phase II shows that the phase II HapMap, if consistent with the chromosome 2 data, will agree completely with ENCODE in this respect. The chromosome 2 data from phase I is presented for comparison.

Discussion

We set out to systematically evaluate whether different estimates of LD—such as SNP ascertainment, sample size, region length, and marker density—are fully explained by known bias in study design. Whereas a naive answer might have been that the different studies are in strong discord (fig. 2), and a theoretical answer that these factors must make the different data sets more similar, it is valuable to demonstrate that almost all differences can be straightforwardly reconciled by deconvoluting these known issues. Specifically, our analyses document that, when the known effects of allele frequency and sample size are taken into account, SNPs of given frequencies show highly consistent results across studies. Since causal alleles of all frequencies likely contribute to disease (Reich and Lander 2001; Pritchard and Cox 2002), having a clear picture of LD around variants of each specific frequency stratum (fig. B1) is a very meaningful insight.

Clearly, estimates of LD around less-common alleles require both sequencing (to ascertain these deeply) and large-enough sample sizes in which to obtain accurate estimates of rare events. From this perspective, it is clear that the samples sizes used even in sequencing studies (from 48–96 chromosomes) are actually too small to accurately estimate properties of alleles with MAF <0.05–0.10; thus, the true properties of LD around rare SNPs remain to be determined.

For common alleles, in contrast, it appears that current estimates are adequate to define the genuine structure of LD in the samples examined, with ENCODE representing the most complete combination of ascertainment, sample size, marker density, and region span (Altshuler et al. 2005). Phase I of HapMap appears to display a slight excess in correlation at a distance, due in large part to the inclusion of many SNPs from a small number of sequenced haplotypes; this bias appears resolved in phase II of HapMap data. The final, practical lesson of this study for geneticists who use HapMap data to study association with common variants is, thus, a message of reassurance: Whereas previous data sets have many issues and biases, phase II HapMap well represents what LD among common alleles really looks like and that their LD is sufficient to be reliably used for mapping them.

Appendix A

Error Bars

According to a binomial model, the SE of evaluating a fraction from millions of data points is very small if data are independent (not shown), but it is underestimated by this theoretical model. To accommodate the empirical error distribution of evaluated values, we took an empirical bootstrap approach. Error bars represent 95% CIs inferred from 100 resampling iterations of a random 90% of the SNPs at a time.

Thinning

Data sets were thinned between 1- and 10-fold. Pairwise LD analyses of data sets thinned more than fivefold (i.e., ENCODE and SeattleSNPs) were averaged over 10 independent thinnings. To verify that the thinning is statistically valid (i.e., does not introduce significant random-sampling noise), we evaluated error bars for the most severe thinning by repeating the analysis 10 times (see fig. A1).

Figure A1.

Robustness of the thinning procedure. To evaluate the effects of resampling, we examined 100 replicates of the most-severe thinnings performed, thinning SeattleSNPs to a flat-allele frequency spectrum (A) and thinning ENCODE by sample size and SNP density (B). We show that pairwise measures of LD, D′ (left panel) and r² (middle panel), require averaging over 10 replicates to provide reproducible averages, whereas single proxy–rate replicates (right panel) provide accurate results.

Equating Marker-Allele Frequency

For equating the minor-allele frequency (MAF) spectrum of a data set to the uniform distribution, we proceeded as follows. First, we sorted all SNPs into bins according to their MAFs, using 10 bins overall (0%–5%, 5%–10%, etc.). Next, we selected the bin with the smallest number of SNPs and then randomly drew an equal number of SNPs from each bin with more SNPs, leaving each bin with the same number.

Equating Length

To equate the lengths of the ENCODE regions to those of the SeattleSNPs regions, we considered every possible pairing between an ENCODE region and a SeattleSNPs region. For each possible pairing, we (1) computed the length of the SeattleSNPs region (kb from first to last SNP), (2) randomly selected a starting SNP along the ENCODE region, and (3) selected the portion of the ENCODE region equal in length to the SeattleSNPs region following the starting SNP. Although each region selected represents only a portion of each ENCODE region, each ENCODE region is sampled 166 times, once for each SeattleSNPs gene.

Equating Density

To set the densities of various data sets, we selected the target density of each given region and multiplied that density by the region’s length (number of kb from first to last SNP), to determine the target number of SNPs for that region. We then randomly drew that number of SNPs from that region, to represent the thinned version.

Equating Sample Size

To set the sample size of each data set, we randomly selected unrelated individuals in each data set (23 individuals in figures 3, 4, and A2 and 20, 40, and 60 in A3).

Order of Operations

Since many of the comparisons required multiple adjustments of data set attributes, we selected the order of sampling operations to prevent any one operation from altering the results of another. For example, setting the MAF spectrum of a region after setting its density will obviously make it less dense than desired. The aforementioned operations were performed in the following order. First, the desired number of individuals (23) was selected. After this, the MAF spectrum was set to the uniform, since selecting individuals after this step would change the MAF spectrum. Next, if necessary for the comparison, the density was thinned. Since this thinning was unbiased with respect to the MAF of each SNP, and since the MAF spectrum was already flat at this point, this thinning was found to not appreciably alter the MAF of a region (data not shown). When length was equated (see fig. 4), the steps of density and MAF thinning were not performed, since the ENCODE and SeattleSNPs were already highly similar with respect to these attributes (see table 1); hence, only the sample size of the ENCODE data set was adjusted before ENCODE was trimmed to the length of SeattleSNPs regions, as detailed above.

Appendix B

Demonstrating the Effects of Attributes on LD with ENCODE

Figure B1 demonstrates the effect of MAF on these pairwise measures of LD by calculating these quantities separately for each quartile of the MAF distribution. For rarer alleles, average D′ is higher and r² is lower. These opposite trends, consistently across distances and populations, are in the same data set—that is, the different curves do not indicate “more” or “less” LD but, rather, the effect of allele frequency on the measures that we use. This picture from different data sets (fig. 2) is similar, which suggests a reconcilable bias resulting from different allele-frequency compositions, rather than a genuine difference in LD.

In addition to the effect of MAF, pairwise LD can also be affected by sample size that varies among data sets. Theoretically, D′ is expected to be particularly inflated among rare SNPs in small samples, since the minor allele of a rare SNP in a small sample may appear on only one chromosome (and, thus, be in perfect LD with that haplotype) (Jorde 2000). Figure A3 demonstrates the consistent effect that differences in sample size are observed to produce.

The maximum pairwise r² achieved by each SNP among its near neighbors is clearly a nondecreasing function of marker density in any given region. Indeed, proxy count is observed to decrease when a given data set is thinned (fig. B2). The fractions of SNPs in each data set with a proxy vary widely, even when allele frequencies are normalized (not shown). To reconcile these, therefore, we must control for density as well.

However, region length is also expected to have an effect for this data set, since the small regions in this data set (average length ∼25 kb) make it less likely that any SNP will have a proxy within its region. Figure B2 demonstrates the effect of region length on proxy count in ENCODE; clearly, regions of 25 kb fall within the range where “edge effects” are nonnegligible in determining proxy count. Therefore, the appropriate comparison would involve the other data sets trimmed to equally short lengths.

Analysis of Genes

Because of the above-described discrepancy between SeattleSNPs and other data sets, we attempted to determine whether genes, on average, are in lower LD than the genomewide average. To investigate this, we analyzed the portions of the two genomewide data sets—HapMap and Perlegen—corresponding to genes and compared them with the genomewide averages for these data sets. Because of low SNP counts in most of the genes, only pairwise D′ and r² were calculated. As figure A2 shows, there is no evidence for lower LD in genes. The higher apparent LD observed in HapMap genes, however, is most likely the result of the HapMap ascertainment strategy (International HapMap Consortium 2003).

We use the ENCODE and HapMap data sets to demonstrate that, even when MAF is held constant, SNPs ascertained in different ways—double-hit, single-hit, or resequencing-based—have different LD properties on average (fig. B3). This is explained by the ascertainment scheme of many public SNPs (fig. B4).