A Relational Approach to Measuring Competition Among Hospitals

Abstract

Objective

To present a new, relational approach to measuring competition in hospital markets and to compare this relational approach with alternative methods of measuring competition.

Data Sources

The California Office of Statewide Health Planning and Development patient discharge abstracts and financial disclosure files for 1991.

Study Design

Patient discharge abstracts for an entire year were used to derive patient flows, which were combined to calculate the extent of overlap in patient pools for each pair of hospitals. This produces a cross-sectional measure of market competition among hospitals.

Principal Findings

The relational approach produces measures of competition between each and every pair of hospitals in the study sample, allowing us to examine a much more “local” as well as dyadic effect of competition. Preliminary analyses show the following: (1) Hospital markets are smaller than thought. (2) For-profit hospitals received considerably more competition from their neighbors than either nonprofit or government hospitals. (3) The size of a hospital does not matter in the amount of competition received, but the larger hospitals generated significantly more competition than smaller ones. Comparisons of this method to the other methods show considerable differences in identifying competitors, indicating that these methods are not as comparable as previously thought.

Conclusion

The relational approach measures competition in a more detailed way and allows researchers to conduct more fine-grained analyses of market competition. This approach allows one to model market structure in a manner that goes far beyond the traditional categories of monopoly, oligopoly, and perfect competition. It also opens up an entirely new range of analytic possibilities in examining the effect of competition on hospital performance, price of medical care, changes in the market, technology acquisition, and many other phenomena in the health care field.

Competition has been a key concept in the market-oriented U.S. health care system in the last 2 decades. Despite its critical importance, many researchers are not satisfied with the existing methods of measuring competition (Bernstein and Gauthier 1998; Gaynor and Haas-Wilson 1999). One reason for such dissatisfaction is that existing methods often fail to capture fine-grained variations in competition in the local market. Most existing methods, following the structural tradition of Stigler and Sherwin (1985), conceptualize competition as an attribute of the market. Even methods that are designed to measure hospital-level competition first define the market for a hospital and then measure competition based on the market so defined (Luft and Maerki 1984/1985; Zwanziger, Melnick, and Mann 1990). Because of their desire to define all-encompassing, autarkic markets, economists tend to prefer using large geographic areas as markets (see Arnould and DeBrock 1986; Morrisey, Sloan, and Valvona 1989). Because of the market focus and the use of large markets, existing methods cannot adequately describe the microcompetitive behavior among hospitals in the local market. With the advent of managed care, however, the importance of local markets is increasing because of the way selective contracting can pit hospitals against one another (Zwanziger, Melnick, and Eyre 1994). As managed care markets mature and hospitals increasingly pay more attention to their immediate neighbors, a new method is called for that is better suited to this changing market context and measures local variations in competition.

The relational approach introduced in this article conceptualizes competition as an attribute of a relationship between two hospitals and measures competition at the level of each pair of hospitals, the smallest unit at which competition can be measured. To some, competition is characterized more by the absence rather than presence of any formal or informal relationships (as illustrated by the phrase “arm's-length ties”). Thus, competition as a relationship may sound like a contradiction in terms. Although hidden and not directly observable, competition “exists” as negative influence that competitors exert on one another, and it can be measured by using observable indicators such as price or patient flow.

Niche overlap theory in organizational analysis provides a theoretical framework for constructing the relational measure of competition. Because all organizations must rely on their environment for critical resources to sustain themselves (Scott 1998), they need to compete for the resources to survive and thrive under the usual conditions of resource scarcity and mutual exclusion (Hannan and Freeman 1989). The theory states that two organizations compete to the extent that they rely on the same resources and that the amount of overlap in resource niches between two hospitals is directly proportional to the amount of competition between them (Baum and Haveman 1997). More formally, then, the relational approach consists of measuring competition between two hospitals using the extent of overlap in their use of common resources.

The relational approach can enrich the study of competition on many different levels of analysis. First, it can be used to identify the strongest competitor. This allows researchers to model the effect of the strongest competitor in many areas of health services research. It is not yet well known how important the strongest competitor is in explaining various hospital behaviors. However, there is no denying that the strongest competitor is the most salient part of a hospital's environment, and as such, its market behavior must be closely monitored and taken into account in some way or another. Its importance may vary depending on the market context; in more locally oriented markets such as those in rural areas, the strongest competitor may assume much more importance than in large and diffuse markets. On the other hand, hospitals in markets dominated by fee-for-service patients may find the strongest competitor less constraining than in those dominated by managed care in which HMOs and PPOs can play hospitals against their strongest competitors to obtain deeper discounts. One can thus imagine that the strongest competitor may gain more significance as managed care markets mature.

Not only does the relational method allow one to identify the strongest competitor, but it also allows one to estimate the strength of competition received from it. In fact, the relational approach can be used to obtain a complete ranked list of competitors by their strength of competition. One can measure how much competitive pressure a hospital receives from its local market competitors such as the first two, three, five, or ten strongest competitors. Furthermore, the sum of competitive pressures from all hospitals can be an indicator of the total competitive pressure a hospital is under.

Pair-wise competition can be used to detect local market structures and to delineate larger groups such as markets or organizational populations (see Van de Ven and Ferry 1980). Using the relational measures, Sohn (1996) detected different structures such as clique, center-periphery, enclave, and diffuse structures formed by a focal hospital and its ten strongest competitors. Because the clique in which all hospitals compete intensely with all others would be a much harsher environment than the other three structures, one would hypothesize that competition has the strongest effect on hospitals in a clique. An enclave in which the focal hospital is not competing with any others in the group but all the others compete intensely with one another would be a market structure that will accord monopolistic benefits to the focal hospital even though it is surrounded by others in such a way that a casual observer finds it involved in the heat of competition.

These three do not exhaust the range of possibilities by any means. However, they illustrate how the relational approach provides opportunities to researchers in measuring competition on different units of observations and how it can be used to obtain new indicators of competition that may bring additional light to what is already known about the functioning of health care markets. In addition, the relational approach can be used effectively in analyzing the increasingly complicated health care markets in which many hospitals join larger units such as health systems, networks, and alliances. In such an environment, a method focused solely on hospitals may not be attractive enough. Even though this article considers competition only among hospitals, the method can be applied to a more diverse group of providers if appropriate mechanism and indicators of competition can be specified and data are found.1

Local Variations In Patient Flow Patterns

The methodological advantages that the relational approach can bring to the analysis of competition have been previously discussed. Some might ask whether local variations in competition are sufficient to warrant a method focusing on pairs rather than markets. To address this issue, six hospitals in Los Angeles, all within 12 miles from one another (mean is 5.8 miles), were examined, and how they share zip codes as patient pools was examined. Table 1 shows the names, bed sizes, and number of patient zip codes of these hospitals. Figure 1 contains a matrix of scatter plots that show the patient flow patterns from patient zip codes to hospitals.

Table 1.

Selected Hospitals in Los Angeles, 1991

Name	Beds*	Total Discharges	Patient Zip Codes
Los Angeles Community Hospital	138	6,353	131
California Medical Center	308	17,361	178
Queen of Angels-Hollywood
Presbyterian Medical Center	433	27,249	206
Hollywood Community Hospital Center	99	1,476	84
Cedars-Sinai Medical Center	922	45,752	393
Midway Hospital Medical Center	230	5,014	91

^*Beds are the average available beds and were obtained from the California OSHPD financial disclosure file. Patient zip codes show the number of zip codes that sent at least five patients to these hospitals. Total discharges are the total number of discharges from these hospitals; patients originated from zip codes with less than five patients are excluded from the total as are patients from outside the state.

Data Source: OSHPD patient discharge abstracts and OSHPD financial disclosure file, 1991.

Figure 1.

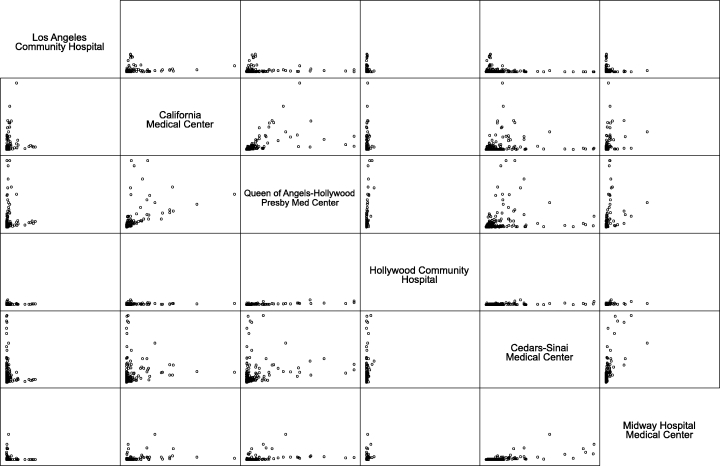
Patterns of Patient Flow for Six Hospitals in Los Angeles, 1991^*

*A dot in this graph represents numbers of patients a zip code area sent to two hospitals on either axis. The maximum for both axes is 2,000 patients, and all axes are in the same scale. Three zip codes that sent more than the maximum are not shown in this graph. Data Source: California OSHPD Patient Discharge Abstracts, 1991.

Each dot represents the number of patients a zip code sent to corresponding hospitals. Dots in the middle that center around the 45^° line indicate zip codes that sent equal or comparable number of patients to both hospitals. Dots scattered along one axis (either X or Y) represent zip codes that sent many more patients to one hospital than to the other. Three patterns generally stand out.

No or Minimal Overlap

This is a pattern in which zip codes are placed along both axes with scarcely any dots in the middle. Zip codes that sent patients to Los Angeles community did not generally send them to Midway and vice versa. A small number of zip codes did, but the magnitude of boundary crossing was small. This pattern indicates that the two hospitals do not share the same patient pool, and according to the niche overlap theory, there must be no or minimal competition between them.

Market Dominance

This is a pattern in which one hospital dominates the other in almost all of their shared patient pools and can be detected by dots scattered close to one axis. An example is the plot for Cedars-Sinai and Hollywood Community. Cedars-Sinai is the largest of all hospitals in this example, whereas Hollywood Community is the smallest.

Unequal Overlap

Unequal overlap is a pattern that falls somewhere between dominance and equal overlap where two hospitals have equal share of patients from all zip codes involved. California Medical, Queen of Angels, and Cedars-Sinai show unequal overlap.

These patterns show that there are indeed considerable local variations in overlap among hospitals. The scatter plots show variations that a market-based approach cannot capture. If an existing method defines all six as belonging in the same market (as most would do), then the researcher would assign the same value (e.g., Hirfindahl-Hirschmann Index [HHI] or number of competitors) to all hospitals, indicating that they are under the same competitive pressure. However, hospitals have markedly different patterns of sharing hospital zip codes, which has implications for the competitive pressure hospitals experience.

On the other hand, the pressure may not be the same within a pair. One hospital in the pair may exercise more competitive pressure toward the other than the other way around. All three patterns are in fact asymmetric in nature. Asymmetry seems to be the norm rather than the exception in competitive relationships among organizations (see Brittain and Wholey 1988). Local variations and asymmetry are two aspects of competition that cannot be adequately captured using existing methods.

Operationalization of Competition As Relationship

A key step in operationalizing competition is to identify the relevant resources that hospitals commonly depend on and the principle by which the resources are organized. As long as the common resources can be correctly identified, one can use the relational approach to measure the extent of competition among organizations from the same population (i.e., competition among hospitals) or from different populations (i.e., competition among nursing homes and home care providers, or among hospitals, systems, and networks). Organizations under study may commonly utilize resources from many disparate resource niches. If so, one needs to identify all of the relevant resource niches as well as the degree to which organizations rely on them.

For hospitals, patients as the ultimate consumers of medical care are the most important resource. Hospitals depend on their patients for survival, and even when they compete for physician affiliation or for medical technology (Robinson and Luft 1985), they do so in order to attract more patients. A zip code of patient residence is used as a niche position for hospitals. Because they usually draw patients from more than one zip code, a collection of them comprises the niche for a hospital. Geographic proximity2 is the main principle by which resources (patients) are organized in the niches (zip codes), and this principle enables one to use a zip code as a niche position. One would prefer using as small a geographic unit as possible to detect the overlap with more precision, but zip code is usually the smallest geographic unit available for patient flow data.

Niche Dimensions

It is important to consider all relevant niche “dimensions” for detecting overlap correctly. Two species may gather food from the same trees, but their niches may not overlap at all if one species feeds on the lower part of the tree while the other feeds on the higher part. In this case, the height of the two species as well as the kind of trees they feed on must be jointly considered. The most crucial niche dimension for hospitals is the extent of service duplication (Fennell 1980,1982; Succi, Lee, and Alexander 1997).

As hospitals differ in the range of services they offer, two hospitals may draw patients from the same pool without competing with each other if they do not offer the same range of services. From the patient's standpoint, two hospitals are not substitutable if they do not provide a similar range of services. To detect true overlap, one needs to stratify patients into service groups that tend to be offered at the same hospital. This stratification scheme will allow one to detect correctly a competitive relationship that involves a small specialty hospital outcompeting a larger one in the narrow range of services the former specializes in.

Zwanziger, Melnick, and Eyre (1994) proposed a classification system based on the Diagnosis Related Groups (DRGs). Their classification is used here with some changes3 to stratify patients into 49 service groups, which serve as niche dimensions in this study.

Competition Coefficient

The amount of niche overlap expressed in numeric values is called the competition coefficient (Levins 1968). Two coefficients C_ij and C_ji are computed for each pair. They represent the intensity or amount of competition from hospital j to i and hospital i to j, respectively. From hospital i 's point of view, C_ij represents the amount of competition that it receives from hospital j and C_ji the amount competition that it generates toward j. As discussed earlier, asymmetry is an important aspect of competition among organizations, and thus, two coefficients are needed to capture it.

Let us suppose that there is an n×m matrix with n hospitals and m zip code areas where patients originate. Each row in this matrix is a vector that contains the numbers of patients from a zip code who were admitted to the hospital that the vector represents. By comparing the two vectors, one can compute the degree of association between two hospitals that indicates how similar they are in terms of their patterns of patient admissions.

Various algorithms have been used to compute the niche overlap, including alpha coefficient (Levins 1968), Euclidean distance (Burt 1992; Burt and Talmud 1993), cosine (Sohn 1996), and some others (McPherson 1983; Podolny, Stuart, and Hannan 1996; D'Aunno, Succi, and Alexander 1997). The first three methods are generally applicable to the niche overlap data just described, but Sohn (2000) demonstrated that they failed to detect overlap correctly. He proposed that a new measure can be systematically derived from the fact that min(x_ik,x_jk) indicates the actual overlap within a niche.4 Consider this formula:

(1)

where the weight, w_ik, indicates the width of each niche position. When the niche states are discrete, the width or relative abundance of resources in the niche positions may be different from position to position. The numerator provides the sum of overlap between hospitals i and j in all niche positions, and the denominator provides the total resource niche of hospital i. C_ij then indicates the proportion of the total resource niche of hospital i that is overlapped by that of hospital j. One of the most intuitive measures of how important a zip code area is to a hospital (e.g., Zwanziger, Melnick, and Mann 1990), p_ik (the proportion of all patients admitted to hospital i who come from zip code k) is an ideal choice for the weight. With w_ik set to p_ik, equation 1 reduces to

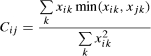(2)

The denominator in equation 2 is the niche size of i, and the numerator is i 's niche overlapped by j 's. The term min(x_ik,x_jk) requires that C_ij lies between 0 (no overlap) and 1 (complete overlap). The competition coefficient, C_ij, can be interpreted as the proportion of the resource niche of a hospital overlapped by a competitor. A competition coefficient of 0.5 means an overlap of 50 percent of a hospital's patient pool.

Direct, Indirect, and Diffuse Competition

The term “competition” has so far been used rather loosely, and the concepts niche overlap and competition are used as if they are interchangeable. To be more precise, three different aspects of competition should be introduced. The first is direct competition that measures the pure effect of competition a hospital receives from a competitor. The competition coefficient is a measure of direct competition.

However, direct competition alone cannot capture the full effect of competition in the market. Even without any overlap in niches, two hospitals can exercise competitive pressure on each other through a third hospital that competes directly with them. The competition between them is called indirect competition. The third and final aspect is diffuse competition, a term that MacArthur (1972) first used. It measures the total competitive effect on a hospital from all other hospitals.

Both indirect and diffuse competition can be estimated from competition coefficients. How indirect competition can be estimated using the simplest case where there are only three hospitals in the universe is illustrated. Hospitals i and j, and j and k are direct competitors. There is no niche overlap between i and k. They are once removed from direct competition but indirectly compete with each other. In general, one can more rigorously conceptualize the pair-wise competition as the sum of direct and indirect competition; namely, the amount of total competition i receives from j is the sum of direct competition j generates toward i and all indirect competition that comes through j:

(3)

where D_ij is the total direct competition hospital i receives from j, and C_ij and C_jk are direct competition that i receives from j and j from k, respectively. Equation 3 assumes multiplicative effect, and w is the attenuation factor that indicates any loss in the strength of indirect competition through the chain of links. The weight of one means the competition j receives from k is transferred to i without loss in strength, whereas the weight of zero means that indirect competition from k does not have any effect on hospital i. The weight will usually be some value between zero and one.

Because of the way the health delivery system is organized in the United States, there are reasons to believe that the weight is very small or close to zero in hospital markets. Zwanziger (1989) points out that hospitals negotiate a complex set of prices with many insurance companies on an annual basis. The negotiated prices are usually confidential, and hospitals are rarely able to respond quickly to price changes on the part of direct competitors, let alone indirect competitors (p. 463; see also Zwanziger, Melnick, and Eyre 1994). More research is needed to determine the appropriate value of the weight for hospitals. However, along with Zwanziger, Melnick, and Eyre, it is assumed that indirect competition is negligible for hospitals, and it is not considered in preliminary analyses discussed later here.

Once the effect of indirect competition is figured out, the estimation of diffuse competition is simple. It can be obtained by summing the competitive effects generated directly or indirectly by all competitors toward a hospital. If the effect of indirect competition is ignored, the diffuse competition can be computed as the sum of competition coefficients from all hospitals 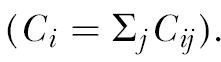5

An Example

To illustrate how these various indices work, a very simple example is used in which there is only one market, the product is homogeneous, and only one niche position can be found.6 One hospital, i, admits 30 percent of all patients from the market, and the rest is equally divided among n other hospitals (subscripted by j ). Table 2 summarizes the changes in various indices for n up to 20.

Table 2.

Various Competition Indices Under a Simplified Condition

Number of competitors to hospital i (n)	Direct competition i receives from j (Cij)	Total competition i receives (Ci)	Direct competition j receives from i (Cji)	Direct competition j receives from j (Cjj)	Total competition j receives (Cj)	Herfindahl Index (HHI)	1-HHI
1	1.0000	1.0000	0.4286	0.0000	0.4286	0.5800	0.4200
2	1.0000	2.0000	0.8571	1.0000	1.8571	0.3350	0.6650
3	0.7778	2.3333	1.0000	1.0000	3.0000	0.2533	0.7467
4	0.5833	2.3333	1.0000	1.0000	4.0000	0.2125	0.7875
5	0.4667	2.3333	1.0000	1.0000	5.0000	0.1880	0.8120
10	0.2333	2.3333	1.0000	1.0000	10.0000	0.1390	0.8610
15	0.1556	2.3333	1.0000	1.0000	15.0000	0.1227	0.8773
20	0.1167	2.3333	1.0000	1.0000	20.0000	0.1145	0.8855

The character of the market is qualitatively different for n<3 and for n>3. In the former, hospital i faces larger competitors in j, whereas in the latter, it is the dominant hospital and faces smaller js. Note that “size” in this example indicates market share; a larger hospital is one with a larger market share. As expected, hospital i receives the maximum competition from j for n up to 2; for n>3, C_ij decreases rapidly at first and slowly as n gets larger. C_jj (direct competition a j receives from another j) is one by definition. The pattern of values for C_i (total competition i receives from all js) shows that it reaches a plateau at n = 3 and does not change as n increases. This raises the concern of whether C_i correctly measures total competition and hence merits some discussion.

This pattern can be explained from two angles. First, it is consistent with what one expects from niche overlap theory. Js divide up 70 percent of the market among themselves, and from i 's standpoint, the amount of total competition it receives from js does not change for n>3 as the total amount of overlap does not change no matter how many js there are in the market. Second, this pattern is consistent with what the HHI measures in general and what one can obtain from the straight-marginal method (Zwanziger, Melnick, and Mann 1990) under the same assumption in particular. Compare the indices in the two relevant columns (C_i and 1-HHI). Even though they are in different scales, the pattern of changes in their values is very similar (r = 0.93 with n = 20).

One can interpret the value of C_i=2.33 as indicating that the total competition i receives from all the other firms in the market is the same as the total competition it receives from 2.33 firms of equal or larger sized competitors. The HHI values show an asymptotic pattern; the numbers-equivalent of firms (1/HHI) reach 5.83 at n = 6 and increase gradually with additional js to 8.73 at n = 20. This number (5.8 effective competitors at n = 6) indicates that the competitiveness in the market is the same as the market with 5.8 hospitals with the same market share. The numbers-equivalent of firms treat new entrants in the market that by assumption can only share 70 percent of the market as if they can also share the rest of the market, and this is the main source of the asymptotic behavior of the HHI. C_i and HHI obviously measure different dimensions of competition (one hospital-specific and the other market-specific), but their similarity is unmistakable.

In contrast, C_j shows a very different pattern; it degenerates into a market crowding measure. This again is consistent with niche overlap theory. From j's point of view, all other hospitals in the same market for n>3 are competitors of equal or larger size. Therefore, the level of competition that i and j face in the same market is fundamentally different; as n increases, i faces progressively smaller but increasing number of competitors, whereas j s face an increasing number of competitors of equal (e.g., other j s) or higher (e.g., i) competitive potential. It stands to reason that the measure of total competition that js face in the market should increase linearly as n increases. The total competition j receives in the market is the same as the number of competitors in the market, because all of its competitors are either equal or stronger competitors to j and all of them generate the maximum amount of competition toward a j.

C_i and C_j demonstrate what the relational approach can do that the traditional market-based approaches cannot. Under this simplified condition, the latter approaches would assign the same values (HHI or market crowding) to all hospitals in the market, whereas the relational approach appropriately recognizes the fact that hospitals i and j face fundamentally different competitive environments in the same market and accordingly assigns different values to C_i and C_j.

This example shows that the relational approach does not “break down” under the limiting condition where one can identify only one niche position. This approach works best when one can detect many niche positions with which to work. The more fine-grained the niche positions are defined, the better this approach will be in detecting the fine shadings of overlap patterns in resource use among hospitals.

Data and Methods

The 1991 California patient discharge abstracts and financial disclosure data compiled by the Office of Statewide Planning and Development (OSHPD) are used to derive a patient origin-destination matrix. This matrix contains information on how many patients originating from one zip code area went to a particular hospital for inpatient service. Hospital-level data were obtained from the OSHPD Financial Disclosure data file for 1991. The data on hospitals' latitudes and longitudes were extracted from TIGER/Line 1992 file from the Bureau of Census. Most of the locations were geocoded with address matching, and some are matched at the zip code level.

Niche overlap among hospitals is measured as follows. The patient discharges are first stratified into 49 service groups and are aggregated to the zip code level to construct one patient origin-destination matrix for each service group. All zip codes that contributed less than three admissions to each hospital are dropped from analysis, as are all admissions from out of state and overseas. All told, there were 429 short-term acute care hospitals in the state in 1991 and 3,233 zip codes. For each service group, niche overlap is computed for every pair of hospitals using equation 2. The competition coefficients obtained at this step measure competition among hospitals in each service group. A weighted average was taken for the overall measure of the hospital-level competition using the proportion of total discharges in each service category as the weight.

A univariate analysis of the competition coefficients based on 429 hospitals was conducted. Descriptive analyses were also done to examine how much direct competition the 10 strongest competitors generate by profit status and how much total amount of diffuse competition hospitals receive and generate by bed size categories. Finally, the relational method was compared with two most popular existing methods, the radial and the straight-marginal approaches, in order to assess how similar they are to each other in measuring competition among hospitals. These analyses are carried out to show (1) that competition coefficients generate patterns of competition consistent with the idea that hospitals compete with a small number of close competitors in the local area, (2) that what competition hospitals receive depends on hospital characteristics as well as the way the local market is structured, and (3) that methods of measuring competition differ widely in identifying competitors.

Results

The univariate distribution of the competition coefficients is extremely skewed left. Sixty-three percent of all pairs in the state have coefficients of 0, indicating no competition; 93 percent have coefficients of. 01 or less, indicating overlap of 1 percent or less. All of these minuscule or 0 coefficients point to the fact that most pairs of hospitals are not competing with each other in any meaningful sense of the term. These are structural holes (Burt 1992) that indicate the absence of competitive relationships. Perhaps more relevant is the distribution of structural holes in the local areas. The statistics for a convenience sample of five metropolitan statistical areas (MSAs) are shown in Table 3.

Table 3.

Univariate Statistics of Competition Coefficients for All Pairs of Hospitals in Five MSAs

			Competition Coefficients
MSA Name	Number of Hospitals	Mean Distance (Miles)	25%	Median	75%	95%	Average
Bakersfield	10	37.4	0.000	0.012	0.229	0.809	0.161
LA—Long Beach	120	20.3	0.001	0.008	0.047	0.328	0.060
Sacramento	14	23.8	0.010	0.066	0.281	0.582	0.168
Salinas	5	25.5	0.005	0.051	0.176	0.559	0.124
San Francisco	22	10.3	0.010	0.067	0.198	0.566	0.148

Among 120 hospitals located in the Los Angeles–Long Beach MSA, half of all possible pairs (n = 14,280) have competition coefficients less than 0.01, and 75 percent of them have coefficients of less than 0.05.7 This shows that most hospitals in the MSA are not competing with one another in any meaningful sense. Four other MSAs (medium-sized and small) also show a consistent pattern; competitive relationships among hospitals in these MSAs are characterized more by their structural holes than by their continuities.

This point can be illustrated again with the San Francisco MSA, which shows a surprisingly low level of overlap among hospitals that are located within a small geographic area. Fifty percent of all pairs had less than 7 percent overlap in their patient pools. When only the hospitals in the peninsula (San Francisco and San Mateo counties) are considered (19 hospitals), 50 percent of all pairs had competition coefficients of more than 1 percent and 25 percent had 3 percent or more.

Hospitals in medium-sized MSAs such as Bakersfield and Sacramento show the highest level of competition (e.g., at the third quartile and on the average) among the MSAs considered here, despite these hospitals being much more geographically dispersed than those in the San Francisco MSA. Even for hospitals in these MSAs, almost 50 percent of all pairs have 7 percent or lower overlap, indicating a large number of structural holes and the potential existence of submarkets within MSAs.

Competition by Bed Size and Ownership

The number of competitors were compared by bed size categories using various cutoffs ranging from 0.1 to 0.9. The cutoff of 0.1 means that if the patient pool of the focal hospital is overlapped by at least 10 percent by its neighbor, these two hospitals are defined as direct competitors. There are a significantly smaller number of direct competitors for the smallest hospitals (less than 100 beds). These smallest hospitals may be located in remote areas, or they specialize in services that do not overlap much with their neighbors' service offerings. There are few very small hospitals that have a large number of competitors. They typically are located at the center of a cluster of hospitals that draw patients from population centers and specialize in services that these hospitals also offer. Bed size is not a good predictor of the amount of direct competition received by a hospital once it reaches 200 beds.

Larger hospitals may not necessarily be subject to more competition. However, do they generate stronger competition toward their neighbors than smaller ones? Figure 2 shows boxplots for the amount of diffuse competition received and generated by bed size category. This graph confirms that the amount of diffuse competition received does not vary much by bed size. However, the amount of diffuse competition a hospital generates differs significantly by bed size (p < 0.0001). This result is not consistent with Barnett and Amburgey (1990), who argued that larger organizations do not necessarily generate stronger competition. Further analyses are needed to resolve this apparent inconsistency.

Figure 2.

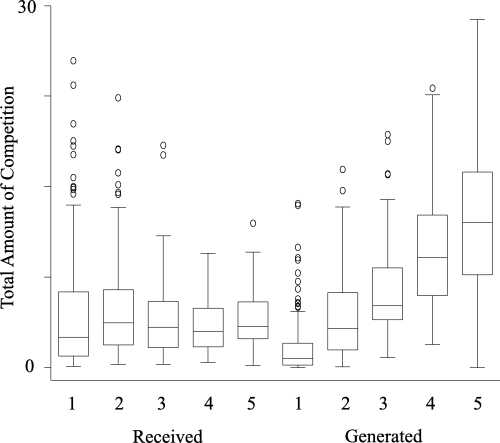
Diffuse Competition Received and Generated by Bed Size Category (n = 429)

Bed size categories are as follows: 1 = less than 100 beds; 2 = 100 to 199 beds; 3 = 200 to 299 beds; 4 = 300 to 399 beds; and 5 = 400 or more beds. Diffuse competition received for hospital i=Σ_jC_ij; diffuse competition generated by hospital i=Σ_iC_ij, where C_ij is the competition coefficient. The diffuse competition received does not vary significantly by bed size categories, where as the diffuse competition generated does (p <0.0001).

Ownership type is expected to be another source of variations in the amount of competition received because hospitals choose locations that are consistent with their missions. Figure 3 shows boxplots for the amount of competition received by the 10 strongest competitors by profit status. For-profit hospitals receive the most intense competitive pressure of the three ownership types (p < 0.0001), whereas government hospitals receive the least. This suggests that government hospitals are appropriately located to serve the population whom other hospitals avoid. However, why do for-profits receive consistently higher amount of competition from their neighbors than not-for-profits? One interpretation is that government hospitals and to a lesser extent not-for-profit hospitals serve communities that are not financially attractive to for-profits. For-profit hospitals tend to operate more in areas that other hospitals also find attractive; hence, more overlap.

Figure 3.

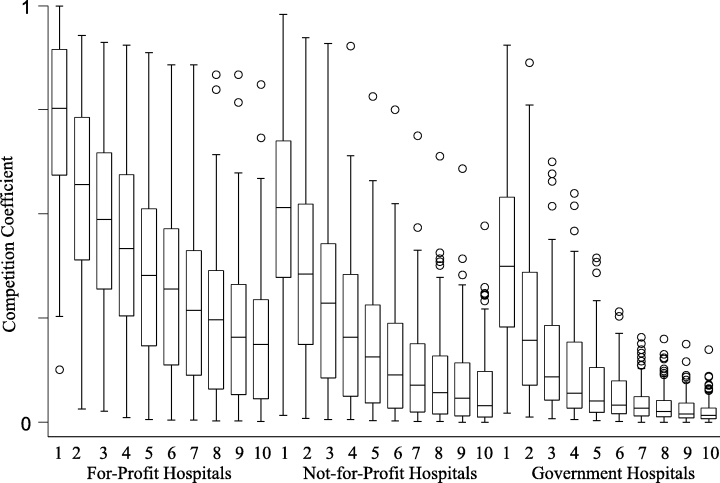
Boxplots of the Amount of Competition Received by Ten Strongest Competitors by Profit Status (n = 429)The numbers on the x-axis identify ten strongest competitors, with one being the strongest and ten being the tenth strongest. Two-way analysis of variance shows that the amount of competition received is significantly different by profit status (p <0.0001). For-profits received the most competition, while government hospitals received the least amount of competition.

Comparison of Methods

How does the relational approach compare with other existing methods? It was compared with two other methods: the radial (Luft and Maerki 1984/1985) and the straight-marginal (Zwanziger, Melnick, and Mann 1990) approaches. The last two methods have their own competitor identification methods. An arbitrary cutoff can be chosen for the relational approach to identify direct competitors as well. Thus, all three methods can be used to produce n×n competition matrices for n hospitals that contain a value of one identifying a competitive relationship and zero otherwise. One way of comparing these three approaches is to compare the resulting binary matrices. Because any difference detected can be attributed to either difference in methods or difference in cutoffs, it is essential to match up the cutoffs in making any meaningful comparisons among these methods.

Three baseline binary matrices with the following cutoffs were constructed: 15 miles for the radial approach, 3 percent for the straight-marginal approach, and 5 percent overlap for the relational approach. Then the density of these baseline matrices was computed, and the cutoffs for the other two methods were iteratively found that produced the same level of density as the baseline matrix. The results are shown in Table 4. The radial approach with 15 miles as the cutoff had 9,044 ties or pairs of competitors (n = 183,612 pairs), resulting in the density of approximately 5 percent. To match this level of density, the straight-marginal cutoff of 1.15 percent (9,034 ties with the density of 0.0491) and the competition coefficient of 0.026 were used (9,017 ties with the density of 0.0492).

Table 4.

Comparison of Radial, Straight-Marginal, and Relational Approaches (n = 183,612)

	Cutoff	Ties	Density	Comparison	Cutoff	Ties	P(C)
(1) Radial Approach	15	9,044	0.0493	(2)	0.0115	9,034	0.553
				(3)	0.026	9,017	0.513
(2) Straight-Marginal	0.03	3,646	0.0199	(1)	8.55	3,650	0.472
Approach				(3)	0.118	3,655	0.447
(3) Relational Approach	0.05	6,353	0.0346	(1)	11.9	6,362	0.476
				(2)	0.0171	6,312	0.532

The last column shows the probability of concordance [P (C)] between the baseline matrix and the matrices with the matching density by the other two methods. To compare two binary matrices, the number of concordant pairs (C) and discordant pairs (D ) are counted. If the corresponding cells in both matrices have a value of one, it is a concordant pair; if only one of them has one, it is a discordant pair. The probability of concordance is

The idea underlying the probability of concordance is found in measures of ordinal association such as gamma, Kendall's tau-b, or Somers'd (Agresti 1990). P(C ) yields the probability of both hospitals identifying the other as a competitor given that either of them identified the other as one. If the two matrices are identical, the probability is 1; if the two matrices are completely discordant, it is 0.

The comparisons show a surprisingly low level of similarity among these three methods. The probability of concordance between any two methods was approximately 0.5 for the same level of density. Almost 50 percent of all pairs identified as competitors in one method are not identified as such in the other. This is a rather substantial difference. The most similar of the three was the radial approach with 15-mile cutoff and the straight-marginal approach at 1.15 percent cutoff [P(C ) = 0.553]. At their own natural cutoffs (15 miles, 3 percent straight-marginal cutoff, and 5 percent overlap), the highest probability of concordance for the three methods was only 0.46.

To understand why these methods are so much different, I chose the largest hospital in the LA–Long Beach MSA (LAC–USC Medical Center) and its nearest neighbor (White Memorial Medical Center), and their competitors are identified using the three methods with their natural cutoffs.

For LAC–USC, the radial method identified 70 competitors. It received competition coefficients of less than 0.015 from half, 0.05 or less from 75 percent of them. Seventeen hospitals generated competition coefficients of 0.05 or more toward LAC–USC and 6 generated coefficients of 0.1 or more. In contrast, the straight-marginal approach identified only 12 competitors. These 12 are all clustered within 13 miles of the focal hospital and 10 of them within 6 miles. Interestingly enough, this method identified as competitors only 5 of the 12 strongest competitors identified using the relational method. The 12 strongest competitors identified using the latter are all within 10 miles from LAC—USC, and 9 of them within 6 miles. Of these 12 hospitals, only 5 were ranked among the top 10 strongest competitors according to the relational method. The 6th was ranked eleventh, but the other 6 were ranked twentieth or lower.

Both straight-marginal and relational measures show that White Memorial is under more competitive pressure than LAC–USC. However, the 15-mile radius method identified the same number of competitors for White Memorial as for LAC–USC. As one goes from large to medium and small MSAs, the radial method identifies fewer competitors than the other two (see Phibbs and Robinson 1993). This indicates the “local” market may be larger in smaller MSAs and rural areas than the radial approach defines.

One source of the difference between the straight-marginal and the relational methods is that the first relies on one significant zip code for the identification of competitors, whereas the latter uses data from all zip codes. For example, two hospitals that share ten zip codes with only 1 percent of overlap will not be identified as competitors under the straight-marginal approach, whereas they may under the relational approach.

From these observations, one can reach two tentative conclusions about the size of markets defined by the different methods. First, the straight-marginal and the relational approaches define markets that are much smaller than the radial method. Second, the competitors identified by the straight-marginal and the relational methods are substantially different. Current literature on comparing various methods suggests that the method is not important because different methods produce comparable measures of competition (see Garnick et al. 1987). This study suggests otherwise. These methods detect different hospitals as competitors to a substantial degree. Using any of these three methods, one runs an almost 50 percent risk of misidentifying a hospital's competitors.

Discussion

Conceptualizing competition as a relationship between a pair of hospitals has several advantages over existing methods. The relational approach allows one to measure the effect of competition at the most fine-grained level possible, namely, direct competition at the pair-wise level. There is evidence that direct competition is an important indicator of market competition. Manheim, Bazzoli, and Sohn (1994) showed that direct competition could pick up competitive effects that diffuse competition (the HHI or the number of hospitals) could not. They found that short-term general hospitals in both 1983 and 1988 in the metropolitan areas in the United States showed negative and significant relationships between cost per admission and the amount of direct competition. This finding is not consistent with the conception of cost-increasing competition before the prospective payment system (Robinson and Luft 1985). Sohn (1996) similarly reported that the direct competition from the strongest competitor was significantly and negatively associated with cost per admission for hospitals in California in 1991. Manheim, Bazzoli, and Sohn (1994) and Sohn (1996) used different measures of direct competition from each other and from the method proposed here. However, they suggest that direct competition is an important predictor of hospital cost. The apparent inconsistency between the effects of direct and diffuse competition on cost requires further investigation.

The competition coefficients can also be used to measure indirect and diffuse competition, to model local market structures, and to define the extent of markets. One can simply set a global cutoff (i.e., the competition coefficient of 0.05) to distinguish hospitals into significant and nonsignificant competitor groups and then define a market for a hospital as consisting of those in the significant group. Better yet, one can use a more sophisticated approach such as the maximum closure (Sohn 1996) to delineate the market boundaries. In other words, competition coefficients as a measure of pair-wise competition can be used as building blocks for deriving measures of competition at higher levels.

The relational approach is not intended to replace existing methods of measuring competition in hospital markets. Existing methods may be more suitable for some purposes, and the relational approach may not be applicable for others because of its limitations. The main limitations of the relational approach are its heavy data and computation requirements. Because it requires detailed patient flow data, which are not currently available for all patients nationally, it cannot yet be applied to all hospitals in the United States.8 This study did not take into account physician affiliations and managed care contracts that are believed to be two important determinants of patient admission patterns. I assumed that even though they may be significant factors, patients would still be subject to distance decay. Data for the latter two resource niches are not currently available. Once they are, the current method can be modified to use these three resource areas for hospitals (e.g., patients, physicians, and managed care organizations).

Policy Implications

In the past decade or so, hospital markets have been undergoing drastic changes. As a result of the procompetition strategies that federal and state governments have pursued in the hope of reducing health care expenditures, hospital markets seem to have made a transition from those based on quality competition to those based on price competition. Ginsburg (1997) notes that “competition in health care today has moved closer to patterns in other service industries. Price is a much more important factor” (p. 364). At the national level, we have experienced lower rates of inflation in health care expenditures in recent years, and particularly impressive is the reduction in hospital costs in the 1990s. By using aggregate numbers, Guterman, Ashby, and Greene (1996) showed that hospital operating costs actually decreased by 1.3 percent in 1994 compared with the previous year.

An important policy question at this point is whether this trend will persist in the long run. We do not clearly understand whether the reduced rates of inflation are due to competition or to transition to a cheaper form of health insurance. If the latter is the case, we may see an upturn in the growth rate of health expenditures in the near future when most of the population has moved into some form of managed care (Ginsburg and Pickreign 1996). If the current competition model based on managed care is not as effective as some numerical indicators suggest, we may reap only one-time savings in health expenditures. However, if the health care industry has undergone structural changes in such a way that hospitals and other providers are going to compete on the basis of price as well as quality for a long time to come, we can say that the procompetition policy has truly succeeded.

As hospital markets are undergoing these profound changes, there are concerns that health care researchers may not have adequate conceptual and methodological tools to examine this trend in a rigorous way (Bernstein and Gauthier 1997; Gaynor and Haas-Wilson 1999; Sage and Hammer 1999). All existing methods that are based on the structural concept of competition are not sophisticated enough to measure accurately local variations in competition, which seems to gain in importance in this brave new world of managed care. Inappropriate measures of competition may give us a picture of the hospital markets that is very different from what is really happening in the real world (Brooks 1995; Rumelt 1991). The relational approach can help in filling some gaps in our knowledge of the functioning of the health care market and the nature of competition among providers.