Abstract
The binding mechanism of sweet proteins to their receptor, a G-protein-coupled receptor, is not supported by direct structural information. In principle, the key groups responsible for biological activity (glucophores) can be localized on a small structural unit (sweet finger) or spread on a larger surface area. A recently proposed model, called “wedge model”, implies a large surface of interaction with the receptor. To explore this model in greater detail, it is necessary to examine the physicochemical features of the surfaces of sweet proteins, since their interaction with the receptor, with respect to that of small sweeteners, is more dependent on general physicochemical properties of the interface, such as electrostatic potential and hydration. In this study, we performed exhaustive molecular dynamics simulations in explicit water of the sweet protein MNEI and of its structural mutant G-16A, whose sweetness is one order of magnitude lower than that of MNEI. Solvent density and self-diffusion calculated from molecular dynamics simulations suggest a likely area of interaction delimited by four stretches arranged as a tetrahedron whose shape is complementary to that of a cavity on the surface of the receptor, in agreement with the wedge model. The suggested area of interaction is amazingly consistent with known mutagenesis data. In addition, the asymmetric hydration of the only helix in both proteins hints at a specific role for this secondary structure element in orienting the protein during the binding process.
INTRODUCTION
The treatment of patients with diseases linked to the consumption of carbohydrates such as diabetes, hyperlipemia, and caries greatly benefits from the design of new sweeteners. The identification and functional expression of the receptor for sweet taste (1–5) opens new perspectives for the rational design of sweet molecules, but owing to the difficulty of direct structural studies on large membrane proteins, the structure of the receptor is still unknown. Therefore, in silico studies of sweeteners and of their interaction with a model for the receptor represent a very useful approach.
The T1R2/T1R3 sweet taste receptor is a G-protein-coupled receptor (GPCR) similar to one of the glutamate receptors, the metabotropic mGluR1 receptor (1–5). The main difference between T1R2/T1R3 and mGluR1 is that whereas the ligands of mGluR1 are either glutamate itself or closely related molecules, the ligands that activate the sweet taste receptor vary widely in chemical constitution and size, ranging from sugars to amino acids, peptides, proteins, and several other classes of organic compounds. The size of sweet proteins is so different from that of other sweeteners that, until very recently, the prevailing belief was that sweet proteins ought to interact with a different receptor. It has now been demonstrated that small molecular weight sweeteners and sweet macromolecules do interact with the same T1R2/T1R3 receptor (6). However, it is not easy to understand how low molecular weight sweet compounds and sweet proteins can activate the same binding site on the receptor.
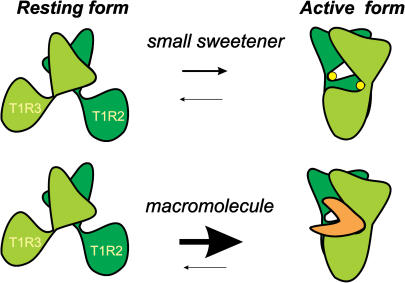
We have recently shown that small molecular weight sweeteners can be hosted by cavities corresponding to the active sites that bind glutamate in the mGluR1 receptor (7), but sweet proteins cannot occupy the same cavities owing to sheer volume incompatibility and because the existence of protruding features (sweet fingers) that can probe this site has been shown to be very unlikely (8). The existence of sweet fingers is not the only possible explanation for the sweetness of proteins: we have hypothesized that sweet proteins interact with an external cavity of the receptor (7–10). The mechanism of interaction, termed “wedge model”, as illustrated by the cartoon of Fig. 1, is based on the fact that proteins can stabilize the active form of the T1R2/T1R3 receptor even in the absence of ligands in the internal active sites. The wedge model is supported by strong indirect evidences, such as the quoted work on the potential sweet fingers of three sweet proteins (8), the survey of the surface of MNEI, a single chain variant of monellin, by means of a paramagnetic probe (11), a structural investigation on G-16A, a peculiar structural mutant of MNEI (12), and specific mutations of MNEI suggested by the model (V. Esposito, thesis work, University of Naples). To explore this model in greater detail, it is necessary to examine the physicochemical features of the surfaces of sweet proteins and of their receptor, particularly because the type of interaction, with respect to that of small sweeteners, depends less on specific pairwise interactions with given residues of the receptor and more on physicochemical properties such as electrostatic potential and hydration. The surface of the receptor can only be examined on homology models (7–10), but those of monellin and of MNEI have been studied experimentally and these studies can be very helpful in describing the interaction with the receptor.
FIGURE 1.
Scheme of the conformational equilibrium between the free forms of the extracellular domain of the T1R2/T1R3 receptor. Binding of a small molecular weight ligand transforms inactive free form I into the complexed form, identical to free form II (upper panel). The lower panel shows that the active free form II can also be stabilized by protein complexation, activating long-lasting signal transmission. The two protomers of the dimeric receptor are dark green (T1R2) and pale green (T1R3), respectively. Small ligands in the two cavities of the complexed form are shown as yellow spheres. The “wedge” protein is orange.
The surface of hydration of monellin has been investigated experimentally by means of femtosecond scanning of the fluorescence of Trp-3, the only tryptophan of this protein (13). This work shows that hydration has contributions both from water molecules that do not interact with the protein and from those bound and interacting significantly with surface sites in dynamical equilibrium in the layer surrounding the protein. This result may be quite relevant to interpret the recognition, by monellin, of the GPCR since, in this process, desolvation is controlled by the timescale of water in the layer. However, this important work gives no clue for the detailed distribution of bound water molecules over the surface of monellin, since the technique used does not have sufficient space resolution. Accordingly, for a detailed comparison of molecular dynamics (MD) simulations, we chose an NMR study that describes the distribution of all bound waters on the surface of MNEI (11).
The survey of the surface accessibility of MNEI (11) was performed by means of an integrated NMR study that combines paramagnetic perturbations and a direct assessment of bound water. The accurate detection of nuclear Overhauser effects (NOEs) between bound water and protein hydrogens (11) was possible both in the absence and in the presence of the paramagnetic probe, thanks to ePHOGSY, a recent pulse sequence (14,15). The results of this NMR study suggested that three MNEI regions are potentially suitable for interactions with other proteins: loop L34, previously referred to as a potential sweet finger, the small N-terminal β-strand containing Ile-6, Asp-7, and Gly-9, and a basic patch containing Arg-72 and Arg-88. These regions are within a larger area suggested by docking calculations between the solution structure of MNEI and a homology model of the human receptor (7,9). It would be interesting to know whether the whole area indicated by docking has hydration features different from noninteracting parts of the surface of MNEI. Hydration and the interaction with the surface of the receptor, in turn, can be influenced by protein flexibility, but it is difficult to examine the interplay of these two parameters experimentally. We decided to investigate these aspects further by analyzing MNEI flexibility and hydration, as derived from molecular dynamics simulations in explicit solvent. We compared the dynamic properties of the molecule with the ones of the G-16A mutant (12), which is of one order of magnitude less sweet than MNEI and, as a control, with those of D-21N, whose sweetness is not reduced by the mutation.
To put hydration in the right perspective from a dynamic point of view, the first step in the analysis of MD data will be dedicated to essential dynamics (ED) (16,17). MD has largely been used to describe the protein hydration at an atomic level spanning from studies on the role of water molecules in DNA binding (18), calculation of solvent density (19) and entropy map (20), estimation of free energy and entropy related to binding of water molecules in buried cavities of proteins (21), calculation of water residence time (22), and many more. The aim of our simulations is to integrate experimental data on the hydration of MNEI with a detailed map of the solvent density at the protein surface. Comparison of MD simulations with surface accessibility deduced from NMR experiments (11) completes the picture of the dynamical behavior of the proteins and of the surrounding solvent, especially in proximity of glucophores. A deeper knowledge of the hydration of a typical sweet protein can add more insights into the understanding of molecular processes involved in eliciting sweetness and eventually favor the design of new sweeteners.
MATERIALS AND METHODS
Molecular dynamics setup
All simulations were performed with the GROMACS package (23) using the GROMOS96 force field (24). The starting structures were those determined in solution for MNEI (Protein Data Bank (PDB) entry 1FA3) (25) and for its G-16A mutant (PDB entry 1M9G) (12). It is worth noting that the numberings of 1FA3 and 1M9G are mutually shifted because of an additional Met at the N-terminal position in the construct of MNEI G-16A. Notwithstanding, throughout this work 1FA3 numbering will be used also for G-16A unless stated otherwise. This choice corresponds to assigning the number zero to the N-terminal Met. The simulations have been carried out in the NPT ensemble with periodic boundary conditions at a constant temperature of 300 K. The Berendsen algorithm (26) has been applied for the temperature and pressure coupling. The bonds were constrained by the LINCS (27) algorithm. The particle-mesh Ewald (PME) method (28) was used to account for the electrostatic contribution to nonbonded interactions (grid spacing of 0.12 nm). To ensure a system pH of 7 the protonation states of pH-sensitive residues were as follows: Arg and Lys were positively charged, Asp and Glu were negatively charged, and His was neutral. The protein's net charge was neutralized by the addition of Cl− and Na+ ions. In each simulation the initial shortest distance between the protein and the box boundaries was 1.5 nm. The remaining box volume was filled using the extended single point charge (SPCE) water model (29). We carried out an initial 500 ps simulation with the restrained positions for the protein atoms to ensure a water relaxation in the box. Energy and root mean-square deviation (RMSD) profiles are shown in the first figure in the Supplementary Material, whereas Table 1 reports general simulation parameters.
TABLE 1.
Simulation parameters
| MNEI | MNEI G-16A | |
|---|---|---|
| Energy (kJ/mol) | E final(Ef) | E final(Ef) |
| Protein-protein (total) | −7630.0 | −7773.0 |
| Protein-protein (LJ) | −3398.9 | −3473.0 |
| Protein-protein (El) | −4231.1 | −4361.9 |
| Protein-solvent (total) | −6728.1 | −6337.8 |
| MNEI | MNEI G-16A | |
| Cα-RMSD (nm)—L23 excl. | 0.199 (0.0220) | 0.233 (0.0282) |
| Starting box size (Å) | 76.9 × 65.5 × 64.7 | 75.4 × 67.3 × 67.6 |
| Water molecules | 10,361 | 10,716 |
Standard deviation in parentheses.
Water density function
The MD solvent density distribution was evaluated from the water oxygen atom positions as described by Lounnas and Pettitt (19). For each frame, the atom coordinates were transformed by superimposing the current model onto a reference one. For the water positions the boundary conditions are applied. The density function is then calculated for a discrete 0.05-nm step three-dimensional (3D) grid. The space surrounding the protein is divided in two shells: the first accounts for the molecular dynamics hydration sites (MDHSs) and comprises the region from the protein center of mass to a maximum distance of 0.6 nm from the protein surface; the second region goes from 0.6 nm to 0.8 nm from the protein surface and represents the bulk solvent shell. The MD hydration sites are assigned as the local maxima of the function with the following restrictions: the maximum ought to be the highest value in a radius of 0.14 nm with a density at least 1.7 times the value of bulk water.
Self-diffusion coefficient map
The Einstein relation (30) is commonly used for determining the diffusion coefficient D by the slope of the mean-square displacement of solvent molecules according to the equation
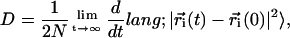 |
(1) |
where the brackets 〈〉 indicate that the average is taken both over time origins and solvent molecules and 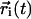 is the position vector of the solvent molecule i at time t. This relation holds in the Brownian regime, hence we do not consider the short time periods during which molecular motion is non-Brownian. Several works have been dedicated to the validation of solvent models by checking water diffusional properties. Although a general favorable agreement exists, some water models apparently fail in the description of water mobility and show D coefficients significantly different from experimental values (31,32). This inconsistency could be imputed to commonly used approximations, for example cutoffs and switching functions in the treatment of long-distance electrostatic interactions (32–35). Additional irregularities in the water diffusion calculations may be introduced by finite system size and periodic boundary conditions (32). The use of PME for electrostatic treatment (28) and a large simulation box can help to overcome these problems.
is the position vector of the solvent molecule i at time t. This relation holds in the Brownian regime, hence we do not consider the short time periods during which molecular motion is non-Brownian. Several works have been dedicated to the validation of solvent models by checking water diffusional properties. Although a general favorable agreement exists, some water models apparently fail in the description of water mobility and show D coefficients significantly different from experimental values (31,32). This inconsistency could be imputed to commonly used approximations, for example cutoffs and switching functions in the treatment of long-distance electrostatic interactions (32–35). Additional irregularities in the water diffusion calculations may be introduced by finite system size and periodic boundary conditions (32). The use of PME for electrostatic treatment (28) and a large simulation box can help to overcome these problems.
Since coefficient D can be influenced by the roughness of the protein surface, it is in order to consider it as a local property (36); hence we calculated the diffusion of water in a grid of step 0.1 nm around the protein. At each grid node, uvw, the Duvw value was computed according to the Einstein relation (Eq. 1), using the following finite difference expression:
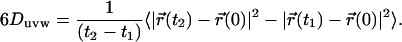 |
(2) |
The values t1 and t2 were fixed at 1 ps and 2 ps, respectively, on the assumption that the diffusional regime would be reached after 1 ps (31,37) but within a time shorter than the average residence time of water molecules within the uvw volume element.
RESULTS AND DISCUSSION
Root mean-square fluctuation and energy components
In this work, we performed 10-ns long MD simulations of the sweet protein MNEI (PDB entry 1fa3) and of its mutants G-16A (PDB entry 1m9g) and D-21N. Simulation statistics for the two main simulations are reported in Table 1. Convergence of the simulations has been tested by evaluating different molecular properties of the system like RMSD analysis and protein-protein and protein-solvent energy contributions during the simulated time (first figure in the Supplementary Material). The dynamical properties of the simulated proteins have been analyzed by extracting significant large-scale components and small amplitude vibrations from the MD sampling. This is made essentially through two complementary analyses: covariance analysis and ED (16,17). When examining flexibility, the most interesting observations come from a comparison of MNEI itself and its G-16A mutant. Gly-16 is placed on a buried edge of the α-helix facing the hydrophobic core of MNEI. It was shown that when G-16 is substituted by an alanine, the sweetness decreases by one order of magnitude, despite the tiny change in the bulkiness of the side chain and the fact that the residue is buried (38). Since a buried residue cannot be involved in a direct interaction with the receptor, this mutation must exert its influence on sweetness in an “allosteric” way, possibly by distorting the protein surface (12). The NMR structure in solution shows that in G-16A the main aspects of the MNEI structure are retained but for a slight pseudorotation of the β-sheets with respect to the helix (12). The protein distortion can be attributed both to a direct sterical effect resulting from the different volumes of a hydrogen atom and of a methyl group and to intrinsic conformational tendencies of the two residues involved. For instance, it is possible that the pronounced conformational flexibility of glycine, although detrimental for the stability of the α-helix, can favor the adaptation of the surface of the helix to that of the β-sheet.
The analysis of the root mean-square fluctuation of the Cα atoms (RMSF profile) for the G-16A mutant presents three maxima corresponding to loops L23, L34, and L45. Conversely, the wild-type plot has the second highest peak at residue Gly-30 (1M9G numbering), which lies on the tether linking the C-term part of the helix to the second β-sheet. We also noted differences in the local hydration profile of the wild-type with respect to the corresponding one of the structural mutant (vide infra). These two observations could be connected in the sense that the G-16A mutation could have a long-range effect on the flexibility of the C-terminal moiety of the helix by restraining the motion of the tether and consequently affecting the hydration properties of the region.
Decomposition of the energy in specific contributions (Fig. 1 in the Supplementary Material) shows a larger difference in the protein-solvent energy term for the initial configuration of G-16A with respect to MNEI. This difference, which is compensated for during the simulation, can be imputed to a different starting conformation of flexible regions in the two molecules, in particular loop L23, which shows multiple conformations also in the NMR ensemble. Indeed, loop L23 in the initial structure of G-16A is particularly well solvated, as reflected by the favorable protein-solvent contribution; during the simulations, because of the L23 flexibility, the corresponding protein-solvent interaction loses efficacy. As a result, in the steady state, the protein-solvent energy terms for MNEI and G-16A reach similar values indicating a convergence of the two simulations.
Covariance analysis
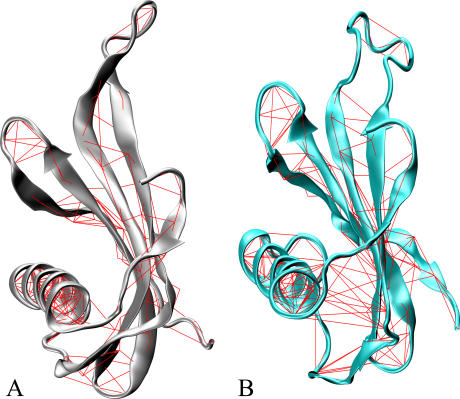
The pairwise covariance matrix can account for correlations in atomic motions. This matrix can be used to highlight protein regions that move coherently. Young et al. (39) described a suitable method of representing the covariance matrix by drawing a line between pairs of atoms with a correlation coefficient higher than a given threshold (covariance web plot). Fig. 2 shows the covariance lines of MNEI (A) and G-16A MNEI (B) with a threshold of 0.5. Such a threshold assures that at least the majority of secondary structure elements will be selected, since their motions are expected to be highly correlated. Covariance and ED analyses of the trajectories have been performed by using the program “Dynamite” (40).
FIGURE 2.
Covariance web plot for MNEI and the G-16A mutant. The pairwise covariance matrix accounts for coherent motions in the protein. The matrix has been computed only considering the Cα atoms. The red lines connect pairs of atoms with a pairwise covariance >0.5. (A) MNEI covariance line plot. Silver ribbons represent the protein backbone. (B) G-16A covariance line plot. Cyan ribbons represent the protein backbone.
For the wild-type, the covariance web plot underlines mainly the network of hydrogen bonds that characterizes elements of secondary structure with only two extra-H-bond correlations. These lines connect Val-37 (strand 2) to Gln-12 and Thr-13 (N-term turn of the helix). The corresponding covariance web plot for the G-16A mutant (Fig. 2 B) shows several extra-H-bond lines between residues of the loop preceding the α-helix (residues 7–10 [1M9G numbering]) and the residues preceding β-strand 2 (residues 40–42 [1M9G numbering]). This finding shows that the G-16A mutation enhances the structural rigidity in the first half segment of the α-helix, whose motion is correlated to the motion of β-strand 2. In addition, modifications in the local flexibility must be associated to differences in the hydration profile of the region (vide infra).
Essential dynamics
ED reduces the dimensionality of the covariance matrix by diagonalization. This method describes global protein motions that are represented by the matrix eigenvectors and eigenvalues. Whereas the covariance web plot highlights regions of concerted atomic motions, ED emphasizes amplitude and direction of dominant protein motions. The two analyses do not necessarily coincide since often the timescales of the respective motions can differ even by many orders of magnitude.
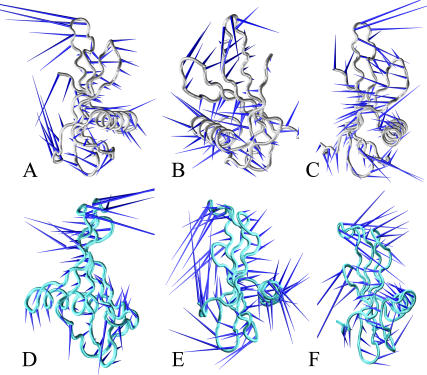
Since the magnitudes of eigenvectors are represented by their eigenvalues, it is possible to evidence the principal components of the protein global motion by sorting them. Usually global motions can be visualized as a movie by projecting the protein trajectory on the respective eigenvector. Rendering these movies in a static picture is not easy. We chose the so-called porcupine plot (40), which is made by cones pointing in the direction of the main movements.
The first three MNEI eigenvectors (Fig. 3, A–C) correspond to 60% of the overall eigenvalues, providing an exhaustive description of the global protein motions. The first mode is a “breathing” motion. Strands 2 and 3 and their connecting loop move toward a region enclosed by the N-term fragment and loop L34, whereas the helix points in an opposite direction. The second and third modes are twisting modes around axes approximately perpendicular to the helix. These latter motions have a rolling effect on the β-sheets. Thus, the ED analysis shows concerted motions of MNEI that involve in general the secondary structure elements.
FIGURE 3.
ED analysis for MNEI and G-16A. ED extracts large protein motions from the covariance matrix. These are sorted on the basis of the eigenvalues that represent the magnitude of the motion. The principal motions are drawn with the porcupine representation. The cones' directions render the global protein motions. The first, second, and third components of MNEI are shown in A, B, and C, respectively. Silver tubes represent the protein backbone. The first, second, and third modes for the G-16A mutant are shown in D, E, and F, respectively. The protein backbone is represented by cyan tubes.
ED of G-16A (Fig. 3, D–F) does not show significant changes with respect to MNEI, with the only exception being a slight reshuffle of the order of the principal motions. In this case, the first and the third motions are twisting modes whereas the second is a breathing mode.
These data show that the G-16A mutation produces alterations of the local flexibility, especially in the helix endpoints, but does not significantly influence the global protein motions.
MNEI solvent density map
The study of protein flexibility combined with the characterization of protein hydration can be extremely useful in evidencing relevant features for potential protein-protein interactions. In particular the map of water density around the protein can account for the accessibility to the surface. This result is actually obtained by exclusion, since the density map evidences the “inaccessibility” to the protein surface due to the presence of tightly bound waters in hydration sites (MDHS), which are defined as local maxima in the water density function (see Methods). Hydration sites on the protein surface are usually connected to increased water localization; they can operate as a protection layer isolating the protein from bulk water (20). Conversely, extended areas lacking defined and localized waters have a propensity to be in contact with dynamical solvent that resembles the bulk solution. It is worth mentioning that the latter regions can be potential “hot spots” for protein interactions because they may be connected to a lower local desolvation energy. In a previous work we have shown that some of these loci are associated with high entropy of the surrounding solvent, making them more “reactive” and therefore more prone to interactions with other molecules (20).
Fig. 4, A and B, shows an overview of the hydration surface of the whole MNEI. We found ∼70 hydration sites uniformly distributed on the MNEI surface. The only notable exception is represented by loop L23, which appears poorly hydrated throughout. This loop is extremely mobile (see RMSF section) and requires a locally restricted reference set in the density map calculation. However it will not be further considered in our analysis since its behavior is due in part to the presence at its extremity of the GF dipeptide linker connecting chains B and A of monellin. This linker, which of course is not a feature of wild-type monellin, contributes to the intrinsic mobility of loop L23 but does not change the biological properties of MNEI with respect to monellin (25).
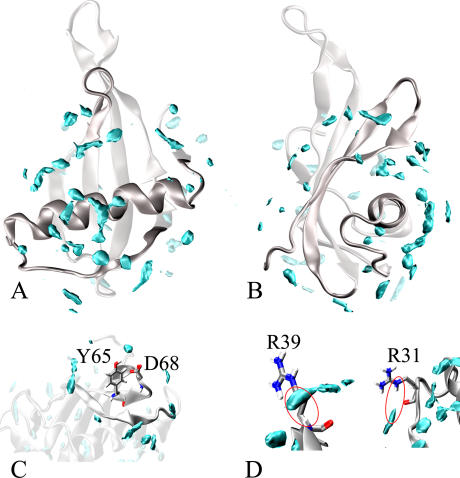
FIGURE 4.
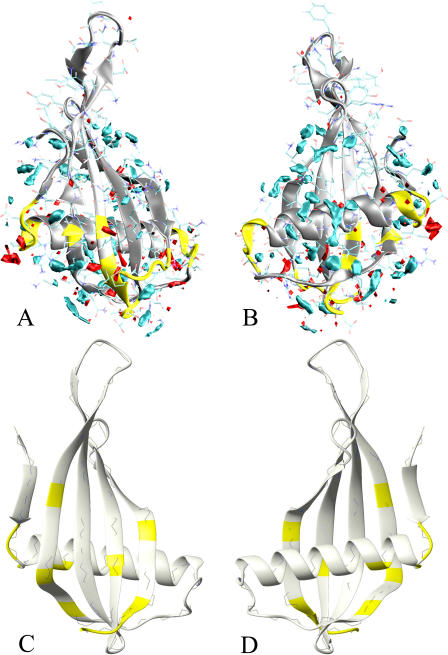
MNEI water density map. The density map provides the location of the MDHS that are defined as local maxima of the function. The MDHS are contoured by cyan surfaces enclosing regions with a value of water density 2.5 times higher than the bulk average density. The MNEI structure (PDB entry 1fa3) is represented by silver ribbons. (A) Overall map of MNEI hydration. (B) Same as (A) but rotated by ∼90°. (C) Close-up view of Y-65 and D-68 hydration: lack of significant MDHS in these regions is consistent with experimental surface accessibility for these residues (11). (D) R31_HE and R39_H hydration. The location of the MDHS suggests that the water interacts with these hydrogen atoms during the simulation.
The solvent density map has been compared to the available experimental data on MNEI hydration. In previous studies (20,41), MD hydration sites have been compared to x-ray data. Correlation with bound waters was systematically poor for surface waters and good for internal waters. One possible cause of these discrepancies was the absence of crystal packing effects in the simulations. In this analysis, we found an encouraging agreement between the MD water density map and the experimental surface accessibility determined by NMR experiments (11). This is probably due to the fact that the simulated protein environment is closer to the experimental conditions in solution but also to the ability of integrated NMR techniques to depict actual accessibility on protein surfaces (42). Probing the protein surface with TEMPOL, a paramagnetic probe, is not limited by water mobility and—when combined with techniques, such as ePHOGSY, that reveal direct interactions between water molecules and proteins' hydrogens—can yield reliable pictures of water surface density (43).
The MNEI density map calculated from our MD simulations outlines regions where MDHSs are less abundant. The main regions found by this analysis are K-25–R-31, M-42–K-44, loop L34, loop L45, and the whole stretch from K-85 to the protein C-terminal. Poor MD water density regions strikingly match those labeled as TEMPOL accessible coupled by weak water-protein NOEs (11). Fig. 4 C shows a close-up of the hydration state of Tyr-65 and Asp-68, two residues at the tip of the L34 loop, classified among the most accessible by the experimental study. It can be seen that there is quite a large area devoid of MDHS around the two residues. Conversely, strong MDHSs have been found near hydrogens that showed significant water-protein NOEs (11), e.g., Arg-31 HE1 and Arg-39 amide H (Fig. 4 D). No buried MDHS have been found in our simulations, except for the internal water molecule placed between residues Val-20 and Leu-31. This molecule has been trapped in the site during the simulation, but it does not show particularly significant interactions with the protein. A list of the highest peaks in the density map and the corresponding nearest residues is reported in Table 2. The unit used for the water density is particles/Å3, which corresponds to a value of 0.05 for the normal water density (1 g cm−3).
TABLE 2.
Highest peaks in the MNEI water density function
| Residues | Water density (particles/Å3) |
|---|---|
| Phe-18 | 0.089 |
| Ile-38 | 0.085 |
| Asp-78 | 0.082 |
| Phe-34 | 0.078 |
| Lys-14 | 0.078 |
| Lys-17 | 0.075 |
| Lys-85 | 0.073 |
| Asp-21 | 0.071 |
| Gly-83 | 0.069 |
| Val-20 | 0.068 |
| Leu-32 | 0.068 |
| Asp-74 | 0.067 |
| Glu-22 | 0.065 |
| Tyr-58 | 0.065 |
| Asn-14 | 0.064 |
1FA3 numbering.
The agreement between the MD solvation map and protein accessibility (11) supports the reliability of current simulations in the description of biological systems. Furthermore, once long simulations in water are available, system properties like the map of self-diffusion coefficients (SDM) (vide infra) can integrate the picture of protein accessibility.
G-16A hydration
The G-16A MD sampling was then used for calculating the corresponding water density map. The hydration profile, characterized by a diffuse distribution of MDHS onto the entire protein surface with the exception of loop L23, resembles that of MNEI. Additionally, as for MNEI, it is possible to recognize regions poor of MDHSs that are potential hot spots for protein interactions. Overall, the lower concentration of MDHSs is on an area limited by the stretch 30–43, loop L34, and segment 92–96.
The main differences in the hydration analyses of the two proteins emerge in the α-helix (Fig. 5 A). As mentioned above, in wild-type MNEI the α-helix presents a large concentration of MDHSs in the (exposed) middle part whereas it is poorly solvated in the N- and C-terminal parts. Conversely, for the G-16A MNEI, the terminal moieties of the helix are extremely solvated, i.e., rich in MDHS, whereas the body of the helix is essentially devoid of hydration sites. It is worth recalling that the helix endpoints showed a different flexibility in the two proteins with a higher rigidity for the mutant. On the other hand, a detailed comparison of the hydration characteristics of L34 and of the protein C-terminal for the wild-type and G-16A suggests that the region enclosed by these stretches is similarly hydrated in both proteins (Fig. 5, B and C).
FIGURE 5.
Comparison of the water density maps of MNEI and G-16A mutant. The overall distribution of the MDHS is similar for the two proteins. The main differences occur in the helix region. Whereas MNEI shows a large concentration of MDHS in the middle region of the helix, the G-16A is more likely to be solvated in the endpoints of the helix. Conversely the L34 loop, a possible “sweet finger”, shows a comparable hydration profile. MD hydration sites are contoured at 2.5 times the bulk solvent value. The color code are cyan for wild-type MDHS, green for G-16A MDHS. The wild-type structure (PDB entry 1FA3) is represented by silver ribbons. G-16A structure (PDB entry 1M9G) is represented by golden ribbons. (A) General proteins hydration with the α-helix outlined. (B) Wild-type close-up view of L34 (pink). (C) G-16A close-up view of L34 (pink).
To put these observations in the right perspective from the point of view of the structure-activity relationship, we performed a control simulation for a mutation that does not cause a reduction in sweetness. D-21 is a surface residue situated on the helix next to G-16 but pointing outside rather than toward the hydrophobic core. When D-21 is mutated into N-21, the sweetness is essentially unaffected; in fact even a slight increase of the sweet power was reported (44). Consequences on hydration of the protein surface caused by the D-21N mutation are decisively smaller than those observed for the G-16A (Fig. 2 in the Supplementary Material). Indeed the density maps of MNEI and D-21N are almost coincident. We find only small hydration perturbations that are locally confined to the point mutation, which can be attributed to the loss of the negative charge implied by the specific mutation. Indeed the loop L34 hydration remains unperturbed (panels B and C). Since protein flexibility as a whole is not affected by the D/N substitution (data not shown), the helix endpoints preserve the same mobility as the wild-type and the associated lower number of MDHSs.
Self-diffusion of water at the MNEI surface
Water at the protein surface forms a layer that has been termed “biological water” since proteins can deeply influence the properties of the surrounding water. As mentioned above, if long enough simulations in explicit water are available, the static information coming from the distribution of MDHSs can be profitably integrated by other system properties like the SDM as calculated from Eqs. 1 and 2. In particular, combination of static and dynamic information can discriminate among the areas characterized by similar low presence of MDHSs and pinpoint loci with particularly high self-diffusional features that could represent possible hot spots for protein-protein interactions (we will refer to these as MD hot spots).
According to the SDM analysis, the region of MNEI most suitable for protein-protein interactions is that approximately delimited by the helix, the C-term residues, and loop L34. Fig. 6, A and B, shows two sides of this region related by a rotation of 180° around a vertical axis. This region is semispherically shaped and presents four main stretches poor of MDHSs and with a correspondently high SDM profile (yellow stretches of Fig. 6 A). Their precise location is defined by the vertices of a tetrahedron with loop L34 at the top (residues 65–69). The region with the weakest presence of MDHSs and highest values for the SDM is the α-helix N-terminal (residues 7–11). The remaining two stretches are the loop after the α-helix (residues 25–30) and the protein C-terminal fragment (residues 91–96). In addition, further isolated residues have to be included in the list, like Arg-39, Pro-40, and Tyr-63. As a matter of fact, two of the three experimentally determined hot spots, the L34 and C-term fragment (25), coincide with the hot spots detected by MD. A list of the highest SDM peaks and the corresponding nearest residues is reported in Table 3. The average value in a layer of 4 Å from the protein surface is 0.680 Å2 ps−1, a value comparable to what was found at the same distance in previous studies (19,36). In analogy with these results (19,36), some regions located on the protein surface present diffusional coefficients even 10 times larger than the average value, showing how strongly the protein can influence local solvent properties. This influence is evidently connected to the physicochemical nature of the surface residues. This may largely be imputed to the hydrophobic/hydrophilic profile of the side chains and to the local charge distribution. In addition, our data show other factors that may affect the hydrodynamic behavior of the protein. In fact, protein shape and local radius of curvature seem to affect the position of MD hotspots that in the MNEI are situated at the vertex of a tetrahedron. Moreover, alterations to the local flexibility are significantly coupled to the hydration profile as evidenced by the differences of the MNEI wild-type and G-16A maps.
FIGURE 6.
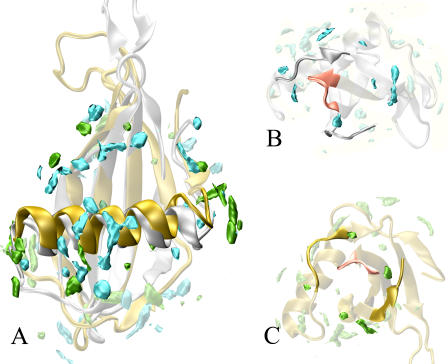
MDHS, SDM, and mutagenesis data compared. The combination of solvent density map and water self-diffusion evidences surface “hot spots” for protein-protein interaction. These are regions poorly surrounded by hydration sites and characterized by high values in the diffusion map. (A and B) MNEI (silver ribbons) and the corresponding hydration maps: cyan for solvent density map, red for SDM. The yellow stretches on the MNEI structure represent residues evidenced by our data to be potential for the protein-protein interaction (D-7–F-11, K-25–G-30, R-39, P-40, Y-63, Y-65–K-69, and G-91–P-96). In the lower panels, C and D, the yellow residues correspond to mutations leading to decrease or loss of sweetness (I-6, D-7, G-9, and R-39 for loss and Q-13, K-36, K-43, R-72, R-88, and P-92–P-96 for substantial decrease). The protein is rotated by 180° around a vertical axis in the two panels.
TABLE 3.
Highest peaks in the MNEI SDM analysis
| Residues | Self-diffusion coefficient (Å2 ps−1) |
|---|---|
| Phe-11 | 6.861 |
| Arg-39 | 6.564 |
| Tyr-63 | 4.857 |
| Asp-7 | 4.548 |
| Pro-10 | 4.396 |
| Thr-12 | 4.103 |
| Gly-9 | 3.953 |
| Gly-91 | 3.843 |
| Pro-40 | 3.713 |
| Leu-70 | 3.671 |
| Val-93 | 3.632 |
| Lys-25 | 3.396 |
| Ile-26 | 3.220 |
| Pro-92 | 3.192 |
| Asp-68 | 2.436 |
1FA3 numbering.
Comparison with mutagenesis studies
Even more interesting is the comparison with the map of mutations leading to a decrease of the sweetening power. Extensive mutagenesis studies performed on monellin and on one of its single chain analogs (44,45) have shown that there are key residues whose mutation leads to substantial loss of activity. The main ones are I-6, D-7, G-9, and R-39, whose mutations causes loss of sweetness of more than two orders of magnitude and Q-13, K-36, K-43, R-72, R-88, and deletion of P-92–P-96 whose mutations cause loss of sweetness of more than one order of magnitude. According to our docking studies (9,10), they cluster on the sides of the “wedge” of MNEI that interacts with the receptor (12). A comparison with the lower panel of Fig. 6 shows that the hot spots derived from the MD analysis are located very close to the regions of crucial mutations.
In addition, our MD study provides new hints for elucidating the protein-receptor binding. Although loop L34 may have a central role in the recognition, being so well identified by the MD hot spot surface, an additional key role could be played by the α-helix. This element is in contact with both static hydration sites (the middle of the helix) and very dynamical sites (the terminal regions). It is likely that this asymmetry is essential in selecting protein orientations in approaching the receptor.
CONCLUSION
In this work, we performed MD simulations of the sweet protein MNEI and its mutant G-16A. The resulting sampling was analyzed by focusing on protein flexibility and protein hydration. The data on the MD solvent density are in agreement with a model requiring a large interface in the MNEI-receptor complex, as implied in the wedge model (7–10). The MD hot spots, identified by a combination of the static MDHS data and the dynamic information supplied by the SDM analysis, point to a specific surface delimited by the following fragments: loop L34 (65–69), 7–11, 25–30, and 91–96. The four stretches are localized at the vertices of a tetrahedron with the loop L34 (65–69) on the top. These findings are amazingly consistent with known mutagenesis data and with the surface predicted by the wedge model (9,10). The entire region of interaction with the receptor proposed by the wedge model is not strongly populated by MDHSs, supporting the hypothesis that the molecular recognition process is made easier by the short time residence water molecules at the protein active site, rendering this region easier to desolvate and more prone to interactions.
Our data further suggest that, owing to the asymmetric hydration of the helix, this secondary structure element could play a specific role in orienting the protein during the binding process. The comparison of wild-type and G-16A hydration better clarified some aspects that emerged from the previous data. The two proteins' hydrations are very similar in correspondence of the L34 and residues 91–96. Since the G-16A basically retains sweetness, our findings reinforce the importance of the role played by L34 and the C-term fragment in the monellin-receptor complex, whereas differences in the helix hydration may help to explain the one order decrease in G-16A sweetness.
The analysis of correlation matrices and RMSF evidenced the connection between the helix hydration and local high frequencies vibrations. The ED showed breathing and twisting mode in both the protein with no significant effects due to the mutation.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
P.A.T. thanks Ministero della Istruzione, Università e Ricerca for financial support.
References
- 1.Max, M., Y. G. Shanker, L. Huang, M. Rong, Z. Liu, F. Campagne, H. Weinstein, S. Damak, and R. F. Margolskee. 2001. Tas1r3, encoding a new candidate taste receptor, is allelic to the sweet responsiveness locus Sac. Nat. Genet. 28:58–63. [DOI] [PubMed] [Google Scholar]
- 2.Montmayeur, J. P., S. D. Liberles, H. Matsunami, and L. B. Buck. 2001. A candidate taste receptor gene near a sweet taste locus. Nat. Neurosci. 4:492–498. [DOI] [PubMed] [Google Scholar]
- 3.Kitagawa, M., Y. Kusakabe, H. Miura, Y. Ninomiya, and A. Hino. 2001. Molecular genetic identification of a candidate receptor gene for sweet taste. Biochem. Biophys. Res. Commun. 283:236–242. [DOI] [PubMed] [Google Scholar]
- 4.Li, X., M. Inoue, D. R. Reed, T. Huque, R. B. Puchalski, M. G. Tordoff, Y. Ninomiya, G. K. Beauchamp, and A. A. Bachmanov. 2001. High-resolution genetic mapping of the saccharin preference locus (Sac) and the putative sweet taste receptor (T1R1) gene (Gpr70) to mouse distal Chromosome 4. Mamm. Genome. 12:13–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sainz, E., J. N. Korley, J. F. Battey, and S. L. Sullivan. 2001. Identification of a novel member of the T1R family of putative taste receptors. J. Neurochem. 77:896–903. [DOI] [PubMed] [Google Scholar]
- 6.Li, X., L. Staszewski, H. Xu, K. Durick, M. Zoller, and E. Adler. 2002. Human receptors for sweet and umami taste. Proc. Natl. Acad. Sci. USA. 99:4692–4696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Morini, G., A. Bassoli, and P. A. Temussi. 2005. From small sweeteners to sweet proteins: anatomy of the binding sites of the human T1R2_T1R3 receptor. J. Med. Chem. 48:5520–5529. [DOI] [PubMed] [Google Scholar]
- 8.Tancredi, T., A. Pastore, S. Salvadori, V. Esposito, and P. A. Temussi. 2004. Interaction of sweet proteins with their receptor. A conformational study of peptides corresponding to loops of brazzein, monellin and thaumatin. Eur. J. Biochem. 271:2231–2240. [DOI] [PubMed] [Google Scholar]
- 9.Temussi, P. A. 2002. Why are sweet proteins sweet? Interaction of brazzein, monellin and thaumatin with the T1R2–T1R3 receptor. FEBS Lett. 526:1–4. [DOI] [PubMed] [Google Scholar]
- 10.Morini, G., and P. A. Temussi. 2005. Micro and macro models of the sweet receptor. Chem. Senses. 30:i86–i87. [DOI] [PubMed] [Google Scholar]
- 11.Niccolai, N., R. Spadaccini, M. Scarselli, A. Bernini, O. Crescenzi, O. Spiga, A. Ciutti, D. Di Maro, L. Bracci, C. Dalvit, and P. Temussi. 2001. Probing the surface of a sweet protein: NMR study of MNEI with a paramagnetic probe. Protein Sci. 10:1498–1507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Spadaccini, R., F. Trabucco, G. Saviano, D. Picone, O. Crescenzi, T. Tancredi, and P. A. Temussi. 2003. The mechanism of interaction of sweet proteins with the T1R2–T1R3 receptor: evidence from the solution structure of G16A-MNEI. J. Mol. Biol. 328:683–692. [DOI] [PubMed] [Google Scholar]
- 13.Peon, J., S. K. Pal, and A. H. Zewail. 2002. Hydration at the surface of the protein Monellin: dynamics with femtosecond resolution. Proc. Natl. Acad. Sci. USA. 99:10964–10969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dalvit, C. 1998. Efficient multiple-solvent suppression for the study of the interactions of organic solvents with biomolecules. J. Biomol. NMR. 11:437–444. [Google Scholar]
- 15.Dalvit, C. 1996. Homonuclear 1D and 2D NMR experiments for the observation of solvent-solute interactions. J. Magn. Reson. B. 112:282–288. [DOI] [PubMed] [Google Scholar]
- 16.Garcia, A. E. 1992. Large-amplitude nonlinear motions in proteins. Phys. Rev. Lett. 68:2696–2699. [DOI] [PubMed] [Google Scholar]
- 17.Amadei, A., A. B. Linssen, and H. J. Berendsen. 1993. Essential dynamics of proteins. Proteins. 17:412–425. [DOI] [PubMed] [Google Scholar]
- 18.Bonvin, A. M., M. Sunnerhagen, G. Otting, and W. F. van Gunsteren. 1998. Water molecules in DNA recognition II: a molecular dynamics view of the structure and hydration of the trp operator. J. Mol. Biol. 282:859–873. [DOI] [PubMed] [Google Scholar]
- 19.Lounnas, V., and B. M. Pettitt. 1994. A connected-cluster of hydration around myoglobin: correlation between molecular dynamics simulations and experiment. Proteins. 18:133–147. [DOI] [PubMed] [Google Scholar]
- 20.De Simone, A., G. G. Dodson, C. Verma, A. Zagari, and F. Fraternali. 2005. Prion and water: tight and dynamical hydration sites play a key role in structural stability. Proc. Natl. Acad. Sci. USA. 102:7535–7540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fischer, S., and C. S. Verma. 1999. Binding of buried structural water increases the flexibility of proteins. Proc. Natl. Acad. Sci. USA. 96:9613–9615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lounnas, V., and B. M. Pettitt. 1994. Distribution function implied dynamics versus residence times and correlations: solvation shells of myoglobin. Proteins. 18:148–160. [DOI] [PubMed] [Google Scholar]
- 23.Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: “A message-passing parallel molecular dynamics implementation”. Comput. Phys. Commun. 91:43–56. [Google Scholar]
- 24.Van Gunsteren, W. F., S. Billeter, A. Eising, P. H. Hunenberger, P. Kruger, A. E. Mark, W. R. P. Scott, and I. G. Tironi. 1996. Biomolecular Simulations: The GROMOS96 Manual and User Guide. VdF: Hoshshulverlag AG an der ETH Zurich and BIOMOS b.v., Zurich, Switzerland/Groningen, The Netherlands.
- 25.Spadaccini, R., O. Crescenzi, T. Tancredi, N. De Casamassimi, G. Saviano, R. Scognamiglio, A. Di Donato, and P. A. Temussi. 2001. Solution structure of a sweet protein: NMR study of MNEI, a single chain monellin. J. Mol. Biol. 305:505–514. [DOI] [PubMed] [Google Scholar]
- 26.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and A. DiNola. 1984. Molecular dynamics with coupling to an external bath. J. Phys. Chem. 81:3684–3690. [Google Scholar]
- 27.Hess, B., H. Bekker, H. J. C. Berendsen, and J. Fraaije. 1997. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 28.Darden, T., L. Perera, L. Li, and L. Pedersen. 1999. New tricks for modelers from the crystallography toolkit: the particle mesh Ewald algorithm and its use in nucleic acid simulations. Struct. Fold. Des. 7:R55–R60. [DOI] [PubMed] [Google Scholar]
- 29.Berendsen, H. J. C., J. R. Grigerra, and T. P. Straatsma. 1987. The missing term in effective pair potentials. J. Phys. Chem. 91:6269–6271. [Google Scholar]
- 30.Allen, M. P., and D. J. Tildesley. 1987. Computer Simulation of Liquids. Clarendon Press, Oxford.
- 31.Lounnas, V., B. M. Pettitt, and G. N. Phillips, Jr. 1994. A global model of the protein-solvent interface. Biophys. J. 66:601–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lau, K. F., H. E. Alper, T. S. Thacher, and T. R. Stouch. 1994. Effects of switching functions on the behavior of liquid water in molecular dynamics simulations. J. Chem. Phys. 98:8785–8792. [Google Scholar]
- 33.Smith, P. E., and B. M. Pettitt. 1991. Peptides in ionic solutions: a comparison of the Ewald and switching function techniques. J. Chem. Phys. 95:8430–8441. [Google Scholar]
- 34.Alper, H. E., D. Bassolino, and T. R. Stouch. 1993. Computer simulation of a phospholipid monolayer-water system: the influence of long range forces on water structure and dynamics. J. Chem. Phys. 98:9798–9807. [Google Scholar]
- 35.Alper, H. E., D. Bassolino, and T. R. Stouch. 1993. The limiting behavior of water hydrating a phospholipid monolayer: a computer simulation study. J. Chem. Phys. 99:5547–5559. [Google Scholar]
- 36.Makarov, V. A., M. Feig, B. K. Andrews, and B. M. Pettitt. 1998. Diffusion of solvent around biomolecular solutes: a molecular dynamics simulation study. Biophys. J. 75:150–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Brooks 3rd, C. L., and M. Karplus. 1989. Solvent effects on protein motion and protein effects on solvent motion. Dynamics of the active site region of lysozyme. J. Mol. Biol. 208:159–181. [DOI] [PubMed] [Google Scholar]
- 38.Iijima, H., and K. Morimoto. 1995. Controlling susceptibility against protease digestion. Ann. N. Y. Acad. Sci. 750:62–65. [DOI] [PubMed] [Google Scholar]
- 39.Young, M. A., S. Gonfloni, G. Superti-Furga, B. Roux, and J. Kuriyan. 2001. Dynamic coupling between the SH2 and SH3 domains of c-Src and Hck underlies their inactivation by C-terminal tyrosine phosphorylation. Cell. 105:115–126. [DOI] [PubMed] [Google Scholar]
- 40.Barrett, C. P., B. A. Hall, and M. E. M. Noble. 2004. Dynamite: a simple way to gain insight into protein motions. Acta Crystallogr. D. 60:2280–2287. [DOI] [PubMed] [Google Scholar]
- 41.Makarov, V. A., B. K. Andrews, P. E. Smith, and B. M. Pettitt. 2000. Residence times of water molecules in the hydration sites of myoglobin. Biophys. J. 79:2966–2974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Niccolai, N., O. Spiga, A. Bernini, M. Scarselli, A. Ciutti, I. Fiaschi, S. Chiellini, H. Molinari, and P. A. Temussi. 2003. NMR studies of protein hydration and TEMPOL accessibility. J. Mol. Biol. 332:437–447. [DOI] [PubMed] [Google Scholar]
- 43.Niccolai, N., A. Ciutti, O. Spiga, M. Scarselli, A. Bernini, L. Bracci, D. Di Maro, C. Dalvit, H. Molinari, G. Esposito, and P. A. Temussi. 2001. NMR studies of protein surface accessibility. J. Biol. Chem. 276:42455–42461. [DOI] [PubMed] [Google Scholar]
- 44.Somoza, J. R., J. M. Cho, and S. H. Kim. 1995. The taste-active regions of monellin, a potently sweet protein. Chem. Senses. 20:61–68. [DOI] [PubMed] [Google Scholar]
- 45.Ariyoshi, Y., and M. Kohmura. 1994. Solid-phase synthesis and structure-activity relationships of analogs of the sweet protein monellin. J. Soc. Synth. Org. Chem. Jpn. 52:359–369. [Google Scholar]