Models of IP₃ and Ca²⁺ Oscillations: Frequency Encoding and Identification of Underlying Feedbacks

Abstract

Hormones that act through the calcium-releasing messenger, inositol 1,4,5-trisphosphate (IP₃), cause intracellular calcium oscillations, which have been ascribed to calcium feedbacks on the IP₃ receptor. Recent studies have shown that IP₃ levels oscillate together with the cytoplasmic calcium concentration. To investigate the functional significance of this phenomenon, we have developed mathematical models of the interaction of both second messengers. The models account for both positive and negative feedbacks of calcium on IP₃ metabolism, mediated by calcium activation of phospholipase C and IP₃ 3-kinase, respectively. The coupled IP₃ and calcium oscillations have a greatly expanded frequency range compared to calcium fluctuations obtained with clamped IP₃. Therefore the feedbacks can be physiologically important in supporting the efficient frequency encoding of hormone concentration observed in many cell types. This action of the feedbacks depends on the turnover rate of IP₃. To shape the oscillations, positive feedback requires fast IP₃ turnover, whereas negative feedback requires slow IP₃ turnover. The ectopic expression of an IP₃ binding protein has been used to decrease the rate of IP₃ turnover experimentally, resulting in a dose-dependent slowing and eventual quenching of the Ca²⁺ oscillations. These results are consistent with a model based on positive feedback of Ca²⁺ on IP₃ production.

INTRODUCTION

The release of Ca²⁺ ions from intracellular stores is a central event in the transduction of hormone and neurotransmitter signals. In a multitude of cell types, the activation of receptors coupled to the phosphoinositide pathway triggers oscillations in the cytoplasmic Ca²⁺ concentration ([Ca²⁺]_c). In many cell types, the strength of the extracellular stimulus is encoded primarily in the frequency of the [Ca²⁺]_c oscillations, which increases with the degree of stimulation. For example, in rat hepatocytes, the periods of [Ca²⁺]_c oscillations range over one order of magnitude, from >250 s for low concentrations of hormones, such as vasopressin and noradrenalin, to ∼30 s for higher hormone doses (1).

A long-standing question has been whether the oscillations are generated by the cellular Ca²⁺ transporters and channels themselves or whether they originate upstream in the signal transduction machinery, between hormone binding to its receptor and the activation of Ca²⁺ fluxes. It has been proposed that the periodic release of Ca²⁺ ions from the endoplasmic reticulum (ER) can be brought about through the regulatory properties of the IP₃ receptor (IP₃R), the main type of ER calcium release channel in nonexcitable cells (2–5). Mathematical models have demonstrated how fast activation and delayed inhibition of the IP₃R by cytoplasmic Ca²⁺ can drive repetitive Ca²⁺ spiking (6–8). In these models, IP₃ is required to initially open the IP₃R and sensitize the channel toward feedback activation by cytoplasmic calcium. Therefore, Ca²⁺ oscillations can occur when IP₃ concentration is held at a constant value. However, models based on a simple description of the IP₃R dynamics generally produce [Ca²⁺]_c oscillations with short periods (∼10–60 s) and thus do not reproduce the long interspike intervals observed experimentally. Long-period oscillations have been obtained when additional mechanisms, such as the regulation of IP₃R by phosphorylation, stochastic gating phenomena or slow calcium buffers, are included (9,10,11).

Recently, it has become possible to monitor IP₃ changes in intact cells. These experiments have shown that, for some of the agonists used, the IP₃ concentration is highly dynamic and can oscillate together with cytoplasmic calcium (12–15). This raises the intriguing possibility that a coupled IP₃-Ca²⁺ oscillator may generate long-period oscillations and underlie the efficient frequency encoding of the hormone dose.

The existence of both positive and negative feedbacks of Ca²⁺ on IP₃ metabolism could mediate fluctuations in cellular IP₃ levels. The production of IP₃ is catalyzed by a diverse family of phosphoinositide-specific phospholipase C (PLC) isoforms (16). All PLC isoforms are activated by Ca²⁺ ions, although their sensitivities to [Ca²⁺] vary greatly (17,18). This feedback can have an important role in Ca²⁺ wave propagation (19–22). IP₃ is removed by phosphorylation or dephosphorylation through IP₃ 3-kinase (IP₃K) or IP₃ 5-phosphatase (IP₃P), respectively. IP₃ removal by IP₃K is activated by Ca²⁺ (23–25). Moreover, it has also been suggested that protein kinase C (PKC), which is activated by receptor-mediated increases in Ca²⁺ and diacylglycerol, may inhibit IP₃ production by inactivating agonist receptors (13,26). However, it is presently not clear what effects such feedbacks have on Ca²⁺ oscillations. Importantly, it is not known whether the involvement of these Ca²⁺-dependent feedback mechanisms serves a physiological role.

Previous models have shown that IP₃-mediated Ca²⁺ release coupled to Ca²⁺-activated PLC can generate oscillations, without any requirement of IP₃R regulation by Ca²⁺ (26,27). These models have been criticized because in some cell types Ca²⁺ oscillations can also be elicited by IP₃ or its nonmetabolizable analogs (3,28,29). The incorporation of Ca²⁺ activation of PLC into a Ca²⁺ oscillator model based on the above-described IP₃R properties has been reported to modulate Ca²⁺ oscillations (30), whereas the inclusion of IP₃K has been found to have practically no effect (31,32).

In this work, we have carried out a systematic modeling study of the interaction between cellular Ca²⁺ transports and IP₃ metabolism. The model includes the dynamics of IP₃, Ca²⁺, and IP₃R and takes into account positive and negative feedback of Ca²⁺ on the IP₃ metabolism. These are mediated by Ca²⁺ activation of IP₃ generation through PLC and Ca²⁺ activation of IP₃ removal by IP₃K, respectively. We have found that each of these Ca²⁺ feedbacks strongly modifies the properties of a core oscillator based on Ca²⁺ and IP₃R dynamics and, in particular, substantially expands the range of oscillation frequencies. Thus IP₃ oscillations may underlie efficient frequency encoding of the hormone signal. The model analysis shows that the lifetime of IP₃ is a critical parameter in the system, the experimental perturbation of which can give information on the feedbacks present. We directly tested this theory in Chinese hamster ovary (CHO) cells by transiently expressing an IP₃ binding protein composed of the N-terminal ligand-binding domain of the type 1 IP₃R fused to green fluorescent protein. The overexpression of this fusion protein exerted a dose-dependent suppression of repetitive agonist-induced Ca²⁺ oscillations that is consistent with an oscillator model including positive feedback of Ca²⁺ on IP₃ generation. Taken together, the experimental data and theoretical analysis suggest that IP₃ oscillations are an essential component of the Ca²⁺ oscillator, expanding the richness in the message conveyed by extracellular stimuli.

MATERIALS AND METHODS

Mathematical model

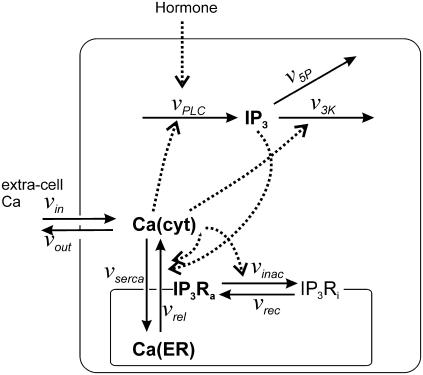
The model accounts for the formation and degradation of IP₃, the main Ca²⁺ fluxes across the ER and plasma membrane, and the IP₃R dynamics (see Fig. 1). It is formulated in terms of four variables: the IP₃ and Ca²⁺ concentrations in the cytoplasm, p and c, respectively; the calcium concentration in the ER stores, s; and the fraction of IP₃R that have not been inactivated by Ca²⁺, r.

FIGURE 1.

Interactions between Ca²⁺ transport processes and IP₃ metabolism included in the model. The solid and dashed arrows indicate transport/reaction steps and activations, respectively. The bold quantities indicate the model variables: IP₃, cytoplasmic IP₃; Ca(cyt), free cytoplasmic Ca²⁺; Ca(ER), free Ca²⁺ in the ER; IP₃R_a, active conformation of the IP₃R. 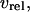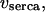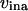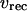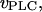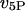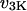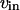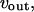The other abbreviations denote: IP₃R_i, inactive conformation of the IP₃R; rate of Ca²⁺ release through the IP₃R; active Ca²⁺ transport into the ER; and rate of Ca²⁺-induced IP₃R inactivation and recovery rate, respectively; production rate of IP₃; and rates of IP₃ dephosphorylation and phosphorylation, respectively; and rates of Ca²⁺ influx and extrusion across the plasma membrane, respectively.

IP₃ dynamics

IP₃ is produced by PLC, whose activity depends on agonist dose and Ca²⁺. The Ca²⁺ sensitivity of PLCβ can be modeled by (33)

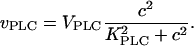(1)

The maximal rate 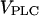depends on the agonist concentration, whereas 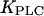characterizes the sensitivity of PLC to Ca²⁺. IP₃ is removed through dephosphorylation by IP₃P and phosphorylation by IP₃K, which we model as

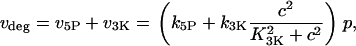(2)

where 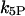and 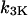are the IP₃ dephosphorylation and phosphorylation rate constants, respectively. The Ca²⁺ dependence of the IP₃K is described by a Hill function with the half-saturation constant 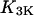(23). According to Fink et al. (34) and Sims and Allbritton (35), one can assume that the two enzymes are not saturated with IP₃, justifying the linear rate law in p.

For the purpose of the subsequent analysis we write the balance equation for the IP₃ concentration in the following form

(3)

where we introduce the characteristic time of IP₃ turnover

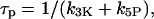(4)

and the ratio of the maximal IP₃K rate to the total maximal degradation rate of IP₃

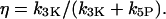(5)

The strength of the positive feedback will be tuned by changing 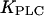(the Ca²⁺ sensitivity of PLC), and the strength of the negative feedback will be tuned by changing (the relative expression level of IP₃K). Although both feedbacks can be present simultaneously, it is useful to first analyze them separately. Therefore, we define the “positive-feedback model” in which PLC is sensitive to Ca²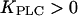⁺ () and IP₃K is not expressed (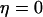), and the “negative-feedback model” in which IP₃K is present (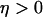) and PLC is assumed insensitive to physiological Ca²⁺ changes ().

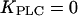Note that the rescaled maximal PLC activity 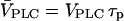equals the steady-state concentration of IP₃ that would be attained in the absence of positive or negative feedbacks.

Calcium and IP₃R dynamics

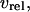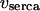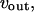The Ca²⁺ release flux through the IP₃R, is modeled according to Li and Rinzel (36). The rate equations for active transport of Ca²⁺ across the ER and plasma membranes, and respectively, follow Lytton et al. (37) and Camello et al. (38). Calcium influx v_in includes a leak into the cell and a stimulation dependent influx. The balance equation for cytoplasmic Ca²⁺ then reads

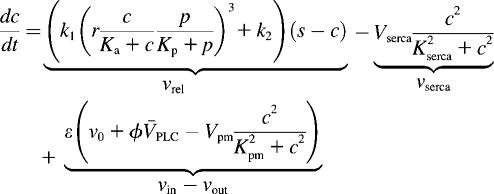(6)

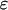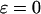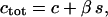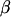The dimensionless parameter measures the relative strength of the plasma membrane fluxes, which is known to be cell-type specific. We first carry out the model analysis for the simpler case that the plasma membrane fluxes are negligible. Setting the total Ca²⁺ concentration in the cell is conserved and can be expressed as where is the ratio of effective cytoplasmic volume to effective ER volume (both accounting for Ca²⁺ buffering). Therefore, we can insert for the ER calcium in Eq. 6, 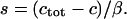In the presence of plasma-membrane fluxes () this conservation no longer holds and a kinetic equation for s must be added:

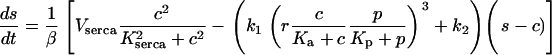(7)

The dynamics of IP₃R inactivation by cytoplasmic Ca²⁺ is described by (35)

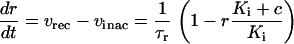(8)

The meaning and numerical values of the kinetic parameters are given in Table 1.

TABLE 1.

Reference parameter values

	Positive feedback	Negative feedback
IP3 dynamics parameters
Half-activation constant of IP3K,	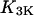0.4 μM	0.4 μM
IP3 phosphorylation rate constant,	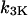0	0.1 s−1
IP3 dephosphorylation rate constant,	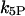0.66 s−1	0
Half-activation constant of PLC,	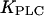0.2 μM	0 μM
Ca2+ transport and structural parameters
Ratio of effective volumes ER/cytosol, β	0.185	0.185
Maximal SERCA pump rate,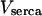	0.9 μM s−1	0.25 μM s−1
Half-activation constant,	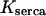0.1 μM	0.1 μM
Maximal PMCA pump rate,	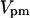0.01 μM s−1	0.01 μM s−1
Half-activation constant,	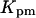0.12 μM	0.12 μM
Constant influx,	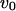0.0004 μM/s	0.0004 μM/s
Stimulation-dependent influx,	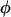0.0047 s−1	0.045 s−1
Strength of plasma membrane fluxes,	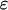0	0
Total Ca2+ concentration (for ),	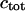2 μM	2 μM
IP3R parameters
Maximal rate of Ca2+ release, k1	1.11 s−1	7.4 s−1
Ca2+ leak, k2	0.0203 s−1	0.00148 s−1
Ca2+ binding to activating site,	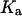0.08 μM	0.2 μM
Ca2+ binding to inhibiting site,	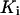0.4 μM	0.3 μM
IP3 binding,	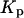0.13 μM	0.13 μM
Characteristic time IP3R inactivation,	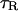12.5 s	6.6 s

The half-saturation constants for PLC and IP₃K were taken from Blank et al. (32) and Communi et al. (22), respectively. The IP₃ degradation rate constants were chosen in accordance to Fink et al. (33) and Sims and Allbritton (34). The maximal rate of PLC, 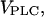is taken as the stimulation-dependent control parameter. In the positive-feedback model (Ca²⁺ activation of PLC), the parameters for the Ca²⁺ transport processes and the IP₃R were taken from Li and Rinzel (35). In the negative feedback model (Ca²⁺ activation of IP₃K), we obtained no substantial effect of the IP₃K on the oscillations with these parameters. However, for different parameters (as given) the IP₃K effects were pronounced. The differences in the Ca²⁺ fluxes between the two models can be accounted for by variations in the expression of the involved proteins. The differences in the Ca²⁺ binding properties to the activating site of the IP₃R can be due to differences in the expression of IP₃R subtypes, with IP₃R subtype I having a higher Ca²⁺ dissociation constant for the activating site than subtypes II and III (52,53). The table gives the reference parameter set; parameters that are varied in specific simulations are indicated in the respective figure legends.

Numerical solutions of the differential equations system, Eqs. 3 and 6–8, were obtained using a fourth-order Runge-Kutta algorithm implemented in XPPAUT (http://www.math.pitt.edu/∼bard/xpp/xpp.html). Bifurcation analyses were done using the program AUTO2000 (39). Calcium waves with the local kinetics given by Eqs. 3 and 6–8 and diffusion of Ca²⁺ and IP₃ were calculated numerically with a finite-difference Crank-Nicholson scheme. Wave speeds for solitary waves were evaluated using AUTO2000.

Experimental procedures

Cell culture

CHO cells were cultured in Ham's F-12 media supplemented with 10% fetal bovine serum (FBS) and antibiotics. Cells were seeded onto poly-D-lysine coated glass coverslips (25 mm) and maintained in culture until 70–80% confluent before experimental protocols.

Plasmid construction and transfection protocols

The cDNA encoding 620 amino acids of the N-terminal rat type 1 IP₃ receptor (40) was ligated in-frame to the C-terminus of the enhanced green fluorescent protein gene in the plasmid pEGFP-C1 (Clontech, Palo Alto, CA) to generate the plasmid pEGFP-LBD. Cell cultures were transiently transfected with either pEGFP-LBD (EGFP-LBD) or pEGFP-C1 (EGFP) using Lipofectamine 2000 (Invitrogen, Carlsbad, CA) according to the manufacturer's protocols. Agonist-evoked [Ca²⁺]_c responses were recorded in transfected cultures after a 16–48-h incubation period.

Imaging measurements of [Ca²⁺]_c and fluorescent proteins

Calcium imaging experiments were performed in a HEPES-buffered physiological saline solution (HBSS) comprising (in mM): 25 HEPES (pH 7.4 at 37°C), 121 NaCl, 5 NaHCO₃, 4.7 KCl, 1.2 KH₂PO₄, 1.2 MgSO₄, 2.0 CaCl₂, 10 glucose, 0.1 sulphobromophthalein, and 0.25% (w/v) fatty acid-free BSA. Cell cultures were loaded with fura-2/AM by incubation with 5 μM fura-2/AM plus Pluronic F-127 (0.02% v/v) for 20–40 min in HBSS. The cells were washed and transferred to a thermostatically regulated microscope chamber (37°C). Fura-2 fluorescence images (excitation, 340 and 380 nm, emission 420–600 nm) were acquired at 3–4-s intervals with a cooled charge-coupled device (CCD) camera as previously described (3). Fura-2 fluorescence intensities were corrected for GFP spillover before calculating fluorescence ratio values, by quenching cytosolic fura-2 with MnCl₂. Cells expressing recombinant proteins were selected by screening for GFP fluorescence (excitation 488 nm, emission 525 nm).

EGFP-LBD concentration was estimated from a standard curve constructed with known concentrations of six His-tagged EGFP (Clontech; molecular weight of 27,000). Calibration solutions were prepared by diluting the recombinant protein in PBS. An aliquot (5 μl) was mixed with low-density mineral oil then sandwiched between two glass coverslips. EGFP containing “bubbles” ranging in size from 10 to 50 μm (the approximate range of cell diameters observed in CHO cultures) were imaged with a Nikon 20×, 0.75 NA Plan Apo objective on a wide-field microscope. The fluorophore protein concentration was converted into molar value assuming a molecular weight of 27,000 for His-tagged EGFP.

RESULTS

Positive and negative feedback models exhibit frequency encoding of agonist dose

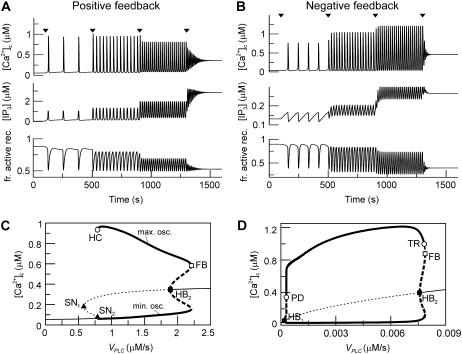
In many cell types, one observes a strong dependence of the frequency of Ca²⁺ oscillations on the dose of the applied receptor agonist, whereas the oscillation amplitude remains nearly constant (1). A stepwise increase of the agonist concentration is accompanied by a prompt rise of the oscillation frequency. In the model, the maximal rate of PLC, 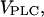is a measure of agonist concentration. We subjected the positive-feedback model, with Ca²⁺ activation of PLC, and the negative-feedback model, with Ca²⁺ activation of IP₃K, to stepwise increases in 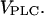The responses are shown in Fig. 2, A and B, respectively, with the time points of 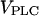increase indicated by arrowheads. Both models exhibit a large range of oscillation frequencies with little change in [Ca²⁺]_c amplitude (Fig. 2, A and B; top traces). The pronounced increase in the rate of spiking with increasing stimulus is the hallmark of the experimentally observed frequency encoding. For very large stimuli, a plateau of elevated [Ca²⁺]_c is reached, again in agreement with experimental data.

FIGURE 2.

Agonist-induced IP₃ and Ca²⁺ oscillations in the positive and negative feedback models. (A) Positive feedback model with Ca²⁺ activation of PLC. Changes in [Ca²⁺]_c, [IP₃], and in the fraction of active receptors (top, middle, and bottom panels) after stepwise increases in the agonist concentration (arrowheads), modeled by an increase in the maximal rate of PLC (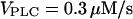 for t < 100 with successive increases to 0.787, 1, 1.5, and 2.5 μM/s). (B) Negative feedback model with Ca²⁺ activation of IP₃K. The response is shown for a step protocol with 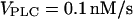for t < 100, followed by increases to 0.45, 2.5, 5.8, and 10 nM/s. (C) Bifurcation diagram for positive feedback model; shown are the maxima and minima of the [Ca²⁺]_c oscillations (thick lines) and the [Ca²⁺]_c steady states (thin lines) as a function of the stimulus (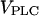). Solid and dashed lines indicate stable and unstable states, respectively. HB, Hopf bifurcation; HC, homoclinic bifurcation; SN, saddle-node bifurcation; FB, saddle node of periodics. (D) Bifurcation diagram for negative feedback model. PD, period doubling; TR, torus bifurcation. Between PD and HB₁ and TR and FB there exist complex oscillations (omitted for clarity). The parameter values used are listed in Table 1.

The [Ca²⁺]_c oscillations in both models consist of a series of sharp spikes with baseline interludes (Fig. 2, A and B). The peak values of [Ca²⁺]_c and [IP₃] occur nearly at the same time. The shape of the [IP₃] oscillations in the two models is different. In the positive-feedback model, [IP₃] exhibits baseline-separated spikes (Fig. 2 A). In contrast, in the negative-feedback model, [IP₃] follows a zig-zag pattern: the occurrence of a [Ca²⁺]_c spike leads to an abrupt decrease in [IP₃], after which [IP₃] slowly builds up again over the whole oscillation period (Fig. 2 B). The IP₃R activities show similar dynamics in both models.

The behavior of the two model systems for different stimulation strengths can be summarized in bifurcation diagrams (Fig. 2, C and D). We computed the steady states of [Ca²⁺]_c and the maxima and minima of [Ca²⁺]_c oscillations as a function of 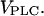For very low PLC activity, both models show a stable steady state of low [Ca²⁺]_c; similarly, an elevated [Ca²⁺]_c plateau is reached at relatively high PLC activity (these stable steady states are indicated by thin solid lines). For an intermediate range of 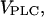the steady states are unstable (thin dashed lines). In these regions, both models exhibit oscillations ([Ca²⁺]_c maxima and minima in stable oscillations are depicted by thick solid lines). The oscillations arise either via Hopf bifurcations (HB), or, in the case of the positive-feedback model, also by a homoclinic bifurcation (HC).

Further bifurcations are indicated and referred to in the figure legend. In particular, a homoclinic bifurcation is associated with the existence of multiple steady states, which arise through saddle-node bifurcations (Fig. 2 C, SN). Such multistationarity is typical for models that neglect the plasma-membrane fluxes of calcium; this point will be discussed in more detail below. In the negative-feedback model, there are two regions near the Hopf bifurcations HB₁ and HB₂ (before the point PD and after the point TR in Fig. 2 D) where irregular and bursting oscillations are observed (results not shown). Because these two regions are extremely narrow, compared to the total stimulation range in the negative feedback model, our focus will be on the regular oscillations.

In the two bifurcation diagrams, one notices that the 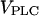values required for oscillations are considerably smaller in the negative-feedback model than in the positive-feedback model. This is primarily a consequence of the different feedback mechanisms. First, in the positive-feedback model the actual PLC activity is Ca²⁺ dependent and, therefore, is lower than 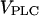at resting [Ca²⁺]_c. Second, owing to the calcium activation of IP₃K in the negative-feedback model, the IP₃ degradation rate at resting [Ca²⁺]_c is much smaller than in the positive-feedback model, requiring a smaller rate of IP₃ production to raise [IP₃] and induce oscillations.

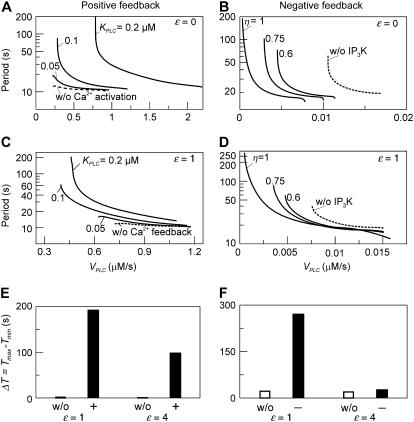
The wide range of oscillation periods is due to interactions of IP₃ and Ca²⁺ dynamics

To elucidate whether the IP₃ dynamics participate in frequency encoding, we compared the oscillation periods in models without any Ca²⁺ feedback on IP₃ (resulting in a constant [IP₃]) and in the two feedback models (with [IP₃] oscillations).

We begin by discussing the positive-feedback model. In the positive-feedback model, we consider Ca²⁺ activation of the agonist-dependent PLCβ. The strength of the positive feedback can be tuned by changing the value of the Ca²⁺ activation constant, 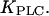For 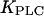being much lower than the basal [Ca²⁺]_c, PLC is always saturated with Ca²⁺ and its activity is independent of variations in [Ca²⁺]_c. In particular, by setting 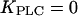positive feedback will effectively be eliminated. This model with constant [IP₃] shows fast calcium oscillations with a period of 10–15 s (Fig. 3 A, dashed line). Introducing positive feedback by setting 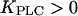causes oscillations with long periods at low stimulation. The frequency encoding of the stimulus becomes very pronounced when the sensitivity of PLC to changes in [Ca²⁺]_c is just above basal [Ca²⁺]_c (Fig. 3 A, solid lines; 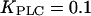and 0.2 μM).

FIGURE 3.

Frequency encoding of agonist stimulus. (A) Positive feedback: oscillation periods observed at different stimulation strengths (varying 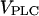). Increasing the half-saturation constant of PLC for Ca²⁺, K_PLC, from 0 (no functional positive feedback) to 0.2 μM (functional feedback) greatly enhances frequency encoding. (B) Negative feedback. Increasing the amount of IP₃K relative to IP₃P (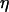) enhances frequency encoding. (C, D) The feedback effects shown in panels A and B are preserved when plasma-membrane fluxes of Ca²⁺ are included in the models (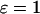). (E) Range of oscillation periods, 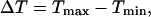in the presence (+) and absence (w/o) of positive feedback for two different strengths of the plasma-membrane Ca²⁺ fluxes (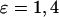). (F) Range of oscillation periods in the presence (−) and absence (w/o) of negative feedback for two different strengths of the plasma-membrane Ca²⁺ fluxes (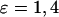). We have found that the IP₃K has an impact on the oscillation period only when the Ca²⁺ fluxes between ER and cytoplasm are comparatively slow and the IP₃R is less sensitive to Ca²⁺ activation. To expose the period effect of the negative feedback, we have chosen different parameter values than in the positive feedback model (see Table 1).

For the negative-feedback model, we recall that there are two removal pathways for IP₃, one catalyzed by the Ca²⁺-insensitive IP₃ 5-phosphatase (IP₃P) and the other by the Ca²⁺-activated IP₃ 3-kinase (IP₃K). We can modify the strength of the negative feedback by taking different concentration ratios of IP₃P and IP₃K. The feedback strength is expressed by the ratio of the maximal IP₃K rate to the total degradation rate of IP_3; 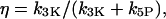where 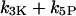has been kept constant in the following calculations. The oscillation periods in the absence of negative feedback (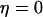), and therefore constant [IP₃], are shown in Fig. 3 B (dashed line). When 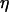is sufficiently high, the negative feedback has a pronounced effect on the range of oscillations periods; for 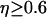there is an increase in the period range (Fig. 3 B, solid lines).

In the positive-feedback model, arbitrarily long periods can be obtained (exceeding the 200 s shown), which are due to the onset of the oscillations via a homoclinic bifurcation (see also Fig. 2 C). The homoclinic bifurcation specifically occurs in the model when the plasma-membrane fluxes of Ca²⁺ are neglected, which is a valid simplification for many cell types in which the contribution of these fluxes to Ca²⁺ oscillations is small (41). We have also studied the more general case when the plasma-membrane Ca²⁺ fluxes are included in the model (see Materials and Methods). Then there is a unique steady state and the homoclinic bifurcation no longer exists. Nevertheless, long-period oscillations are present (Fig. 3 C). Importantly, the dependence of the period range of the oscillations on 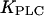remains very similar.

We also introduced plasma-membrane fluxes of Ca²⁺ into the negative-feedback model (Fig. 3 D). We observed a similar picture as without plasma membrane fluxes, provided that the plasma-membrane fluxes were comparatively moderate. However, when the plasma-membrane Ca²⁺ fluxes are large enough, the effect of IP₃K on the oscillation period practically disappears. In contrast, the period behavior in the positive-feedback model is less affected by changes in the magnitude of the plasma-membrane Ca²⁺ fluxes. To show this, we evaluated the range of oscillation periods 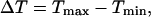where T_max and T_min are the maximal and minimal period that are obtained for low and high stimulation, respectively, for two different strengths of the plasma-membrane Ca²⁺ fluxes ( 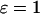and 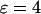). The positive-feedback model exhibits in both cases a much larger period range than the corresponding model without feedback (Fig. 3 E). In contrast, the increase of the period range through negative feedback is only seen when the plasma-membrane Ca²⁺ fluxes are comparatively small, 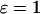(Fig. 3 F).

In summary, both positive and negative feedbacks of Ca²⁺ on IP₃ may serve a physiological role by greatly enhancing the range of frequency encoding of the agonist stimulus. The frequency encoding supported by the positive feedback is more robust against variations in the kinetic parameters of the Ca²⁺ transport processes.

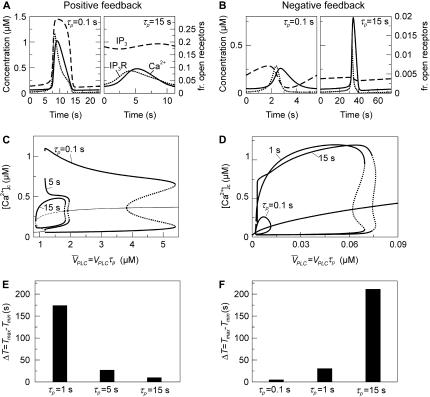
Positive and negative models respond differently to changes in feedback IP₃ turnover time

In the model simulations, we noticed that the characteristic time of IP₃ turnover 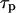has a decisive impact on the Ca²⁺-IP₃ oscillators. The measured IP₃ turnover times span a relatively wide range, from 0.1 to >10 s depending on cell type and experimental conditions (34,35). We have found that fast IP₃ turnover (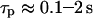) is associated with long oscillation periods in the positive-feedback model. Conversely, the negative-feedback model exhibits long-period oscillations when the IP₃ turnover is comparatively slow ().

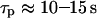Insight into the origin of this difference between the two models can be gained by looking at the time courses of the model variables. In the positive feedback model, fast IP₃ turnover (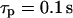) yields high-amplitude oscillations in [Ca²⁺]_c and [IP₃] (Fig. 4 A, solid and dashed lines, respectively). [Ca²⁺]_c and [IP₃] rise simultaneously, and IP₃-induced Ca²⁺ release and Ca²⁺-activated IP₃ production coincide. After termination of the [Ca²⁺]_c spike, [IP₃] returns quickly to a basal level, because Ca²⁺-activated IP₃ production has ceased and IP₃ degradation is fast. Also, the IP₃Rs close efficiently after the spike (Fig. 4 A, dotted line showing the fraction of open IP₃R). For slow IP₃ turnover (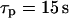) [IP₃] does not sufficiently decline after the [Ca²⁺]_c spike, leading to an increased basal opening of the IP₃R, lower ER Ca²⁺ store loading and, consequently, much less pronounced [Ca²⁺]_c spikes (Fig. 4 A).

FIGURE 4.

IP₃ turnover time controls feedbacks. (A) Positive-feedback model. Dynamics of [Ca²⁺]_c, [IP₃], and the fraction of open IP₃Rs (solid, dashed, and dot-dashed lines, respectively) during an oscillation period; the fraction of open IP₃Rs is given by 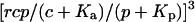(see Eq. 6). Fast IP₃ turnover yields a pronounced spike (left panel, 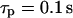), whereas slow IP₃ turnover supports only a small-amplitude response (right panel, 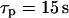). (B) The negative-feedback model shows the opposite behavior, with a small-amplitude response for fast IP₃ turnover (left panel, 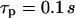) and a sharp spike for slow IP₃ turnover (left panel, 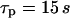). (C) Positive-feedback model. Bifurcation diagram showing the maxima and minima of the [Ca²⁺]_c oscillations as a function of the stimulus for different values of the IP₃ turnover. The bifurcation diagrams for different values of 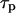are compared by plotting them against the product 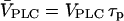; in this way, the steady-state concentrations of Ca²⁺ and IP₃ are identical for a given 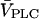(solid and dashed lines indicate stable and unstable states, respectively; the stability of the steady state is shown for 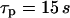). Both amplitude and range of stimuli leading to oscillations increase with faster IP₃ turnover. (D) The corresponding bifurcation diagrams for the negative-feedback model show the opposite behavior. The amplitude and range of stimuli leading to oscillations increase with slower IP₃ turnover. (E, F) Dependence of frequency encoding on IP₃ turnover in the positive and negative feedback models, respectively. Shown are the differences 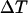between the largest (for low stimulation) and smallest (for high stimulation) oscillation period.

Not only the spike characteristics but also the oscillation period and the range of agonist stimuli that give oscillations are affected by the IP₃ half-life. For fast IP₃ turnover, oscillations in the positive-feedback model are observed over a wide range of stimuli (Fig. 4 C, 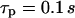). Slower IP₃ turnover leads to reduced oscillation ranges and also much smaller amplitudes (Fig. 4 C, 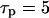and 15 s). Importantly, also, the capacity for frequency encoding of the stimulus, as measured by the period range of oscillations, is high when the IP₃ turnover is fast (Fig. 4 E).

In the negative-feedback model, changing the timescale of IP₃ turnover has the opposite effect. When IP₃ turnover is fast (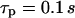), a rise in [Ca²⁺]_c triggers, via activation of IP₃K, a pronounced decrease in [IP₃], which in turn limits further Ca²⁺ release (Fig. 4 B). Therefore, the [Ca²⁺]_c spikes are relatively small and [IP₃] shows strong variations (solid and dashed lines, respectively, in Fig. 4 B). When the IP₃ lifetime is larger (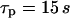), [IP₃] remains at a relatively high level throughout and the [Ca²⁺]_c spikes are accordingly more pronounced (Fig. 4 B). Moreover, for slow IP₃ degradation, the range of stimuli where oscillations occur is larger (Fig. 4 D). The capacity for frequency encoding as measured by the range of oscillation periods, 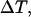strongly increases with the IP₃ half-life (Fig. 4 F). This finding agrees with the frequent observation that negative feedback is more prone to oscillate when the controlled variable (here IP₃) responds slowly.

To summarize, frequency encoding in the two feedback models poses opposite requirements on IP₃ turnover: positive and negative feedbacks are efficient frequency modulators when the IP₃ turnover is fast and slow, respectively. The critical IP₃ lifetimes estimated in the model indicate that both cases could be realized physiologically.

Period control is shared by all processes

The calculations have shown that the inclusion of IP₃ dynamics strongly alters the frequency properties of the oscillator and, particularly, leads to long-period oscillations. We have, therefore, quantified the control of the IP₃ dynamics and the other processes present in the model on the oscillation period. To this end, we have used the following sensitivity measure

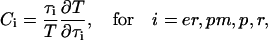(9)

which we refer to as period control coefficients (see also Wolf et al. (42)). The 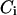set the change of the oscillation period T in proportion to the change in the characteristic time 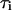of an individual process i. We analyzed the control of the following processes: IP₃ metabolism (with 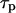as defined in Eqs. 3 and 4), the IP₃R dynamics (with 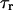as defined in Eq. 8), Ca²⁺ transport across the ER membrane (achieved by scaling 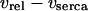with 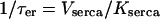in Eq. 6), and Ca²⁺ transport across the plasma membrane (achieved by scaling 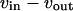with 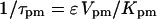in Eq. 6). A positive period control coefficient implies that a slowing of the respective process (i.e., increase in 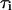) raises the period. At any point, the period control coefficients sum to unity, 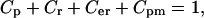so that each coefficient quantifies the relative contribution of a single process to the oscillation period (43).

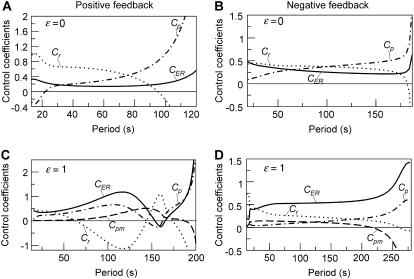
The control coefficients were calculated for various levels of stimulation in the positive and negative feedback models. Because these levels correspond to different oscillation periods, we can plot the C_i against the period. Fig. 5, A and B, depict the result for the model without plasma-membrane fluxes of Ca²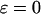⁺ (). Positive and negative feedback models yield a similar picture. The control is distributed between the dynamics of IP₃, Ca²⁺, and IP₃R. In long-period oscillations, the IP₃ turnover has the leading control (dot-dashed lines). The IP₃R dynamics contributes more significantly to setting the period of fast oscillations, especially in the positive-feedback model (dotted lines).

FIGURE 5.

Control coefficients for the oscillation period. (A, B) Positive and negative feedback models, respectively, in the absence of Ca²⁺ fluxes across the plasma membrane (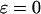); control coefficients of Ca²⁺ exchange across the ER membrane (C_er, solid line), IP₃ metabolism (C_p, dashed line), and IP₃R dynamics (C_r, dotted line) as function of the period of the oscillations. A positive period control coefficient signifies that a slowing of the corresponding process increases the oscillation period. (C, D) Period control coefficients in the positive and negative feedback models, respectively, in the presence of plasma-membrane fluxes of Ca²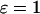⁺ (). The dash-dotted line indicates the control exerted by Ca²⁺ exchange across the plasma membrane (C_pm).

The distribution of control becomes more complex when the plasma-membrane fluxes of Ca²⁺ are included (Fig. 5, C and D; 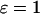), although, interestingly, the plasma-membrane fluxes exert very little period control themselves (dashed lines). There are several notable features. First, the fast oscillations in the positive-feedback model are no longer dominated by the IP₃R dynamics. There is even a rather counterintuitive behavior at intermediate periods where acceleration of the IP₃R dynamics would result in a slowing of the oscillations (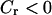). Second, the overall tendency that the IP₃ dynamics are more relevant for slow oscillations is preserved. However, the dynamics of ER Ca²⁺ release and refilling now play a more pronounced role in setting the period.

This quantification of period control reveals that no process can be singled out as a unique period controlling factor. Depending on the oscillation mechanism and the reference period, the IP₃ turnover, the ER Ca²⁺ fluxes, and the IP₃R dynamics can all exert strong control.

How to distinguish Ca²⁺ feedbacks on IP₃ metabolism experimentally: model predictions

Our analysis has shown that oscillation mechanisms involving Ca²⁺-activated PLC or IP₃K are sensitive to the timescale of IP₃. This offers the possibility to experimentally interfere with the oscillation mechanism by perturbing the IP₃ turnover.

The overexpression of IP₃ metabolizing enzymes would accelerate the IP₃ turnover and also decrease [IP₃] (see Eqs. 3–5). Overexpression of either IP₃ 5-phosphatase or IP₃ 3-kinase can abolish Ca²⁺ and IP₃ oscillations. In the case of IP₃P overexpression, this effect can be revoked by an increase in agonist dose, while quenching of oscillations with overexpression of the Ca²⁺-dependent IP₃K is predicted to be irreversible. However, positive- and negative-feedback models behave in the same way (see Supplementary Material, Fig. S1).

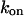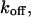A different result is obtained if the IP₃ turnover is slowed by introducing IP₃-binding proteins (IP₃ buffer) into the cell. To be specific, we assume a monovalent IP₃ buffer with on- and off-rate constants and respectively. The IP₃ balance equation (Eq. 3) is then modified to

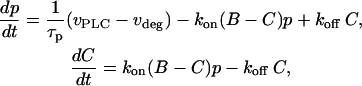(10a,b)

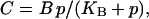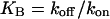where p as before stands for [IP₃], B denotes the total concentration of the introduced IP₃ buffer, and C is the concentration of occupied IP₃ buffer. If the binding of IP₃ to the buffer is fast compared to the IP₃ degradation rate, the amount of occupied buffer will be in equilibrium with [IP₃]. This implies where is the dissociation constant. Summing Eqs. 10a and 10b, and using the equilibrium relation for C, one obtains for the dynamics of unbound IP₃

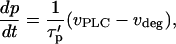(11)

with the modified characteristic time of IP₃ turnover

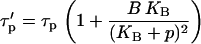(12)

The IP₃ buffer creates an additional bound pool of IP₃ that is protected from degradation. Then the buildup of free [IP₃] after PLC activation is delayed, because the buffer binding sites also need to be filled. Similarly, the decay of free [IP₃] is slowed, because IP₃ molecules dissociate from the buffer as cellular [IP₃] decreases. Precisely these two effects are accounted for by the modified time constant 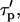which increases with the buffer concentration (Eq. 12). Note that the balance between the rates of IP₃ production and degradation is unaffected by the buffer. In particular, the IP₃ buffer would not change the steady-state concentration of free IP₃ attained when 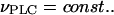(The endogenous IP₃ binding sites have already been accounted for by the characteristic time of IP₃ turnover, 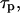defined in the absence of the exogenous IP₃ buffer.)

Introducing an exogenous IP₃ buffer into a core Ca²⁺ oscillator model operating with constant PLC activity and Ca²⁺-insensitive degradation (such as the model discussed above in the absence of Ca²⁺ feedbacks on IP₃), will delay the rise in [IP₃] after PLC activation. However, eventually the same steady-state concentration of free [IP₃] would be reached as without buffer. Therefore, Ca²⁺ oscillations may set in with an increased latency, whereas spike shape and period would be unaffected by the presence of the IP₃ buffer.)

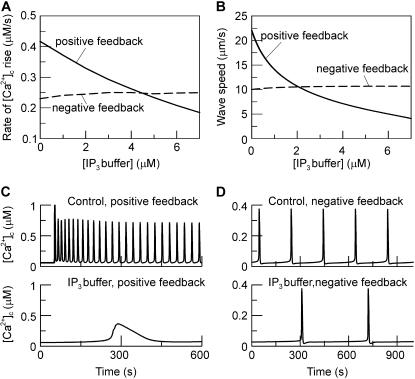
When introducing the IP₃ buffer into the positive- and negative-feedback models, we find that for low concentrations of IP₃ buffer (0 < B < 10 μM for 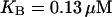) the oscillations persist in both models. However, depending on which type of Ca²⁺ feedback is present, IP₃ buffer affects the kinetic properties of the [Ca²⁺]_c oscillations in very different ways. In the positive-feedback model, the IP₃ buffer slows the Ca²⁺ responses. The rate of [Ca²⁺]_c rise in an individual spike is predicted to be decreased by the buffer in a dose-dependent manner (Fig. 6 A, solid line). Another characteristic property of [Ca²⁺]_c oscillations is the wave speed—the velocity at which a calcium spike propagates through the cell. To evaluate the effect of IP₃ buffer on wave propagation, we added to the model diffusion of Ca²⁺ and IP₃ in the cytoplasm and solved the resulting reaction-diffusion equations numerically on a one-dimensional domain. The propagation speed of a Ca²⁺ spike shows a very similar behavior as the rate of [Ca²⁺]_c rises: it decreases strongly as a function of IP₃ buffer concentration in the positive-feedback model (Fig. 6 B, solid line). In contrast, in the negative-feedback model, the IP₃ buffer will cause hardly perceptible increases in the rate of Ca²⁺ rise (Fig. 6 A, dashed line) and the wave speed (Fig. 6 B, dashed line). These two properties are well suited for experimental measurements, because they have been found to be remarkably constant in cells not perturbed by IP₃ buffer (44–46).

FIGURE 6.

Slowing of the IP₃ turnover with an IP₃ buffer. (A) The maximal rate of [Ca²⁺]_c rise during a [Ca²⁺]_c spike decreases as a function of IP₃ buffer concentration in the positive-feedback model (solid line), whereas it is barely affected in the negative-feedback model (dashed line). The results are shown for 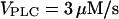(positive feedback) and 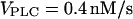(negative feedback); similar results are obtained for other values. (B) The intracellular wave speed decreases as a function of IP₃ buffer concentration in the positive-feedback model (solid line), whereas it is barely affected in the negative-feedback model (dashed line). A solitary Ca²⁺ wave is initiated by a local increase in [IP₃]; [Ca²⁺]_c and [IP₃] diffuse with diffusion constants of 20 and 280 μm²/s, respectively; 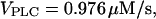(positive feedback) and 0.217 nM/s (negative feedback). (C) High IP₃ buffer concentration abolishes oscillations in the positive-feedback model ( 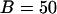μM, 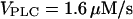). (D) Oscillations persist in the presence of IP₃ buffer in the negative feedback model ( 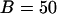μM, 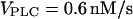). In all panels the IP₃ buffer dissociation constant is 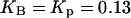μM. For the positive-feedback calculation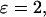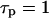s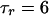: s, s, 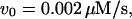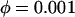/s. For the negative-feedback model 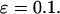Other parameters are as listed in Table 1.

For higher concentrations of IP₃ buffer (B>20 μM), the differences between the positive- and negative-feedback models are even clearer. In the positive-feedback model, the IP₃ buffer completely abolishes the [Ca²⁺]_c oscillations, and instead a single slow [Ca²⁺]_c transient is observed (Fig. 6 C). In the negative feedback model, the [Ca²⁺]_c oscillations persist even for very high concentrations of IP₃ buffer, although the oscillation period is increased (Fig. 6 D).

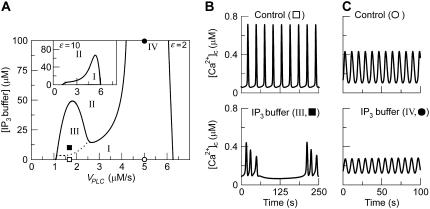
As IP₃ buffering causes the strongest effects in the positive-feedback model, we have analyzed this case in more detail. Fig. 7 A summarizes the results by showing the regions of oscillatory behavior as a function of the stimulus (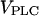) and the concentration of exogenous IP₃ buffer. Four different regions can be distinguished. In region I, the IP₃ buffer slows the oscillations with respect to rise time and propagation speed (see solid lines in Fig. 6, A and B). In region II, high enough IP₃ buffer concentrations abolish the oscillations (shown in Fig. 6 C). In region III, IP₃ buffer can cause more complex oscillations, such as the bursting oscillations shown in Fig. 7 B. For a large range of stimuli, the oscillations disappear when sufficiently high amounts of IP₃ buffer are added (transition into region II). However for strong stimulation, there can be an additional domain, region IV (Fig. 7 A). Here, the oscillations persist even at very high IP₃ buffer concentration but have strongly diminished amplitude (Fig. 7 C). Note that in the presence of sufficiently high IP₃ buffer, only fast oscillations (at high stimulation) can be retained. The long-period oscillations, which depend on Ca²⁺ feedback on PLC are invariably abolished by the IP₃ buffer.

FIGURE 7.

Complex responses to an IP₃ buffer in the positive-feedback model. (A) Bifurcation diagram showing the region of oscillations as function of stimulus (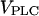) and IP₃ buffer concentration (gray-shaded area; the solid lines indicate the locus where the steady state becomes unstable via a Hopf bifurcation). In region I, regular oscillations have a decreased rate of [Ca²⁺]_c rise with increased [IP₃ buffer] as shown in Fig. 6 A. In region II, the IP₃ buffer abolishes the Ca²⁺ oscillations completely, as shown in Fig. 6 C. In region III, bursting [Ca²⁺]_c oscillations are observed (the lower boundary of this region is determined by a period doubling bifurcation, dotted line). We have indicated an additional region IV, which is characterized by oscillations persisting even at high [IP₃ buffer]. The parameters are as in Fig. 6, with 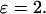When the strength of the Ca²⁺ plasma-membrane fluxes is increased (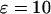), regions III and IV disappear (inset). (B) Example of bursting oscillations observed in region III (top panel, control without IP₃ buffer; bottom panel, [IP₃ buffer] = 10 μM; 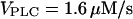). (C) Example of oscillations in region IV (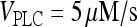; [IP₃ buffer] = 100 μM), which are characterized by high frequency and low amplitude.

Whether regions III and IV exist, depends on the kinetic parameters of the Ca²⁺ fluxes. The inset in Fig. 7 A shows a situation where the Ca²⁺ fluxes across the plasma membrane were increased fivefold. Then only regions I and II remain, and sufficiently high buffering of IP₃ always suppresses oscillations. Closer analysis revealed that if the system can oscillate for constant [IP₃] then IP₃ buffer never completely abolish the oscillations and a region IV exists (A. Politi, unpublished data).

Expression of an IP₃ buffer suppresses Ca²⁺ oscillations

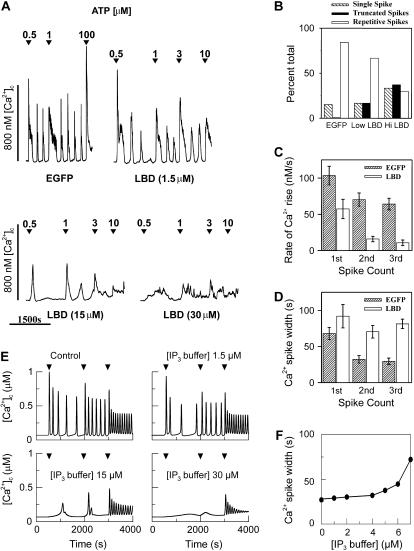
The most significant difference in the responses of the positive-feedback and negative-feedback models to the IP₃ buffer is that agonist-induced oscillations always persist in the latter model whereas they can be abolished in the former. To examine the model predictions experimentally, we took advantage of a molecular IP₃ buffer developed in our laboratory, which consists of the N-terminal ligand binding domain of rat type 1 IP₃R linked to enhanced green fluorescent protein (EGFP-LBD; (47); L. Gaspers, P. Burnett, J. Johnston, A. Politi, T. Höfer, S. Joseph and A. Thomas, unpublished data). CHO cells were transiently transfected with EGFP or EGFP-LBD then challenged with submaximal and maximal ATP concentrations. The subsequent [Ca²⁺]_c responses were monitored via changes in the fura-2 fluorescence ratio. EGFP fluorescence was utilized to distinguish transfected from nontransfected cells in a given field of view and to estimate the intracellular concentration of the transgene (see Materials and Methods).

The addition of low ATP concentrations elicited periodic [Ca²⁺]_c spikes in >85% of the CHO cells expressing EGFP (Fig. 8, A and B) or nonexpressing cells from cultures transfected with EGFP-LBD (not shown). Agonist-evoked [Ca²⁺]_c oscillations required functional ER Ca²⁺ stores (i.e., they were thapsigargin-sensitive), but ceased abruptly upon removing extracellular Ca²⁺ suggesting that plasma membrane Ca²⁺ fluxes are relatively strong in this cell type (not shown). In both GFP-expressing and nonexpressing cells, the [Ca²⁺]_c increase immediately after agonist challenge was more prolonged and the rate of Ca²⁺ rise faster than subsequent [Ca²⁺]_c oscillations (Fig. 8, A and C). No systematic differences were evident in agonist sensitivity or the pattern of the [Ca²⁺]_c spiking between EGFP expressing and nonexpressing cells suggesting that neither EGFP nor the transfection reagents per se had significant effects on Ca²⁺ signaling. By contrast, the presence of EGFP-LBD had a dose-dependent effect on the agonist-dependent Ca²⁺ oscillations in CHO cells (Fig. 8 A). High levels of EGFP-LBD expression correlated with a loss of repetitive [Ca²⁺]_c spiking and the appearance of low amplitude [Ca²⁺]_c increases (Fig. 8, A and B). Moreover, EGFP-LBD expression significantly slowed the rate of [Ca²⁺]_c rise (Fig. 8 C; p < 0.01) and significantly broadened the width of the [Ca²⁺]_c spike (Fig. 8 D; p < 0.05) compared to EGFP expressing cells. For these data, we only analyzed EGFP-LBD expressing cells where low ATP challenge (0.5 or 1 μM) evoked at least three sequential baseline-separated Ca²⁺ spikes. This was observed predominately in cells expressing low levels of EGFP-LBD and, thus we probably underestimated the actions of IP₃ buffering on the kinetics of [Ca²⁺]_c oscillations.

FIGURE 8.

The effects of a molecular IP₃ buffer on ATP-evoked [Ca²⁺]_i oscillations in CHO cells. CHO cells (n = 5 independent cultures) were transiently transfected with pEGFP-LBD (EGFP-LBD) or pEGFP-C1 (EGFP). The cells were loaded with fura-2/AM 16–48 h posttransfection and challenged with the indicated ATP concentrations. The traces (A) show typical ATP-evoked [Ca²⁺]_c spikes in CHO cells transiently expressing EGFP or different levels of EGFP-LBD. The intracellular EGFP-LBD concentration was estimated as described in Materials and Methods. (B) Data show the effects of increasing EGFP-LBD expression on ATP-evoked Ca²⁺signals. CHO cells expressing EGFP-LBD were arbitrarily divided into low (489 ± 66 units; n = 18 cells) or high (3170 ± 480 units; n = 27 cells) categories using a cutoff of 1000 fluorescence intensity units. The estimated mean EGFP-LBD concentration was 6 ± 0.8 or 38 ± 6 μM, respectively. The mean EGFP fluorescence intensity was 7400 ± 615 units (89 ± 7 μM; n = 198 cells). Truncated spikes are defined as low amplitude [Ca²⁺]_c oscillations similar to those shown in the bottom traces of panel A. The initial rates of [Ca²⁺]_c rise (C) and the widths of the [Ca²⁺]_i spike (D) were calculated in cells expressing EGFP (n = 52 cells) or EGFP-LBD (n = 20 cells) where ATP challenge (0.5 or 1 μM) evoked at least three sequential baseline-separated Ca²⁺ spikes. The width of the [Ca²⁺]_c spike were determined at half-peak height. (E) The positive feedback model, Ca²⁺ activation of PLC, with different IP₃ buffer concentrations (as indicated) shows a good agreement with the EGFP-LBD experimental data shown in panel A. An increase in ATP is simulated by an increase in the maximal activity of PLC (arrowheads). (F) In the positive feedback model we also observe a significant increase in spike width (calculated at half-peak height). To match the Ca²⁺ oscillations in CHO cells all variables have been slowed by a factor 10, reference parameter set as in Fig. 6 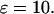In panel E, 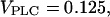0.2, 0.4 μM/s. Initial condition at 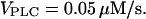In panel F,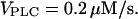

According to the theoretical results, the disappearance of the oscillations and a slowing of the Ca²⁺ rise suggests that IP₃ oscillations driven by positive feedback of Ca²⁺ on IP₃ production are involved in this system. We have simulated the positive-feedback model with relatively strong plasma-membrane Ca²⁺ fluxes as observed in CHO cells. At high concentrations of IP₃ buffer (Fig. 8 E), the model exhibits single transients (for lower agonist dose), and repetitive truncated spikes (for high agonist dose). Both responses closely resemble the experimentally observed patterns in cells expressing high amounts of EGFP-LBD. The Ca²⁺ oscillations at lower concentrations of IP₃ buffer (Fig. 8 F) exhibit a broadening of the individual spikes, which is very similar to the experimental observation in cells expressing low amounts of EGFP-LBD. Also the observed decrease of the rate of Ca²⁺ rise is reproduced by the model (data similar to Fig. 6 A). A model with negative feedback could account for none of the experimental findings (see Fig. 6).

DISCUSSION

There has been increasing evidence that hormone-evoked periodic Ca²⁺ spiking can be accompanied by oscillations of the Ca²⁺-releasing second messenger IP₃ (12–15). The experimental findings raise the questions of i), the underlying mechanisms of IP₃ oscillations and ii), their potential functional role. The theoretical analysis and experiments presented here provide insight into both issues.

Several processes could be involved in the generation of IP₃ oscillations. Feedbacks of IP₃ and the second product of the PLC reaction, diacylglycerol, on PLC and upstream agonist receptor/G-protein could produce IP₃ oscillations without involvement of Ca²⁺ (26,48). Alternatively, feedbacks on IP₃ metabolism may be mediated by Ca²⁺, resulting in coupled IP₃-Ca²⁺ oscillators (27,30,32,49). In this work, we have focused on the latter type of feedback oscillators because they can naturally account for the experimental observations of i), Ca²⁺ oscillations at clamped IP₃ concentration and ii), coupled IP₃ and Ca²⁺ oscillations. We considered prototypical positive and negative feedbacks of Ca²⁺ ions on IP₃ metabolism: Ca²⁺ activation of PLC and Ca²⁺ activation of IP₃ 3-kinase, respectively.

The incorporation of such feedbacks into a core Ca²⁺ oscillator model based on the regulatory properties of the IP₃ receptor can greatly expand the sensitivity of signal transduction to the hormonal stimulus. The presence of either feedback increases the range of agonist concentrations where one observes Ca²⁺ oscillations and enhances the ability to frequency-encode the agonist dose. Thus Ca²⁺ feedbacks on IP₃ metabolism represent a possible mechanism for the generation of robust long-period oscillations. This is likely to be an important component of frequency-modulated Ca²⁺ signals, because physiological responses are controlled in this lower frequency range (50,51). Thus our model points to a physiological role of IP₃ oscillations.

For the positive feedback to modulate the oscillation properties, the Ca²⁺ sensitivity of PLC needs to be only somewhat above basal [Ca²⁺]_c (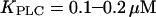). Such values are in agreement with experimental data (33). This feedback delays the onset of the Ca²⁺ spike, because both [IP₃] and [Ca²⁺]_c must rise to a certain level for triggering explosive opening of the IP₃R. In this way, long oscillation periods arise for low levels of stimulation, whereas for strong stimuli the high IP₃ level obviates the need for additional Ca²⁺ activation of PLC. We have here specifically assumed that Ca²⁺ and agonist act on the same isoform of PLC (e.g., PLCβ). However, similar results were obtained in a model variant when the isoform PLCδ is also included in the model, which is a Ca²⁺-sensitive but agonist-insensitive PLC isoform (results not shown).

Negative feedback exerts control on the Ca²⁺ oscillations when IP₃ removal takes place predominantly via IP₃K rather than by the IP₃P (>60% of the removal flux at high [Ca²⁺]_c carried by IP₃K). Long oscillation periods are generated when [IP₃] drops in the wake of a Ca²⁺ spike due to IP₃K activation and subsequently recovers slowly to the level needed to activate the IP₃R. We have found that this mechanism requires a finely tuned interplay between IP₃ metabolism and Ca²⁺ fluxes. This sensitivity may explain the discrepancy to the work of Dupont and Erneux (32), who reported only small effects of IP₃K on [Ca²⁺]_c oscillation periods. In contrast, the effects of the positive feedback were found to be robust with respect to the properties of the core Ca²⁺ oscillator.

The different modes of action of positive and negative feedbacks are reflected by opposing requirements on the lifetime of IP₃. In the case of positive feedback, IP₃ turnover must be fast to support long-period oscillations, allowing for i), coincidence of Ca²⁺ and IP₃ spikes and ii), for the rapid removal of IP₃ in the wake of a spike. In the case of negative feedback, slow IP₃ turnover is required for the slow recovery of IP₃ levels in between spikes. In different cellular systems, either one of the IP₃ feedbacks could play a significant role in controlling Ca²⁺ oscillations, depending primarily on the underlying turnover rate of IP₃. However, they cannot be expected to act synergistically.

A critical question is the experimental identification of the mechanisms that drive IP₃ oscillations. The theoretical analysis showed that slowing the IP₃ turnover by means of an IP₃ buffer can be used to distinguish between the two feedback mechanisms. An IP₃ buffer can quench the oscillations generated by an IP₃-Ca²⁺ oscillator based on positive feedback of Ca²⁺ on IP₃, but not by one based on negative feedback. Our preliminary modeling results indicate that the weak response of the negative-feedback oscillator to IP₃ buffering could be a general property not limited to a mechanism operating through IP₃ 3-kinase. We obtained very similar results with an alternative mechanism acting through PKC-dependent inactivation of the agonist receptors.

To test this theoretical prediction, we overexpressed the ligand binding domain of the type 1 IP₃R in a mammalian cell line, which acts as an IP₃ buffer. The observed dose-dependent suppression of Ca²⁺ oscillations demonstrates that the IP₃ dynamics play a critical role in the oscillator mechanism. Moreover, the detailed agreement between the experimental data and the simulations of the positive-feedback model is consistent with a coupled IP₃-Ca²⁺ oscillator based on Ca²⁺ activation of PLC.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.