Structures of Protonated Arginine Dimer and Bradykinin Investigated by Density Functional Theory: Further Support for Stable Gas-Phase Salt Bridges

Abstract

The gas-phase structures and energetics of both protonated arginine dimer and protonated bradykinin were investigated using a combination of molecular mechanics with conformational searching to identify candidate low-energy structures, and density functional theory for subsequent minimization and energy calculations. For protonated arginine dimer, a good correlation (R = 0.88) was obtained between the molecular mechanics and EDF1 6-31+G* energies, indicating that mechanics with MMFF is suitable for finding low-energy conformers. For this ion, the salt-bridge or ion–zwitterion form was found to be 5.7 and 7.2 kcal/mol more stable than the simple protonated or ion–molecule form at the EDF1 6-31++G** and B3LYP 6-311++G** levels. For bradykinin, the correlation between the molecular mechanics and DFT energies was poor (R = 0.28), indicating that many low-energy structures are likely passed over in the mechanics conformational searching. This result suggests that structures of this larger peptide ion obtained using mechanics calculations alone are not necessarily reliable. The lowest energy structure of the salt-bridge form of bradykinin is 10.6 kcal/mol lower in energy (EDF1) than the lowest energy simple protonated form at the 6-311G* level. Similarly, the average energy of all salt-bridge structures investigated is 13.6 kcal/mol lower than the average of all the protonated forms investigated. To the extent that a sufficient number of structures are investigated, these results provide some additional support for the salt-bridge form of bradykinin in the gas phase.

Introduction

Molecular mechanics methods play an important role in structural studies of biopolymers. In combination with information obtained from experimental methods, such as two-dimensional NMR, molecular mechanics calculations have been used to obtain the tertiary structure of many peptides and small proteins.^1–3 Molecular docking programs are used to study the interactions of potential substrates with binding pockets of receptors.⁴ Using structures obtained by X-ray crystallography or NMR as starting geometries, both steric and energetic effects of substrate–receptor binding can be investigated. Binding constants for substrate–receptor complexes are calculated from molecular mechanics or from empirical interaction energies.⁵ Chemical databases can be searched for new substrates, and the influence of substrate binding on the structure of the complex can be investigated.⁵

Another area where molecular mechanics is an important partner with experiment is in structural studies of polymers in the gas phase. For example, molecular mechanics calculations are essential for interpreting data from ion mobility measurements of large biopolymers.^6–8 In these experiments, ion cross sections are determined by measuring ion flight times in a drift tube. Information about the ion structure can be obtained by comparing the measured cross sections to those determined from calculated low-energy structures.^6–8 Mechanics calculations have also been used to obtain information from gas-phase ion dissociation^9,10 and H/D exchange experiments^11,12 with the goal of deducing structural information.

Critical to the successful application of these methods to large molecules is (1) the ability to find minimal energy structures from the enormous number of possible conformers and (2) the accuracy with which the potential energy surface of a large ion can be calculated with mechanics. Several methods have been developed to sample the conformational energy surface of large molecules. Of these methods, internal coordinate conformation searching has emerged as one of the most effective ways of finding minimal conformers of molecules containing less than 12 torsion angles.¹³ For such molecules, most internal conformation searching methods are successful at finding ~99% of the conformers with energies within 3 kcal/mol of the minimum.¹³ Recently, conformational searching methods using mode-following techniques have been shown to be promising for larger molecules. The low-mode technique of Kolossvary and Guida¹⁴ was used to find all known minima of C₃₉H₈₀ and identified a previously unknown global minimium.

In molecular mechanics, the potential energy surface of a molecule is calculated using classical force fields. These force fields are parameterized to fit experimental or high-level computational data for a set of small molecules that can include amino acids, nucleobases, etc. One critical question is how accurately these force fields represent the potential energy surface of larger molecules. Friesner and co-workers¹⁵ evaluated the accuracy of a variety of different mechanics force fields for calculating conformational energies of Ala₄. Energies of 10 different conformers of Ala₄ were determined from local MP2 calculations and were compared to the relative energies computed by several force fields. Of 20 different force fields investigated, the Merck molecular force field (MMFF) had the lowest rms deviation in conformational energies (1.2 kcal/mol).¹⁵ Gundertofte et al.¹⁶ tested 10 force fields on their ability to correctly reproduce the conformational energy differences measured experimentally for 42 organic molecules. Halgren also performed a similar study on a larger database of 147 molecules.¹⁷ In these comparisons, the energy differences calculated with the MMFF reproduced the experimentally derived differences as well as, or better than, the other force fields tested.

Until recently, extending the comparison of mechanics energies of large molecules to those calculated by ab initio methods has been limited to molecules with ~50 atoms or less.¹⁸ Application of ab initio methods to larger molecules is limited primarily by the time required for evaluation of the electron repulsion integrals.¹⁹ In the recent past, the computation time required for this has scaled with the second to third power of the number of atoms in the molecule.¹⁹ New algorithms for evaluating the electron repulsion integrals have reduced this scaling to linear with molecular size for both density functional and Hartree–Fock calculations. One method, the continuous fast multipole method of White et al.,²⁰ enables ab initio calculations on molecules consisting of up to 200 atoms.

Recent progress in the formulation of new density functionals has also made a significant impact in the ability to apply ab initio methods to large molecules. A particularly attractive feature of density functional theory (DFT) is that it includes electron correlation, which is required to accurately determine the strength of hydrogen bonds.²¹ Binding energies of hydrogen-bound molecules calculated using DFT, especially the B3LYP functional, are in very good agreement with experimentally measured values and with values calculated using high-level methods.²¹ Density functional methods are effective at reproducing energies of several different conformers of small polypeptides calculated at the MP2 level.²² Density functional theory is also effective at reproducing experimentally measured gas-phase basicities for a range of small organic molecules^23,24 and for polyglycines up to 10 residues in length.²⁵

Here, we use the combination of molecular mechanics and DFT to evaluate the structure of two biomolecule ions, protonated arginine dimer and protonated bradykinin, for which experimental evidence indicates that these ions form salt bridges in the gas phase.^10,26–28 The dissociation energies of both of these ions and a series of their analogues have been measured using blackbody infrared radiative dissociation.^10,26 The protonated dimer of arginine has a significantly higher dissociation energy than protonated methyl ester dimers of arginine, consistent with the higher binding energy expected for a salt-bridge vs an ion–molecule interaction (a salt bridge cannot be formed in arginine methyl ester dimers).²⁶ Bradykinin is a small peptide consisting of nine amino acids with arginine residues on both the N-and C-termini. Dissociation energies of bradykinin and a series of analogues suggest that a salt bridge is formed between the two terminal arginines and the C-terminal carboxylate.¹⁰ Other experimental evidence for salt bridges occurring within the gas-phase structure of bradykinin has also been reported.²⁷ The results presented here suggest that mechanics calculations are suitable for finding low-energy conformers of protonated arginine dimers, but molecules the size of bradykinin are significantly more problematic. These calculations indicate that the salt-bridge structure of protonated arginine dimer is more stable than the ion–molecule form, and they also provide some support for the salt-bridge form of bradykinin.

Methods

Molecular mechanics using the Merck molecular force field (MMFF) and conformational searching were used to find candidate low-energy structures. The protonated ions were built in the Macromodel program (v6.5, Schrodinger Inc., Portland, OR). For the salt-bridge and ion–molecule forms of protonated arginine dimer, conformation searching was carried out using a Monte Carlo²⁹ search with 2000 steps. After the Monte Carlo run, an additional 3000 steps were performed with the low-mode (LMOD) conformational searching technique.³⁰ From the results of the search, several low-energy conformers were selected as starting geometries for density functional calculations.

Bradykinin contains 33 torsional bonds, which makes it much more conformationally complex than protonated arginine dimer. Three isomers of bradykinin were studied: (1) the salt-bridge form, where the guanidinium side chains of both the C- and N-terminal arginines are protonated and the C-terminal carboxylic acid is deprotonated, (2) the C-terminal protonated form, where the side chain of the C-terminal arginine is protonated, and (3) the N-terminal form, where the side chain of the N-terminal arginine is protonated. Initially, the conformational search of bradykinin was carried out by running a 5000-step Monte Carlo search in Macromodel v6.5 for each isomer. Then a 5000-step LMOD search was carried out on the lowest energy conformation. The following procedure was used to test whether a global minimium or a structure with an energy close to the global minimum was found. The lowest energy conformer from the 5000-step LMOD search was used as the initial structure in a new 2500-step LMOD search. The lowest energy conformer from this search was compared to the initial structure. If the two structures differed, then another 2500-step search was carried out. This process was carried out iteratively until no new structures were found. In all, the conformational search for each isomer of bradykinin required 22 500 steps or more of conformational searching.

The Xcluster³¹ program was used to identify conformers that are similar, and to group them into clusters or families of similar structures. A conformational difference, d_i, is determined from the difference in position of the ith atom between two structures. The two structures are placed in a family if the root mean square, (∑d_i2/N)1/2 (N = total atoms) or d_rms, of these atomic distances is lower than a certain threshold.

The Qchem v1.1 ab initio program³² was used for all density functional calculations. For the arginine dimer, the convergence criterion for the rms gradient was set at 2 × 10⁻³ hartree/bohr with an energy change of 8 × 10⁻⁵ hartree. An integral cutoff threshold of 10⁻⁸ au was used, except for calculations with diffuse basis functions, where a value of 10⁻⁹ au was used. Both the B3LYP and EDF1 hybrid functionals were used. For bradykinin, the convergence criterion was set at 2 × 10⁻³ hartree/bohr. Energy changes per optimization cycle were higher for bradykinin relative to arginine dimer, ~1 × 10⁻⁴ hartree. Although values lower than this are desired, this value appears to be a reasonable compromise between getting minimized structures with low gradients and CPU time consumed. The integral cutoff used for calculations on bradykinin was set equal to 10⁻⁷ au. Only the EDF1 functional was used in the density functional calculations for bradykinin.

Results and Discussion

Arginine Dimer. Molecular Mechanics.

Three structural isomers of protonated arginine dimer, (Arg·Arg + H)⁺, were investigated (Figure 1). One is a salt-bridge or ion–zwitterion structure (structure I) where the guanidine side chain of one arginine molecule is protonated and the other arginine is a zwitterion in which the guanidine group of the side chain is protonated and the carboxylic acid group is deprotonated. The other two structures (II and III) are ion–molecule structures in which the guanidine side chain of one arginine is protonated and the other arginine is neutral (Figure 1). The latter two structures differ by which nitrogen of the neutral arginine side chain is deprotonated (II, R = −(CH₂)₃–N–C(NH₂)₂; III, R = − (CH₂)₃–NH–C(NH₂)(NH)).

Figure 1.

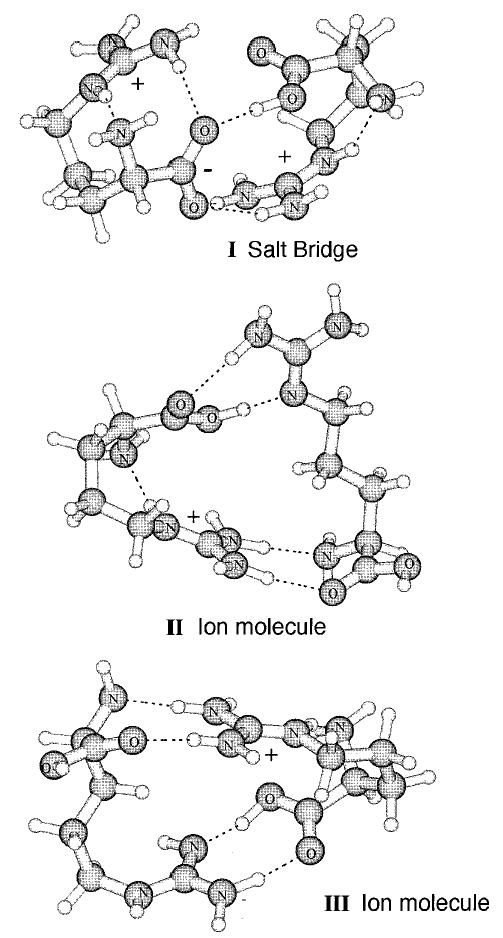
Lowest energy conformer of each isomer of protonated arginine dimer calculated at the EDF1 6-31+G*//6-31G*.

The LMOD (low-mode) conformation searching method is both efficient and effective for molecules with ~20 torsional bonds.^14,30 The protonated dimer of arginine contains 16 variable torsional bonds. Thus, the LMOD method should be suitable for finding low-energy candidate structures for this ion. For each of the (Arg·Arg + H) ⁺ isomers, conformation searching resulted in 23, 12, and 7 conformers with energies within 5 kcal/mol of the lowest energy structure for I–III, respectively. A cluster algorithm³¹ was used to sort these structures into “families” or groups of similar conformation. A distance threshold of 0.5 Å was used. A total of seven, five, and four families were found for structures I–III, respectively. The energies of the minimal conformers for each of these families are given in Table 1. Throughout this paper, all structural isomers are indicated by bold roman numerals, e.g., I, and the conformational isomers are indicated by the arabic numeral that follows. Also included in this table are energies calculated using MMFF for two minimal conformers found previously with CVFF and semiempirical calculations (I8 and II6).²⁶ These latter structures are higher energy structures when using the MMFF. Two additional higher energy structures are also included for II. These structures extend the energy range for comparison with DFT results. Thus, the total numbers of conformers appearing in Table 1 are eight, eight, and four for structures I–III, respectively.

TABLE 1.

Relative Energies within a Family of Structures for the Conformers of (Arg·Arg + H)⁺ Calculated Using Mechanics (MMFF) and DFT (EDF1 6-31+G*//EDF1 6-31G*)^a

conformer	drms,min (Å)	rel energy (MMFF) (kcal/mol)	EDF1//EDF1 energy (hartrees)	rel energy (EDF1) (kcal/mol)
Salt Bridge (I)
1	0.8	0.0	−1213.723 978	0.0
2	0.5	2.7	−1213.717 993	3.8
3	0.5	2.8	−1213.714 672	5.8
4	0.8	3.1	−1213.722 417	1.0
5	0.8	3.8	−1213.722 482	0.9
6	1.5	4.8	−1213.713 150	7.0
7	0.8	5.1	−1213.718 635	3.4
8	1.6	9.3	−1213.711 385	7.9
Ion–Molecule (II)
1	0.6	0.0	−1213.711 205	0.0 (8.0)
2	0.6	2.9	−1213.712 192	−0.6 (7.4)
3	1.0	3.1	−1213.701 312	6.2 (14.2)
4	1.0	4.5	−1213.706 606	2.9 (10.9)
5	1.8	5.0	−1213.702 797	5.3 (13.3)
6	1.8	8.8	−1213.692 727	12.2 (18.2)
7	1.9	9.6	−1213.692 044	12.6 (18.6)
8	1.8	17.0	−1213.683 011	17.7 (25.7)
Ion–Molecule (III)
1	1.7	0.0	−1213.712 470	0.0 (7.2)
2	0.8	3.3	−1213.705 170	4.6 (11.8)
3	0.8	5.4	−1213.697 273	9.5 (16.7)
4	1.7	5.7	−1213.705 553	4.3 (11.5)

^aThe values in parentheses are the DFT energies of the conformer relative to the most stable conformer (I1).

For each conformer listed in Table 1, a root-mean-square distance, d_rms, is calculated between it and all other conformers listed in Table 1. For example, for conformer I1, seven values of d_rms are calculated since there are a total of eight structures for I. The smallest value d_rms,min is listed in Table 1 for all conformers. This value is a measure of the uniqueness of each structure. The actual structures are available as Supporting Information.

Density Functional Theory.

Each of the minimal structures in Table 1 found from mechanics calculations were geometry optimized using the EDF1 functional and the 6-31G* basis. A single-point energy with the 6-31+G* basis for each of these structures is given in Table 1. The relative energies of each of the structures calculated with mechanics vs those calculated using the EDF1 functional are shown in Figure 2 (the relative energies are normalized to the lowest energy structure equal to zero for each isomer). The data in Figure 2 have a linear correlation coefficient of 0.88. The lowest energy structures for both I and III calculated at the mechanics level are also the lowest energy structures at the DFT level. For structure II, the lowest energy structure at the DFT level is not the same as that obtained with mechanics. However, the difference in energy between these conformers is only 0.6 kcal/mol at the DFT level, which is not a significant difference. While the ordering of the different structures based on energies calculated at the mechanics level differ somewhat from the order based on DFT calculations, it would appear that energies calculated using MMFF track energies calculated at the EDF1 6-31+G*//EDF1 6-31G* level within a few kilocalories per mole.

Figure 2.

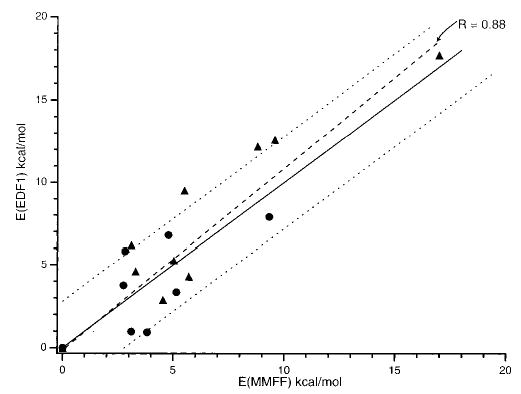
Comparison of the relative energies of 12 ion–molecule (▴) and 8 salt-bridge (•) conformers of (Arg·Arg + H)⁺ calculated at the EDF1 6-31G+*//6-31G* and mechanics MMFF levels. Perfect correlation (solid line) and least-squares regression (dashed line) are shown. Data points which are located within the dotted lines have a deviation of <2 kcal/mol from perfect correlation.

The lowest energy conformer obtained at the DFT level for each of these isomers is shown in Figure 1. At the DFT level, the ion–molecule structures II and III are comparable in energy, differing by only 0.2 kcal/mol. This difference is lower than that reported for Arg·M⁺, (M = Li, Na, K, Cs), where the R = –(CH₂)₃–NH–C(NH₂)(NH) isomer was found to be 2–3 kcal/mol more stable than the R = – (CH₂)₃–N–C(NH₂)₂ isomer.³³ The salt-bridge structure is lower in energy than either ion–molecule structure by more than 7 kcal/mol. The average absolute deviation of the relative energies of all 20 (Arg·Arg + H)⁺ structures calculated at the MMFF level compared to the energies at the EDF1 6-31+G* level is 1.9 kcal/mol. The difference in energy between the salt-bridge structure and either ion–molecule structure is much greater than the deviation between the mechanics and DFT energies. These results would suggest that, to the extent that the conformational search is adequate and that energies can be accurately calculated by DFT, molecular mechanics is suitable for identifying low-energy candidate structures for this ion.

Effects of the Basis Set and Functionals.

To determine whether the difference in energy between the salt-bridge and ion–molecule structures is significant, the effects of the basis set and functionals were investigated. Energies for both the minimal salt-bridge and ion–molecule structures were calculated at the EDF1 6-31++G**//6-31++G** level (Table 2). At this level, the salt-bridge structure (I) is more stable by 5.7 kcal/mol. For comparison, this difference calculated at the B3LYP 6-31+G*//6-31+G* and B3LYP 6-311++G**//6-31+G* levels is 10 and 7.7 kcal/mol, respectively. The energy difference decreases with increasing basis set for both functionals, although the energy difference between isomers is still relatively large. The results obtained for the EDF1 calculation with the smaller basis set are comparable to the results of the B3LYP calculation with the larger basis set. This may be due to parameterization built into the EDF1 functional which was derived using the 6-31+G* basis.²⁴ One might expect that, for a smaller basis set, the EDF1 functional will provide more accurate results than other functionals.

TABLE 2.

Difference in Energy between the Most Stable Salt-Bridge Conformer (I1) and the Most Stable Ion–Molecule Form (III1) Calculated Using Density Functional Theory^a

functional	basis	energy diff (kcal/mol)
EDF1	6-31+G*//6-31G*	7.2
EDF1	6-31++G**//6-31++G**	5.7
B3LYP	6-31+G*//6-31+G*	10.0
B3LYP	6-311++G**//6-31+G*	7.7

^aA positive value indicates that the salt bridge is more stable.

Dissociation Energies.

The dissociation energies for both the salt-bridge form of protonated arginine, I1, and the protonated dimer of the arginine methyl ester, (ArgME·ArgME + H)⁺, were estimated using density functional theory. A salt-bridge form of protonated arginine methyl ester dimer is not possible due to the absence of an acidic hydrogen. A dissociation energy was estimated from eq 1, where E_DH⁺ is the energy (EDF1

$$E_0=E_{\text{DH}+}-E_{\text{MH}+}-E_{\text{M}}$$ (1)

6-31+G*) of the protonated dimer minimized at the EDF1 (6-31G* basis) level. E_MH⁺ and E_M are the energies (EDF1 6-31+G*) of the protonated monomer and neutral monomer, respectively. The initial geometries of the monomers were taken from their geometries within the optimized dimer and minimized using the EDF1 functional (6-31G* basis). The geometry of the transition state was not modeled explicitly. Thus, the values we report are estimates of the true E₀ values.

For (Arg·Arg + H)⁺, the calculated value of E₀ is 1.50 eV. This value is slightly higher than the value of 1.33 ± 0.08 eV obtained from Blackbody infrared radiative dissociation (BIRD) experiments.²⁶ For (ArgME·ArgME + H)⁺, the calculated value is 0.98 eV, slightly lower than the 1.05 ± 0.05 eV obtained from BIRD experiments.²⁶ The higher dissociation energy of the salt-bridge form of (Arg·Arg + H)⁺ is due to the large electrostatic interaction. These results indicate that the energies calculated at the EDF1 6-31+G*//EDF1 6-31G* level are reasonably consistent with experimental measurements for these dimer ions.

Bradykinin. Molecular Mechanics.

Bradykinin is a nine-residue peptide (Arg-Pro-Pro-Gly-Phe-Ser-Pro-Phe-Arg) with arginine residues at both the N- and C-termini. Calculations were done on three isomers of protonated bradykinin. Structure IV is one in which a salt bridge occurs between the two terminal arginines (Figure 3). The other two structures (V and VI) correspond to simple protonated structures, with the proton located at the guanidine group of the N- and C-terminal arginines, respectively. There are many additional possible sites of protonation. These two structures were chosen on the basis of the high gas-phase basicity of the guanidine group³⁴ and of isolated arginine itself.³⁴ Arginine has the highest gas-phase basicity of any of the individual amino acids.

Figure 3.

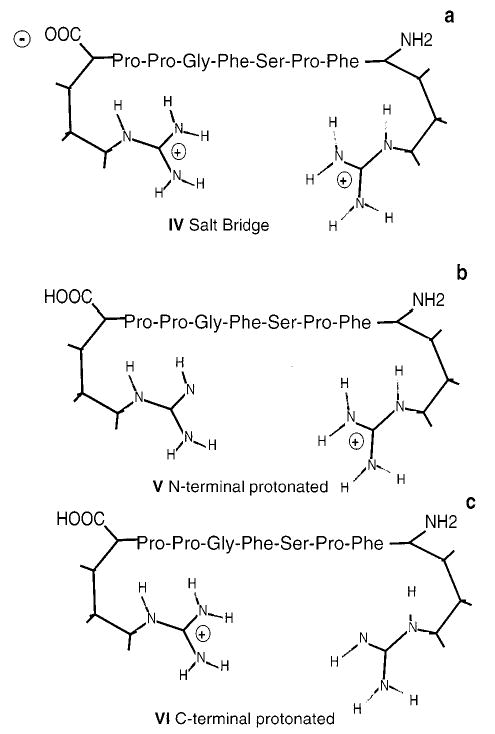
The three general isomers of bradykinin studied: (a) salt-bridge form in which both the side chains of the C-terminal and N-terminal arginines are protonated and the carboxylic acid is deprotonated, (b) isomer in which only the N-terminal arginine side chain is protonated, and (c) isomer in which only the C-terminal arginine side chain is protonated.

Conformational searching is clearly a significant problem with molecules the size of bradykinin, for which there are 33 torsional bonds. Searching runs were carried out until the energy of the minimal structure did not change over the course of 2500 searching steps. This required a minimum of 22 500 searching steps for each isomer. As was the case with protonated arginine dimer, many conformers of similar structure and energy were found. These similar structures (within a distance threshold of 0.7 Å) were again clustered into families.³¹ For structure IV, 13 distinctly different structures with energies within ~5 kcal/mol of the lowest energy structure were identified. Of these 13 structures, 6 were selected randomly as starting geometries for the DFT calculations. An additional higher energy conformer (IV7) was also selected. The same method was used for conformers V and VI. After clustering, three conformers of V and two conformers of VI were chosen and minimized using DFT. One higher energy protonated structure was chosen (VI3) as well.

The d_rms,min values for all of the structures of bradykinin are listed in Table 3. This value provides a measure of the differences between these conformers. As an illustration, the two conformers with the smallest value of d_rms,min are shown as superimposed structures in Figure 4a (structures IV3 and IV4, d_rms,min = 0.8 Å). These two conformers are very similar, differing only by small variations in the peptide backbone and side-chain angles. In contrast, two superimposed structures that have a d_rms,min = 2.3 Å (structures IV1 and IV6) are shown in Figure 4b. These structures are significantly different, even though the two terminal arginines interact in both conformers, which greatly reduces the conformational space. The two terminal arginine residues in the charge-solvated structures do not always interact, so that the differences between conformers of these forms of the ion are more different than the differences between the salt-bridge forms. The charge-solvated conformers all have d_rms,min > 2 Å, which reflects this difference. The ψ/φ angles for all structures are given in Table 1 in the Supporting Information.

TABLE 3.

Relative Energies within a Family of Structures for the Conformers of Protonated Bradykinin Calculated Using Mechanics (MMFF) and DFT (EDF1 6-31G*//EDF1 6-31G*)^a

conformer	drms,min (Å)	rel energy (MMFF) (kcal/mol)	EDF1//EDF1 energy (hartrees)	rel energy (EDF1) (kcal/mol)
Salt Bridge (IV)
1	1.2	0.0	−3599.063 036	5.6
2	0.9	1.2	−3599.066 052	3.7
3	0.8	4.0	−3599.057 249	9.3
4	0.8	4.7	−3599.072 021	0.0
5	1.7	5.0	−3599.070 107	1.2
6	2.3	5.7	−3599.055 085	10.6
7	0.9	9.3	−3599.058 632	8.4
N-Terminal (V)
1	2.1	0.0	−3599.038 599	2.3 (21.0)
2	2.1	6.6	−3599.035 441	4.3 (23.0)
3	3.1	5.7	−3599.042 316	0.0 (18.7)
C-Terminal (VI)
1	2.2	0.0	−3599.042 027	5.9 (18.8)
2	2.2	3.5	−3599.051 392	0.0 (12.9)
3	3.5	12.1	−3599.039 154	7.7 (20.6)

^aThe values in parentheses are the DFT energies of the conformer relative to the most stable conformer (IV4). The number of conformers which contain two β turns (from Arg¹ to Gly⁴ and from Ser⁶ to Arg⁹) are in bold typeface.

Figure 4.

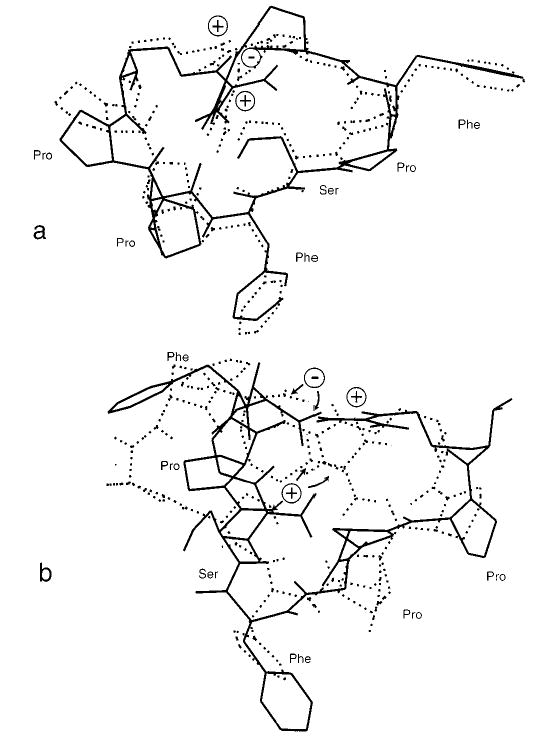
(a) Superposition of bradykinin structures IV3 (dotted lines) and IV4 (solid lines) that have a d_rms,min = 0.8 Å and (b) superposition of bradykinin structures IV1 (dotted lines) and IV6 (solid lines) that have a d_rms,min = 2.3 Å. All structures were calculated at the molecular mechanics level.

Density Functional Theory.

The energies of the conformers for each of the structures (IV, V, and VI) calculated at the EDF1 6-31G*//6-31G* level are given in Table 3. The relative energies calculated at the mechanics vs DFT level are shown in Figure 5. There is significant scatter in these data; the linear correlation coefficient is 0.28. The average deviation between the EDF1 and MMFF relative energies is 4.0 kcal/mol. For structure IV, the lowest energy structure calculated by MMFF is 5.6 kcal/mol higher in energy than the lowest energy conformer calculated by DFT. This suggests that many potential low-energy structures are missed in the conformational search using MMFF. In addition to the errors inherent in DFT calculations on large molecules, these results indicate that the ability to find low-energy structures using mechanics may be a limiting factor in combining mechanics and DFT calculations for determining detailed structures of large molecules in the absence of any other structural information, such as that obtained from experiment. Additional information, such as interproton distances obtained from NMR, can dramatically limit the number of possible conformations. This can make possible accurate determination of the higher order structure of large peptides and proteins in solution. Similarly, collisional cross section measurement obtained from ion mobility experiments or gas-phase H/D exchange data can be used to limit the number of possible conformers in these gas-phase calculations.

Figure 5.

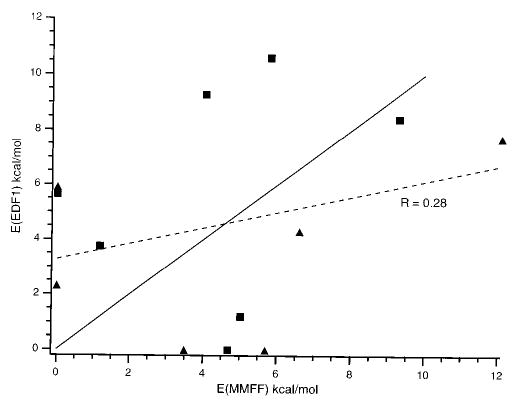
Comparison of the relative energies of 6 ion–molecule (▴) and 7 salt-bridge (▪) conformers of (bradykinin + H)⁺ calculated at the EDF1 6-31G*//6-31G* and mechanics MMFF levels. Perfect correlation (solid line) and least-squares regression (dashed line) are shown.

Despite the large scatter in these energetic data, there is a clear trend in the relative stability of the salt-bridge vs ion–molecule structures. The lowest energy conformer of V is 5.8 kcal/mol higher in energy than conformer VI. The difference in energy between the most stable salt-bridge conformer (IV1) and the most stable non-salt-bridge conformer (VI1) is 13.0 kcal/mol (the salt bridge is more stable). The mean energy of all structure IV conformers is 13.6 kcal/mol less than the mean of all structure V and VI conformers. If the error in the energy calculations were random, these two structures would be different with a confidence level of >99%. This is overly optimistic since the error is almost certainly not random. However, this does suggest that it may be possible to obtain some meaningful structural information on large ions by performing higher level calculations on large numbers of candidate structures identified by mechanics.

A single-point energy calculation was performed on the most stable salt bridge and simply protonated conformer (IV4 and VI2) using the EDF1 functional and the 6-311G* basis. The salt bridge (IV4) is 10.6 kcal/mol more stable. As with protonated arginine, the energy difference between the salt bridge and simple protonated structure decreases slightly with the larger basis set.

Geometry Optimization.

The time required for a full geometry optimization at the EDF1 6-31G* level is greater than 170 h on a DEC Alpha500au computer. In contrast, only ~12 h is required for calculating a single-point energy. Thus, the geometry optimization takes the vast majority of the computer time necessary for these calculations. More than a 10-fold increase in the number of conformers could be sampled if only a single-point energy calculation was done. To determine whether the MMFF geometries are sufficient, single-point energies at the EDF1 6-31G* level were performed with MMFF-optimized geometries for the salt-bridge isomer of bradykinin (Table 4). The average absolute deviation of the EDF1 6-31G*//MMFF relative energies to the EDF1 6-31G*//6-31G* relative energies is 3.5 kcal/mol. This is only minimal improvement over the relative MMFF energies themselves. Thus, full optimization appears to be required for even a modest level of accuracy.

TABLE 4.

Relative Energies of the Salt–Bridge Isomer of Bradykinin (IV) Calculated at the MMFF and EDF1 Density Functional Levels^a

conformer	rel energy (MMFF) (kcal/mol)	EDF1//MMFF energy (hartrees)	rel energy (EDF1//MMFF) (kcal/mol)
1	0.0	−3599.003 735	0
2	1.2	−3598.996 902	4.3
3	4.0	−3599.006 408	−1.7
4	4.7	−3599.006 158	−1.5
5	5.0	−3599.000 186	2.2
6	5.7	−3598.997 043	4.2
7	9.3	−3598.986 379	10.9

^aThe total and relative energies at the EDF1 level (6-31G* basis) are calculated using MMFF geometries.

Solution-Phase Structure.

The structure of bradykinin has been studied extensively in a number of solvent environments with both NMR^2,35–38 and circular dichroism.^36,39 In aqueous solution, bradykinin rapidly interconverts among many different structures.³⁶ There is no persistent secondary structure, although some evidence for a β turn⁴⁰ between Ser⁶ and Arg⁹ has been reported.³⁶ This β turn is stabilized in nonaqueous solvents, including trifluoroethanol,³⁵ dimethyl sulfoxide,^2,36,38 9:1 diox-ane/water,^2,37 and 6.9 mM sodium dodecyl sulfate.³⁹ A β turn between Arg¹ and Gly⁴ has also been observed in trifluoroethanol and dimethyl sulfoxide.^2,36,38 Evidence for electrostatic interaction between two terminal arginine residues of bradykinin in dimethyl sulfoxide has also been reported.³⁸ Sejbal et al.¹ reported that the bradykinin antagonist B-9340 contains a salt bridge in 280 mM sodium dodecyl sulfate on the basis of results from NMR and molecular dynamics. B-9340 has arginines on both termini and has a secondary structure similar to that of bradykinin.¹

The lowest energy conformer from our EDF1 calculation is shown in Figure 6 (IV4). In this conformation, β turns extending from Ser⁶ to Arg⁹ and from Arg¹ to Gly⁴ are present. The conformers that contain both β turns are indicated in bold in Table 4. Of the seven salt-bridge conformers, four have both β turns, whereas only one of the six non-salt-bridge conformers has both β turns. The two lowest energy structures for bradykinin, IV4 and 5, contain both β turns. Wyttenbach et al.⁸ investigated the gas-phase structure of bradykinin using mechanics with the AMBER force field. They reported that only 5 of the 100 lowest energy structures for the salt-bridge conformer of bradykinin contain a Ser⁶ to Arg⁹ β turn.⁸

Figure 6.

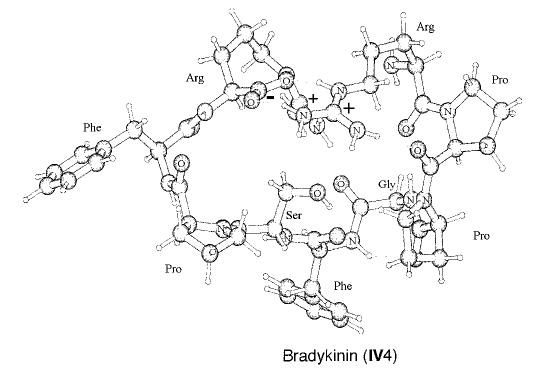
Lowest energy conformer of protonated bradykinin (salt-bridge conformer IV4). Hydrogens bonded to carbon have been omitted for clarity.

Electrostatic Interactions of I and IV.

Previous studies indicate that one of the factors that limits the accuracy of mechanics calculations is the manner in which electrostatics are calculated.¹⁵ Most available force fields use charges located at the atom center.⁴¹ This limitation appears to be particularly acute for larger ions. The dipole moment of the most stable arginine dimer (I1) calculated at the MMFF, AM1, and EDF1 6-31+G* level is 7.4, 5.8, and 4.2 D, respectively. However, for the most stable structure of bradykinin (IV4), the dipole moment calculated by MMFF is 53 D! Semiempirical AM1 calculations also give an anomalous dipole moment of 54 D, indicating that the semiempirical treatment of bradykinin is also inadequate. These values are much higher than that calculated by density functional theory, which gives a more reasonable dipole moment of 12 D.

Different dielectric constants were used in the mechanics calculations to see whether this value affects the stability of the lowest energy conformer. When all the conformers of IV are reminimized using a dielectric of 1.2, conformer 2 is the most stable. In contrast, a reminimization of all I conformers using a dielectric of 1.2 does not affect their stability ordering. Since a small change in the dielectric used affects stability ordering of IV, this suggests that better representation of electrostatic interactions would improve the performance of the molecular mechanics for larger ions.

Conclusions

The structure and energetics of two gas-phase biomolecule ions, protonated arginine dimer and protonated bradykinin, were investigated using a combination of molecular mechanics and density functional theory. Molecular mechanics calculations using MMFF and conformational searching using Monte Carlo and low-mode conformation searching techniques were used to find candidate low-energy structures. These structures were grouped into families of similar structure. The lowest energy structure from each family was used as a starting geometry in subsequent density functional calculations.

For protonated arginine dimer, the correlation between the MMFF and EDF1 6-31+G*//6-31G* energies is good (linear correlation coefficient 0.88). These results suggest that mechanics energies using MMFF are sufficient to identify structures within a few kilocalories per mole of the lowest energy structure for this ion. To the extent that the conformational search is comprehensive, these calculations indicate that the salt-bridge or ion–zwitterion form is more stable than the charge-solvated or ion–molecule structure by 5.7 and 7.7 kcal/mol at the EDF1 6-31++G**//6-31++G** and B3LYP 6-311++G**//6-31+G* levels, respectively. This result is in excellent agreement with the experimental results that indicate that the salt-bridge form is more stable.²⁶ Dissociation energies estimated at the EDF1 6-31+G* level are in good agreement with experimentally measured values, providing support for the energetics calculated at this level of theory.

The success of this computational approach applied to protonated bradykinin is more ambiguous. The correlation between the mechanics MMFF and DFT energies is poor (linear correlation coefficient 0.28), suggesting that mechanics is not suitable for identifying the lowest energy structures of this particular peptide ion. Clearly, similar calculations on additional large ions should be done to indicate the generality of this result. However, the result for bradykinin does suggest that gas-phase structures of large ions calculated at the mechanics level, as is typically done to obtain structural information in a number of experimental approaches, must be approached with significant caution when no experimental constraints are available. Despite the limited sample set and lack of experimental constraints for bradykinin in this study, there is a clear trend in the relative stabilities of the salt-bridge vs simple protonated forms of this ion calculated at the DFT level. The lowest energy structures of the salt-bridge and simple protonated forms differ by 13 kcal/mol, with the salt-bridge structure being more stable. The average difference between all the salt-bridge and simple protonated forms is 14 kcal/mol (the salt-bridge form more stable). These calculations are in good agreement with experimental results that indicated that protonated bradykinin contains a salt bridge in the gas phase.^10,27 The structures are also in good agreement with experimentally determined structures in nonaqueous solution. The results presented here suggest that it may be possible to obtain meaningful structural and energetic information from larger ions even in the absence of experimentally determined constraints, by investigating large numbers of low-energy mechanics structures by DFT.