Abstract
Objective
To develop a method for predicting concurrently both hospital survival and length of stay (LOS) for seriously ill or injured patients, with particular attention to the competing risks of death or discharge alive as determinants of LOS.
Data Sources
Previously collected 1995–1996 registry data on 2,646 cases of injured patients from three trauma centers in Maine.
Study Design
Time intervals were determined for which the rates of discharge or death were relatively constant. Poisson regression was used to develop a model for each type of terminal event, with risk factors on admission contributing proportionately to the subsequent rates for each outcome in each interval. Mean LOS and cumulative survival were calculated from a combination of the resulting piecewise exponential models.
Principal Findings
Age, Glasgow Coma Scale, Abbreviated Injury Scores, and specific mechanisms of injury were significant predictors of the rates of death and discharge, with effects that were variable in different time intervals. Predicted probability of survival and mean LOS from the model were similar to actual values for categorized patient groups.
Conclusions
Piecewise exponential models may be useful in predicting LOS, especially if determinants of mortality are separated from determinants of discharge alive.
Keywords: Mortality, length of stay, prediction, injury, trauma, piecewise exponential models, Poisson regression
Predicting the outcome of serious illness or injury is increasingly important for the planning and assessment of interventions in the health-care system, as well as for its more traditional role in providing a prognosis for individual cases. Mortality is obviously one important outcome variable, but the use of additional outcome variables might allow different perspectives in comparing groups of patients or evaluating interventions. In particular, hospital length of stay (LOS) is a potentially useful measurement of morbidity and a major determinant of the cost of medical care.
Constructing models to predict LOS will be more complicated in the presence of a significant mortality risk. In this case, the hospital stay can be terminated either by an undesirable event (death) or by a desirable event (discharge alive). The least sick patients will have relatively short LOS, and somewhat sicker patients will have longer LOS, but the sickest patients will also have short LOS terminating in death. Factors increasing the rate of one outcome may have no effect or an opposite effect on the rate of the other outcome, and effects may not be uniform throughout the hospital stay.
We have previously described an approach that distinguishes between these “competing risks” by using time to discharge alive as an outcome variable (Clark and Ryan 1997). The cumulative incidence of this desirable event can be estimated using standard software by considering the time until this event occurs to be infinite for patients who die. This formulation provides a simple way to evaluate both LOS and mortality, and is particularly useful for graphical comparisons. However, time to discharge alive is not by itself a measure of morbidity or cost.
In this study, we have continued the adaptation of traditional time-to-event methods (Cox and Oakes 1984) to produce a model for the prediction of LOS itself, with provision for the problem of competing risks and the possibility that risk factors will affect LOS differently in survivors and nonsurvivors. We present below some concepts of piecewise exponential modeling and an application to patients hospitalized in trauma centers. This approach may be particularly suited to the study of seriously injured patients and others for whom a significant hospital mortality must be anticipated.
Piecewise Exponential Models
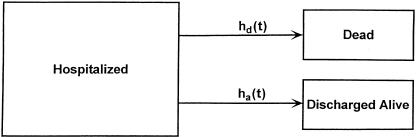
Consider a cohort of seriously injured or ill patients admitted to a hospital, whose hospital stay may be terminated either by death or discharge alive (Figure 1). The simplest predictive model of this sort would assume that the hazard (instantaneous rate) for leaving the hospital is equal to some constant, multiplied by a factor involving various risk factors or covariates. This would result in an exponential proportional hazards model for each outcome. That is, if the hazard function h(t) is equal to some constant k, the proportion of the original cohort remaining at time t will be exp(−kt). The parameter k can be estimated from the regression model
Figure 1.
A multistate model showing hospitalization resulting either in death or discharge alive. Note that the transition rate (hazard) for each outcome may vary with time
 |
where c1…cn are coefficients corresponding to the covariates x1…xn. A Poisson regression model (Kleinbaum et al. 1988) is mathematically equivalent to an exponential proportional hazards model, and may be more familiar or easier to use.
If we disregard the nature of the event that terminates the hospitalization, a single proportional hazards model could be constructed to predict the effect of risk factors on LOS, and this simplification might be reasonable when the number of deaths is small. When hospital mortality is significant, however, it makes more sense to construct a separate proportional hazards model for each outcome, especially since factors affecting the probability of one outcome may have no effect or even an opposite effect on the other.
In practice, the baseline hazards for discharge or death will rarely be constant. We are particularly considering patients with serious injuries or illnesses who would be unlikely to go home immediately after admission, might be more likely to go home after treatment in the next several days or weeks, but then might be less likely to go home if they remain in the hospital many weeks or months. Conversely, we might expect that the early death rate would be relatively high, followed by a period of stabilization, and finally the death rate of those who could not be discharged from the hospital might gradually increase. However, if the rates for certain intervals of time were relatively constant, we might still be able to construct valid exponential proportional hazards models for each of these intervals, and then combine them into a “piecewise” exponential model.
Piecewise exponential models can be very flexible. Although analysis of their mathematical properties is somewhat more involved than for simple exponential models, the necessary calculations are not difficult. If time intervals are made progressively shorter, a piecewise exponential model becomes approximately equivalent (at least in large sample settings) to a nonparametric Cox proportional hazards model (Friedman 1982), although the conceptual and computational advantages from using the exponential function will diminish if more than a few time intervals are used. If the number of time intervals is not too large, a model can be constructed with different regression coefficients (or even different values for the covariates) in different intervals.
For a given set of covariates determined at the time of hospital admission, the present study estimated rates of death and discharge alive as constants, kd and ka, for each of several time intervals. For a hospitalized cohort entering an interval at time ti, the proportion still hospitalized at time t later in the same interval can thus be estimated as 
. Further calculations based upon a piecewise exponential model using the combined hazards allow estimation of the mean time spent in the hospital (mean LOS) and the cumulative proportion discharged alive (probability of survival).
We used Stata (Stata Corporation 2001) for model estimation, and Mathematica (Wolfram 1996) for other programming and graphing. Further details of the theoretical background and programming used in this study are described in the corresponding software manuals.
Methods
Data on hospitalized injured patients in Maine have been collected in a statewide trauma registry since 1995, using the same software (HTR, Cales Associates, Alameda, CA) for all participating hospitals. These data have been periodically sent to Maine Emergency Medical Services (MEMS) and electronically imported into a system trauma registry (STR, Cales Associates).
The STR data from 1995 to 1996 from the three largest hospitals in the state (which have since been designated as trauma centers) were used for this study, following MEMS confidentiality rules. Cases transferred from a trauma center to another hospital were excluded, as were cases for which a data element was missing or out of range. The maximal Abbreviated Injury Scores (Keller et al. 1971) for each of six body regions (head, face, chest, abdomen, extremities, and general) were calculated from International Classification of Diseases, 9th revision (ICD-9) diagnosis codes by the STR. Indicator variables (1=yes, 0=no) were created for motor vehicle crashes (ICD-9 E-codes E810–E819), burns (E890–E899, E924), and penetrating injuries (E920, E922, E955, E956, E965, E966). Glasgow Coma Scale scores (Teasdale and Jennett 1976) were categorized such that Categories 0–4 corresponded respectively to raw scores of 3, 4–5, 6–8, 9–12, and 13–15. An indicator variable was set equal to 1 if admission systolic blood pressure was less than 90. If a patient had been transferred from another hospital to a trauma center, an indicator variable was set equal to 1 and the variable LOS was set equal to the LOS at the receiving hospital, otherwise LOS was equal to the LOS at the first and only hospital. If a LOS of 0 was recorded, this was replaced with an LOS of 1 day.
The time scale was arbitrarily apportioned into ten intervals of LOS, attempting to place similar numbers of events into each interval while also allowing for the entire range of values to be represented (Table 1). A Poisson regression model, without covariates but including time at risk for each case within each time interval, was estimated for each type of terminating event (death or discharge alive). The model was progressively simplified to involve only five time intervals by assigning the same indicator variable to adjacent intervals (starting with the longest LOS) as long as a likelihood ratio test showed no significant difference (p>0.05) as a result of consolidating the intervals.
Table 1.
Arbitrary categorization of hospital length of stay (LOS), with the number of cases entering that time interval, days at risk, deaths, and discharges. Days at risk exclude days for patients who have died or been discharged prior to or during a given time interval, and are used as a denominator to calculate daily incidence rates for each outcome
| LOS | Number entering | Days at risk | Deaths (rate) | Discharges (rate) |
|---|---|---|---|---|
| 1 | 2,646 | 2,646 | 64 (0.0242) | 495 (0.1871) |
| 2 | 2,087 | 2,087 | 13 (0.0062) | 300 (0.1437) |
| 3 | 1,774 | 1,774 | 6 (0.0034) | 288 (0.1623) |
| 4 | 1,480 | 1,480 | 5 (0.0038) | 251 (0.1696) |
| 5–6 | 1,224 | 2,256 | 6 (0.0027) | 345 (0.1530) |
| 7–9 | 873 | 2,217 | 7 (0.0032) | 323 (0.1457) |
| 10–14 | 543 | 2,119 | 11 (0.0052) | 247 (0.1166) |
| 15–22 | 285 | 1,647 | 8 (0.0049) | 139 (0.0844) |
| 23–43 | 138 | 1,790 | 4 (0.0022) | 80 (0.0447) |
| 44–172 | 54 | 1,465 | 4 (0.0027) | 50 (0.0341) |
Having thus determined with some objectivity the number of time intervals which fairly reflected variations in baseline incidence rate for each possible outcome, we subsequently assumed that the daily baseline incidence rates were constant during each interval. Models were constructed for each outcome (death or discharge alive) with indicator variables for each time interval. Covariates were added in a stepwise fashion (Cox and Oakes 1984), and temporarily retained in a model if the Wald p-value associated with that term was no more than 0.10. Squared terms were evaluated for categorized variables, but more complicated data transformations were not attempted. A few clinically relevant interactions between covariates were considered, but were not significant.
Basic predictive models were constructed without interaction terms between covariates and time intervals. Covariates were retained in the basic model for each outcome if the Wald p-value associated with that term was less than 0.05 for either outcome.
After exploratory modeling, a final Poisson model for each outcome was then developed containing indicator variables for each interval, all covariates which had been significant in any individual model, and terms for the interaction of each time interval with each covariate. For each outcome, the full model with all possible time interval interactions was then simplified in a stepwise fashion (again starting with the longest LOS), by eliminating covariates that were not statistically significant in a given time interval and combining the covariate effects from adjacent intervals wherever these modifications did not significantly change the likelihood ratio, with significance again taken as p < 0.05.
For any set of covariates (e.g., those for any given case or category), expected time in the hospital (LOS) and the cumulative incidence of each outcome were then calculated from a piecewise exponential model with the hazard in each interval equal to the sum of the hazards for death and for discharge alive. The LOS predicted by combining the best fitting piecewise exponential models was compared with the actual LOS for each case using ordinary linear regression. Mean predicted LOS and predicted survival were compared with actual LOS and survival for several subgroups of the patient population.
Results
There were 2,847 patient records in the STR contributed by one or another of the three trauma centers. After the exclusions described above, 2,646 (92 percent) were available for analysis. Of these 2,646 cases, 952 (36 percent) had been transferred from other hospitals to a trauma center, while the remaining 1,694 had been primarily admitted to one of the centers. Included were 1,611 (61 percent) male and 1,035 female. One hundred twenty-eight (5 percent) died in hospital, while the remainder were discharged alive after an LOS ranging from 1 to 172 days (median 4 days). Other characteristics of this population are shown in Table 2.
Table 2.
Characteristics of study population, with comparison of actual to predicted results from the final model with time-varying parameters for the categories shown. LOS=Mean actual LOS, LOSpred=Mean LOS predicted by the model, SURV=Actual percentage surviving, SURVpred=Probability of survival predicted by the model
| CASES | LOS | LOSpred | SURV | SURVpred | |
|---|---|---|---|---|---|
| Age < 55 | 1,830 (69%) | 6.73 | 7.09 | .966 | .968 |
| 55 ≤ Age ≤ 70 | 355 (13%) | 8.63 | 7.93 | .961 | .958 |
| Age > 70 | 461 (17%) | 8.90 | 8.96 | .889 | .902 |
| Penetrating | 143 (5%) | 4.76 | 5.95 | .902 | .911 |
| Burns | 92 (3%) | 15.47 | 15.85 | .978 | .975 |
| Vehicle Crashes | 944 (36%) | 9.69 | 10.02 | .918 | .931 |
| HeadAIS > 2 | 609 (23%) | 10.76 | 11.37 | .865 | .876 |
| FaceAIS > 2 | 19 (1%) | 19.21 | 16.56 | 1.000 | .992 |
| ChestAIS > 2 | 347 (13%) | 12.90 | 13.92 | .841 | .861 |
| AbdomenAIS > 2 | 131 (5%) | 12.77 | 14.84 | .870 | .874 |
| ExtremityAIS > 2 | 557 (21%) | 10.54 | 9.88 | .953 | .955 |
| GeneralAIS > 2 | 15 (1%) | 24.40 | 28.98 | .933 | .935 |
| Best GCS <13 | 250 (9%) | 14.26 | 14.77 | .664 | .707 |
| Worst SBP <90 | 86 (3%) | 10.62 | 13.72 | .709 | .812 |
| All Cases | 2,646 | 7.36 | 7.53 | .952 | .955 |
Modeling incidence rates without covariates for discharge alive, with progressive simplification of the model as described above, resulted in consolidation of the ten arbitrary time intervals (Table 1) to five intervals with distinct incidence rates, corresponding to t1=1, t2=9, t3=14, and t4=22. A similar process for death rates distinguished a difference only between the first day and the rest of the hospitalization. However, in subsequent modeling with covariates, the five intervals were retained for both outcomes.
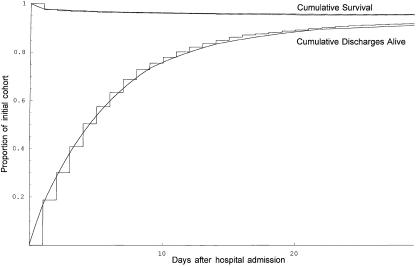
Piecewise exponential models without covariates showed a good fit when compared graphically to Kaplan-Meier plots based on time to death and time to discharge alive. The crude daily incidence rates (not considering risk factors) for death were 0.0242 in the first time period and 0.0038 thereafter. The crude daily incidence rates for discharge alive from the hospital in the five time periods were respectively 0.1871, 0.1537, 0.1166, 0.0844, and 0.0400. The observed curves for survival and the cumulative incidence of discharge alive are compared to the models without covariates in Figure 2.
Figure 2.
Plots of the actual survival curve from the data and actual cumulative incidence of discharge alive from the data, with superimposed theoretical piecewise exponential curves from the model without covariates
When covariates were added to the models, squares of the categorized GCS and the maximal AIS scores for each body region produced better fitting models than the untransformed variables, consistent with the known nonlinear effect of anatomic injury severity on outcomes (Baker 1974). Age, decreased GCS, and increased severity of head, chest, or abdominal injury had the expected effects of decreasing time to death while increasing time to discharge alive. Hypotension and penetrating trauma independently increased mortality rate but not rate of discharge alive; transfers and burns did not result in an increased mortality rate but had a reduced rate of discharge alive. More severe facial or skeletal injuries had both a lower rate of death and a lower rate of discharge alive (Table 3).
Table 3.
Estimated covariate effects for daily rates of leaving the hospital, when effects were assumed uniform over all time intervals. Point estimates with 95% confidence intervals (in parentheses) are given. A negative value indicates that the event is less likely in the presence of a given covariate, while a positive value indicates that the event is more likely
| OUTCOME | ||||
|---|---|---|---|---|
| COVARIATE | Discharged Alive | Died | ||
| Age (years) | −0.013 | (−0.015, −0.011) | 0.031 | (0.024, 0.039) |
| (GCSmax)2 | 0.056 | (0.040, 0.072) | −0.166 | (−0.203, −0.128) |
| (HeadAIS)2 | −0.041 | (−0.050, −0.032) | 0.037 | (0.013, 0.060) |
| (FaceAIS)2 | −0.056 | (−0.089, −0.023) | −0.236 | (−0.419, −0.052) |
| (ChestAIS)2 | −0.055 | (−0.067, −0.044) | 0.055 | (0.028, 0.081) |
| (AbdomenAIS)2 | −0.084 | (−0.100, −0.068) | 0.029 | (−0.012, 0.070) |
| (ExtremityAIS)2 | −0.071 | (−0.083, −0.059) | −0.074 | (−0.129, −0.020) |
| (GeneralAIS)2 | −0.039 | (−0.062, −0.016) | −0.109 | (−0.225, 0.006) |
| Penetrating | −0.006 | (−0.199, 0.187) | 1.171 | (0.506, 1.836) |
| Burn | −1.496 | (−1.728, −1.264) | 0.570 | (−0.899, 2.034) |
| Vehicle Crash | −0.178 | (−0.270, −0.086) | 0.439 | (−0.013, 0.891) |
| Transfer | −0.232 | (−0.318, −0.146) | 0.015 | (−0.372, 0.403) |
| Hypotension | 0.158 | (−0.103, 0.418) | 0.592 | (0.081, 1.103) |
| Day 1 | 0.396 | (0.187, 0.605) | 3.339 | (2.540, 4.138) |
| Days 2–9 | 0.471 | (0.281, 0.661) | 1.562 | (0.747, 2.378) |
| Days 10–14 | 0.551 | (0.334, 0.768) | 1.464 | (0.520, 2.408) |
| Days 15–22 | 0.451 | (0.210, 0.692) | 1.236 | (0.235, 2.238) |
| Constant | −1.764 | (−2.091, −1.436) | −7.230 | (−8.342, −6.119) |
The models with time-varying parameters showed interesting differences from one time period to another, as well as between the two potential causes of leaving the hospital (Table 4). Physiologic or anatomic evidence of severe neurologic injury was a strong predictor of death in the first few days. Patients with penetrating injuries and those with serious thoracic or abdominal injuries were more likely to die, but hypotension was no longer an independent predictor of death. Patients who survived transfer from other hospitals were less likely to die in the first 9 days, but more likely to die thereafter. Older patients tended to stay in the hospital longer, and increased severity of injury in each body region was also associated with increased LOS. Patients with penetrating trauma still in the hospital after 9 days were less likely to go home during days 10 to 22. Burn patients and patients transferred from other hospitals stayed longer in the trauma centers. Patients injured in motor vehicle collisions were more likely to go home on the first day, but less likely thereafter.
Table 4.
Estimated covariate effects for daily rates of leaving the hospital during the specified time intervals. Parentheses indicate estimates that have been grouped in adjacent intervals as described in the text. Effects of variables not listed or left blank in a given interval were not statistically significant
| COVARIATES | 1 day | 2–9 days | 10–14 days | 15–22 days | 22 days |
|---|---|---|---|---|---|
| For discharge alive | |||||
| Age (years) | −0.023 | (−0.010 | −0.010 | −0.010 | −0.010) |
| (GCSmax)2 | (0.065 | 0.065 | 0.065) | ||
| (HeadAIS)2 | −0.066 | (−0.039 | −0.039 | −0.039 | −0.039) |
| (FaceAIS)2 | −0.186 | (−0.036 | −0.036 | −0.036 | −0.036) |
| (ChestAIS)2 | −0.156 | −0.060 | (−0.024 | −0.024 | −0.024) |
| (AbdomenAIS)2 | −0.246 | −0.094 | (−0.051 | −0.051) | |
| (ExtremityAIS)2 | −0.131 | −0.076 | −0.033 | −0.033 | −0.033) |
| (GeneralAIS)2 | (−0.042 | −0.042 | −0.042 | −0.042 | −0.042) |
| Penetrating | (−1.436 | −1.436) | |||
| Burn | (−1.727 | −1.727) | (−0.876 | −0.876 | −0.876) |
| Vehicle Crash | 0.020 | (−0.222 | −0.222 | −0.222 | −0.222) |
| Transfer | (−0.223 | −0.223 | −0.223 | −0.223) | |
| Constant | −0.906 | −1.520 | −1.758 | −0.967 | −1.805 |
| For death | |||||
| Age (years) | (0.020 | 0.020) | (0.064 | 0.064 | 0.064) |
| (GCSmax)2 | −0.248 | (−0.089 | −0.089 | −0.089 | −0.089) |
| (HeadAIS)2 | 0.036 | 0.109 | |||
| (FaceAIS)2 | (−0.259 | −0.259 | −0.259 | −0.259 | −0.259) |
| (ChestAIS)2 | (0.057 | 0.057 | 0.057 | 0.057 | 0.057) |
| (AbdomenAIS)2 | (0.051 | 0.051 | 0.051 | 0.051 | 0.051) |
| Penetrating | (0.731 | 0.731 | 0.731 | 0.731 | 0.731) |
| Transfer | (−0.387 | −0.387) | (0.917 | 0.917 | 0.917) |
| Constant | −2.660 | −6.639 | (−9.085 | −9.085 | −9.085) |
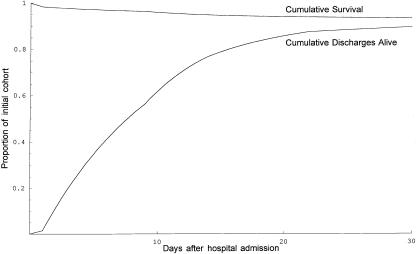
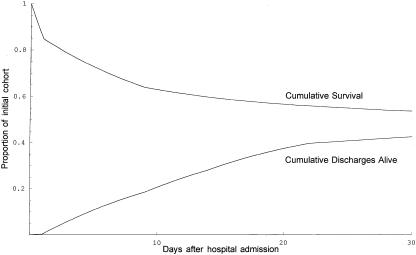
Outcome curves (survival and cumulative discharge alive) were graphed for numerous theoretical patient cohorts (e.g., Figures 3 and 4). In these graphs, the expected probability of survival for a given cohort is seen as the height where the curves meet, while expected LOS corresponds to the area between the curves.
Figure 3.
Predicted survival curve and cumulative incidence of discharge alive for patients 80 years of age with serious injury to the chest (AIS=4)
Linear regression of actual LOS against predicted LOS for the combined model without time-varying parameters showed a relatively weak ability to predict the actual LOS. The fitted equation was
 |
The combined model allowing for time-varying parameters showed better accuracy and better (although still modest) precision. The fitted equation was
 |
Results for different subsets of patients are given in Table 2.
Discussion
We have previously described some of the problems with implementation of time-to-event methods in the presence of competing risks (Clark and Ryan 1997). Nevertheless, proportional hazards methodology is a powerful tool (Cox and Oakes 1984), and the piecewise exponential approach presented here retains its ability to express the effect of risk factors in an understandable way, while allowing for competing risks and time-varying effects. Mullins et al. (1997) have pointed out the need to separate predictors of early and late hospital mortality from trauma. Blackstone (1996) has advocated the use of hazard functions (incidence rates) to analyze LOS after valvular heart surgery. Our adaptation of these suggestions may be useful in predicting outcomes for seriously injured patients and others in whom hospital mortality is not infrequent.
With reference to Table 4, for example, the model with time-varying effects predicts that a hypothetical 80-year-old man admitted directly to one of our centers with multiple rib fractures (AIS = 4) but normal GCS (category 4) would have a risk of dying on the first day approximately equal to exp
, then a risk of dying during each of the next 8 days approximately equal to 
. His chance of being discharged alive on the first day would be predicted as 
. Figure 3 shows the theoretical curves representing the proportion of such patients expected to die or to be discharged alive over time. The area between these curves represents expected LOS (9.5 days), and the height of their convergence represents expected survival (92.6 percent). If our theoretical patient also suffered a serious head injury (AIS=4) with moderate neurologic impairment (categorized GCS=3, corresponding to a raw GCS of 9 to 12), the outcome curves shown in Figure 4 enclose an expected LOS of 13.1 days and converge to an expected survival of only 48.9 percent.
Figure 4.
Predicted survival curve and cumulative incidence of discharge alive for patients 80 years of age with serious injury to the chest (AIS=4) and head (AIS=4, GCS category 3)
The models demonstrate effects of several covariates that agree with clinical intuition, including several that affect one outcome but not the other. Although it may initially seem paradoxical that increased severity of facial injury should reduce mortality, inclusion in the model is conditioned upon admission to a trauma center, so that patients admitted because of a severe (but generally nonlethal) facial injury requiring specialized surgery will be at lower risk for death than the majority of patients admitted with head or truncal injury. We expect that with a larger set of data, especially with more victims of penetrating injury, it would be possible to demonstrate more of an effect from physiologic variables on early mortality. The differing registry inclusion criteria of hospitals in Maine may also be obscuring some effects, especially those anticipated in the first few days. The small number of patients still hospitalized after 22 days hinders estimation of covariate effects in the last time interval.
Any model involves simplification of reality, while attempting to retain its essential features. This process includes minimizing the number of parameters to be estimated. A theoretical argument could be made that our models for death and discharge alive should have the same covariates if they are to be combined. However, when interactions with multiple time intervals were also being considered, we felt that it was preferable to estimate a single parsimonious model for each outcome. Some of the “insignificant” parameters are thereby included in the constant term for a given outcome and time interval.
Others have attempted to model hospital length of stay after acute trauma, and have also encountered the problems we have discussed. MacKenzie et al. (1989) limited analysis of LOS to survivors, predicting the logarithm of LOS from ordinary linear regression of explanatory variables. In the published discussion of this study, MacKenzie stated that model complexity had forced them to abandon the original intent to include nonsurvivors. Siegel et al. (1994) adapted this approach, including mortality as the most influential of several predictors of LOS; however, using one outcome (mortality) as an independent variable to predict another outcome (LOS) complicates interpretation of the model.
Schwartz et al. (1996) limited their attention to patients with hip fractures. They first estimated a probability of survival, p, for each case (presumably derived using logistic regression) and then included p and p2 in regression models to predict LOS. This allowed both low and high values of p to affect their models, but they did not report which was more influential. They also found that a logarithmic transformation of LOS did not produce better fitting models, and obtained values of R2 ranging from 0.04 to 0.17.
Rutledge and Osler (1998) created an International Classification of Diseases Injury Severity Score (ICISS) and adapted it to predict LOS for injured patients. Their approach involves linear regression of up to 15 diagnoses and 15 procedures against the observed values of LOS for each of several hundred diagnoses or procedures coded using ICD-9 and contained in a large reference database. While the authors were able to demonstrate good correlation between predicted and actual LOS in hospital discharge data (R2=.50), their model also includes information not available on admission (e.g., procedures performed during hospitalization).
None of the above approaches is comparable to ours. In particular, the use of certain outcomes (such as death or procedures during hospitalization) to explain another outcome (LOS) cannot be compared to predictions using only data available at the time of admission. While the former approach may have some useful purposes, interpretation is problematic since death must be considered as an outcome, not a predictor. Procedures performed during hospitalization also may reflect variation in medical practice or be influenced by intermediate outcomes (complications). We would also emphasize that one should be cautious about the use of R2 in evaluating nonlinear models (Kvalseth 1985), and cannot use this statistic to compare models constructed from different data.
More recently, Ho et al. (2000) have studied outcomes after hip fracture using a competing risks model, which shares theoretical features with our approach. The authors assumed an underlying log–logistic hazard function, and estimated constant covariate effects on rates of death and discharge alive. They did not calculate LOS or probability of survival for given patient cohorts, but found that increased age, male sex, and several premorbid conditions increased the rate of death and decreased the rate of discharge alive.
We believe that piecewise exponential models such as we have described are conceptually and computationally easier, are able to model underlying hazards more flexibly, can incorporate time-varying effects, and are therefore preferable for implementation of a competing risks analysis. Since our formulation essentially describes a multistate model, it could furthermore be generalized to include outcomes in addition to death and discharge alive (e.g., rehabilitation hospital or nursing home).
We have been primarily interested in exploring theoretical and computational issues, and recognize that our sample may not be large enough to make strong inferences about specific effects of covariates on the outcomes of injured patients. A model of this sort could be made more precise by applying it to a larger database, which would also enable more specific categorization of mechanisms of injury, physiologic data, premorbid conditions, and descriptors of injury. Interactions and other data transformations might provide additional insight into the factors responsible for mortality or prolonged hospitalization. Subsequent testing of such an improved model on an independent database would then be warranted, and might allow it to be used more generally for predicting injury outcomes.
References
- Baker SP, O'Neill B, Haddon W, Jr, Long WB. “The Injury Severity Score: A Method for Describing Patients with Multiple Injuries and Evaluating Emergency Care.”. Journal of Trauma. 1974;11(3):187–96. [PubMed] [Google Scholar]
- Blackstone EH. “Outcome Analysis Using Hazard Function Methodology.”. Annals of Thoracic Surgery. 1996;61(2 Suppl):S2–S7. doi: 10.1016/0003-4975(95)01075-0. [DOI] [PubMed] [Google Scholar]
- Clark DE, Ryan LM. “Modeling Injury Outcomes Using Time-to-Event Methods.”. Journal of Trauma. 1997;42(6):1129–34. doi: 10.1097/00005373-199706000-00025. [DOI] [PubMed] [Google Scholar]
- Cox DR, Oakes D. Analysis of Survival Data. London: Chapman & Hall; 1984. [Google Scholar]
- Friedman M. “Piecewise exponential models for survival data with covariates.”. Annals of Statistics. 1982;10(1):101–13. [Google Scholar]
- Ho V, Hamilton BH, Roos LL. “Multiple Approaches to Assessing the Effects of Delays for Hip Fracture Patients in the United States and Canada.”. Health Services Research. 2000;34(7):1499–518. [PMC free article] [PubMed] [Google Scholar]
- Keller WK, Dillihunt RC, Fenner HA, Jolley FL, Keeney AH, Weygandt PL, Hames LM. “Rating the Severity of Tissue Damage: I. The Abbreviated Scale.”. Journal of the American Medical Association. 1971;215(2):277–80. doi: 10.1001/jama.1971.03180150059012. [DOI] [PubMed] [Google Scholar]
- Kleinbaum DG, Kupper LL, Muller KE. Applied Regression Analysis and Other Multivariable Methods. Boston: PWS-KENT; 1988. [Google Scholar]
- Kvalseth TO. “Cautionary note about R2.”. American Statistician. 1985;39(4):279–85. [Google Scholar]
- MacKenzie EJ, Morris JA, suffix, Edelstein SL. “Effect of Pre-existing Disease on Length of Hospital Stay in Trauma Patients.”. Journal of Trauma. 1989;29(6):757–65. doi: 10.1097/00005373-198906000-00011. [DOI] [PubMed] [Google Scholar]
- Mullins RJ, Mann NC, Brand DM, Lenfesty BS. “Specifications for Calculation of Risk-adjusted Odds of Death Using Trauma Registry Data.”. American Journal of Surgery. 1997;173(5):422–5. doi: 10.1016/s0002-9610(97)89581-5. [DOI] [PubMed] [Google Scholar]
- Rutledge R, Osler T. “The ICD-9-based Illness Severity Score: A New Model That Outperforms Both DRG and APR-DRG as Predictors of Survival and Resource Utilization.”. Journal of Trauma. 1998;45(4):791–9. doi: 10.1097/00005373-199810000-00032. [DOI] [PubMed] [Google Scholar]
- Schwartz M, Iezzoni LI, Ash AS, Mackiernan YD. “Do Severity Measures Explain Differences in Length of Hospital Stay? The Case of Hip Fracture.”. Health Services Research. 1996;31(4):365–85. [PMC free article] [PubMed] [Google Scholar]
- Siegel JH, Shafi S, Goodarzi S, Dischinger PC. “A Quantitative Method for Cost Reimbursement and Length of Stay Quality Assurance in Multiple Trauma Patients.”. Journal of Trauma. 1994;37(6):928–37. doi: 10.1097/00005373-199412000-00010. [DOI] [PubMed] [Google Scholar]
- Stata Corporation. Stata Statistical Software: Release 5.0. College Station TX: Stata Corporation; 2001. [Google Scholar]
- Teasdale G, Jennett B. “Assessment and Prognosis of Coma after Head Injury.”. Acta Neurochirurgica. 1976;34(1–4):45–55. doi: 10.1007/BF01405862. [DOI] [PubMed] [Google Scholar]
- Wolfram S. The Mathematica Book. Cambridge UK: Cambridge University Press; 1996. [Google Scholar]