Binding Energies of Proton-Bound Dimers of Imidazole and n-Acetylalanine Methyl Ester Obtained by Blackbody Infrared Radiative Dissociation

Abstract

The dissociation kinetics of protonated n-acetyl-L-alanine methyl ester dimer (AcAlaME_d), imidazole dimer, and their cross dimer were measured using blackbody infrared radiative dissociation (BIRD). Master equation modeling of these data was used to extract threshold dissociation energies (E_o) for the dimers. Values of 1.18 ± 0.06, 1.11 ± 0.04, and 1.12 ± 0.08 eV were obtained for AcAlaME_d, imidazole dimer, and the cross dimer, respectively. Assuming that the reverse activation barrier for dissociation of the ion–molecule complex is negligible, the value of E_o can be compared to the dissociation enthalpy (ΔH_d°) from HPMS data. The E_o values obtained for the imidazole dimer and the cross dimer are in agreement with HPMS values; the value for AcAlaME_d is somewhat lower. Radiative rate constants used in the master equation modeling were determined using transition dipole moments calculated at the semiempirical (AM1) level for all dimers and compared to ab initio (RHF/3-21G*) calculations where possible. To reproduce the experimentally measured dissociation rates using master equation modeling, it was necessary to multiply semiempirical transition dipole moments by a factor between 2 and 3. Values for transition dipole moments from the ab initio calculations could be used for two of the dimers but appear to be too low for AcAlaME_d. These results demonstrate that BIRD, in combination with master equation modeling, can be used to determine threshold dissociation energies for intermediate size ions that are in neither the truncated Boltzmann nor the rapid energy exchange limit.

Introduction

Knowledge of gas-phase ion thermochemistry is essential in many areas including the chemistry of plasmas and interstellar space as well as understanding the role of solvent in the condensed phase. Thermochemical methods which make possible the measurement of accurate dissociation energies have provided information that is critical for relating fragmentation observed in a tandem mass spectrum back to the identity of the original ion. This information has improved the ability of tandem mass spectrometry to provide structural information from unknown samples as well as identify compounds present in complex mixtures at trace levels. Of key importance in measuring thermochemical data is knowledge of the internal energy of the ion population. High-pressure mass spectrometry (HPMS), in which the ion population has a Boltzmann distribution, has been used to provide accurate thermochemical values since the 1960s.^1,2 Elegant state-to-state techniques, such as guided ion beam³ and photoelectron–photoion coincidence (PEPICO)⁴ spectroscopy, have been used to measure accurate dissociation energies. These and other methods have been recently reviewed by Armentrout and Baer.⁵

More recently, blackbody infrared radiative dissociation (BIRD) has been used to obtain dissociation activation energies for a variety of ions ranging from small weakly bound clusters to large proteins.^6–13 In this method, ions are trapped at low pressure in the cell of a Fourier transform mass spectrometer where they can absorb blackbody photons emitted from the vacuum chamber walls. The steady-state internal energy of the ion population depends on the relative rates of dissociation, photon absorption, and emission. For large ions, equilibration with the blackbody radiation field can occur.^6,14 This results in a population with a Boltzmann distribution of internal energies. Under these conditions, the measured Arrhenius parameters are the same as those that would be measured under high-pressure conditions.⁶ We have called this the rapid energy exchange (REX) limit. In this limit, information about both the activation energy and transition-state entropy can be obtained directly from the experiment. The effect of various factors that lead to kinetics in the REX limit are discussed elsewhere.¹⁴

For small ions or weakly bound clusters, dissociation occurs rapidly when ions are excited above the threshold dissociation energy (E_o). This results in a population of ions that have an internal energy distribution that is similar to a Boltzmann distribution but is depleted at higher energies. Measured Arrhenius parameters are lower than those that would be measured in an HPMS experiment. However, true threshold dissociation energies can be obtained from these data by modeling. For small ions with low E_o’s, Dunbar has shown that accurate values of E_o can be obtained using either a simple truncated Boltzmann model or a master equation model.^7,8,15–17 For example, the measured zero-pressure dissociation activation energy of SiMe₃⁺–Me is 0.43 ± 0.07 eV.¹⁷ Values of E_o of 0.70 ± 0.07 and 0.67 ± 0.05 eV are obtained using the truncated Boltzmann model and master equation modeling, respectively. These values are in excellent agreement with values of 0.72 ± 0.06 and 0.70 eV obtained by guided ion beam experiments and ab initio (MP2/6-31G*) calculations.¹⁷ Sena and Riveros¹⁸ have also used master equation modeling to simulate measured dissociation kinetics of acetophenone activated by photons generated from a heated tungsten filament. Assuming that ions activated above E_o dissociate immediately (the truncated Boltzmann assumption), a value of E_o was obtained.¹⁸

For intermediate-size ions in which radiative energy transfer and microcanonical dissociation rates are competitive, neither the truncated Boltzmann nor the REX limit analysis applies. For these ions, master equation modeling can be used to obtain E_o.9 The master equation is a set of coupled differential equations that describes the time evolution of a reacting system. Radiative absorption, emission, and dissociation rate constants are included in the model to simulate the BIRD experiment. Our implementation of the model contains three adjustable parameters: the threshold dissociation energy (E_o), transition dipole moments (μ), and the transition-state frequency set.⁹ These values are varied within a reasonable range to fit the experimentally measured data. This method has been used to determine the threshold dissociation energies from BIRD kinetics of proton-bound dimers of several amino acids and N,N-dimethylacetamide; these dissociation processes are in neither the truncated Boltzmann nor REX limit.⁹ The value of E_o obtained from the master equation modeling of N,N-dimethylacetamide was 1.25 ± 0.05 eV,⁹ which is the same as that obtained from HPMS data.¹⁹

To assess the accuracy with which E_o can be obtained from BIRD and master equation modeling of intermediate-size ions, the dissociation of three proton-bound dimmers–n-acetyl-L-alanine methyl ester dimer (AcAlaME_d), imidazole dimer (Im_d), and their cross dimer (AcAlaME·Im)–was measured using BIRD. Values of E_o are determined from master equation modeling of the BIRD data and compared to values that have been previously measured by Meot-Ner using HPMS.^19,20 If the reverse activation barrier for dissociation of these ion–molecule complexes is negligible, then the value of E_o should be equal to the binding energy of these complexes. The results of this experiment demonstrate that this method can provide dissociation energies for ions that are in neither the truncated Boltzmann nor REX limit with similar accuracy and precision as obtained by HPMS experiments. In addition, these results indicate that BIRD and master equation modeling can provide accurate dissociation energies for intermediate-size molecules, such as peptides, for which little thermochemical data are known.

Experimental Section

Materials.

Imidazole was purchased from the Aldrich Chemical Co. (Milwaukee, WI) and was used without further purification. The methyl ester of n-acetyl-L-alanine was synthesized by adding 1 drop of concentrated sulfuric acid to ~15 mL of a methanol solution of n-acetyl-L-alanine (Sigma Chemical Co., St. Louis, MO) and allowing the mixture react at room temperature for ~24 h. This solution was diluted to ~10⁻⁴ M with methanol and was used to form the dimer of n-acetyl-L-alanine methyl ester by electrospray. Imidazole was added to this solution to form the mixed dimer. The imidazole dimer was electrosprayed from a ~10⁻⁴ M solution of 80:20 methanol:water with ~1% acetic acid added.

Mass Spectrometry.

All BIRD measurements were done on an external ion source ESI-FTMS with a 2.7 T superconducting magnet. The instrumentation has been described in detail elsewhere.^10,11 A shutter is opened to allow ions to pass into the ultrahigh-vacuum chamber for a period of 3–12 s. This time is adjusted for each set of kinetic data in order to maximize signal. During ion accumulation, a pulse valve is opened to introduce nitrogen gas into the chamber at a pressure of ~2 × 10⁻⁶ Torr in order to assist in trapping and thermalization of the ions. After the shutter is closed, a 2 s delay is used to allow the chamber to be pumped to a background pressure of ≤3 × 10⁻⁸ Torr. The protonated dimer is isolated using a combination of SWIFT, chirp, and single-frequency excitation waveforms. A variable reaction delay of up to 600 s is used prior to detection. Data are acquired with an Odyssey data system (Finnigan FTMS, Madison, WI) using an excitation sweep rate of 3200 Hz/μs.

The vacuum chamber surrounding the ion cell is resistively heated, and its temperature is controlled using an Omega proportionating temperature controller (Stamford, CT, model 4002A). The ion cell temperature is measured by thermocouples located on either side of the cell. The temperature of the ion cell varies by less than ±0.5 °C over the time required to obtain a kinetic data set. However, even this slight variation leads to some scatter in the kinetic data.

Calculations.

Minimum-energy structures for all protonated and neutral monomers and protonated dimers were obtained from molecular mechanics using the consistent valence force field (CVFF) of the Insight/Discover Suite of programs (Biosym Technologies, San Diego, CA). For protonated n-acetyl-L-alanine methyl ester and its dimer, the proton was placed on the amide oxygen of one n-acetyl-L-alanine methyl ester unit.¹⁹ For the protonated imidazole species as well as the mixed dimer, the proton was placed on N3 of the imidazole monomer. A total of 120 structures were generated for each molecule by running molecular dynamics at 500 K for 4 ps followed by simulated annealing to 200 K over 8 ps and then energy minimization to 0 K. The lowest energy structure was then used as the initial geometries for semiempirical calculations. Geometry minimization and force calculations were done with MOPAC 6.0 using the AM1 force field. Vibrational frequencies and transition dipole moments (μ) were determined for each species. To compare semiempirical and ab initio values for transition dipole moments, ab initio geometry minimization and force calculations were performed on all monomer units and the imidazole dimer using the semiempirical structures as starting coordinates. All ab initio calculations were done at the RHF/3-21G* level using GAUSSIAN 92 (Gaussian, Inc., Pittsburgh, PA). Frequencies from ab initio calculations were scaled by 0.91 for subsequent radiative absorption calculations because HF calculations are known to systematically overestimate vibrational frequencies.²¹

Up-pumping rates for comparison of semiempirical and ab initio integrated transition dipoles were calculated using a very simple model. The values given are the rate of photon absorption for an ion at 0 K inside a blackbody at the middle of the experimental temperature range used. These values are calculated for comparison purposes only and are not used in the master equation modeling.

Master equation modeling was done using software written in this laboratory. A detailed description of this is given elsewhere.⁹ The master equation is a set of coupled differential equations that can be represented as the product of a transport (or J) matrix with a vector describing the initial population of the energy levels of a system. The solution to the master equation is insensitive to choice of initial population; in our model, we take the initial population of energy levels to be a Boltzmann. The elements of the J matrix are the detailed rate constants for population and depopulation of each energy state. An energy state can be populated through radiative absorption from a state of lower energy and stimulated or spontaneous emission from a state of higher energy. These rates are calculated using Einstein A and B coefficients and using the Planck distribution for the radiation density at a given temperature. Similarly, a state can be depopulated by means of absorption, emission, or dissociation. Rate constants for dissociation are calculated using RRKM theory.

Results and Discussion

Blackbody Infrared Dissociation Kinetics.

Dissociation of the protonated dimers results exclusively in formation of protonated monomer within the range of temperatures investigated. For AcAlaME·Im, only protonated imidazole is formed. The proton affinities (PA) of AcAlaME and Im are 223.7¹⁹ and 222.3 kcal/mol,²² respectively. While Im has a lower PA, the BIRD results show that Im has a higher gas-phase basicity (GB). The different relative values of PA vs GB are presumably due to the entropy change arising from the coordination of the proton to both carbonyl groups in the AcAlaME monomer.¹⁹ The dimers were dissociated over a minimum temperature range of 57 °C. Unimolecular dissociation rate constants are determined at each temperature from the slope of ln{[D⁺]/([D⁺] + [M⁺])} vs time, where [D⁺] and [M⁺] are the abundances of protonated dimer and monomer, respectively. These kinetic data are shown in Figure 1 a–c. All the plots have zero y-intercepts and excellent linear fits (R ≥ 0.992), indicating that the ion population is in a steady state at the start of the reaction delay in each experiment.

Figure 1.

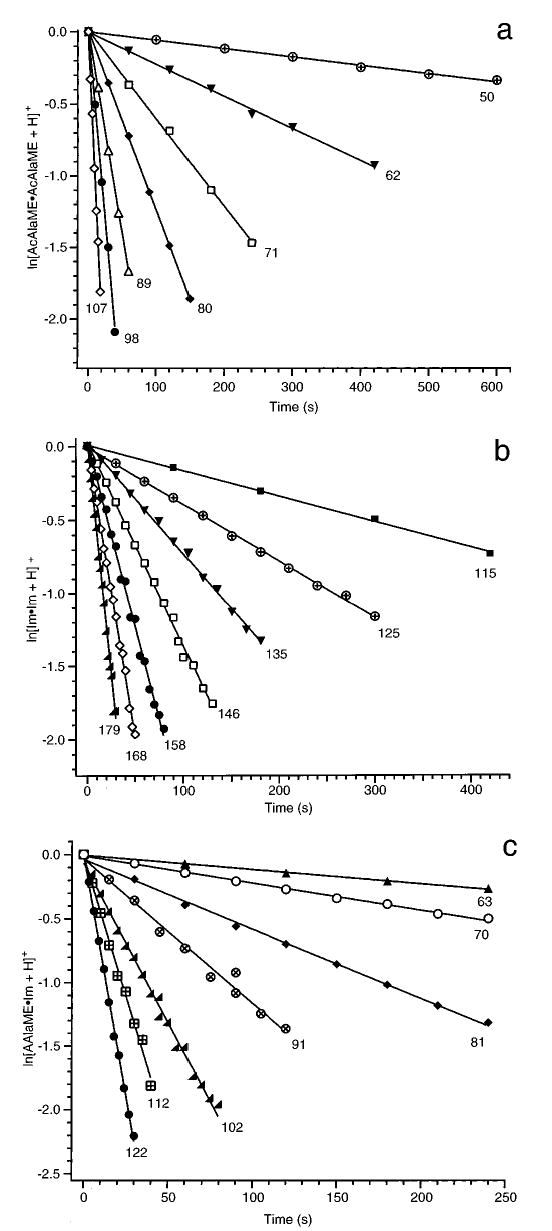
Blackbody infrared radiative dissociation data of protonated (a) n-acetyl-L-alanine methyl ester dimer, (b) imidazole dimer, and (c) (n-acetyl-L-alanine methyl ester)·(imidazole) fit to first-order kinetics. Temperatures (in °C) are indicated on the plot.

Arrhenius Plots.

From the temperature dependence of the dissociation rate constants, Arrhenius activation parameters are obtained. The Arrhenius plots are shown in Figure 2. The measured zero-pressure values for preexponentials (A) and activation energies (E_a) are given in Table 1. The error given is the standard deviation of the linear least-squares best fit line. The measured preexponentials are substantially lower than those for an entropically favorable dissociation process from a Boltzmann distribution of ions. This indicates that these dissociation processes are not in the REX limit.

Figure 2.

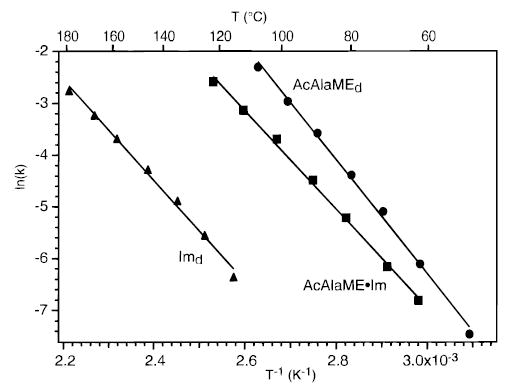
Zero-pressure limit Arrhenius plot for the dissociation of the proton-bound dimers of (^) n-acetyl-L-alanine methyl ester, (▴) imidazole, and (▪) their cross dimer.

TABLE 1.

Measured Zero-Pressure Arrhenius Parameters for Proton-Bound Dimers

Dimmer	measured Ea (eV)	measured log A
AcAlaMEd	0.95 ± 0.02	11.6 ± 0.3
Imd	0.83 ± 0.03	8.2 ± 0.3
AcAlaME·Im	0.82 ± 0.02	9.4 ± 0.3

Parameters in the Master Equation Model.

Because these dissociation processes are not in the REX limit, modeling is required in order to extract threshold dissociation energies (E_o) from the measured Arrhenius parameters. The master equation is a set of coupled differential equations describing the time evolution of the population of internal energy states of a system. Combining expressions for absorption and emission of infrared radiation with microcanonical dissociation rate constants to describe energy-transfer processes, the solution to the master equation numerically simulates the BIRD experiment. There are three adjustable parameters in this model: E_o, transition dipole moments (μ), and the high-pressure preexponential (A^∞). The latter two parameters are varied over a range of reasonable values (vide infra) to find the range of E_o that match the experimentally measured data. The criteria for a fit are that the calculated zero-pressure E_a and preexponential match the measured values within experimental error and that the calculated absolute dissociation rate constants are within a factor of 2 of the measured values.

To calculate radiative absorption and emission rate constants, it is necessary to determine vibrational frequencies, their corresponding transition dipole moments, and the density of the blackbody radiation field. The latter is given by the Planck distribution. Vibrational frequencies can be calculated with reasonable accuracy. However, calculated values of transition dipole moments for these dimers have much greater uncertainty. Transition intensities for small neutral molecules calculated at the RHF/3-21G* level are larger than measured values by a factor of ~2.^23,24 There is only limited comparison data for ions.²⁵ Results of both Dunbar and co-workers⁷ and Price et al.⁹ indicate that master equation modeling using integrated radiative rate constants calculated with ab initio derived transition dipole moments provides a reasonably accurate fit to BIRD kinetic data for small ions.

BIRD can be used to investigate ions of virtually any size; ab initio methods cannot. For this reason, it is useful to model larger ions using semiempirical methods as well. The integrated radiative rate constants for imidazole and its dimer were evaluated using values of μ calculated at both the semiempirical (AM1) and ab initio (RHF/3-21G*) level. The up-pumping rate of the imidazole dimer using ab initio values is 4.4 times higher than that obtained from semiempirical calculations. Thus, the semiempirical derived transition dipoles for this ion can be multiplied by a factor of ~√4.4 = 2.1 in order to obtain integrated radiative rates equal to those from the ab initio calculations.

Due to the larger size of the other dimers, ab initio calculations were done only on the protonated and neutral monomers. The up-pumping rate for the dimer was then approximated by simply taking the sum of the frequencies and their corresponding values of μ. These values are then compared to the up-pumping rate of the dimer calculated at the semiempirical level. For imidazole, the ratio of the up-pumping rate of the sum of protonated and neutral monomer calculated at the ab initio level vs the protonated dimer at the semiempirical level is 2.9. This corresponds to a multiplying factor of 1.7 for semiempirical derived transition dipoles, which is in reasonable agreement with the value of 2.1 calculated explicitly for the dimer. This indicates that it is not an unreasonable approximation to calculate up-pumping rates of larger ions using this procedure. For AcAlaME_d and AcAlaME·IM, this multi-plying factor is 2.2 and 1.9, respectively. These results indicate that the radiative rate constants obtained from semiempirical calculations at the AM1 level are about a factor of 4 lower than those obtained from ab initio calculations.

To account for the large uncertainty in the radiative rate constants, the transition dipoles calculated at the semiempirical AM1 level are multiplied by factors of 1, 2, and 3 in the master equation modeling fitting procedure. This corresponds to a 9-fold change in the integrated radiative rates and should be a reasonable estimate of the errors in these values. By comparison, small changes in the vibrational frequencies used in the model have an extremely small effect on the calculated radiative rates.¹⁴ Thus, the semiempirical frequencies are used directly.

Microcanonical dissociation rate constants are calculated using RRKM theory. Reactant frequencies are obtained from the semiempirically minimized structures. Transition-state frequency sets are constructed from those of the reactant by removing a single frequency (74–250 cm⁻¹) corresponding to a low-energy stretch between monomer units and systematically varying five other frequencies below 500 cm⁻¹ to provide A^∞ values of 10^14.0, 10^15.0, 10^16.2, and 10^17.5 s⁻¹. A single value or at least a narrower range of A^∞ values could be obtained by modeling the transition-state structure or structures explicitly. Accurate transition-state structures would improve the precision of the master equation modeling. However, dissociation of even relatively simple dimers, such as AcAlaME_d, in which several internal hydrogen bonds exist can be complicated to model. The range of A^∞ values used in the master equation model covers a wide range of “loose” transition states expected for dissociation of these proton-bound dimers and circumvents the problem of calculating the transition state explicitly.

Master Equation Model Fitting Procedure.

At the experimental temperatures used, considerable molecular motion in these ion–molecule complexes occurs. Thus, multiple structures may exist. For example, two minimized structures of AcAlaME_d were found to have energies within 0.4 kcal/mol at the semiempirical AM1 level (Figure 3). These structures have slightly different integrated radiative transition rates and frequencies. The range in the parameters calculated for the different structures is significantly smaller than the range that we use as uncertainties in the master equation modeling. Thus, the choice of structure has virtually no effect on the value of E_o obtained from the modeling (vide infra). If the range of transition dipole multiplication factors or the range of A^∞ is reduced, then the choice of structures may be more critical.

Figure 3.

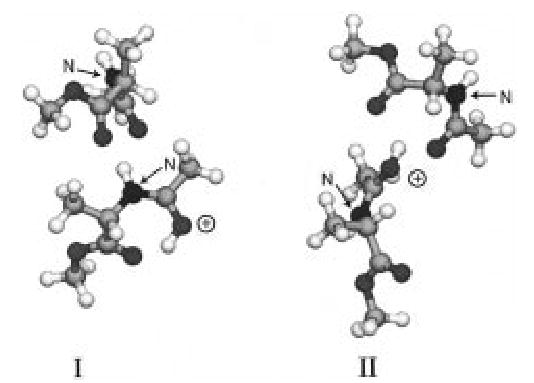
Two structures of AcAlaME_d minimized at the AM1 semiempirical level. Structure I is lower in energy by 0.4 kcal/mol. The N-terminus and protonated amide oxygen of each dimer are labeled.

The general procedure used to fit the experimental data is illustrated in Figure 4 for AcAlaME_d using structure II (Figure 3) which gives the widest range of E_o values. The solid line is the best fit to the experimentally measured values. The dotted and dashed lines are calculations using A^∞ values of 10¹⁴ and 10^17.5 s⁻¹, respectively. Results using values of μ directly from semiempirical force calculations (multiplication factor of 1) are shown in Figure 4a. Absolute dissociation rate constants roughly matching those of the experiment can be obtained with an E_o = 1.00 eV over the entire range of A^∞ values. However, the calculated zero-pressure Arrhenius activation energies are 0.70 and 0.50 eV for A^∞ 10¹⁴ and 10^17.5 s⁻¹, respectively. These values are significantly lower than the measured values and are well outside the experimental error. The Arrhenius activation energy can be reproduced using an E_o = 1.27 eV for A^∞ of 10^17.5 s⁻¹. However, the zero-pressure A factor and magnitude of the rate constants obtained with these parameters are more than 5 times too low. Thus, the experimental data cannot be fit using the values of μ directly from the semiempirical calculations. Similarly, no fits are obtained using a multiplication factor of 2, i.e., integrated radiative rates that are 4 times higher.

Figure 4.

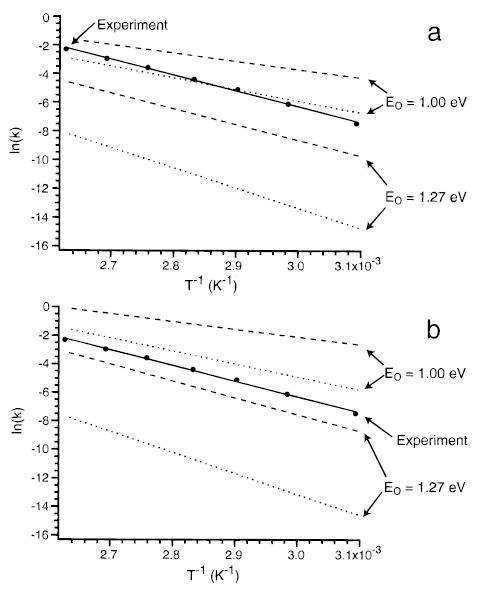
Results from master equation modeling for the proton-bound dimer of n-acetyl-L-alanine methyl ester using E_o’s of 1.00 and 1.27 eV and transition dipole multiplication factors of (a) 1.0 and (b) 3.0. The dotted and dashed lines correspond to master equation dissociation rates calculated with preexponentials (A^∞) of 10¹⁴ and 10^17.5 s⁻¹, respectively. The solid lines are the best fit to the experimental data (●).

Figure 4b shows the results of using integrated transition intensities that are a factor of 9 higher than the semiempirical values (multiplication factor of 3). Dissociation rates similar to those measured experimentally can be obtained using E_o’s between 1.0 and 1.27 within a range of A^∞ values. However, not all these values reproduce the experimentally measured Arrhenius parameters. Using an A^∞ = 10¹⁵–10^17.5 s⁻¹, these data can be fit with an E_o between 1.12 and 1.24 eV. The zero-pressure Arrhenius plots calculated with the minimum and maximum E_o values obtained are shown in Figure 5a. These represent the entire range of E_o’s that fit the experimental data within our criteria. Thus, we report the E_o for this dissociation process as 1.18 ± 0.06 eV. Although calculated dissociation rate constants are lower than experimental ones at both extremes of E_o, sets of parameters within this range can lead to calculated rate constants that are equal to or larger than the measured values. For example, lowering the E_o from the maximum value of 1.24 to 1.21 eV (ΔE_o = 0.03 eV) with an A^∞ of 10^17.5 s⁻¹ leads to a calculated dissociation rate at 380 K that is equal to the measured rate. The uncertainty in the master equation E_o’s not only includes the experimental error but also reflects the 9-fold range of integrated radiative rates and 1000-fold range in A^∞ values used in these calculations. We believe that these should be reasonable estimates of the error in these calculations.

Figure 5.

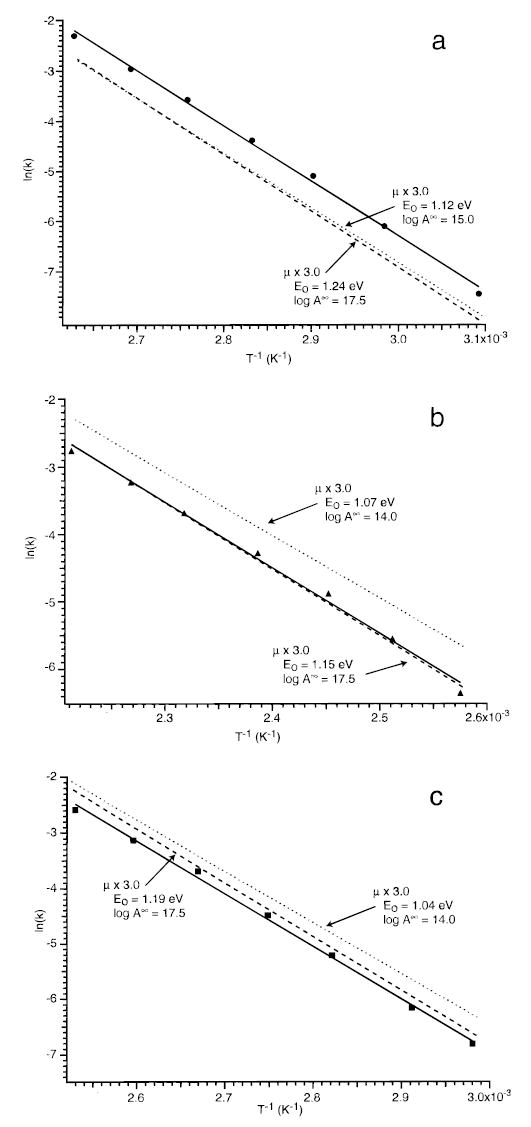
Zero-pressure Arrhenius plots showing limits of E_o calculated using master equation modeling of the experimental data for the proton-bound dimers of (a) n-acetyl-L-alanine methyl ester, (b) imidazole, and (c) their cross dimer. Dotted and dashed lines correspond to the lowest and highest E_o’s which fit the experimental data. The values of the transition dipole multiplication factor and A^∞ used in the modeling are indicated.

Modeling the experimental data using structure I results in a value of E_o = 1.18 ± 0.06 eV, the same result as obtained for structure II. However, to obtain fits with A^∞ = 10¹⁵ s⁻¹, a transition dipole multiplication factor of 3.5 was necessary. Even using a structure in which the amide nitrogen is protonated (7 kcal/mol higher in energy at the semiempirical AM1 level), the E_o obtained is 1.19 ± 0.06 eV. Thus, the choice of structure used in the modeling has virtually no effect on the value of E_o obtained. Hence, finding the lowest energy structure is not critical to this method.

Values of E_o for each of the proton-bound dimers were obtained similarly by using a range of A^∞ and transition dipole multiplication factors. The results are given in Table 2. Figure 5 illustrates the limits of E_o that can reproduce the experimental data.

TABLE 2.

Comparison of Master Equation Derived Threshold Dissociation Energies with HPMS Values

name	trunc Boltzmann Eo (eV)	μa	up-pump rate (eV/s) (350 K)	master eq Eo (eV) fits	master eq Eo (eV)	HPMS ΔHd° (eV)b
AcAlaMEd	1.71	1.0	0.18		1.18 ± 0.06	1.31 ± 0.04 (~500 K)
		2.0
		3.0		1.12–1.24
Imd	1.09	1.0	0.11		1.11 ± 0.04	1.03 ± 0.04 (~480 K)
		2.0		1.13–1.14
		3.0		1.07–1.15
AcAlaME·Im	1.33	1.0	0.16		1.12 ± 0.08	1.20 ± 0.04 (~460 K)
		2.0		1.07–1.19
		3.0		1.04–1.19

^aTransition dipole multiplication factor of AM1 value.

^bValues from refs 19 and 20.

None of the experimental data could be accurately modeled using the integrated radiative rates obtained directly from the semiempirical calculations. Both Im_d and AcAleMe·Im could be modeled by multiplying these values by a factor of 2. Fits for all three dimers could be obtained using a multiplication factor of 3, although the range in A^∞ for AcAlaME_d was limited (vide supra). These results suggest that the semiempirical values of μ are consistently low, a conclusion supported by previous results for other proton-bound dimers.⁹ Even the integrated radiative rates obtained from ab initio calculations appear to be low. These and earlier results⁹ suggest that multiplying the transition dipole moments from semiempirical AM1 calculations by a factor of 2–3 provides reasonable estimates of the integrated radiative rates for these dimers. The extent to which this holds true for other ions is under further investigation.

Effect of Transition-State Frequency Set.

The choice of the frequencies used to produce the transition-state frequency set influences the energy dependence of the microcanonical dissociation rate constants (k_d) and hence influences the values of E_o obtained from the master equation modeling. Transitionstate frequency sets are constructed from the semiempirical reactant frequency sets by removing one frequency corresponding to the reaction coordinate and by lowering five other frequencies to simulate the conversion of vibrational degrees of freedom in the reactant dimer to translational and rotational degrees of freedom in the product monomers. A normal mode corresponding to a low-frequency stretch between monomers was selected as the reaction coordinate. This frequency was between 74 and 225 cm⁻¹ for the three dimers. Five other frequencies below 500 cm⁻¹ were varied to produce the desired rapid energy exchange limit preexponentials that bracket a range of “loose” transition states.

The imidazole monomers have no frequencies below 450 cm⁻¹. The homodimer of imidazole has six frequencies below 170 cm⁻¹ and none between 170 and 450 cm⁻¹. Thus, these six lowest frequencies were varied to produce the transition-state frequency sets.

For AcAlaME_d, many low-frequency modes are present. Due to the potential for multiple transition-state structures involving different hydrogen bonds, we do not model the transition state explicitly but rather vary the transition-state frequencies to produce a range of REX limit preexponentials. However, the choice of frequencies used to produce a given A^∞ can influence the value of E_o obtained from the master equation modeling.

To illustrate this effect, several transition-state frequency sets resulting in the same A^∞ value were constructed for AcAlaME_d (Table 3). Vibrational frequencies below 500 cm⁻¹ are associated with cooperative modes between the monomers. Six of these frequencies were chosen to construct frequency sets I and II. These frequency sets are similar except they have a different frequency eliminated as the reaction coordinate. The magnitude of k_d over all energies is nearly identical for these two frequency sets, and the range of E_o values obtained from the master equation modeling is virtually identical. For set III, five vibrational frequencies at or below 100 cm⁻¹ were varied, and a low stretching frequency at 74 cm⁻¹ was taken as the reaction coordinate. This represents an extreme in the choice of frequency sets. The monomers have nine vibrational frequencies at or below 100 cm⁻¹ while the dimer has 12; i.e., the dimer has only three additional frequencies in this range. A range of E_o’s between 1.13 and 1.27 eV is obtained with this frequency set. Set IV represents the opposite extreme. In this set, a vibration at 2000 cm⁻¹ (a carbonyl stretch) is taken as the reaction coordinate, and five frequencies between 500 and 1500 cm⁻¹ are varied. A range of E_o values between 1.07 and 1.15 eV are obtained from master equation modeling using this frequency set.

TABLE 3.

Effect of Transition-State Frequency Set on Master Equation Derived Threshold Dissociation Energies^a

		changed frequency (cm−1)
set	log A							Eo (eV)
I	15.0	20 (63)	b (74)	30 (100)	60 (174)	80 (225)	90 (449)	1.12–1.23
	17.5	10 (63)	b (74)	10 (100)	20 (174)	20 (225)	20 (449)
II	15.0	25 (63)	35 (74)	50 (100)	60 (174)	b (225)	70 (449)	1.12–1.24
	17.5	10 (63)	10 (74)	10 (100)	20 (174)	b (225)	30 (449)
III	15.0	5 (12)	10 (30)	15 (47)	b (74)	20 (82)	20 (100)	1.13–1.27
	17.5	2 (12)	3 (30)	5 (47)	b (74)	5 (82)	5 (100)
IV	15.0	200 (618)	250 (766)	400 (999)	500 (1202)	200 (1419)	b (2038)	1.07–1.15
	17.5	50 (618)	90 (766)	100 (999)	100 (1202)	100 (1419)	b (2038)

^aValues in parentheses are reactant frequencies that were varied to produce the transition-state frequency set.

^bFrequency removed as reaction coordinate.

These results show that the choice of frequencies used to construct the transition-state frequency set for a given A^∞ does influence the final value of E_o obtained from master equation modeling although this effect is relatively small. In general, the magnitude of this effect will depend on several factors. The influence of these particular transition-state frequency sets on the energy dependence of the k_d is shown in Figure 6 for a dissociation process with an E_o = 1.2 eV and A^∞ = 10^17.5 s⁻¹. Also shown is a Boltzmann distribution for AcAlaME_d at the middle of the experimental temperature range (352 K). The four frequency sets result in k_d’s that are by definition the same at the extremes in energy. However, there is up to a 6000-fold difference in these values over the range of energies for which there is a significant population that has sufficient energy to dissociate (1.2 to ~1.5 eV).

Figure 6.

Microcanonical rate constants for the dissociation of the proton-bound n-acetyl-L-alanine methyl ester calculated by RRKM theory for four different transition-state frequency sets using an E_o of 1.2 eV and A^∞ = 10^17.5 s⁻¹. Frequency sets I and II (overlapping, solid line), III (dashed line), and IV (dotted line) are described in Table 3. Plotted on the same energy scale is a Boltzmann distribution at the middle of the experimental temperature range for dissociation.

The range of E_o’s we report for this dimer is obtained from frequency sets I and II and does not include the extreme frequency sets. Transition-state frequency sets for the mixed dimer were constructed similarly.

Truncated Boltzmann.

Also reported in Table 2 are the values of E_o obtained using the truncated Boltzmann model of Dunbar.^9,15 For imidazole, the value of E_o is nearly the same as that obtained from master equation modeling. For both AcAlaME_d and the cross dimer, the values obtained from the truncated Boltzmann model are larger than those obtained from master equation modeling. The up-pumping rates for these three dimers at 350 K are also given in Table 2. The radiative rates for AcAlaME_d and the cross dimer are significantly larger than for the imidazole dimer. For the truncated Boltzmann model to apply, rates of radiative emission must be significantly smaller than rates of dissociation. For ions such as AcAlaME_d and the cross dimer for which this is not the case, the truncated Boltzmann will overestimate the true value of E_o.

Binding Energies.

To the extent that these dissociation processes do not have reverse activation barriers, the value of E_o we obtain should be equal to the binding energy of the dimers. Values for ΔH_d° have been measured by Meot-Ner for each of these dimers using HPMS.^19,20 Table 2 compares our master equation derived values of E_o with ΔH_d°. These parameters are nearly equal; the difference in these values is estimated in the Appendix. For Im_d and AcAlaME·Im, the values of E_o we obtain are in agreement with values derived from Meot-Ner’s data. HPMS is widely regarded as a highly accurate method for measuring thermochemical values. The agreement indicates that the reverse activation barriers for these dissociation processes are negligible.

For AcAlaME_d, however, the value of E_o we obtain (1.18 eV) is lower than that obtained by Meot-Ner (1.31 eV) and is outside of the experimental error reported by both techniques. With a log A^∞ of 19.8 in the master equation model, a value of E_o equal to the HPMS value is obtained. However, this frequency factor is larger than one would expect for a simple dissociation process. For small neutral molecules that dissociate by very loose transition states, a log A^∞ = 18 represents an upper limit to what has been reliably measured.²⁶ A log A^∞ = 19.8 corresponds to a transition-state entropy (ΔS^‡) of 31.7 cal/(mol K). This value is about the same as the ΔS_d° (31.5 cal/(mol K)) measured by HPMS. The transition state should be more constrained than the products. Thus, ΔS^‡ should be smaller than ΔS_d°. Because the dissociation process of AcA-laME_d may be more complicated than typical for small molecules, we cannot rule out the possibility that log A^∞ may be greater than 18. However, this value must be lower than 19.8. This indicates that Meot-Ner’s value for the binding enthalpy may be too high.

Conclusions

In combination with modeling, blackbody infrared radiative dissociation appears to be a highly reliable method for obtaining binding energies of small molecules and clusters. Measured zero-pressure limit Arrhenius parameters are lower than the “true” values that would be measured if the ion population has a Boltzmann distribution (the rapid energy exchange limit). The threshold dissociation energy can be obtained from BIRD kinetic data using master equation modeling. The accuracy with which this can be done depends both on the uncertainties in the experimental measurements and on the uncertainties in the modeling parameters. For ions that dissociate by “loose” transition states, such as proton-bound dimers or clusters, the greatest uncertainty in the modeling lies in the calculated radiative rate constants which depend strongly on the values of the transition dipole moments used in the calculations. Additional uncertainty exists in the choice of frequencies used to construct the transition-state frequency set. By investigating the dissociation energetics of proton-bound dimers with ΔH_d° values that have been previously measured, the accuracy of the modeling process can be evaluated.

For two of the proton-bound dimers investigated here, the values of E_o determined by modeling of the BIRD data are in agreement with ΔH_d° values measured by Meot-Ner using HPMS.^19,20 This indicates that the BIRD method can provide values of E_o with high accuracy. In fact, despite the wide range of values for the adjustable parameters used in these calculations, the error of this method appears to be only slightly larger than that obtained by HPMS. For the three dimers investigated here, the errors are estimated to be ≤0.08 eV. The major portion of this error is due to uncertainty in the parameters that go into the master equation modeling. Improvements to the calculation of these parameters can greatly improve the precision of this method. The value of E_o we report for AcAlaME_d is significantly lower (by 0.13 eV) than ΔH_d° obtained by HPMS.²⁰

For small to intermediate size ions that are not in the REX limit and for which little or no information about transition-state entropy (A^∞) is known, the ability of this method to obtain an E_o is highly dependent on the accuracy with which the radiative rate constants can be calculated. Results to date suggest that the integrated radiative rate constants calculated at the semiempirical AM1 level are roughly a factor of 4–9 too low. Integrated radiative rates calculated at the RHF/3-21G* level are about a factor of 4 larger than AM1 values but still may be too low to fit BIRD data for all the systems investigated. The extent to which these correction factors can be applied to other ions is currently under investigation. The ability to accurately calculate integrated radiative rate constants would result in a corresponding improvement in the accuracy with which E_o could be obtained for dissociation processes for which no information about the transition-state entropy is known.

Appendix

The enthalpy (ΔH_d°) of the reaction

$${\text{M}}_2{\text{H}}^{+}\to {\text{MH}}^{+}+\text{M}$$

is related to the change in energy (ΔE_d) by eq 1.

$$\mathrm{\Delta }{H}_{\text{d}}{}^{\circ }=\mathrm{\Delta }{E}_{\text{d}}+RT$$ (1)

If there is no reverse activation barrier, ΔE_d at the temperature of the HPMS experiment can be related to E_o by making a temperature correction. With equipartition of energy, E_o is given by eq 2.

$$E_{\text{o}}=\mathrm{\Delta }{H}_{\text{d}}{}^{\circ }-\mathrm{\Delta }{E}_{\text{vib},T}-\mathrm{\Delta }{E}_{\text{rot},T}-\mathrm{\Delta }{E}_{\text{trans},T}-RT$$ (2)

where ΔE_vib,T, ΔE_rot,T, and ΔE_trans,T are the difference in vibrational, rotational, and translational energy between the products and reactants at the temperature of the HPMS experiment (400–520 K). At these temperatures, it is reasonable to treat the translations and rotations classically. Equation 2 then reduces to eq 3.

$$E_{\text{o}}=\mathrm{\Delta }{H}_{\text{d}}{}^{\circ }-\mathrm{\Delta }{E}_{\text{vib},T}-4RT$$ (3)

If the vibrations are not significantly populated, ΔE_vib,T can be approximated using the harmonic oscillator assumption. This correction can then be evaluated using the semiempirical or ab initio frequency sets. With these assumptions, and taking T to be the middle of the HPMS experimental range, E_o − H_d° is less than +0.06 eV. The magnitude of this correction depends primarily on the low-energy (<500 cm⁻¹) frequencies. At the HPMS temperatures, frequencies below ~100 cm⁻¹ are significantly populated. Thus, the harmonic oscillator approximation is not ideal for these frequencies and results in an overestimate of this correction.