Tropical drying trends in global warming models and observations

Abstract

Anthropogenic changes in tropical rainfall are evaluated in a multimodel ensemble of global warming simulations. Major discrepancies on the spatial distribution of these precipitation changes remain in the latest-generation models analyzed here. Despite this uncertainty, we find a number of measures, both global and local, on which reasonable agreement is obtained, notably for the regions of drying trend (negative precipitation anomalies). Models agree on the overall amplitude of the precipitation decreases that occur at the margins of the convective zones, with percent error bars of magnitude similar to those for the tropical warming. Similar agreement is found on a precipitation climate sensitivity defined here and on differential moisture increase inside and outside convection zones, a step in a hypothesized causal path leading to precipitation changes. A measure of local intermodel agreement on significant trends indicates consistent predictions for particular regions. Observed rainfall trends in several data sets show a significant summer drying trend in a main region of intermodel agreement: the Caribbean/Central-American region.

Climate model global warming simulations (1–8) include substantial changes in tropical rainfall. It has been difficult to quantify what precipitation changes should be expected, however, because climate models tend to agree poorly on standard measures of such changes (9, 10).

We evaluate tropical precipitation response in the latest multimodel ensemble of simulations under the Intergovernmental Panel on Climate Change Special Report on Emissions Scenarios A2 scenario (10) for anthropogenic forcings, each continued from a 20th-century radiative forcing run. Here we seek aspects of the simulations on which some level of model agreement can be found. For brevity, we present figures for a single season, choosing June–August (JJA) because of the relationship to an observed trend discussed in Observed Trends for the Caribbean/Central-American Region. Drying (precipitation reduction) trends are highlighted both because of their potential impacts and because some aspects emerge more clearly in the analysis.

A physical hypothesis for two related mechanisms (11, 12) for the tropical precipitation changes provides background for the diagnostics. This hypothesis offers plausible reasons for model sensitivity and for the localization of the dry anomalies and suggests that some features of the spatial pattern of the precipitation change should remain stable with time. The “upped-ante” mechanism (11) for drought tendency hypothesizes a differential moistening between convective and nonconvective regions as warming increases the “ante” of moisture required to sustain convection. Decreases in precipitation occur on the margins of the convection zones in regions of strong low-level inflow into the convection zones, as has been shown to occur in two model studies (12, 13). This mechanism depends on the details of the simulated wind climatology relative to the moisture gradient, and thus the location of the drying is hypothesized to be sensitive among models. A given climatology and relationship between warming and convective moistening, however, may be expected to yield precipitation reduction patterns that grow in place. The “anomalous gross moist stability” or “rich-get-richer” mechanism (12) hypothesizes that the upped-ante differential moisture increase will yield increased precipitation within the convection zones because of enhanced moisture convergence. This mechanism also contributes to drying outside the strong convection zones and likewise should yield an approximately fixed spatial pattern whose amplitude grows in time with the tropospheric warming.

Patterns and Amplitude Measures for Precipitation Changes

Dry Region Spatial Patterns.

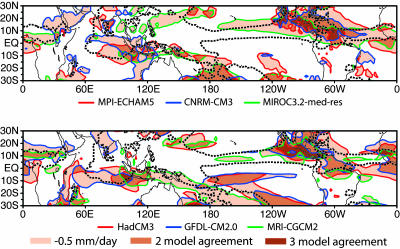
Fig. 1 shows an overlay of the “dry” regions (negative precipitation anomalies) for several models for a 30-year average at the end of the 21st century relative to a 1901–1960 base period for the JJA season. Regional anomalies can be large, exceeding 3 mm day⁻¹ in some cases. Dry anomalies often occur in relatively intense, localized regions at the margins of the convection zones. Weak negative anomalies (not seen at the contour interval shown) also extend more broadly through the climatological descent regions. Very substantial differences in the regional distribution of strong anomalies occur among the models. Some differences in the Southeast Pacific and South Atlantic are attributable to errors in the position of the simulated climatological convergence zones (Figs. 7 and 8, which are published as supporting information on the PNAS web site, provide an assessment of model climatological precipitation and the full spatial pattern of precipitation change for each model). More typically, intermodel differences are in position or extent along a particular convective margin.

Fig. 1.

Examples of dry region precipitation change in the JJA season for 2070–2099 relative to 1901–1960 (mm day⁻¹) from six of the ocean–atmosphere climate models, for the Special Report on Emissions Scenarios A2 global warming scenario. Contour line colors correspond to different models. Model acronyms are given in Methods. Shading denotes precipitation decreases exceeding 0.5 mm day⁻¹, with darker shading where these regions overlap for more than one of the three models shown on each panel. The dashed black contour gives the observed climatological 4 mm day⁻¹ contour, which typifies the shape of the mean convection zones.

Amplitude Growth.

Precipitation anomalies evaluated earlier in the century (2010–2039 and 2040–2069 changes relative to the same 20th-century base period; data not shown) are smaller in amplitude, but most features of the spatial pattern correspond to those in Fig. 1. To provide a measure of amplitude growth, we project each model's precipitation change field onto spatial patterns that are constant in time and are chosen to reflect each model's typical precipitation response for dry and “wet” regions (negative and positive anomalies), respectively. The two spatial patterns for each model are defined by the precipitation change for 2070–2099 (relative to the 1901–1960 base period) in the tropics (lat 23°S to lat 23°N). This pattern is divided into negative and positive anomalies, each normalized by their respective spatial rms. The late-21st-century precipitation change is used to characterize each model's preferred pattern because the anomalies are well established above internal variability by this time. For each model the precipitation change for a sliding 30-year window is then projected onto that model's own wet and dry patterns to give an amplitude (in mm day⁻¹), which is displayed at the 15th year of the window.

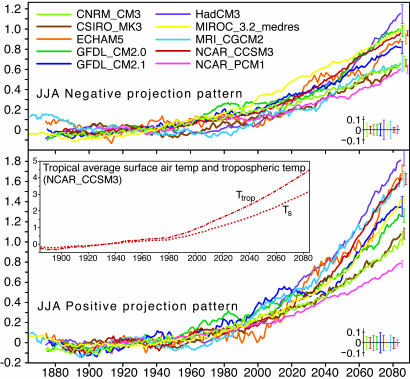
Fig. 2 shows this projected amplitude as a function of time for the JJA season. The growth of both dry and wet anomaly amplitude approximately tracks the warming in tropical surface and tropospheric temperature (Fig. 2 Inset). Time evolution for other seasons (data not shown) is comparable. Although interdecadal variability is substantial in some models, the anthropogenic signal emerges from the internal variability estimated from the control runs early in the 21st century. Note that increasing amplitude for the dry case corresponds to regional decreases in precipitation. This measure, which approaches a spatial rms value in late 21st century, captures the amplitude of spatially varying precipitation anomalies, which are much larger than the tropical mean precipitation change. Magnitudes are on the order of those associated with the interannual El Niño/Southern Oscillation phenomenon, but these anthropogenic changes persist on far longer time scales. Although the models tend to differ in the exact spatial distribution of wet/dry anomalies, the amplitude agreement among models appears to be unprecedented for a regional precipitation-related quantity.

Fig. 2.

Amplitude of dry and wet precipitation changes (30-year running mean, relative to 1901–1960) for JJA from 10 ocean–atmosphere climate models for the Special Report on Emissions Scenarios A2 global warming scenario. The anomaly at each year is projected onto the normalized spatial pattern of late-21st-century (2070–2099 average) negative and positive precipitation change, respectively. Units are mm day⁻¹. The error bars on the model lines, repeated at bottom right, are ±1 standard deviation values of the same projection quantity evaluated for internal variability in the control runs for each model. Inset shows the increase of tropical average surface air temperature, ΔT_s, and vertical average tropospheric temperature (275–900 hPa), ΔT_trop, for a single model that has late-21st-century warming close to the multimodel ensemble mean.

Per-T Climate Sensitivity.

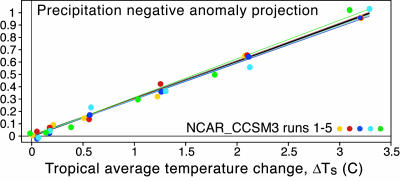
As a prelude to quantifying this intermodel agreement, we first present the relationship of the precipitation anomaly to the tropical mean temperature. This relationship is quantified in Fig. 3 for the dry region projection for a model that has an ensemble of five runs available. Although in general precipitation behavior need not be linear (for instance if a particular region were reduced to zero precipitation) for average quantities and these amplitudes, the precipitation change amplitude grows approximately linearly with temperature. This behavior also holds for the wet region projection and for moisture increases (data not shown). We thus define a per-T climate sensitivity, i.e., change per tropical-average surface air temperature change, applied in Fig. 4 to several quantities relevant to changes in the hydrological cycle. The per-T sensitivity is useful in relating these changes to a widely studied quantity ΔT_s and in taking into account that amplitude increases with temperature within each model. However, the main purpose of using per-T sensitivity here is to clarify that scatter in precipitation among models is not primarily due to temperature, because the leading temperature dependence for each model is approximately removed. For instance, the model that is an outlier with small temperature increase in Fig. 4a lies within the range of the other models in terms of precipitation impact per unit warming in Fig. 4c.

Fig. 3.

Precipitation anomaly dry region projection (as in Fig. 2), ΔPrecip_dry, as a function of tropical average temperature for NCAR-CCSM3 for JJA. Colors denote different ensemble runs. The slope of the heavy line shown gives the per-T climate sensitivity for ΔPrecip_dry (lines for fits to individual ensemble members are also shown). Values are for 30-year averages centered on 1934, 1964, 1994, 2024, 2054, and 2084 (10 years earlier for NCAR-CCSM3 ensemble member 5 because of missing data at the end).

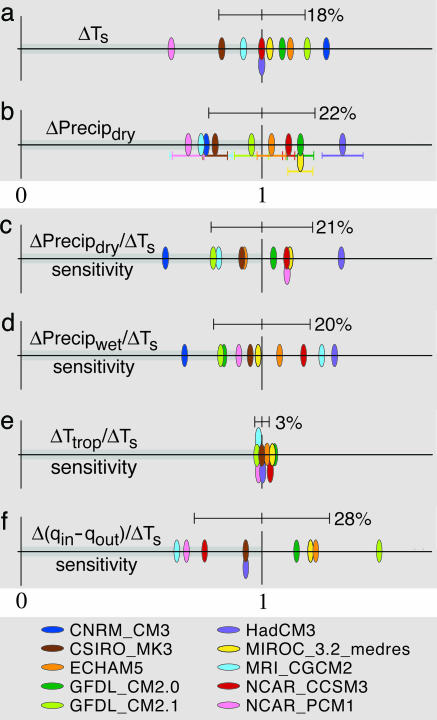
Fig. 4.

Late-21st-century changes (2070–2099 minus 1901–1960) and per-T climate sensitivities for tropical precipitation, temperature, and moisture in JJA. Each variable is normalized by the mean of the multimodel ensemble so that the intermodel range relative to the multimodel mean (the interval 0–1, highlighted in gray) may be compared across climate variables. Multimodel ensemble standard deviations are shown as error bars, with values as a percent of the multimodel mean marked. All axes are nondimensional. (a) Tropical average (lat 23°S to 23°N) surface air temperature, ΔT_s. (b) rms negative precipitation change, ΔPrecip_dry (with error bars as in Fig. 2). In c and d, variables are given as per-T climate sensitivities, defined as change per unit increase in tropical average surface air temperature, ΔT_s. (c) ΔPrecip_dry per ΔT_s. (d) rms positive precipitation change, ΔPrecip_wet per ΔT_s. (e) Tropospheric temperature increase (275- to 900-hPa vertical average above the surface boundary layer), ΔT_trop per ΔT_s. (f) Differential tropospheric moisture increase inside convection zones minus increase outside Δ(q_in − q_out) per ΔT_s. Colors denote model.

Model Agreement in Global Tropics Measures.

Fig. 4 quantifies the degree of intermodel agreement for the amplitude of late-21st-century precipitation changes as measured by the dry and wet region projections, i.e., for spatial rms measures across the tropics. This analysis is motivated by the hypothesis that the model regional responses have underlying similarities even if the spatial distribution differs. The scatter among models for the negative region precipitation change (Fig. 4b) is only slightly larger, relative to the multimodel ensemble mean, than the range for tropical-average surface temperature (Fig. 4a), the intermodel standard deviations being 22% and 18% of the multimodel mean, respectively. When the precipitation change is expressed as a precipitation climate sensitivity per unit surface temperature change (Fig. 4c), the intermodel standard deviation for negative region amplitude drops only slightly, to 21% of the mean, suggesting that the scatter is not primarily due to differences in warming. The per-T precipitation-increase sensitivity (Fig. 4d) has roughly comparable intermodel standard deviation. Overall, the amplitude of the precipitation anomalies exhibits a level of agreement in the multimodel ensemble that, while clearly leaving room for improvement, is roughly comparable to intermodel agreement on the warming itself. Considering that these amplitudes measure regional precipitation changes, on which poor intermodel agreement has been found, the agreement on this measure is fairly remarkable. It may be interpreted as indicating that the potential for regional drying should be taken seriously.

Fig. 4 also shows two variables potentially associated with the causal chain contributing to precipitation changes. The free tropospheric temperature climate sensitivity has particularly low scatter (14) (Fig. 4e). A measure of the moisture gradient increase between regions inside and outside of strong convective zones (Fig. 4f) shows that the models all produce this key step in the hypothesized mechanisms discussed in the Introduction. Reasonable agreement on the differential moisture increase within convection zones is no doubt a factor in why the models would agree on precipitation change amplitude even while exhibiting differences in regional distribution. However, the per-T sensitivity for the differential moisture increase has larger intermodel scatter than that for tropospheric temperature, suggesting that intermodel differences begin already at the step of establishing increased free tropospheric moisture in convective regions.

Local Trend and a Measure of Local Model Agreement

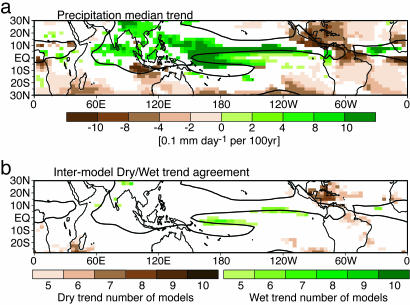
A typical spatial distribution is seen in Fig. 5a, which shows the precipitation trend of the multimodel ensemble median (see Methods for details). Substantial drying trends occur in particular locations along the convective margins, for which the 4 mm day⁻¹ contour of the median climatology serves as a rough indicator. Among these are drying regions in Central America, the Caribbean, equatorial South America, and along the Atlantic intertropical convergence zone. Precipitation increases tend to occur inside the convection zones, including increases in the Southeast Asian summer monsoon. Increased precipitation also occurs in the equatorial Pacific, associated with changes in the dynamics of the equatorial cold tongue and local sea-surface temperature increase (15–18). The drying trends tend to be larger as a fraction of the climatological rainfall: trends in much of the wet region are <20% of median climatology per 100 yr, whereas the dry region trends noted above often exceed 30% per 100 yr. Although the amplitudes of these trends are sufficient to raise concern, we wish to ask a more stringent question: are there precipitation trends on which the models agree at the point-by-point level?

Fig. 5.

Multimodel local precipitation trend measures. (a) Precipitation trend for JJA of the multimodel ensemble median from 1979 to 2099. Shading indicates >99% significance by the Spearman-rho test. The black line gives the 4 mm day⁻¹ contour from the median climatology (1900–1999 average) of the models to indicate a typical boundary of the convection zones. (b) Model agreement on the predicted local precipitation trend from 1979 to 2099 for JJA. The number of models at each location that agree on a dry trend or a wet trend exceeding 99% significance and exceeding a minimum amplitude change (20% of the median climatology per century) is given by the brown or green color bars, respectively. Only regions with five or more of the 10 models agreeing are shaded.

Intermodel scatter tends to be high at the local level, so we used the following measure: at each point count the number of models (fraction of the multimodel ensemble) that have a trend of the same sign and amplitude sufficiently large to (i) pass a given significance level and (ii) exceed a minimum percent change (here 20%) per century of climatological seasonal rainfall. Fig. 5b shows this measure of local intermodel agreement for both dry and wet trends. Majority agreement on precipitation increases occurs in a very restricted subset of the areas with significant median trend within the equatorial Pacific and certain parts of the Indian/Southeast-Asian monsoon. Drying trends fare slightly better in terms of the area over which majority model agreement occurs, although some areas exhibiting agreement in the subtropical winter hemisphere have small trend amplitudes. The largest area of high intermodel agreement occurs for a drying trend in the Caribbean/Central-American region. The model median amplitude of this trend is between 0.5 and 1 mm day⁻¹ per 100 yr over most of the region, exceeding this at some locations. This amplitude is substantial because this region sits at the margin of the strong convection zones, with ≈2 mm day⁻¹ rainfall in this season in the current climate. The individual model reduction in rainfall averaged over the region (long 90–60°W, lat 13–25°N) for a 30-year average at the end of the century (relative to 1901–1960 average) ranges up to 54% with a median of 25%. Locally the percent reduction can be higher for particular models.

Observed Trends for the Caribbean/Central-American Region

We now consider evaluation of precipitation trends in observations, which face several challenges. Full spatial coverage by means of satellite retrievals is available only since 1979. Land station rain gauge data has longer temporal records in some locations but limited tropical spatial coverage. Projection methods such as are used in Fig. 2 hold future promise, especially as the satellite record lengthens, but require an estimate of spatial pattern, on which models currently agree poorly. Finally, for estimation of local trends the models are far from agreement on when detection of statistically significant trends should be expected. Even in regions where high model agreement is obtained in late 21st century when the signal is large, agreement by measures that require point-by-point statistical significance degrades for earlier times (Fig. 9, which is published as supporting information on the PNAS web site, provides an example). Part of this scatter is due to internal variability. For example, for the National Center for Atmospheric Research Community Climate System Model, version 3 (NCAR-CCSM3), the earliest model to achieve statistical significance in the Caribbean/Central-American region, area average (long 92–58°W, lat 11–23°N) rainfall trends starting from 1979 pass the 95% significance level of a Spearman-rho test (19) at different years for the five runs, ranging from 1994 to 2029. For trends evaluated starting from 1950, all NCAR-CCSM3 runs pass this criterion by 2004. However, to reach model agreement takes longer: five models pass this criterion before 2044, and seven pass by 2054.

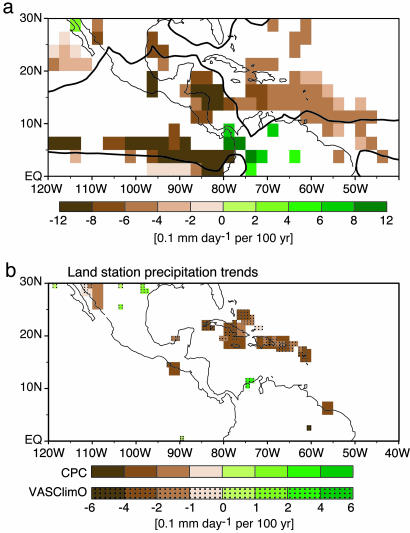
With these caveats in mind, examination of four observational rainfall data sets yields a significant drying trend in the Caribbean/Central-American region. A satellite estimate and two land-only station data sets are shown in Fig. 6 over their periods of availability, since 1979 and since about 1950, respectively, with a Spearman-rho test applied at each grid point. The coarser-resolution Hulme land rainfall data (20) give similar results (data not shown). The station-based local negative trends fall in the range of 5–30% of the mean rainfall per 100 yr; the shorter satellite-based trend is somewhat larger.

Fig. 6.

Precipitation trend from observed estimates for JJA. (a) Climate Prediction Center Merged Analysis of Precipitation satellite-only product for 1979–2003. The 4 mm day⁻¹ contour from the climatological average over this period is shown in black for reference. (b) Gridded station data (partial land and island coverage only) from two data sets: Climate Prediction Center (34) (CPC; 2.5° resolution, 1950–2002) and Variability Analyses of Surface Climate Observations (33) (VASClimO; overlaid at 1° resolution, 1951–2000). Shading indicates regions exceeding the 95% significance level by the Spearman-rho rank-based test. Note that the color bar in a is at double the interval of that in b.

In the absence of observed time series to characterize regional interdecadal variability, we present a multimodel ensemble probability distribution of 50-year trends from the control runs (Fig. 10, which is published as supporting information on the PNAS web site). Because of the difficulty of validating the model interdecadal precipitation variability, the comparison of the observed trend to this distribution shows only that 50-year trends of the observed magnitude in the region are not common in the models. One cannot at this time exclude the possibility that the observed trend is due to natural interdecadal variability; standards of attribution for temperature trends (21) are not yet met. Observed sea-surface temperature trends in this region are estimated to be small or positive (22, 23), which would favor increased rainfall, so any impact from oceanic interdecadal variability would have to come via a remote pathway. Possible natural variability linkages include El Niño/Southern Oscillation and the North Atlantic Oscillation (24).

Observed rainfall trends have been noted in other regions (25–27), but we do not in the present models find strong intermodel agreement on global warming-related trends for these regions. The drying trend in sub-Saharan Africa observed over past decades has been noted to continue in future in some models (28, 29) but exhibits poor agreement in the ensemble considered here. A region of drying in southern Africa and surrounding oceans exhibits reasonable intermodel agreement by our measures but should be treated with caution because most models overestimate precipitation in the related Southern Hemisphere mid-latitude storm tracks (see Fig. 7 for details). We do note a region of strong model agreement on drying in the eastern subtropical South Pacific in southern spring and summer that has a corresponding negative trend in satellite observations (data not shown). However, we have not found consistent supporting evidence in station data from islands in that region. The Caribbean/Central-American region trend, colocated with the region of largest local intermodel agreement and predicting substantial percent rainfall reduction, thus stands out as demanding attention and may provide a prototype for other regions that are as yet undetectable.

Summary

Understanding, detection, and attribution of precipitation changes under global warming lags by at least a decade behind the corresponding problem for temperature, especially in the tropics. While recognizing considerable model differences that challenge climate modelers, the results here extract sufficient agreement to consider the following changes likely: tropical precipitation decreases in certain areas along the margins of the convection zones and increases within the convection zones, with amplitude increasing with warming. The drying trends outside the convection zones are likely to be concentrated in particular regions, among which the Caribbean/Central-American region is a leading candidate.

A trend is shown in observed station and satellite data in this region, although attribution of this trend to anthropogenic effects should as yet be regarded as plausible but uncertain.

Methods

The model ensemble was chosen based on completeness of data availability (including three-dimensional fields) at the Program for Climate Model Diagnosis and Intercomparison archive and a model grid size that is smaller than 4° by 3°, because phenomena at convective margins are being considered. The models included are as follows: Centre National de Recherches Météorologiques Coupled Global Climate Model, version 3 (CNRM-CM3); Commonwealth Scientific and Industrial Research Organization (Australia) climate system model, version 3 (CSIRO-MK3); Max Planck Institute for Meteorology fifth-generation atmospheric general circulation model (ECHAM5); Geophysical Fluid Dynamics Laboratory, National Oceanic and Atmospheric Administration, global coupled climate model, versions 2.0 and 2.1 (GFDL-CM2.0 and GFDL-CM2.1); Hadley Centre coupled model, version 3 (HadCM3); Center for Climate System Research, University of Tokyo, Model for Interdisciplinary Research on Climate, version 3.2, medium resolution (MIROC-3.2-medres); Meteorological Research Institute, Japan, coupled global climate model, version 2.3.2a (MRI-CGCM2); NCAR-CCSM3; and National Center for Atmospheric Research Parallel Climate Model, version 1 (NCAR-PCM1). Although GFDL-CM2.0 and GFDL-CM2.1 differ primarily in the dynamic core, their precipitation response is very different (Fig. 7), and so they are treated here as different models. The Canadian Climate Centre model (CCCma) was evaluated and has consistent results but was excluded from the multimodel ensemble here because of a nonnegligible trend affecting JJA tropical precipitation (0.15 mm day⁻¹ century⁻¹ in the ΔPrecip_dry projection) in its 500-year control run, presumably because of imperfect equilibration of the spin-up run.

In Fig. 1, the observed climatology contour is from the Climate Prediction Center Merged Analysis of Precipitation data set. In Fig. 2, the projection procedure is simpler than the one known as optimal “fingerprinting” (30) but closely related in that a distinctive pattern of the anthropogenic impact is being defined. The main difference in the application here is that different patterns are used for each model to focus on amplitude, given the differences in spatial distribution among models. Difficulties using standard fingerprinting in face of model disagreement were shown in ref. 31. The standard deviations from the control runs shown as error bars in Fig. 2 are evaluated by taking the same spatial pattern for the projection (i.e., from the 2070–2099 change) and projecting on the control run precipitation differences from an ensemble of all possible 30-year means minus nonoverlapping 60-year means. Control runs all exceed 340 years (500 years for most models). The curves in Fig. 2 are for a single realization for each model for consistency among models (because most models did not have an ensemble available). Evaluation of other ensemble members where available yields similar results, consistent with the error bars evaluated from the control. Projections similar to the wet and dry patterns in Fig. 2 but using the full late-21st-century precipitation change pattern (not divided into wet and dry regions) yield similar curves that lie between those for the wet and dry region amplitudes for each model.

The per-T climate sensitivity illustrated in Fig. 3 can be estimated either as a linear fit (through zero) or simply from ratio in the late-century signal (when this sufficiently exceeds the internal variability). The latter is used here for simplicity. Although tropospheric temperature is more relevant to the hypothesized physical pathway, we use values per tropical average surface air temperature change because it is a more widely known indicator of global warming and the two are closely linked in the models (Fig. 4e). This sensitivity measure follows methods standard for climate feedback parameter estimates (10) but applied here to impacts of the warming rather than to feedbacks onto it.

In Fig. 4, the multimodel ensemble mean values by which the axes are normalized are as follows: 3.2 K for ΔT_s, 0.84 mm day⁻¹ for ΔPrecip_dry, 0.26 mm day⁻¹ K⁻¹ for ΔPrecip_dry/ΔT_s, 0.43 mm day⁻¹ K⁻¹ for ΔPrecip_wet/ΔT_s, 1.4 K/K for ΔT_trop/ΔT_s, and 0.37 mm K⁻¹ for Δ(q_in − q_out)/ΔT_s. In Fig. 4f, the differential moisture increase Δ(q_in − q_out) is estimated as an average moisture increase in the 900- to 650-hPa layer for tropical regions with climatological precipitation >4 mm day⁻¹ minus the average over those with smaller precipitation. Although this is a crude estimator of local gradients, it clearly shows a substantially larger moisture increase within strongly convecting regions.

In Figs. 5 and 6, the trend is computed for each grid point for the given season. Rank regression is used for temporal trend computation; i.e., the sum of squares minimized in the standard regression computation is replaced by a product of the usual variable times its value in centered rank space. This is a more robust estimator for non-Gaussian variables such as precipitation (32). In Fig. 5, the model data are first averaged to a common 3.75° by 2.5° grid (that of the coarsest-resolution model, HadCM3). For Fig. 5a, a model median is computed for the seasonal precipitation values at every grid point and year. This procedure creates a positive definite time series for each grid point that characterizes median properties of the models and on which the same operations can be done as on any other precipitation time series, including the computation of the climatology and long-term trend shown in the figure. For Fig. 5b, the trend over 1950–2099, its Spearman-rho statistic, and the climatology are computed separately for each model. Because we are requiring primarily agreement on sign, we wish to exclude counts of trends with questionable sign or low potential consequence, and so we count only the number of models at each grid point that pass the confidence and fractional change criteria stated in the text. In Fig. 6, the gridded station data sets include some of the same stations. The VASClimO project included a large effort to gather additional stations, and aggregation of station data is by Kriging interpolation to minimize risk of temporal inhomogeneities due to varying station densities (33). The Climate Prediction Center Merged Analysis of Precipitation satellite precipitation estimate that does not include land stations is chosen for independence in Fig. 6.

Abbreviations

JJA

June–August

NCAR-CCSM3

National Center for Atmospheric Research Community Climate System Model, version 3.