Modeling lung cancer risk in case-control studies using a new dose metric of smoking

Abstract

Many approaches have been taken to adjust for smoking in modeling cancer risk. In case-control studies, these metrics are often used arbitrarily rather than being based on the properties of the metric in the context of the study. Depending on the underlying study design, hypotheses and base population, different metrics may be deemed most appropriate. We present our approach to evaluating different smoking metrics. We examine the properties of a new metric, “logcig-years”, that we initially derived from utilizing a biological model of DNA adduct formation. We compare this metric to three other smoking metrics, namely pack-years, square-root pack-years, and a model in which smoking duration and intensity are separate variables. Our comparisons use generalized additive models and logistic regression to examine the relationship between the logit probability of cancer and each of the metrics, while adjusting for other covariates. All models were fit using data from a lung cancer study of 1275 cases and 1269 controls that has focused on gene-smoking relationships. There was a very significant, linear relationship between logcig-years and the logit probability of lung cancer in this sample, without any need to adjust for smoking status. These properties together were not shared by the other metrics. In this sample, logcig-years captured more information about smoking that is important in lung cancer risk than the other metrics. In conclusion, we provide a general framework for evaluating different smoking metrics in studies where smoking is a critical variable.

Introduction

The nature of the relationship between smoking and lung cancer as estimated from a statistical model depends in large part on how “smoking” itself is coded. Coding methods include using indicator variables to differentiate between current, former, and never smokers, using pack-year categories, or using a continuous variable such as pack-years itself or its constituent factors.

Models that use categories assume that, conditional on other model covariates, the risk of lung cancer within a category is constant. Categorizing a continuous variable does not make full use of all the available data [1] and the choice of cutpoints between categories may influence the estimated smoking-lung cancer risk relationship [2]. Furthermore, if the underlying variable used to define the categories is measured with error, then the categorization may create nondifferential measurement error, since a value close to the cutpoint is more likely to be misclassified than a value in the mid-range of the category [3].

Continuous smoking metrics used in the literature include pack-years, the square-root of pack-years [4, 5, 6, 7], or including smoking duration and intensity as separate variables [8, 9, 10]. Previous papers have found non-linear relationships between pack-years and lung cancer [11, 12]. In our own lung cancer case-control sample, an approximately linear relationship between square-root pack-years and lung cancer risk was found, but indicator variables to distinguish between current, former, and never smokers were necessary for improved model performance [4]. The multistage model of carcinogenesis [13, 14, 15] has motivated several authors to separate smoking duration and intensity in modeling lung cancer risk. However, when never smokers are included in the model, relative risks associated with duration for a fixed intensity and vice versa are difficult to interpret [16], because duration and intensity are always zero for never smokers. Other continuous variables that may be important include age of smoking initiation and years since smoking cessation; however these variables, together with smoking duration, are highly collinear with age, another variable commonly included in cancer risk models.

In addition to these issues, some studies appropriately limit their populations to current smokers [8], ever-smokers [17] or use separate models for current and former smokers [10]. Such analyses require defining cutpoints in smoking duration, timing and/or intensity to define these samples. Not only do the choice of cutpoints determine which subjects are excluded, but studies differ in their choice of cutpoints, which can ultimately affect results [12].

In many circumstances, different smoking metrics may provide reasonably similar results such that the choice of metric is not critical. However, when smoking becomes integral to the study hypothesis, such as is the case with gene-smoking analyses [4, 5, 6, 7, 10, 18, 19, 20], it may be important to compare how different metrics perform within the study population. The primary aim of this paper is to provide a general approach for evaluating the performance of different metrics through the use of a concrete example of how this approach can be applied in a specific study.

Our comparison includes a new metric which we call “logcig-years”, which we define to be log(cigarettes smoked per day + 1) × years of smoking. We compare the performance of four different metrics using data from a large lung cancer case-control study, and also explore how the performance of these metrics compare to results from Doll and Peto’s model of smoking and cancer [14]. Throughout this paper we use “log” to mean the natural logarithm. We define cigpday as cigarettes smoked per day, logcigp as log(cigpday + 1), cigtime as years of smoking, yrsquit as years since smoking cessation, and agestart as age of smoking initiation.

Methods

Study population

The data used in this analysis was derived from a case-control study approved by the Human Subjects Committees of Harvard School of Public Health and Massachusetts General Hospital. Details of the study design have been described previously [11]. Briefly, the sample consists of histologically confirmed, newly diagnosed lung cancer patients presenting at Massachusetts General Hospital between December 1992 and September 2000. Controls were friends or nonblood-related family members of the cases, and were not specifically matched to cases. When the above potential controls were not available, controls were recruited from friends or family members of non-lung cancer patients.

As we have previously, in this paper we included data from all Caucasians with complete data on age, gender, smoking status, cigpday and cigtime (for ever smokers), and yrsquit (for former smokers).

Motivation of the logcig-years metric

The logcig-years metric was derived in part from a model relating smoking to DNA adducts. The formation of DNA adducts from polycyclic aromatic hydrocarbons (PAHs, such as benzo[a]pyrene) in tobacco smoke is widely believed to be on the causal pathway from smoking to lung cancer [21, 22, 23, 24]. Given certain assumptions, it follows from the solution to a set of differential equations relating adducts to smoking that the logarithm of the number of DNA adducts can be modeled as an additive function of the logarithm of smoking intensity. The logarithmic transformation of adduct numbers, while not universal, is fairly standard both in models relating smoking and adducts [25, 26] and in models relating adducts to lung cancer risk [27]. Since adduct formation is believed to be on the causal pathway to lung cancer, one could model the probability of cancer initiation as a function of the number of adducts, on some scale. If the logarithmic transformation of smoking intensity is useful for a model of the logarithm of DNA adducts, and if the cumulative log(adduct) burden is directly related to cancer risk, this suggests that cumulative log(smoking intensity) may be a useful smoking metric. Pack-years, which is cumulative smoking intensity on the untransformed scale, is widely used but does not necessarily represent the best way to combine smoking intensity and duration into a single cumulative metric. The logcig-years metric is one alternative to pack-years, and is also a cumulative smoking metric.

Like other simple smoking metrics, the logcig-years metric does not take into account all of the many steps that occur between cancer initiation and tumor detection. These steps may depend on factors such as the age at which an individual started smoking and the age at which the individual stopped smoking (if ever). In this paper we do not attempt to model the process of carcinogenesis or to better understand the true complexity of how smoking leads to cancer development. For this we refer the interested reader to papers on the multistage model of carcinogenesis [13, 14, 15] and related papers [28, 29, 30, 31, 32]. Instead, our goal in this paper is simply to compare the performance of the logcig-year metric with more standard smoking metrics.

Statistical analyses

We examined the relationship between the logit probability of cancer and each of four continuous smoking metrics separately, using first generalized additive models (GAM) [33], and then logistic regression. The smoking metrics we considered were pack-years, square-root pack-years, logcig-years, and the “two metrics” model in which smoking duration and intensity were separate metrics in the same model. In the “two metrics” model, we used cigtime as the duration variable, and logcigp as the intensity variable. This transformation of smoking intensity was chosen in part because of the nonlinearity between the logit probability of lung cancer and the untransformed smoking intensity observed here (not shown) and in a previous paper using data from this study [10]. This nonlinearity has also been noted by Rachet et al [9], who used GAM to develop models relating smoking to lung cancer risk in a case control study, using duration of smoking and smoking intensity as separate variables.

GAM is a powerful statistical tool that extends the generalized linear models framework to allow the shape of the relationship between the outcome and each continuous variable to be an arbitrary smooth function with the shape determined by the data. GAM was used to examine the nature of the relationship between cancer risk and each smoking metric separately, in a model that adjusted for age, years since quitting smoking (defined here and in other papers [4, 5, 6, 7] to be zero for never smokers), smoking status (as two indicator variables to distinguish between never, former, and current smokers), and gender. Each continuous variable was allowed to have a possibly non-linear effect on cancer risk. Specifically, the GAM models we fit to ever and never smokers together are of the form

$$\text{logit }P\text{(cancer) }={\beta }_{\text{0}}+s\text{(}smokingmetric\text{)}+s\text{(}age\text{)}+s\text{(}yrsquit\text{) }+{\beta }_{1}former+{\beta }_{2}current+{\beta }_{3}gender,$$

where smoking metric is one of the four smoking metrics mentioned above, and former, current, and gender are indicator variables for former smokers, current smokers, and female, respectively. The notation “s(.)” indicates a smooth term that we fit using a smoothing spline with 4 degrees of freedom. In the “two metrics” model, s(smoking metric) was replaced by s(cigtime) + s(logcigp).

We also used GAM to examine similar adjusted relationships among smokers only. In the smokers-only model, we can potentially adjust for age of smoking initiation, a variable that is meaningless for never smokers. However due to the collinearity between this variable, years of smoking, age, and years since smoking cessation, it is not possible to adjust for all these variables in the “two metrics” model. Instead, in all smokers-only models we categorized age of smoking initiation and included an indicator variable for whether or not the smoker started smoking prior to age 18. The value of 18 was chosen to represent the approximate age at which lung development is nearing completion. In the smokers-only models we did not include the current smoking indicator since the former smoker indicator was sufficient to distinguish between current and former smokers.

All GAM models were fit using the S-plus software [34, 35]. In addition to examining the GAM plots, we tested for nonlinearity between the outcome and each continuous variable using the approximate chi-squared test for the nonlinear contribution of the non-parametric terms [36], supplied by S-plus.

Any smoking metric that did not have a significant departure from a linear relationship with the logit probability of cancer in the adjusted model was then considered further in logistic regression models, also fit in S-Plus. Any covariate other than the smoking metric that had a nonlinear relationship with cancer risk was transformed such that the relationship using the transformed variable was approximately linear. The transformed covariate was then used in the logistic regression models. Two logistic regression models were fit using these smoking metrics. In the first logistic regression model (the “full model”), in addition to adjusting for the covariates as described above, we also included an interaction term between smoking status and the smoking metric, to allow the slope relating the smoking metric and cancer risk to differ for current versus former smokers. For the “two metrics” model, this meant we included a pair of interaction terms, one for smoking intensity and one for duration. The second logistic regression model (the “all covariates” model) included all covariates described, but did not include the interaction term(s). The necessity of considering these interactions is motivated by our earlier work [4, 6].

Results

Baseline characteristics

After excluding non-Caucasians and individuals missing key model covariates, the resulting sample contained 2544 observations: 1275 lung cancer cases and 1269 controls. Among the cases, there were 85 never smokers, 675 former smokers, and 515 current smokers, whereas among the controls there were 445 never smokers, 578 former smokers, and 246 current smokers. Never smokers were defined to have smoked fewer than 100 cigarettes in their lifetime, and former smokers were defined to have quit smoking one or more years ago. The 1190 ever-smoking cases tended to be heavier smokers than the 824 ever-smoking controls, with mean (standard deviation) pack-years of 59.8 (36.8) and 31.8 (27.2) respectively.

Results from assessing linearity between the smoking metrics and risk, using GAM

In our sample, the adjusted relationship between pack-years and the logit probability of cancer was significantly non-linear (p < .001 for the nonlinear contribution) both in a model fit using all individuals (i.e. both ever and never smokers, Figure 1), and in a model fit using only smokers. This indicates that in our sample, pack-years is not appropriate to use as a continuous variable in logistic regression models. In separate models, square-root pack-years and logcig-years were linearly related to the logit probability of cancer, after adjusting for other model covariates (p > .10 for the nonlinear contribution), when all individuals were included (Figure 1), and when only ever smokers were included. The corresponding plots for the smokers-only models were very similar (not shown).

Figure 1.

The contribution of each smoking metric (x-axis, labeled on plot heading) to the logit probability of lung cancer (y-axis) among all individuals, from a generalized additive model adjusting for age (as a smooth function), gender, smoking status (as two indicator variables), and years since smoking cessation (as a smooth function). Each plot in the upper row is fit from a separate model, while the two plots on the lower row are fit in a single model. Dashed lines give pointwise approximate 95% confidence intervals for the fitted curve.

In the “two metrics” model, the adjusted relationships between the logit probability of cancer and both logcigp and cigtime in a model fit using all individuals were approximately linear (see bottom plots in Figure 1). In the model fit using smokers only, there was weak evidence of nonlinearity between the logit probability of cancer and logcigp (p ≈ .07 for the contribution of the non-linear terms).

In all models just described, the adjusted relationship between the logit probability of cancer and years since quitting smoking was approximately linear. However in our sample the adjusted relationship between the logit probability of cancer and age was significantly non-linear in all models (p < .001). The corresponding GAM plots indicated that the relationship with age was approximately linear up to about age 70, and approximately linear thereafter, but with a change in slope at about age 70 (see Figure 2). This observed age effect is partly due to the difference in age distribution among cases and controls in this sample.

Figure 2.

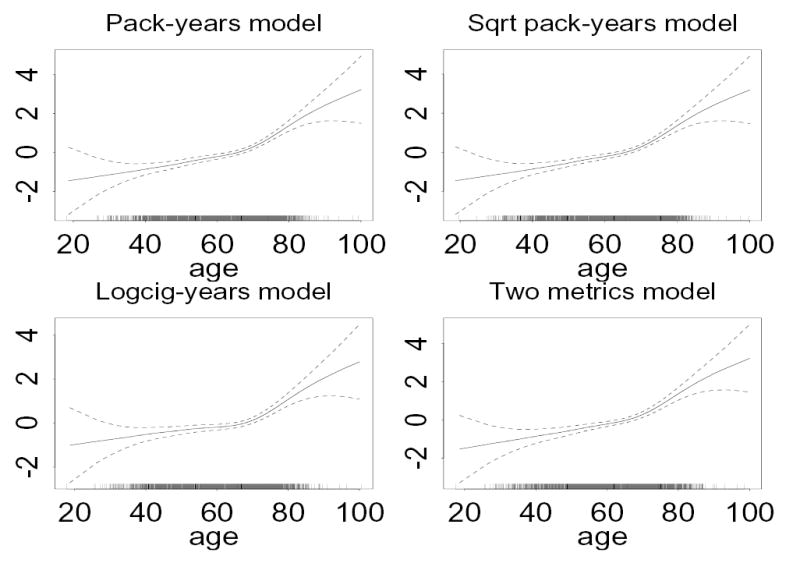
The contribution of age (x-axis) to the logit probability of lung cancer (y-axis) among all individuals, from generalized additive models adjusting for the metric indicated in the heading (as a smooth function), gender, smoking status (as two indicator variables), and years since smoking cessation (as a smooth function). Each plot is fit from a separate model. Dashed lines give pointwise approximate 95% confidence intervals for the fitted curve.

Results from modeling smoking and lung cancer risk, using logistic regression

For the logistic regression models we focus on three metrics that are linearly related to the logit probability of cancer: square-root pack-years, logcig-years, and the “two metrics” model. In the models using square-root pack-years and logcig-years, these smoking metrics were very significant predictors of cancer risk (p < .001). In the “two metrics” model, logcigp was a very significant predictor (p < .001), but cigtime was a significant predictor only in the model using all individuals (p < .01).

Due to the nonlinearity associated with the age effect, in all logistic regression models we adjusted for age using a piecewise linear model, in which we allowed one slope for age less than 70, and a different slope for age greater than 70, with the constraint that the slopes join at age 70. In all cases the slopes before and after age 70 were significantly different from each other (p < .001). Gender was not significant in any of the models.

We started by considering the “full model”, which includes the interaction between smoking status and the smoking metric, for each of the three remaining smoking metrics. In models using all individuals and in the smokers only models, the interactions between smoking status and the smoking metric were significantly different from zero for the square-root pack-years models, and for the “two metrics” models (in which the interactions were only significant for logcigp but not for cigtime), but not for the logcig-years models.

Next we considered the “all covariates” models that did not include the interactions mentioned above, but adjusted for all remaining covariates. In models fit using all individuals, and ever smokers only, yrsquit was a significant predictor (p < .01) in models with square-root pack-years and in the “two metrics” model, but was of borderline significance or not significant in the models with logcig-years (p ≈ .06 for all individuals, p ≈ .64 for smokers only). In the model fit using all individuals, the smoking status indicator variables were significant predictors in the model using square-root pack-years and the “two metrics” model, but not in the model using logcig-years. For models fit using smokers only, smoking status was not significant for any of the three metrics. The indicator variable for starting smoking before age 18, only included in smoker-only models, was significantly different from zero only in the model using logcig-years as the smoking metric. The logistic regression models are summarized in Table 1.

Table 1.

Regression coefficients from logistic regression models for lung cancer using different smoking metrics and adjusting for other model covariates as shown^a. Models that include interactions (former^*metric) were fit separately. Residual deviances were calculated from models without interaction terms.

											Residual deviance
	smoking metric		former	current	age	age >70	yrsquit	start < 18	former* metric		Unadj	Adjusted
	Logcig-years								former * logcigyrs
Everyone	.02***		.36	.40	.02*	.10***	−.01†		−.001		2735	2663
Smokers	.02***		−.07		.002	.12***	−.004	−.40**	−.001		2266	2201
	Sqrt-pack								former*sqrt-pack
Everyone	.28***		.55*	.71**	.03***	.10***	−.03***		−.13*		2806	2648
Smokers	.29***		−.17		.04***	.12***	−.03***	−.21†	−.14*		2335	2186
	Log-cigp	Cig-time							former* logcigp	former*cigtime
Everyone	.83***	.03**	−1.26**	−1.13*	.03**	.10***	−.03**		−.63**	.004	2790	2648
Smokers	.90***	.02	−.16		.05**	.11***	−.04**	−.15	−.64**	.003	2265	2186

^aModels fit using everyone include never-smokers, and contain the following variables: smoking metric (as indicated), a former smoker indicator, a current smoker indicator, age, age > 70 (which is 0 if age < 70, and is age if age ≥ 70), years since quitting smoking, and gender. In a separate model, the interaction between the smoking metric and the former smoker indicator was also included. Models fit using smokers only include the smoking metric, a former smoker indicator, age, age > 70, years since quitting smoking, gender, and start < 18 (which is 1 if started smoking before age 18, and 0 otherwise). Gender was not significant in all models. In models with log (cigarettes smoked per day + 1) and years of smoking, the models include both the two smoking metrics. Significance of the coefficients is indicated by superscripts.

^†= (p > .05 but p < .10),

^*= (p < .05),

^**= (p < .01),

^***= (p < .0001)

The last two columns of Table 1 give the residual deviances of the models - both for an unadjusted model including only the smoking metric (two variables for the “two metrics” model), and for the adjusted model which also adjusts for the covariates in the “all covariates” model. In the unadjusted models, the residual deviances for the logcig-years models were substantially smaller than for all other comparable models, except for the smokers only models in which the residual deviance using logcig-years was approximately the same as for the “two metrics” model. The residual deviance can be thought of as a measure of discrepancy of a generalized linear model [37] such as logistic regression, analogous to the sum of squared residuals in a normal linear regression. This suggests that as a single metric, logcig-years explains more of the variability in lung cancer than the other metrics (except possibly the “two metrics” model for smokers only). However when adjusted for the other model covariates, the residual deviances for the logcig-years models were somewhat larger than for the corresponding models using the other metrics. This suggests that in models using all the covariates considered here, models other than the logcig-years model explained more of the variability in lung cancer. When the model requires smoking status indicator variables, the smaller deviance comes with a price of abrupt changes in estimated cancer risk upon changes in smoking status.

Sensitivity of the logcig-years metric

We explored the sensitivity of the logcig-years metric to the scale on which smoking intensity is measured. Specifically, we considered generalized metrics of the form log(α cigpday + 1) × cigtime, for a range of values of α. We found that the residual deviance of the unadjusted model is smallest for metrics based on values of α between 0.5 and 1.5, but the residual deviance for the adjusted model is smallest for metrics based on values of α < 1, suggesting that a metric based on α between 0.5 and 1 may be somewhat better than the logcig-years metric which uses α = 1. In the adjusted smokers-only model using α = 0.5, smoking status and yrsquit remained not statistically significantly, whereas in the model based on all individuals using α = 0.5, yrsquit and the current smoking indicator both became borderline significant.

We also investigated the sensitivity of the logcig-year metric to adding the constant of one to cigpday before taking the logarithm. For all individuals and separately for smokers only, we fit three additional logistic regression models (and three analogous GAM models) in which logcig-years was replaced with log (cigpday + k) × cigtime, for k = 2, 3 and 4 in turn. For smokers only, we also fit a fourth model in which logcig-years was replaced with log(cigpday) × cigtime. Each model adjusted for the same covariates as the logcig-years model. In all cases the GAM plot was visually indistinguishable from the GAM plot using logcig-years, neither smoking status nor yrsquit were statistically significant, and the coefficient for the alternative metric continued to be approximately 0.02.

Addressing possible confounding by age

In our sample, the median case age was almost 7 years larger than the median control age. Thus the observed age effect in this study, as in any case-control study which is not perfectly age-matched, reflects a combination of the direct age effect and the difference in age distribution between cases and controls.

In order to remove the possible confounding with age, we fit the logcig-years model to current, former and never smokers together, separately by 4 age strata. Following the example of Flanders et al [8], we fit separate GAM and logistic regression models within age deciles of 40–49, 50–59, 60–69, and 70–79. Each model included covariates of logcig-years, current and former smoking indicator variables, yrsquit, age, and gender. The reason for including age was to allow for a possible age effect within age decile. Age was only significant in the 70–79 year group. Logcig-years was statistically significant in all 4 age strata models (p < .005), and the coefficient for logcig-years ranged from 0.014 to 0.023 within age strata. This coefficient was smallest (0.014–0.015) for the 40–49 and 60–69 age groups, and largest (0.022–0.023) for the 50–59 and 70–70 age groups. Our results imply reasonable robustness of our metric in different age group strata.

Addressing possible confounding by age of smoking initiation

Among ever smokers, we also explored models in which age of smoking initiation was included as a continuous variable (results not shown). In the “two metrics” model, this meant we were not able to adjust for age, and in this model larger values of age of smoking initiation and larger values of years since quitting smoking were both associated with increased cancer risk. Under the multistage model of carcinogenesis, the effect of a carcinogen will depend on age of smoking initiation, time since initial exposure, or both, depending on the stage(s) in which the carcinogen has an effect [38]. The results just described are consistent with cigarette smoke carcinogens acting on both early and late stage transitions [38], as other studies have suggested. However the implication that years since smoking cessation is positively related to lung cancer risk is neither biologically reasonable nor consistent with other studies. In this data, age of smoking initiation ranged from 6 to 61 years, with 78 smokers starting at age 30 or greater, including 8 who started smoking after age 50. In the “two metrics” model, age of smoking initiation as a continuous variable, years of smoking and years since quitting smoking together comprise the overall age effect, possibly explaining the apparent positive association between cancer risk and years since quitting smoking in this model.

Our decision to dichotomize age of smoking initiation allows us to also adjust for age in models using each smoking metric. It has been suggested that the lung is most sensitive to the effects of smoking during lung development [39, 26]. Dichotomizing age of smoking initiation at age 18 is meant to capture whether smoking started before or after lung development was essentially complete. However this dichotomization does not capture smoking initiation effects which may be important at a later age, such as cancer promotion in intermediate-stage cancer cells. Individuals who started smoking earlier were on average heavier smokers who smoked longer than those who started smoking later. There was no evidence of an interaction between this indicator variable and logcig-years.

Addressing the definition of years since quitting smoking for never smokers

We defined yrsquit to be zero for never smokers, yet it could be argued that yrsquit, like agestart, is not meaningful for never smokers. For smokers, the variable age is the sum of agestart, cigtime, and yrsquit. For never smokers this suggests defining yrsquit to be zero and agestart to be age. In a model that includes never smokers and adjusts for yrsquit (defined to be zero for never smokers), whether or not never smokers are influential in determining the coefficient for yrsquit can be visually assessed by examining the GAM plot for yrsquit. In all models discussed here, the adjusted relationship between yrsquit and the logit probability of cancer for never smokers was consistent with the relationship for ever smokers.

Exploring smoking-lung cancer risk implications of each metric

Here we compare what each smoking metric implies about lung cancer risk predictions over a range of different values of smoking intensity and duration. For pack-years, the increase in predicted cancer risk is the same for a doubling in smoking intensity (for fixed duration) as it is for a doubling in number of years smoked (for fixed intensity). The same is true for square-root pack-years. In contrast, for logcig-years the predicted increase in cancer risk for a doubling of smoking duration (for fixed intensity) is much larger than it is for a doubling in smoking intensity (for a fixed duration).

In Figure 3 we give contours of these three smoking metrics, as well as a two-dimensional smooth of estimated cancer risk as a function of smoking intensity and smoking duration estimated from the lung cancer data from the model

Figure 3.

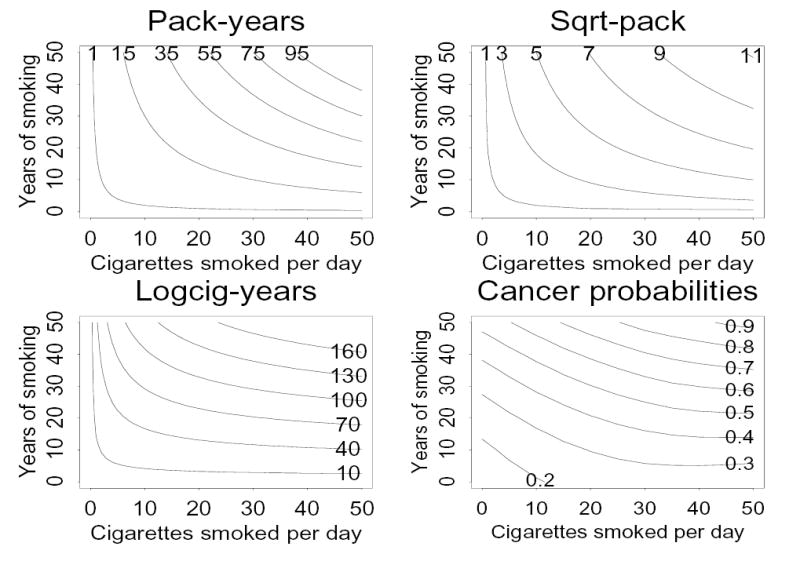
Lines of constant values of pack-years (upper left), square-root pack-years (upper right), and logcig-years (lower left), and from a two-dimensional smooth of cancer risk estimated from the lung cancer data (lower right), as a function of cigarettes smoked per day and years of smoking.

$$\text{logit P(cancer) }=s\text{(}cigtime,cigpday\text{)}\text{.}$$

In the three contour plots, for fixed values of other model covariates the estimated cancer risk is constant along any given contour of the smoking metric (shown as curves in the plot), and cancer risk is estimated to increase when moving from one contour to another with a larger value of the smoking metric. The contour plot for the “two metrics” model depends on the coefficients for cigtime and logcigp. For the values given in Table 1, the contour plot for the “two metrics” model (not shown) is similar to that for the logcig-years model. The two-dimensional smooth fit from the data using all individuals (Figure 3, lower right) and fit using smokers only (very similar to Figure 3 lower right, not shown) differ from the three contour plots most dramatically where smoking intensity is zero, and to a lesser extent where years of smoking is zero. Any two-dimensional smooth is less accurate at the plot edges where extrapolation is needed, than in the center of the plot. The two-dimensional smooth fit from the data does suggest that cancer risk increases more rapidly with increasing years of smoking (for fixed intensity) than it does with increasing intensity (for fixed duration), consistent with logcig-years and “two metrics” models, but not with the pack-years or square-root pack-years models.

In the “two metrics” model, adjusting for duration and intensity separately assumes that the effect of smoking intensity (on the logarithmic scale) and smoking duration are additive, an assumption which is not made for the other smoking metrics considered here. Under the “two metrics” model, a specific increase in years of smoking is predicted to increase cancer risk by the same amount for light smokers as for heavy smokers, whereas under the logcig-years model, the predicted increase is greater for heavier smokers. A similar conclusion can be reached about differences in estimated cancer risks for a specific increase in smoking intensity for a fixed smoking duration.

In Figure 4 we show the estimated lung cancer relative risk on the logarithmic scale, for ever smokers relative to never-smokers using the logcig-years model which included only the significant or borderline significant covariates (logcig-years, age as a piecewise linear term, and years since quitting smoking). The estimated log relative risk was .019 × logcig-years − .009 × yrsquit. Since smoking status was not needed in this model, the estimated relative risk does not change abruptly when smoking cessation occurs. This feature is not shared by any of the other smoking metrics when fit to data using all individuals.

Figure 4.

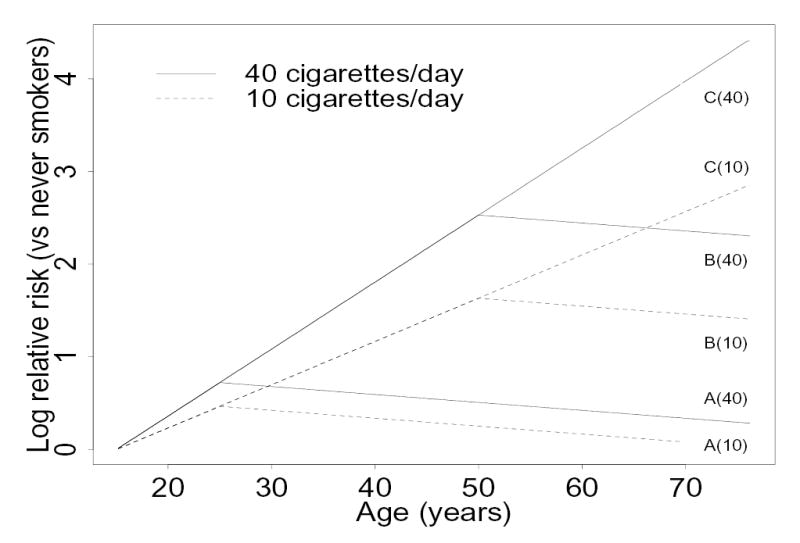
Estimated log relative risks of lung cancer for ever smokers versus never smokers of the same age using the logcig-years model, assuming smoking initiation at age 15. For two different smoking intensities, relative risks are shown for smoking cessation at age 25, (labeled as A), cessation at age 50 (B) and for current smokers (C).

Assessing our sample using the Doll and Peto equation

We now explore differences in our choice of metrics with the gold standard one of Doll and Peto [14] in their landmark study. In a cohort study, Doll and Peto found that among male never smokers and current smokers aged 40–79 who started smoking between age 16 and 25 and who smoked 40 or fewer cigarettes per day, the annual lung cancer incidence was proportional to (cigpday + 6)² × (age – 22.5)^4.5, where age − 22.5 was used as a proxy for smoking duration (cigtime). We tried to fit an analogous model in our data by using the log odds ratio to approximate the log incidence rate ratio among the n = 177 male never smokers and n = 137 male current smokers in our sample which met Doll and Peto’s criteria. We assumed a baseline risk of age^4.5 for never smokers. Because we are modeling the log odds ratio rather than incidence itself, and furthermore we are using case control data rather than cohort data, our model results are not strictly comparable to Doll and Peto’s results. One consequence of using the logarithmic scale is that we must add a constant (we chose to add one) to cigtime so as to not exclude never smokers when taking the logarithm. In a model for incidence this is not necessary. Among this subsample, we examined the relationship between the logit probability of cancer and log(cigpday + 6), log(cigtime+1) and log(age), using both GAM and logistic regression. Our results would be consistent with Doll and Peto’s model if the coefficients in the logistic regression model were 2, 4.5, and -4.5 respectively.

Adding one to cigtime before taking the logarithm resulted in a very bimodal distribution for this variable. Among the n = 137 current male smokers meeting Doll and Peto’s criteria, the smallest cigtime was 9, so the variable log(cigtime+1) had n = 177 values of 0, and n = 137 values between 2.30 and 4.11. The GAM plot indicated that the logit probability of cancer was strongly and positively related to log(cigtime+1) among current smokers, but that the adjusted relationship for never smokers did not fit this pattern. As a result, the inclusion of never smokers caused the overall relationship to be extremely nonlinear. In the adjusted logistic regression model, the coefficient (SE) for log(cigpday + 6) was 2.70 (0.70), consistent with the Doll and Peto model. The coefficient (SE) for log(age) was 1.35 (0.85), whereas the coefficient of −0.35 for log(cigtime+1) is not meaningful due to the nonlinearity noted above. The age distributions among cases and controls in our overall case control study and in the subset used for this analysis is not necessarily representative of the corresponding age distributions in the population. The age effect seen here partly reflects this difference, which could explain why our estimated age effect differs from Doll and Peto’s estimate. Other reasons why our results did not more closely match Doll and Peto’s could include our assumption of the baseline risk among never smokers, and the fact that cigarette smoke exposure characteristics have changed over the past four decades, which may also affect the smoking metric. In fact, Flanders et al [8] performed a more recent cohort analysis, and also found major differences with Doll and Peto. In this data subset, logcig-years continued to be linearly related to the logit probability cancer with a regression coefficient (SE) of 0.02(0.002).

The Doll and Peto sample did not include former smokers in their base population, and this subset comprised over half of the ever smokers in our sample. Differences in the epidemiology of lung cancer in former smokers and current smokers (for example, proportion of adenocarcinomas, peripheral versus central lung cancers, etc.) suggest possible differences in lung carcinogenesis, and this too may affect the smoking metric. Thus, choosing an appropriate metric may be affected by differences in study design and population.

Discussion

We compared the performance of several metrics in a large case-control study to illustrate how we evaluate smoking metric(s) for use in our gene-smoking models. Three of the metrics have been used in published studies (pack-years, square-root pack-years, and the “two metrics” model), while the fourth, logcig-years, has not been considered previously. In our sample, we showed that the contribution of pack-years to the logit probability of lung cancer was highly non-linear. The remaining three metrics passed this first hurdle and were approximately linearly related to the logit probability of lung cancer. Both the square-root pack-years model and the “two metrics” model require inclusion of smoking status as a covariate, especially in models that include never-smokers, implying that risk estimates may change drastically upon smoking initiation and smoking cessation. The model using logcig-years did not have this drawback because smoking status (and its interaction with logcig-years) were not significant predictors of cancer risk, after adjusting for other model covariates. Models that include smoking status may be sensitive to the cutpoints used to differentiate between never, former, and current smokers. Such a sensitivity has been noted by Leffondre et al [12] for the estimated hazard ratio for lung cancer in a Cox model. We note that although the logcig-years metric performed well in our data, whether or not it performs well in other datasets would need to be determined on the basis of its performance relative to other metrics in those datasets.

Our general approach to evaluating continuous variable smoking metrics can be summed up as follows: (i) evaluate each metric for linearity with disease outcome using the appropriate link function (e.g. the logit probability of cancer, for logistic regression), in one’s study population; (ii) evaluate the effect on risk estimates by inclusion of other potentially clinically important variables along with your metric(s) of interest. Examples include smoking status (never, current, or former smokers), year since quitting smoking, age of smoking initiation, and/or age; (iii) compare the implications of the different smoking metrics for lung cancer risk predictions; and (iv) explore possible reasons why the metric that performs best in your study population may be different from other metrics chosen in other studies or for other hypotheses. The best performing continuous smoking metrics appear to have the following three properties: (i) a linear relationship with disease risk using the appropriate link function, since this is a model assumption; (ii) the ability to include or exclude never smokers from the model without substantial changes in choice of model covariates or estimated disease risk in smokers; and (iii) an insensitivity of disease risk estimates to changes in smoking status for fixed values of other model covariates. Models that include smoking status imply a jump in estimated risk at the age of smoking initiation and/or smoking cessation, an assumption that is appropriate for certain types of analyses but not for others, and one that is somewhat implausible from the biologic perspective.

A limitation of this study concerns the derivation of the logcig-years metric, which was based on several simplifying assumptions. Our derivation only considered PAH formation from smoking, but other substances such as well done red meat are also sources of PAHs. We did not account for other possible sources of PAHs in this paper (but see Cortessis and Thomas [40] who model smoking and well-done red meat consumption jointly). Although we have stated various limitations of the logcig-years metric, it should be noted that all metrics suffer from an inability to explain or account for many biological premises associated with tobacco carcinogenesis. Although initially motivated by a DNA adducts model, our metric was chosen mainly because in this sample dataset, it performed better than other metrics. It should be understood that in other contexts, other metrics, including those not mentioned in this paper, may be most appropriate for analysis. In all circumstances, the derived metric should have at least face validity.

In summary, we recommend that a process such as we outlined here be followed before assuming that a particular smoking metric suitably adjusts for or evaluates smoking in a statistical model. Different studies may use different metrics, since the base population and study designs may differ between studies. We do not recommend that this comprehensive approach be used for all studies that incorporate smoking variables, but that the process be adapted to evaluate smoking metrics in studies where smoking is an integral part of the biologic of the disease or the study hypothesis.