Comparing different estimates of cochlear compression in listeners with normal and impaired hearing

Abstract

A loss of cochlear compression may underlie many of the difficulties experienced by hearing-impaired listeners. Two behavioral forward-masking paradigms that have been used to estimate the magnitude of cochlear compression are growth of masking (GOM) and temporal masking (TM). The aim of this study was to determine whether these two measures produce within-subjects results that are consistent across a range of signal frequencies and, if so, to compare them in terms of reliability or efficiency. GOM and TM functions were measured in a group of five normal-hearing and five hearing-impaired listeners at signal frequencies of 1000, 2000, and 4000 Hz. Compression values were derived from the masking data and confidence intervals were constructed around these estimates. Both measures produced comparable estimates of compression, but both measures have distinct advantages and disadvantages, so that the more appropriate measure depends on factors such as the frequency region of interest and the degree of hearing loss. Because of the long testing times needed, neither measure is suitable for clinical use in its current form.

I. INTRODUCTION

Physiological studies of the healthy mammalian cochlea have shown that the response of the basilar membrane is highly compressive for tones presented at characteristic frequency (Rhode and Robles, 1974; Robles et al., 1986; Murugasu and Russell, 1995; Ruggero et al., 1997; Russell and Nilsen, 1997; Rhode and Recio, 2000). A loss of this nonlinearity may underlie many of the difficulties experienced by hearing-impaired listeners: abnormal loudness growth, reduced frequency selectivity, reduced rate of decay of forward masking, and larger-than-normal gap-detection thresholds in narrow-band noise can all be accounted for by a loss or reduction of compression on the basilar membrane (Yates, 1990; Glasberg and Moore, 1992; Oxenham and Moore, 1997; Oxenham and Bacon, 2003). A reliable behavioral measure of cochlear compression may therefore be of clinical value.

Forward masking of tonal signals is one psychophysical method that has been used in human listeners to derive estimates of the magnitude of cochlear compression. Forward masking lends itself to estimating cochlear response because the nonsimultaneous presentation of the masker and signal eliminates concerns regarding possible nonlinear peripheral interactions, such as suppression. The compression values derived from such measures tend to be quantitatively similar to those obtained using physiological techniques in animals (e.g., Oxenham and Plack, 1997; Rosen et al., 1998; Baker et al., 1998; Glasberg et al., 1999; Hicks and Bacon, 1999; Plack and Oxenham, 2000; Wojtczak et al., 2001; Nelson et al., 2001; Moore et al., 2002; Lopez-Poveda et al., 2003; Plack and Drga, 2003).

The two most commonly used forward-masking techniques for estimating compression are growth of masking (GOM) (e.g., Oxenham and Plack, 1997) and temporal masking (TM) (e.g., Nelson et al., 2001). Both paradigms derive compression values by comparing off-frequency masker levels (i.e., masker frequency less than or equal to 0.6 times signal frequency) with on-frequency masker levels (i.e., masker frequency equal to signal frequency). In line with the available physiological data (usually taken from the base of the cochlea) it is assumed that basilar membrane compression is limited to frequencies around the characteristic frequency and that the response to a tone half an octave or more below characteristic frequency is approximately linear (Yates et al., 1990; Ruggero et al., 1997). While this assumption is probably valid for high characteristic frequencies, some recent physiological and psychophysical studies have questioned its validity at low characteristic frequencies (e.g., Rhode and Cooper, 1996; Oxenham and Dau, 2001, 2004; Lopez-Poveda et al., 2003; Plack and Drga, 2003). For the details of further assumptions, see Oxenham and Plack (1997) and Nelson et al. (2001).

In the case of GOM, masker levels necessary to just mask a signal are measured at several fixed signal levels. The slope of a GOM function is thought to reflect relative differences in the response of the basilar membrane to the masker and signal at the place on the basilar membrane where the signal is detected. For on-frequency maskers when both the signal and the masker are nearly equal in level, the GOM function has a slope roughly equal to one, presumably because both the signal and masker are subjected to similar amounts of compression. Off-frequency masking produces functions with a slope less than one, especially at medium signal levels, because the response to the signal is compressed while the response to the masker is not. The ratio of the slopes of straight lines fit to the off- and on-frequency data, for a given signal frequency, provides an estimate of the magnitude of compression.

In the case of TM, masker levels necessary to just mask a fixed low sensation level signal are measured as a function of the time delay between the offset of the masker and the onset of the signal. For the on-frequency masker, the change in masker level as a function of delay is thought to reflect the effects of compression and the more central recovery from forward masking; for the off-frequency masker, which is assumed to be processed linearly, the function should reflect only the recovery from forward masking, which is known to be independent of masker frequency (e.g., Nelson and Pavlov, 1989). Thus, the effects of compression and decay of the response to the masker can be separated by plotting off-frequency masker levels as a function of on-frequency masker levels, paired according to signal delay (Nelson et al., 2001; Lopez-Poveda et al., 2003; Plack and Drga, 2003). The resulting function can be viewed as a derived basilar membrane input-output function.

Despite these procedural differences, both GOM and TM purport to measure the same thing, namely basilar membrane compression. However, no study has yet made a direct comparison of the two methods in the same listeners. Such a comparison is of interest for at least two reasons. First, it tests the assumption that the two techniques do indeed provide estimates of the same underlying phenomenon; second, it allows a direct comparison of the two measures in terms of efficiency and reliability. In the current study, GOM and TM curves were measured in five normal-hearing listeners (experiment I) and five hearing-impaired listeners (experiment II).

II. EXPERIMENT I: NORMAL-HEARING LISTENERS

A. Methods

1. Stimuli and procedure

GOM and TM curves were measured at signal frequencies (f_s) of 1, 2, and 4 kHz with an on-frequency (f_m=f_s) and off-frequency (f_m=0.55f_s) forward masker. Both the signal and masker tones were gated with raised-cosine ramps of 5 ms in the 1- and 2-kHz signal frequency conditions and 2.5 ms in the 4-kHz condition. The signal and the masker had steady-state portions of 0 and 100 ms, respectively.

In the GOM paradigm, the level of a forward masker needed to just mask the signal was measured as a function of signal level (50, 55, 60, 65, 70, and 75 dB SPL). These signal levels were selected because this is the level region where the maximum amount of compression is expected (e.g., Oxenham and Plack, 1997). The silent interval between masker offset and signal onset (i.e., signal delay) was 0 ms, defined in terms of the zero-points in the envelope. In order to limit the effects of off-frequency listening, an ipsilateral background noise was presented at a spectrum level 40 dB below the level of the signal. It is important to ensure that the level of the background noise is not intense enough to mask the signal itself. At the specified spectrum level, the highest signal level (75 dB SPL) was at least 20 dB above the simultaneous masked threshold of the signal measured in the background noise alone. The bandwidth of the high-pass background noise was 6 kHz with a lower cutoff frequency of 1.2f_s. To avoid detection of the signal in the contralateral ear, a contralateral masking noise was presented at an overall level 20 dB below the level of the signal, with a pass band extending from 0.8f_s to 1.2f_s. Both the ipsilateral and contralateral noises were gated on 50 ms before masker onset and gated off 50 ms after signal offset.

In the TM paradigm, the level of a forward masker needed to mask a 10 dB SL signal was measured as function of signal delay (10 to 100 ms at 10-ms intervals). This range of signal delays was selected to ensure that on-frequency masked thresholds would be measured in the level region where maximum compression is expected (i.e., 50 to 75 dB). No background noises were presented in either ear; the signal level was always so low that neither off-frequency listening nor detection in the contralateral ear was deemed likely.

All stimuli were generated digitally and played out via a soundcard (LynxStudio LynxOne) with 24-bit resolution and a sampling frequency of 32 kHz. The stimuli were then routed to a programmable attenuator (TDT PA4) and headphone buffer (TDT HB6) before being presented to the listener via Sennheiser HD 580 headphones. Listeners were seated in a double-walled sound-treated room. A trial consisted of three observation intervals, separated by interstimulus intervals of 500 ms. The masker was presented in all three intervals and the signal was randomly presented in one of the three intervals. Thresholds were tracked using a two-up one-down adaptive procedure that estimates the masker level at the 70.7% correct point on the psychometric function (Levitt, 1971). In the adaptive procedure, the masker level was initially varied with a step size of 8 dB. After the first two level reversals, the step size was reduced to 4 dB and after an additional two reversals to 2 dB. The threshold estimate was taken as the mean of the last eight reversals with a 2-dB step size. The maximum allowable masker level was set at 102 dB SPL; if the tracking procedure attempted to exceed this level more than six times, the run was aborted. Thresholds are only reported for conditions that resulted in no aborted runs. For the GOM data, which involved six data points per curve, each reported threshold is the mean of at least four estimates. When the standard deviation of four estimates exceeded 4 dB, an additional two estimates were made and the mean of all six estimates was recorded as threshold. Approximately 50% of the reported GOM thresholds are the mean of six estimates. The TM data involved more data points per curve (up to ten), so initially only two estimates per condition were made. However, the standard deviation of the two estimates exceeded 4 dB in about 80% of the conditions; in those cases an additional two estimates were made and the mean of all four estimates was recorded as threshold. Thus, on average, GOM and TM involved about 30 and 36 runs per curve, respectively, for each listener. Data collection did not begin until a listener had a minimum of 4 h of practice with each of the two experimental paradigms. The order of presentation of the experimental paradigms was randomized across subjects. Testing was completed for all conditions of a given paradigm before testing with the other paradigm began. Listeners N1, N2, and N5 were tested first with GOM while listeners N3 and N4 were tested first with the TM paradigm. The presentation of signal frequency conditions was also randomized within a masking paradigm.

2. Subjects

GOM and TM curves were measured in five normal-hearing listeners who ranged in age from 18 to 32 years. Listeners were verified as having absolute thresholds better than 20 dB HL (ANSI, 1996) for octave frequencies between 250 and 8000 Hz. Listeners were recruited from the M.I.T. student population and were compensated monetarily for their time. Test sessions typically lasted for 2 h (including breaks) and listeners were tested two to three times per week. The total testing time per listener was about 45 h.

B. Results

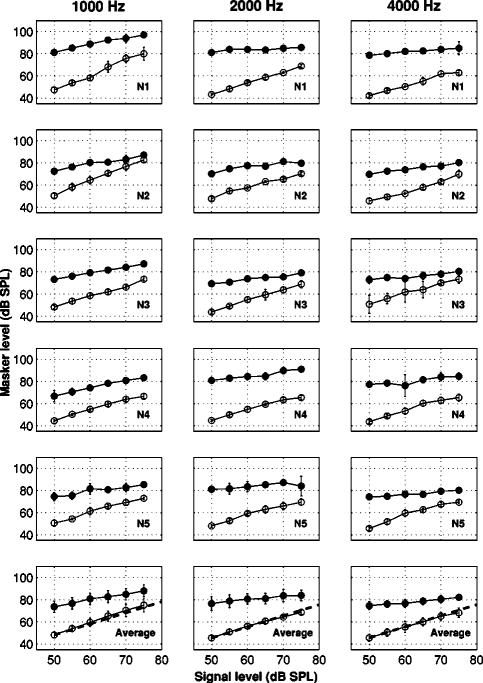
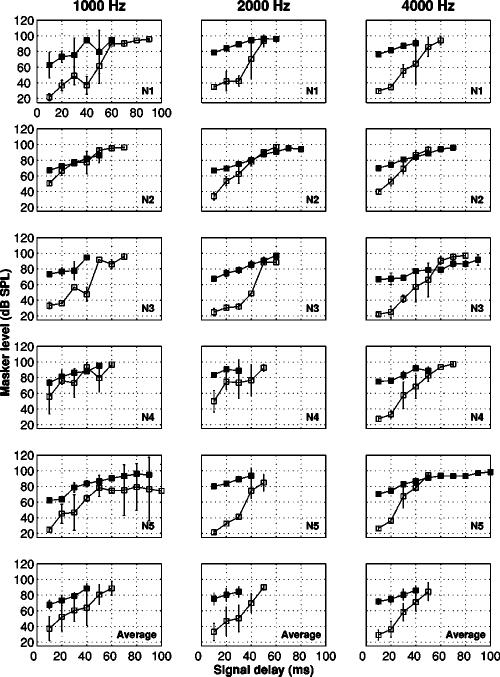
GOM curves are shown in Fig. 1 and TM curves are shown in Fig. 2 for signal frequencies of 1, 2, and 4 kHz. Each row corresponds to a different listener, and the final row shows the mean data. Mean thresholds are reported only for conditions where data were available for all five listeners. On- and off-frequency masked thresholds are plotted with open and filled symbols, respectively. Error bars represent ±1 standard deviation. As can be seen, within-subject standard deviations across measurements were generally larger for the TM data, particularly in the on-frequency masking condition.

FIG. 1.

GOM functions measured at signal frequencies of 1, 2, or 4 kHz for normal-hearing listeners in experiment I. Each row represents a different subject or the mean data. Filled symbols represent off-frequency masked thresholds and open symbols represent on-frequency masked thresholds. Error bars represent ±1 standard deviation. The dotted lines plotted in the bottom row represent a straight line with a slope of one.

FIG. 2.

TM curves measured at signal frequencies of 1, 2, or 4 kHz for normal-hearing listeners in experiment I. Each row represents a different subject or the mean data. Filled symbols represent off-frequency masked thresholds and open symbols represent on-frequency masked thresholds. Error bars represent ±1 standard deviation.

The GOM data (Fig. 1) show that, in agreement with previous studies, the slope of the off-frequency masker functions is in most cases much less than unity, while the slope of the on-frequency masker functions is close to unity (e.g., Oxenham and Plack, 1997). The dashed line shown with mean data (Fig. 1; bottom row) represents a straight line with a unity slope.

Also in agreement with previous studies, the TM data (Fig. 2) show that masker levels increased with signal delay, and the rate of increase differed for the on- and off-frequency masking data (e.g., Nelson et al., 2001; Lopez-Poveda et al., 2003; Plack and Drga, 2003). In most cases, the slope of the on-frequency curve varies over the range of time intervals measured, and there is a region of the on-frequency masking curve that is substantially steeper than the off-frequency masking curve. For the off-frequency conditions, the slope of a given curve tends to be more constant, although there may be a trend for the slope to become shallower at the highest levels. Plack et al. (2004) found a similar, and significant, trend for the slope of the off-frequency masking curve to become shallower at higher masker levels (and larger masker-signal intervals) for their 4-kHz signal frequency (2.2-kHz masker). Although such a trend seems to exist in some of our data, it failed to reach significance, either with a simple correlation of off-frequency masker slope and masker level (R=−0.18; p=0.34), or with an attempt to find a quadratic component to the regression (p>0.05).

There is also a trend for the off-frequency curves to become shallower with increasing signal frequency. The mean slope of the off-frequency masking functions is 0.39 (s.e.=0.04) at a signal frequency of 4 kHz, 0.43 (s.e.=0.05) at 2 kHz, and 0.53 (s.e.=0.04) at 1 kHz. This feature has been reported before (Lopez-Poveda et al., 2003; Plack and Drga, 2003) and is discussed further below.

C. Estimating compression values

In the following sections, compression values are derived from the TM and GOM data, and results from the two paradigms are compared. In previous studies (Nelson et al., 2001; Plack and Drga, 2003), third-order polynomials were found to provide relatively good fits to the data, although in some cases the minimum derivative was a negative number (Plack and Drga, 2003). Recently, Plack et al. (2004) suggested fitting the data with a multiphase (i.e., three-segment) linear regression function. With this method, the slopes of the lower and upper segments are fixed at unity and a straight line is fit to the middle segment. The horizontal distance, in dB, between the upper and lower segments can be used to estimate the maximum gain applied by the cochlear active mechanism, if it assumed that the gain at high levels (in the upper segment) is zero (see Plack et al., 2004, for details). An alternative to a generic polynomial is a function that is specifically designed to capture certain features of the basilar membrane input-output function, such as the more compressive mid-level region. The sum of a linear and a sigmoidal function (LS) has been used in a number of studies (e.g., Moore et al., 1996; Oxenham and Moore, 1997; Glasberg and Moore, 2000). In this study, we use a version of this that describes the basilar membrane response (R) for a given input level (L) as

$$R=0.9L+A+B+(1-(1/(1+\exp (-0.05(L-50))))),$$ (1)

where

$$A=-0.0894G_{\max }+V+10.894,$$ (2)

$$B=1.1789G_{\max }-11.789,$$ (3)

and where G_max determines the maximum gain (in dB) applied by the active mechanism. The slope of the response curve at very low and very high input levels is nearly linear, as defined by the constant 0.9, and varies slightly with level. The compressive middle region of the function spans the range of input levels between about 20 to 80 dB, the midpoint of which is defined by the constant 50 (in dB SPL). The value of G_max is a free parameter that is allowed to vary to provide the best fit to the data. The free parameter V allows a vertical shift of the function. The values of A and Bare specified so that the calculated basilar membrane response is 100 dB for L=100 dB and V=0. The minimum of the function's first derivative can be used as an estimate of the maximum compression. Here we use all these approaches in deriving compression estimates from the first experiment.

1. Temporal masking

Estimating compression values from TM curves typically involves the interim step of deriving a basilar membrane response curve by plotting off-frequency masker levels as a function of on-frequency masker levels. The fact that off-frequency curves tend to become shallower with increasing signal frequency has been interpreted as evidence that off-frequency curves only reflect truly linear processing of the masker at high signal frequencies (Lopez-Poveda et al., 2003; Plack and Drga, 2003). At lower characteristic frequencies, compression may be applied not only to on-frequency but also to off-frequency stimuli, making the assumption of linear processing of the off-frequency masker invalid. This was taken into account in our analysis by fitting a straight line to the 4-kHz off-frequency masker levels (f_m=2.2 kHz) for each subject, and using that as the linear reference against which to plot the on-frequency masker data, as suggested by Lopez-Poveda et al. (2003).

Basilar membrane response curves derived from the TM data are shown in Fig. 3. Each row represents a different listener and the final row shows the mean data. Each symbol represents an off-frequency masker level (f_m=2.2 kHz) plotted as a function of on-frequency masker level (f_m=f_s), paired by signal delay. Using a higher frequency off-frequency masker eliminates the need to rely on the assumption that compression is frequency specific in more apical basilar membrane regions. Using a straight line fit to the off-frequency data, as opposed to the raw data itself, allows f_m=2.2 kHz thresholds to be used as the linear reference even for signal frequency conditions where on-frequency masked thresholds were obtained for a greater number of signal delays.

FIG. 3.

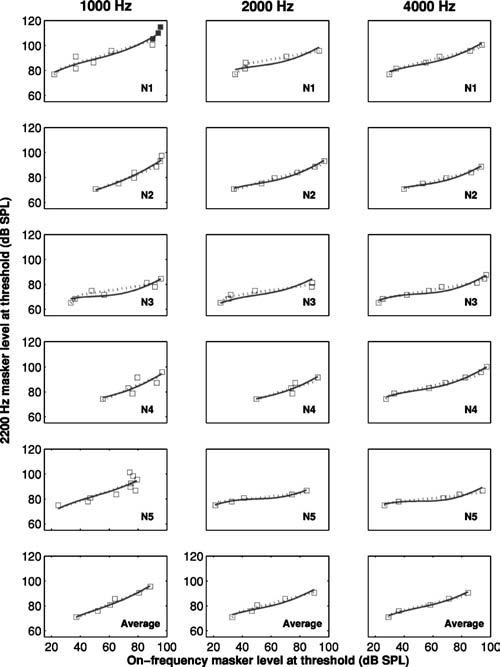
Basilar membrane response curves derived from TM data for normal-hearing listeners in experiment I. Each row represents a different subject or the mean data. The LS function fit to the data is plotted as a solid line. The multiphase regression function is plotted as a dashed line. A straight line fit to the off-frequency TM curve measured at f_m=2.2 kHz was used as the linear reference.

Plotted with a solid line in Fig. 3 is the LS function, fit to the data using a least-squares approach. G_max and V were allowed to vary as free parameters; for every estimated value of G_max, the value of V that produced the best fit to the data was determined. The values of G_max and V that minimized the sum of squared errors for the predicted masked levels were accepted as the final parameter values. The resulting LS function was evaluated and is plotted as a solid line in Fig. 3. The Matlab functions nlinfit and fminsearch were used to generate the fitted function.

Using an approach similar to Plack et al. (2004), a multiphase regression function was also fit to the TM data and is plotted with a dotted line in Fig. 3. The lower breakpoint (LBP), upper breakpoint (UBP), lower segment intercept (LI), and slope of the middle segment (MS) were allowed to vary as free parameters. The slope of the lower and upper segments was fixed at 1. The fitting function (nlinfit) was constrained so that the middle segment contained a minimum of three data points. The resulting least-squares, three-segment function was evaluated. In general, the sum of squared errors associated with the multiphase regression function was considerably smaller than the LS function, although this may simply reflect the fact that the multiphase regression function has twice as many free parameters as the LS function.

The minimum of the first derivative of each LS function plotted in Fig. 3 is shown in the right-hand column of Table I. Also shown in Table I are minimum slope values for the TM data using a straight line fit to the off-frequency masker levels (f_m=0.55f_s) as the linear reference. The minimum slope value for each of the multiphase regression functions plotted in Fig. 3 is shown in the right-hand column of Table II. Minimum slope values derived from the TM data using off-frequency masker levels (f_m=0.55f_s, rather than f_m=2.2 kHz) as the linear references are also shown in Table II. This allows a more direct comparison with the GOM data, where it is not possible to use the same high off-frequency reference for all signal frequencies.

TABLE I.

Estimates of compression calculated from the LS function fit to basilar membrane response curves derived from GOM and TM data, for each signal frequency in experiment I. Values in the “Mean” rows show parameters fitted to the mean data, only including points for which values from all five subjects were available.

Subject	GOM	TM Reference=0.55fS	TM Reference=2.2 kHz
		fs=1000 Hz
N1	0.38	0.39	0.29
N2	0.32	0.43	0.37
N3	0.54	0.38	0.07
N4	0.75	0.36	0.25
N5	0.43	0.56	0.34
Mean	0.48	0.42	0.26
		fs=2000 Hz
N1	0.11	0.07	0.15
N2	0.41	0.19	0.19
N3	0.35	0.23	0.04
N4	0.45	0.06	0.25
N5	0.19	0.15	0.04
Mean	0.30	0.14	0.13
		fs=4000 Hz
N1	0.26	0.21	0.21
N2	0.37	0.16	0.16
N3	0.24	0.07	0.07
N4	0.35	0.18	0.18
N5	0.20	0.01	0.01
Mean	0.28	0.13	0.13

TABLE II.

Estimates of compression calculated from the ratio of slopes of the GOM data and from the multiphase regression function fit to basilar membrane response curves derived from the TM data in experiment I. GOM slope values at f_S=6 kHz are from experiment IA. Values in the “Mean” rows show parameters fitted to the mean data, only including points for which values from all five subjects were available.

Subject	GOM Slope ratio	TM Reference=0.55fS	TM Reference=2.2 kHz
		fs=1000 Hz
N1	0.46	0.42	0.35
N2	0.42	0.46	0.42
N3	0.58	0.40	0.17
N4	0.75	0.54	0.46
N5	0.47	0.60	0.40
Mean	0.53	0.48	0.36
		fs=2000 Hz
N1	0.14	0.18	0.21
N2	0.44	0.32	0.32
N3	0.37	0.22	0.16
N4	0.48	0.22	0.35
N5	0.22	0.20	0.13
Mean	0.33	0.23	0.23
		fs=4000 Hz
N1	0.28	0.29	0.29
N2	0.41	0.27	0.27
N3	0.32	0.20	0.20
N4	0.37	0.26	0.26
N5	0.25	0.13	0.13
Mean	0.33	0.23	0.23
		fs=6000 Hz
N1	0.28	…	…
N2	0.18	…	…
N3	0.22	…	…
N4	0.16	…	…
N5	0.09	…	…
Mean	0.19	…	…

Minimum slope values derived from the TM data were analyzed using a three-factor repeated-measures analysis of variance (fixed effects), using signal frequency (1, 2, or 4 kHz), fitting function (LS or multiphase regression), and linear reference (f_m=0.55f_s or f_m=2.2 kHz) as within-subject factors. Here and throughout this paper, p values less than 0.05 are considered significant. The results showed a signifi-cant main effect of signal frequency [F(2,8)=15.44, p=0.002] and fitting function [F(1,4)=65.47, p=0.001]. There was no main effect of linear reference [F(21,4) =2.64, p=0.18], but the interaction between signal frequency and linear reference was significant [F(2,8)=7.39, p=0.02]. Posthoc Fisher's LSD tests showed a significant (p<0.05) difference between slope values at f_s=1 kHz vs. f_s=2 kHz or 4 kHz. There was also a significant (p<0.05) difference between slope values at f_s=1 kHz using f_m=0.55f_s as the linear reference vs. f_m=2.2 kHz.

The significant effect of fitting function reflects, at least in part, the fact that the LS-function estimate is the slope value at the point where the derivative of the function reaches its minimum. In contrast, by definition the slope of the linear regression analysis is defined over at least three data points and thus represents the average slope over a larger region of the level range.

The significant interaction between linear reference and signal frequency suggests that the choice of linear reference is an important factor only for signal frequencies less than 2 kHz. This is consistent with the finding of Lopez-Poveda et al. (2003) that the slope of off-frequency TM curves was constant for signal frequencies greater than or equal to 2 kHz. Posthoc analysis (Fisher's LSD test) also showed that even when f_m=2.2 kHz was used as the linear reference, slope values at a signal frequency of 1 kHz (average across subjects=0.31 dB/dB) were still significantly larger than values at f_s=2 kHz (average=0.18 dB/dB) or 4 kHz (average=0.18 dB/dB). This finding, suggesting that compression is reduced at lower frequencies, is in contrast to results reported by Lopez-Poveda et al. (2003) and Plack and Drga (2003), who found equal compression at low and high frequencies. It is not clear what accounts for this discrepancy, although it may in part be traced back to the results of listeners N2 and N4. For these listeners the TM curves at 1 kHz start at a fairly high level, meaning that the data may not include the most compressive regions of their data.

2. Growth of masking

The magnitude of compression was estimated from the GOM data (see Fig. 1) by calculating the ratio of the slopes of straight lines fit to off- and on-frequency masker levels. In contrast to the TM paradigm, it is not possible to use the high-frequency off-frequency masker curves as a linear reference, and so all comparisons involve the off-frequency masker at f_m=0.55f_s . Slope values are shown in Table II. As the data generally fell on a single straight line in the level region tested (50–75 dB SPL), calculating the ratio of the slopes is essentially equivalent to fitting the derived basilar membrane response curve with the three-segment multiphase linear regression function.

Basilar membrane response curves were also derived from the GOM data by plotting off-frequency data as a function of on-frequency data, paired by signal level. The resulting curves were fit with the LS function and minimum slope values are shown in Table I. A comparison of values in Tables I and II indicates that both methods of deriving estimates of compression from GOM data produce similar results.

3. Comparisons of TM and GOM estimates of compression

One goal of this study was to determine whether the GOM and TM paradigms produce consistent intrasubject slope estimates. To address this question, minimum slope values derived from the LS function were analyzed using a two-factor repeated-measures analysis of variance (fixed effects), using masking paradigm (GOM or TM) and signal frequency (1, 2, or 4 kHz) as within-subject factors. In the most comparable conditions, when f_m=0.55f_s was used as the linear reference for each TM signal frequency condition, results showed a significant main effect of signal frequency [F(2,8)=16.29, p=0.002]. There was a trend towards a main effect of masking paradigm, although it failed to reach significance [F(1,4)=5.76, p=0.07]. This (nonsignificant) trend reflects the fact that the TM estimates tended to be lower (stronger compression) than the GOM estimates. The interaction between masking paradigm and signal frequency was not significant [F(2,8)=1.08, p=0.39]. An identical pattern of results, in terms of significant differences and interactions, was found for compression values derived from the GOM data using the slope ratios and from the TM data using the multiphase regression functions. The result from the ANOVA showing no significant difference in the compression estimates between the two paradigms is supported by the fact that the correlation between the two measures was significant (Pearson correlation coefficient of 0.54; p =0.039).

Significant differences between the two paradigms did arise if the comparison was made between GOM and TM with a linear reference of f_m=2.2 kHz. This is expected because, as noted above, the same difference was found between the two TM measures, f_m=2.2 kHz and f_m=0.55f_s, with the latter probably underestimating compression, due to the failure of the assumption that the off-frequency response is linear.

Test reliability was examined by constructing 0.95 confidence intervals around G_max values used to calculate the minimum slope values reported in Table I for individual listeners. The Matlab function nlparci was used to determine the confidence interval for a given value of G_max (i.e., nonlinear least-squares parameter estimate) using the residuals and the Jacobian matrix (an analog of the X matrix in the standard linear regression model) at the solution (Table III). A two-factor repeated-measures analysis of variance (fixed effects), using paradigm (GOM and TM) and signal frequency (1, 2, or 4 kHz) as within-subject factors, showed a significant main effect of paradigm [F(1,4)=10.03, p=0.03]. The effect of signal frequency [F(2,8)=3.67, p=0.07] and the interaction of paradigm and signal frequency [F(2,8)=2.25, p=0.17] were not significant. Given that both paradigms involved measuring a similar number of data points, this finding suggests that the GOM paradigm provides a less variable measure than TM.

TABLE III.

The mean width of 0.95 confidence intervals around compression estimates derived from individual normal-hearing listeners' GOM and TM data in experiment I, using the LS function. The confidence intervals (CI) were constructed using the Jacobian matrix at the solution to the function.

	Width of CI
Signal frequency (kHz)	GOM	TM
1	0.06	0.31
2	0.06	0.16
4	0.07	0.11

4. Possible effects of “confusion”

For forward masking with brief masker-signal intervals, researchers have often found evidence for “confusion,” where signal thresholds are elevated because listeners have difficulty distinguishing the signal from the offset of the masker (e.g., Neff, 1985). Nelson et al. (2001) addressed this in their study of TM curves and found that, although some thresholds were changed by the presence of a cue tone (designed to eliminate confusion), their estimates of compression were unchanged. We completed pilot experiments on several listeners with and without cue tones. We found that, after considerable practice, there were no substantial changes, either in individual thresholds, or in estimates of compression. Thus, we conclude that the present data are unlikely to be contaminated by effects of confusion.

D. Discussion

TM and GOM paradigms produced comparable estimates of basilar membrane compression, although there was a trend towards TM estimates being more compressive than GOM estimates. To the extent that a difference is present, it may be due in part to the fact that the signal level for the TM curves is always 10 dB SL, whereas the signal level from the GOM curves was as high as 75 dB SPL. This highlights an important difference between the two measures: For TM, the use of a fixed signal level ensures that the listener is using the same place or the same limited frequency region on the basilar membrane to detect the signal, regardless of masker level. For GOM, where signal level is varied, the place used to detect the signal will probably be different at high levels than at low levels because the peak of the traveling wave shifts as a function of level (e.g., McFadden, 1986; Moore et al., 2002). Since the growth in the peak of the traveling wave is more linear than the growth at the place with a characteristic frequency equal to the signal, it follows that the GOM paradigm may underestimate compression, particularly at high levels. Thus, the TM paradigm may be thought of as measuring the response function to a signal at the (invariant) characteristic frequency, whereas the GOM paradigm may measure something closer to the response function to a signal at the best frequency, the place of which varies with level.

The difference in compression estimates between the two fitting procedures (linear regression versus LS function) is not surprising, given that the LS compression value is based on a single point in the function, whereas the regression value is based on an average across a level range of at least 10 dB. In fact, when the LS slope is averaged over a similar level range, the values for the two paradigms become much more comparable.

There is, however, a theoretical reason to question the use of the LS function. In a study of hearing loss and basilar membrane compression, Plack et al. (2004) have reported that the maximum gain applied by the active mechanism and the magnitude of maximum compression on the basilar membrane are not statistically correlated. The original LS function assumes that these two auditory functions are intimately related; the value of G_max (i.e., y intercept) is equal to the maximum gain and determines the minimum slope of the fitted function. While the LS function, with the inclusion of the V parameter that shifts on the entire function along the y axis, decouples the two auditory functions to some extent, they still cannot be viewed as being completely independent of one another; the range of input levels over which compression applies and maximum gain are still coupled.

In summary, both GOM and TM paradigms produce similar behavioral estimates of basilar membrane compression when comparable fitting techniques are used. Both GOM and TM (f_m=0.55f_s) paradigms probably underestimate compression at signal frequencies below 2 kHz, presumably because the assumption of a linear response to the off-frequency masker is violated. This can be remedied with TM by using a high-frequency linear off-frequency reference curve (f_m=2.2 kHz), but cannot be remedied with GOM (Lopez-Poveda et al., 2003). Finally, for given measurement effort, estimates using GOM provide less variable estimates of compression, with confidence intervals nearly half those found for the TM data. However, this comes at the expense of biased estimates at lower signal frequencies.

III. EXPERIMENT IA

Slope values derived from GOM functions measured in experiment I tend to decrease with increasing signal frequency (see Table II). In agreement with other psychoacoustic studies, results from experiment I suggest that a lack of frequency specificity of the compression mechanism may account for the substantially larger slope values at f_s=1 kHz. However, even at signal frequencies of 2000 and 4000 Hz there are several slope values that exceed 0.3 dB/dB. This finding is somewhat puzzling given that other studies using GOM have measured compression values of around 0.2 or less at a signal frequency of 6000 Hz (Oxenham and Plack, 1997; Nelson et al., 2001). The purpose of the current experiment was to determine if the observed trend for slope values to decrease continues at higher signal frequencies, approaching a value of 0.2 dB/dB across listeners at 6 kHz.

A. Methods

Stimuli and procedure

GOM functions were measured at f_s=6 kHz in the same five normal-hearing listeners who participated in experiment I. Stimulus parameters and experimental procedures were identical to those used in experiment I, except that the signal and masker tones were gated with raised-cosine ramps of 2 ms, and that the ipsilateral background noise was presented at a spectrum level 45 dB below the level of the signal. These modifications were made to replicate as closely as possible the parameters used by Oxenham and Plack (1997).

B. Results

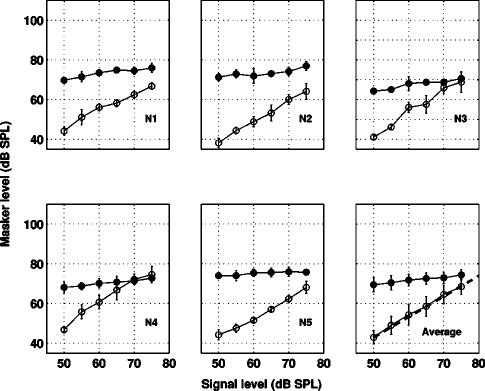
Results are shown in Fig. 4. Each panel corresponds to a different listener, with the last panel showing the mean data. On-frequency masked thresholds are plotted with open symbols and off-frequency masked thresholds are plotted with filled symbols. Error bars represent ±1 standard deviation. The ratio of the slopes of straight lines fit to the off- and on-frequency data are shown in Table II. The slope values for most listeners continue to decrease with increasing signal frequency. Furthermore, all slope values measured at f_s=6 kHz are less than 0.3 dB/dB. A single-factor repeated measures analysis of variance (fixed effects), using signal frequency (1, 2, 4, or 6 kHz) as a within-subject factor, was performed to determine the significance of observed differences. Results showed a significant main effect of signal frequency [F(3,12)=11.39, p=0.001]. A test of within-subject (linear) contrasts was also significant [F(1,4)=18.34, p=0.01]. These findings are indicative of a systematic increase in compression estimates as a function of signal frequency.

FIG. 4.

GOM functions measured at a signal frequency of 6 kHz for normal-hearing listeners in experiment IA. Each panel represents a different subject or the mean data. Filled symbols represent off-frequency masked thresholds and open symbols represent on-frequency masked thresholds. Error bars represent ±1 standard deviation. The dotted line plotted in the bottom panel titled “Average” represents a straight line with a slope of one.

C. Discussion

The slope values measured at f_s=6 kHz are in good agreement with earlier GOM studies (e.g., Oxenham and Plack, 1997; Nelson et al., 2001). Previous studies using GOM at low signal frequencies that have measured slope values exceeding the range of 0.2 to 0.3 dB/dB either failed to prevent off-frequency listening and/or used simultaneous masking (e.g., Stelmachowicz et al., 1987; Hicks and Bacon, 1999; Moore et al., 1999). As mentioned above, the most likely explanation for the apparently decreasing compression exponent with decreasing signal frequency is not that on-frequency compression decreases, but that off-frequency compression increases as the compression itself becomes less frequency selective. This interpretation is consistent with an increasing body of literature (Lopez-Poveda et al., 2003; Plack and Drga, 2003; Oxenham and Dau, 2004). Where our data remain unclear is the point at which the off-frequency response begins to become more compressive: our GOM data suggest that this may be as high as 6 kHz, whereas other data suggest that the point may only be reached between 1 and 2 kHz (Lopez-Poveda et al., 2003).

One potential reason might relate to our use of a very short temporal gap between the masker and signal in GOM, which could in principle result in physical overlap between the masker and signal in the auditory periphery. This might result in effective simultaneous masking, which in turn might reduce the estimated compression. Arguing against this is the fact that no such overlap has been found in the past for frequencies of 1 kHz and above (Vogten, 1978; Shailer and Moore, 1987; Carlyon, 1988). Another possible explanation is that the larger slope values observed at 2000 and 4000 Hz are indicative of (subclinical) cochlear damage. Again, this explanation seems unlikely given that participants were young listeners with audiometrically normal hearing. Furthermore, using methods similar to Shera et al. (2002), we measured auditory filter shapes at 1, 2, and 4 kHz in these same listeners. This particular notched-noise paradigm more closely resembles the procedures used in the measurement of neural tuning curves (i.e., near-threshold signal levels, non-simultaneous masking, and constant signal level), and, as such, is thought to be a sensitive and accurate behavioral measure of cochlear tuning. Filter equivalent rectangular bandwidths derived from our listeners' data fell within the normal range observed by Shera et al. (2002). Thus, we have no entirely satisfactory explanation of the seemingly continuous increase in estimated compression across the range of frequencies tested here, in contrast to the relatively constant estimates found in previous studies (Plack and Oxenham, 2000; Lopez-Poveda et al., 2003).

IV. EXPERIMENT II: HEARING-IMPAIRED LISTENERS

As discussed in the Introduction, a reliable measure of cochlear compression may be of clinical value because a loss or reduction of compression may explain many of the perceptual difficulties experienced by hearing-impaired listeners. Results from experiment I suggest that GOM produces less variable estimates of compression in listeners with normal hearing at the expense of underestimating compression at lower signal frequencies. While neither GOM nor TM in their present forms are suitable for clinical use because of lengthy test times, the purpose of the following experiment was to determine which of the two masking paradigms is better suited for listeners with impaired hearing.

A. Methods

1. Stimuli and procedure

GOM and TM curves were measured in five hearing-impaired listeners. Stimulus parameters and experimental procedures were identical to those used in experiment I with the following exceptions:

1. For GOM functions, the signal was presented at levels between 5 dB SL and the upper limit of maximum comfort, in 5-dB intervals. For most listeners, the signal levels tested were considerably higher than those tested in the group of normal-hearing listeners. Absolute thresholds were measured at the beginning of each test session to verify that the signal was audible.

2. For TM curves, the signal was presented at 5 dB SL (instead of the 10 dB SL used in experiment I). This facilitated measurements at a greater number of signal delays than would have otherwise been possible. Absolute thresholds were measured at the beginning of each test session to verify that the signal was audible.

3. With the exception of listener I4, GOM and TM curves were measured at signal frequencies of 1, 2, and 4 kHz. In the case of listener I4, thresholds were measured at 1, 2, and 3 kHz because of the severity of his hearing loss at 4 kHz.

2. Subjects

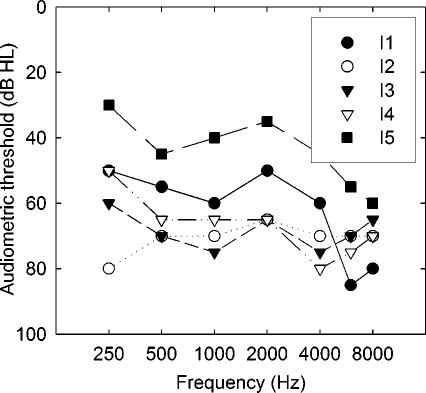
Five hearing-impaired listeners with relatively flat audiometric thresholds between 500 and 4000 Hz were included as subjects in experiment II. Absolute thresholds and (presumed) etiology of each listener's hearing loss are shown in Fig. 5 and Table IV, respectively. Listeners were recruited from a large audiology clinic in the Boston area and were compensated monetarily for their time. Test sessions typically lasted for 2 h (including breaks) and listeners were tested two to three times per week.

FIG. 5.

Audiometric thresholds of the ear tested for each hearing-impaired subject in experiment II.

TABLE IV.

Presumed etiology of each hearing-impaired subject's hearing loss.

Subject	Ear tested	Etiology
I1	left	Meniere's
I2	left	unknown, congenital
I3	right	Norrie disease
I4	right	unknown
I5	right	presbycusis

B. Results

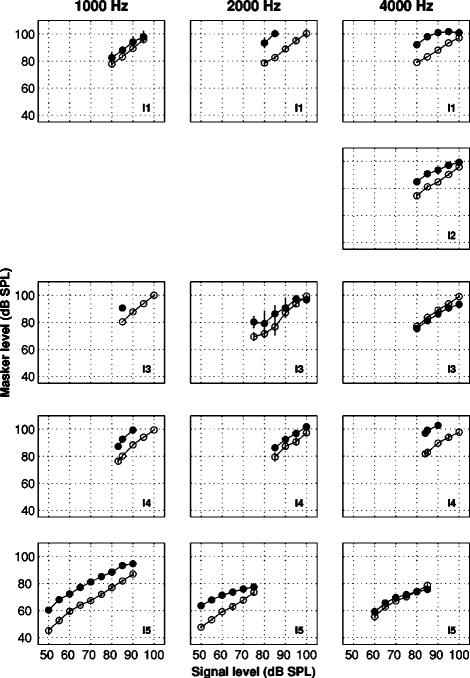
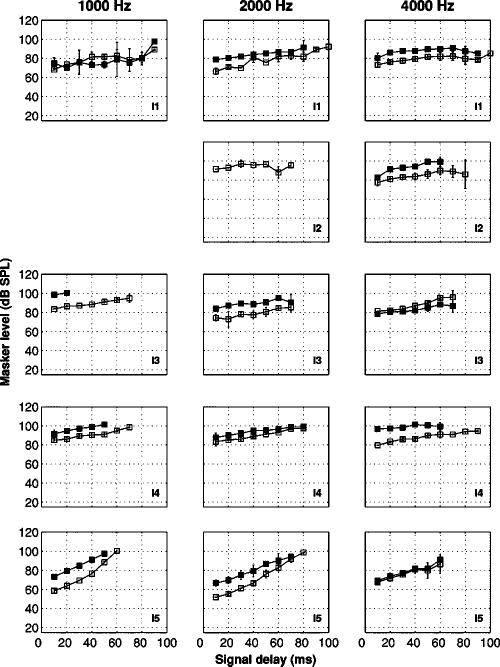
Results for the hearing-impaired listeners are shown in Figs. 6 (GOM) and 7 (TM). Each row corresponds to a different listener. On- and off-frequency masked thresholds are plotted with open and filled symbols, respectively. Error bars represent ±1 standard deviation. Due to maximum level discomfort issues and the output limitation of 102 dB SPL, on-and off-frequency masked thresholds could not be collected in all listeners in every condition. For example, neither GOM nor TM curves could be measured in listener I2 at a signal frequency of 1 kHz, as the signal remained detectable at the highest allowable masker level.

FIG. 6.

GOM functions measured at signal frequencies of 1, 2, or 4 kHz for hearing-impaired listeners in experiment II. Each row represents a different subject. Filled symbols represent off-frequency masked thresholds and open symbols represent on-frequency masked thresholds. Error bars represent ±1 standard deviation.

FIG. 7.

TM curves measured at signal frequencies of 1, 2, or 4 kHz for hearing-impaired listeners in experiment II. Each row represents a different subject. Filled symbols represent off-frequency masked thresholds and open symbols represent on-frequency masked thresholds. Error bars represent ±1 standard deviation.

With the exception of listener I5, TM thresholds varied little with increasing signal delay. This is in contrast to the listeners tested in experiment I and previously described findings regarding normal-hearing listeners (e.g., Nelson et al., 2001). Reduced rate of decay for forward masking in impaired listeners has been attributed to reduced compression on the basilar membrane (e.g., Glasberg and Moore, 1992; Oxenham and Moore, 1997). However, this hypothesis can only be applied to on-frequency masking data, which is thought to reflect both compression of the masker and decay of the internal representation of the masker. Off-frequency TM curves (particularly at higher frequencies) should only reflect decay of the masker and so should not be affected by a loss of or reduction in the magnitude of basilar membrane compression. Plotting masker threshold in dB SPL as a function of masker-signal delay (ms) and excluding the data of listener I5, the mean slope of the off-frequency masking curve for each signal frequency was 0.17 (s.e.=0.07) at 4 kHz, 0.15 (s.e.=0.01) at 2 kHz, and 0.23 (s.e.=0.02) at 1 kHz. These values are less than half the slope values measured in the normal-hearing listeners. Slope values for listener I5, who had the mildest hearing loss, were close to normal: 0.39 at 4 kHz, 0.48 at 2 kHz, and 0.60 at 1 kHz. These findings suggest either the presence of a true temporal processing deficit unrelated to the effects of cochlear compression or loss of compression (cochlear or more central) that is not restricted to on-frequency stimuli. A similar effect has been found by Plack et al. (2004) in more mildly impaired listeners. However, in contrast to their results, the shallower slopes found here seem unlikely to result simply from the somewhat higher masker levels used with the hearing-impaired listeners. The range of levels used was fairly similar across the two groups and, furthermore, no correlation was found between masker level and off-frequency TM slope for the normal-hearing listeners.

For listener I1, higher on-frequency masker levels were needed to just mask the 1-kHz signal for the 0-ms delay condition (GOM paradigm) than for the 10-ms delay condition (TM paradigm) (compare leftmost open data points in Figs. 6 and 7 for listener I1, 1-kHz signal condition). While it is not unusual to find little or no change in threshold with initial increases in forward masking interval with impaired listeners (e.g., Glasberg et al., 1987), increases are less common. The difference may be related to the context in which the conditions were run: in GOM the gap was always 0 ms, and so listeners had ample opportunity to build a perceptual “template,” whereas in TM the gaps changed from run to run, perhaps making the detection process in some listeners less “optimal.”

C. Estimating compression values

Basilar membrane response curves derived from the TM data are shown in Fig. 8. Each row corresponds to a different listener. A straight line fit to the 2.2-kHz masking curve (i.e., off-frequency masking curve measured in the 4-kHz signal condition) was used as the linear reference for all conditions. For listener I4, the 3-kHz signal off-frequency (i.e., 1.65-kHz) masking curve was used as the linear reference. The LS function and the multiphase regression function were fit to the response curves and are shown by the solid and dashed lines, respectively. Minimum slope values derived from the fitted functions are shown in Tables V and VI. As was sometimes the case with the normal-hearing listeners in experiment I, the choice of fitting function sometimes produced substantially different compression values for the same data set. In some conditions, both functions produced implausibly small (as well as a few negative) values. The LS function may be particularly unsuited to dealing with basilar membrane response curves measured in listeners with more severe hearing loss, because the equation defines the function's compressive region to be between 20 and 80 dB and assumes a linear response for input levels exceeding 80 dB. In some listeners the majority of data points fall well above 80 dB and the derived response functions are rather shallow (for example, see listener I4 in Fig. 8). In such cases, the LS function produces minimum (or negative) slope values for input levels that are below the range over which data could be collected. In all cases, however, the slope values quoted in the tables correspond to the minimum values that occurred within the range of levels actually measured for a given listener.

FIG. 8.

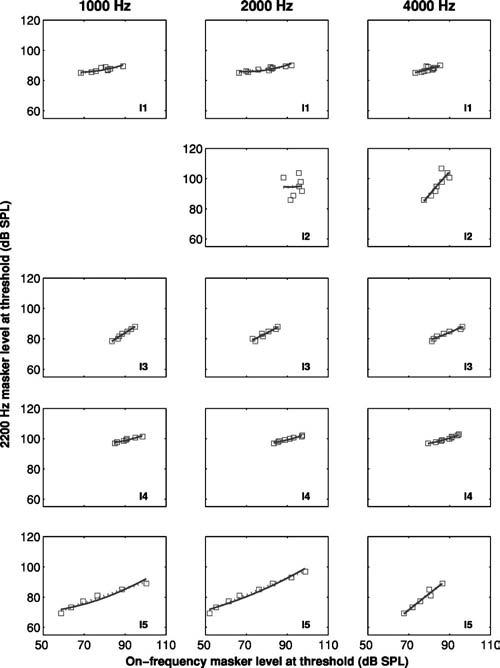
Basilar membrane response curves derived from TM data for hearing-impaired listeners in experiment II. Each row represents a different subject. The LS function fit to the data is plotted as a solid line. The multi-phase regression function is plotted as a dashed line. A straight line fit to the off-frequency TM curve measured at f_m=2.2 kHz was used as the linear reference.

TABLE V.

Estimates of compression calculated from the LS function fit tobasilar membrane response curves derived from GOM and TM data, for each signal frequency in experiment II. Dashed lines indicate conditions where estimates could not be calculated due to an insufficient number of thresholds.

Subject	GOM	TM Reference=0.55fs	TM Reference=2.2 kHz
		fs=1000 Hz
I1	0.85	0.80	0.02
I2	…	…	…
I3	…	1.20	0.85
I4	1.3	1.1	−0.18
I5	0.83	0.62	0.25
		fs=2000 Hz
I1	1.40a	0.42	−0.07
I2	…	…	0.01
I3	0.48	0.50	0.66
I4	0.85	0.67	0.18
I5	0.51	0.61	0.43
		fs=4000 Hz
I1	0.31	0.27	0.27
I2	0.58	1.70	1.70
I3	0.80	0.45	0.45
I4	0.82	0.24	0.24
I5	0.66	1.10	1.10

^aBased on two data points.

TABLE VI.

Estimates of compression calculated from the ratio of slopes of the GOM data and from the multiphase regression function fit to basilar membrane response curves derived from GOM data and TM data in experiment II. Dashed lines indicate conditions where estimates could not be calculated due to an insufficient number of thresholds.

Subject	GOM Slope ratio	GOM-multiphase regression function Reference=0.55fs	TM-multiphase regression function Reference=0.55fs	TM-multiphase regression function Reference=2.2 kHz
		fs=1000 Hz
I1	0.86	…	0.82	0.21
I2	…	…	…	…
I3	…	…	1.30a	0.86
I4	1.06	…	1.04	0.33
I5	0.85	0.83	0.70	0.46
		fs=2000 Hz
I1	1.25a	1.34a	0.54	0.19
I2	…	…	…	0.10
I3	0.63	0.44	0.56	0.69
I4	0.85	…	0.74	0.36
I5	0.54	0.48	0.67	0.56
		fs=4000 Hz
I1	0.46	−0.20	0.37	0.37
I2	0.67	0.67	1.55	1.55
I3	0.84	0.75	0.55	0.55
I4	0.86	0.70	0.36	0.36
I5	0.71	0.70	1.07	1.07

^aBased on two data points.

Further examination of Fig. 8 highlights a potential difficulty in using the TM paradigm for estimating compression in impaired listeners, regardless of which fitting function is used. Because of the extremely shallow slopes of the TM curves, the derived input-output function poorly describes the response of the basilar membrane, as most of the data points are clustered in one small region. In principle it would be possible to carefully choose masker-signal intervals to span a wider range of masker levels. However, this would require extensive individual pilot testing, which would further increase the duration of the already very long experiment. In contrast, the GOM technique measures compression over a range of levels that is determined by the signal level, which is one of the experimental parameters.

The slope ratios of the GOM functions (see Table VI) seem to produce compression estimates that are generally consistent with peripheral-based hearing loss (e.g., Ruggero et al., 1996; Oxenham and Moore, 1995), even in listeners with severe hearing loss. However, because of level discomfort issues, the number of GOM thresholds that could be measured was sometimes small. Furthermore, for listeners who demonstrate compression values that approach normal, the issue of the compression's frequency specificity is a factor at lower signal frequencies. For example, compare compression values for listener I5 derived from GOM and TM curves at a signal frequency of 1 kHz. While the minimum slope derived from the TM data (using f_m=2.2 kHz) is close to normal, the GOM slope ratio approached unity. However, if f_m=0.55f_s is used as the linear reference for the derived basilar membrane response curve, compression values calculated using the two forward-masking paradigms are more similar (0.62 using the LS function and 0.70 using the regression function). As was the case with normal-hearing listeners in experiment I, this finding suggests that the GOM paradigm may not produce accurate estimates of compression at lower signal frequencies, possibly because of a more extensive compressive region at these characteristic frequencies.

Using a TM paradigm, Plack et al. (2004) observed that maximum compression in many listeners with mild to moderate hearing loss approaches normal values, albeit over a reduced range of input levels. In contrast, most of our listeners showed more linearized response functions throughout the level range. This may reflect the fact that our listeners were more severely impaired, and so had less (or no) residual cochlear amplification. It may also be due to the more restricted range of threshold levels that could be measured. An exception to this is seen in listener I5's TM data at f_s=1 kHz (see Fig. 8, bottom left-hand panel). The multiphase regression function fit to the derived basilar membrane response curve indicated the presence of a compressive region between about 60 and 100 dB, with a minimum slope value of 0.46 dB/dB. Examination of the GOM functions also suggests the presence of a reduced region of compression for listener I1 at f_s=4 kHz (see Fig. 6, upper right-hand panel).

To allow a more direct comparison between the TM and GOM data, the LS function and the multiphase regression function were fit to response curves derived from the GOM data by plotting off-frequency masker levels as a function of on-frequency masker levels, paired according to signal level. Whenever possible the actual off-frequency data points were used. In cases where the number of on-frequency data points exceeded the number of off-frequency points, a straight line fit to the off-frequency data was used. Compression values are shown in Table V (column 1) and Table VI (column 2). For listener I4, the multiphase regression function could not be used for signal frequencies of 1000 and 2000 Hz because the number of data points did not exceed the number of parameters in the fitting function. For listener I1 at f_s=4 kHz, the multiphase regression function indicated the presence of a compressive region between about 90 and 100 dB, with a minimum slope value of −0.2 dB/dB. While this slope value is implausible, it does suggest the presence of compressive activity at this frequency. Furthermore, the results of the regression function indicate that calculating the slope ratio from single straight-line fits to the entire data range would underestimate the magnitude of compression.

Consistent with the results from the normal-hearing listeners, there was no systematic difference between compression estimates from GOM and TM when the 0.55f_s reference was used (paired t-test: t=0.5; p=0.6). However, in contrast to the results from the normal-hearing listeners, there was no significant correlation between the two measures (R=0.03; p=0.9). This suggests that either or both measures may not produce results that are reliable enough to distinguish between different listeners. TM seems to produce more scattered results, with some slope estimates being greater than one (suggesting expansion) and others implying strong compression, whereas the GOM estimates tend more generally to imply less-than-normal compression, which is expected based on the degree of hearing loss. However, without independent physiological confirmation it is not possible to say which measure is more accurate in absolute terms.

Test reliability of the GOM and TM paradigms was examined by constructing 0.95 confidence intervals around minimum slope values derived from the LS function using the Jacobian matrix at the solution (Table VII). While the statistical significance of differences in confidence interval width could not be easily assessed due to an unequal number of estimates across the different conditions (GOM and TM curves could not be measured in all listeners at every signal frequency), TM confidence intervals were slightly smaller at 1 kHz but more than twice as large at 2 and 4 kHz. This is similar in trend to the results from normal-hearing listeners, showing that GOM tends to produce less variable estimates of compression.

TABLE VII.

The mean width of 0.95 confidence intervals around compression estimates derived from individual hearing-impaired GOM and TM data in experiment II, using the LS function. The confidence intervals were constructed using the Jacobian matrix at the solution to the function.

	Width of CI
Signal frequency (kHz)	GOM	TM
1	0.19	0.17
2	0.21	0.50
4	0.11	0.23

In summary, hearing-impaired listeners showed shallower on- and off-frequency TM curves than normal-hearing listeners. The shallower off-frequency curves may indicate a reduction in temporal acuity or the presence (in normal hearing) of substantial off-frequency compression, even at 4 kHz. The resulting basilar membrane compression estimates indicated a general loss of compression, in line with that found in earlier studies (e.g., Oxenham and Plack, 1997). In contrast to the results from more mildly impaired listeners (Plack et al., 2004), there was generally no level region in which normal compression was observed. TM curves produced more variable estimates of compression, which were often difficult to interpret, due to the very restricted range of masker levels covered. This could be remedied by using a wider range of masker-signal temporal gaps, but at the cost of even longer testing times.

V. CONCLUSIONS

The main purpose of this study was to determine whether GOM and TM produce within-subject estimates of compression that are consistent across a range of signal frequencies, and which of the two paradigms is a more efficient measure. Results from normal-hearing listeners in experiment I suggest that while GOM is a less variable measure of compression (i.e., smaller confidence intervals for a similar number of data points), it may also underestimate compression at 1 kHz (and possibly at higher frequencies), most likely due to the reduced frequency specificity of compression in more apical regions (e.g., Plack and Drga, 2003). In the TM paradigm, this concern can be addressed by using a high-frequency off-frequency masking function as the linear reference for all signal frequencies. The two fitting procedures(LS and multiphase regression) produced somewhat different estimates of compression, but this could be ascribed to the different level ranges over which the estimates were valid. LS was considered less desirable because of its implicit assumption that cochlear gain is related to the maximum amount of compression.

The limitations of the LS function were further highlighted in the results of experiment II, which showed that the function failed to capture the trends in the data from the hearing-impaired listeners. Again, the GOM function produced less variable estimates of compression overall, with the caveat that the results may not be accurate at low signal frequencies.

Experiment II produced unexpected results in that the off-frequency TM curves were shallower than normal for the hearing-impaired listeners. Further work will be required to decide whether this reflects a general temporal deficit or whether some other mechanism, such as a non-frequency-specific compression, can account for the effect.

In summary, the advantages of GOM are as follows:

1. It provides relatively stable estimates of compression: GOM confidence intervals were generally smaller than those for TM.

2. The level range over which compression is estimated can be defined in advance, without the need for pilot testing: For TM curves, either a large range of masker-signal intervals must be tested to ensure that the level range of interest is covered, or pilot testing must be undertaken.

The advantages of the TM paradigm are as follows:

1. It uses a low signal level, which avoids issues related to off-frequency listening and the basal shift of the traveling wave. The issue with off-frequency listening in GOM may be particularly difficult with hearing-impaired listeners, where it may be difficult to ensure off-frequency masking without inadvertently producing on-frequency interference.

2. It is possible to estimate compression at low signal frequencies by using off-frequency masking curves from higher signal frequencies: with GOM, compression estimates at lower signal frequencies may be biased and there is no obvious way to compensate for it.

In their current forms, neither paradigm is clinically useful, because of the very long testing times required to derive a full function. However, it remains possible that an abbreviated version can be developed, in which compression over a very limited level range is targeted.