Terminal Restriction Fragment Length Polymorphism Data Analysis for Quantitative Comparison of Microbial Communities

Abstract

Terminal restriction fragment length polymorphism (T-RFLP) is a culture-independent method of obtaining a genetic fingerprint of the composition of a microbial community. Comparisons of the utility of different methods of (i) including peaks, (ii) computing the difference (or distance) between profiles, and (iii) performing statistical analysis were made by using replicated profiles of eubacterial communities. These samples included soil collected from three regions of the United States, soil fractions derived from three agronomic field treatments, soil samples taken from within one meter of each other in an alfalfa field, and replicate laboratory bioreactors. Cluster analysis by Ward's method and by the unweighted-pair group method using arithmetic averages (UPGMA) were compared. Ward's method was more effective at differentiating major groups within sets of profiles; UPGMA had a slightly reduced error rate in clustering of replicate profiles and was more sensitive to outliers. Most replicate profiles were clustered together when relative peak height or Hellinger-transformed peak height was used, in contrast to raw peak height. Redundancy analysis was more effective than cluster analysis at detecting differences between similar samples. Redundancy analysis using Hellinger distance was more sensitive than that using Euclidean distance between relative peak height profiles. Analysis of Jaccard distance between profiles, which considers only the presence or absence of a terminal restriction fragment, was the most sensitive in redundancy analysis, and was equally sensitive in cluster analysis, if all profiles had cumulative peak heights greater than 10,000 fluorescence units. It is concluded that T-RFLP is a sensitive method of differentiating between microbial communities when the optimal statistical method is used for the situation at hand. It is recommended that hypothesis testing be performed by redundancy analysis of Hellinger-transformed data and that exploratory data analysis be performed by cluster analysis using Ward's method to find natural groups or by UPGMA to identify potential outliers. Analyses can also be based on Jaccard distance if all profiles have cumulative peak heights greater than 10,000 fluorescence units.

Culture-independent methods of microbial community analysis involve the analysis of signature biochemicals extracted directly from environmental samples. Molecular genetic techniques, utilizing extracted genomic or ribosomal nucleic acids, allow microbial community analysis to be coupled with a phylogenetic framework (1, 29). The use of such techniques has shown that methods relying on growth of the organisms ex situ reveal a small fraction of the diversity present in soil microbial communities (see, for example, references 27 and 28). This uncultured diversity includes both species that are closely related to cultured organisms and species that represent virtually uncultured phylogenetic lineages (6, 8, 12).

Most molecular methods involve the separation of PCR amplicons based on differences in DNA sequence of genes of functional or phylogenetic interest, often the 16S rRNA gene. These include denaturing gradient gel electrophoresis (20), ribosomal intergenic spacer analysis (2), single-strand conformation polymorphism (25), amplified ribosomal DNA restriction analysis (19), and terminal restriction fragment length polymorphism (T-RFLP) (3, 16). These methods do not reveal diversity per se unless the community is very simple, since only a fraction of the species indicated by DNA rehybridization rates or sequence analysis of a clone library can be visualized on a gel (4, 21). These methods do provide a way to determine the relative abundance of common species present in a sample, free of the constraint that the organisms must be amenable to growth in the laboratory. They are valuable as rapid methods of finding major differences between communities and testing hypotheses based on a comparison of samples.

T-RFLP has been shown to be effective at discriminating between microbial communities in a range of environments (26). It involves tagging one end of PCR amplicons through the use of a fluorescent molecule attached to a primer. The amplified product is then cut with a restriction enzyme. Terminal restriction fragments (T-RFs) are separated by electrophoresis and visualized by excitation of the fluor. T-RFLP analysis provides quantitative data about each T-RF detected, including size in base pairs and intensity of fluorescence (peak height). T-RF sizes can be compared to a database of theoretical T-RFs derived from sequence information (for example, see references 5 and 18). T-RFLP profiles have been shown to be relatively stable to variability in PCR conditions (22, 23).

Presently, the least-well-defined technical aspect of T-RFLP is the data processing and analysis of profiles. A wide range of methods has been used in the literature. The goal of this study was to find an optimal procedure for use in comparing complex environmental T-RFLP profiles, resulting in the lowest probability of type II errors (not finding differences between profiles when they are actually different). Analytical replicates were used in this assessment so that the actual relationships between some of the profiles would be known with certainty, allowing us to test the statistical methods themselves. Several aspects of analysis of T-RFLP data were examined, including (i) rules for including peaks in analysis, (ii) the basis for how differences between aligned profiles are measured (i.e., the distance metric used), and (iii) analysis of the relationships between profiles. The sensitivity of statistical methods to these factors is dependent not only on the analytical consistency of replicate profiles, but also on the degree of divergence between communities. We used four sets of samples, representing a range of biological complexity and environmental differentiation, to determine the relative utility of different methods of statistical analysis of T-RFLP profiles.

MATERIALS AND METHODS

(i) KBS soil fractions.

Soil samples were collected from agricultural field plots of the Long-Term Ecological Research (LTER) site and the Living Field Lab at the W. K. Kellogg Biological Station (KBS) in southwestern Michigan. Soils at this site are Typic Hapludalfs and are approximately 43% sand and 40% silt (24). Samples were 0.9 to 1.3% organic matter, with a pH of 6.2 to 6.7. Field treatments included continuous alfalfa, conventionally managed continuous corn, and organically managed first-year corn in a corn-corn-soybean-wheat rotation with cover crops (10) (http://lter.kbs.msu.edu). Three intact soil cores, weighing approximately 350 g, were excavated and pooled for each of four field plots of each treatment. Sampling depth was 10 cm. The soil was fractionated into rhizosphere, shoot residue, and light and heavy fractions from various sizes of soil macroaggregates (C. Blackwood and E. Paul, submitted for publication). Samples were stored at 4°C until fractionation was complete, which was within 8 weeks.

(ii) Bioreactor samples.

Bioreactor samples were taken from a fluidized-bed reactor with activated carbon as the particulate carrier. The reactor was inoculated with an anaerobic enrichment culture derived from Milan soil (see below) and fed continuously with ethanol and essential nutrients. Samples were removed, pelleted, and stored at −20°C until needed.

(iii) KBS alfalfa soil samples.

Ten-gram soil samples were collected from five locations within a 1.5- by 2-m plot within an alfalfa field at the KBS LTER site. Samples were collected from the layer of soil 2 to 4 cm deep. Samples were immediately placed on dry ice and kept frozen until processing. These samples were part of a larger study of the spatial structure of soil microbial communities.

(iv) Multiregion soil samples.

Soils were collected from Sault Saint Marie, Mich., Milan, Tenn., and Hawthorne, Nev. (pH 7.0, 6.3, and 7.9, respectively; the Nevada and Tennessee soils were provided by Robert Hickey, RETEC Group, Inc.). One 500-g sample of soil was removed from the top 5 cm of soil, homogenized, and aliquoted to 100-ml specimen containers. Samples were stored at −20°C until needed.

T-RFLP experiments 1 and 3.

Mixed community DNA was extracted from 0.2- to 0.3-g soil fractions with the Ultraclean soil DNA extraction kit (Mo Bio Laboratories, Solana Beach, Calif.), including a 10-min. bead-beating step performed with a vortexer. DNA was extracted from the 10-g alfalfa soil samples by using the large-scale Ultraclean soil DNA extraction kit, including a 30-min. incubation at 65°C with rotary shaking with beads. Optimization of PCR was performed for each sample by adjusting the amount of genomic DNA extract used (0.4 to 2 μl) to obtain a strong band on an agarose gel, without visible nonspecific product. This method was found to be more efficient than quantitation of the DNA in each sample, which did not necessarily result in optimal PCR conditions. PCR was performed by using a reaction mixture of 0.2 μg of bovine serum albumin (Boehringer Mannheim Biochemicals, Indianapolis, Ind.)/μl, 160 μM each deoxynucleoside triphosphate, 3 mM MgCl₂, 0.05 U of Gibco Taq DNA polymerase/μl, 1× PCR buffer (Gibco BRL, Gaithersburg, Md.), and 0.4 μM each primer. The primers used were the general eubacterial primer 8-27F (AGAGTTTGATCCTGGCTCAG, with Escherichia coli numbering and with sequences derived from reference 1) (manufactured by Integrated DNA Technologies, Coralville, Iowa) and the universal primer 1392-1406R (ACGGGCGGTGTGTACA) amplifying the 16S ribosomal gene. PCR was performed in a Perkin-Elmer 9600 thermocycler by using an initial denaturation step of 95°C for 3 min, followed by 22 cycles of a program consisting of denaturation at 94°C for 30 s, primer annealing at 55°C for 30 s, and extension at 72°C for 30 s. PCR tubes were placed in the thermocycler when the block temperature reached 80°C. A final extension at 72°C for 7 min was performed after the programmed number of cycles was complete.

PCRs (50 to 75 μl) were performed in triplicate under the optimal conditions found previously, except that the forward primer was 0.6 μM hexachlorofluorscein (hex)-labeled 8-27F (Integrated DNA Technologies). PCR replicates were then pooled and purified by using the Promega PCR Preps Wizard kit as directed by the supplier, except that elution was performed with 19 μl of sterile water heated to 55 to 65°C. Five microliters of purified PCR product (approximately 600 ng) was mixed with 5 μl of restriction enzyme master mix containing 1.5 U of restriction enzyme (RsaI)/μl and 1× reaction buffer (Gibco). Restriction reactions were incubated for 3 h at 37°C, followed by 16 min at 65°C to denature the restriction enzyme. Three microliters of the restricted PCR product was mixed with 1 μl of 2500 TAMRA size standard (Applied Biosystems Instruments, Foster City, Calif.). DNA fragments were separated by size by electrophoresis at 1,800 V for 14 h on an ABI 373 automated DNA sequencer at Michigan State University's DNA sequencing facility. The 5′ terminal fragments were visualized by excitation of the hex molecule attached to the forward primer. The gel image was captured and analyzed by using Genescan version 3.1 analysis software. A peak height threshold of 50 fluorescence units was used in the initial analysis of the electropherogram. Negative controls (no genomic DNA) were conducted with every PCR and run on several Genescan gels. Contamination in PCRs was not detected. Small peaks occasionally appeared in negative control lanes on Genescan gels, but the cumulative peak height was always below 1,000 units.

T-RFLP experiments 2 and 4.

Amplifications of bioreactor and multiregion soil samples were performed as above with the following modifications. The reverse primer used was 1492R (GGTTACCTTGTTACGACTT), and one 100-μl PCR was performed per sample with 0.2 mM deoxynucleoside triphosphates, 1.5 mM MgCl₂, 0.4 μM hex-labeled 8-27F primer, 0.2 μM 1492R primer, 0.1 μg of bovine serum albumin/μl, 0.2 ng of template DNA/μl, and 0.05 U of Taq polymerase (PE Amplitaq)/μl. Thermocycling was performed in a GeneAmp 2400 PCR System thermal cycler (Perkin Elmer, Norwalk, Conn.) at 94°C for 5 min followed by 30 cycles of 94°C for 50 s, 55°C for 50 s, and 72°C for 1 min 30 s, with a final extension step at 72°C for 7 min. Amplifications were cleaned and concentrated by using Microcon YM-100 centrifugal filters (Millipore Corp., Bedford, Mass.). Restrictions with HhaI, MspI, and RsaI were performed independently.

Replication experiments.

For the set of KBS soil fraction samples, one PCR replicate (generated by pooling three PCRs) was digested per sample. Two aliquots of digest from each of 32 samples were run on two different Genescan gels. Hence, replication was at the level of the Genescan gel.

For the remaining sets of samples, two PCR replicates were generated for each sample. For the alfalfa soil samples, six PCRs were run per sample, and three of these were pooled for each PCR replicate, while for the bioreactor and multiregional samples, each PCR replicate was from one PCR. The PCR replicates were then restricted, and two aliquots of each restriction were run on a Genescan gel, resulting in a total of four replicate T-RFLP profiles per sample. Replication was at the level of the PCR, restriction, and Genescan lane.

Data processing.

Data sets were constructed by using minimum peak height thresholds of 50, 100, and 200 fluorescence units. Rarefaction was also used as a method of determining which small peaks should be included in the analysis (7). Occasionally, the baseline fluorescence of the T-RFLP electropherograms was elevated (i.e., fluorescence did not reach zero between widely spaced peaks). If the value of the baseline could be ascertained, the baseline was subtracted from peak height in that region. If the baseline varied inconsistently, the sample was rerun. Data sets were also created by using either all profiles or only profiles with a cumulative peak height greater than 10,000 fluorescence units. T-RFLP profiles were aligned by inspection of the electropherogram and by manual grouping of the peaks into categories. Alignment of peaks by manual inspection was based primarily on the size of peaks in base pairs, although the pattern of peaks was also used to determine their alignment when groups of overlapping peaks were found between samples. The identities of samples were concealed during manual alignment.

Statistical analyses.

Several different distance metrics were compared, including Euclidean distance between profiles calculated from either raw or relative peak heights, Hellinger distance, and Jaccard distance (JD) (equal to 1 minus Jaccard's coefficient). Hellinger distance is equivalent to the Euclidean distance between profiles after square root transformation of relative peak heights (14). Jaccard's coefficient is based on binary variables of peak presence and is equal to the ratio of the number of matching T-RFs to the total number of T-RFs present in either profile (15).

Statistical methods of analyzing the relationships between T-RFLP profiles that were compared included redundancy analysis and two methods of hierarchical cluster analysis, namely, the unweighted-pair group method using arithmetic averages (UPGMA) and Ward's method (SAS Institute, Inc.) (9). The cophenetic correlation was calculated for dendrograms by using an algorithm written in SAS IML. Evaluation of clustering errors was performed by using dendrograms showing the hierarchical relationships between T-RFLP profiles as found by the clustering procedure. The number of clusters examined was chosen to be the number required to explain a constant arbitrary proportion of the variance in the entire data set (50 percent). An error was counted when two replicate T-RFLP profiles (i.e., profiles derived from the same DNA extract) were clustered into different groups.

Statistical significance of the difference between samples, and, as a corollary, the similarity of replicate profiles, was tested by using redundancy analysis with Canoco software (Microcomputer Power, Ithaca, N.Y.). This compares a pseudo-F statistic, calculated from the proportion of the total variance explained by sample identity, to the values of F of 9,999 random permutations of the sample identities of the profiles (15). Redundancy analysis was also used to test the significance of differences between replicate PCRs, with permutation restricted by sample. Distance-based redundancy analysis was used to determine significance when using JD (13), with calculation of the JD matrix and its principal coordinates being performed by using an algorithm written in SAS IML, adapted from original code provided by Carl Ramm at Michigan State University. SAS code is available from C. Blackwood upon request.

RESULTS

(i) KBS LTER soil fraction samples.

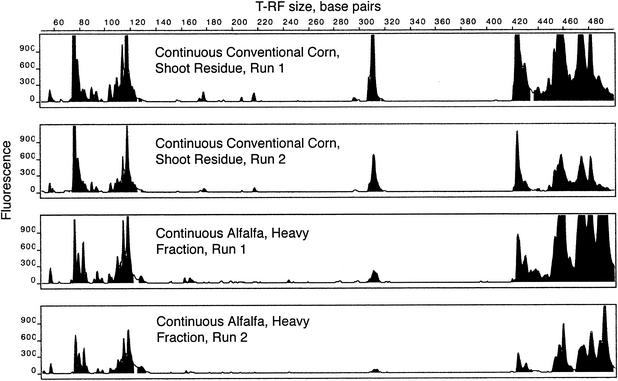
In the first set of samples, there were 32 replicated profiles. An example of two replicated profiles is shown in Fig. 1. There are differences between these two profiles, such as the prominent peak at 310 bp in corn and the 85-bp peak in alfalfa. The analytical replicates also differ, primarily because of differences in peak height, although there is some noise in the size of fragments as well.

FIG. 1.

Example of analytical replicates of T-RFLP profiles from two soil eubacterial communities. PCR fragments were cut with RsaI.

The mean value of the fragment size ranges for T-RF categories resulting from the alignment procedure was 1.4 bp (the maximum range was 4.4 bp). Clustering using raw, unstandardized peak height consistently resulted in the greatest number of errors (Table 1). Use of relative peak height (peak height divided by the cumulative peak height of the given sample) resulted in the fewest number of errors. Clustering using binary variables (JD) had an error rate higher than that for relative peak height but still much lower than that for raw peak heights (Table 1). Neither deletion of peaks with heights of less than 100 fluorescence units or less than 1% of the cumulative peak height nor rarefaction resulted in improvement of clustering, relative to results with the use of all peaks with heights of more than 50 units. Deleting all peaks with heights of less than 200 units increased the number of errors (Table 1). Use of the Hellinger transformation resulted in an increase of up to two errors over the analogous dendrogram based on relative peak height. UPGMA clustering typically contained one to two fewer errors than clustering by Ward's method and also resulted in a higher cophenetic correlation (or correlation between elements of the original distance matrix and a distance matrix constructed from the results of the cluster analysis). However, clustering by Ward's method required fewer clusters to explain 50 percent of the variance in the data set.

TABLE 1.

Dendrogram characteristics for cluster analyses of T-RFLP profiles of KBS soil fractions by using a variety of data processing methods and clustering algorithms

Variablea	Baselineb	Ward's method		UPGMA
		No. of errors (out of 32)	No. of clusters	No. of errors (out of 32)	No. of clusters
Height	50	14	6	12	9
	100	14	6	12	9
	200	18	6	12	9
Relative height	50	2	6	1	10
	100	2	6	1	8
	200	3	6	5	7
	Rarefaction	2	6	1	9
	1%	2	6	1	10
Hellinger transformed	50	2	11	1	13
	100	2	11	1	13
	200	7	11	5	12
	Rarefaction	4	11	2	12
	1%	3	11	2	12
JD	50	6	6	5	8
	100	11	5	5	7
	200	8	4	9	4
	Rarefaction	7	7	3	9
	1%	5	7	4	7

^aAll profiles were included in analysis; the minimum cumulative peak height is 4,000 fluorescence units. See the text for a description of the results when profiles with less 10,000 fluorescence units are excluded.

^bBaseline refers to a minimum peak height cutoff (fluorescence units) or other method of determining how small peaks are excluded.

Deletion of samples with cumulative peak height of less than 10,000 fluorescence units resulted in 22 replicated profiles. There were one or zero errors for all combinations of clustering methods and distance metrics tested.

(ii) Bioreactor samples.

The bioreactors were treated identically, so their communities should be very similar to each other. Hence, a statistical method with a high level of sensitivity is required to tell apart the T-RFLP profiles, or errors in determining which profiles are derived from the same samples will occur.

The various methods of data processing and analysis did not greatly affect the error rate of clustering of bioreactor replicates, and no method appeared to perform best (see Table 2). This was consistent for RsaI, MspI, and HhaI digests analyzed separately, as well as for analysis of all three digests simultaneously. There were typically nine errors in each dendrogram (out of a potential 18 possible errors). For this set, each sample was represented by two replicate PCRs, each of which was run twice. Approximately half of the errors could be traced to differences between replicate PCRs, with the two profiles of one PCR clustering together but apart from the two profiles of the other replicate PCR of the same sample (as opposed to random errors due to lane-to-lane variability of the gel).

TABLE 2.

Dendrogram characteristics for cluster analyses of T-RFLP profiles of bioreactor samples by using a variety of data processing methods and clustering algorithms

Statistics for MspI, RsaI, and HhaI	Variablea	Baselineb	Ward's method			UPGMA
			No. of errors (out of 18)	No. of clusters	Cophenetic correlation	No. of errors (out of 18)	No. of clusters	Cophenetic correlation
Average, analyzed	Height	100	9.7	3.3	0.81	10.3	3.3	0.92
separately	Relative height	100	8.3	3.7	0.80	9.7	3.7	0.94
	Relative height	Rarefaction	8.3	3.7	0.79	9.7	3.7	0.94
	Hellinger transformed	100	9	4	0.82	9	4.3	0.96
	Hellinger transformed	Rarefaction	8.7	3.7	0.82	9	4	0.96
	JD	100	9.7	3.4	0.74	6.3	3.7	0.94
	JD	Rarefaction	7.3	3.3	0.75	7.7	3.3	0.94
Analyzed together	Height	100	13	4	0.79	12	4	0.94
	Relative height	100	13	5	0.77	14	5	0.95
	Relative height	Rarefaction	11	4	0.78	14	5	0.94
	Hellinger transformed	100	13	5	0.80	8	5	0.97
	Hellinger transformed	Rarefaction	13	5	0.81	8	5	0.97
	JD	100	5	4	0.74	8	4	0.97
	JD	Rarefaction	7	4	0.78	6	4	0.97

^aAll sample profiles had cumulative peak heights of >10,000 fluorescence units except some RsaI profiles.

^bBaseline refers to a minimum peak height (fluorescence units) cutoff or other method of determining how small peaks are excluded.

The significance of the differences between sample profiles was tested by using redundancy analysis of standardized peak heights, Hellinger-transformed peak heights, and principal coordinates of JD. The sample identities were found to explain a significant amount of variance in the data set for the RsaI and HhaI profiles analyzed separately and for the RsaI, MspI, and HhaI profiles analyzed together (see Table 3). Sample identities were significant for the MspI profiles only for JD. P values for all digests were lowest for analysis of JD and highest for standardized peak heights, except for the RsaI profile, where analysis of JD had the highest P value. The RsaI data set included several profiles where the cumulative peak height was less than 10,000 fluorescence units.

TABLE 3.

Redundancy analysis results from testing the null hypothesis that there is no difference between bioreactor sample T-RFLP profiles

Profilea	Variable	Sample		PCR replicate
		Proportion explained (%)	P value	Proportion explained (%)	P value
RsaI	Relative height	46	0.0017	—b	0.22
	Hellinger transformed	35	0.0003	—	0.19
	JD	35	0.012	—	0.37
MspI	Relative height	23	0.19	41	0.034
	Hellinger transformed	22	0.15	36	0.070
	JD	24	0.0054	—	0.34
HhaI	Relative height	33	0.024	38	0.072
	Hellinger transformed	33	0.0061	32	0.072
	JD	29	0.0005	—	0.19
MspI, RsaI, and	Relative height	30	0.0071	31	0.073
HhaI	Hellinger transformed	28	0.0032	30	0.073
	JD	26	0.0003	—	0.34

^aAll sample profiles had cumulative peak heights of >10,000 fluorescence units except some RsaI profiles.

^b—, variability explained is not significant at the P = 0.1 level.

PCR replicate identity explained approximately as much variability as did sample identity, but PCR replicate identity was only marginally significant for relative and Hellinger-transformed heights (Table 3). For JD, the variability explained by PCR replicate was not significant. The residual variability after accounting for sample identity and PCR replicate is due to random lane-to-lane variability.

(iii) Alfalfa soil samples.

Like the bioreactor samples, the adjacent alfalfa soil samples are likely to harbor similar communities, resulting in errors in determining which profiles came from the same samples when statistical methods that are not sensitive enough are used. While clustering using JD resulted in the lowest number of errors for the alfalfa soil samples, all dendrograms had error rates that were quite high (Table 4). Clustering by PCR replicate did not occur. Redundancy analysis detected significant differences between community profiles with analysis of Hellinger-transformed variables and of principal coordinates of JD but not with analysis of relative peak height variables (Table 5). PCR replicate identity accounted for slightly less variability than did sample identity and was not significant for any distance metric.

TABLE 4.

Dendrogram characteristics for the set of alfalfa soil samples

Variablea	Ward's method			UPGMA
	No. of errors (out of 30)	No. of clusters	Cophenetic correlation	No. of errors (out of 30)	No. of clusters	Cophenetic correlation
Relative height	15	3	0.83	16	4	0.90
Hellinger transformed	21	5	0.76	14	5	0.95
JD	13	4	0.68	9	5	0.92

^aAll sample profiles had cumulative peak heights of >10,000 fluorescence units.

TABLE 5.

Redundancy analysis results for the set of alfalfa soil samples

Variablea	Sample		PCR replicate
	Proportion explained (%)	P value	Proportion explained (%)	P value
Relative height	30	0.12	—b	0.45
Hellinger transformed	31	0.0093	—	0.61
JD	32	0.0001	—	0.16

^aAll sample profiles had cumulative peak heights of >10,000 fluorescence units.

^b—, variability explained is not significant at the P = 0.1 level.

(iv) Multiregional soil samples.

No errors were observed in cluster analysis of replicate profiles from the multiregional set of soil samples by any method of processing and analysis (data not shown). This result was consistent for RsaI, MspI, and HhaI digests. In general, two groups were required to explain 50% of the variance in the data set. This grouping divided all four replicate profiles of one sample from the eight replicate profiles of the remaining two samples. Three groups explained 75 to 85 percent of the total variance in the data set, with each group being made up by all of one sample's replicate profiles.

Peak height baseline.

Deletion of the smallest peaks by using any of a variety of algorithms had relatively little effect on the error rate of analyses, except that an increase in the number of errors was observed where larger peaks started to be deleted (i.e., peaks with heights between 100 and 200 fluorescence units; see Table 1).

Comparison of community distance metrics.

Analysis of relative peak height and Hellinger-transformed peak height resulted in similar error rates (Tables 1, 2, and 4). The Hellinger transformation did consistently result in a greater number of groups being required to account for 50 percent of the variance in the data set, although other changes in the topologies of the dendrograms were minor. Cluster analyses based on Euclidean distance calculated from raw peak heights resulted in an unacceptable number of errors for all sets of samples except the most divergent (Tables 1 and 2). The Hellinger transformation consistently resulted in a lower P value when redundancy analysis was performed to test the significance of the differences between samples (Tables 3 and 5). This reduction in P value was dramatic for the set of closely spaced alfalfa soil samples. Other data transformations examined by Legendre and Gallagher (14) were discarded either in preliminary analyses (i.e., the chord distance) or because of the heavy weighting of rare T-RFs (e.g., the chi-square distance). The latter property makes a distance metric inappropriate for T-RFLP data, since rarity of a T-RF might not reflect rarity of the associated genotype but may simply reflect sampling variability in detection of small peaks (see references 14 and 15 for discussions on weighting of rare species).

The use of JD when some profiles had low cumulative peak heights (<10,000 fluorescence units) resulted in a large number of errors in cluster analysis (Table 1) and a higher P value in redundancy analysis (Table 3). When all profiles analyzed had cumulative peak heights of >10,000 units, clustering with the use of JD was as good as that with the use of relative or Hellinger-transformed peak heights, and redundancy analysis was more sensitive (with a lower P value; see Tables 2 to 5). Analysis of JD was also the least sensitive to variability between PCR replicates, with P values of >0.15 in all cases (Tables 3 and 5). However, there was no corresponding decrease in the total variability in the JD data sets, which implies that JD was more sensitive to random lane-to-lane variability.

Comparison of statistical methods.

The number of errors found in cluster dendrograms was dependent on the set of samples being analyzed. The error rate was lower by UPGMA than by Ward's method if some profiles had cumulative peak heights of less than 10,000 fluorescence units (Table 1). The two methods had essentially equivalent error rates if all samples had cumulative peak heights greater than 10,000 units. UPGMA clustering was more true to the original distances between samples, as indicated by higher cophenetic correlation (9), and is more sensitive to outliers. This is reflected in the increased number of groups required to explain 50 percent of the total variance in the data sets in UPGMA analyses. Redundancy analysis was able to detect significant differences between samples and, as a corollary, significant similarities between analytical replicates, for both data sets tested (Tables 3 and 5).

DISCUSSION

This study was designed to aid in the choice of methods to process and analyze quantitative T-RFLP data. The results of the analyses are different, in absolute terms, for each of the sets of samples examined because the sets represent a wide range in degree of sample divergence; however, the trends in the sensitivity of data analysis methods were consistent across this gradient and resulted in some methods being clearly preferable. The best method of data analysis would find significant differences between samples in spite of PCR and lane-to-lane variability. Variability between PCR replicates was more significant for the bioreactor samples than for alfalfa soil samples. Each PCR replicate was formed by pooling three PCRs for the alfalfa soil samples, while in the bioreactor samples, each PCR replicate was from an individual PCR.

The fact that deletion of the smallest peaks either had little effect on the dendrogram error rate or increased it is surprising, because small peaks were thought to be the most inconsistent. These results imply that there were a number of T-RFs that occurred frequently and were important for distinguishing samples, yet had small peaks. Generally the statistical methods examined here deal with random PCR and gel variability but do not correct for other sorts of artifacts, such as PCR bias, which can, for instance, cause abundant organisms to generate small T-RF peaks. The effects of these artifacts, strictly on comparisons of communities, are reduced by treating all samples identically, although further research into the causes of artifacts is needed. The effects of PCR bias on peak height can also be reduced in the statistical analysis by using a metric such as JD, which accounts for presence or absence of peaks only. However, JD performed as well as Hellinger distance only if cumulative peak height, primarily affected by DNA load, was uniformly high and the presence of small peaks was stabilized.

Hellinger distance was more sensitive than relative peak height in redundancy analysis (see Tables 3 and 5) and was equally sensitive in cluster analysis. Hellinger distance is also recommended by Legendre and Gallagher (14) based on theoretical considerations and simulations, and it was used by Lukow et al. (17) in an attempt to normalize peak height distribution.

The goal of hierarchical cluster analysis is to summarize as much variability in a data set as possible within a dendrogram; hence, cluster analysis is essentially a tool for exploratory data analysis (11). The goal of redundancy analysis is to explicitly test whether that variability which can be attributed to the differences between experimental groups is significant. Therefore, it would be expected that redundancy analysis detected significant differences between samples in the less divergent sample sets, while cluster analysis often failed to show them, because these differences accounted for only 25 to 40% of the variance in the data sets. Calculation of a P value by random permutation avoids the assumption of multinormality and restrictions on the number of variables that can be analyzed (13).

Ward's method of hierarchical cluster analysis sacrifices some precision in clustering compared to UPGMA, but it is more efficient at identifying major groups within T-RFLP datasets. Also, the scale of the dendrogram plot is more heterogeneous across different levels in the hierarchy, resulting in the ability to more easily choose the number of major groups in the dendrogram. The UPGMA method may be considered a more conservative method of finding natural groups and outliers within sets of T-RFLP profiles (9). The problems associated with choosing the number of important groups that are present when comparing dendrograms with differing scales were avoided in the current study by examining whatever number of groups was required to account for 50% of the total variance. This was done to compare error rates of dendrograms on an equal basis, but it is not recommended for applications of cluster analysis other than assessing error rates, since the 50% level may not correspond to a biologically meaningful number of groups.

CONCLUSIONS

Given statistical analyses that were sensitive enough (low probabilities of type II error), it was possible to use T-RFLP to reject the null hypotheses that communities were identical in replicate bioreactors or in soil samples collected within two meters of each other. With this level of sensitivity, the utility of T-RFLP in quantitative comparison of microbial communities is obvious. If the experimental design is such that appropriate hypotheses can be formulated, redundancy analysis of Hellinger-transformed peak height and/or JD (if all profiles have a cumulative peak height greater than 10,000 fluorescence units) are recommended as the most sensitive methods to distinguish between groups of profiles. If the goal of data analysis is exploratory, clustering by using both Ward's method (to find natural groups) and UPGMA (to identify potential outliers) is recommended. The validity of clustering results are basically equivalent with the use of relative peak height, Hellinger-transformed peak height, or JD (if all samples have cumulative peak height greater than 10,000 units). This study was not an exhaustive examination of all multivariate statistical methods that could be used for T-RFLP data. Future work could examine the potential of other distance metrics and other methods of data analysis, such as correspondence analysis, principal coordinates plots, and the use of artificial neural networks, as well as more complex methods of defining the fluorescence baseline. The use of quantitative statistical analysis coupled with molecular methods creates new opportunities for addressing applied and ecological problems in microbial community analysis.