Diffusion of Calcium and Metabolites in Pancreatic Islets: Killing Oscillations with a Pitchfork

Abstract

Cell coupling is important for the normal function of the β-cells of the pancreatic islet of Langerhans, which secrete insulin in response to elevated plasma glucose. In the islets, electrical and metabolic communications are mediated by gap junctions. Although electrical coupling is believed to account for synchronization of the islets, the role and significance of diffusion of calcium and metabolites are not clear. To address these questions we analyze two different mathematical models of islet calcium and electrical dynamics. To study diffusion of calcium, we use a modified Morris-Lecar model. Based on our analysis, we conclude that intercellular diffusion of calcium is not necessary for islet synchronization, at most supplementing electrical coupling. Metabolic coupling is investigated with a recent mathematical model incorporating glycolytic oscillations. Bifurcation analysis of the coupled system reveals several modes of behavior, depending on the relative strength of electrical and metabolic coupling. We find that whereas electrical coupling always produces synchrony, metabolic coupling can abolish both oscillations and synchrony, explaining some puzzling experimental observations. We suggest that these modes are generic features of square-wave bursters and relaxation oscillators coupled through either the activation or recovery variable.

INTRODUCTION

An important control center in glucose homeostasis is the insulin-secreting pancreatic β-cell, localized in the islets of Langerhans. Insulin secretion is a complex multicellular process, which relies on interactions between β-cells within an islet as well as on the interactions between islets in the pancreas. Under normal conditions, glucose stimulation evokes well-synchronized oscillations of cytosolic Ca²⁺ concentration ([Ca²⁺]_i) in the β-cells in an islet, which in turn trigger pulses of insulin secretion (1–5). On the other hand, in islets of ob/ob mice, desynchronization of the glucose-induced [Ca²⁺]_i oscillations disturbs the regularity of the corresponding pulses of insulin secretion (6). It has been suggested (6) that such a mechanism could contribute to the irregularity of insulin oscillations in diabetic patients with Type II Diabetes mellitus (7). Thus, it is of interest to gain a better understanding of the mechanisms underlying the coordination of the pancreatic β-cell activity.

In the islets of Langerhans, gap junctions represent the functional cellular connections that are responsible for electrical and metabolic coupling (8–16). Intercellular communication through gap junctions, formed by protein subunits called connexins, plays an important role in synchronizing the activity of the pancreatic β-cells and thus in maintaining the normal physiological function of the pancreatic islets of Langerhans. There is a great deal of experimental data suggesting that connexins contribute to the control of cell function both in vitro and in vivo (11,13,16–18).

The role of electrical coupling in aiding the propagation of bursts of action potentials among coupled β-cells associated with coordinated elevations in [Ca²⁺]_i and pulsatile insulin secretion is well-established (9,10,14,16). The role of gap-junctional diffusion of calcium, shown to be crucial for synchronization in some nonexcitable cells such as hepatocytes and pancreatic acinar cells (19,20), is not clear for β-cells, however.

The extent of metabolic coupling and its influence on islet cells coordination is similarly unclear. It has been verified experimentally (14) that signaling molecules, such as intermediate products of glycolysis, can also diffuse through gap junctions in the islet cells of transgenic RIP-Cx32 mice that show enhanced junctional conductance. Moreover, it has been demonstrated (8) that signals generated in the early steps of the glycolytic pathway, in particular glucose 6-phosphate (G6P), can also propagate among islet cells.

In this article, we use mathematical modeling to study the effects of different intercellular messengers on the behavior of pancreatic β-cells diffusively coupled through gap junctions. First, we analyze the effects of intercellular calcium diffusion in a simple, Morris-Lecar-like β-cell model (21). Surprisingly, the diffusion of calcium through gap junctions, if too strong, can have a desynchronizing effect by promoting oscillator death, a phenomenon first identified in coupled chemical oscillators (22). Based on this result, we conclude that calcium gap-junctional diffusion does not make an important contribution to the normal function of pancreatic islets of Langerhans.

Next, we investigate the role that metabolic coupling plays in regulating the oscillatory behavior of islet cells. Specifically, we study the effects of gap-junctional diffusion of fructose 1-6-bisphosphate (FBP) and glucose 6-phosphate (G6P), which are intermediate products of glycolysis. For that purpose, we use a recent mathematical model that combines pancreatic islet calcium and electrical dynamics with glycolysis (23,24). Applying techniques from bifurcation theory, we show that there are different possible modes of organized collective behavior depending on the coupling messenger. The glycolytic oscillator itself, as a part of this model, is of relaxation type. Sufficiently strong coupling through the activation variable (FBP) synchronizes glycolytic oscillations while coupling through the recovery variable (G6P) kills the glycolytic oscillations. The death of the glycolytic oscillations alters qualitatively the collective behavior of the full ionic-metabolic system, providing a possible explanation of some puzzling experimental observations in islets with enhanced coupling (25) and when glucose is removed and re-added (23).

In Models and Methods, we introduce the models and explain their details, and in the section following, we present the results. We begin by showing simulations of the effects of coupling through the recovery variables or, in other words, the variables that provide negative feedback. Then, using bifurcation analysis, we study how strong coupling through both activation and recovery variables affects the collective behavior of these systems. In addition, we investigate the effects of heterogeneity among β-cells.

Although the models we consider and the questions we address in this study refer to pancreatic β-cells, the results are applicable to any system of relaxation oscillators coupled through the activation or recovery variable. Such systems, for example, include coupled chemical oscillators (22,26,27), coupled systems of neurons or coupled genetic oscillators (28). We conjecture that the oscillator death phenomenon is a general feature of systems of relaxation oscillators coupled through the recovery variable. Importantly, it is not the molecular identity of the coupling messenger that determines the behavior but its dynamical role.

MODELS AND METHODS

Morris-Lecar-like β-cell model

We extend the original model of membrane potential for barnacle muscle fiber, proposed by Morris and Lecar (21), to obtain the bursting dynamics of β-cells. In this form, it is essentially equivalent to the original Chay-Keizer model for β-cell bursting (29). We have chosen it as the simplest model that can exhibit both bursting and oscillator death but have verified that a more elaborate model (30) has the same response to Ca²⁺ coupling.

The Morris-Lecar model is a two-variable model in which the variables V and n represent the membrane potential and the fraction of open voltage-gated K⁺ channels, respectively. The modified Morris-Lecar equations are

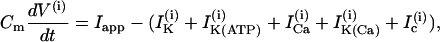(1)

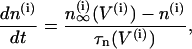(2)

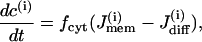(3)

where the variables V and n have been augmented by the cytosolic calcium concentration [Ca²⁺]_i, denoted c. The three dependent variables and all expressions are indexed by the cell number, (i). The value C_m is the membrane capacitance, and f_cyt is the fraction of free to total cytosolic Ca²⁺. Values of all parameters used in the model simulations are given in Table 1. The currents included in the model are

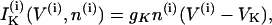(4)

(5)

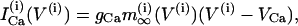(6)

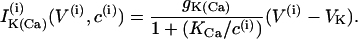(7)

TABLE 1.

Parameter values of the Morris-Lecar-like β-cell model

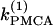	0.15 ms−1	Iapp	0 pA
fcyt	0.001	φ	0.035 ms−1
Cm	5300 fF	gK(Ca)	2000 pS
VK	−75 mV	VK(ATP)	−75 mV
VCa	25 mV	gK	2700 pS
gK(ATP)	150 pS	gCa	1000 pS
V1	−20 mV	V2	24 mV
V3	−16 mV	V4	11.2 mV
KCa	5.0 μM	α	4.5 × 10−6 fA−1μM ms−1

The activation functions and the time constant for n are

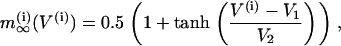(8)

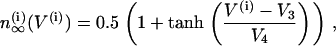(9)

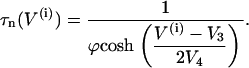(10)

The rate of change of the membrane potential (V) is given by a balance equation (Eq. 1) for the ion currents involved in its dynamics. To the currents originally included in this model we add a Ca²⁺-sensitive potassium current, I_K(Ca), which is directly activated by Ca²⁺ (7). As in other β-cell models, fast spikes during the burst result from interaction between voltage-dependent calcium and potassium currents I_Ca and I_K given in Eqs. 6 and 4, respectively. The slow modulation that drives the shifts between active and silent phases is provided by the intracellular calcium concentration c, which is a negative feedback variable acting on I_K(Ca).

The rate of change of c is also given by a balance equation (Eq. 3). The Ca²⁺ flux across the plasma membrane 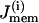is given by the difference between the Ca²⁺ influx, represented by the voltage-gated calcium current, and Ca²⁺ efflux through the plasma membrane Ca²⁺ pump,

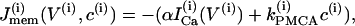(11)

where α converts current to flux, and 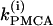is the plasma membrane Ca²⁺ ATPase pump rate. In the case of two coupled cells we define 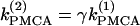to introduce heterogeneity between the cells.

Since we are interested in the effects of coupling through various messengers, we incorporate both electrical and calcium coupling of the cells by adding the following gap-junctional coupling terms to the equations for V and c, which are Eqs. 1 and 2, respectively,

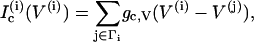(12)

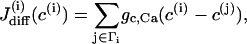(13)

where g_{c, V} and g_{c, Ca} are the coupling conductance and the gap-junctional permeability for Ca²⁺, and the sum is taken over the set Γ_i of nearest-neighbor cells to which cell (i) is coupled. We are particularly interested in how the ratio

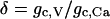(14)

of the coupling strengths through voltage and calcium affects the behavior of the coupled system. The parameters δ, g_{c, V} and g_{c, Ca} are varied in the simulations and their values are given in the figure legends.

Glycolytic oscillator model

To study metabolic coupling, we consider a recent β-cell model proposed by Bertram et al. (23), which incorporates a metabolic subsystem in addition to the feedback by [Ca²⁺]_i onto Ca²⁺-sensitive K⁺ channels. This enables the model to produce very slow oscillations in [Ca²⁺]_i governed by glycolytic oscillations. We first study only the glycolytic oscillator component, which is based on an earlier model for glycolytic oscillations in muscle extracts (31). This model is a classic example of a biochemical relaxation oscillator in which the product, fructose 1-6-bisphosphate (FBP), is the activation variable and the substrate, glucose 6-phosphate (G6P), is the recovery variable. The positive feedback is due to FBP, which activates the allosteric enzyme phosphofructokinase (PFK), and the negative feedback is due to depletion of G6P. As in the Morris-Lecar β-cell model described above, the cells are indexed by the cell number (i).

We consider a simplified version of this model, which includes equations only for G6P and FBP,

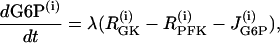(15)

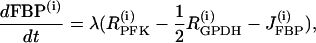(16)

where λ = 0.005 is a parameter that converts milliseconds to seconds and adjusts the timescale of the glycolytic oscillations to agree with experimental observations. The value 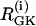is the constant glucokinase (GK) reaction rate. We introduce heterogeneity by assuming different levels of GK activity in the cells. The glyceraldehyde 3-P dehydrogenase (GPDH) reaction rate 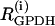is given by the expression

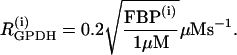(17)

The PFK reaction rate, 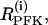includes the binding of activators (AMP and FBP), an inhibitor (ATP), and the substrate fructose 6-phosphate (F6P = 0.3 G6P). The function describing the reaction rate of PFK is rather complex and is completely defined in Bertram et al. (23) and Pedersen et al. (24).

Similarly to the Morris-Lecar-like β-cell model, the gap-junctional coupling terms are added to the equations for G6P and FBP, which are Eqs. 15 and 16, respectively, and take the form

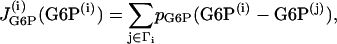(18)

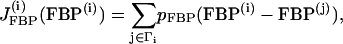(19)

where p_G6P and p_FBP are the gap-junctional permeabilities for G6P and FBP, respectively, and the sum is taken over the set of cells Γ_i to which cell (i) is coupled. In this case we consider again the nearest-neighbor coupling scheme.

Computational methods

The model equations for the Morris-Lecar-like β-cell (Eqs. 1–3) and the model equations for the glycolytic oscillator (Eqs. 15 and 16) in the case of two coupled cells were solved numerically using the software package XPPAUT (32). The bifurcation analysis was performed with AUTO 2000 (33). The model definition files used in the simulations can be downloaded from http://lbm.niddk.nih.gov/sherman/.

RESULTS

Coupled Morris-Lecar-like β-cells

The Morris-Lecar-like β-cell model belongs to the class of square-wave burster models. The effects of electrical coupling in such models have been comprehensively investigated (34–36). The most typical result is that the bursts synchronize, but the spikes may not synchronize unless the coupling is very strong. If the cells are heterogeneous, stronger coupling is required to achieve synchrony. If the cells are sufficiently different and the coupling strong enough, the slow oscillations are still able to phase-lock nearly in-phase, but the fast spiking oscillations die (35).

In this study we focus on the effects of coupling through the recovery (negative feedback) variable in addition to already present electrical coupling as well as on their relative strengths, represented by the parameter δ (Eq. 14). We avoid the complex behaviors observed when the coupling is weak by assuming that the electrical coupling is sufficiently strong, so that the only stable spiking modes are the in-phase or nearly in-phase, when the cells are identical or nonidentical, respectively.

Calcium coupling can kill the bursting

The recovery variable in the Morris-Lecar-like β-cell model is c. Although the electrical coupling among β-cells is well-documented experimentally (9,10,14,16), the diffusion of calcium through gap-junctions, feasible from the experimental point of view (37), has not been addressed theoretically.

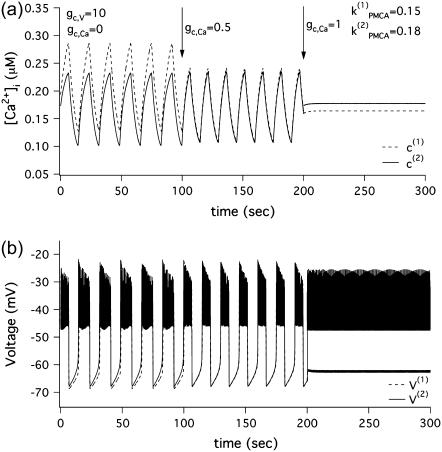
In Fig. 1 we show two coupled Morris-Lecar-like β-cells where one of the cells (dashed) has stronger Ca²⁺ pumping than the other (solid). Initially, the two cells are coupled only through the membrane potential (0 ≤ t ≤ 100 s). The spikes in Fig. 1 b are synchronized nearly in-phase with nearly identical amplitude. The cytosolic Ca²⁺ concentrations (Fig. 1 a) oscillate in phase, but, since the cells are nonidentical, their amplitudes are different; the cell with stronger pumping has lower [Ca²⁺]_i. Addition of calcium coupling (100 < t ≤ 200 s) equalizes the amplitudes of the [Ca²⁺]_i oscillations and leads to better synchronization of the voltage bursts. In this case, diffusion of Ca²⁺ through gap-junctions facilitates synchronization of the coupled system. However, increasing the coupling strength of Ca²⁺ further (200 < t ≤ 300 s) results in the disappearance of the slow calcium oscillations (Fig. 1 a) and splitting of the voltage solutions into two levels, a high, spiking level, and a low, silent level (Fig. 1 b). Thus, incorporation of sufficiently strong gap-junctional diffusion of calcium in addition to electrical coupling kills the slow component of the bursting voltage solution, leaving only the fast spikes.

FIGURE 1.

Simulations of Morris-Lecar-like β-cell model with two heterogeneous cells 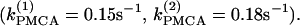(a)[Ca²⁺]_i solutions. (b) Voltage solutions.

A physiological interpretation of this phenomenon can be given as follows. The effect of diffusive Ca²⁺ coupling is to equalize the [Ca²⁺]_i, which provides negative feedback for bursting. Since the Ca²⁺ pumps are not identical, the cells require different amounts of [Ca²⁺]_i to exhibit bursting. Therefore, when the concentration of Ca²⁺ in the two cells is equalized the cells can no longer burst. Instead, the cell with the stronger pump fires continuously at a depolarized level because [Ca²⁺]_i is too low, whereas the other cell is repolarized because [Ca²⁺]_i is too high. In the next section we will show that the cells do not need in fact to be heterogeneous. When the cells are identical, a symmetry-breaking pitchfork bifurcation can also lead to a situation in which one cell has too much [Ca²⁺]_i and the other too little.

Bifurcation analysis—identical cells

To understand why and under what circumstances intercellular calcium diffusion can result in oscillator death, we perform a bifurcation analysis of the Morris-Lecar-like β-cell model (Eqs. 1–3). As mentioned above, the Morris-Lecar-like β-cell model is a square-wave bursting model in the range of parameter values that we have chosen for our study. Because of the fast-slow nature of this type of system, it is computationally challenging to construct numerically bifurcation diagrams of the full system. However, we are interested in how coupling through calcium affects the behavior of the coupled system. Therefore we simplify the full system by removing the fast spiking component. To achieve that we set the fast voltage-gated K⁺ channels activation variable which allows us study only the slow oscillatory behavior of the system. The reduced system of Eqs. 1 and 3 is a coupled system of relaxation oscillators where the voltage (V) can be regarded as the activation variable and the [Ca²⁺]_i (c) as the recovery variable. Note that this approach differs from the usual fast-slow analysis used in previous studies of coupling (34–36), in which the recovery variable was used as a bifurcation parameter.

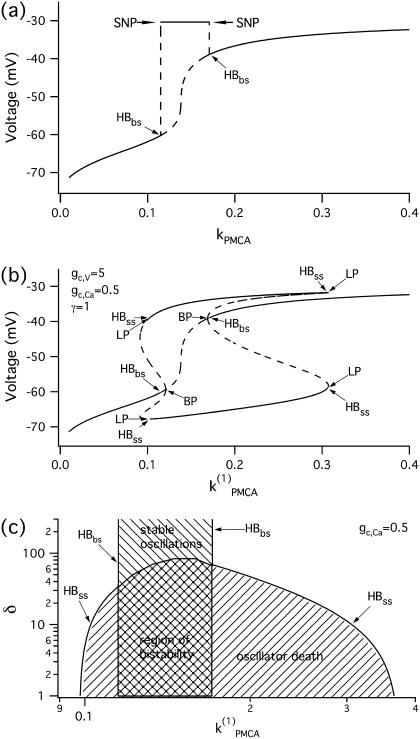
We start with the single-cell bifurcation study, using the plasma membrane calcium (PMCA) pump rate k_PMCA as a bifurcation parameter. This is a natural choice because varying the PMCA pump rate takes the model through the three experimentally observed modes. As the value of k_PMCA increases, the behavior of a single β-cell changes from silent to bursting. Further increase in PMCA pump rate brings the cell to a continuous firing regime. This behavior is summarized in Fig. 2 a, which shows that there is range of (k_PMCA) values where the steady state loses stability, between the two Hopf bifurcation points labeled HB_bs. The Hopf bifurcation points give rise to a branch of periodic orbits, which rises nearly vertically and is initially unstable but becomes stable at a saddle-node-of-periodics (SNP) turning point. The stable (nearly horizontal) portion corresponds to the slow component of the bursting solution of the full system. For values of the parameter (k_PMCA) that are on the left side of the leftmost Hopf bifurcation point the system is silent. To the right of the rightmost Hopf bifurcation point the reduced system goes to a high-voltage steady state, which means that the full system would fire continuously.

FIGURE 2.

Bifurcation diagrams of the Morris-Lecar-like β-cell model. (a) Bifurcation diagram in the case of a single cell, showing the maximum of the periodic orbits as a function of k_PMCA; (b) bifurcation diagram in the case of two identical cells, showing the nonhomogeneous steady-state solutions as a function of k_PMCA; periodic branch omitted for clarity. (c) Two-parameter bifurcation diagram in (k_PMCA, δ)-space for fixed g_c,Ca = 0.5; the cross-shaded region indicates bistability; plotted on logarithmic axis scale. (HB, Hopf bifurcation; BP, symmetry-breaking (pitchfork) point; LP, saddle node; SNP, saddle node of periodics.) The broken lines denote instability.

We continue with a study of the coupled system in the case of two identical cells, coupled through both voltage and calcium. When the cells are identical, the coupled system is symmetric, and identical behavior of the two cells is always a solution, though not necessarily stable. Indeed, coupling through calcium may cause the original symmetry of the system to break through a subcritical pitchfork bifurcation of the homogeneous steady state, labeled BP in Fig. 2 b. As a result, the homogeneous (symmetric) steady-state branch becomes unstable and splits into two additional branches, which gain stability through Hopf bifurcations denoted by HB_ss. The homogeneous steady state in Fig. 2 b is the same as the steady state for a single cell (Fig. 2 a). The periodic branch (not shown in Fig. 2 b but the same as in Fig. 2 a) that connects the two Hopf bifurcation points (HB_bs), which are detected at the same parameter (k_PMCA) values in both cases, corresponds to synchronous in-phase bursting solutions of the coupled full system (Eqs. 1–3). The Hopf bifurcation points HB_ss in Fig. 2 b give rise to additional branches of periodic solutions, but these are unstable and are therefore omitted for clarity. Note that between the two Hopf bifurcation points HB_bs the coupled system is bistable, i.e., in the corresponding parameter range stable slow oscillations (bursting solutions in the full system) coexist with stable nonhomogeneous steady-state solutions that result from the pitchfork bifurcation BP.

Oscillator death via a pitchfork bifurcation has previously been described and analyzed by Bar-Eli (22) in a system of coupled chemical oscillators, the Brusselator. This form of oscillator death differs from that in a similar bursting model (35) mentioned above, in which the fast spikes disappear due to heterogeneity and strong electrical coupling and only the slow oscillations persist. In contrast, the effect of diffusive Ca²⁺ coupling is to destroy the slow calcium oscillations and hence the slow component in the bursting voltage solution, while the fast oscillations persist. Moreover heterogeneity, which is necessary for the existence of oscillator death due to electrical coupling, is not required in the case of oscillator death resulting from calcium coupling. We will use the abbreviations PFOD to denote oscillator death due to pitchfork bifurcations and HBOD to denote oscillator death involving dynamical transitions through Hopf bifurcations.

Since we saw in Fig. 1 that a little coupling through calcium enhances synchrony, but a lot prevents oscillations, we next investigate how oscillator death depends on the strength of coupling through voltage and calcium. In particular, we continue the Hopf bifurcation points HB_bs, which give rise to a branch of synchronized bursting solutions, and the Hopf bifurcation points HB_ss, where the nonhomogeneous steady states gain stability (Fig. 2 c) in two parameters, the PMCA pump rate (k_PMCA) and the ratio (δ = g_{c, V}/g_{c, Ca}), of the coupling strengths through voltage and calcium. Fig. 2 c shows that although there is bistability between the bursting and steady-state solutions, the parameter region where the nonhomogeneous steady-state solution is stable is bigger than the region corresponding to stable bursting solutions. The nonhomogeneous steady state is stable only for parameter values below the curve labeled HB_ss in Fig. 2 c. This means that oscillator death occurs only if g_{c, V} is <∼100 times as large as g_{c, Ca}. This may explain why such behavior has not been observed experimentally: unless the calcium coupling is sufficiently strong compared to the electrical coupling, oscillator death due to intercellular calcium diffusion would never be encountered.

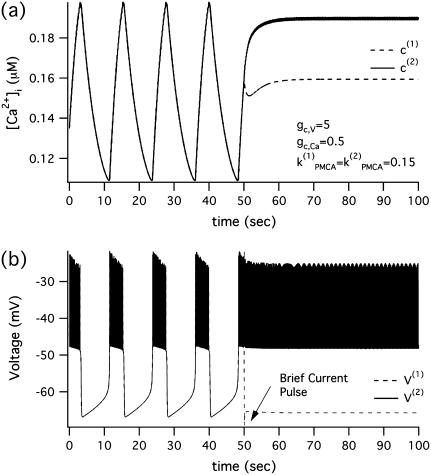
Fig. 2, b and c, imply that brief perturbations can switch the system between the synchronous oscillatory and the PFOD steady state. A typical example for k_PMCA = 0.15, g_{c, Ca} = 0.5, and δ = 10 is shown in Fig. 3, where brief current pulses of opposite polarity change the behavior from a synchronous bursting solution to a stable nonhomogeneous steady state.

FIGURE 3.

Morris-Lecar-like β-cell model reset from nonoscillating to oscillating in the case of identical cells with parameter values taken from the region of bistability 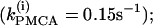at t = 50 s, pulses of equal amplitude but opposite polarity are applied for 100 ms. (a) [Ca²⁺]_i; (b) membrane potential.

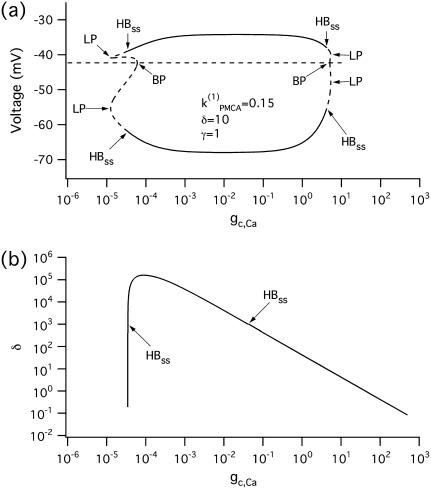
To show that the form of oscillator death in our system is the same as that studied by Bar-Eli (22) and Marek and Schreiber (38), we choose a particular value of the parameter k_PMCA = 0.15 and study the collective behavior of two identical β-cells as the coupling strength through calcium (g_{c, Ca}) is varied (Fig. 4 a). Similar to those studies (e.g., Fig. 1 in Bar-Eli (22)), we find that in our system the homogeneous steady state is unstable. For a range of g_c,Ca values, a subcritical pitchfork bifurcation of the homogeneous steady state gives rise to a pair of nonhomogeneous steady-state solutions, which gain stability through Hopf bifurcation points labeled HB_ss in Fig. 4 a. Specifically, in the case of δ = 10, for very small (≲10⁻⁴) or for large (≳10) values of g_{c, Ca} the coupled system has only a stable bursting solution, while for 10⁻⁴ < g_{c, Ca} < 10 the coupled system is bistable, i.e., the stable bursting solution coexists with the stable nonhomogeneous steady-state solutions.

FIGURE 4.

Bifurcation diagrams of the Morris-Lecar β-cell model in the case of identical cells, with parameter values taken from the region of bistability 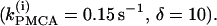(a) Bifurcation diagram in the case of two identical cells, showing the nonhomogeneous steady-state solutions as a function of g_{c, Ca}. (b) Locus of the pair of Hopf bifurcation points, HB_ss in the two-parameter (g_{c, Ca}, δ)-space. (HB, Hopf bifurcation; BP, symmetry-breaking (pitchfork) point; LP, saddle node.) The broken lines denote instability.

The behavior of the system depends on the strength of the electrical coupling as well. Similarly to Fig. 2 c, the two-parameter (g_c,Ca, δ) bifurcation diagram of the Hopf bifurcation points HB_ss in Fig. 4 b indicates that oscillator death occurs for values of δ below the curve HB_ss, i.e., only if the ratio δ = g_{c, V}/g_c,Ca is not too big.

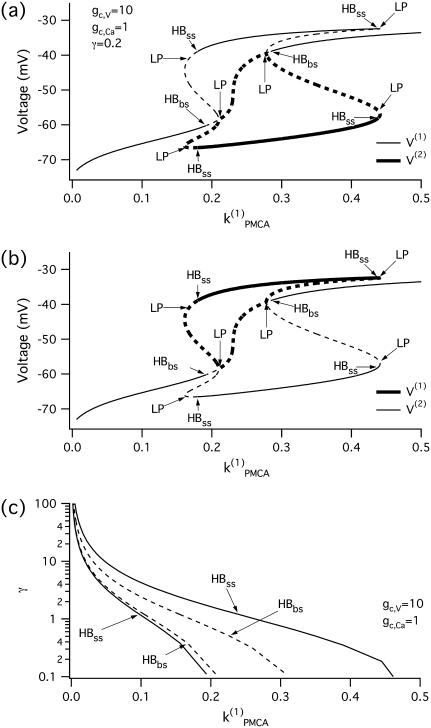
Bifurcation analysis—nonidentical cells

Although the assumption that the cells are identical facilitates the analysis and is helpful in capturing the basic bifurcation structure of the coupled system, the case of nonidentical cells is closer to reality. Therefore, we introduce heterogeneity in our system of two coupled cells by defining the ratio 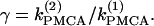The bifurcation diagram of the coupled system for a fixed degree of heterogeneity γ = 0.2, using 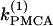as a bifurcation parameter, is displayed in Fig. 5, a and b. Since the cells are nonidentical, the steady state is not symmetric: the symmetric steady state seen when the cells were identical (Fig. 2 b) here breaks into two pairs of asymmetric steady-state solutions, given in thin and thick solid lines in Fig. 5, a and b. The pitchfork bifurcation becomes a saddle-node bifurcation and the nonhomogeneous steady states gain stability through Hopf bifurcation points labeled HB_ss. For clarity, in Fig. 5, a and b, the periodic branch, which connects the Hopf bifurcation points HB_bs and corresponds to stable, nearly in-phase bursting solutions of the full system (Eqs. 1–3), as well as the unstable branches of periodic orbits that emanate from the points HB_ss, are not shown. Although the symmetry of the coupled system is lost in the case of nonidentical cells, Fig. 5, a and b, illustrate that, regarding the phenomenon of oscillator death, the behaviors in both cases are similar. Hence, the case of nonidentical cells can be treated as a perturbation of the case of identical cells that preserves the oscillator death phenomenon.

FIGURE 5.

(a,b) Bifurcation diagrams of the Morris-Lecar β-cell model in the case of nonidentical cells (γ = 0.2) showing the nonhomogeneous steady-state solutions as a function of 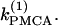(c) Loci of the Hopf bifurcation points of the Morris-Lecar β-cell model in the case of nonidentical cells in the two parameter ( 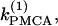γ)-space. (HB, Hopf bifurcation; LP, saddle node.) The broken lines denote instability.

In Fig. 5 c we continue in two parameters 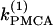and γ the loci of the Hopf bifurcation points HB_bs that give rise to a branch of synchronized, nearly in-phase bursting solutions and the loci of the Hopf bifurcation points HB_ss, where the nonhomogeneous steady states gain stability. The lines labeled HB_ss outline the region in the ( 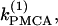γ) parameter space of stable nonhomogeneous steady-state solutions, whereas the lines labeled HB_bs outline the region of stable, nearly synchronous bursting solutions. Fig. 5 c illustrates that, for the heterogeneous case as well, the coupled system is bistable. An example of behavior in that regime is shown in Fig. 1, a and b. Fig. 5 c also demonstrates that the range of parameter 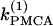values where the nonhomogeneous steady state is stable is approximately twice as big as the range where the system is bistable. Interestingly, the other type of oscillator death (HBOD) (35,36) can be found in Fig. 5 c when the degree of heterogeneity γ is very large. We see that all the branches represented in this figure come closer together and eventually coincide as γ increases. This leads to disappearance of the HB_bs and HB_ss points, and hence in this case the dynamics of the coupled system is represented by a single stable steady state.

Coupled glycolytic oscillators

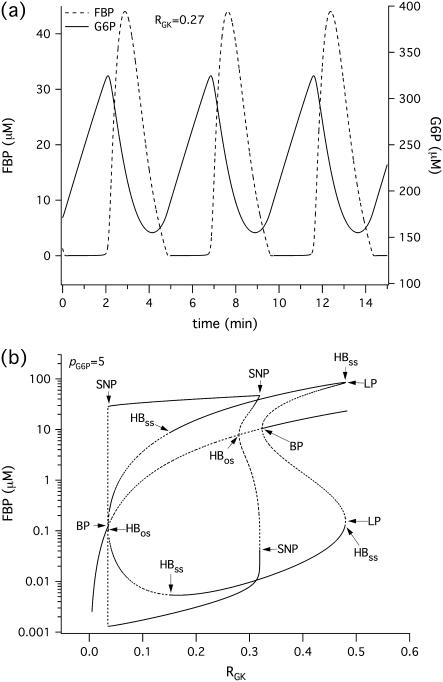
The glycolytic oscillator model, described by Eqs. 15 and 16, is characterized by a gradual buildup of the glucokinase (GK) product, glucose 6-phosphate (G6P), which is then discharged as the concentration of the PFK product, fructose 1-6-bisphosphate (FBP), rises (Fig. 6 a). Therefore, similarly to the reduced Morris-Lecar β-cell model (Eqs. 1 and 3), it is of relaxation type, where FBP is the activation variable and G6P is the recovery variable. We then expect to detect oscillator death of the PFOD type (22,38) in a system of glycolytic oscillators coupled through G6P. Indeed, as shown in Fig. 6 b, the bifurcation diagram for FBP of two coupled identical glycolytic oscillators has the same basic structure as the corresponding bifurcation diagram (Fig. 2 b) of two coupled Morris-Lecar β-cells. In Fig. 6 b we have used the rate of GK (R_GK), which reflects the level of glucose stimulation, as a bifurcation parameter. The homogeneous (symmetric) steady state splits into two nonhomogeneous steady states through a pitchfork bifurcation, labeled BP in Fig. 6 b. There are also two Hopf bifurcation points (HB_os) connected by a branch of stable periodic orbits, which correspond to synchronous (in-phase) oscillations in FBP concentration. Analogously, the nonhomogeneous steady-state branches gain stability through Hopf bifurcation points (HB_ss). These nonhomogeneous stable steady states correspond to PFOD.

FIGURE 6.

(a) Simulations of the glycolytic subsystem in model of Bertram et al. (23) for a fixed level of stimulation R_GK = 0.27s⁻¹. (b) Bifurcation diagram of the above glycolytic subsystem showing the maximum and minimum of the periodic orbits as well as the nonhomogeneous steady-state solutions as a function of R_GK. (HB, Hopf bifurcation; BP, symmetry-breaking (pitchfork) point; LP, saddle node; SNP, saddle node of periodics.) The broken lines denote instability.

In the case of coupled glycolytic oscillators, the existence and stability of this phenomenon depends again on the ratio between the coupling strengths through FBP (p_FBP) and G6P (p_G6P). In particular PFOD occurs as long as p_FBP is not ≫p_G6P and p_FBP ≤ 0.01 s⁻¹ (computations not shown). Moreover, similar to Fig. 2 c and Fig. 4 b for coupled Morris-Lecar β-cells, in the case of coupled glycolytic oscillators the region in the parameter space where stable, nonhomogeneous steady-state solutions exist increases (not shown) when the coupling strength for the recovery variable increases compared to the coupling strength for the activation variable (i.e., when δ decreases). Finally, in the case of coupled heterogeneous glycolytic oscillators as well as in the case of more than two coupled cells we expect behavior similar to that of the Morris-Lecar-like β-cell model.

A biochemical interpretation of PFOD for glycolytic oscillators similar to that for the electrical oscillators can be given as follows. Two glycolytic oscillators that require different amounts of the substrate G6P to produce FBP oscillations will stabilize when driven by coupling through G6P to equalize the levels of the substrate. They settle into a steady state where one of them has high and the other low FBP. For the former, the concentration of the substrate G6P is more than the maximum allowable for oscillations, and for the latter, it is below the minimum for oscillations.

Combining electrical and metabolic oscillators

The Morris-Lecar β-cell model, although very useful as a theoretical tool for studying the collective behavior of coupled cells, does not take into account many of the mechanisms that influence the dynamics of pancreatic islets. It reproduces the fast electrical activity (<60 s) of this cell type, but cannot simulate very slow as well as compound (mixed) bursting. Moreover, pulsatile insulin secretion has a period of 2–5 min (7,18), which is comparable to the period of slow or compound electrical bursting and [Ca²⁺]_i oscillations. It has been proposed (23,39,40) that metabolic oscillations, in particular glycolytic, underlie the slow oscillations in [Ca²⁺]_i. There is experimental evidence for glycolytic oscillations in single islets of Langerhans (40–43).

To study the effects of metabolic coupling on the slow dynamics of pancreatic islets, we use a recent model (23) that incorporates the glycolytic oscillator discussed in the previous section. Complete model details as well as the parameter values can be found in Bertram et al. (23). This model is capable of reproducing a wide range of oscillation frequencies depending on the parameter regimes. In the parameter regimes where glycolysis oscillates, electrical bursting and the concomitant oscillations in [Ca²⁺]_i result from the combined influence of two independent but connected oscillators—fast electrical and slow glycolytic. In the simulations below, we examine electrical coupling and metabolic coupling through both FBP and G6P. We do not consider intercellular calcium diffusion because there are no experimental observations of the oscillator death phenomenon due to Ca²⁺ coupling, which we discussed in the previous sections.

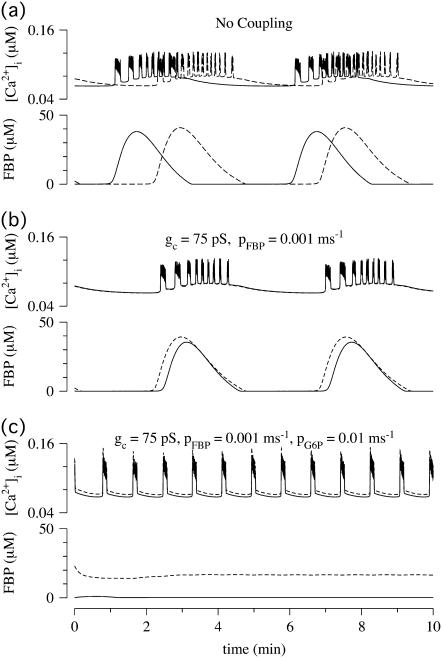
The first example (Fig. 7) illustrates the behavior of two uncoupled nonidentical β-cells (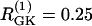 and 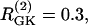representing different levels of sensitivity to glucose. For this choice of parameters, interaction of the electrical and glycolytic oscillators within each of the coupled cells results in compound oscillations because the electrical oscillations are much faster than the glycolytic ones (Fig. 7 a). Cell 2 (dashed) has slightly higher frequency than Cell 1 (solid). If the cells are only electrically coupled, their membrane potentials and [Ca²⁺]_i synchronize, but the metabolic oscillations do not synchronize, resulting in complex aperiodic behavior (not shown). (In principle, electrical coupling can synchronize even the metabolic oscillations due to the effects of Ca²⁺ on mitochondrial ATP production, and hence indirectly on PFK (24), but with the parameters used here the effect is weak and only works if the cells are identical or nearly so.) Addition of coupling through FBP, on the other hand, strongly synchronizes the glycolytic oscillations as well as the slow oscillations in [Ca²⁺]_i and voltage (Fig. 7 b). Finally, including gap-junctional diffusion of G6P (Fig. 7 c), we provoke oscillator death as predicted by the analysis in the previous section (Fig. 6 b).

FIGURE 7.

Simulations of the model of Bertram et al. (23) for two coupled heterogeneous cells. 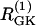= 0.2 s⁻¹ (solid); 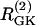= 0.25 s⁻¹ (dashed); 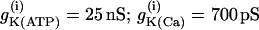; and r⁽ⁱ⁾ = 1.0. (a) When uncoupled, both cells are compound bursters with slightly different frequencies. (b) When coupled via membrane potential (g_{c, V} = 75 pS) and FBP (p_FBP = 0.001 ms⁻¹), the electrical and metabolic oscillations synchronize. (c) When coupled as well by G6P (p_G6P = 0.01 ms⁻¹), the slow oscillations are abolished, leaving fast, synchronized Ca²⁺ oscillations.

In this case, however, oscillator death does not result in stabilization of the whole system. Although the glycolytic oscillations are abolished, the electrical/[Ca²⁺]_i oscillations persist (Fig. 7 c), and are well synchronized due to electrical coupling. In other words, increase in the gap-junctional permeability transforms slow voltage/calcium oscillations into fast oscillations. In fact, there is experimental evidence (25) that overexpression of gap-junctional connexins Cx36 and Cx43 converts slow voltage and calcium oscillations (period ∼5 min) into fast ones (period <1 min). In those experiments, the gap-junctional conductance was measured to increase after overexpression, which, according to our simulations, would not itself convert slow oscillations to fast oscillations. We hypothesize that the conversion was instead due to increase in the intercellular diffusion of G6P.

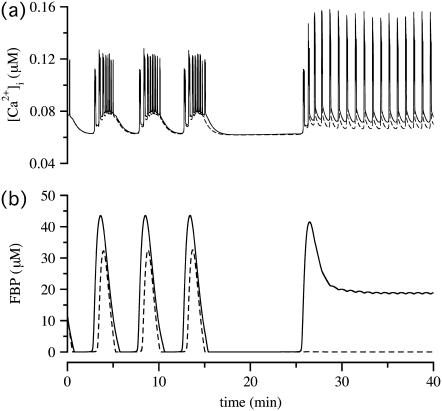
In the simulation of Fig. 7 c, the system is actually bi-stable, so annihilation of the slow oscillation depends on the initial conditions. We exploit this to simulate another experimental observation, conversion of slow to fast oscillations by removal and re-addition of glucose (Fig. 4 in (23)). In that article, it was suggested that the conversion was due to intrinsic bistability in the glycolytic oscillator subsystem within each cell. Here we show an alternative scenario—that bistability results from coupling through G6P.

PFOD is favored by heterogeneity, so we accentuated the difference in 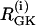values. (Both cells are still compound bursters, but the frequencies are more discrepant than in Fig. 7.) Fig. 8 a begins with synchronized compound voltage and calcium oscillations, here due to coupling through G6P and voltage, but not FBP, which is also expected to favor PFOD. (Note that coupling through FBP is not needed to synchronize the metabolic oscillations if coupling through G6P is present.) At t = 15 min, removal of glucose is simulated by reducing 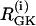by 80% and setting coupling to 0, as coupling has been shown to increase with glucose (44). At t = 25 min, re-addition of glucose is simulated by restoring 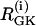and coupling. The cells now go into the PFOD solution.

FIGURE 8.

Simulations of the model of Bertram et al. (23) for two coupled heterogeneous cells. Parameters as in Fig. 7 except: 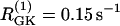(dashed), 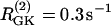(solid), p_FBP = 0, and p_G6P = 0.0025 ms⁻¹. (a) Cytosolic Ca²⁺; (b) FBP. Initially the cells synchronize at a slow oscillation. At t = 15 min, glucose removal is simulated by decreasing 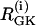by 80% and setting coupling to 0. Glucose is re-added and coupling restored at t = 25 min. The cells now go to the oscillator death solution. (Compare Fig. 4 in Bertram et al. (23).)

In summary, Figs. 7 and 8 show that coupling through membrane potential may not be sufficient to synchronize slow, metabolically driven oscillations in membrane potential and [Ca²⁺]_i. Coupling through either of the metabolic variables, FBP or G6P, or both, robustly synchronizes the slow oscillations. Coupling through G6P, but not coupling through FBP, can kill the slow oscillations.

DISCUSSION

As a representative of the endocrine cell family, the pancreatic β-cell expresses the connexin 43 (Cx43) isoform of the connexin channel family (13,15). Recent experimental evidence indicates that connexin 36 (Cx36) is coexpressed in these cells (15). It has been shown (12,15,16) that Cx36 is directly involved in the synchronization of glucose-induced Ca²⁺ oscillations and insulin secretion in pancreatic islets. Therefore, the properties of this channel in terms of permeability to specific signaling ions and molecules will determine the overall behavior of an islet where thousands of β-cells are coupled together. Unfortunately, there are limited experimental studies and many possible intercellular messengers that could diffuse through gap junctions and thus affect β-cell behavior. We have used mathematical modeling to study the effects of diffusion of several intercellular messengers. We do not focus on electrical coupling since it has already been studied extensively both experimentally (9,10,14,16) and theoretically (34–36). In this article, we instead investigate how the exchange of other intercellular signals influences a system of coupled β-cells, assuming the presence of electrical coupling. In particular we have addressed diffusive coupling of calcium and the glycolytic metabolites FBP and G6P through gap-junctions and their effects on β-cell dynamics. Furthermore, we have shown how metabolic communication could account for experimental results that cannot be easily explained solely by electrical coupling.

Diffusive calcium coupling

Calcium gap-junctional diffusion has been shown (19,20) to play an important role in synchronization of calcium responses in coupled hepatocytes and pancreatic acinar cells. However, our analysis demonstrates that gap-junctional diffusion of calcium, if close in magnitude to the voltage-coupling strength, can kill the slow component in the bursting electrical activity of coupled β-cells (Fig. 1). This effect is a manifestation of the oscillator death phenomenon described by Bar-Eli (22). This form of oscillator death is due to a symmetry-breaking pitchfork bifurcation, which generates new asymmetric steady-state solutions that compete with or replace the synchronous oscillatory solution (Fig. 2).

Thus, substantial diffusion of calcium through gap-junctions appears to have a negative effect on the electrical bursting as well as oscillatory Ca²⁺ dynamics. Since such an effect has not been encountered experimentally, it might be that the electrical coupling is sufficiently strong compared to the calcium coupling to prevent oscillator death. Indeed, it has been reported (45) that in smooth muscle cells, for instance, voltage coupling is orders-of-magnitude stronger than diffusion of Ca²⁺ through gap-junctions. Another example are the heart cells where Ca²⁺ waves can be propagated through both mechanisms—either only through diffusion of calcium or accompanied by action potentials (46). In the former case, the wave speed reported experimentally is ∼30 μM/s compared to ≈120–150 μM/s in the latter case, which is 4–5 times higher, indicating that the effective diffusion coefficient for membrane potential is at least 1–2 orders-of-magnitude larger than for calcium. The relative contributions of cytoplasmic diffusion and gap-junctional permeability would be different in islets, which have different geometrical characteristics. Although the electrical space constant in pancreatic islets has been calculated to be ≈90 μM (44), there have been no direct measurements of Ca²⁺ diffusion coefficient or wave propagation velocity. Thus, it is a matter for future experimental work to confirm or reject the model prediction.

Further possible explanation of such a difference between the strengths of calcium and electrical coupling could be the selectivity of the gap-junctional channels for particular ions and molecules reported in Goldberg et al. (47,48). That is, Cx36, which preferentially connects β-cells, might disfavor the intercellular exchange of calcium and thus preserve the normal function of the coupled β-cells by preventing oscillator death. We note that Serre-Beinier et al. (13) showed reduction of gap-junctional calcium coupling in the presence of increased levels of [Ca²⁺]_i. In any case, the β-cell must possess a sufficient set of mechanisms to prevent oscillator death. However, a small degree of calcium coupling could contribute to synchronizing the Ca²⁺ oscillations, especially if the cells are heterogeneous (Fig. 1 a).

Metabolic coupling

Although acknowledged as possible (7,8,12,14,15), the effects of metabolic coupling on the behavior of pancreatic β-cells have not been experimentally investigated. Nevertheless, Kohen et al. (8) have demonstrated transfer of glycolytic intermediates, specifically G6P, between pancreatic islet cells. In addition, Quesada et al. (14) have shown that molecules of molecular weight 376.320 and electrical charge and volume similar to those of fluorescent carboxyfluorescein (CF) cannot permeate Cx36 channels. The latter finding is consistent with the ability of G6P to pass through the gap-junctions connecting islet cells since the molecular weight of G6P is only 257.113, considerably smaller than that of CF. However, FBP has a molecular weight of 340.117, which is comparable to that of CF. This suggests that diffusion of FBP may well be significantly smaller in magnitude than that of G6P. These experimental data also suggest that gap-junctional diffusion of ADP or ATP among pancreatic β-cells is unlikely, considering their molecular weights of 427.204 and 507.183, respectively. All of the above is also consistent with the experimental evidence for selective exchange of metabolites through gap-junctions built up from different connexins reported by Goldberg et al. (47,48).

We have shown that while gap-junctional diffusion of FBP synchronizes the glycolytic oscillations, diffusion of G6P through gap-junctions promotes oscillator death, provided that it is sufficiently strong compared to coupling through voltage and FBP (Fig. 7). Given the differences in the molecular weights of the two molecules and the permeability properties of Cx36 channels (14), it is plausible that if islet cells are strongly coupled metabolically, then the effect will be death of the glycolytic oscillations. Furthermore, there is experimental evidence (14) that even though under normal physiological conditions electrical coupling of native islet cells is more extensive than dye coupling, molecules smaller than CF freely diffuse through gap-junctions when junctional permeability is enhanced.

Combining the experimental data discussed above with our theoretical results, we are able to offer an explanation (Fig. 7) of recent experimental observations of the effect of overexpression of Cx36 or Cx43 in mouse pancreatic islets (25). In those experiments, increase in the gap-junctional conductance transformed slow (>2 min) bursts of membrane potential/oscillations in calcium into fast (<60 s) electrical/calcium activity. Assuming that the slow oscillations are governed by oscillations in glycolysis, we hypothesize that enhancement of gap-junctional permeability leads to substantial diffusion of G6P through gap-junctions and kills the glycolytic oscillations, leaving only the fast electrical activity (Fig. 8). We have found no support in the simulations (not shown) for the alternate hypothesis that increased electrical coupling alone could eliminate the slow bursting component. There could, of course, be other reasons that we have not explored for the increase in oscillation frequency.

Coupling via diffusion of G6P, like coupling via Ca²⁺, makes the system bistable, in this case between fast, purely electrical oscillations, and slow, combined electrical/glycolytic oscillations (Fig. 8). This offers an alternative explanation for the conversion between fast and slow oscillations by removal and re-addition of glucose previously described in Fig. 4 in Bertram et al. (23). Unlike coupling via Ca²⁺, however, we would not expect to be able to reset the system by brief ionic perturbations; the metabolic variables would have to be perturbed. More generally, the occurrence of fast versus slow oscillations in islets may depend on whether the system lies in the basin of attraction of the oscillator death solution or not, a previously unsuspected explanation for this much-studied issue. Variation in intrinsic parameters, such as rates of glycolysis and channel conductances, likely also contributes, as previously discussed (23).

The above phenomena have been illustrated by simulations of two cells. Pancreatic islets, however, contains hundreds or thousands of β-cells. Our computations with four cells of the Morris-Lecar-like model (not shown) indicate that the range of parameters in which the system of coupled cells may become stable is larger than for two cells. This is consistent with the oscillator death (PFOD) behavior of coupled chemical oscillators previously reported by Bar-Eli (22), who found that the basin of attraction of the oscillator death solution increased with population size. We thus expect that the larger the number of coupled cells, the higher the probability that the coupled system would stabilize. We have confirmed that the phenomena of Figs. 7 and 8 occur with larger populations (125 cells) and indeed appear to be more robust, but systematic study of the effects of population size is left for future work.

Comparison with other systems

Oscillator death resulting from a pitchfork bifurcation (PFOD) was discovered in a coupled system of chemical oscillators (22). In this study we demonstrate this phenomenon in a Morris-Lecar-like β-cell model, which is a model of Hodgkin-Huxley type (Figs. 2 and 4). Moreover, we identify the coupling through the recovery variable (calcium) as the cause for the occurrence of this phenomenon. The Hodgkin-Huxley formalism is widely applied in modeling excitable systems, and our results indicate that PFOD of the oscillations in such systems will occur if these cells are coupled through the recovery (negative feedback) variable and the ratio of the electrical coupling strength to the recovery variable coupling strength is not too big. For example, the Morris-Lecar-like β-cell can be converted to a model of a neuron with Ca²⁺-dependent adaptation by increasing the time constant of the voltage-dependent K⁺ current (e.g., by decreasing φ). Such a system also exhibits PFOD when Ca²⁺ is allowed to diffuse.

In contrast, in models of calcium dynamics of electrically nonexcitable cells, such as hepatocytes and pancreatic acinar cells (19,20), Ca²⁺ plays an important role in synchronization. The main difference between the two classes of models is the dynamical role of Ca²⁺. In the former case, Ca²⁺ is the activation variable, whereas in the latter case, Ca²⁺ provides negative feedback, and thus plays the role of recovery variable. We have shown that sufficiently strong coupling through the activation variable produces synchrony while coupling through the recovery variable can provoke PFOD in addition to synchrony (Figs. 1–5). Similarly, for the glycolytic oscillator model, coupling through the activation variable FBP results in synchrony, whereas coupling through the recovery variable G6P can result in oscillator death (Figs. 6–8). Thus, PFOD is a consequence of the dynamical role of the recovery variable, which provides negative feedback for oscillations in the activation variable, rather than its biological nature per se.

Other forms of oscillator death

PFOD must be distinguished from a different type of oscillator death that involves stabilization of the steady state due to disappearance of Hopf bifurcation (HBOD) as a result of a great degree of heterogeneity in the coupled system (Fig. 5 c). In contrast, PFOD does not require heterogeneity; it is a property of the symmetric system in the idealized case when the cells are assumed to be identical (Fig. 2). Indeed, it is the breaking of the symmetry that kills the oscillation by introducing a new pair of stable steady states. PFOD does, however, persist in the presence of heterogeneity (Fig. 5). The type of oscillator death reported in (35) was an example of HBOD in which the fast spikes within the active phase of a burst disappear and therefore the coupled system of two heterogeneous β-cells exhibits relaxation oscillations. In PFOD it is the slow oscillations that die, while the fast oscillations are preserved.

Another scenario for oscillator death has been reported, based on anti-phase periodic orbits that end in infinite-period bifurcation and give way to an asymmetric steady state (26,27). Similar to these studies, we have also found anti-phase periodic solutions in the Morris-Lecar model when the coupling strength is weak and upon increasing the stiffness parameter f to 0.1 instead of 0.001. However, in the cases we focus on in this article, they are unstable or do not exist. Interestingly, our numerical computations with the Morris-Lecar-like β-cell model reveal that, when present, the anti-phase periodic orbits terminate by going heteroclinic to the nonhomogeneous steady-state solutions, which arise through pitchfork bifurcation of the symmetric steady state, as the coupling strength increases. Thus, oscillator death via pitchfork bifurcation of a steady state and via antiphase oscillations appear to be related, but the exact relationship is left as an open question for future investigation.

Predictions

Our study enables us to make two major predictions about the dynamical effects of diffusive cell coupling via gap-junctions on the collective behavior of coupled β-cells:

• Prediction 1. Calcium either does not diffuse through gap-junctions among the pancreatic islets β-cells, or if it does diffuse, the electrical coupling is much stronger than calcium coupling.

• Prediction 2. Glucose-6-phosphate (G6P) does diffuse through gap-junctions among the pancreatic islets β-cells. Moreover, sufficiently strong coupling through G6P can kill the glycolytic oscillations.