Force-Induced Adsorption and Anisotropic Growth of Focal Adhesions

Abstract

Focal adhesions are micrometer-sized protein aggregates that connect actin stress fibers to the extracellular matrix, a network of macromolecules surrounding tissue cells. The actin fibers are under tension due to actin-myosin contractility. Recent measurements have shown that as the actin force is increased, these adhesions grow in size and in the direction of the force. This is in contrast to the growth of condensed domains of surface-adsorbed molecules in which the dynamics are isotropic. We predict these force-sensitive, anisotropic dynamics of focal adhesions from a model for the adsorption of proteins from the cytoplasm to the adhesion site. Our theory couples the mechanical forces and elasticity to the adsorption dynamics via force-induced conformational changes of molecular-sized mechanosensors located in the focal adhesion. We predict the velocity of both the front and back of the adhesion as a function of the applied force. In addition, our results show that the relative motion of the front and back of the adhesion is asymmetric and in different ranges of forces, the adhesion can either shrink or grow in the direction of the force.

INTRODUCTION

Biological cells of various types establish diverse types of specialized contacts to their environment. These highly organized adhesions play an important role in cell-cell communication and signaling, cell development, or cell movement. In this article, we focus on the properties of focal adhesions (FA), relatively stable and large cell cytoskeleton-matrix connections, that play an important role in cell differentiation, motility, and wound healing, as well as apoptosis (1–4). When shear stress is applied to the contact area, the adhesion is observed to grow in size (5–7). In contrast to the symmetric domain growth generally observed in the adsorption of nonbiological molecules onto substrates, FA show highly anisotropic growth dynamics in which the additional proteins are mostly accumulated in the direction of the force exerted by the cytoskeleton on the FA. When intracellular actin-myosin contractility is disrupted, FAs do not develop (8,9). However, myosin II-dependent cell contractility is not needed when artificially induced, external forces are applied to the cell, leading to the formation of focal adhesions (5,10). These experiments show that exerted force (either intracellular or external) activates signaling cascades that are essential for the formation and growth of FA. The theoretical treatment of the origin of the mechanosensitivity of FA and the dynamics of their anisotropic growth as discussed in this article results in predictions for the growth velocities of both the front and back of the FA as a function of force. Comparison of theory and experiment in various biological contexts can then be used to refine the model and differentiate between various microscopic mechanisms.

The elastic response of FA to force was discussed by Nicolas et al. (11,12), who analyzed the elastic deformation of a focal adhesion that is subject to a spatially localized stress. The proteins comprising the FA are modeled as a thin elastic layer; the fact that force is localized means that the layer shows compression at the front edge and dilation at the back edge of the force region. This symmetry breaking was suggested to be the origin of the anisotropic adsorption of additional FA proteins and hence the asymmetric growth of the focal adhesion. Using these ideas for the elastic response of the FA, we present in this article a theory for the dynamics of growth of the FA. The link between the elasticity and the dynamics is the assumption that aggregation of cytoplasmic proteins to the plaque is favored when the plaque proteins in the FA are either stretched or exposed to in-plane compression. The role of force in stretching integrin molecules and thus activating their association with other plaque proteins has recently been discussed by Bruinsma (13) in the context of focal complexes, which are the precursors of FAs, discussed here. Our dynamical model predicts the growth velocity of both the front and the back of the adhesion site as a function of the force exerted on the FA. We find that the force must exceed a critical value for the FA to grow, but when growth occurs it occurs preferentially in the direction of the force. Isotropic growth (or shrinking) can be initiated by direct stretching of the proteins by the actin-myosin force; anisotropic growth is caused by the elastically induced in-plane compression of the plaque proteins. These two mechanisms compete with each other, leading to four force regimes in which the adhesion site shows different growth behavior. Three of these growth regimes have indeed been observed qualitatively in experiments. More biologically oriented readers may omit the calculations and proceed to the final sections, namely, Variety of Growth Behavior in Different Force Regimes and Discussion, where we depict the qualitative results of the model in a simple way.

In addition, we focus on the differences between our model and one recently presented by Shemesh et al. (14), which assumes a particular geometry of FA that also leads to growth in the direction of the force. In contrast, our model considers a symmetric domain and predicts that the anisotropic growth of FA is the result of spontaneous symmetry breaking caused by the intrinsic elastic response of the FA to spatially confined stress. In this last section we also suggest specific experiments that can be used to test and refine the various theoretical models.

BIOLOGY OF FOCAL ADHESION FORMATION

Cultured cells show integrin-mediated contacts that undergo several stages of morphology and composition during their development. The nascent association of a cell and the extracellular matrix (ECM) is called an initial adhesion or IA. The IA is generally located at the edge of a lamellipodia. It contains the transmembrane glycoprotein integrin, which binds on the one hand to proteins located in the ECM, and on the other, to additional linker proteins such as talin that connect the integrin molecules to actin stress fibers of the cytoskeleton in the cell (the contractile and force-generating myosin II apparatus). This initial connection to the actin is generally weak and small in extent; therefore the IA can slip under applied forces in the pico-Newton (pN) range (15). The initial contacts can be transformed by force to so-called focal complexes. In focal complexes, the link to the actin is reinforced and new proteins such as vinculin are recruited from the cytoplasm. These larger and more robust assemblies of proteins are able to transmit forces of the nano-Newton (nN) range (16) to the substrate. As shown by Choquet et al. (17) and Pelham and Young (18), nascent adhesion sites regulate the force they exert on the substrate in a manner that depends on the substrate rigidity. Bruinsma (13) developed a two-state model for the energetics of dynamically fluctuating, isolated, adhesion sites to explain the force-induced transition from initial contacts to focal complexes as a function of the substrate rigidity. The central idea relates the binding and unbinding processes to the force that the contractile apparatus exerts over a certain time: the force-loading rate. On a stiff substrate it is easier for the cell to build up a certain force; hence the force loading rate increases with the substrate rigidity (19,20).

In this article, we focus on the later stage of the growth process after the initial focal complexes have developed into stable and growing focal adhesions (FA). The dynamics of the anisotropic growth of mature focal adhesion are driven by cytoskeletal forces and the availability of additional proteins from the cytoplasm. The FAs appear as elongated, 3–10-μm large, streaklike structures. They contain, in addition to the transmembrane protein integrin, many connective plaque proteins, e.g., talin, vinculin, paxilin, and others (21). When shear stress is applied to the contact area, the focal adhesion grows in size and in the direction of the force. This was demonstrated in experiments by Riveline et al. (5), in which the shear stress was produced by a microneedle that was first brought to the periphery of the cell and then moved to the cell-center without affecting the cell membrane. In doing so, the microneedle exerted forces on the actin filaments of the cytoskeleton that are connected to focal adhesions in the cell periphery. Thus, the microneedle exerted a certain shear force also on the FA. On a timescale of minutes, the FA was observed to grow on a micrometer scale in the direction of the force. This coupling of the growth to the applied shear stress and the force direction is the focus of our model and its predictions. The growth-inducing forces can originate from either the cell's own contractile apparatus (22) or from external devices such as a micropipette (5). But the presence of force is indispensable for FA growth since experiments show that disruption of the actin-myosin contractility disrupts the growth of FA (5,8,9,22). These experiments indicate that FA can be regarded as micron-sized mechanosensors that show anisotropic growth under the application of forces.

A quantitative analysis revealed that the growth itself must be understood in the context of the adsorption of additional proteins from the cytoplasm to the adhesion site (5). In this vein, we emphasize that for other types of adsorption processes (e.g., surfactant molecules at an interface or proteins on a substrate), in which the molecules interact with each other in an isotropic manner to form a condensed phase, the domain growth is expected to be isotropic. In contrast, the growth of FA is highly anisotropic and controlled by the shear stress.

Since the force initiates the growth, one must understand how the force is able to modify the properties of the contact region and make it favorable for the adsorption of additional cytoplasmic proteins. As proposed by Nicolas et al. (11,12), the adhesion site can be regarded as an elastic layer that deforms mechanically under shear stress in an anisotropic manner depending on whether one looks at the front or back of the region over which the force is applied. We build on this elastic model to predict the dynamics of adsorption and hence the domain growth. Our model extends the results of Nicolas et al. (11) and its considerations of the free energy of mechanosensitive molecules situated in the elastic layer of the focal adhesion site, to predict the dynamics of FA.

PHYSICAL MODEL OF FOCAL ADHESIONS

Focal adhesions contain many different types of interacting proteins. The microscopic interaction potentials are not known in detail. To study the physics, one must abstract from the known biological structure the most important properties that govern the phenomenon of force-induced growth. In this section, we present a simplified physical picture of FA and discuss how this model interprets and simplifies the complex biological situation.

We begin with the extracellular matrix (ECM) outside the cell. The major proteins of the ECM are collagen fibers to which various proteins are associated. Some of these, such as the ECM protein fibronectin, are able to bind to the transmembrane protein integrin located in the cell membrane. This protein offers the R-G-D sequence which is recognized as a binding site by several members of the integrin family. In reality, the ECM itself must be treated as an elastic medium. To simplify matters, we begin with a model that is relevant for experiments with cells that are cultured on stiff substrates like silicon or glass and treat the ECM as an infinitely stiff medium. The effects of a soft ECM on FAs have been elucidated by Nicolas and Safran (23). In principle, one can extend our model in a similar way.

A very important component in the development of FA is the transmembrane protein integrin that connects the inside to the outside of the cell and the supporting surface. Integrin is a major candidate for the mechanosensor that transmits and translates applied or actin forces to the growth of focal adhesions. Admittedly, integrin may not be the only force-sensitive protein that affects the release or adsorption of plaque proteins from FA. Our model focuses on relatively large length scales at which the detailed molecular nature is not resolved. Since the molecular interaction potentials are not known, we cannot identify any one protein as the mechanosensor. We thus focus on integrin and its association with at least one other mechanosensitive protein. At the micron-length scales of interest for the prediction of the growth of FA, we model this mechanosensitive assembly of proteins as one entity and refer to the integrin-protein unit as the sensor.

Integrin itself is connected to the actin stress fibers by additional linker proteins. Biologists have identified dozens of different plaque proteins that are involved in this connection, such as talin, paxilin, vinculin, and others. Although some parts of this biochemical topology are known (21), little is known about the protein-protein interaction potentials in the plaque and how these interactions are influenced by force. There is evidence that zyxin, for example, can only be located in the adhesion plaque if force is exerted on that region. This would show that not only the growth but also the composition of the adhesion plaque is force-dependent to some extent. Due to the complexity of the protein plaque and the unknown interdependencies of the different proteins, constructing a model that tracks every single protein type is not only impossible but is also not very useful from the physical point of view. After all, we want to predict growth on the micron-length scale at which all the microscopic details cannot be crucial. We therefore use a coarse-grained model in which several microscopic components are lumped into one. In this model we treat the adsorption or desorption properties of all passive (non-force-sensitive) proteins in the same manner. This is in contrast to the mechanosensitive proteins we mentioned above, that associate with or dissociate from the other plaque proteins depending on their configurational state, as determined by the force.

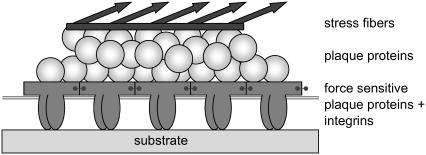
The picture used in our model is thus the following (compare Fig. 1):

1. For simplicity, we first focus on infinitely stiff substrates and therefore do not treat the substrate elasticity in detail (it is known that stiff substrates favor FA growth, so our treatment of an infinitely stiff substrate is a reasonable limiting case).

2. The FA itself is divided into two layers: The lower layer—close to the substrate—contains the mechanosensitive protein that changes their configuration and association energies when shear stress is applied. We lump in this manner all mechanosensitive proteins that are involved in focal adhesion. These proteins are grafted to the substrate via the integrin molecules. These units are later modeled as discrete objects that we consider in the elastic description of the focal adhesion.

3. The second, upper layer is closer to the actin stress fibers than the lower layer and is composed of the proteins that are insensitive to external forces but that do associate with the protein assemblies in the lower layer. These proteins are passive with respect to force but their association with the proteins in the lower layer depends on the force-induced configurational state of the proteins in this lower layer. In addition, these proteins of the upper layer are directly connected to the actin and transmit the force to the lower layer.

FIGURE 1.

A schematic picture of a focal adhesion (FA) site with the actin stress fibers on top, which are connected to the plaque proteins, the so-called upper layer. The FA is grafted to the substrate by the integrin proteins. The integrin proteins together with force-sensitive plaque proteins build up the so-called lower layer.

ELASTICITY OF FOCAL ADHESIONS

In order to account for the observed, anisotropic association of proteins and the subsequent anisotropic domain growth in the direction of the force, one must identify how the applied force breaks the symmetry of the problem. We follow the suggestion by Nicolas et al. (11) that the anisotropic growth of focal adhesions can be explained by coupling the elasticity to the configurational states of the molecules in the FA; these states determine the energetics of association of cytoplasmic proteins with the molecules of the FA. We therefore assume that in addition to direct stretching, in-plane compression also activates the FA molecules to associate with the cytoplasmic proteins. The symmetry can then be broken by the exerted force if it is applied in a finite region of the FA (11,12).

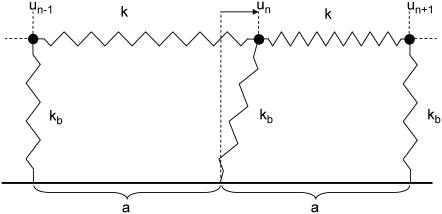
We now review the energetic, elastic treatment by Nicolas et al. (11,12) and generalize the theory in a subtle manner that accounts for the coupling of the FA molecules to the actin. To simplify the elastic treatment, we model the interactions between these units via springs of stiffness k that connect the sensors to each other and result in a linear, elastic chain. The grafting of the chain by the integrins to the substrate is accounted for by springs of stiffness k_b (compare Fig. 2). The resulting continuum equation obtained by balancing the spring forces and the applied force due to the actin is given by Nicolas et al. (11):

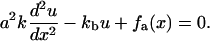(1)

FIGURE 2.

The lower layer of integrin-protein units is modeled as a one-dimensional linear elastic chain that is anchored to the substrate. Each integrin-protein unit is represented by a particle that is connected via springs of stiffness k to its neighbors. The grafting to the surface is accounted for by a spring of stiffness k_b that connects the integrin-protein unit to the substrate. The average spacing between two integrin-protein units is given by a and u_n is the displacement of the n^th particle from its equilibrium position in the absence of force. The anchoring to the substrate by the springs of stiffness k_b gives rise to a local restoring force f_a,n = −k_bu_n. Eq. 1 is a continuum representation of this discretized illustration. A derivation is given in Nicolas et al. (14).

Here, a is the average distance between two integrin-protein units and u(x) is their displacement. The first term originates from the spring force in the chain whereas the second term accounts for the grafting of the chain to the substrate by springs of stiffness k_b. This anchorage gives rise to the local restoring force, −k_bu. The last term, f_a(x), is the actin force exerted on the FA, transmitted to the lower layer at position x.

Note that the derivation of Eq. 1 requires an infinitely extended, preformed layer of integrin-clusters. However, this is a rather weak assumption for the following reasons: The range of the elastic deformations close to the edges of the FA is mainly determined by the detailed boundary conditions. This can be seen from the model by Nicolas et al. (11) that regards the FA as a thin elastic layer on a relatively rigid substrate. In this case, the decay length of the elastic deformation is mainly determined by the thickness of the elastic thin film (∼100 nm). Therefore, the region of the FA that is not acted upon by the actin force need only be several film-thicknesses in size (that is, a few integrin spacings ∼20–70 nm (24)) for the elastic model to be valid. It is in this region that the stress is transmitted by the elasticity even though there is (not yet) any direct coupling to the actin. These arguments have been given earlier in Nicolas et al. (11).

The transmitted actin force, f_a(x) is coupled to the plaque protein concentration for the following reason: The integrin-protein units in the lower layer are only connected to the actin via their association with the plaque proteins in the upper layer. A given integrin-protein unit at position x is acted upon by the actin-myosin force only if a plaque protein is associated with this unit and transmits the force. In the opposite case, if the integrin-protein unit is not associated with a plaque protein and thus not connected to actin, the actin force is not transmitted to the units in the lower layer and the integrin-protein units feel no force. In the following we assume that the force that acts on an integrin-protein unit is linearly dependent on the plaque protein concentration, and thus write

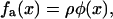(2)

where ρ is a constant that represents the average force an integrin-protein unit in the lower layer feels when it is completely connected (via its association with the plaque proteins of the upper layer) to the actin fibers. In this equation, φ is the local volume fraction of the plaque proteins in the upper layer and is thus a dimensionless quantity. If the upper layer is fully occupied by the plaque proteins, φ is equal to unity. We will refer to φ as the plaque protein concentration. This consideration yields the elastic equation:

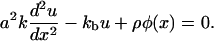(3)

This equation determines the displacement of the integrin-protein units as a function of the plaque protein concentration, including any spatial dependence of the distribution of plaque proteins. This allows us to calculate the elastic deformations of the integrin-protein units; these deformations in turn determine the molecular configurations of these units that affect the energetics of their association with the plaque proteins. Thus, the elasticity determines the probability of adsorption of additional cytoplasmic plaque proteins to the FA. In some cases, the deformations may make adsorption more probable and in others, the plaque proteins may in fact desorb from the integrin-protein units to the cytoplasm, thus shrinking the FA. In this manner, the elasticity is coupled to the adsorption kinetics. Because the concentration of the plaque protein adsorbed to the adhesion is not homogenous on the scale of the FA, this will induce an anisotropic deformation and hence also an anisotropic growth of the FA due to plaque protein adsorption.

The elastic force balance equation, Eq. 3, is a second-order ordinary differential equation, whose Green's function has an exponential form. This allows us to solve this equation for u(x) for any spatial distribution of the plaque protein concentration φ(x), and we find

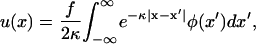(4)

where we have introduce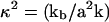d and .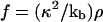

We assume that the spring constant k_b, which is related to the vertical tilting/stretching of the grafted integrin-protein unit in the lower layer, is stiffer than the lateral spring constant k that couples these units with each other. This is a reasonable approximation, since the deformation of a single molecular unit should be of higher energy than a change in the spacing between two such units. We therefore assume that κ ≫ 1. We note that the largest contribution to the integral is in the vicinity of the point x′ = x where the exponential is close to unity. Outside this region, the exponential factor causes the integrand to be small. If φ(x′) is varying slowly in this region we can expand the concentration about the point x and find the general solution for u(x) for any spatially dependent concentration, φ(x):

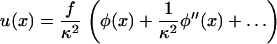(5)

ADSORPTION KINETICS

We will use an analogy to surfactant adsorption, which we will then generalize to treat the adsorption of plaque proteins from the cytoplasm, and its association with the mechanosensitive integrin-protein units in the lower layer. The adsorption process can be split into two steps: In the first step, free plaque proteins dissolved in the cytoplasm must diffuse to the adhesion site. Once a plaque protein is in the proximity of the lower layer, it can associate with an integrin-protein unit that has been activated—either by direct stretching or by in-plane compression; both these processes are related to the forces exerted by the cytoskeleton on the adhesion site. In general, the adsorption kinetics of molecules in solution (e.g., surfactants) to a surface can be treated in two limiting cases: the diffusion-limited or kinetically limited adsorption (DLA- or KLA-limit, (25)). A scaling analysis of the adsorption kinetics indicates that the association of the plaque proteins with the integrin-protein units in the lower layer is the rate limiting step for the growth of focal adhesions, thus the KLA-limit is applicable (A. Besser and S. A. Safran, 2005, unpublished). We found the timescale for the slow process, the association of plaque proteins with the integrin-protein units, to be of order 𝒪(1 s); whereas the fast process of the bulk diffusion of the proteins occurs on much shorter timescales, < 𝒪(10 ms). This separation of timescales allows us to simplify the mathematical treatment without losing any physical significance: the integrin-protein units are assumed to adjust instantaneously to the local plaque protein concentration and are thus treated as being in equilibrium, with a time- and space-dependent plaque protein concentration whose kinetics are written in the KLA-limit (25):

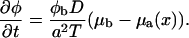(6)

This equation describes the adsorption kinetics of the cytoplasmic proteins to the integrin-protein lower layer where a is the average distance between two units in this layer and T is the temperature. D is the diffusion constant of the plaque proteins and φ_b and μ_b are concentration and the chemical potential of the plaque proteins in the bulk. In the KLA limit, appropriate to our situation, the bulk concentration and chemical potential, φ_b and μ_b, respectively, can be considered as constants in both space and time. In contrast, the concentration of plaque proteins near the lower layer, φ(x, t), is both space- and time-dependent; it is only large in the vicinity of those integrin-protein units that have been activated by the force; the activation implies a conformational change that makes the association of the plaque proteins with the integrin-protein units energetically favorable. The space and time evolution of φ(x, t) is determined by Eq. 6, where μ_a(x) is the chemical potential of plaque proteins on the integrin surface. Because the mechanosensitive units in the lower layer change their conformations in response to the elastic deformation induced by the actin-myosin force, and because these conformational changes modify the energies of association of these units with the plaque proteins, the chemical potential of the plaque proteins in the vicinity of the lower layer, μ_a, is spatially dependent. Only those mechanosensitive units that are coupled to the cytoskeleton force can be activated to associate with the plaque proteins. This depends on the region over which the force acts as well as the spatial extent of the coupling of the mechanosensitive units of the lower layer to the force.

A more precise treatment of the spatial dependence of the chemical potential would lead to an additional in-plane diffusion term in the kinetic equation that would be proportional to the in-plane Laplacian of the concentration. However, once associated with the integrin-protein units and thus bound to the lower layer, the in-plane mobility of the proteins is expected to be small and we ignore this in-plane term compared with the KLA equation written above. By defining the coefficients

(7)

we arrive at the following kinetic equation that focuses on the association kinetics of the plaque proteins in the vicinity of the lower layer:

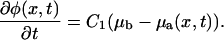(8)

The kinetic equation for the plaque protein concentration depends on the chemical potential μ_a of the plaque proteins near the lower layer. This is a function of the binding energy of these proteins to the lower layer, which is, in turn, a function of the conformational state of the integrin-protein units in the lower layer. The state of these units—activated or nonactivated for association with the plaque proteins—depends on the stretching or in-plane compression of these units, both of which are related to the cytoskeletal force. This then results in a coupling of the adsorption dynamics to the force and the compression, which is determined by the elastic equations. We thus have a closed set of equations for both the mechanical displacement and the protein concentration at the integrin layer. The goal that remains is the determination of the chemical potential, μ_a(x), and its dependence on the force.

ACTIVATION STATISTICS OF THE MECHANOSENSORS

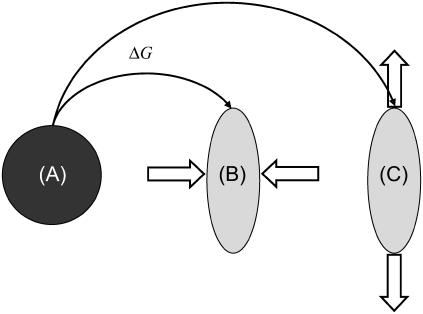
Although the detailed microscopics of the activation of the mechanosensors is not yet known, we now present a simple but concrete model to treat the statistics of this process; this general model can be applied to a wide variety of microscopic situations. To make the statistical model more specific we imagine that the conformation of the nonactivated state of the mechanosensitive, integrin-protein unit has a spherical shape, whereas the conformation of the activated state is more elongated (prolate ellipsoid) (compare Fig. 3). The energetics of association with plaque proteins of the activated state of the integrin-protein units is favorable, while those of the nonactivated state involve an energy cost. To deform the inactive spherical conformation to the ellipsoidal, active state, it is sufficient to either stretch or to compress the integrin-protein unit. More generally, one can model the statistics of activation by assuming that the mechanosensitive, integrin-protein units can be in only two states: an activated state, s_i = 1, or a nonactivated state, s_i = 0, where s_i is a variable that denotes the conformation of the integrin-protein unit at a given site, i, in the lower layer. To change conformation from the nonactivated to the activated state, the mechanosensor must overcome an energy barrier, ΔG. This energy can be provided by the external force that can either compress or stretch the mechanosensor units; we assume that either in-plane compression or stretching can lead to the same conformational change in the force-sensitive proteins, but with different energetics. The cytoskeletal force thus modulates the activation of the sensor units and hence governs the association energy of these mechanosensitive integrin-protein units with the plaque proteins. The statistics of this process are derived from the energetics of the activation and we write a Hamiltonian that accounts for the conformational changes of the integrin-protein units:

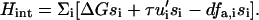(9)

FIGURE 3.

A possible, concrete but schematic picture of the activation process of mechanosensors: Assume that the conformation of the nonactivated state of the force-sensitive proteins has a spherical shape (A), whereas the conformation of the activated state has an elongated shape (B,C). The difference in energy between the activated and nonactivated states is ΔG > 0. This energy can be provided by the external force either by compressing (B) or by stretching the sensor (C), so that the activated state is favored energetically. In-plane compression originates from elastic interaction between neighboring sensors in the lower layer, whereas stretching is due to the direct coupling of the sensor to the actin stress fibers.

If there is no force applied to the adhesion site, the displacement, u_i, of the integrin-protein units at a given site, i, and the actin force transmitted to these units, f_a,i, is zero; the energetic cost for a conformational change (where s_i goes from zero to unity) is ΔG, which we take to be positive and much greater than the thermal energy. In this case of no force, the Boltzmann factor for the probability of a conformational change will be exponentially small. In our model, in-plane compression or stretching lowers the energy of the activated state. Thus, in Eq. 9, the second term represents the energy gain if the sensor is both compressed and in the activated state. The statistical probability for conformational change associated with this term depends on the amplitude of the compression, whose absolute value is expected to be highest at the edges of the focal adhesion site. To relate the discrete site variable, u_i, to our previous discussion of the continuum elasticity, we write u′_i to denote the local change of integrin-protein deformation at site i; this is a measure of the relative change of the integrin density, which in the continuum model we write as 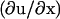. Therefore u′_i < 0 represents an in-plane compression of the local integrin-protein density in the lower layer, and u′_i > 0 an expansion. The value τ is a proportionality factor that relates the compression u′ to the conformational energy and is dependent on the initial density of the uncompressed layer as well as on the elastic properties of the sensors. At the front edge of the region over which the actin force acts, the layer is compressed and the integrin-protein units are activated; at the back edge, they are expanded and do not change conformation (11,12). Thus, association of the integrin-protein mechanosensitive units with new plaque proteins in their vicinity is energetically favorable near the front edge of the force and unfavorable at the back. This effect is at the origin of the symmetry breaking and the anisotropic growth of FA in our model.

In addition to in-plane compression, we also include the effect of the direct stretching of the mechanosensitive units by the cytoskeletal forces that makes the activated state energetically favorable, as suggested by Bruinsma for focal complexes (13). This is a purely local effect and cannot transmit information in the plane of the lower layer, in contrast to the compression effect discussed above. This additional energy gain is represented by the third term in Eq. 9, where f_a,i is the local actin force which is transmitted to an integrin-protein unit at site i and d is a length scale of the order of the molecular deformation of the sensors during the conformational change. If the sensor is both stretched and in the activated conformation, s_i = 1, its energy is lowered and the probability for conformation change (and hence association with the plaque proteins) is enhanced. This effect ensures that the association of the integrin-protein units with the plaque proteins remains stable (is energetically favorable) under the application of force. This term does not differentiate between the different regions in the plane and causes only isotropic force-induced growth of the FA.

The local actin force, f_a,i, which is transmitted to an integrin-protein unit at site i, is dependent on the plaque protein concentration since those molecules couple the integrin-protein units to the actin stress fibers. Similar to the discussion of the continuum elastic model, we write in our discrete representation for the local actin force, f_a,i = ρt_i, where t_i = 1 (t_i = 0) signifies the presence (absence) of a plaque protein adjacent to site i in the lower layer. We rewrite the Hamiltonian of Eq. 9 as

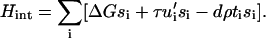(10)

From this we derive the statistical probability of integrin activation at site i by considering the balance between the energetics of activation and the entropy,

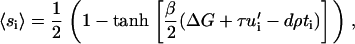(11)

where β = 1/T (we set the Boltzmann constant to unity). For simplicity, and because the physically relevant case only involves small density changes, we treat u′_i as a small quantity and expand 〈s_i(t_i)〉, disregarding terms of order O[u′²]. In this approximation we find that the probability of conformational change is given by

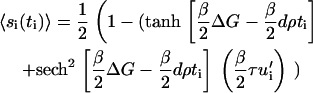(12)

INTERACTIONS AMONG THE ADSORBED PLAQUE PROTEINS

The main goal that still remains is the derivation of the chemical potential μ_a of the plaque proteins in the vicinity of the lower layer where the integrin-protein mechanosensitive units have been activated to associate with the plaque proteins by the actin force in some limited region. Before embarking on the detailed calculation, we outline the main points: First, we discuss the Hamiltonian that governs the energetics of the plaque proteins adsorbed to the lower layer. In doing so, we include the integrin-protein activation statistics described in the previous section. From this Hamiltonian and from entropic considerations we derive an expression for the free energy of the plaque proteins. Finally, we calculate the chemical potential of the plaque proteins from the derivative of the free energy.

The Hamiltonian that governs the energetics of the plaque proteins near the integrin-protein lower layer is given by

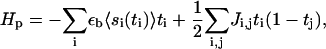(13)

where t_i ∈ {0, 1} is the site-variable for plaque proteins: t_i = 1 means that a plaque protein is located at site i (i is the in-plane coordinate) near the lower layer. The first term accounts for the energy that a plaque protein gains if it binds to an activated integrin-protein unit. If there is a plaque protein at site i, (t_i = 1), it gains the binding energy ε_b, but this energetic gain must be multiplied by the probability 〈s_i〉 that the integrin-protein unit at site i is activated so that complexation with the plaque protein is energetically and statistically favorable.

In addition, in accord with the experimental observations of a condensed protein plaque, we consider an effective attraction between neighboring plaque proteins. This attraction is given phenomenologically in our theory. It can arise from van der Waals interactions, or from more specific microscopic, molecular attractions due to specific functional groups. The microscopic origin does not change the theory; it influences only the numerical value of the parameter denoted by J, which is the net energy gain when two plaque proteins come into close contact with each other. The attraction causes condensation of the plaque proteins and hence of the FA. This assumption is motivated by the experimental observation of condensed plaque proteins in FA—at least once the actin force is in the appropriate regime. In the language of liquid-gas type phase separation, the FA would correspond to the high density phase, and the remaining region near the lower layer, which is not yet densely occupied by plaque proteins, can be regarded as the low density phase.

Using the final result of the previous section for the integrin activation probability, 〈s_i〉, Eq. 12, we derive from this Hamiltonian the free energy of the plaque proteins. In a mean-field approximation, the free energy is the sum of the internal energy (average value of the Hamiltonian) and the entropy of the plaque proteins, which can be evaluated in a lattice-gas approximation (28). For convenience, we replace the discrete quantities in Eq. 13 by their continuum counterparts:

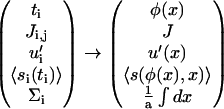(14)

For simplicity, and because the microscopic nature of the interactions is not known, we consider only nearest-neighbor interactions among plaque proteins; hence, the interaction matrix J_i,j is written as an interaction constant J. Furthermore, to enable an analytic solution, we use the Ginsburg-Landau expansion (see (28)) of the free energy about the concentration at the interface between the dense region where φ ≈ 1 and the dilute region where φ ≈ 0 and define ψ = φ – 1/2. Since we focus on the motion of the interface, the region where φ ≈ 1/2 or ψ ≈ 0 is the most important regime. (A detailed derivation of the free energy including a discussion of the continuum limit is given in the Appendix A.) The free energy, F, of the plaque proteins adjacent to the lower layer is

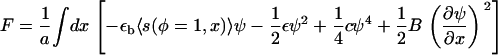(15)

The first term is the total binding energy of the plaque proteins to the integrin-protein units in the FA. The second and the third term come from the Ginsburg-Landau expansion of the free energy and are related to the interactions among the plaque proteins and to their translational entropy. The fourth term represents the continuum representation (28) of the line energy of the interface that separates the high-density domain of plaque proteins that is the FA, from the low-density region where very few plaque proteins have adsorbed to the lower layer. Using this approximation for the free energy, we derive the chemical potential, which is proportional to the change of the free energy with the concentration. In the continuum picture, one uses a functional derivative and we write the chemical potential of the plaque proteins adsorbed to the lower layer as

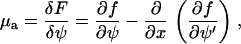(16)

where f is the integrand of Eq. 15. Thus we obtain an equation for the chemical potential of the plaque proteins,

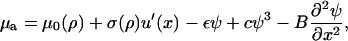(17)

with

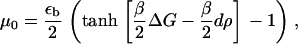(18)

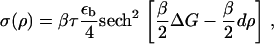(19)

and

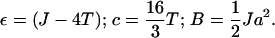(20)

The first term, μ₀(ρ), on the right-hand side of Eq. 17, is the force-dependent contribution to the chemical potential that comes from the stretching of individual proteins by the cytoskeletal force, whereas the second term, σ(ρ) u′(x), which is also force-dependent, comes from the activation induced by lateral interactions between proteins. The three remaining terms are not force-dependent and appear in the usual theory of domain growth of condensed phases. They would result in isotropic domain growth, provided the chemical potential is appropriate.

SOLUTION OF THE MODEL

In a previous section (Elasticity of Focal Adhesions), we derived the local, elastic equilibrium of the focal adhesion. The integrin-protein unit deformation, u(x), depends on the actin force exerted by the stress fibers. Since the plaque proteins are crucial in order to mediate the force from the actin to the mechanosensitive integrin-protein lower layer, the transmitted actin force, ρφ(x), and thus the integrin deformation, is coupled to the plaque protein concentration,

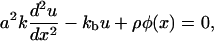(21)

which has the solution

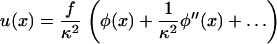(22)

We then described the process of protein adsorption to the FA and showed that the change of the plaque protein concentration in time is proportional to the difference of the chemical potential of plaque proteins in the bulk solution μ_b and that of the plaque proteins adsorbed to the lower layer, μ_a(x, t):

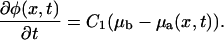(23)

The chemical potential, μ_a(x, t), of the plaque proteins adjacent to the lower layer depends on the elastic deformation of the mechanosensors. Hence, this chemical potential is dependent on the actin force and the sensor compression, u′(x) (this dependence is discussed in the two preceding sections):

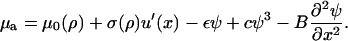(24)

We now have a closed set of equations for both the local mechanical equilibrium of the lower layer and the plaque protein concentration adsorbed to this layer. We will next combine these two equations into one dynamic equation for the plaque proteins adsorption kinetics that allow us to predict the growth of the FA.

By substituting the elastic equation, Eq. 21, and the equation for the chemical potential, Eq. 24, into the kinetic equation, Eq. 23, we find

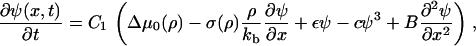(25)

where

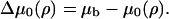(26)

This is a single, partial differential equation that describes the change in the plaque protein concentration adsorbed to the lower layer and its relation to the actin force. The solution of this equation for the plaque protein concentration, ψ(x, t), as a function of both space and time, will define the plaque protein concentration profile in the upper layer and hence the shape of the FA. The elastic deformations induced by the actin force result in asymmetric changes in the plaque protein profile and by following the dynamics of both the front and the back of the FA we are able to predict the growth and the overall motion of the FA.

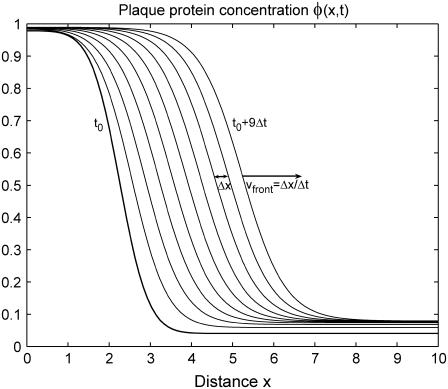
To get a quick feeling for the plaque protein concentration profile dynamics, we solved this equation numerically. As an initial condition, we assumed a steplike but smooth concentration profile of the plaque proteins, ψ(x, t = 0), and assume that the control parameter ρ, the force per sensor, is constant. Our results show (compare Figs. 4 and 5) that the concentration profile changes its initial shape over a short, initial time; afterwards the front begins to move in a self-similar manner that preserves the shape of the domain, and in the direction of the force. After the initial equilibration process, the concentration profile reaches a steady-state which then moves with a constant velocity in the direction of the force. These numerical results motivate us to make an ansatz for the analytical solution for the concentration profile that provides predictive insight into the problem. We consider a steady-state profile of the plaque protein concentration, φ = ψ + 1/2, that moves with a constant velocity v:

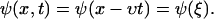(27)

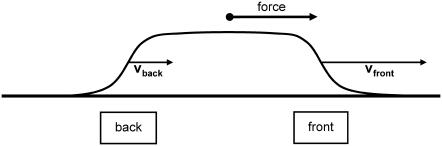
FIGURE 4.

The direction of the force exerted on the FA determines its front and its back edge. In the absence of artificially applied forces, the force direction is given by the actin stress fibers and generally points to the cell body. We will refer to the edge of the FA that points toward the force center (and in the ordinary case to the center of the cell) as the front edge; and the opposite boundary (generally furthest away from the center of the cell) is called the back edge. The region of FA is tracked by the plaque protein concentration profile (obtained by a cross section through the FA along the force). By calculating the change in time of plaque protein concentration at the front edge and at the back edge, experiments can separately measure the dynamics of the front and the back edges of the FA.

FIGURE 5.

Numerical solution of Eq. 25 for the plaque protein concentration as a function of space and time for a constant force in the regime of a growing domain. The initial concentration profile at t = t₀ is a smooth, steplike function. At early times, the front undergoes an equilibration process and the shape of the plaque protein concentration profile varies. However, after a certain time, the front begins to move in the direction of the force, in a self-similar manner that preserves the shape of the domain.

The velocity υ is the velocity of the front edge (the edge which is moving in the direction of the force, see Fig. 4) which we will later refer to as: υ_front. The value υ is a free parameter in this ansatz and has not yet been determined. We next evaluate Eq. 25 with this ansatz,

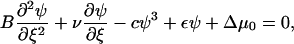(28)

with

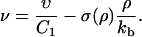(29)

We will later show (see Eq. 37) that the coefficient ν is proportional to the overall growth velocity υ_tot of the FA (that is, the time-rate of change of the size of the FA). The solution of Eq. 28 has the form (26)

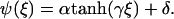(30)

Here, 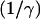is the width of the interface of concentration profile that separates the high density, condensed region from the low density, dilute region. The parameters α and γ are related to the asymptotic concentrations in the condensed (ψ(−∞)) and the dilute (ψ(+∞)) domains. For ξ→±∞, the function 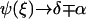if γ is negative. Thus δ is proportional to the sum of the concentrations in the condensed and the dilute domains, 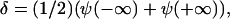whereas α is proportional to their difference, .

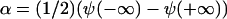We determine the set of parameters (α, γ, δ, ν) by inserting Eq. 30 in Eq. 28. Since ν determines the growth velocity of the FA, this is the main parameter of interest. As a result, ν can be simply written in terms of the parameter δ:

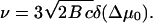(31)

The parameter δ is still a complicated function of Δμ₀ (Eq. 26 and Eq. 18). (At this point we remind the reader that Δμ₀ is force-dependent.) For convenience, we expand the function δ(Δμ₀) for small values Δμ₀:

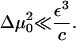(32)

We will see that Δμ₀ = 0 when the force is at the critical value at which the condensed domain changes from one that shrinks in time to one that grows. This is obviously the most interesting and relevant regime, since FAs in cells are highly dynamic structures whose growth can be rapidly changed from shrinking to growing by the cell's own contractile apparatus. Thus, the region of small values of Δμ₀ is of interest. It thus appears that cells sustain a value of the actin stress so that the FAs operate near this critical level.

A Taylor series expansion for ν in this critical regime yields

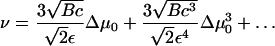(33)

Δμ₀ is given by Eqs. 26 and 18 and depends on the actin force proportional to ρ. This relationship together with Eq. 29 allows us to calculate the growth velocity of the FA at both the front and back edges (see Fig. 4). For the velocity of the front edge we find

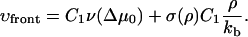(34)

For the velocity of the back edge of the FA, we obtain

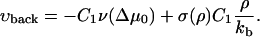(35)

The second term in the expressions for both the front and the back velocity originates from the elastic compression term. For the usual case of domain growth (e.g., of surfactants adsorbed to a surface), this symmetry breaking term is absent and both the back and the front edges of the condensed domain grow symmetrically into the dilute domain for appropriate values of the chemical potential difference. In our model, the vector of growth velocity points away from the center of the condensed domain. Thus the minus sign in Eq. 35 accounts for the direction of the growth at the back edge of the FA.

The second term in the expressions for the velocities of both the front and back edges has a plus sign. The reason for this is that at the front edge, this term induces additional growth stimulated by compression, so the front edge tends to grow into the dilute domain—to the right (see Fig. 4). Since the region near the back edge of the FA is dilated by the actin force, the integrin-protein units are deactivated. This causes any plaque proteins adsorbed to this region to desorb, thus inducing a shrinking of the back edge of the FA. This depletion and shrinking effect, that is totally dependent on the actin force and its effect on the elasticity of the lower layer, tends to move the back edge of the FA to the right.

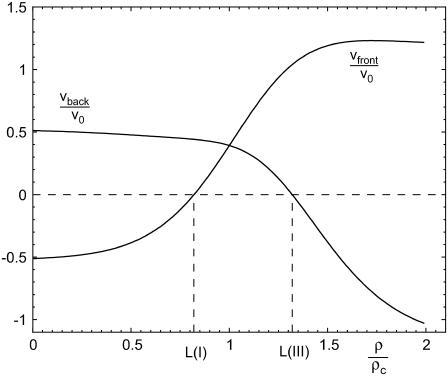
The growth velocity of both the front and back of the FA is plotted in Fig. 6, in which we scale the velocities by the factor

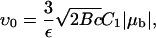(36)

and the force by the factor ρ_c, which is the critical force level where Δμ₀(ρ) = 0 (see below). For small forces, the mechanosensors in the adhesion plaque are not sufficiently activated and protein aggregation occurs neither at the back edge or the front edge. If a condensed domain of plaque proteins were nucleated by some occurrence it would desorb plaque proteins at both edges and shrink; therefore the velocity at the front is negative and at the back positive (compare Fig. 6). When the force is increased, the activation of the mechanosensors is enhanced and the overall loss of proteins is reduced. Because the elastic compression term induces activation of the mechanosensors at the front of the FA, but deactivation (due to dilation) at the back, it is the front edge that first reaches the state of no motion (i.e., at which there is a balance between the shrinking due to the deactivation by the insufficiently large direct force, and the growth due to the activation by the compressive effect). We will refer to this force level for the front as LI and for the back as LIII (see Fig. 6). For very high forces both the front and back edges of the FA are strongly activated and the aggregation of proteins is favored.

FIGURE 6.

Velocity of the front and the back end of the FA as a function of the force. To obtain dimensionless units, the velocities are scaled by the factor υ₀ (Eq. 36) and the force is scaled by the factor ρ_c, which is the critical force level at which the FA neither shrinks nor grows and Δμ₀ = 0.

The overall growth velocity of the domain that determines the time-rate of change of its size is given by

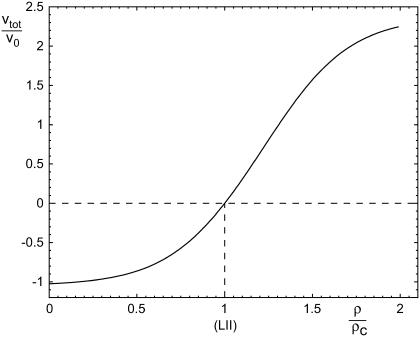
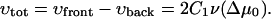(37)

This formula together with Eq. 33 indicates that for Δμ₀ = 0, the FA is in a critical state that neither grows nor shrinks (see Fig. 7, level (LII)). The total size of the FA remains constant but if the force is slightly increased, Δμ₀ will become positive because more integrin-protein units will become activated and additional adsorption of the plaque proteins from the solution will be favored. Hence the FA switches into a state of overall growth. However, if the force is decreased from the value at which Δμ₀ = 0, the FA will react in the opposite direction and will begin to shrink.

FIGURE 7.

The overall growth velocity υ_tot of the FA as a function of the force. This represents the time rate of change of the overall size of the FA. The velocity is again scaled by the factor υ₀ and the force by ρ_c.

VARIETY OF GROWTH BEHAVIOR IN DIFFERENT FORCE REGIMES

The different types of growth behavior predicted by our model arise from the competition between two terms. One term, related to the local chemical potential difference, Δμ₀, is force-dependent,

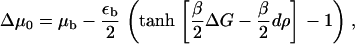(38)

and induces a symmetric growth or shrinking of the FA as a result of the activation of the sensor due to the direct stretching of the integrin-protein units by the actin force. We call this the symmetric term. For small values of the force (when Δμ₀ < 0) it induces shrinking of the condensed domain; when the force is such that Δμ₀ > 0, the domain grows. The second term, related to the elastic deformation u′(x, t), originates from the activation of the integrin-protein units by in-plane compression (at the front edge) and their deactivation by dilation (at the back edge); it is this effect that breaks the symmetry of the problem and induces the anisotropic growth of the FA in our model. At the front edge, both terms enhance the adsorption of additional plaque proteins from solution as the force is increased. However, at the back edge of the FA, these two terms operate in opposite directions. The term related to Δμ₀ also induces growth at the back edge of the FA, whereas the elastic term favors the desorption of plaque proteins to the bulk.

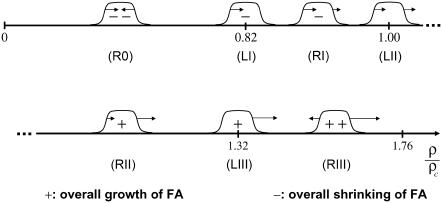
For weak forces, the compression term becomes negligible and the stretching term dominates the growth process. Since for small forces the mechanosensors in the lower layer are rarely activated, the previously adsorbed plaque proteins tend to desorb into the cytosol. As a result, in the regime of small forces, the symmetric term induces shrinking at both ends (see Fig. 8, range R0).

FIGURE 8.

Our model predicts different growth behavior in the different regimes of applied or actin-myosin-induced force: For small values of the force, the direct stretching of the integrin-protein units is not large enough to overcome the energy required for conformational change and the FA shrinks (R0). As the force is increased, the mechanosensors in the FA are activated; they then associate with plaque proteins from the cytosol and the loss of proteins is reduced. Because the compression term induces activation at the front edge, but deactivation by dilation at the back edge of the FA, it is the front edge that first changes (LI) its growth behavior from shrinking to a net gain of proteins (RI). For a certain force level, corresponding to a critical value of the plaque proteins' chemical potential, Δμ₀ = 0, the loss at the back is exactly compensated by the aggregation of new proteins at the front (LII) and the focal adhesion neither shrinks nor grows in size. When the force is increased from this critical value, the adhesion begins to grow in size (RII). Since cells are highly dynamic structures whose growth can be rapidly changed from shrinking to growing by their contractile apparatus, cells may regulate the actin stress so that FA operates near this critical force level (LII). In the regime of very high forces the model predicts that even the back of the adhesion tends to grow (in the opposite direction of the force) due to the direct stretching effect that dominates the dilation effect (RIII). A detailed description of each force regime is given in the text.

With increasing actin force, the mechanosensors in the lower layer are increasingly activated to associate with additional plaque proteins from solution. The shrinking induced by the symmetric term is reduced while the compression term becomes more significant. At the front edge of the FA, the compression term induces growth while at the back edge it induces an additional dissociation of plaque proteins from the lower layer and into the cytoplasm. When the actin force reaches high-enough values, the compression term precisely compensates the loss at the front edge due to the symmetric term, while the back is still shrinking due to the desorption of the plaque proteins. As a result, the front edge stays fixed while the back edge is shrinking (see Fig. 8, level LI).

If the actin force is increased above this value, the activation of the integrin-protein units at the front edge is enhanced by both the compression and the stretching terms to such an extent that the FA begins to grow at the front. Since at the back edge the elastic effect reduces the activation caused by the stretching term, the back—for a given range of force—may still show desorption of the plaque proteins and consequentially shrinks. For a specific range of forces, the loss at the back is higher than the gain at the front; hence one observes an overall shrinking of the FA—that is, its overall size decreases in time (see Fig. 8, range RI).

For a critical value of the force ρ_c, the loss of plaque proteins at the back is precisely compensated by the gain of plaque proteins at the front; at this critical value, the FA changes from overall shrinking to growing. As discussed above, this occurs at values of the force at which Δμ₀ = 0. However, at this critical force value, the shape and the size of the adhesion remains fixed while the center of mass of the domain does move as directed by the force (see Fig. 8, level LII).

For even higher values of the force the overall size of the FA begins to increase with time; this means the growth at the front is faster than the loss of plaque proteins at the back (see Fig. 8, range RII).

When the force reaches an even higher value, the activation of the integrin-protein units at the back edge of the FA caused by stretching is large enough to compensate the elastic-term-inducing deactivation of these units. For this value of the force, the back of the FA does not move while the front grows quickly (see Fig. 8 level LIII).

For even larger values of the force, our model predicts that in addition to growth of the front edge of the FA due to the adsorption and association of new plaque proteins from the cytoplasm with the lower layer, even the back edge begins to adsorb more plaque proteins and grow. This can happen because the activation of the integrin-protein units at the back edge by stretching overcompensates the desorption of plaque proteins from the deactivated integrin-protein units of the lower layer induced by the dilation of this layer due to the elastic effect (see Fig. 8, range RIII).

DISCUSSION

In this section, we explain the differences between our model and that of Shemesh et al. (14). Since the two models make different assumptions, we suggest here crucial experiments that can test these assumptions and elucidate the dominant mechanisms responsible for the anisotropic growth of FA. Shemesh et al. (14) regard the FA site as a bundle of plaque proteins that is stretched (over a scale comparable with the size of the FA) by the actin stress fibers. They propose that the driving force for plaque protein aggregation is the thermodynamic response of this self-assembly under tension: an aggregate that is stretched counteracts this change in density by attracting additional molecules from solution. This restores the equilibrium density of molecules and the stress in the aggregate is relieved. To obtain an effective stretching of the plaque protein bundle in response to the actin force, Shemesh et al. (14) assume a particular geometry of the focal adhesion: For the case of a growing adhesion there must be an imbalance between the number of points of force application and of points of anchoring (via the integrin). This is the case, e.g., if the density of anchor points differs from the density of bonds to the actin fibers. Furthermore, the front edge of the adhesion site must be connected to the stress fibers but must not be grafted to the substrate. On the other hand, they require that the back is grafted to the substrate but not attached to the actin. As a result, the adhesion site is effectively stretched caused by the local imbalance of the restoring force of the anchor points and the applied actin force. If the FA was considered to be symmetrical, namely the density of anchor points equals the density of bonds to the actin fibers, the FA would not be stretched and would not grow according to the model by Shemesh.

In our model, growth still occurs due to the coupling of the actin force and the density gradients at the front and the back that have differing signs and different effects on the activation of the mechanosensor. This points out the importance of the mechanosensor in our model; Shemesh et al. (14) do not require any mechanosensitivity in their thermodynamic treatment. In contrast to the stretching model of Shemesh, our theory makes no assumptions about the geometry of the FA. Despite this static symmetry of the adhesion in our model, the growth process is asymmetric because the elasticity of the lower layer spontaneously breaks the symmetry of the system. This is due to the compression term, which is an intrinsic, elastic response to the spatially constrained stress arising from the force exerted by the actin. The front and back of the FA only differ by the sign of their density gradients in a relatively narrow interfacial region in which the density of the plaque proteins changes from high to low values.

Another important difference between the two models is the driving force for protein aggregation. In our model, the reduction of chemical potential is driven by the activation of single integrin-protein units, which then prefer to either associate or dissociate with plaque proteins that have diffused from the cytoplasm. The elastic response of the FA to the actin force results in a net loss of proteins at the back and in enhanced adsorption of proteins at the front. This is in contrast to the prediction of the model by Shemesh, which predicts that the additional proteins are adsorbed in a gradual manner over the whole adhesion site once the stress exceeds a critical value. (If the stress is too small, there is no adsorption and growth of the FA.)

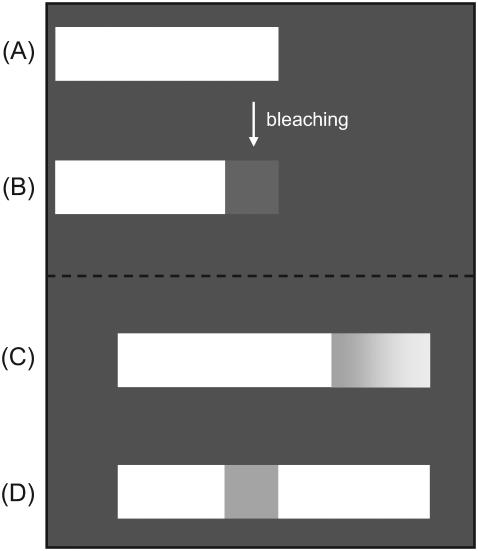
The differences between the two models for the dynamics of plaque protein aggregation allow us to suggest fluorescence-recovery-after-photobleaching experiments that can test the models and their predictions. Assume that one of the plaque proteins involved in FA assembly (e.g., paxilin or vinculin) is stained with a fluorescent dye (29) and the fluorescent light is tracked under a microscope. Next, a laser beam is placed in the vicinity of the front edge of the elongated adhesion plaque; this bleaches the proteins at the front (compare Fig. 9, A and B). Afterwards, the force exerted on the focal adhesion is increased (5), which induces protein aggregation and growth of the FA. Both models predict that additional plaque proteins from the cytoplasm associate with the FA as the force is increased, but the predictions for the pattern of the recovered fluorescence differ from each other:

• The model of Shemesh et al. (14) predicts that the concentration of additional, cytoplasmic plaque proteins that associate with stressed FA is proportional to their distance from the back edge. Therefore the bleached region will be filled with a smoothly varying concentration of plaque proteins from the cytosol, higher at the front than at the back. After a while, these additional proteins would establish a gradient of the fluorescence intensity in the once-bleached region. As additional proteins aggregate to relieve the stress, the once-bleached region also begins to grow in size and will be shifted in the direction of the force, since the additional proteins also elongate the plaque protein bundle behind the bleached region (see Fig. 9 C).

• The model presented here predicts a different distribution of the fluorescent intensity once new plaque proteins associate with the bleached FA. In our model, the cytoplasmic plaque proteins associate with the FA only near the very front where fluorescent intensity is thus recovered; near the back, proteins dissociate from the FA due to the dilation effect (for small values of the force). The main body of the FA is unchanged in our picture and we would predict that the bleached region maintains its size and position relative to the substrate. Since our model does allow thermal exchange of proteins over the whole adhesion site the fluorescence intensity may increase in time to some degree in the bleached region, but the model predicts no gradient in the reestablishment of the fluorescence intensity, except near the very front of the FA (see Fig. 9 D).

FIGURE 9.

(A) The light-colored rectangle schematically represents an FA stained with a fluorescent dye. (B) The front of the FA is bleached with a laser beam. Predicted development of the bleached region after the stimulation of the intracellular contractile apparatus or application of an external force: (C) by the model of Shemesh et al. (14); (D) by the model presented in this article.

However, both models allow that proteins are constantly exchanged between the FA and the cytoplasm due to thermal fluctuations. This exchange of proteins (resulting in recovery of the fluorescence) over the whole length of the adhesion site may smear the patterns described above. Fluorescence-recovery-after-photobleaching experiments with β3-GFP-integrins by Ballestrem et al. (27) showed that the fluorescence signal is recovered after 10 min due to thermal fluctuations, whereas the growth of FA stimulated by external force elapses in ∼3 min (5). Nevertheless, the gap between the two timescales may be sufficient to elucidate the nature of the stressed region of FAs and distinguish between the two models. This is indicated by an experiment, very similar to the one we propose, performed by Wehrle-Haller et al. (30). They show that totally bleached, sliding FAs recover their fluorescence intensity strongly at the very front of the bleached region (see Fig. 4 b in (30)). These results suggest that the activation mechanism proposed in this article may indeed be responsible for the growth of FAs. However, more detailed and more quantitative data is needed for a clear distinction between the two models.

In summary, our model suggests that the anisotropic growth response of FA is stimulated by conformational changes of mechanosensitive proteins located in the adhesion plaque. The transition from a nonactivated to an activated state is induced by external forces. Activation can occur by either stretching or in-plane compression and the latter process enables us to relate protein adsorption to the elastic deformations of the FAs and thus to the actin force. By solving the coupled elastic and dynamic equations we predict how FAs grow or shrink in different force regimes. In particular, we calculated the velocity of both the front and the back edges of the adhesion site as a function of the force. We predict a critical value of the force at which the FA changes from shrinking to growing and that the force-dependent chemical potential, Δμ₀, is the appropriate control parameter that determines the growth behavior. When the force is such that Δμ₀ = 0, the FA neither grows nor shrinks. When the force is slightly increased above this critical value, the condensed domain of plaque proteins begins to grow in size. This is obviously the most physically interesting and biologically relevant regime, since FAs in cells are highly dynamic structures whose growth can be rapidly changed from shrinking to growing by the contractile apparatus of the cell. This suggests that cells may regulate the actin stress so that the FA operates near this critical force level.

An additional feature of our model is its ability to predict different growth behaviors in various force regimes. Although it is difficult to predict absolute numbers for the growth velocities and critical forces, the trends and their implications for experiment are well established by our calculations. Measurements of these force regimes in future experiments may provide an important test of the theory. Such an experiment could be performed by exposing cells to a drug that inhibits the contractility of the actin-myosin apparatus. By varying the concentration of the administered drug one can thus control the intracellular forces in an quantitative manner. Comparison of theory and experiment can then be used to refine the model and differentiate between various microscopic mechanisms.

APPENDIX A: FREE ENERGY

In this Appendix we present a detailed derivation of the free energy given in Eq. 15. In Eq. 12, we wrote the activation probability for the sensor at site i. Here, we rename it for convenience as

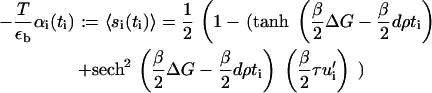(A1)

As described in Interactions Among the Absorbed Plaque Proteins, we make the following ansatz for the Hamiltonian of the plaque proteins (now in terms of α_i(t_i)):

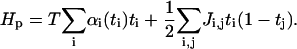(A2)

The partition function for this Hamiltonian is difficult to evaluate because of the coupling between the sites in the last term. Following the derivation in Safran (28), we use the variational method and consider a model Hamiltonian, H_p0, that contains terms that only involve single sites:

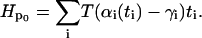(A3)

The parameters γ_i are determined by the minimization implied by the variational method (28). The partition function of the model system is

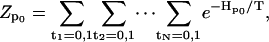(A4)

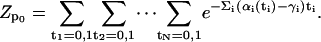(A5)

Since H_p0 does not involve coupling between the sites, we find an expression for the partition function that is a simple product,

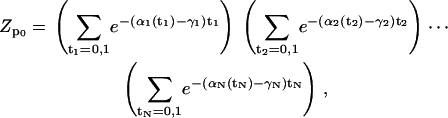(A6)

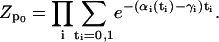(A7)

Evaluation yields

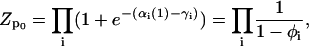(A8)

where 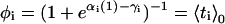is the equilibrium average value of the local concentration variable t_i in the ensemble described by H_p0. This is obtained by considering

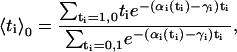(A9)

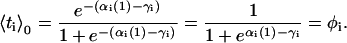(A10)

One can do the same for

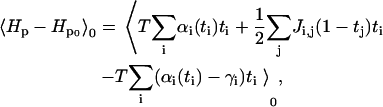(A11)

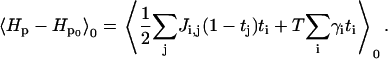(A12)

Since t_i and t_j are not correlated,

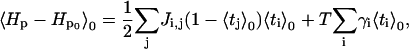(A13)

so

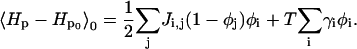(A14)

The free energy, F, is given by the variational principle (28):

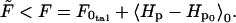(A15)

Using our results from Eq. A14,

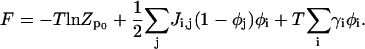(A16)

The value γ_i is known from Eq. A10,

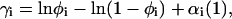(A17)

and Z_p0 is known from Eq. A8. This yields for the free energy F:

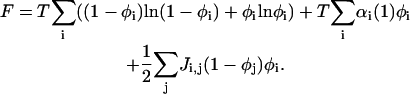(A18)

The last term of Eq. A18 can be rewritten as

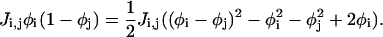(A19)

We now perform the continuum limit, which allows us to convert the differences (φ_j–φ_i) to a gradient. The precise form of this gradient depends on the coupling matrix J_{i, j}. For the case of short-range interaction, we can consider only nearest-neighbor interactions, and we write

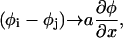(A20)

where a is the distance between nearest-neighbors, which leads to

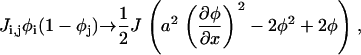(A21)

and the other functions are transformed like

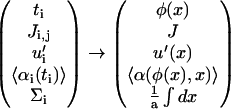(A22)

This yields the expression for the free energy of

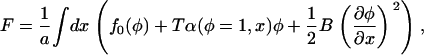(A23)

with 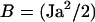and

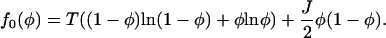(A24)

In our model, most of the protein dynamics such as adsorption or desorption take place at the edges of the FA site. In this region, the plaque protein concentration drops from a value of ∼1 (condensed domain of plaque proteins, the FA) to a low value ≈0 (the low density domain). Thus the interface between the two phases can be considered to be at 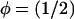. For convenience we introduce 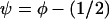and expand about ψ = 0, the region of interest, and arrive at

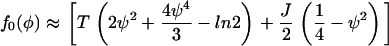(A25)

The total free energy is then written as (eliminating α by its definition in Eq. A1)

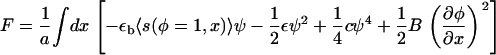(A26)

Because we are only interested in the chemical potential (which is a functional derivative of the free energy) we drop the constant terms and define the coefficients as

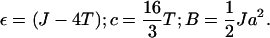(A27)