Entropy-Driven Genome Organization

Abstract

DNA and RNA polymerases active on bacterial and human genomes in the crowded environment of a cell are modeled as beads spaced along a string. Aggregation of the large polymerizing complexes increases the entropy of the system through an increase in entropy of the many small crowding molecules; this occurs despite the entropic costs of looping the intervening DNA. Results of a quantitative cost/benefit analysis are consistent with observations that active polymerases cluster into replication and transcription “factories” in both pro- and eukaryotes. We conclude that the second law of thermodynamics acts through nonspecific entropic forces between engaged polymerases to drive the self-organization of genomes into loops containing several thousands (and sometimes millions) of basepairs.

INTRODUCTION

Specific interactions between monomers (e.g., H-bonds) are known to mediate biomolecular assembly. Paradoxically, nonspecific entropic forces can also drive self-assembly. Thus, the environment within a living cell is crowded, with 20–30% of the volume occupied by macromolecules (1,2); then, aggregation of the largest particles can lower the free energy of the system through an increase in entropy of the many smaller particles (3). In Fig. 1 A, the centers of mass of the small spheres can access the yellow volume, but not the gray volumes surrounding each large sphere or abutting the perimeter wall. When one large sphere approaches another, these excluded volumes overlap (Fig. 1 A, overlap volume 1) and this allows the small spheres to access a greater volume. The resulting increase in entropy of the many small spheres generates what has been called a “depletion attraction” between the large ones. The attractive energy at contact is ∼3/2(D/d)n k_BT, where D and d are the diameters of the large and small spheres, n is the volume fraction of the small spheres, k_B is the Boltzmann constant, and T is the absolute temperature (3). The attraction falls to zero at a distance d between the two large spheres. A related attraction drives a large sphere to the surrounding wall (Fig. 1 A, overlap volume 2). Enough is known about these attractions that they are being used to model the formation of helices in proteins (4) and position particles within man-made nanostructures (5). The free-energy gains can be several k_BT, which can be compared with the energy associated with a single van der Waals interaction (∼0.1 k_BT), a single H-bond (∼1.5 k_BT, or ∼1 kcal/mol), and a covalent bond (10–100 k_BT).

FIGURE 1.

The depletion attraction. (A) The schematic shows a suspension of large and small spheres in a box. The shaded regions around the four large spheres are excluded to the center of masses of the small spheres. When one large sphere contacts another, their excluded volumes overlap (overlap volume 1) to increase the volume available to the small spheres (increasing their entropy); then, aggregation of the large spheres paradoxically increases the entropy of the system. An analogous effect is found when a large sphere contacts the wall (2). The attraction can also be viewed as an osmotic phenomenon; small spheres cannot enter excluded volumes, and a force equivalent to their osmotic pressure acts on each side of the two touching large spheres to force them together (or on one side of the large sphere at the wall to force it to the wall). (B) Spheres bound to each end of a string will also tend to aggregate or associate with the wall, to loop the connecting string (which has an associated entropic cost). The type of overlap involved is indicated.

Here we describe how this depletion attraction might drive genome organization. (For various models of genome structure, see Manuelidis (6), Cook (7), Sachs et al. (8), Marshall et al. (9), Munkel and Langowski (10), Belmont (11), Ostashevsky (12), and Kleckner et al. (13).) When DNA is replicated or transcribed, the resulting polymerizing complexes are large enough relative to the crowding agents that they will tend to aggregate. We consider a range of different complexes in bacteria and man, and in almost every case, the depletion attraction is sufficient to explain the observed organization—the clustering of active DNA and RNA polymerases into “factories” to form loops that may be several millions of basepairs in length (14–17).

METHODS

The depletion attraction

We first review the original formulation of the entropic depletion attraction. Consider two hard (chemically noninteracting) spheres of diameter D dispersed in a solution of hard spheres of diameter d (usually the case d < D is considered). The center of mass of the small spheres is excluded from a shell surrounding the large spheres (Fig. 1 A). As one large sphere approaches the other, these excluded volumes overlap (Fig. 1 A, overlap volume 1) and the small spheres can access a greater volume; there is a net free-energy gain due to the increase in the entropy of the small spheres. The minimum of this potential is attained when the two large spheres are in contact, and is given by Asakura and Oosawa's formula (3)

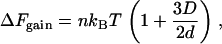(1)

where n is the volume fraction of small spheres, k_B the Boltzmann constant, and T the absolute temperature. Eq. 1 is an approximation and applies to values of n up to ∼30%; it then becomes less reliable until ΔF changes sign. If the two spheres are moved apart, the attraction declines progressively as the overlap volume falls. For values of D and d used here, the average attraction in the range of full to zero overlap is approximately half that given by Eq. 1.

We now generalize to different and arbitrary shapes. The scale of the free energy gain depends significantly on the shape of the large objects. For example, Eq. 1 can be generalized to two different large spheres (3) with diameters D₁ and D₂, where D₁ > D₂:

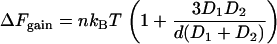(2)

A special case is that of a wall, in which D₁ = 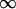; the overlap volume is larger than that with another sphere (Fig. 1 A, compare overlap volumes 1 and 2), so the resulting attraction is larger and given by

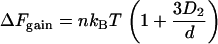(3)

ΔF_gain is even larger with a convex wall like a bacterial cell membrane (18).

Most biological interactions involve nonspherical objects like ligands that fit snugly into irregularly shaped receptors. In the most general case, theory (3) predicts that the free-energy gain for irregular objects is

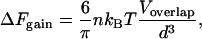(4)

where V_overlap is the increase in volume available to the small objects. We approximate proteins and RNA here as spheres as they usually fold into globular structures.

“Soft” beads

Most situations we discuss involve interactions between polymerases bound to DNA, and individual enzymes are modeled as hard spheres. However, we also discuss interactions between two clusters of polymerases where each cluster contains many enzymes (e.g., DNA polymerases in replication factories). In such cases, the biology suggests that individual enzymes intermingle when the two clusters come into contact; we call these clusters “soft,” and allow individual hard spheres in one cluster to intermingle on contact with their counterparts in the other. The result is one large cluster with the combined volume of the two original ones. This problem is complicated by the large number of possible arrangements of individual spheres within a cluster, and of one cluster relative to the other. Therefore, we restrict analysis to simple limiting cases. At the coarsest level, each cluster can be treated as one macrosphere with volume (or surface) corresponding to the total of all individual spheres. This approach is used for the “hard” gains in Fig. 2, rows 9–13. However, for Fig. 2, rows 3, 4, and 14 (hard gains), all polymerases are attached to DNA and a better model is obtained by considering the cluster of N polymerases as a linear (straight) succession of N closely packed beads; then, the free energy gained by putting two such clusters in longitudinal contact is N times the gain for two individual beads. This holds if the polymer is very stiff (i.e., its persistence length is larger than N times the diameter of a polymerase). If, on the other hand, the polymer is flexible, so that the cluster diameter is much larger than the persistence length (or if there are many individual spheres in one cluster), we allow individual spheres in one cluster to intermingle freely with their counterparts in the other (with the gain as in Eq. 5, below). This approach is used for the soft gains in Fig. 2, rows 3 and 9–14.

FIGURE 2.

Energy gains (ΔF_gain from the depletion attraction) and losses (ΔF_loss due to looping). ΔF_gain is the maximum obtained for hard spheres or soft clusters at closest contact; n = 0.2, and d = 5 nm (except in row 2, where d = 1 nm). Cartoons illustrate the structures analyzed: blue, DNA; red, RNA; green, DNA polymerases; pink, RNA polymerases (pols). See Methods plus Results and Discussion for details.

If the two clusters of large spheres (total diameter of each cluster = D) are soft and can fuse to give one larger sphere of size 2^1/3D (i.e., with conservation of volume), the entropic gain is proportional to the gain in volume excluded to the small macromolecules. This gain is given by

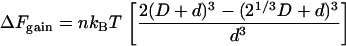(5)

If spheres in the two clusters are allowed to intermingle, the overlap volume is considerable and the entropic gain now depends on D²/d² (Eq. 5); this compares with D/d for hard spheres (Eq. 1).

Two beads on a string

We now come to the central case of interest here (Fig. 1 B), which has not yet been analyzed: two large spheres threaded on a connecting (genomic) string. We assume the tethering string can be modeled as a polymer in a good solvent (19). Whether there is a net attraction between spheres depends on the balance between ΔF_gain and ΔF_loss, where ΔF_gain is the entropic attraction between spheres (given by Eq. 1 or 5 for hard or soft spheres, respectively) and ΔF_loss is the entropic penalty that must be paid to loop the string. This loss arises due to the tethering constraint, and is well approximated by (20,21):

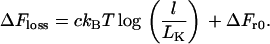(6)

The constant c has been the subject of debate between theoretical physicists (see Hanke and Metzler (20) and references therein) and depends on loop conformation; it typically increases with string density from 1.5 for an ideal random walk or freely jointed chain, through 2.2 for the “four-legged” loop as in Fig. 1 B (22), to higher values if the density is very high (below). l is loop length, and L_K is the (statistical) Kuhn length of the string. ΔF_r0 is a constant that is independent of loop length; it is physically related to the dimensions of the overlap volume (and so to the diameter of the small spheres), and to the range r₀ of (short) distances between the two beads that we consider sufficient to form a loop. ΔF_r0 for self-avoiding walks is generally estimated by simulation and can be significant in the cases we consider. Note that we consider the looping costs of both a freely jointed chain (in bacteria) and a self-avoiding loop (in eukaryotes); costs for the latter have not been determined previously.

The entropic attractions between two free or tethered spheres differ qualitatively in an important respect. The most probable state for two untethered spheres is to lie apart as they diffuse in three-dimensional space, and the fraction of spheres that do pair—f_pairing—can be found using the van't Hoff relation (neglecting three and higher body interactions):

(7)

where K_eq is the equilibrium constant of the reaction and C_b is the concentration of unbound large spheres. In contrast, two spheres threaded on a string can often be together if the interaction is large enough. Treating the thread as a freely jointed chain, we can calculate semianalytically the (“looping”) probability of finding the two within the overlap volume (Fig. 3 A). This probability is found by weighing the probability of the two spheres being at a distance r through the depletion attraction (3). Even if the attractive interaction cannot bring the two spheres permanently together, it can still ensure that the two pair for at least some finite time (τ_pairing, see below). This qualitative distinction can lead to large quantitative differences. For example, of the ∼8000 molecules of RNA polymerase (diameter ∼10 nm) in an Escherichia coli cell (volume ∼0.8 μm³ (23)), we calculate (24) that only 2% are paired (i.e., 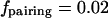); this compares with the essentially complete pairing of two sets of 70 threaded polymerases (Results and Discussion).

FIGURE 3.

Dependence of looping on attractive energy, chain length, and sphere diameter. Cartoons illustrate forms existing under different conditions. See Methods for details. (A) Probability of forming loops at different attractive energies (in k_BT). Structures modeled are two large beads (D = 10 nm) connected by freely-jointed chains of different lengths; a loop is considered to exist if sphere surfaces lie within 5 nm. Sharp transitions between unbound (unlooped) and bound (looped) states occur within ∼5 k_BT. (B) Effects of minimum diameter (D) of large spheres and length of freely-jointed chain on looping; lines mark transitions between unlooped and looped forms for hard and soft spheres.

Examples

The E. coli genome is modeled as a freely jointed chain—a succession of infinitely thin penetrable segments, each of length L_K of 0.3 kbp (calculated assuming a persistence length for B DNA of 50 nm (25)). The eukaryotic chromatin fiber is modeled (26) as a self-avoiding tube (persistence length 40 nm or ∼3.6 kbp, assuming a packing of 1 kbp/11 nm). Note that the volume fraction, n, is known in bacteria but not in eukaryotes, whereas local DNA structure is known in eukaryotes but not in prokaryotes. As zig-zagging models have supplanted those involving 30-nm solenoids (27), tube diameter is set at 20 nm in eukaryotes to reflect a wider zig-zagging fiber that can interpenetrate to some extent.

We model pro- and eukaryotic genomes differently mainly because the thickness/persistence length ratios are so different. In bacteria, there is no evidence of proteins bound stably to DNA, and DNA diameter (∼2.5 nm) is smaller than persistence length (∼50 nm); therefore, it seems appropriate to neglect thickness and use the analytically tractable freely jointed chain. In eukaryotes, we know that DNA is folded first into nucleosomes and then into higher-order structures; as a result, diameter (20 nm) is a significant fraction of persistence length (40 nm) and it seems more appropriate to use the tube model (which includes self-avoidance, but is less tractable analytically). Self-avoidance is included by ensuring that all circles going through any triplet of points taken along the tube center-line have radii larger than half the tube thickness (26). Calculation of looping costs requires Monte Carlo simulations, as existing theory does not enable us to compute ΔF_r0 analytically. To calculate the looping probability, we adapt the method used previously to determine the probability that a point on a loop attached to one sphere might bind to a specified binding zone on the surface of that sphere (26). Here, we have two beads attached to each end of a flexible tube. We fix the position of the center of one bead, divide the surrounding volume into concentric shells of increasing radii, and compute for each pair of contiguous shells the conditional probability that the other end of the tube is found in the inner of these two shells, given that it is constrained to lie within the outer of the two shells.

In Fig. 2, values for ΔF_loss in E. coli for equivalent structures tend to be higher than those for man. This arises for two reasons. First, bacterial DNA is less compact (above), so loops are longer (giving a higher entropic cost); if it proves to be more condensed, values for ΔF_loss will be smaller. Second, the beads tend to have smaller diameters in bacteria, so values for ΔF_r0—which depend on the range of distances between the two beads considered sufficient to form a loop—tend to be larger; they were 5.7 k_BT in Fig. 2, rows 3–5 and 7 (calculated assuming a depletion attraction in the range 10–15 nm between sphere centers), 3.2 k_BT, 3.5 k_BT, and 3.5 k_BT (assuming a range of 43–48 nm, 37–42 nm, and 37–42 nm) in Fig. 2, rows 6, 8, and 9, respectively. In Fig. 2, rows 11–17, we assumed interaction in the range between sphere centers of 30–35, 30–35, 75–80, 25–30, 25–30, 40–45, and 25–30 nm, respectively, and calculated the entropic loss via Monte Carlo simulations (26).

For Fig. 2, rows 3 and 4, the distance between rrn operons is genome length (i.e., 4.6 Mbp) divided by operon number (i.e., 7). In LB, there are ∼70 polymerases per operon (23), and ΔF_gain is calculated assuming either that 70 closely packed impenetrable spheres lie in straight lines at each end of a 650-kbp thread (for hard), or that each one of the 70 hard spheres at one end can intermingle with any other sphere (for soft). These two extremes correspond to very stiff and very flexible threads, respectively, and the real situation is likely to lie in between. In contrast to other cases, here the gain given by the soft cluster (which is proportional to the number of polymerases exposed to the solvent on the surface) is smaller than that given by hard polymerases. For Fig. 4 C, we consider the topology in Fig. 4 B, and calculate the probabilities that different operons cluster together into f foci (where f is between 1 and 22). To make the problem tractable, we assume the following. 1), An observable focus corresponds to one operon (or more), with each associated with 70 polymerases tagged with green fluorescent protein (GFP) (note that 70% polymerases are engaged on rrn operons (23)). 2), Neighboring operons cluster first, the next nearest neighbor is then added to the cluster, and so on. 3), We compute the separate probabilities of having f_i foci for the four arms in the network (i.e., two arms containing rrnC,A,B,E,F,G,D and two with rrnC,A,B,E). Via the convolution of these quantities, we can find the probabilities of the whole system having f foci. 4), Operons are connected by a freely jointed chain (as ΔF_r0 can be calculated exactly). We also assume a not-further-specified interaction between active operons, calculate the probability of observing f foci (with f = 0–6 (28)), and adjust the interaction to fit the data. We have repeated the calculation assuming that two operons must be in the same site to be detected as a focus and found a slightly smaller value for the interaction (i.e., 13 k_BT instead of 16.5 k_BT). For Fig. 2, rows 5–8, average spacings between active polymerases are from M. Bon, S. McGowan, and P. R. Cook (unpublished). For Fig. 2, rows 5 and 7, a gain of 0.8 k_BT is nevertheless sufficient to increase the time spent together by 30%; the gain also doubles if transcripts are included as 10-nm hard spheres. If we model each polymerase, transcript, plus associated ribosomes as one 10-nm hard sphere (the polymerase) plus coplanar contacting hard spheres (diameter 21 nm) representing ribosomes, the gain increases by 1.46 k_BT for each ribosome (estimated by considering the configuration where the two planar clusters are stacked in register so that equal-sized spheres are in contact).

FIGURE 4.

The rrn operons of E. coli. See Methods for details. (A and B) Typical genome topologies. Positions of the origin (ori), terminus (ter), and seven operons encoding ribosomal RNA (rrnA–G (shaded letters)) are shown (23). In M9 + glucose, replication began at the origin, and the two forks progressed only a little away around the genome. In LB, an origin fired, the two replication forks progressed most of the way to the terminus, and duplicated origins refired. (C) Probabilities that cells contain different numbers of foci marking rrn operons. Experimental data (gray line (40)) can be fitted (red line (33)) assuming that all cells contain structures like that illustrated in B with 22 rrn operons, and an attraction of 16.5 k_BT between rrn operons that brings one or more together so they appear as one focus; this compares with a maximum attraction of 31–56 k_BT calculated in Fig. 2, row 3.

For Fig. 2, row 9, we consider slowly growing cells with only two forks (as in Fig. 4 A); the entropic cost of looping is given by

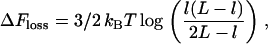(8)

where l and L (expressed in Kuhn lengths) denote distance between forks and total genome length, respectively. The cost in Eq. 8 is that to make one loop, as joining the two forks only creates one extra loop. Eq. 8 is valid for 1 ≪ l ≪ L, and has been derived by first writing down the probability that three distinct freely jointed chains (of length l, l, and L − 2l) have the same initial and final point, which we call 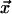and 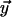respectively, and then by taking the limit 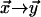of this quantity.

For row 10, each fork is associated with a cluster of 25 hard spheres and is attracted to the membrane. ΔF_gain (hard) is calculated assuming that each fork is associated with one larger hard sphere that can accommodate the 25 tightly packed spheres (when the entropic gain is given by Eq. 3). We compute ΔF_gain soft by comparing the volume excluded to the crowding macromolecules by a sphere cap abutting the wall, where the cap has the same volume as the 25 spheres. The gain is given by the maximum over h in the range [0,D] of the function:

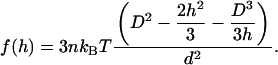(9)

On the other hand, confining one of the forks in the topology of Fig. 4 A to a distance x₀ from the wall costs some entropy, which if the chain is a freely jointed chain reads (l ≪ L, and both L and l are much larger than 1, with erf denoting the error function):

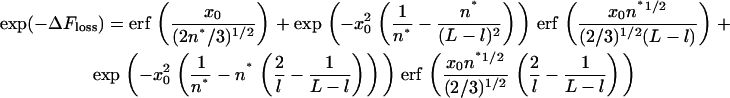(10)

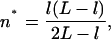(11)

where x₀, l, and L are all measured in Kuhn lengths. To arrive at Eq. 10, we calculated the probability of having a network of freely jointed chains with the topology in Fig. 4 A, integrating over the intermediate points and requiring that this freely jointed network is rooted at a point. (The axes are such that the bacterial surface lies at z = 0.) The exact entropic cost in Fig. 2, row 10, is computed assuming that the network is displaced from 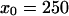nm (the center of the cell) to within the range of the entropic attraction to the surface. The calculations leading to Eq. 10 are cumbersome but straightforward and are omitted here.

For Fig. 2 rows 14–17, ΔF_gain is found as for rows 3–8. For row 17, we model each polymerase, transcript, and spliceosome as three coplanar contacting hard spheres (a 15-nm polymerase, 20-nm transcript plus bound proteins, and 24-nm spliceosome). The free-energy gain is estimated by considering the configuration where the two planar clusters are stacked in register (so that equal-sized spheres are in contact). For rows 15–17, the entropy gain is less than the loss due to looping, and so is insufficient to ensure that the two transcription units are always together. However, the interaction is sufficient to drive a temporary association, which keeps the two together for a time, τ_pairing, which can be estimated using Kramer's theory (25) applied to the potential resulting from the radial integration of the entropy depletion interaction (3), complemented with a Morse potential that forbids the two large spheres to interpenetrate more than 0.1 nm. The resulting expression is

(12)

For large spheres with a diameter of 10–20 nm, τ₀ is typically ∼5 μs. This estimate is based on the assumptions that the friction experienced obeys Stokes' law and the viscosity of the cell interior (η) is ∼10 centipoise (29,30). Applied to the case in Fig. 2, row 17, Eq. 12 provides an estimate for of 0.3 ms. We now consider cooperative effects as three large spheres cluster (Fig. 5 C). It appears natural to assume that the activation free energy leading to the breaking of the cluster involves the loss of two contacts at a cost of ∼8 k_BT. The estimated lifetime for the cluster is therefore ∼0.1 s. Since the viscosity of the cell interior grows rapidly with particle size >∼25 nm (29,30), this estimate (based on a nominal value for η) provides a lower bound for pairing time. We conclude that pairing lasts for a nonnegligible fraction of the ∼5 min it takes to transcribe a typical human gene (31).

FIGURE 5.

Cooperative effects. See Methods for details. (A and B) Monte Carlo simulations of 21 beads (green, terminal beads; red, internal ones) threaded every 20 kbp along a (self-avoiding) 0.4-Mbp chromatin fiber (blue). Each bead represents three spheres (15-nm RNA polymerase II, 20-nm transcript, 24-nm spliceosome). Starting with a linear string, fiber segments are allowed to diffuse while being subjected to an attraction between any two beads of 4 k_BT (Fig. 2, row 17). In panel B, the string was first compacted using an initial interaction of 8 k_BT. After reaching equilibrium, typical structures are visualized using RasMol software. The numbers of beads in each cluster are indicated, which in both panels A and B is more than the approximately five expected in the absence of cooperative effects (from Fig. 2, row 17, calculated as for Fig. 3 A). (C) Trade-off between entropic gains and losses. When two complexes pair, the entropic gain involves one overlap volume (Fig. 1 A) relative to the cost of forming one loop. Adding a third involves two more overlap volumes but only one more looping cost; adding a fourth involves three more overlap volumes but only one more looping cost. Adding more beads is progressively less favored as crowding increases the looping cost; moreover, entanglement becomes significant with more than around eight beads (52), and this limits the maximum number of beads in a cluster.

For Fig. 5, A and B, we model each mRNA-producing complex as three coplanar, contacting, hard spheres (a 15-nm polymerase, 20-nm transcript plus bound proteins, and 24-nm spliceosome), although each triplet is represented as one bead in the figure. The simulation began with a linear string, the (final) attraction between any two triplets is modeled as a two-body square well with a width of 5 nm and minimum equal to 4 k_BT (Fig. 2, row 17). In Fig. 5 B, the string was first compacted using an initial interaction of 8 k_BT.

RESULTS AND DISCUSSION

The small crowding molecules in the cell have diameters (d) of ∼5 nm, and a volume fraction (n) of ∼0.2; these commonly accepted values (1,32) will be used throughout, except for one extracellular case—the 100-mers (below). In Fig. 2, various cases are listed according to their complexity; each example is accompanied by an estimate (the “gain”) of how much the free energy is lowered upon contact of the large spheres.

Sphere/sphere interactions

Actin

To put our analysis in context, we first consider a simple example—the polymerization of two actin monomers. The major energy source driving actin polymerization comes from ATP hydrolysis; however, calculation shows that the depletion attraction makes a contribution even though it cannot provide directional assembly (which must be determined by other factors). Modeling monomers as noninteracting hard spheres (D = 5 nm) in the presence of many small spheres (d = 5 nm, n = 0.2) gives an entropic gain (i.e., ΔF_gain) of ∼0.5 k_BT (Fig. 2, row 1), compared to a measured free-energy change of 1–2 k_BT (33,34). We conclude that the depletion attraction adds to other specific ones between molecules, and we will argue that the same is true of the cases discussed below. We can then calculate (using Kramer's theory) that monomers remain paired for three times longer in the presence of crowding molecules (see Methods).

Prebiotic RNA genomes

We now consider two of the simplest genomes. Current theories for the evolution of life involve RNA molecules able to catalyze their own synthesis (35,36). But in this “RNA world” lacking cell membranes, how are the critical components prevented from diffusing apart to maintain the high local concentrations necessary for continued evolution? Possible solutions include binding to charged surfaces, and capture within a confined space (e.g., a hydrothermal vent, a puddle on a charged surface). However, the depletion attraction could contribute. Thus, modeling two 100-mers of RNA as 4-nm spheres in a crowded solution of smaller molecules (d = 1 nm, n = 0.2) gives an attraction (gain) of ∼1.4 k_BT (Fig. 2, row 2). Here, too, pairing lasts roughly three times longer than in the absence of the depletion attraction.

Two beads threaded on a string

We now turn to the central case of interest here, where the two large spheres are threaded on a string; the spheres represent active polymerases and the string hydrated DNA (in prokaryotes) or a chromatin fiber (in eukaryotes). It is well known that specific interactions between spheres can drive genome looping. Thus, if two DNA-binding proteins present at ∼1 nM interact together with a K_d of 10⁻⁷ M (values typical for nuclear proteins), <1% will be complexed together in the absence of DNA (37). But if they bind to the same DNA molecule at sites 10 kbp apart, the resulting local concentration ensures that two-thirds will be in the complex to loop the connecting DNA (37). Our central thesis here is that the nonspecific depletion attraction can also make a significant contribution in the crowded cell (Fig. 1 B). Whether aggregation occurs depends on the balance between the depletion attraction (i.e., ΔF_gain; Eq. 1 in Methods) and ΔF_loss (the entropic penalty that must be paid to loop the connecting string). This loss is well approximated by ck_BT log(l/L_K) + ΔF_r0 (Methods). The constant c depends on loop conformation; it typically increases with string density from 1.5 for an ideal random walk or freely jointed chain, through 2.2 for the four-legged loop as in Fig. 1 B (22), to higher values if the density is high. l is loop length, and L_K the Kuhn length (a measure of string stiffness). Notice that we include self-avoidance in the case of the thick eukaryotic string (i.e., no two segments of the fiber are allowed to occupy the same volume). ΔF_r0 is a constant that is independent of loop length; it is physically related to the dimensions of the overlap volume and the range r₀ of distances between the two beads considered sufficient to form a loop (in our case ≤5 nm). In the cases modeled here, the spheres are polymerases that remain irreversibly bound to their templates while active.

Two free (untethered) spheres in a crowded cell will diffuse in three-dimensional space and spend little time together, and the extent of the small paired fraction can be determined using van't Hoff's relation (Eq. 7 in Methods). If the two spheres are tethered to each other, the inevitable high local concentration plus depletion attraction ensure that the paired fraction is greater. The (looping) probability of finding the two spheres close enough together for their excluded volumes to overlap is illustrated in Fig. 3 A, which gives results for a freely jointed chain. (Similar results (not shown) are found for self-avoiding and worm-like chains (which differ by the presence of a nonzero stiffness parameter (25)).) Sharp transitions are seen between the unbound (unlooped) and bound (looped) states with chains of different lengths. The diameter of the large spheres (D) and length of connecting string are important determinants of whether or not a loop forms (Fig. 3 B); above the upper (orange) line, two spheres will eventually come together to form a loop. As before, the time the two spend together can be estimated using Kramer's theory (Methods).

“Soft” beads

Individual polymerases bound to DNA are modeled as hard (impenetrable) spheres. However, we also discuss interactions between clusters of bound polymerases where each cluster contains many active enzymes (e.g., DNA polymerases in replication factories). Although modeled as two clusters of (polymerase-sized) spheres or as two larger spheres, individual enzymes probably intermingle when the two clusters come into contact. Therefore, we also model such clusters as “soft,” and allow individual hard spheres in one cluster to intermingle on contact with their counterparts in the other. The result is one large cluster with the combined volume of the two original ones. Intermingling ensures that the overlap volume is considerable, and the entropic gain now depends on D²/d² (Eq. 5 in Methods), compared to D/d for hard spheres (Eq. 1 in Methods). As a result, soft clusters are more likely to come together to form a loop, and smaller diameters are needed to ensure looping (Fig. 3 B, lower red line). These two cases (hard and soft) represent extremes; true values are likely to lie between the two, and (conservatively) we generally consider here the former.

Tunable interactions

The transition to the looped form occurs over a narrow free-energy range of ∼10 k_BT (Fig. 3 A), roughly equivalent to ∼7 H-bonds. It then might be advantageous for the cell to ensure that DNA-binding complexes are of a size that can exploit this transition (e.g., by creating or destroying only a few H-bonds). The depletion attraction puts an upper limit on the size of complexes that permit such tuning; if too large (i.e., with diameters of ∼100 and 40 nm for hard and soft clusters, respectively), Fig. 3 B shows that there is a good chance they will always aggregate to give loops. As we shall see, Nature seems to set diameters so that the resulting depletion attraction lies in this tunable range.

This prompts the question: why do not all complexes in the cell—whether tethered or not—end up in one aggregate? (The fraction in the aggregate can be found using Eq. 7 and Fig. 3 for untethered and tethered components, respectively.) We suggest that they will do so if the concentration of components is high enough—for example, with hemoglobin S in the red cells of patients with sickle cell anemia (38), and with over-expressed proteins in bacteria (which sometimes form inclusion bodies). Where both the concentration and scale of the depletion effect are large enough to form aggregates, but where experimental observations yield no evidence of aggregation, it also seems likely that energy from other sources must be spent to prevent aggregation.

Examples

Bacterial rrn operons

The genome of E. coli encodes 7 rrn operons separated on average by ∼650 kbp (Fig. 4 A). In Luria broth (LB)—a rich medium supporting division every 30–45 min—demand for rRNA is high; ∼70% of the RNA polymerase in the cell transcribes one or other of these operons, and each rrn operon is associated with ∼70 active enzymes (23). As an origin (ori) often fires and refires before genome segregation, a cell typically has a genome structure like that in Fig. 4 B, with ∼22 active rrn operons (23). Treating each polymerase as a hard sphere (D = 10 nm), and each operon as a linear string of 70 closely packed spheres, we find that the entropic attraction (i.e., ΔF_gain) between two operons significantly exceeds the penalty that must be paid to loop the intervening DNA (i.e., ΔF_loss; Fig. 2, row 3). (Including nascent transcripts (average length ∼2500 nucleotides, or half the length of the completed transcript) as spheres (D = 10 nm) attached to polymerases ensures that the attraction is even higher (not shown).) This suggests that entropy depletion inevitably drives two active operons together.

In a nutrient-poor media like M9 + glucose, cells divide every 90–170 min and biosynthetic capacity switches away from ribosome genesis; the genome structure is like that in Fig. 4 A, and each rrn operon now associates with only about four polymerases (23). As a result, the loss due to looping outweighs the gain (Fig. 2, row 4), and rrn operons are unlikely to be together.

These results are consistent with experimental data (28). Tagging with the GFP reveals that in LB the polymerases (and so the ∼22 operons to which ∼70% are bound) are clustered in one to six foci that disappear on transfer to M9 + glucose. The distribution of foci in LB (28) can be fitted assuming that there is an attractive interaction of ∼16.5 k_BT between each operon (Fig. 4 C); this compares with the value we calculate for the (maximum) attraction of 31-56 k_BT (Fig. 2, row 3).

Bacterial open reading frames

Engaged RNA polymerases are scattered every ∼24 and ∼8.6 kbp along the bacterial genome in LB and M9, respectively (M. Bon, S. McGowan, and P. R. Cook, unpublished). If we include only the polymerase, the gain is insufficient to overcome the cost and so unlikely to bring two lone and adjacent polymerases together (Fig. 2, rows 5 and 7). However, translation occurs cotranscriptionally, so ∼10 (in LB) or 6 ribosomes (in M9 (23))—each with a diameter of ∼21 nm—are typically attached to the nascent transcript (length ∼500 nucleotides, equivalent to half that of a typical mRNA); this increases the gain so it now roughly equals the cost (Fig. 2, rows 6 and 8), and adjacent polymerases are likely to be together much of the time. (Treating ribosomes as soft spheres and including cooperative effects (below) increases clustering even further.) Unfortunately, we currently lack experimental data to confirm this prediction.

Bacterial replication factories

GFP-tagging shows that active DNA polymerases in living bacteria are concentrated in discrete factories containing at least 25 polymerases often associated with the cell membrane (39,40). We model a cluster of 25 polymerases at a fork as one 37-nm hard sphere. Soon after initiation in a poor medium (when little intervening DNA has been replicated), the gain (2.4 k_BT) is greater than the loss due to looping (not shown), and we would expect the two forks to be together. But as replication generates more DNA between forks, the loss increases to a maximum of 15.5 k_BT (Fig. 2, row 9), when we would expect the two forks to have separated. It has been shown experimentally that the two forks do indeed separate when ∼30% of the genome has been replicated (40), and we calculate that a looping cost of 11 k_BT balances the gain at this stage. This lies between values predicted for hard and soft spheres (i.e., 2.4 and 16.9 k_BT), so the depletion attraction can alone account for the observed dynamics with reasonable accuracy. It can also force spheres to associate with the membrane for some time (Fig. 2, row 10). Therefore, it provides a good explanation of why the two forks separate when they do, and their location. However, we would also expect that later the forks would aggregate again as they converge toward the terminus (when looping costs decrease); this is not observed experimentally (40), presumably because the segregation machinery prevents it.

Human replication factories

Replication begins at origins scattered every 50–100 kbp along a human chromosome, and several pairs of the resulting replication forks are clustered in small replication factories (diameter ∼75 nm); on passage through S phase, these factories grow into enormous structures (diameter ∼1000 nm) containing thousands of forks (14). As in bacteria, the entropic gain is greater than the loss immediately after initiation, when little replicated DNA lies between forks (not shown), so forks will be together (Fig. 2, row 11). Again as before, the loss due to looping increases to a maximum as more DNA is replicated (Fig. 2, row 11); therefore, forks are likely to separate. Even so, the gain is still sufficient to allow dynamic interactions lasting seconds (Methods). Moreover, if the clusters at forks are soft, they should remain together as the gain exceeds the loss (Fig. 2, row 11). The same applies to two origins that have just fired (Fig. 2, row 12), and to two distant factories (Fig. 2, row 13). We conclude that the depletion attraction is sufficient to bring together forks, active origins, and even factories separated by 1 Mbp—as is seen. Moreover, as more origins fire, we would expect them to aggregate with existing clusters—as they do.

Human rDNA genes

Each of the 10 loci encoding rRNA in the diploid human genome contains ∼80 tandem repeats, each with an ∼13-kbp transcription unit and an ∼30-kbp “spacer”; ∼100 RNA polymerase I complexes transcribe each active unit in the array. Active rDNA genes—but not inactive ones—aggregate to form nucleoli (41). As the cluster of active polymerases is so large and the spacer so short, the entropic gain due to the depletion attraction far outweighs the loss due to looping, and adjacent transcription units will inevitably aggregate (Fig. 2, row 14). Once again, the attraction can account for the organization seen.

Human open reading frames

RNA polymerase II transcribes most human genes. In a HeLa cell, the active enzyme is concentrated in nucleoplasmic factories, each containing about eight active enzymes engaged on a different transcription unit (14,15). As RNA processing occurs cotranscriptionally (42), each mRNA-producing complex typically contains a polymerase (diameter ∼15 nm), a nascent transcript (average length of ∼8400 nucleotides (43)) with compacted diameter ∼14 nm plus its bound proteins, and attached capping, splicing (one subcomplex has dimensions of 27 × 22 × 24 nm (44)) and polyadenylation machineries. Modeling such complexes as 25- or 40-nm hard spheres gives a ΔF_gain slightly less than ΔF_loss (Fig. 2, rows 15 and 16), so they will be paired between 1% and 5% of the time (Methods). Modeling the polymerase, transcript, and spliceosome as three hard spheres (a 15-nm polymerase, 20-nm transcript plus bound proteins, and 24-nm spliceosome) ensures that they are paired 12% of the time. Thus, this simple model (in which the size of the polymerizing complex is almost certainly underestimated) also explains why active genes tend to cluster.

Many beads on one string: cooperative effects

We now consider 21 beads (each representing one mRNA-producing complex) threaded every 20 kbp along a 0.4 Mbp of an active region of the human genome. Using Monte Carlo methods (Methods), we model an attraction of 4 k_BT between beads (Fig. 2, row 17); simulations yield two populations with energy minima depending on the approach used. Starting with a linear string, segments diffuse to give structures with ∼30% beads in clusters (Fig. 5 A). If the string is first compacted (a more likely representation of what happens in vivo), ∼80% are in clusters (Fig. 5 B). This compares with the ∼12% found above. We attribute most of the extra clustering to cooperative effects arising from the nonlinear increase in number of overlap volumes as more and more beads join a cluster (Fig. 5 C). Two factors may further increase clustering: the mRNA-producing complex is probably larger than we model, and—once such large structures come together—the high nucleoplasmic viscosity will slow diffusion apart (Methods). These results reinforce the idea that the depletion attraction contributes to the observed clustering and looping; moreover, similar cooperativity should be seen with all other strings discussed.

CONCLUSIONS

We treat active polymerizing complexes as spheres threaded on a DNA/chromatin string, and find that entropic forces drive aggregation of the complexes to loop the intervening DNA. This counterintuitive result is obtained despite the looping costs, which are outweighed by the entropy gained by the many small molecules that are packed into the cell. We suggest that Nature exploits such nonspecific aggregation to organize genomes. We do not wish to suggest such attractive entropic forces are the sole ones driving self-assembly; rather, they will augment other specific interactions (e.g., involving H-bonds, electrostatic interactions) that also position monomers precisely.

Our results help explain several aspects of genome organization. First, we predict that active (but not inactive) genomes will inevitably be looped, and they are (14,15,17). For example, old evidence shows that loops are present in active cells (from bacteria to man) but not in inactive ones (e.g., chicken erythrocytes, human sperm); moreover, loops are lost progressively as active chicken erythroblasts mature into inactive eythrocytes (45). Recent evidence also shows that three mouse genes spaced ∼10 kbp and ∼15 Mbp apart on the genetic map are attached to one factory when transcribed (with consequential looping), but not when inactive (46). Moreover, inhibiting transcription in living pro- and eukaryotes disperses their DNA (47–49), presumably by releasing loops. Second, we can explain why bacterial replication forks initially lie together before separating (40), and why bacterial and eukaryotic replication complexes tend to be found at the cell membrane or in factories (14,39). Third, we can predict the fraction of bacterial rrn operons found together in transcription factories (28) with reasonable accuracy, and why—in eukaryotes—active RNA polymerases I and II cluster in nucleoli and nucleoplasmic factories (Cook, 1999). (It is likely that energy must be spent to prevent polymerase I factories from aggregating with polymerase II factories.) These results are consistent with a model for genome organization in which active RNA polymerases cluster to loop the intervening DNA (15).

Our approach can readily be extended to other aspects of genome and cellular organization. For example, the interactions discussed here occur independently of scale. Then we can model local effects (e.g., the aggregation of hard nucleosomes into a soft cluster to form a chromatin fiber, with the depletion attraction augmenting electrostatic interactions (50)) as well as global ones (e.g., the aggregation of heterochomatic clumps as chromosomes condense during mitosis). Moreover, we deliberately consider only one string here to simplify analysis; nevertheless, it is easy to imagine that the depletion attraction drives the formation of nucleoli and chromocenters (as active rDNA genes or centromeric heterochromatin on different chromosomes aggregate), as well as the pairing of meiotic chromosomes (as homologous transcription complexes aggregate (51)). Finally, the depletion attraction probably contributes to the formation of many other large structures in cells (e.g., inclusion bodies, interchromatin granule clusters), and—where large structures like the cytoskeleton do exist—energy must be spent to counteract the attraction from driving them into one large aggregate.