Low-Temperature Glass Transitions of Quenched and Annealed Bovine Serum Albumin Aqueous Solutions

Abstract

To investigate the glass transition behaviors of a 20% (w/w) aqueous solution of bovine serum albumin, heat capacities and enthalpy relaxation rates were measured by adiabatic calorimetry at temperatures ranging from 80 to 300 K. One series of measurements was carried out after quenching from 300 down to 80 K and another after annealing in 200–240 K. The quenched sample showed a heat capacity jump indicating a glass transition temperature T_g = 170 K, and the annealed sample showed a smaller jump with the T_g shifted toward the higher temperature side. The temperature dependence of the enthalpy relaxation rates for the quenched sample indicated the presence of two enthalpy relaxation effects: one at around 110 K and the other over a wide temperature range (120–190 K). The annealed sample showed three separate relaxation effects giving 1) T_g = 110 K, 2) 135 K, and 3) temperature higher than 180 K, whereas nothing around 170 K. These effects were thought to originate, respectively, from the rearrangement motions of 1) primary hydrate water forming a direct hydrogen bond with the protein, 2) part of the internal water localized in the opening of a protein structure, and 3) the disordered region in the protein.

INTRODUCTION

A fully hydrated protein at room temperature is known to undergo conformational changes over time. These conformational changes are directly related to the biological activity; therefore, understanding the dynamic properties of the hydrated protein is a key area of interest in protein sciences (1–3).

The conformational perturbation is known to weaken upon decreasing the temperature. Further, at ∼160–200 K, the dynamic behavior of the protein suddenly changes from anharmonic (like a liquid) to harmonic motions (like a solid). This phenomenon is understood as the glass transition and/or dynamical transition of the protein molecule. The biological activity of the protein ceases in the glassy state because the conformational perturbation of the protein is frozen. The glass transition of proteins has been demonstrated through a change in the temperature dependence of the mean-square displacement of the atoms using Mössbauer spectroscopy (4), neutron scattering (5–7), and x-ray scattering (3,8). Infrared spectroscopic (9–18), dielectric (19), and calorimetric (9,20–27) approaches have also been applied to examine the glass transition. Based on these experimental observations, the glass transition of a hydrated protein is thought to depend strongly on the dynamic property of the solvent and occurs over a wide temperature range as a result of the wide distribution in the structural relaxation times of molecules. This broad distribution is attributed to the formation of numerous different configurations among the protein and solvent molecules. However, the majority of the research in this area has reported results of multicomponent systems, such as those including buffer reagents. The included extra components potentially affected the original glass transition behavior of the hydrated protein. Thus the glass transition property of a purely hydrated protein, that is, a binary system consisting of a protein and water, has not been investigated enough. Furthermore, the broad and weak glass transition of the hydrated protein has only been determined to take place in rough temperature intervals because of the limits in experimental precision. As a result, little is known about the fundamental nature of the glass transition that occurs over a wide temperature range.

Adiabatic calorimetry works as a kind of low frequency spectrometry operating in a time domain roughly from 10⁶ to 10² s. The low frequency character is important in that the lower the frequency, the more clearly the different molecular rearrangement processes are potentially separated. Considering that all of the configurational degrees of molecular aggregation contribute to thermodynamic quantities, it is worth noticing that any process can be detected as long as the configurational change concerning the process contributes appreciably to heat capacity (C_p) at the glass transition temperature (T_g). In addition, the enthalpy relaxation rates, which are evaluated by measuring a series of C_p values, enable continuous and sensitive detection of the glass transition behavior. The detectable limit of the enthalpy relaxation rates depends on the amount of the sample used in the calorimetric experiment; an enthalpy relaxation rate measurement with a larger amount of sample is more effective for a detailed investigation of a minute glass transition behavior, such as β-relaxation process (28) or rearrangement of water molecules confined within silica gel pores (29). However, few studies have applied this method to a protein aqueous solution.

The purpose of this investigation was therefore to evaluate the glass transition behavior of a protein aqueous solution through precise measurements of enthalpy relaxation rates using adiabatic calorimetry with a large amount of sample and to examine the effect of hydration on the glass transition behavior of the hydrated protein. Thus, a 20% (w/w) aqueous solution of bovine serum albumin (BSA) was used as a typical hydrate protein system. The absolute values of the C_p and the enthalpy relaxation rates of two samples with different degrees of hydration were investigated in 80–300 K; one was quenched and the other annealed in the temperature range at which water tends to crystallize into ice.

MATERIALS AND METHODS

Determination of the presence of a glass transition with enthalpy relaxation rates

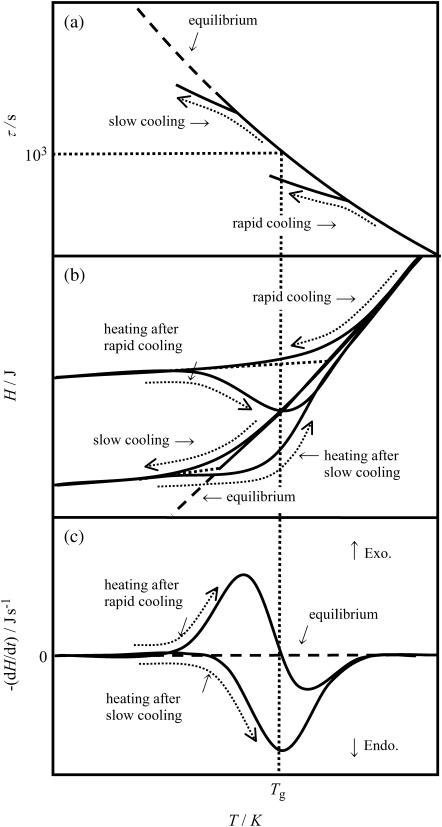
The relaxation accompanying a glass transition is from nonequilibrium to equilibrium states. Therefore, the enthalpy relaxation rate is affected by the thermal history such as the precooling rate. This thermal history depends on how the sample was brought to the nonequilibrium glassy state and how far it is from the equilibrium state. To explain the way of determining the presence of a glass transition based on the systematic temperature dependence of an enthalpy relaxation rate, the general relation among the relaxation time of molecular rearrangement (τ), the enthalpy (H), and the enthalpy relaxation rate (−dH/dt) for the glass transition of a liquid with a single molecular relaxation process is illustrated in Fig. 1. When the liquid vitrifies through rapid cooling, the H becomes much higher than the equilibrium one. With increasing the temperature of the glass, the τ becomes short and gradually approaches a calorimetric timescale between 10⁶ and 10² s. Then, first, an exothermic enthalpy relaxation effect is observed as the H starts to relax toward its equilibrium value; the −dH/dt increases with increasing the temperature. Further increase in the temperature brings the H to cross the equilibrium line at around T_g and to turn to a lower state than the equilibrium one; the −dH/dt exhibits a positive peak and then becomes a negative value. As the temperature increases furthermore, the τ becomes shorter than 10² s and the liquid exhibits no relaxation phenomenon in the calorimetric timescale; the −dH/dt returns to zero while the glass reaches its equilibrium state within the duration of the order of 10² s. On the other hand, when the liquid vitrifies through slow cooling, the H is considerably lower than that of the rapidly cooled liquid. On heating it, an endothermic enthalpy relaxation appears after the H crosses and becomes lower than the equilibrium one with increasing temperature; the −dH/dt exhibits a negative peak giving a top at around the T_g. As the τ becomes shorter with increasing temperature, the H, which has once departed downward from the equilibrium line, approaches gradually and gets on the curve at essentially the same temperature as for the rapidly cooled liquid.

FIGURE 1.

General relation found among the relaxation time (τ) (a), enthalpy (H) (b), and enthalpy relaxation rate (−dH/dt) (c) in the case of a glass transition due to freezing of a single relaxation process.

The height of −dH/dt peaks observed depends not only on the magnitude of C_p jump in the glass transition, but also on the difference between the rates of precooling and heating for measurement. Moreover, the width of the temperature range where the relaxation is observed depends on the distribution of τs. Thus, the enthalpy relaxation measurements enable us to detect an obscure glass transition sensitively and continuously. As has been noted, the observation of a set of exothermic and endothermic −dH/dt for the rapidly and slowly cooled samples indicates the existence of a glass transition. Then, the T_g at which the τ becomes 10³ s has been determined empirically as the temperature at which the endothermic relaxation rate for the slowly cooled sample shows its maximum (28–30).

Preparation of BSA sample

BSA (initial fractionation by heat shock, fraction V, above 98% purity by electrophoresis) was purchased from Sigma-Aldrich (St. Louis, MO). The contents of small particles such as salt ions potentially present were reduced by dialyzing 10% (w/w) aqueous BSA against distilled water for 3 days at 278 K. The BSA aqueous solution thus purified was lyophilized at 10⁻⁴ Pa over 2 days with warming gradually from 233 to 298 K. A 20% (w/w) aqueous solution of BSA (pH = 6.1) was prepared by dissolving a specified quantity of the lyophilized BSA into distilled water.

Heat capacity and enthalpy relaxation measurements with an adiabatic calorimeter

The 20% (w/w) aqueous BSA sample was loaded into a calorimetric cell. The mass of the sample used was weighed to be 10.54 g. The heat capacities were measured using an intermittent heating method with an adiabatic calorimeter (30). The average heating rate for measurements was ∼0.1 Kmin⁻¹. The dH/dt was evaluated based on the following experimental principle. When spontaneous heat evolution or absorption takes place due to glass/phase transitions of a sample, a corresponding spontaneous temperature rise or fall in the calorimetric cell is observed in the thermometry period. The temperature drift rate (dT/dt) can be transformed to the dH/dt per mole of BSA using the following expression.

where n_BSA is the quantity of the BSA used, and a minus sign on the left-hand side indicates the correlation between the spontaneous temperature rise/fall of the cell and the enthalpy decrease/increase in the sample, respectively. A value of 66,267 g mol⁻¹ was used as the average molecular weight of BSA in this work (31).

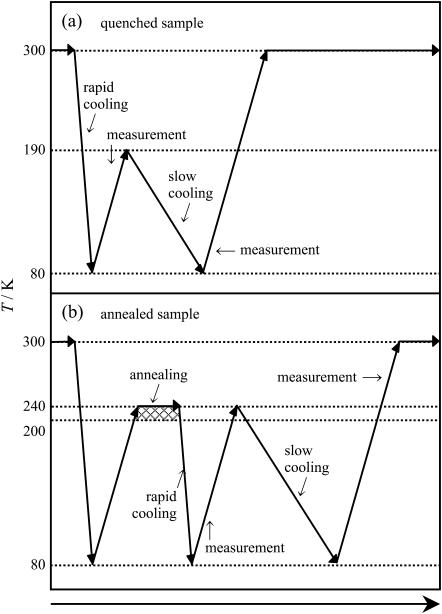
C_p and the −dH/dt were measured for the two kinds of BSA samples; they were quenched and annealed, respectively, in advance resulting in different hydration degrees. The temperature sequence for the quenched BSA sample is shown in Fig. 2 a. The sample was cooled rapidly from 300 K down to 80 K at ∼10 Kmin⁻¹, and the C_p and the −dH/dt measurements were executed up to 190 K, above which water crystallization potentially occurs. The sample was then recooled slowly from 190 K down to 80 K at 20 mKmin⁻¹, and the C_p and the −dH/dt were measured from 80 K up to 300 K. On the other hand, the temperature sequence for the annealed sample is shown in Fig. 2 b. The annealed sample was cooled rapidly from 300 K down to 80 K at ∼10 Kmin⁻¹ and heated up to 200 K. Then, the sample was annealed in 200–240 K to reduce the degree of hydration due to enhancement of the water crystallization. The annealed sample was cooled rapidly down to 80 K at ∼10 Kmin⁻¹, and the C_p and the −dH/dt were then measured up to 240 K, above which ice melting potentially occurs. The sample was recooled slowly from 240 K down to 80 K at 20 mKmin⁻¹, and the C_p and the −dH/dt were measured from 80 K up to 300 K.

FIGURE 2.

Temperature sequence in C_p and −dH/dt measurements for quenched sample (a) and annealed sample (b).

RESULTS

Heat capacities of the quenched and annealed samples

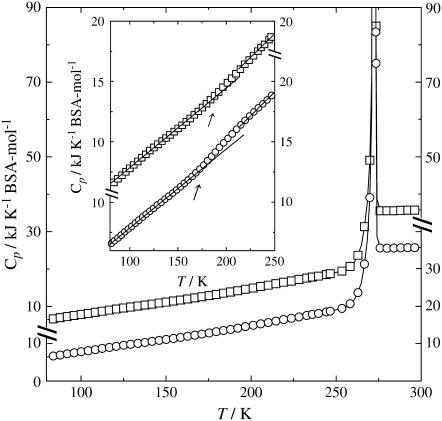
The C_p data of the quenched sample are plotted with open circles in Fig. 3. The effect of the cooling rate below 190 K on the C_p was rather small, and thus only the results of the measurements after the slow cooling are shown there. A gradual jump in the C_p was observed over a range of 170–200 K, as shown in the inset of the figure. This jump was thought to be caused by a glass transition. The transition temperature, evaluated as the point of the onset of the jump, was T_g = 170 K. This result is in good agreement with values previously reported; Inoue and Ishikawa investigated the glass transitions of 40%, 30%, and 20% (w/w) aqueous solutions of BSA using DSC, and the T_g values were estimated to be 172–177 K (26). Similarly, Sartor et al. reported the T_g values of well-hydrated metmyoglobin, methemoglobin, and lysozyme quenched using DSC as 172, 167, and 162 K, respectively (20,25). Further, Green et al. reported those of well-hydrated myoglobin and cytochrome c as 150–170 K (24). Thus, the value of T_g = 170 K for the quenched aqueous solution of BSA obtained in this work was thought to be within a reasonable range.

FIGURE 3.

Heat capacities of the quenched (circle) and annealed (square) samples. The inset shows the heat capacities on an enlarged vertical scale for the region T = 80–250 K. For clarity, the C_p data of the annealed sample have been shifted upward by 10 kJK⁻¹BSA-mol⁻¹ in the main figure and 5 kJK⁻¹BSA-mol⁻¹ in the inset. Arrow indicates the T_g.

The C_p data of the annealed sample are presented with open squares in Fig. 3. For clarity, the data are shifted upward compared with those of the quenched sample by 10 kJK⁻¹BSA-mol⁻¹ in the main figure and by 5 kJK⁻¹BSA-mol⁻¹ in the inset. The C_p data for the annealed sample was rather independent of the cooling rate, and thus the results of the measurements after slow cooling are shown there. Further, the jump in the C_p was significantly smaller than that for the quenched sample. The temperature range of the jump shifted toward the higher temperatures by a few tens of Kelvin. These observations were also consistent with those reported by other researchers (20–22,25,27).

Enthalpy relaxation rates of the quenched and annealed samples

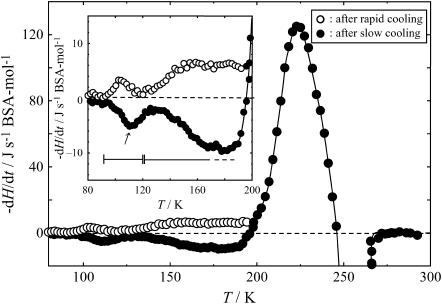
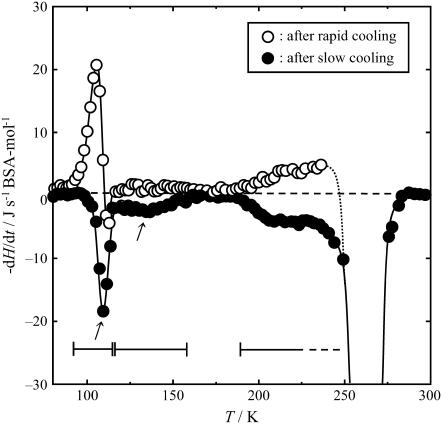
Fig. 4 shows the −dH/dt data for the quenched sample. Open and solid circles represent the results of the measurements after rapid cooling from 300 K to 80 K and after slow cooling from 190 K to 80 K, respectively. The inset shows them on an enlarged scale in 80–200 K. The −dH/dt data of the quenched sample after rapid cooling and after slow cooling showed two sets of peaks below 200 K that were positive and negative, respectively. A large exothermic effect was observed due to the crystallization of freezable water above 200 K. The systematic cooling-rate dependence of the −dH/dts indicated the existence of two glass transitions: the first in the range between 90 and 120 K, and the second over a wide range between 120 and above 190 K. The T_g of the first glass transition was determined to be 110 K, the temperature at which the endothermic effect showed its maximum. It should be noted that, as far as the authors know, this glass transition has not been reported previously. The second glass transition exhibited a wide distribution in relaxation times, namely in the circumstances where rearranging units were located. Moreover, since the endothermic effect due to the glass transition overlapped with the exothermic peak due to the crystallization of freezable water, the T_g could not be determined as a single characteristic temperature. However, judging from the temperature range of the exothermic/endothermic effects observed, the second glass transition was thought to be associated with the C_p jump observed in 170–200 K.

FIGURE 4.

Temperature dependence of −dH/dt for the quenched sample. Horizontal bar and arrow indicate the glass transition region and the T_g, respectively. Inset shows enlargement of T = 80–200 K region.

Fig. 5 shows the −dH/dt data for the annealed sample. Open and solid circles represent the result of the measurements after rapid cooling and after slow cooling, respectively. The large endothermic effect starting at around 250 K upon heating was attributed to the melting of ice. Three glass transitions were observed, as shown in Fig. 5. The enthalpy relaxation behavior of the glass transition occurring at around 110 K was in a similar temperature range as that for the quenched sample but was sharper and clearer in comparison. The subsequent enthalpy relaxation over the wide range above 120 K in the quenched sample almost disappeared and split into two regions. A small enthalpy relaxation effect appeared in one region of 120–160 K, indicating a transition at T_g = 135 K and a broad relaxation effect in the other region starting at 180 K. It was difficult to determine accurately the T_g because the effect of ice melting above 250 K overlapped with the glass transition effect. The second glass transition was related to the small C_p jump observed at around 190 K.

FIGURE 5.

Temperature dependence of −dH/dt for the annealed sample. Horizontal bar and arrow indicate the glass transition region and the T_g, respectively.

DISCUSSION

The observations based on the C_p measurements are in good agreement with those reported for other hydrated proteins (20–22,25,27). Unlike these studies, however, this study obtained the temperature dependence of the enthalpy relaxation effects for samples subjected to different precooling treatments. A glass transition that has not been observed using other techniques was identified at around 110 K, as shown in Figs. 4 and 5. Further, the enthalpy relaxation effect ranging 120–190 K clarified the presence of an extremely broad distribution of relaxation times. This broad distribution reflects the presence of a variety of circumstances of the rearranging molecules. Furthermore, it was disclosed that the annealing induces the broad distribution to partition into two groups; one undergoes a glass transition at 135 K and the other at above 180 K. Discussion of the origins of these glass transitions follows.

The BSA aqueous solution used in this study was dialyzed extensively in the sample preparation. Nevertheless some kinds of ions would remain essentially in the system. The amount of residual ions was estimated roughly from the relationship between the pH of the dialyzed solution and the concentrations and dissociation constants of the and COO⁻ groups in BSA molecules to be only one ion per hundreds of water molecules. Since the enthalpy relaxation signals were found clearly in the present measurements with a large amount of sample, it is thought that the existence of the residual ions little affects the results and the enthalpy relaxation effects are attributable to the spectrum of relaxation times of the rearrangement motions of water and protein molecules.

The enthalpy relaxation observed above 180 K for the annealed sample is attributed, based on the observed temperature, to the glass transition of an amorphous peptide chain within the BSA molecule that is plasticized by water. Globular proteins including BSA are primarily composed of two different polypeptide regions: an ordered region (e.g., α-helix) and an amorphous region (i.e., random coil). The amorphous polypeptide within a globular protein molecule is expected to show the glass transition above the temperature at which the surrounding water molecules start to rearrange. However, the T_g depends on the water content, similarly to the dependence observed in water-soluble amorphous polymers. The presence of such glass transitions has been confirmed in globular proteins at moisture levels below 45% (w/w) (32–35). The heat capacity jump associated with the glass transition has been demonstrated to increase with decrease in the folding region of the protein, which corresponds to increase in the amorphous polypeptide regions within the protein molecule (32,33,35). In an aqueous solution of the protein, the amorphous polypeptide region is in a more fluid state, giving rise to a glass transition at lower temperatures. However, the crystallization of water during cooling and further annealing of the solution induces a freeze concentration of hydrated protein including the amorphous region. Consequently, the T_g of the amorphous region of the hydrated protein would increase up to above 180 K upon reduction in the degree of hydration. The change in glass transition temperature that proceeds with freeze concentration is well known as a common feature of aqueous solutions of glass-forming solutes; the T_g is commonly marked as T_g′ (36,37). Therefore, the glass transition observed for the annealed sample beginning at 180 K corresponds to the T_g′ of aqueous BSA.

The origins of the enthalpy relaxation effects observed in 90–120 K for both the quenched and annealed samples, in 120–190 K for the quenched sample, and in 120–160 K for the annealed sample are discussed in the following. Considering that the amorphous polypeptide regions within the protein molecule are immobile at such low temperatures, these glass transitions are thought to originate from freezing of the motion of water molecules. In reality, similar low-T_g glass transitions for water confined within silica gel pores have been reported. Maruyama et al. investigated the glass transition behavior of water confined within silica gel pores (sizes 3–50 nm) by monitoring the enthalpy relaxation rates using an adiabatic calorimeter (29). Two glass transitions were observed in their work at 132–115 K and 160 K. The former transition was interpreted to originate from freezing of the motion of the interfacial water molecules interacting with silanol groups, and the latter from freezing of the motion of the internal water interacting only with other water molecules. They suggested that interfacial water always exists irrelevantly to the treatments of quenching or annealing of the sample and turns into a glassy state at low temperatures. On the other hand, internal water generally crystallizes, whereas some internal water that exists within a narrow pore remains vitreous, exhibiting a glass transition. Although the water in hydrated proteins does not behave in completely the same manner as the water confined within silica gel pores, similar behaviors are expected.

As well known, water molecules around a protein molecule exist as a shell, namely, a “hydration shell” (38–42). A water molecule in the primary hydration shell, which is denoted as primary hydrate water here, is strongly fixed by a direct hydrogen bond with hydrophilic groups on the protein molecule and never crystallizes, even if kept for a long period at subzero temperatures. Only the primary hydrate water is formed in the hydration range up to 0.3–0.4 g per gram of protein (20,23,25,43). Meanwhile, the secondary hydration shell indicates the water molecules of some layers around primary hydration shell. The molecules are locked by the hydrogen bonds with those in the primary hydration shell but are able to diffuse over a long period of time. Although they fall completely into a glassy state upon quenching, they are ordinarily drawn out of the narrow region to form a larger aggregate of water molecules and then crystallize over the course of warming up to 200 K or during annealing above this temperature. The secondary hydration shell is constituted in the hydration range between 0.4–0.7 g per gram of protein (20,23,25,43). Bulk water appears above this hydration range, and abrupt increase in the diffusion rate in the system and in the critical cooling rate necessary for vitrification is observed. Consequently, in such protein aqueous solutions when cooled down to subzero temperature, almost all the water molecules in the secondary shell crystallize together with bulk water. However, the primary hydrate water and the “vitreous, but freezable water” left within small pore regions remain as unfrozen water. The vitreous, but freezable water indicates unfrozen water except the primary hydrate water and corresponds with the nearest neighbors to the primary hydration shell and the water confined within a small opening of protein structures (20,25,43). The existence of such water molecules or water clusters was pointed out by Saenger; he described the characteristic water molecules as “internal water” and suggested that the internal water is an integral part of a protein structure (44). It is expected that most of the internal water is crystallized by the annealing treatment but that part of the internal water remains within the small pores depending on the location of rugged protein structure.

From the above viewpoint, it should be noted that the primary hydrate water and internal water localized in the opening of a protein structure are intimately connected with the interfacial and internal water molecules confined within silica gel pores, respectively. Then, the enthalpy relaxation effects in 90–120 K for both the samples and in 120–190 K for the quenched sample and/or in 120–160 K for the annealed sample are interpreted reasonably as originating from the glass transitions of the primary hydrate water and the internal water, respectively. This interpretation is reasonable based on two considerations. The first consideration is based on consistency with the experimental results. Quenching brings numerous internal water molecules into the vitreous state, and these water molecules show glass transitions. Thus, it is thought that the relaxation effects at 90–120 K and 120–190 K for the quenched sample are connected with the motions of the primary hydrate water and the internal water, respectively. On the other hand, annealing treatment crystallizes the numerous internal water molecules and decreases the distribution of molecular relaxation times. Hence, the annealed sample was thought to exhibit a drastic decrease in the enthalpy relaxation effect in 160–180 K and a sharpening of the effect around 110 K, as compared with those in the quenched sample. And also, the small enthalpy relaxation effects in 120–160 K would be due to the glass transition of the internal water that has been kept from the crystallization, for example, the internal water confined within the small pores depending on the location of rugged protein structure. The other consideration is based on differences in development of the hydrogen-bond network of water molecules. The relaxation time for the rearrangement of water molecules at some temperature is determined by the activation energy and largely by the energy of breaking the hydrogen bonds in the rearranging process. The number and strength of the bonds to be broken depend on the development of the network: The more developed the network, the larger the activation energy and the higher the glass transition temperature. In the aqueous solution at room temperature, the water in a primary hydration shell is thought to form hydrogen bonds with fixed hydrophilic groups on the protein molecule, whereas the water in a secondary hydration shell and analogously bulk water are thought to be mobile. However, this trend is expected to change at low temperatures: The hydrogen-bond network of the water molecules in a primary hydration shell does not change significantly and remains incomplete even at low temperatures. This is thought to arise because the arrangement of the hydrophilic groups of the protein is fixed independently of the temperature, indicating rather temperature-independent activation energy. On the other hand, water molecules that are surrounded by other water molecules tend to form four tetrahedral hydrogen bonds and thus an extended hydrogen-bond network. This network is observed even in the liquid state, in which the water molecules change their positions to develop a more tightly bound network of hydrogen bonds. This indicates a remarkable increase in the activation energy with decreasing temperature. Therefore, at low temperatures, the internal water is expected to be more immobile than the hydrate water. Thus, the primary hydrate water shows its glass transition at comparatively lower temperatures.

The so-called solvent-slaved glass transition has been mentioned in relation to the glass transition of atoms in a protein molecule; the word “slaved” indicates that the motion and thus freezing depend strongly on the solvent (14,15,45). Such motions are thought to be active above the glass transition temperatures of the molecular rearrangements of both the primary hydrate water and internal water. The rearrangement dynamics of hydrated proteins and water is frozen below the temperature of the glass transition (110 K) due to the primary hydrate water.

CONCLUSIONS

The dissolution of proteins into a large amount of water enables the formation of numerous different protein-water configurations. Further, this dissolution enables the protein molecule to be mobile at room temperature. These properties give rise to a wide distribution in the relaxation times for the conformational changes. The present investigation on the enthalpy relaxation in a 20% (w/w) aqueous solution of BSA revealed that three distinguishable glass transitions exist in the subzero temperature range and that the primary hydrate water becomes perfectly immobile below 110 K. These findings will help in further understanding protein dynamics and will provide important insights into the low-temperature molecular dynamics of other biological systems.