Scaling Behavior in Mitochondrial Redox Fluctuations

Abstract

Scale-invariant long-range correlations have been reported in fluctuations of time-series signals originating from diverse processes such as heart beat dynamics, earthquakes, and stock market data. The common denominator of these apparently different processes is a highly nonlinear dynamics with competing forces and distinct feedback species. We report for the first time an experimental evidence for scaling behavior in NAD(P)H signal fluctuations in isolated mitochondria and intact cells isolated from the liver of a young (5-month-old) mouse. Time-series data were collected by two-photon imaging of mitochondrial NAD(P)H fluorescence and signal fluctuations were quantitatively analyzed for statistical correlations by detrended fluctuation analysis and spectral power analysis. Redox [NAD(P)H / NAD(P)⁺] fluctuations in isolated mitochondria and intact liver cells were found to display nonrandom, long-range correlations. These correlations are interpreted as arising due to the regulatory dynamics operative in Krebs' cycle enzyme network and electron transport chain in the mitochondria. This finding may provide a novel basis for understanding similar regulatory networks that govern the nonequilibrium properties of living cells.

Living cells are open systems that operate far from equilibrium (1–5). Experimental studies reporting various manifestations of nonlinear dynamics in clinical pathology have revolutionized our perspectives on health and disease (6,7). Despite this realization, a fundamental understanding of these nonequilibrium processes at the level of a single cell is still lacking. Demands of cellular homeostasis under such nonequilibrium conditions require coordinated response of many regulatory networks so as to maintain constant levels of metabolites and cofactors. These regulatory networks comprise transcription factors and regulatory proteins, and form the hub of the cellular decision-making process—under normal and stressed conditions. To understand the synergetic roles of mechanisms that govern regulatory networks at the single cell level, it is important to develop innovative strategies for monitoring specific in vivo responses in real time.

To this end, we present a novel application of a statistical correlation analysis tool to gain insight into the enzyme kinetics of a classical mitochondrial enzyme network, the Krebs' cycle. The rationale for the choice of this system is based on two observations: i), generation of ATP by mitochondria occurs in a highly controlled manner (supply-on-demand) determined by the cytosolic ADP levels and mitochondrial substrate availability and ii), regulation of key enzymes in the Krebs' cycle is governed by substrate availability and product inhibition. The mitochondrial electron transport chain couples these two processes at the biochemical level by feeding the output of the Krebs' cycle (NADH and FADH₂) to generate ATP and by utilizing the ATP levels to activate/inhibit the Krebs' cycle. As can be seen, this is a classical situation of nonlinear feedback regulation where the output information (in this case, ADP/ATP ratio) is fed as the input to regulate the main process of electron transport mediated by the Krebs' cycle enzymes.

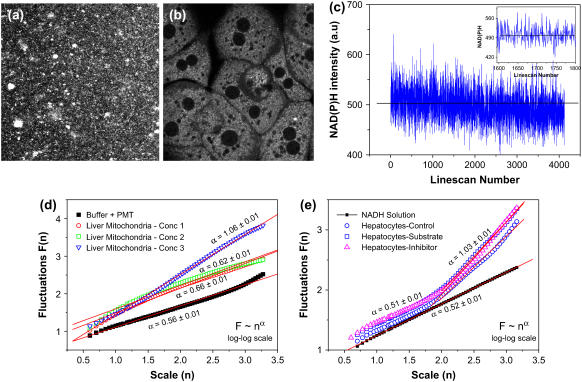
Having recognized the existence of a nonlinear feedback regulation mechanism operative in mitochondrial Krebs' cycle, we then asked a simple question: what is the experimental manifestation of such a regulatory network ? It is known that complex I of the electron transport chain oxidizes NADH generated by the Krebs' cycle thereby initiating the electron flow. Under normal circumstances, NADH level determines both (ADP/ATP) ratio as well as the activity of the Krebs' cycle enzymes (product inhibition). We therefore reasoned that monitoring statistical correlations in redox (NADH/NAD⁺) fluctuations will be a promising experimental approach for understanding the regulatory dynamics of the Krebs' cycle enzymes. We measured NAD(P)H fluorescence in living primary hepatocytes (liver cells) isolated from young (5-month-old) mouse as well as in intact mitochondria isolated from these hepatocytes (8,9). The latter allowed us to investigate the effects of eliminating nonmitochondrial NAD(P)H contributions in the observed signal fluctuations. Spatially resolved fluorescence images were collected by a homebuilt two-photon imaging microscope (see Supplementary Material). Steady-state NAD(P)H fluorescence was collected in XY surface scan mode (512 × 512 pixels; ∼5 s/scan; 730 nm excitation; 440/90 emission) and NAD(P)H fluctuations were measured in XT line scan mode (time-series data; 512 × T; ∼30 ms/scan). Fig. 1, a and b, show representative steady-state fluorescence images of individual mitochondria and intact liver cells. In both the cases, NAD(P)H signals were significantly above the instrument background. The representative time-series data (c) show that the NADH signal fluctuate around the mean value. The inset shows the enlarged view of the fluctuations in a shorter time range. We sought to look for underlying correlations in these fluorescence fluctuations, by a novel application of detrended fluctuation analysis (DFA), originally developed by Peng et al. (10). This algorithm calculates root mean square fluctuations F(n) as a function of scale (window) sizes (n) from the original time series to yield a scaling function F(n) = n^α (Supplementary Material). The scaling exponent α characterizes nonrandom correlations (α < 0.5 for anticorrelations and 0.5 < α < 1.5 for positive correlations) or uncorrelated randomness (white noise limit α = 0.5 or brown noise limit α = 1.5) in the signal. A special case is when α = 1, which corresponds to scale-free power-law correlations. Fig. 1 d shows representative DFA plots (log-log scale, F vs. n) obtained after analysis of the original time-series NAD(P)H data from isolated mitochondria. As can be seen, there is a concentration-dependent increase in positive correlations (α ∼ 0.62, 0.66, and 1.09 corresponding to different mitochondrial concentrations, expressed in terms of protein concentrations 1.86, 3.72, and 37.2 mg/ml) suggesting that viable mitochondria display nonrandom, non-Gaussian correlations. Also shown for comparison is the DFA plot calculated for the buffer medium (no mitochondria). As expected, we obtained white noise value of α ∼ 0.56. This further confirms that the scaling exponents obtained for isolated mitochondria indeed correspond to the underlying correlations and are not affected by instrumental or other artifacts. Fig. 1 e shows DFA plots obtained in intact hepatocytes. For shorter scale sizes (0.75 < log n < 1.75) the scaling exponent α ∼ 0.5 resembling white noise also is evident in 100 μM NADH solution. However, for larger scales (1.75 < log n <3.25), there is a significant deviation of α, which assumes a value α ∼ 1 (power law correlations). Conventional fast Fourier transform methods showed similar positive correlations (Supplementary Material). Also plotted in Fig. 1 e are the scaling functions obtained from time-series data in hepatocytes while they are metabolizing the mitochondrial substrate (5 mM pyruvate/glutamate) or when electron transport chain complex I activity is inhibited by 10 μM rotenone. The fact that the scaling exponents in these two cases are similar to the one observed in control cells confirms that there is a tight regulation in mitochondrial metabolism even during acute metabolic perturbations. Digman et al. recently analyzed images obtained in scanning fluorescence correlation spectroscopy experiments and interpreted the observed spatial correlations in terms of molecular diffusion processes in various timescales (11). Our results are consistent with similar diffusion mechanisms in isolated mitochondria suspended in buffer medium and the dependence of scaling exponent on mitochondrial density (protein concentration) may be reasoned as due to diffusion-limited mitochondrial aggregations. However, we also observed in the case of intact hepatocytes that there is a crossover in scaling exponent from “uncorrelated” randomness (α ∼ 0.5) to persistent positive correlations (α ∼ 1.0) whereas there is no such crossover observed in the case of isolated mitochondria. Although this observation needs more detailed analysis, we speculate that this difference may arise from additional sources of time correlations stemming from regulatory dynamics of enzyme network in intact cells. Because the cellular redox poise has both mitochondrial and nonmitochondrial influences, intact cells are anticipated to display more complex dynamics than isolated mitochondria. It is possible that in intact cells, there exists a hierarchial organization of redox regulation that may modulate mitochondrial redox status in an interdependent manner. Such a scheme might be abolished or reduced when mitochondria are isolated from the cells. Considering the fact that the equilibrium constants of NAD⁺-linked dehydrogenases in liver tissues are ∼8 × 10⁻² mM (12), it is conceivable that intact cells possess more coupled activity of these dehydrogenases than isolated mitochondria. Similar crossover in scaling exponent α has earlier been reported in heart beat dynamics where it was attributed to multiscale fractality (1,13). Regardless, the scaling behavior observed in mitochondrial redox fluctuations provide a quantitative basis for understanding metabolic networks in living cells.

FIGURE 1 .

(a–b) Steady-state multiphoton NAD(P)H images of isolated mitochondria and living hepatocytes; (c) representative NAD(P)H intensity fluctuations plotted from the time-series data; (d) log-log plot of fluctuations (F) and scale size (n) obtained after detrended fluctuations analysis of time-series data in isolated mitochondria for different protein concentrations as described in the text; (e) scaling functions for hepatocytes NAD(P)H time series; see text for details.

Recent studies indicate the critical roles that mitochondria play in a variety of metabolic syndromes including cancer and in aging process (14). It will be intriguing to see how our scaling analysis approach can be exploited to offer insights into the modifications of regulatory dynamics during aging and other disease processes. A logical next step will be to explore the modifications of scaling behavior by selectively knocking out the genes of regulatory enzymes (for example, by siRNA interference) to determine the specific role every member plays in the overall adaptive performance of the regulatory network.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.