Wavelength Dependent Cis-Trans Isomerization in Vision

Abstract

The primary event in vision is the light-driven cis-trans isomerization of the 11-cis-retinal chromophore in the G-protein coupled receptor rhodopsin. Early measurements showed that this photoisomerization has a reaction quantum yield Φ of ∼0.67 [Dartnall (1936) Proc. R. Soc. A 156, 158-170; Dartnall (1968) Vision Res. 8, 339-358] and suggested that the quantum yield was wavelength independent [Schneider (1939) Proc. Natl. Acad. Sci. U.S.A. 170, 102-112]. Here we more accurately determine Φ ₅₀₀) = 0.65 ± 0.01 and reveal that Φ surprisingly depends on the wavelength of the incident light. Although there is no difference in the quantum yield between 450 and 480 nm, the quantum yield falls significantly as the photon energy is reduced below 20 000 cm^-1 (500 nm). At the reddest wavelength measured (570 nm), the quantum yield is reduced by 5 ± 1% relative to the 500 nm value. These experiments correct the long-held presumption that the quantum yield in vision is wavelength independent, and support the hypothesis that the 200 fs photoisomerization reaction that initiates vision is dictated by nonstationary excited-state vibrational wave packet dynamics.

Schroödinger first proposed in “What is Life?” (1) that a true appreciation of biology requires understanding the quantum mechanics associated with biomolecular function. This early insight is well illustrated in the molecular response of the visual pigment rhodopsin to photon absorption. The extraordinarily high sensitivity of the visual process [allowing even single photon detection (2)] relies fundamentally on both static and dynamic quantum mechanical phenomena. Wald (3) was the first to show that the molecular basis of the primary photoevent was an 11-cis → all-trans isomerization. Later studies determined that the photoisomerization is complete in only 200 fs (4) and results in the storage of 35 kcal/mol (5) or 60% of the incident 500 nm photon energy. The high reaction quantum yield of ∼0.67 (6) has long been thought to be wavelength independent (7) and our understanding of the primary event in vision has historically incorporated this belief. Here we present results showing that this ∼60 year old belief is incorrect and that the reaction quantum yield in vision is wavelength dependent as predicted by the nonstationary isomerization model we introduced in 1994 (8).

The idea that the photophysical properties of rhodopsin might diverge from the traditional condensed phase picture of vibrational relaxation in the excited state prior to product formation appeared as early as 1979 (9). The observation of vibrational coherence in the photoproduct of rhodopsin following femtosecond excitation (8), the dependence of fluorescence upon excitation wavelength (10 ), and the correlation between reaction speed and quantum yield (11) convincingly demonstrate that the excited-state reactive motion exceeds the rate of vibrational dephasing and relaxation. In rhodopsin, the chromophore excited-state lifetime is so short (τ₁ ≈ 50 fs) (10) that internal conversion must proceed via nonstationary vibrational states instead of fully thermalized ones. Intuitive understanding in a simplified one-dimensional projection is provided by the classical Landau-Zener model (12,13) that expresses the reaction quantum yield Φ (probability of crossing adiabatic surfaces) as a function of wave packet velocity ν along the reaction coordinate, Φ exp(—k/ν), where k depends on the energy difference and slopes of the ground and excited state potential energy surfaces. In this description, the reaction efficiency depends intimately upon the nuclear motion of the excited chromophore. Recent it calculations exploring the multidimensional nature of the reaction coordinate provide a more sophisticated quantum mechanical picture of the photoreaction. These calculations suggest the presence of a conical intersection which similarly predicts a highly efficient S₁ to S₀ decay channel (14,15). The dynamic internal conversion model and the supporting calculations predict that a change in the excess energy of the wave packet should alter its torsional velocity and hence the quantum yield (16). We were thus encouraged to make more careful measurements of Φ as a function of incident wavelength to test this prediction.

MATERIALS AND METHODS

Rhodopsin Preparation. Rod outer segments (ROS) were isolated from bovine retinae and purified by sucrose flotation followed by sucrose density gradient centrifugation (17). The isolated ROS were lysed in water, solubilized in 5% Ammonyx-LO (Exciton, Inc.), and purified by hydroxyapatite chromatography (18). The protein was eluted with a phosphate step gradient (30-150 mM PO ₄^3-, pH 7), yielding ∼12 nmol of rhodopsin/retina. All samples used in the experiment had an OD ₅₀₀/cm of <0.7, corresponding to the region in which Beer's law is valid (data not shown), and an OD ₂₈₀/ OD ₅₀₀ absorbance ratio of < 1.8. The samples were filtered twice to remove particles greater than 0.22 μm in diameter and fresh NH ₂OH was added to a final concentration of 2 mM.

Data Acquisition. A dual-beam SLM-Aminco DW2 UV—Vis absorption spectrophotometer was used to measure kinetic bleaching curves of rhodopsin as a function of incident wavelength. A 420 nm long pass filter and a 44mm focal length cylindrical lens were placed in the sample and reference beam paths to eliminate second-order light and to focus the beams onto the sample and reference cuvettes. In addition, a calibrated ∼30% broadband beam splitter (Melles Griot, model 03BTF001) was used to pick off a fraction of the sample beam and send it to a NIST-calibrated silicon photodiode (Hamamatsu S2281) in order to determine the incident irradiance on the sample. The current from the photodiode was measured with a lock-in amplifier (Stanford Research Systems SR830) using the chopper signal of ∼274 Hz from the spectrophotometer as a reference. In each experiment, 1.305 mL of rhodopsin solution was placed in the sample cuvette and stirred by a magnetic bar. Teflon covers were placed over the cuvettes and the temperature of the solutions was held constant at 10 ± 1 °C by placing the cuvettes on a copper block cooled by a circulating bath. Dry nitrogen was blown onto the front and back faces of the cuvettes to prevent condensation. The rhodopsin solution was bleached under constant irradiation at a given wavelength with 10 nm bandwidth light emerging from the spectrophotometer. To verify that all observed changes in rhodopsin concentration were due to photobleaching, the baseline reproducibility of the spectrophotometer was checked after each experiment and thermal bleaching of the sample was measured usinga1nm band-pass from the spectrophotometer and found to be negligible.

Each experiment consisted of measuring kinetic decays with a set of three incident wavelengths λ = 500 nm (green), λ < 500 nm (blue), and λ > 500 nm (red). This allowed for the measurement of quantum yields relative to that measured at 500 nm. The total range of incident wavelengths was 450-570 nm. For each set of incident wavelengths, the experiment was performed by recording the bleaching kinetics of a single 1.305 mL sample of rhodopsin under constant illumination. Kinetic decays with λ) 500 nm were measured at the beginning and end of each experiment to monitor for systematic drift. The change in optical density was ∼6% over the bleaching time of 10-50 min/wavelength and the bulk bleach at the end of the experiment was ∼24%. To verify that the difference in optical density at each wavelength did not affect the results, a second set of experiments was performed in which three separate samples of equal OD were used. In these experiments, a single sample was bleached three times (∼8% each time) by one of green, blue, or red wavelengths until ∼24% of the total sample was photolyzed. Afterward a new sample was placed in the cuvette and the same bleaching sequence was followed at a new wavelength. These equal OD experiments had larger error relative to the single sample experiments due to the movement of cuvettes and volumetric errors; however, the results were identical within the error for the two different procedures.

Quantum Yield Determination. Dartnall's method of photometric curves (19) was used to determine the absolute value of Φ₅₀₀ as well as the relative ratios of quantum yields Φ_λΦ₅₀₀. The photobleaching of sample under constant irradiance was monitored via the sample absorbance and incorporated in Dartnall's function:

$$f\left(\mathrm{OD}\right)=-2.303\left[{\mathrm{OD}}_{\lambda }\right(t)-{\mathrm{OD}}_{\lambda }(\infty \left)\right]-\ln [1-\exp (-2.303\left[{\mathrm{OD}}_{\lambda }\right(t)-{\mathrm{OD}}_{\lambda }(\infty \left)\right]\left)\right]$$

OD_λ(t) is the absorbance obtained from bleaching kinetics and OD_λ(∞) is the absorbance of the completely bleached sample. The time derivative of f(OD) is used to calculate the absolute and relative quantum yields using the equations

$${\Phi }_{\lambda }=\frac{N_{\mathrm{A}}\frac{\partial f}{\partial t}}{I_{\lambda }\cdot 2303{\varepsilon }_{\lambda }{l}_{\lambda }{m}_{\lambda }}{\mid }_{\lambda }$$

$$\frac{{\Phi }_{\lambda }}{{\Phi }_{500}}=\frac{\frac{\partial f}{\partial t}{\mid }_{\lambda }{I}_{500}{\varepsilon }_{500}{m}_{500}}{\frac{\partial f}{\partial t}{\mid }_{500}{I}_{\lambda }{\varepsilon }_{\lambda }{m}_{\lambda }}$$

where I_λ is the incident photon flux per unit sample volume (photons cm^-3 s^-1)(corrected for cuvette backreflection), N_A is Avogadro's number, ɛ _λ is the molar decadic extinction coefficient (M^-1 cm^-1), l _λ is the path length (1 cm for all wavelengths), and m_λ is a correction factor due to other absorbing species. Data obtained in a typical experiment for three different incident wavelengths are presented in Figure 1.

FIGURE 1.

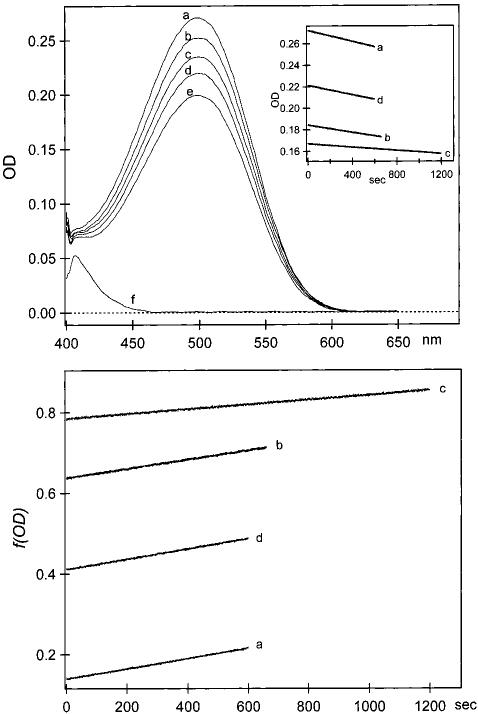
Sequential measurements of rhodopsin bleaching using one sample. Top inset: Kinetic bleaching curves during photolysis with λ) = 500 nm (a), λ = 530 nm (b), λ = 460 nm (c), and λ = 500 nm (d). (Top) Absorption spectrum of rhodopsin before bleaching (a); spectra after bleaching with λ = 500 nm for 10 min(b); λ = 530 nm for 11 min (c); λ = 460 nm for 20 min (d); λ = 500 nm for 10 min (e); and totally bleached sample (f). (Bottom) Plot of f(OD) in eq 1 as a function of time for λ = 500 nm (a); λ = 530 nm (b); λ = 460 nm (c); and λ = 500 nm (d). Linear fits yielded slopes used to calculate absolute and relative ratios of quantum yields in eqs 2 and 3. The slopes for traces a — d were 1.27 χ 10^-4, 1.39 χ 10^-4, 5.77 χ 10^-5, and 1.27 χ 10^-4 S^-1 respectively. The error for each slope was ± <0.2%.

High accuracy and precision were crucial for these measurements of absolute and relative quantum yields. The random error for each Φ_λ result was minimal and arose primarily from uncertainties in relative extinction coefficients (< 0.3%), photon irradiance (< 0.2%), and slopes (< 0.2%). For the absolute quantum yield determination, systematic error (2%) accounted for most of the total uncertainty. At all wavelengths, there was a nearly equal and reproducible linear decrease in ∂f/∂t|_λ as a function of initial concentration. Over half of this systematic error could be attributed to a slight deviation from Beer's law linearity, presumably due to aggregates at higher rhodopsin concentration. Since the systematic error affects all the values of Φ_λ equally, we did not include this error in our reported ratios of Φ_λ/Φ₅₀₀. Error in Φ_λ/Φ ₅₀₀. Error in Φ_λ/Φ ₅₀₀ arose primarily from the change in ∂f/∂t|_λ associated with the decrese in rhodepsin conectration during a single experiment and was ± <0.8% over the relevant concentration range. Each Φ_λ/Φ₅₀₀ was determined a total of 2-7 times, and the corresponding total error was calculated accordingly (20).

RESULTS AND DISCUSSION

We first measured the absolute quantum yield for excitation at 500 nm using eq 2. Typical values of I_λ,∂f/∂t|₅₀₀ and m₅₀₀ are 1.25 χ 10¹² photons cm^-3 S^-1, 1.27 χ 10^-4 S^-1 and 1.00, respectively. The resulting value for Φ₅₀₀ is 0.65 ± 0.01 based on ɛ_λ = 40 600 M^-1 cm^-1. Given the ≤2% absolute error limit of our experiment, this is the most accurate determination of the quantum yield to date. It is reassuring that our result falls well within the larger error limits determined in earlier experiments (6,21).

The wavelength dependence of Φ was determined relative to the 500 nm value (using eq 3) to eliminate the contribution of any systematic error in the absolute quantum yield at 500 nm. A summary of these results along with the absorption spectrum of rhodopsin are presented in Figure 2. The quantum yield is constant within the error limits from 450 to 500 nm; however there is a clear decrease in the reaction quantum yield from 500 to 570 nm. The decrease in excitation energy as the incident wavelength is raised from 500 to 570 nm lowers the excess energy initially deposited in the excited state. This is expected to result in a lower excited-state torsional velocity, and hence the observed decrease in isomerization quantum yield as predicted by the Landau-Zener or similar multidimensional models. When the photon energy is raised above 20 000 cm^-1 (λ < 500 nm) no further increase in quantum yield is observed. There are two possible explanations for this observation. First, a higher lying one-photon forbidden “A-state” [λ_max ∼440 nm (22)] may alter the electronic character of the allowed absorption band and thus affect the observed quantum yield in this region. However, in view of the negligible one-photon cross-section of the “A-state” across the full spectrum, this explanation is unlikely. We propose instead that the wavelength independence of the quantum yield below 500 nm is due to differential partitioning of the excess energy into photochemically active and inactive Franck-Condon modes as the incident wavelength is changed (Figure 3). Similar mode-specific activity on the excited state has already been observed experimentally (23). Multimode calculations of the absorption spectrum of rhodopsin (to be published) based on detailed Franck Condon parameters determined by Raman intensity analysis (24) show that at wavelengths shorter than 500 nm, unreactive high frequency (primarily ethylenic) modes become more significant within the Franck Condon profile whereas at wavelengths longer than 500 nm, the reactive torsional modes are more dominant. Thus, the torsional (reactive) velocity is more strongly dependent upon excess photon energy in the 500-570 nm wavelength region.

FIGURE 2.

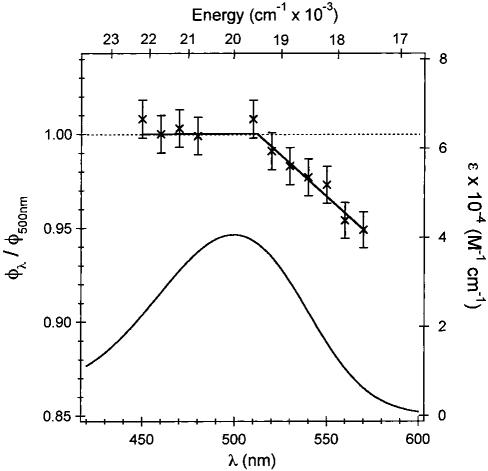
Summary of results for the wavelength dependence of the reaction quantum yield of rhodopsin (Φ_λ) relative to Φ ₅₀₀ along with the rhodopsin absorption spectrum. The linear fit to the Φ_λ/ Φ 500 data points is added as a guide. Errors are reported as ±1σ. The observed wavelength dependence of Φ cannot be explained in terms of an excited-state barrier. The fact that the quantum yield is temperature independent (21,27) from 400 to 590 nm (36) coupled with the extreme rapidity of the reaction (200 fs) and the presence of coherent photoproduct (8) indicate that the isomerization reaction in rhodopsin must occur on a barrierless excited-state surface.

FIGURE 3.

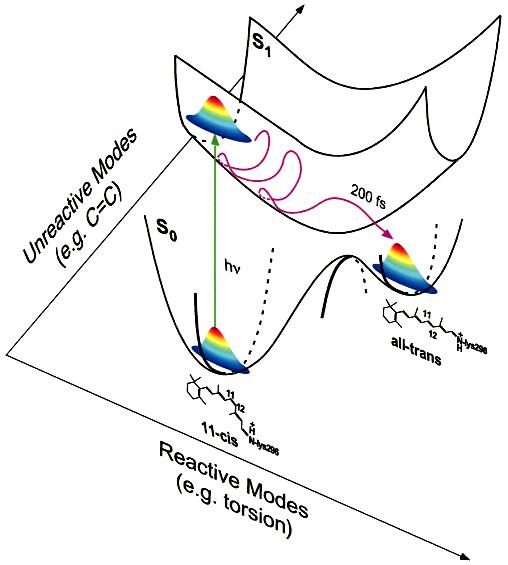
Multidimensional model of the excited state potential energy surface in rhodopsin indicating schematically both the reactive torsional dynamics and one of the many higher frequency unreactive vibrational degrees of freedom. As expected from multidimensional Franck-Condon analysis, the excitation projects onto reactive low-frequency torsional modes as well as high-frequency unreactive modes. Excitation with energy greater than 20 000 cm^-1 (_λ < 500 nm) preferentially increases the projection onto higher frequency unreactive modes. Thus, the wavelength dependence of the quantum yield is best observed with excitation below 20 000 cm^-1 where the low-frequency torsional modes dominate the Franck-Condon envelope.

The high accuracy of our measurement of the wavelength dependent quantum yield for rhodopsin is a significant improvement upon previous experiments. In the earliest seminal work, Lythgoe and co-workers concluded that the photosensitivity (ɛ_λ.Φ_λ) of rhodopsin was wavelength independent to within ∼± 20% in the 440-560 nm range (7). Later it was determined that the quantum yields for isomerization with 500 and 540 nm light at 77 K agreed with one another as well as with Φ₅₀₀ at room temperature within ∼±8% (21). It is apparent that the errors associated with these previous experiments were simply too large to observe the 5% variation in quantum yield measured in our experiment. By necessity, past studies have utilized the wavelength independent value of Φ to obtain results such as the quantum yields associated with the reactions batho →rho and iso ↔ batho (25) and the enthalpy of formation of bathorhodopsin (26). Furthermore, the vast majority of the models for the primary event in vision have been implicitly or explicity based on excited-state equilibration with a wavelength independent quantum yield (21, 27, 28) and therefore did not predict the ultrafast isomerization time. Our result that the quantum yield is wavelength dependent will impact previous models and results and thereby prompt improved understanding of rhodopsin's photochemistry.

The observation of a wavelength-dependent quantum yield supports our nonstationary state dynamic model for the primary event in vision (8) because the photochemical outcome depends on the energetics of the initially prepared excited state. As illustrated in Figure 3, upon photon absorption the ground-state wave packet projects onto Franck-Condon active modes of the chromophore in the excited state and evolves rapidly to produce ground state photoproduct before significant torsional dephasing has occurred. This picture of protein reaction dynamics is unique in many ways. First, there is a breakdown of the BornOppenheimer approximation; the electronic wave function is a rapidly changing function of nuclear geometry in the crossing region and as a result the isomerization proceeds via a nonadiabatic pathway. Second, a Fermi Golden Rule analysis of the internal conversion in rhodopsin is inapplicable because there is insufficient time for excited-state equilibration or relaxation before product formation. Finally, the cistotrans isomerization occurs so rapidly that the equipartition limit is not reached and the excited state vibrational phase space is only partially occupied (29). This results in a dynamic coupling between ground and excited states where the strength of the coupling depends intimately on the kinetic energy of the wave packet along reactive torsional degrees of freedom as it enters the surface crossing region. This description of a coherent nonadiabatic path toward photoproduct is entirely consistent with the presence of a conical intersection between the S₁ and S₀ potential energy surfaces. In the vicinity of such a surface funnel, extremely strong and localized nonadiabatic coupling can result in rapid and efficient internal conversion prior to excited-state equilibration (30). Such an excited-state surface funnel has been reported in it studies of retinal (14, 15). It will be interesting to see if such it calculations can successfully provide a more in-depth description of the unrelaxed and multimodal nature of the photochemical reaction in rhodopsin including the wavelength dependence of the quantum yield uncovered here.

The photochemistry of vision is a unique and remarkable example of the importance of quantum mechanics and femtosecond molecular dynamics in a biological process. The wavelength-dependent quantum yield for the barrierless photoisomerization reaction in vision is a result of the highly specific and unique environment provided by the protein opsin (31). When the 11-cis protonated Schiff base retinal is photoisomerized in a conventional solvent such as methanol, there are striking differences in its chemistry such as a decreased quantum yield (32), a slower reaction rate (33), and contrasting energetics (34). These observations suggest that the well-defined protein-binding pocket plays an important role in directing the dynamics of this photochemical reaction (35). Multidimensional theoretical modeling of these quantum yield results is now needed to gain further insight into the nonstationary vibrational dynamics of the protein-solvated chromophore. It is remarkable that our most important sense and a key biological process depends so intimately on femtosecond excited-state molecular dynamics.