Abstract
Composite interval mapping was used to identify life-span QTL in F2 progeny of three crosses between different pairs of inbred lines. Each inbred line was derived from a different outbred population that had undergone long-term selection for either long or short life span. Microsatellite loci were used as genetic markers, and confidence intervals for QTL location were estimated by bootstrapping. A minimum of 10 QTL were detected, nine of which were located on the two major autosomes. Five QTL were present in at least two crosses and five were present in both sexes. Observation of the same QTL in more than one cross was consistent with the hypothesis that genetic variation for life span is maintained by balancing selection. For all QTL except one, allelic effects were in the direction predicted on the basis of outbred source population. Alleles that conferred longer life were always at least partially dominant.
DROSOPHILA melanogaster has been a model organism for study of the genetics and evolution of life span for over 80 years (Pearl 1922). Its life span shows moderate heritability (e.g., Service 2000), and average life span can be modified quite easily by laboratory selection experiments (Luckinbill et al. 1984; Rose 1984; Partridge and Fowler 1992; Zwaan et al. 1995). In particular, it has been used extensively to address questions about evolutionary genetic mechanisms of senescence, about the physiological correlates of increased life span, and about cellular and biochemical mechanisms of aging (e.g., Service et al. 1985, 1988; Mueller 1987; Graves et al. 1992; Stearns et al. 1993; Chippindale et al. 1994; Hughes and Charlesworth 1994; Leroi et al. 1994; Orr and Sohal 1994; Charlesworth and Hughes 1996; Promislow et al. 1996; Tatar et al. 1996; Deckert-Cruz et al. 1997; Vossbrink 1997; Pletcher et al. 1998; Resler et al. 1998; Harshman et al. 1999; Arking et al. 2000).
Given its extensive use as a model organism for investigation of aging, it is natural that the techniques of quantitative trait locus (QTL) mapping should be applied to the analysis of life span in D. melanogaster (Nuzhdin et al. 1997; Curtsinger et al. 1998; Resler et al. 1998; Leips and Mackay 2000; Pasyukova et al. 2000; Vieira et al. 2000; Curtsinger and Khazaeli 2002; Luckinbill and Golenberg 2002; Reiwitch and Nuzhdin 2002; De Luca et al. 2003). There are several reasons to undertake such studies. Identification of life-span genes will provide an understanding of the biochemical basis of heritable life-span variation and, therefore, test various physiological/biochemical theories of aging (e.g., theories based on oxidative damage; Sohal and Weindruch 1996). We will also gain insight into the mechanisms that help to maintain heritable variation for life span, a significant unsolved problem. For example, we might obtain evidence for or against various forms of balancing selection (overdominance, antagonistic pleiotropy, sexual antagonism, etc.). Finally, we expect that identification of life-span genes can give us evidence regarding evolutionary genetic theories of senescence (antagonistic pleiotropy and mutation accumulation; Rose 1991). Ultimately, answers to these sorts of questions will require that we have the actual genes responsible for life-span variation “in hand.” That is generally not possible with QTL studies based on some variation of interval mapping, a very common design. At best, we hope to identify chromosomal regions that contain loci that influence life span. That information can then provide a basis for more detailed, fine-scale mapping studies, perhaps using other types of experimental designs such as deficiency mapping (Pasyukova et al. 2000; De Luca et al. 2003).
In this article, we report the results of a replicated mapping experiment designed to locate life-span QTL regions in D. melanogaster. We used an experimental design based on analysis of F2 progeny produced by crosses between homozygous (inbred) parental lines that were derived from outbred populations that had been selected to have divergent mean life spans. Three different mapping crosses, each based on a different pair of parental lines, were analyzed. This is the first study to report the results of such multiple crosses. One advantage of replicated mapping crosses is that they may provide some evidence regarding the mechanisms underlying genetic variation. For example, if some form of balancing selection, such as antagonistic pleiotropy, is responsible for much of the natural genetic variance in life span, then we might expect that relatively few loci are involved and that segregating QTL alleles would be at intermediate frequencies in outbred populations. If that is so, then our replicated crosses should identify similar QTL. On the other hand, if much of the natural genetic variance for life span is due to a large number of loci that are segregating for relatively rare deleterious mutations—the mutation accumulation hypothesis (Medawar 1946)—then multiple crosses are likely to reveal different QTL. We identified a minimum of 10 life-span QTL. Three of our QTL regions were common to all three crosses, and two more were shared by two crosses. We also present the first extensive analysis of the dominance relations of alleles at life-span QTL, information that is not available from analysis of recombinant inbred lines (e.g., Nuzhdin et al. 1997; Curtsinger and Khazaeli 2002). Our results also bear on other issues, such as the sex specificity of life-span QTL (Nuzhdin et al. 1997; Leips and Mackay 2000; Vieira et al. 2000; Curtsinger 2002; Mackay 2002; Reiwitch and Nuzhdin 2002).
MATERIALS AND METHODS
Mapping crosses:
The inbred lines used for the mapping crosses were derived from laboratory populations of D. melanogaster that have been under long-term selection in the laboratory for either short or long life span. Five replicate populations with relatively short mean life span are designated B1–B5 and five replicate populations with relatively long life span are designated O1–O5. All 10 populations were derived from a common ancestral population. Details concerning the ancestral population, the selection procedure, and maintenance of the populations can be found elsewhere (Rose 1984; Charlesworth and Charlesworth 1985; Service 1993; Service and Vossbrink 1996). Average adult life spans for the B and O populations are ∼25 and 61 days, respectively (Service et al. 1998). In 1993, 20 inbred lines were started from each of the B and O populations. Inbred lines were propagated by a single mated female in each generation for the first 34 generations, after which lines were maintained by using several males and females as parents for each generation. At the time of the present experiments, the inbred lines had been through >100 generations. Therefore, each line should have been completely homozygous, which was subsequently confirmed by marker genotyping. Life spans of the inbred lines were not assayed because of probable inbreeding depression. Instead, we proceeded on the assumption that each inbred line would probably be fixed for alleles at life-span QTL that were segregating at high frequency in that line's parental (B or O) outbred population. We chose to use inbred lines from three different pairs of B and O outbred populations to encompass as much variation as possible within our experiments. The choice of pairings was based on maximizing genetic distances that were calculated from AFLP polymorphisms (Vossbrink 1997). Although the present experiments used microsatellite markers (see below), we reasoned that maximizing AFLP genetic distance would increase the likelihood of between-line polymorphisms at microsatellite loci. Cross 1 used a B4 and an O5 inbred line, cross 2 used a B2 and an O3 inbred line, and cross 3 used a B5 and an O4 inbred line. The three mapping crosses were done consecutively during an 11-month period.
We used an F2 mapping design. Each mapping experiment was initiated by a reciprocal cross between parental inbred lines. After 2 weeks, the F1 adults from the reciprocal crosses were mixed and distributed to fresh medium in 20 or 30 vials (95 × 25 mm). F2 larval density was not tightly controlled. However, each cross produced ∼1500–2500 F2 adults. For crosses 2 and 3, only a portion of the F2 adults were used for the life-span assay (Table 1). To reduce mortality from overcrowding, we elected to assay fewer adults. In the case of crosses 2 and 3, we established F2 adult densities at ∼200/cage. For each cross, F2 adults were maintained in six mixed-sex cages that were constructed from 1-liter plastic wide-mouth food storage jars following the design of Fukui and Kirscher (1993). Temperature (25°) and food medium were the same as for the B and O source populations and the parental inbred lines. The cages were checked twice a day, roughly every 12 hr, for dead flies. Those flies that had died were collected, sexed, phenotyped (day of death), and stored at −80° for later genotyping. The durations of the cage experiments were 79, 81, and 83 days for crosses 1, 2, and 3, respectively.
TABLE 1.
Sample sizes and likelihood-ratio test thresholds
| Likelihood-ratio test thresholda
|
|||||
|---|---|---|---|---|---|
| Sex | Total no. | Sample size (%) | Overall | Additive | Dominance |
| Cross 1 | |||||
| Female | 1114 | 141 (12.7) | 15.25 | 12.10 | 29.60 |
| Male | 1058 | 138 (13.0) | 15.19 | 13.00 | 35.15 |
| Cross 2 | |||||
| Female | 604 | 149 (24.7) | 15.50 | 12.56 | 35.35 |
| Male | 481 | 133 (27.7) | 15.92 | 13.72 | 40.00 |
| Cross 3 | |||||
| Female | 564 | 142 (25.2) | 14.97 | 12.26 | 137.24 |
| Male | 453 | 140 (30.9) | 14.92 | 12.23 | 30.06 |
See text for an explanation of the overall, additive, and dominance tests and for the method of determining significance thresholds.
Microsatellite markers:
To obtain a set of polymorphic microsatellite markers that spanned the three major D. melanogaster chromosomes, we screened 118 candidate microsatellite loci. Initially, we screened loci listed in two data bases (Schug et al. 1998; Goldstein 2001). Markers for testing were chosen at ∼10-cM intervals along the length of each chromosome. The X chromosome is ∼66 cM while the two major autosomes are each slightly >100 cM. Markers were screened for polymorphisms in the pairs of inbred lines used for our crosses, and those that were polymorphic in at least one pair were retained for QTL mapping. The published microsatellite data bases did not provide enough polymorphic markers for a sufficiently dense marker map. We found additional, “new” microsatellite loci by screening the on-line D. melanogaster genomic sequence (National Center for Biotechnology Information 2000) in regions where there were gaps in our marker maps. Microsatellites were found by analyzing sequences with SSRfinder (Gur-Arie et al. 2000), and primers for the “new” microsatellites were constructed using PrimerSelec v5.0 software (DNASTAR, Madison, WI). To increase our chances of finding scoreable differences among alleles, we focused mainly on tri- and tetra-nucleotide motifs with a minimum of eight repeats. In all, there were 22, 26, and 23 markers for crosses 1, 2, and 3, respectively. (Information about the microsatellite loci is in supplemental Table A at http://www.genetics.org/supplemental). Many individual markers were polymorphic for more than one cross. The average distance between markers was ∼11.4 cM on the standard D. melanogaster genetic map (FlyBase 1999). Marker alleles that were present in the B and O inbred parental lines will be referred to as B alleles and O alleles, respectively.
DNA extraction and visualization of microsatellites:
Individual flies were sexed for a second time before the extraction procedure began to ensure proper identification. Genomic DNA was isolated from individual flies using a Puregene DNA isolation kit (Gentra Systems) and processed using conventional methods. The PCRs were run in 96-well plates with 2 wells reserved for parental controls. The PCR products were separated by electrophoresis in 3% MetaPhor agarose gels (Cambrex). Gels were digitally photographed after separation of PCR products had occurred and were scored on a UV light table to provide further accuracy.
Selective genotyping:
Selective genotyping was used in each of the crosses to reduce the number of individuals that had to be processed. This powerful method requires sampling only the extreme phenotypes that will most likely contain the vast majority of linkage information. Table 1 shows the percentage of each cross that was sampled. Selective genotyping increases the power to detect QTL, but it can also overestimate the QTL effects (Lynch and Walsh 1998). In all three crosses, ∼140 individuals were sampled from each of the two tails of the phenotypic distribution. Many markers contained a small fraction of individual failures and these were simply treated as missing data. The sex ratio of the sampled flies was kept close to 1:1 to assure adequate sample sizes for each sex separately. Inspection of daily mortality indicated a few days that had an unusually high number of deaths at early ages. The large number of deaths was most likely due to environmental causes such as degradation of medium between food changes or fouling of cages between cleanings. Individuals on these anomalous days were not included in the genotyped samples.
Marker linkage maps:
Because previous studies have indicated sex-specific effects of life-span QTL (Nuzhdin et al. 1997; Leips and Mackay 2000; Pasyukova et al. 2000; Vieira et al. 2000), we did separate mapping analyses for each sex as well as each cross (six analyses in all). Mapmaker/Exp 3.0 (Lander et al. 1987; Lincoln et al. 1992, 1993) was used to determine a marker linkage map using the Haldane mapping function. The linkage map generated by Mapmaker was generally shorter (average marker spacing ∼8.2 cM) than the standard map due to lack of recombination in F1 males and to underrepresentation of recombinants in the tails of the F2 phenotypic distributions that were used for mapping. The QTL mapping software used the linkage maps that were produced by Mapmaker and estimated QTL positions were placed on those maps, all six of which were unique. To compare results of different crosses, we present all results with marker and QTL positions converted to the standard D. melanogaster recombination map. The adjustment procedure for QTL locations used a linear function that related the positions for flanking markers that were reported by Mapmaker to their approximate positions on the standard map. For example, suppose the standard map positions of a pair of neighboring markers were 30 and 40, that the positions estimated by Mapmaker were 22 and 28, and that a likelihood peak for QTL location was found at 27 on the Mapmaker map. The estimated position of this QTL on the standard map was then calculated as 38.3 [= 30 + ([(27 − 22)/(28 − 22)] × [40 − 30])].
QTL analyses and hypothesis tests:
QTL mapping analyses were done with QTL Cartographer software (Basten et al. 1994, 2001). We used composite interval mapping (model 6 in the Zmapqtl program module) to control for effects of both linked and unlinked QTL (Zeng 1994). Conditioning markers were chosen by the forward-backward stepwise regression method (SRmapqtl module), with P(Fin) and P(Fout) being adjusted for each analysis so that at least five markers were selected. We restricted the analyses so that only five conditioning markers were used. After some experimentation, we settled on a 5-cM window size for all analyses. Variation in results due to window size has been found in other studies (Nuzhdin et al. 1997; Leips and Mackay 2000; Reiwitch and Nuzhdin 2002). The 5-cM window size was selected because there was little variation between the likelihood peaks that were identified with 5-, 10-, and 15-cM window sizes, and the 5-cM window generally produced the narrowest and most well-defined QTL peaks. The Eqtl program module was used to identify the peaks in the likelihood maps that exceeded the threshold levels for statistical significance (see below). All analyses of the actual data (i.e., excluding permutations and bootstraps) were run on untransformed and log-transformed phenotype data (age of death). Results did not differ substantially, and all results are therefore presented for untransformed data. With an F2 design, it is possible to test for dominance as well as additive effects of alleles. In our analyses the following genotypic values were assigned: BB = 0, BO = a + d, and OO = 2a. At each test position on a chromosome, the null hypothesis is no QTL, for which the likelihood of the data is evaluated with a = 0 and d = 0. Three alternative hypotheses may be tested that correspond to a ≠ 0 and d ≠ 0, a ≠ 0 and d = 0, and a = 0 and d ≠ 0. We analyzed all three tests, which we refer to as the overall, additive, and dominance tests.
Permutation tests and bootstrapping:
Permutation tests (Churchill and Doerge 1994) were run within the QTL Cartographer package to determine significance thresholds for likelihood-ratio test statistics. For each of 1000 permutations in a given data set, the largest experiment-wise test statistic for each of the three hypothesis tests was found. The 95th percentile value of these 1000 largest test statistics was used to set the threshold for a 5% experiment-wise type I error rate for each hypothesis (Table 1). We used bootstrapping to estimate confidence intervals for QTL locations. Each of the six data sets (two sexes from three crosses) was bootstrapped 200 times (Visscher et al. 1996; Bennewitz et al. 2002). Each bootstrap sample was analyzed with the Zmapqtl program module, and the Eqtl module was used to identify likelihood-ratio peaks that exceeded the previously established significance thresholds (Table 1). All three hypotheses were bootstrapped using the same samples. Background markers were the same as those used for the actual data. The bootstrap frequency distributions of the likelihood-ratio maxima were often asymmetrical. We determined noncentral 95% confidence intervals by finding the shortest region that contained the point estimate for QTL location (from the actual experiment) and that also included ∼190 significant likelihood-ratio peaks (190/200 = 0.95). In a few cases, likelihood peaks in the actual data were too poorly supported by bootstrapping to yield useful confidence intervals. That is, it was not possible to specify a reasonable map region around a point estimate that included ∼190 bootstrap maxima. We did not consider those cases any further.
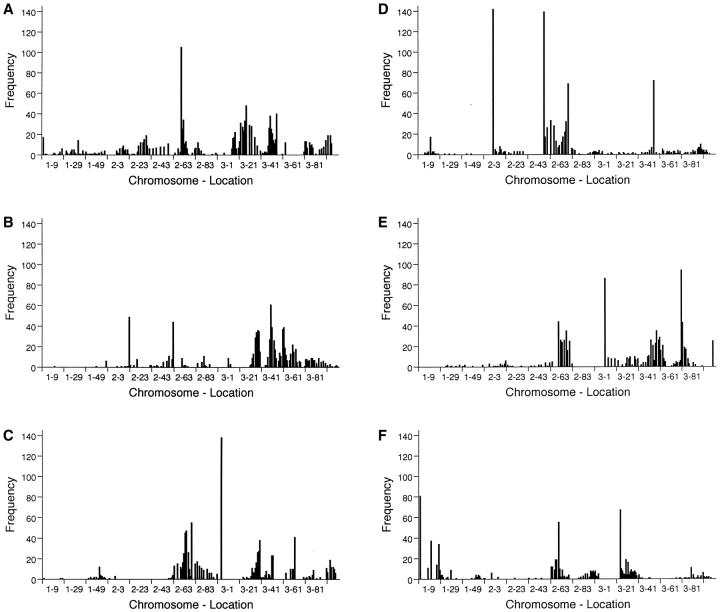
Our procedures included some strategies that appear to improve bootstrap confidence intervals in some circumstances. By retaining only those likelihood-ratio peaks in our bootstrap samples that exceeded significance thresholds, we incorporated one aspect of selective bootstrapping (Lebreton and Visscher 1998). Our method for determining the upper and lower bounds of confidence intervals is similar to the method suggested for noncentral intervals by Bennewitz et al. (2002). We show the complete results of our bootstrap analyses (Figure 1). These empirical posterior bootstrap distributions may provide information about QTL location beyond that given just by the confidence interval (Visscher et al. 1996) and may suggest the presence of QTL that were not detected in the actual data.
Figure 1.—
Posterior bootstrap distributions (N = 200 samples) for the overall hypothesis test. Only those bootstrap maxima that exceeded significance thresholds are shown. (A–C) Females; D–F, males. (A and D) cross 1; (B and E) cross 2; (C and F) cross 3.
RESULTS
Single-marker ANOVA tests:
One-way analysis of variance was used to test for differences in mean life span among the genotypes at each marker locus. These tests must be evaluated cautiously because there are many of them (142) and because of nonindependence of linked markers and probably nonindependence of unlinked markers due to similar phenotypic effects and selective genotyping. Most autosomal marker loci showed highly significant genotypic effects (detailed results are given in supplemental Table B at http://www.genetics.org/supplemental). Genotypic effects for X-linked markers, however, were present only in cross 1 females and cross 3 males. In almost every case in which there was a significant genotypic effect, O homozygotes had a longer life span than B homozygotes. Thus, alleles at segregating QTL in each cross had the effect on life span that would be predicted from their populations of origin. Furthermore, whenever there were significant genotypic effects, there was a pervasive pattern of at least partial dominance of O alleles. There was only slight evidence for overdominance.
QTL mapping:
There were six separate QTL mapping analyses (three crosses by two sexes). Likelihood maps for each of the three major chromosomes are provided in the supplemental material (http://www.genetics.org/supplemental). Likelihood map peaks that exceeded the significance thresholds for the overall, additive, and dominance tests are listed in Table 2, along with confidence intervals for peak locations and estimates of additive and dominance parameters and the proportion of phenotypic variance explained. In a few cases, peaks were too poorly supported by bootstrapping to yield useful confidence intervals. Considering just the overall hypothesis test, there were 26 significant maxima, which were evenly divided among the three crosses and between the two sexes. Only two peaks were on the X chromosome (both in cross 3 males). The additive test yielded 17 significant maxima, and the dominance test 7 maxima. All of the significant dominance test maxima were in cross 1, and 6 of the 7 were observed in females. Three of the additive test peaks (point estimates 3-50.9 in cross 1 females, 3-0.5 in cross 2 males, and 2-59.4 in cross 3 males) and two of the dominance test peaks (point estimates 2-45.1 and 3-73.2 in cross 1 females) either were undetected or did not give useful confidence intervals by the overall hypothesis tests. Four maxima by the overall hypothesis tests did not produce useful confidence intervals. Thus, we have 27 supported likelihood map peaks: 22 by overall hypothesis tests (and possibly by additive and/or dominance tests as well), plus 3 by additive and 2 by dominance tests. We combined these 27 maxima into 10 putative life-span QTL, which were designated qtl1–qtl10 (Table 3). Combining was done when point estimates for QTL location were similar and/or there was substantial overlap of the confidence intervals for location. In some cases, such as for qtl8 and qtl10, point estimates were very close. In other cases, such as for qtl9, there was considerable range in the point estimates. However, for qtl9, confidence intervals for three of the point estimates were completely contained within the confidence interval for the fourth estimate (Table 2). Our procedure was conservative in the sense that it might underestimate the actual number of QTL, and we consider our estimate of 10 life-span QTL to be a minimum.
TABLE 2.
Significant likelihood-ratio test statistic peaks, confidence intervals for peak locations, and estimates of QTL effects
| Cross | Sex | Locationa | Bootstrap peaks in same intervalb |
95% C.I. (N)c | R2d | ae | df |
|---|---|---|---|---|---|---|---|
| A. Overall testg | |||||||
| 1 | F | 2-28.8 | 81 (19) | 0.09 | 8.0 | 14.7 | |
| 1 | F | 2-61.0 | 195 (105) | 58.9–65.6 (191) | 0.21 | 10.9 | 19.3 |
| 1 | F | 3-14.6 | 141 (27) | 11.3–21.9 (204) | 0.14 | 9.4 | 17.5 |
| 1 | F | 3-20.6 | 131 (29) | 15.2–29.7 (187) | 0.13 | 16.2 | 16.8 |
| 1 | F | 3-41.8 | 182 (21) | 37.4–48.5 (199) | 0.24 | 12.8 | 23.3 |
| 1 | M | 2-2.3 | 170 (142) | 2.3–30.2 (188) | 0.07 | 9.6 | 6.9 |
| 1 | M | 2-48.1 | 139 (139) | 47.4–55.2 (215) | 0.10 | 10.3 | 5.5 |
| 1 | M | 2-53.9 | 117 (33) | 47.4–55.2 (215) | 0.10 | 13.5 | 4.7 |
| 1 | M | 2-68.4 | 168 (32) | 55.2–69.1 (209) | 0.09 | 12.4 | 3.1 |
| 2 | F | 3-28.0 | 176 (36) | 20.3–30.7 (176) | 0.36 | 19.5 | 2.2 |
| 2 | F | 3-41.4 | 199 (39) | 36.8–45.9 (189) | 0.46 | 22.1 | 6.9 |
| 2 | F | 3-51.9 | 151 (39) | 43.3–58.8 (191) | 0.12 | 15.7 | 7.2 |
| 2 | M | 2-64.3 | 171 (24) | 60.7–71.9 (196) | 0.21 | 14.2 | 4.3 |
| 2 | M | 3-3.6 | 117 (9) | 0.13 | 12.2 | 2.6 | |
| 2 | M | 3-46.3 | 91 (6) | 0.21 | 15.2 | 4.1 | |
| 2 | M | 3-51.0 | 163 (29) | 42.1–54.4 (203) | 0.23 | 16.1 | 4.7 |
| 2 | M | 3-70.7 | 184 (94) | 68.0–77.4 (191) | 0.25 | 13.5 | 9.5 |
| 3 | F | 2-64.3 | 182 (45) | 58.8–68.2 (191) | 0.14 | 1.5 | 19.5 |
| 3 | F | 2-72.5 | 142 (15) | 64.9–78.1 (186) | 0.10 | 10.7 | 14.2 |
| 3 | F | 2-96.8 | 145 (138) | 78.1–96.8 (187) | 0.09 | 12.8 | 6.3 |
| 3 | F | 3-27.9 | 204 (26) | 25.8–47.7 (193) | 0.20 | 4.2 | 22.7 |
| 3 | F | 3-61.4 | 30 (10) | 29.2–62.7 (190) | 0.06 | 8.3 | 11.5 |
| 3 | M | 1-1.4 | 92 (81) | 1.4–20.8 (190) | 0.08 | −6.7 | |
| 3 | M | 1-11.0 | 51 (37) | 1.4–20.8 (190) | 0.08 | −6.6 | |
| 3 | M | 2-59.4 | 84 (19) | 0.10 | 14.9 | 4.2 | |
| 3 | M | 3-18.6 | 191 (4) | 15.0–35.4 (190) | 0.14 | 11.9 | 6.6 |
| B. Additive testg | |||||||
| 1 | F | 2-48.5 | 140 (74) | 0.16 | 11.8 | 14.9 | |
| 1 | F | 2-61.0 | 189 (85) | 49.7–65.6 (187) | 0.21 | 10.9 | 19.3 |
| 1 | F | 3-50.9 | 84 (61) | 38.3–55.2 (191) | 0.19 | 13.9 | 19.3 |
| 1 | M | 2-48.1 | 131 (131) | 47.4–55.2 (186) | 0.10 | 10.3 | 5.5 |
| 1 | M | 2-56.6 | 119 (36) | 47.4–57.9 (222) | 0.10 | 13.3 | 4.7 |
| 1 | M | 2-69.8 | 167 (76) | 57.9–73.6 (206) | 0.09 | 12.1 | 3.2 |
| 2 | F | 3-28.0 | 173 (33) | 18.0–30.7 (173) | 0.36 | 19.5 | 2.2 |
| 2 | F | 3-40.1 | 199 (57) | 35.5–44.6 (189) | 0.46 | 22.1 | 6.7 |
| 2 | F | 3-50.6 | 128 (41) | 0.12 | 16.2 | 7.1 | |
| 2 | M | 2-66.0 | 171 (29) | 60.7–71.9 (196) | 0.21 | 14.4 | 4.1 |
| 2 | M | 3-0.5 | 145 (95) | 0.5–25.3 (197) | 0.12 | 12.1 | 2.3 |
| 2 | M | 3-48.4 | 164 (35) | 42.1–53.1 (191) | 0.22 | 15.7 | 4.4 |
| 2 | M | 3-73.7 | 188 (36) | 70.2–79.8 (193) | 0.26 | 13.8 | 9.4 |
| 3 | F | 2-96.8 | 138 (125) | 82.6–96.8 (177) | 0.09 | 12.8 | 6.3 |
| 3 | M | 1-1.4 | 87 (67) | 1.4–29.6 (165) | 0.08 | −6.7 | |
| 3 | M | 2-59.4 | 98 (28) | 53.6–67.5 (174) | 0.10 | 14.9 | 4.2 |
| 3 | M | 3-15.0 | 188 (87) | 15.0–49.9 (188) | 0.12 | 11.0 | 6.1 |
| C. Dominance testg | |||||||
| 1 | F | 2-45.1 | 189 (57) | 30.9–48.5 (189) | 0.10 | 12.8 | 15.4 |
| 1 | F | 2-61.0 | 184 (131) | 54.3–66.4 (190) | 0.21 | 10.9 | 19.3 |
| 1 | F | 3-14.6 | 93 (25) | 12.6–21.9 (199) | 0.14 | 9.4 | 17.5 |
| 1 | F | 3-23.2 | 191 (44) | 17.6–31.5 (195) | 0.13 | 15.6 | 17.0 |
| 1 | F | 3-38.8 | 313 (23) | 35.4–42.3 (186) | 0.25 | 12.6 | 23.6 |
| 1 | F | 3-73.2 | 231 (42) | 70.0–76.2 (189) | 0.08 | 3.4 | 14.2 |
| 1 | M | 2-15.7 | 179 (33) | 11.6–30.2 (204) | 0.03 | −4.2 | 6.7 |
Point estimates for the map positions of all likelihood-ratio test maxima that exceeded threshold values for statistical significance (i.e., possible QTL).
The number of statistically significant likelihood-ratio test maxima in 200 bootstrap samples that occurred in the same marker interval as for the actual data. The number in parentheses is the number of bootstrap peaks at exactly the same location as for the actual data.
The approximate 95% confidence interval for QTL location as described in the text. The number in parentheses is the actual number of bootstrap peaks used to form the confidence interval. The number of bootstrap peaks should be 190 for a 95% confidence. A number <190 is used when justified by inspection of the posterior bootstrap peak distributions (Figure 1). A number >190 may occur due to the discontinuous nature of the bootstrap distribution. In a few cases, no confidence interval is given because the location was poorly supported by the bootstrapping and the number of significant bootstrap peaks within a reasonable distance from the point estimate was much <190.
R2 is the proportion of phenotypic variance in life span explained by a QTL at the test position, conditioned on background markers (Basten et al. 2001, p. 56).
The estimated additive effect (days) of a QTL at the test position. Positive values indicate that the O allele (derived from a long-lived population) confers greater longevity. Estimates for X-linked QTL in males are not adjusted for hemizygosity.
The estimated dominance effect (days) associated with a QTL at the test position. Estimates are not shown for X-linked QTL in males. Positive values indicate that the O allele (derived from a long-lived population) is dominant.
See text for an explanation of the overall, additive, and dominance tests.
TABLE 3.
Minimal set of life-span QTL
| 95% C.I.b
|
|||||||
|---|---|---|---|---|---|---|---|
| QTL | Point estimate(s) | Analysesa | Geneticc | Cytogenetic | R2d | ad | dd |
| X chromosome | |||||||
| qtl1 | 1.4, 11.0 | 3M | 1–21 (190) | 3A-7C | 0.08 | −6.6 | — |
| Chromosome 2 | |||||||
| qtl2 | 2.3 | 1M | 2–30 (188) | 21F-28E | 0.07 | 9.6 | 6.9 |
| qtl3 | 45.1e, 48.1, 53.9 | 1F, 1M | 45–59 (381) | 33A-44E | 0.10 | 12.2 | 8.5 |
| qtl4 | 61.0, 68.4, 64.3, 64.3, 72.5, 59.4f | 1F, 1M, 2M, 3F, 3M | 59–73 (976) | 44E-51D | 0.14 | 10.8 | 10.8 |
| qtl5 | 96.8 | 3F | 78–97 (187) | 52E-58A | 0.09 | 12.8 | 6.3 |
| Chromosome 3 | |||||||
| qtl6 | 0.5f | 2M | 0.5–25 (197) | 61D-66D | 0.12 | 12.1 | 2.3 |
| qtl7 | 14.6, 20.6, 28.0, 27.9, 18.6 | 1F, 2F, 3F, 3M | 13–31 (763) | 64C-67C | 0.19 | 12.2 | 13.1 |
| qtl8 | 41.8, 41.4 | 1F, 2F | 38–47 (384) | 68F-77A | 0.35 | 17.5 | 15.1 |
| qtl9 | 50.9f, 51.9, 51.0, 61.4 | 1F, 2F, 2M, 3F | 40–62 (780) | 70A-90E | 0.15 | 13.5 | 10.7 |
| qtl10 | 73.2e, 70.7 | 1F, 2M | 71–78 (389) | 93C-94E | 0.16 | 8.5 | 11.8 |
Except where noted, all point estimates for QTL location are based on likelihood-ratio test maxima using the overall hypothesis test (i.e., the combined test for additive and dominance effects).
The analyses in which a given QTL was detected. 1F refers to cross 1 females, etc.
The approximate 95% bootstrap confidence interval for QTL location. A composite confidence interval is given if a QTL was detected in more than one analysis. For a QTL detected in n analyses, the confidence interval is the shortest region that contains (200 × 0.95)n significant peaks using the n combined bootstrap distributions. For example, qtl8 appears in two analyses and an exact 95% confidence interval would be the region that contains 380 bootstrap maxima. Confidence intervals on the cytogenetic map were estimated by approximating cytogenetic locations to recombination map locations.
The number in parentheses is the number of bootstrap maxima used to construct the confidence interval (see footnote b).
See Table 2 for explanations of R2, a, and d. Where more than one point estimate is given for QTL location, mean values are given for R2, a, and d. No estimate of d is given for qtl1 because that QTL is X linked and was detected in males only. Also, estimates of a for qtl1 are not adjusted for hemizygosity.
A significant likelihood-ratio peak by dominance test.
A significant likelihood-ratio peak by additive test.
QTL effects:
For autosomal QTL, the estimated additive effects (a) ranged from 8.5 to 17.5 days, and dominance effects (d) ranged from 2.3 to 15.1 days (Table 3). Because we used selective genotyping and because effects are likely to be overestimated for those QTL that are actually detected (Beavis 1995), these numbers should not be taken at face value but may be useful for comparison of the relative magnitudes of the effects of the QTL. The average additive effect was 12.1 days, and the average dominance effect was 9.5 days. Qualitatively, these results are consistent with the ANOVA tests: there was a general pattern of support for the idea that alleles that confer longer life are at least partially dominant to those that confer shorter life. For example, 24 of 24 dominance parameter estimates in Table 2A are positive. However, in only a few cases was it possible to reject the null hypothesis of no dominance (d = 0) by likelihood-ratio tests (Table 2C). Evidence for overdominance was very limited. R2 for the 10 QTL ranged from 7 to 35% (Table 3). Again, these numbers are likely to be overestimates (Beavis 1995).
Confidence intervals for QTL location:
Bootstrap distributions of likelihood-ratio test peaks for the overall hypothesis tests are shown in Figure 1, and confidence intervals for peak locations are given in Table 2. If a particular QTL was detected in more than one analysis, then a composite confidence interval was calculated by pooling bootstrap results across analyses (Table 3). Confidence intervals for QTL detected in only one analysis were quite long. On the other hand, the average length of confidence intervals for QTL that were detected in more than one analysis was 14 cM. The shortest confidence intervals (7–9 cM) were for QTL for which there was close agreement among point estimates for location (qtl8 and qtl10).
DISCUSSION
We have identified a minimum of 10 life-span QTL in D. melanogaster from three different pairs of populations. One concern with using inbred lines to study the genetic basis of phenotypes that show inbreeding depression, such as life span, is that the results will not apply to outbred populations. Specifically, the genetic variation revealed in crosses between inbred lines can be the result of mutations that arise during inbreeding or of chance fixation of rare deleterious alleles that were present in the source populations from which the inbred lines were derived. Our results indicate that the use of inbred lines was not problematic. With one exception (qtl1), allelic effects were consistent with expectation based on population of origin. That is, QTL alleles derived from populations with evolutionarily increased life span (O populations) conferred greater longevity than did alleles from populations with shorter life span (B populations). That consistent relationship would not be expected if the life-span QTL that we detected were due to the vagaries of inbreeding. On the other hand, it is exactly the result that would be expected if the inbred lines were fixing genetic variation responsible for life-span variation in outbred populations.
Sex-specific QTL:
Half of the life-span QTL identified in this study were sex limited. Other studies have reported similar sex specificity (e.g., Nuzhdin et al. 1997; Leips and Mackay 2000; Vieira et al. 2000). If many life-span QTL are sex specific, then sexual dimorphism in the molecular and cellular mechanisms of aging is implied—an interesting possibility. However, Curtsinger (2002) has argued that sex specificity of life-span QTL may be a consequence of the relatively low power of most mapping experiments. Most of our sex-specific QTL were detected in only one analysis, and an argument could be made that our sex-limited QTL are the ones that we had lower power to detect. The bootstrap results may be helpful in assessing sex specificity. For example, qtl8 was detected in females of crosses 1 and 2 at about position 3-41. Cross 1 males also show a large spike in the frequency of significant bootstrap maxima at very nearly the same position (Figure 1D). This suggests that qtl8 would not be sex limited in a more powerful study (or that there may be two tightly linked sex-specific QTL). Similar but weaker cases can be made for qtl5 in cross 3 (Figure 1, C and F) and for qtl6 in cross 2 (Figure 1, B and E). Comparisons among studies may also suggest that sex specificity is not strongly supported. For example, our female-specific qtl8 corresponds quite well with a male-specific QTL located by Nuzhdin et al. (1997) at position 3-44. Lastly, the mating status of the flies used for life-span measurements may affect conclusions about the sex specificity of life-span QTL: sex-specific effects may be apparent only when unmated flies are used for life-span assays (Reiwitch and Nuzhdin 2002).
Evolutionary genetic mechanisms for life-span variation—cross-specificity of QTL:
Five of our QTL were detected in two or three crosses (Table 3). The presence of the same QTL in multiple crosses is consistent with the hypothesis that genetic variation for life span is associated with some form of balancing selection, such as antagonistic pleiotropy (Rose 1982). In such cases, we might expect that the same loci would contribute to the evolutionary difference in life span between several pairs of B and O populations and that those loci would be detected in replicated crosses. On the other hand, condensing our results into 10 QTL may have led us incorrectly to identify the same QTL in more than one cross. For the two QTL detected in two crosses (qtl8 and qt10), point estimates of QTL location were in close agreement (Table 3). However, for the three QTL assigned to all three crosses (qtl4, qtl7, and qtl9), there was more spread in the point estimates, and the claim that the same QTL were present in all three crosses may be less well supported. An opposing concern is that we might underestimate the number of crosses in which particular QTL were actually present because of limited power to detect QTL. For example, qtl1 was detected in cross 3 males and was near the left end of the X chromosome (Figure 1F). There was some suggestion of a QTL at a similar location in cross 1 males and females (Figure 1, A and D), but not in cross 2 males or females (Figure 1, B and E). qtl8 was located at approximately position 3-41 in females of crosses 1 and 2. Females of cross 3 showed a clear spike in the bootstrap distribution at the same location (Figure 1, A–C), suggesting that qtl8 might actually have been present in females of all three crosses. However, in general, the bootstrap results tended to reinforce the conclusion that qtl2, qtl3, qtl5, and qtl6 were each limited to a single cross. Finding a QTL in only one cross does not rule out the possibility that genetic variance for the locus is maintained by balancing selection because there is an element of chance in which alleles become fixed during inbreeding. But taken at face value, limitation of QTL to a single cross is perhaps more consistent with mutation accumulation than with balancing selection.
Evolutionary genetic mechanisms for life-span variation—dominance:
We could estimate dominance for nine QTL (Table 3), and the dominance effects were in the direction of longer life in each case. Assuming an equal chance that alleles conferring longer or shorter life will be dominant, the probability that all nine loci would show dominance in the same direction is 0.004 (two-tailed binomial test). We suggest two possible explanations based on antagonistic pleiotropy and mutation accumulation. Antagonistic pleiotropy is most likely to maintain genetic polymorphisms if there is recessive deleterious gene action (Rose 1982; Curtsinger et al. 1994). If shorter life span is deleterious (all other things being equal) and if antagonistic pleiotropy is responsible for genetic variation in life span, then we would expect alleles that confer shorter life span to be recessive. The difficulty is that evidence for the involvement of antagonistic pleiotropy in life span in D. melanogaster is equivocal. Most of the support comes from antagonistic correlated responses to selection (Luckinbill et al. 1984; Rose 1984; Service et al. 1988, 1998; Zwaan et al. 1995). But correlated selection responses may be due to causes other than pleiotropy, and not all selection experiments show antagonistic correlated responses (Partridge and Fowler 1992). Wayne et al. (2001) and Curtsinger and Khazaeli (2002) found no evidence that life-span QTL had antagonistic pleiotropic effects on other fitness components. Direct estimates of genetic covariances between life span and other life history components in D. melanogaster are generally positive for fitness (Hughes 1995; Service 2000) or variable (Scheiner et al. 1989). Mutation accumulation might also be expected to result in a general pattern of recessiveness of alleles responsible for shorter life span, again assuming that shorter life span is deleterious. The majority of deleterious mutations appear to be fully or partially recessive (Wright 1977, p. 509). Furthermore, recessive deleterious mutations will have a higher equilibrium frequency than dominant ones under mutation selection balance (Crow and Kimura 1970; Charlesworth 1980) and are therefore more likely to be observed in life-span QTL mapping experiments. Thus, recessiveness, with regard to life span of alleles that shorten life span, is expected under both theories of senescence. A similar result (dominance of long-life alleles) appears to have been obtained by Leips and Mackay (2002), but was not discussed. A chromosome substitution experiment, however, yielded opposite results (Buck et al. 1993).
Conclusions:
Our primary objective in undertaking these experiments was to identify chromosomal regions that contain genes affecting life span. We also sought information about gene action at life-span QTL and about the value of replicated mapping experiments in distinguishing between antagonistic pleiotropy and mutation accumulation as mechanisms underlying genetic variance for life span. The number of life-span QTL that we detected falls within the range found in other studies, and 9 of our 10 QTL coincided reasonably with QTL found in at least one other study (Nuzhdin et al. 1997; Resler et al. 1998; Leips and Mackay 2000; Vieira et al. 2000; Curtsinger and Khazaeli 2002; Luckinbill and Golenberg 2002; Reiwitch and Nuzhdin 2002). On the basis of the results of this study and comparisons with other studies, qtl3, qtl7, qtl8, and qtl9 appear to be the most promising regions for more intensive mapping efforts designed ultimately to locate the actual genes responsible for life-span variation in outbred fly populations. Three of these loci are located on chromosome 3, a result that is consistent with other studies that support a dominant role for that chromosome in life-span determination (Luckinbill et al. 1988; Buck et al. 1993). qtl4, which was well supported by our experiments, but had rather less support in other studies, might also be a promising region for additional investigation. Strategies for finer-scale mapping of QTL include the use of advanced intercross lines (Darvasi and Soller 1995), replication of individual genotypes by means of recombinant inbred lines (e.g., Nuzhdin et al. 1997; Curtsinger and Khazaeli 2002), and complementation tests (Pasyukova et al. 2000; De Luca et al. 2003). De Luca et al. (2003), building upon earlier work (Pasyukova et al. 2000), used complementation tests and sequencing to identify Dopa decarboxylase (Ddc) as a probable life-span gene. The recombination map location of Ddc is ∼2-53.9 (FlyBase 1999), which corresponds exactly with one of our point estimates for the location of qtl3 (Table 3).
Our results can be interpreted as support for both mutation accumulation and antagonistic pleiotropy (or balancing selection). Five of our QTL were present in more than one cross, a result that is consistent with balancing selection. On the other hand, the remaining five QTL were each confined to one cross, a result that is more in accord with mutation accumulation. However, given both lack of precision in estimating QTL location and limited power to detect QTL, these conclusions can only be provisional. Also, our finding that alleles that confer greater longevity are generally at least partially dominant is consistent with both antagonistic pleiotropy and mutation accumulation. Ultimately, resolution of these issues will probably require the identification of specific life-span genes, determination of their allele frequencies in natural populations, and evaluation of their pleiotropic effects, if any. One test that has so far been missing from all life-span QTL mapping studies in D. melanogaster is a demonstration that the QTL respond to selection that changes mean life span. Such an experiment would provide independent validation of life-span QTL. In an accompanying article, we present the results of such a selection experiment (Valenzuela et al. 2004, this issue).
Acknowledgments
We thank S. Barnes, K. Borg, C. Clark, M. Dickey, D. Hilchey, G. Lawrence, J. Migdalene, A. Taba, T. Tsosie, and W. Young for help in various phases of this research. This research was supported by National Science Foundation grant DEB-9707706 and National Institutes of Health grant R25-GM56931.
References
- Arking, R., V. Burde, K. Graves, R. Hari, E. Feldman et al., 2000. Forward and reverse selection for longevity in Drosophila is characterized by alteration of antioxidant gene expression and oxidative damage patterns. Exp. Gerontol. 35: 167–185. [DOI] [PubMed] [Google Scholar]
- Basten, C. J., B. S. Weir and Z-B. Zeng, 1994 Zmap—a QTL cartographer, pp. 65–66 in 5th World Congress on Genetics Applied to Livestock Production: Computing Strategies and Software, edited by C. Smith, J. S. Gavora, B. Benkel, J. Chesnais, W. Fairfull et al. Organizing Committee, 5th World Congress on Genetics Applied to Livestock Production, Guelph, Ontario, Canada.
- Basten, C. J., B. S. Weir and Z-B. Zeng, 2001 QTL Cartographer, Version 1.15. Department of Statistics, North Carolina State University, Raleigh, NC.
- Beavis, W. D., 1995 The power and deceit of QTL experiments: lessons from comparative QTL studies. Proceedings of the Forty-ninth Annual Corn and Sorghum Industry Research Conference, ASTA, Washington, DC, pp. 252–268.
- Bennewitz, J., N. Reinsch and E. Kalm, 2002. Improved confidence intervals in quantitative trait loci mapping by permutation bootstrapping. Genetics 160: 1673–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buck, S., R. A. Wells, S. P. Dudas, G. T. Baker III and R. Arking, 1993. Chromosomal localization and regulation of the longevity determinant genes in a selected strain of Drosophila melanogaster. Heredity 71: 11–22. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1980 Evolution in Age-Structured Populations. Cambridge University Press, Cambridge, UK.
- Charlesworth, B., and D. Charlesworth, 1985. Genetic variation in recombination in Drosophila. I. Responses to selection and preliminary genetic analysis. Heredity 54: 71–83. [Google Scholar]
- Charlesworth, B., and K. A. Hughes, 1996. Age-specific inbreeding depression and components of genetic variance in relation to the evolution of senescence. Proc. Natl. Acad. Sci. USA 93: 6140–6145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chippindale, A. K., D. T. Hoang, P. M. Service and M. R. Rose, 1994. The evolution of development in Drosophila melanogaster selected for postponed senescence. Evolution 48: 1880–1899. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., and R. W. Doerge, 1994. Empirical threshold values for quantitative trait mapping. Genetics 138: 963–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, J. F., and M. Kimura, 1970 An Introduction to Population Genetics Theory. Harper & Row, New York.
- Curtsinger, J. W., 2002. Sex-specificity, lifespan QTLs, and statistical power. J. Gerontol. A Biol. Sci. Med. Sci. 57: B409–B414. [DOI] [PubMed] [Google Scholar]
- Curtsinger, J. W., and A. A. Khazaeli, 2002. Lifespan, QTLs, age-specificity, and pleiotropy in Drosophila. Mech. Ageing Dev. 123: 81–93. [DOI] [PubMed] [Google Scholar]
- Curtsinger, J. W., P. M. Service and T. Prout, 1994. Antagonistic pleiotropy, reversal of dominance, and genetic polymorphism. Am. Nat. 144: 210–228. [Google Scholar]
- Curtsinger, J. W., H. H. Fukui, A. S. Resler, K. Kelly and A. A. Khazaeli, 1998. Genetic analysis of extended life span in Drosophila melanogaster I. RAPD screen for genetic divergence between selected and control lines. Genetica 104: 21–32. [DOI] [PubMed] [Google Scholar]
- Darvasi, A., and M. Soller, 1995. Advanced intercross lines, an experimental population for fine genetic mapping. Genetics 141: 1199–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deckert-Cruz, D. J., R. H. Tyler, J. E. Landmesser and M. R. Rose, 1997. Allozymic differentiation in response to laboratory demographic selection of Drosophila melanogaster. Evolution 51: 865–872. [DOI] [PubMed] [Google Scholar]
- De Luca, M., N. V. Roshina, G. L. Geiger-Thornsberry, R. F. Lyman, E. G. Pasyukova et al., 2003. Dopa decarboxylase (Ddc) affects variation in Drosophila longevity. Nat. Genet. 34: 429–433. [DOI] [PubMed] [Google Scholar]
- FlyBase, 1999. The FlyBase database of the Drosophila genome projects and community literature. Nucleic Acids Res. 27: 85–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukui, H. H., and A. W. Kirscher, 1993. Thanatometer II: a chamber designed for large mixed-sex populations of Drosophila melanogaster. Dros. Inf. Serv. 72: 72–73. [Google Scholar]
- Goldstein, D. B., 2001 The Drosophila microsatellite database (http://www.ucl.ac.uk/biology/goldstein/ms_db).
- Graves, J. L., E. C. Toolson, C. Jeong, L. N. Vu and M. R. Rose, 1992. Desiccation, flight, glycogen, and postponed senescence in Drosophila melanogaster. Physiol. Zool. 65: 268–286. [Google Scholar]
- Gur-Arie, R., C. J. Cohen, Y. Eitan, L. Shelef, E. M. Hallerman et al., 2000. Simple sequence repeats in Escherichia coli: abundance, distribution, composition, and polymorphism. Genome Res. 10: 62–71. [PMC free article] [PubMed] [Google Scholar]
- Harshman, L. G., K. M. Moore, M. A. Sty and M. M. Magwire, 1999. Stress resistance and longevity in selected lines of Drosophila melanogaster. Neurobiol. Aging 20: 521–529. [DOI] [PubMed] [Google Scholar]
- Hughes, K. A., 1995. The evolutionary genetics of male life-history characters in Drosophila melanogaster. Evolution 49: 521–537. [DOI] [PubMed] [Google Scholar]
- Hughes, K. A., and B. Charlesworth, 1994. A genetic analysis of senescence in Drosophila. Nature 367: 64–66. [DOI] [PubMed] [Google Scholar]
- Lander, E., P. Green, J. Abrahamson, A. Barlow, M. Daley et al., 1987. Mapmaker: an interactive computer package for constructing primary genetic linkage maps of experimental and natural populations. Genomics 1: 174–181. [DOI] [PubMed] [Google Scholar]
- Lebreton, C. M., and P. M. Visscher, 1998. Empirical nonparametric bootstrap strategies in quantitative trait loci mapping: conditioning on the genetic model. Genetics 148: 525–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leips, J., and T. F. C. Mackay, 2000. Quantitative trait loci for life span in Drosophila melanogaster: interactions with genetic background and larval density. Genetics 155: 1773–1788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leroi, A. M., A. K. Chippendale and M. R. Rose, 1994. Long-term laboratory evolution of a genetic life-history trade-off in Drosophila melanogaster. 1. The role of genotype-by-environment interaction. Evolution 48: 1244–1257. [DOI] [PubMed] [Google Scholar]
- Lincoln, S., M. Daley and E. Lander, 1992 Constructing Genetic Maps With Mapmaker/Exp 3.0, Ed. 3. Whitehead Institute, Cambridge, MA.
- Lincoln, S., M. Daly and E. S. Lander, 1993 Mapmaker/QTL 1.1 Manual. Whitehead Institute, Cambridge, MA.
- Luckinbill, L. S., and E. M. Golenberg, 2002. Genes affecting aging: mapping quantitative trait loci in Drosophila melanogaster using amplified fragment length polymorphisms (AFLPs). Genetica 114: 147–156. [DOI] [PubMed] [Google Scholar]
- Luckinbill, L. S., R. Arking, M. J. Clare, W. C. Cirocco and S. A. Buck, 1984. Selection for delayed senescence in Drosophila melanogaster. Evolution 38: 996–1003. [DOI] [PubMed] [Google Scholar]
- Luckinbill, L. S., J. L. Graves, A. H. Reed and S. Koetsawang, 1988. Localizing genes that defer senescence in Drosophila melanogaster. Heredity 60: 367–374. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998 Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.
- Mackay, T. F. C., 2002. The nature of quantitative genetic variation for Drosophila longevity. Mech. Ageing Dev. 123: 95–104. [DOI] [PubMed] [Google Scholar]
- Medawar, P. B., 1946. Old age and natural death. Modern Quarterly 2: 30–49. [Google Scholar]
- Mueller, L. D., 1987. Evolution of accelerated senescence in laboratory populations of Drosophila. Proc. Natl. Acad. Sci. USA 84: 1974–1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- National Center for Biotechnology Information, 2000 Drosophila melanogaster genome (http://www.ncbi.nih.gov/mapview/map_search.cgi?taxid=7227).
- Nuzhdin, S. V., E. G. Pasyukova, C. L. Dilda, Z-B. Zeng and T. F. C. Mackay, 1997. Sex-specific quantitative trait loci affecting longevity in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 94: 9734–9739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, W. C., and R. C. Sohal, 1994. Extension of life span by overexpression of superoxide dismutase and catalase in Drosophila melanogaster. Science 263: 1128–1130. [DOI] [PubMed] [Google Scholar]
- Partridge, L., and K. Fowler, 1992. Direct and correlated responses to selection on age at reproduction in Drosophila melanogaster. Evolution 46: 76–91. [DOI] [PubMed] [Google Scholar]
- Pasyukova, E. G., C. Vieira and T. F. C. Mackay, 2000. Deficiency mapping of quantitative trait loci affecting longevity in Drosophila melanogaster. Genetics 156: 1129–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl, R., 1922 The Biology of Death, Being a Series of Lectures Delivered at the Lowell Institute in Boston in December 1920. J. B. Lippincott, Philadelphia.
- Pletcher, S. D., D. Houle and J. W. Curtsinger, 1998. Age-specific properties of spontaneous mutations affecting mortality in Drosophila melanogaster. Genetics 148: 287–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Promislow, D. E. L., M. Tatar, A. A. Khazaeli and J. W. Curtsinger, 1996. Age-specific patterns of genetic variance in Drosophila melanogaster. I. Mortality. Genetics 143: 839–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiwitch, S. G., and S. V. Nuzhdin, 2002. Quantitative trait loci for lifespan of Drosophila melanogaster affect both sexes. Genet. Res. 80: 225–230. [DOI] [PubMed] [Google Scholar]
- Resler, A. S., K. Kelly, G. Kantor, A. A. Khazaeli, M. Tatar et al., 1998. Genetic analysis of extended life span in Drosophila melanogaster II. Replication of the backcross test and molecular characterization of the N14 locus. Genetica 104: 33–39. [DOI] [PubMed] [Google Scholar]
- Rose, M. R., 1982. Antagonistic pleiotropy, dominance, and genetic variation. Heredity 48: 63–78. [Google Scholar]
- Rose, M. R., 1984. Laboratory evolution of postponed senescence in Drosophila melanogaster. Evolution 38: 1004–1010. [DOI] [PubMed] [Google Scholar]
- Rose, M. R., 1991 Evolutionary Biology of Aging. Oxford University Press, New York.
- Scheiner, S. M., R. L. Caplan and R. F. Lyman, 1989. A search for trade-offs among life history traits in Drosophila melanogaster. Evol. Ecol. 3: 51–63. [Google Scholar]
- Schug, M. D., K. A. Wetterstrand, M. S. Gaudette, R. H. Lim, C. M. Hutter et al., 1998. The distribution and frequency of microsatellite loci in Drosophila melanogaster. Mol. Ecol. 7: 57–70. [DOI] [PubMed] [Google Scholar]
- Service, P. M., 1993. Laboratory evolution of longevity and reproductive fitness components in male fruit flies: mating ability. Evolution 46: 387–399. [DOI] [PubMed] [Google Scholar]
- Service, P. M., 2000. The genetic structure of female life history in D. melanogaster: comparisons among populations. Genet. Res. 75: 153–166. [DOI] [PubMed] [Google Scholar]
- Service, P. M., and R. E. Vossbrink, 1996. Genetic variation in “first” male effects on egg laying and remating by female Drosophila melanogaster. Behav. Genet. 26: 39–48. [DOI] [PubMed] [Google Scholar]
- Service, P. M., E. W. Hutchinson, M. D. MacKinley and M. R. Rose, 1985. Resistance to environmental stress in Drosophila melanogaster selected for postponed senescence. Physiol. Zool. 58: 380–389. [Google Scholar]
- Service, P. M., E. W. Hutchinson and M. R. Rose, 1988. Multiple genetic mechanisms for the evolution of senescence in Drosophila melanogaster. Evolution 42: 708–716. [DOI] [PubMed] [Google Scholar]
- Service, P. M., C. A. Michieli and K. McGill, 1998. Experimental evolution of senescence: an analysis using a “heterogeneity” mortality model. Evolution 52: 1844–1850. [DOI] [PubMed] [Google Scholar]
- Sohal, R. S., and R. Weindruch, 1996. Oxidative stress, caloric restriction, and aging. Science 273: 59–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stearns, S. C., M. Kaiser and E. Hilleshiem, 1993. Effects on fitness components of enhanced expression of elongation factor EF-1α in Drosophila melanogaster. I. The contrasting approaches of molecular and population biologists. Am. Nat. 142: 961–993. [DOI] [PubMed] [Google Scholar]
- Tatar, M., D. E. L. Promislow, A. A. Khazaeli and J. W. Curtsinger, 1996. Age-specific patterns of genetic variance in Drosophila melanogaster. II. Fecundity and its genetic covariance with age-specific mortality. Genetics 143: 849–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valenzuela, R. K., S. N. Forbes, P. Keim, and P. M. Service, 2004. Quantitative trait loci affecting life span in replicated populations of Drosophila melanogaster. II. Response to selection. Genetics 168: 313–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vieira, C., E. G. Pasyukova, Z-B. Zeng, J. B. Hackett, R. F. Lyman et al., 2000. Genotype-environment interaction for quantitative trait loci affecting life span in Drosophila melanogaster. Genetics 54: 213–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher, P. M., R. Thompson and C. S. Haley, 1996. Confidence intervals in QTL mapping by bootstrapping. Genetics 143: 1013–1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vossbrink, R., 1997 An analysis of Drosophila melanogaster populations divergent in longevity using amplified fragment length polymorphism markers. M.S. Thesis, Northern Arizona University, Flagstaff, AZ.
- Wayne, M. L., J. B. Hackett, C. L. Dilda, S. V. Nuzhdin, E. G. Pasyukova et al., 2001. Quantitative trait locus mapping of fitness-related traits in Drosophila melanogaster. Genet. Res. 77: 107–116. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1977 Evolution and the Genetics of Populations, Vol. 3: Experimental Results and Evolutionary Deductions. University of Chicago Press, Chicago.
- Zeng, Z-B., 1994. Precision mapping of quantitative trait loci. Genetics 136: 1457–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwaan, B., R. Bijlsma and R. F. Hoekstra, 1995. Direct selection on life span in Drosophila melanogaster. Evolution 49: 649–659. [DOI] [PubMed] [Google Scholar]