Quantitative Trait Loci Affecting Life Span in Replicated Populations of Drosophila melanogaster. II. Response to Selection

Abstract

Three selection experiments were used to identify chromosome regions that contain QTL affecting late-life and early-life fitness in Drosophila melanogaster. The selection experiments were initiated by crossing pairs of inbred lines that had been derived from outbred laboratory populations that had different mean life spans. QTL regions were located by association with microsatellite markers that showed significant selection responses. Regions between recombination map positions 54 and 81 on chromosome 2, between 0 and 30 on chromosome 3, and near locations 49 and 81 on chromosome 3 had the strongest support as locations of life-span QTL. There was good general agreement between the life-span QTL regions that were identified by selection and those that were identified in a companion recombination mapping experiment that used the same fly stocks. Many marker loci responded in opposite directions to selection for late- and early-life fitness, indicating negative genetic correlations or trade-offs between those traits. Indirect evidence suggested that some negative genetic correlations were due to antagonistic pleiotropy.

SELECTION experiments are one of the most commonly used methods in classical quantitative genetic analysis. A directional selection response is evidence of additive genetic variance for a phenotype, and selection may be used to estimate the realized heritability of a quantitative trait. Also, correlated selection responses of two or more phenotypes are evidence of genetic covariance among traits. Furthermore, the availability in recent years of numerous highly polymorphic genetic markers means that selection experiments can be used to identify chromosome regions that contain quantitative trait loci (QTL). Hitchhiking by markers has been used to infer QTL for 6-week weight in mice (Keightley and Bulfield 1993) and for bristle number in flies (Nuzhdin et al. 1998). Selection experiments can be an important component of an overall QTL mapping strategy. For example, selection may be much more powerful than recombination mapping experiments for detecting QTL (Keightley and Bulfield 1993). And agreement between selection experiments and recombination mapping experiments with respect to QTL location increases confidence that QTL regions have been properly identified. Nevertheless, selection experiments have not been widely used for QTL mapping, perhaps because they are too time consuming for most species.

In this article, we report the results of selection experiments that were designed to identify chromosome regions that contain genes affecting late-life and early-life fitness in Drosophila melanogaster. One of our expectations was that selection for increased late-life fitness would identify a set of QTL that corresponded to life-span QTL found in a recombination mapping experiment in the accompanying article (Forbes et al. 2004, this issue). Our second expectation was that the selection experiments would provide some information on the importance and mechanistic basis of life history trade-offs in D. melanogaster. Trade-offs among fitness components (reproduction, life span, etc.) have played a central role in the development of ecological and evolutionary life history theory (e.g., the r- and K-selection theory of MacArthur and Wilson 1967). Trade-offs also are the basis of the antagonistic pleiotropy model for the evolution of senescence (Williams 1957), and antagonistic pleiotropy has been proposed as a mechanism for the maintenance of genetic variation in life history traits (Rose 1982, 1985). The Williams-Rose model specifically postulates antagonistic pleiotropic effects between early-life and late-life fitness components.

Evidence for the involvement of antagonistic pleiotropy in Drosophila life history is mixed. Selection experiments frequently, but not always, indicate trade-offs between life span and early-age fecundity (Luckinbill et al. 1984; Rose 1984; Partridge and Fowler 1992; Service 1993; Service et al. 1998). However, experiments that are designed to estimate genetic covariances among fitness components frequently detect few or no negative correlations (Scheiner et al. 1989; Hughes 1995; Service 2000). Even when negative genetic correlations between life history traits are detected, such correlations are only suggestive of antagonistic pleiotropy. Negative genetic correlations that are inferred from correlated phenotypic responses to selection can arise from inadvertent simultaneous direct selection on a pair of traits and thus not be indicative of life history trade-offs at all. This is most likely to be a problem in “natural” (as opposed to artificial) selection experiments designed to modify life span, such as those that have typically been carried out with D. melanogaster (Luckinbill et al. 1984; Rose 1984; Chippindale et al. 1994; Service et al. 1998). Also, genetic correlations and correlated responses to selection can arise from linkage disequilibrium. Because the present experiments can be suggestive only in distinguishing between antagonistic pleiotropy and linkage as causes of negative genetic correlations, we will for the most part simply discuss the evidence for negative correlations (trade-offs) without attributing any particular underlying cause, except in so far as our analysis permits.

We selected for increased late-life fitness in some populations and for increased early-life fitness in other populations. In both cases, we assayed changes in life span and changes in the frequencies of alleles at microsatellite marker loci. Marker loci that responded to selection for increased late-life fitness point to possible life-span QTL. Marker loci that responded to selection for increased early-life fitness point to QTL that influence early-life fitness components, including, possibly, egg-adult development rate and early-age reproductive success. Marker loci that responded in opposite directions to both selection regimes are evidence for negative genetic correlations between late- and early-life fitness. We argue that if such marker loci are more frequent than would be expected by chance, then there is indirect evidence that at least some QTL have antagonistic pleiotropic effects.

MATERIALS AND METHODS

Populations, inbred lines, and crosses:

Reciprocal crosses were made between three different pairs of inbred lines. One line of each pair was derived from an outbred population that had a relatively short mean life span (B population), and the other line was derived from a population that had a relatively long mean life span (O population). We will refer to inbred lines as either B or O lines, depending upon their origin. In all, six inbred lines were used, each line having been derived from a different outbred population. The inbred line crosses were the same as those described in our accompanying article (Forbes et al. 2004, this issue), with one minor exception. The B inbred line for cross 2 was different from, but closely related to, that used in Forbes et al. (2004). Analysis of >20 microsatellite loci did not reveal any differences between these two B lines.

The outbred populations and the inbreeding procedures are described in the accompanying article (Forbes et al. 2004, this issue). Here it is sufficient to note that the B and O outbred populations were a subset of those originally described by Rose (1984). The average adult life span of O flies is more than twice that of B flies (Service et al. 1998). Because of possible inbreeding depression, we did not expect our B and O inbred lines to display similar differences in longevity, and we did not assay the life spans of inbred lines. However, we did expect that the inbred lines would most likely be fixed for at least a subset of the alleles responsible for the evolutionary difference in mean life span between the B and O selection regimes. Therefore, similar selection applied to the progeny of crosses between inbred lines should tend to reproduce the longevity differences seen between the B and O outbred source populations.

Selection experiment:

For each cross, the F₂ was randomly divided into six populations. Three populations were assigned to a short-generation selection regime (S populations), and three populations were assigned to a long-generation selection regime (L populations). Considering all three crosses, there were nine S and nine L populations. Short-generation selection was done by culturing S populations with 2-week-long discrete generations. The culture procedures and conditions were identical to those used for the ancestral B outbred populations. Each population consisted of 20 vials with ∼1000–2000 flies in each generation. L populations were also maintained in discrete generations. However, generation lengths were increased to 9 weeks from 2 weeks. Some generations were stopped short of 9 weeks due to diminishing population size. Like their O outbred counterparts, the L populations were maintained as adults in 2-liter population cages, each population cage contained ∼1000 flies, and each population consisted of two cages. At the end of each generation, eggs from the L populations were collected and transferred to vials, and emerging adults were transferred to population cages 2 weeks later. The L culture procedures and conditions were similar to those used for the O ancestral populations. All populations were maintained at 25°. After a number of generations of selection (Table 2), 15 males and 15 females were randomly collected from each replicate population and frozen at −80° for subsequent genotyping. Hence, 90 individuals were genotyped for each selection regime of a given cross. Except for cross 1, there were more generations of selection in the S populations than in the L populations when flies were sampled for genotyping (Table 2).

TABLE 2.

Selection response by cross

		L selection		S selection
Marker	Location	Mean (95% C.I.)a	t-Testb	Mean (95% C.I.)a	t-Testb	Responsec	Forbes et al. (2004) QTLd
A. Cross 1 [S 13 (2.2), L 13 (9.1)]e
AF047180	1-0	0.59 (0.08)	4.30*	0.12 (0.28)	−4.35**	LS
DROPCXGEN	1-0.9	0.55 (0.14)	0.10 (0.19)	−5.93**	S
DMSGG3	1-1.3	0.61 (0.17)	0.10 (0.19)	−5.93**	S	1 (3)
DMU56661	1-11	0.44 (0.09)	0.09 (0.11)	−10.47***	S	1 (3)
AE003438	1-18	0.43 (0.15)	0.12 (0.06)	−18.38***	S	1 (3)
DROSEV2	1-33.4	0.57 (0.21)	0.15 (0.19)	−6.08**	S
DMTROPONI	1-57.6	0.81 (0.28)	3.94*	0.29 (0.10)	−8.80***	LS
AC004441	2-3	0.63 (0.24)	0.22 (0.06)	−18.81***	S	2 (1)
AC005555	2-31.5	0.46 (0.10)	0.27 (0.17)	−5.35**	S
AC006302	2-48.5	0.57 (0.19)	0.23 (0.02)	−43.28***	S	3 (1)
DL	2-52.9	—	0.35 (0.04)	−15.11***	—	3 (1)
AC004759	2-54.3	0.69 (0.15)	5.30**	0.34 (0.02)	−27.01***	LS	3 (1)
AC006472	2-61	0.71 (0.10)	7.95***	0.35 (0.04)	−15.11***	LS	4 (1–3)
MAM	2-70.3	—	0.38 (0.17)	−2.98*	—	4 (1–3)
DMU19731	2-71	0.72 (0.07)	12.23***	0.38 (0.15)	−3.33*	LS	4 (1–3)
AC004641	2-81	0.73 (0.13)	6.92**	0.46 (0.43)	L	5 (3)
ELF1	2-87	—	0.42 (0.30)	—	5 (3)
AC004307	2-90	0.53 (0.19)	0.37 (0.27)	5 (3)
DS08011	2-101	0.52 (0.10)	0.45 (0.13)
DMRHOb	3-0.2	0.87 (0.11)	10.56***	0.57 (0.38)	L	6 (2)g
AC004343	3-0.5	0.86 (0.13)	9.02***	0.56 (0.38)	L	6 (2)
DMCPDR	3-1.5	—	0.57 (0.38)	—	6 (2)
AC004658	3-8	0.87 (0.22)	4.86**	0.54 (0.46)	L	6 (2)
DMU14395	3-18	0.82 (0.08)	15.02***	0.43 (0.05)	−5.76**	LS	6 (2), 7 (1–3)
DROLAMB2A	3-28	0.78 (0.08)	12.89***	0.39 (0.17)	L	7 (1–3)
DMSGS378	3-41.4	0.59 (0.17)	0.42 (0.42)	8 (1, 2), 9 (1–3)
DRO11DC7Z	3-47	0.71 (0.06)	13.50***	0.43 (0.21)	L	8 (1, 2), 9 (1–3)
DMTRXIII	3-54.2	0.66 (0.17)	3.83*	0.32 (0.18)	−4.18*	LS	9 (1–3)
DRONANOS	3-67	0.45 (0.11)	0.22 (0.28)	−3.95*	S
AE003744	3-80	0.78 (0.29)	3.50*	0.16 (0.13)	−9.20***	LS	10 (1, 2)h
AE003768	3-98	0.67 (0.19)	3.79*	0.18 (0.15)	−7.69***	LS
B. Cross 2 [S 24 (2.0), L 12 (8.2)]e
DMSGG3	1-1.3	0.98 (0.06)	10.55***	0.95 (0.11)f	L	1 (3)
DELTEX	1-17	0.78 (0.20)	5.42**	0.32 (0.63)	L	1 (3)
DMTROPONI	1-57.6	0.18 (0.22)f	0.16 (0.22)	−5.27**	S
AE003585	2-3	0.73 (0.12)	7.47***	0.59 (0.10)	L	2 (1)
AC005555	2-31.5	0.53 (0.15)	0.66 (0.02)f
DMU12269	2-39	0.51 (0.23)	0.63 (0.11)f
CAD	2-54	0.66 (0.21)	3.20*	0.44 (0.17)	L	3 (1)
DROGPAD	2-60	0.68 (0.04)	18.15***	0.43 (0.07)	−3.99*	LS	4 (1–3)
AC006472	2-61	0.69 (0.03)	23.00***	0.39 (0.07)	−6.98**	LS	4 (1–3)
DMU19731	2-71	0.71 (0.10)	7.95***	0.24 (0.26)	−3.67*	LS	4 (1–3)
AC004641	2-81	0.73 (0.12)	7.47***	0.31 (0.21)	−3.77*	LS	5 (3)
DS08011	2-101	0.61 (0.23)	0.51 (0.20)
AC004343	3-0.5	0.77 (0.20)	9.91***	0.62 (0.19)	L	6 (2)
DMU36477	3-10	0.70 (0.20)	3.28*	0.49 (0.12)	L	6 (2)
DMPROSPER	3-50	0.79 (0.06)	16.98***	0.29 (0.09)	−9.72**	LS	9 (1–3)
DMCP017G	3-62	0.75 (0.14)	4.39**	0.51 (0.36)	L	9 (1–3)
DMTF125	3-81.5	0.77 (0.10)	8.24***	0.32 (0.03)	−25.09**	LS	10 (1, 2)h
AE003768	3-98	0.32 (0.02)f	0.05 (0.08)	−12.01**	S
C. Cross 3 [S 19 (2.1), L 8 (6.9)]e
DMSGG3	1-1.3	0.42 (0.10)	0.35 (0.25)	1 (3)
DMU56661	1-11	0.53 (0.30)	—	—	1 (3)
AE003438	1-18	0.52 (0.14)	0.36 (0.29)	1 (3)
DROSEV2	1-33.4	0.68 (0.23)	3.31*	0.40 (0.29)	L
DROYP3	1-44	0.69 (0.09)	8.45***	0.58 (0.15)	L
DROEXO2	1-51.5	0.41 (0.08)f	0.63 (0.06)f
AE003588	2-1	0.66 (0.26)	0.58 (0.26)
DROYANETSB	2-4	0.35 (0.07)f	0.54 (0.17)	2 (1)
AE003615	2-22.5	0.47 (0.24)	0.23 (0.23)	2 (1)
AC005555	2-31.5	0.45 (0.21)	0.41 (0.36)
AC006472	2-61	0.59 (0.16)	0.36 (0.10)	−6.05**	S	4 (1–3)
DMMASTER	2-70.3	0.66 (0.10)	6.66**	0.29 (0.02)	−34.67**	LS	4 (1–3)
AC004307	2-90	0.78 (0.02)	44.28***	—	—	5 (3)
AC004365	2-97.5	0.75 (0.30)	3.39*	0.31 (0.10)	−7.63**	LS
AE003482	3-13	0.61 (0.25)	0.39 (0.20)	6 (2), 7 (1–3)
DMSGS378	3-41.4	0.52 (0.13)	0.35 (0.20)	−3.15*	S	8 (1, 2)
DRO17DC2Z	3-47	0.59 (0.15)	0.41 (0.06)	−6.36**	S	8 (1, 2), 9 (1–3)
DROABDB	3-59	0.56 (0.10)	0.33 (0.14)	−4.87**	S	9 (1–3)
AE003744	3-80	0.75 (0.12)	8.37***	0.38 (0.10)	−4.94**	LS	10 (1, 2)h
DROROUGH	3-91.1	—		0.49 (0.02)		—

^aFrequency of the marker allele from the O (long-lived) parental inbred line used for each cross. Confidence intervals (95%) are given by the mean ± (95% C.I.), where the 95% confidence limit is calculated as t_0.05[2] × SEM, and t_0.05[2] = 4.303 (two-tailed). Data were not angularly transformed for these calculations.

^bOne-tailed t-test with n = 3 population means, as explained in the text. For L selection, the alternative hypothesis is that the mean O-allele frequency is >0.5. For S selection, the alternative hypothesis is that the mean O-allele frequency is <0.5. Data were angularly transformed for these tests. Results are not shown for tests that were not significant (α = 0.05). *P < 0.05, **P < 0.01, ***P < 0.001.

^cSee text for explanation.

^dThe marker is located within the 95% confidence interval for the indicated QTL of Forbes et al. (2004)(Table 3). The number(s) in parentheses indicates the cross(es) in which the QTL was identified. For example, the marker DMSGG3 is located within the confidence interval for qtl1 of Forbes et al., which they detected in cross 3.

^eThe number of generations of selection that preceded collection of flies for estimation of marker allele frequencies. Numbers in parentheses are mean generation lengths in weeks.

^fSignificantly different from 0.5 in the direction opposite to expectation. This is a two-tailed test using the 95% confidence interval.

^gMarker located just to the left of the confidence interval for qtl6 (2-0.5–2-25), for which the point location estimate was 2-0.5.

^hMarker located just to the right of the confidence interval for qtl10, which was between map positions 3-71 and 3-78 (Forbes et al. 2004, Table 3). In all crosses, this is the marker closest to the confidence interval for qtl10.

Longevity assays:

Longevity assays were done to confirm that the L and S selection protocols produced different life spans. Eggs were sampled from the L and S populations and flies were reared at controlled density (100 eggs/vial) for two generations. Second-generation adults were transferred to population cages based on the design of Fukui and Kirscher (1993). Two cages were used for each replicate S or L population, and there were ∼200 flies/cage. Cages were checked every other day, at which time dead flies were removed and sexed. All populations of a given cross were assayed at the same time. Therefore, the S lines had experienced more generations of selection than the L lines (Table 1). Doing the assays at different times (e.g., after the same number of generations of selection) would have potentially introduced confounding environmental effects into the comparison of life spans. However, concurrent assays raise the likelihood that selection responses will be asymmetrical. In particular, we might expect more pronounced responses in the S lines. For the first cross, we also did a longevity assay of flies derived from the F₂ generation (i.e., before selection). That assay provided a standard for evaluating selection responses, albeit with possible confounding temporal effects. The initial life-span assay for cross 3 did not reveal a statistically significant difference between selection regimes. Therefore, we repeated that assay (Table 1). Assays (longevity or allele frequency) were not done after the same number of generations of selection in all three crosses (Tables 1 and 2). Rather, the timing of assays depended upon workload and availability of personnel.

TABLE 1.

Longevity assay results

	Mean life span (days)				ANOVAb
Cross and treatment	Female	Male	Combined	Generations of selectiona	Treatment	Sex
Cross 1
F2	26.0	28.7	27.4	NA	0.601
S	24.0	20.5	22.2	39 (2.0)	385.53***	4.302
L	33.8	31.5	32.7	8 (9.4)
Cross 2
S	28.1	29.0	28.6	19 (2.0)	15.323*	1.409
L	33.0	34.1	33.5	5 (7.6)
Cross 3 (assay 1)
S	18.0	36.0	27.0	27 (2.1)	3.056	64.265**
L	27.9	37.4	32.7	7 (7.1)
Cross 3 (assay 2)
S	18.8	31.4	25.1	48 (2.0)	41.687**	7.168
L	30.1	37	33.6	12 (8.1)

^aNumber of generations of selection preceding the longevity assays. Numbers in parentheses are average generation lengths in weeks.

^bNumbers are F-values. *P < 0.02, **P < 0.01, ***P < 0.0001. F-values without asterisks were not significant (P > 0.05). For the F₂ generation of cross 1, the analysis was by one-way ANOVA of six values (mean male and female life span per replicate cage by three replicate cages) with sex as the factor. All other analyses were three-factor ANOVAs with n = 24 (two treatments × two sexes × three replicate populations/treatment × two cages/population). Treatment (i.e., selection regime) and sex were fixed main effects, and population was a nested random effect within treatment. The F-ratio for the treatment effect was MS_treatment/MS_{population(treatment)}. The F-test for the sex effect was MS_sex/MS_{sex×population(treatment)}. Population (treatment) and the interaction effects—sex × treatment and sex × population (treatment)—were not statistically significant (P > 0.05) in all four three-factor analyses.

Marker loci, genotyping, and analysis of marker allele frequencies:

We used microsatellites for genetic markers (see supplemental Table A, http://www.genetics.org/supplemental). The procedures used to identify useful markers are described by Forbes et al. (2004), and most of the microsatellites used in these experiments are the same as those used by Forbes et al. DNA extraction, PCR amplification, and electrophoresis generally followed the same procedures as described by Forbes et al. All allele frequency data are presented in terms of the frequencies of the marker alleles that were derived from the O inbred parental lines, which we simply refer to as the O alleles. Allele frequency responses to selection were evaluated by t-tests. The null hypothesis of no selection response at a marker locus was equivalent to the expectation that the O allele frequency of a set of replicate populations was 0.5. The alternative hypothesis for the L populations was that the mean O allele frequency would be >0.5. In contrast, the alternative hypothesis for the S populations was that the O allele frequency would be <0.5. Hence, tests were one-tailed. t-Tests were performed on angularly transformed O allele frequencies with each population mean taken as a datum (n = 3 populations/selection regime). A conventional Bonferroni correction for multiple tests is most appropriate when variables have low correlations (Manly 1997a, p. 108), which is unlikely to be the case for linked markers that are responding to selection. Manly (1997a) suggests an alternative method based upon randomization. We could not implement that procedure fully because our sample size (six populations/cross) was too small to accurately estimate the randomization distribution for the experiment-wise error rate. There are only 20 possible assignments of three populations each to the S and L treatments, two of which are the actual ones. Nevertheless, we repeated our analyses for all 18 additional orderings. This enabled us to determine the number of significant selection responses that we might have expected by chance.

We tested for consistency of selection responses among two or more crosses by using the mean O allele frequency of a selection regime within a cross as the basic datum of analysis. A separate t-test was performed for each marker locus that was used in at least two crosses. In cases where the same marker locus was not used in multiple crosses, we were frequently able to “lump” nearby markers to perform the analysis. The criterion for lumping different loci among crosses was that they be within 5 cM of each other. We also calculated product moment correlations of mean marker frequencies between L and S treatments. Statistical significance of correlation coefficients was evaluated by randomization tests (Manly 1997b). When two markers were very close to each other (<1–2 cM), we used only one if the allele frequencies were very similar and the choice of marker would have no impact on the analysis.

Comparisons with companion QTL mapping experiments:

We calculated product-moment correlations between marker allele frequencies in our selection experiments and the number of likelihood-ratio (LR) peaks from the bootstrap analyses in the recombination mapping experiment in the accompanying article (see Forbes et al. 2004, this issue, Figure 1). A likelihood map peak is a point estimate for the position of a QTL. The number of peaks at a given location in a bootstrap analysis gives an indication of the confidence that a QTL is at that location. The number of likelihood-ratio peaks was obtained by summing the bootstrap distributions over a 5-cM symmetrical window around the marker position, and bootstrap results for males and females were combined, as were bootstrap results for the three effect hypotheses (additive and dominance effects, additive effects only, and dominance effects only). Only those bootstrap maxima that exceeded significance thresholds were included, and the number of bootstrap maxima was log transformed. The statistical significance of correlations was evaluated by randomization tests.

Figure 1.—

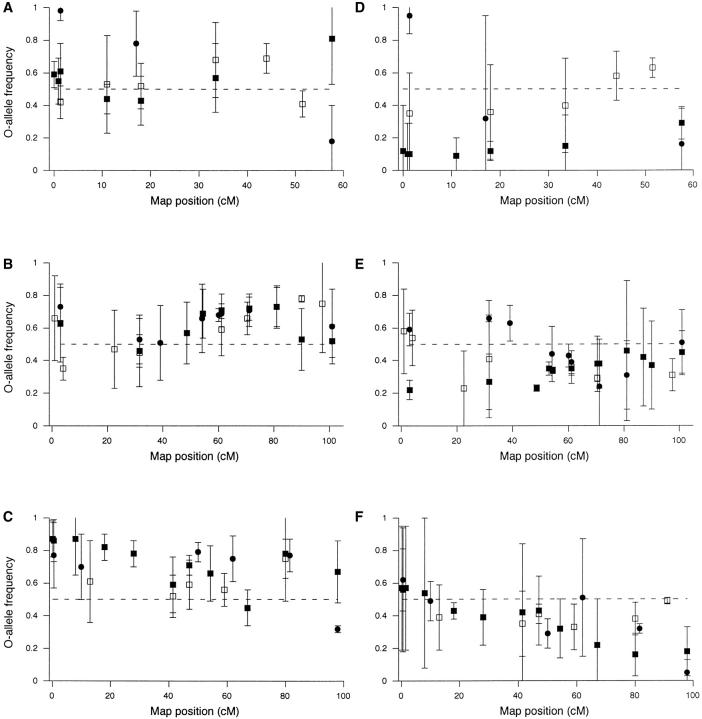
Marker locus selection responses. Each point is the mean frequency, over three replicate lines, of the marker allele derived from the O (long-lived) parental inbred line used for each cross. Error bars are 95% confidence limits (mean ± 4.303 SEM, d.f. = 2). The horizontal dashed line is the expected allele frequency, 0.50, under the null hypothesis of no selection response. Statistical tests for marker selection response (Table 2) are one-tailed, as explained in the text. (A–C) L selection response; (D–F) S selection response. (A and D) X chromosome; (B and E) chromosome 2; (C and F) chromosome 3. Solid squares, cross 1; solid circles, cross 2; open squares, cross 3.

RESULTS

Longevity assays:

As expected, the average adult life span of the L population flies was greater than that of the S population flies (Table 1). L population life span was 17–47% greater than S population life span, and the difference was positively correlated with the length of selection (L or S) that preceded the longevity assays (r > 0.72, n = 4). The F₂ flies of cross 1 (i.e., before selection) had a mean adult life span that almost exactly split the subsequent difference between the S and L lines of that cross. All three were significantly different from each other, indicating that the selection regimes had resulted in both longer and shorter life spans when compared to that of the F₂. That suggests that the cumulative phenotypic selection responses were quite similar in the S and L populations, despite the fact that the S populations experienced many more generations of selection.

Marker selection responses:

In all, there were 131 tests of the null hypothesis that marker allele frequencies were equal to 0.5 (Table 2). Selection responses were observed for at least some markers on all three chromosomes in all crosses (Table 2, Figure 1). However, the proportion of significant selection responses was lowest for the X chromosome (14/31 = 45.2%) and higher for chromosomes 2 and 3 (28/54 = 51.9% and 27/46 = 58.7%, respectively). The mean O allele frequency deviated from 0.5 by at least ±0.1 in 86 cases. Of those, 78 were in the expected direction: the O marker allele increased in frequency in the L populations and decreased in the S populations. Of the 131 allele frequency tests, 69 were significant by one-tailed tests (i.e., showed significant deviations in the expected direction). Of those, 34 were in the L treatment and 35 were in the S treatment. There were only 8 cases (4 L and 4 S) in which marker allele frequencies deviated significantly from expectation in the opposite direction, 4 of which were associated with the X chromosome (Table 2). These results argue strongly that the great majority of the selection responses of marker loci resulted from linkage to alleles that conferred high fitness in the ancestral B and O populations (and in the S and L treatments). There was very little evidence that the responses of marker loci were due to linkage to low-frequency deleterious alleles that might have become fixed during inbreeding. Given that two markers may flank a QTL, we expect that the actual number of QTL detected by our procedure is less than the number of markers that responded to selection. On average there were 20.7 markers/cross that were present in both L and S treatments and that could therefore be used for randomization tests. In the actual data, an average of 12.7 markers showed significant selection responses per cross and treatment combination (by one-tailed test, regardless of direction). In the randomizations, the corresponding number was 2.5 significant results. In almost every case, markers that had significant test statistics in the randomizations were ones that responded in the same direction in the L and S treatments. Therefore, we may have less confidence in the results for those markers. Markers that responded significantly to selection in opposite directions (the LS response, Table 2) never gave significant test statistics in the randomizations.

Selection responses in L populations:

The L selection regime produced strong directional selection for longevity and fertility at late ages. Therefore, the selection responses of marker loci in the L populations were expected to indicate the location of life-span and/or late-life fertility QTL. X chromosome markers responded significantly to L selection in all three crosses, although there was little consistency among crosses (Table 2, Figure 1A). Chromosome 2 presented a much more consistent picture. Considering all three crosses, 10 of 11 tests for markers located between map positions 54 and 81 were significant (Table 2, Figure 1B). In addition, there were significant selection responses for markers located at the left end of chromosome 2 in cross 2 and at the right end of chromosome 2 in cross 3. Most chromosome 3 markers showed significant L selection responses in crosses 1 and 2 (Table 2, Figure 1C). For cross 3, O allele frequencies were consistently >0.5 in the L populations, but significantly so only for the marker locus at position 80. The overall picture, then, was that the evidence for life-span QTL was strongest for chromosomes 2 and 3. For chromosome 2, the most important region appears to be between map positions 54 and 81 (Figure 1B). For chromosome 3, the most likely regions for life-span QTL appear to be 0–30, 47–62, and 80 (Figure 1C). These conclusions are supported by tests that combined the results for all three crosses (Table 3).

TABLE 3.

Selection analysis of combined crosses

	L selection		S selection
Location	Mean (SE)	t (d.f.)a	Mean (SE)	t (d.f.)a
Chromosome 2
2-54.2	0.675 (0.015)	11.168 (1)*	0.390 (0.050)	−2.171 (1)
2-61	0.663 (0.037)	4.297 (2)*	0.367 (0.012)	−10.854 (2)***
2-70.7	0.697 (0.019)	10.095 (2)***	0.303 (0.041)	−4.587 (2)**
2-81	0.728 (0.002)	127.858 (1)****	0.385 (0.075)	−1.517 (1)
Chromosome 3
3-48.5	0.697 (0.058)	3.240 (2)*	0.377 (0.044)	−2.745 (2)
3-80.8	0.767 (0.009)	27.074 (2)***	0.287 (0.066)	−2.981 (2)*

Results are shown only for markers that had statistically significant (P < 0.05) selection responses over all crosses included in an analysis.

^aData are frequencies of the marker allele from the O inbred parental line used for each cross. The mean allele frequency in each cross is the basic datum of analysis. One-tailed t-test with n = 3 or 2 cross means, as explained in the text. For L selection, the alternative hypothesis is that the mean O-allele frequency is >0.5. For S selection, the alternative hypothesis is that the mean O-allele frequency is <0.5. Data were angularly transformed for these tests.

^*P < 0.05,

^**P < 0.025,

^***P < 0.005,

^****P < 0.0001.

Selection responses in S populations:

The S treatment was expected to select directly for traits that enhanced fitness in a 2-week culture regime. Such early-life fitness traits presumably include rapid preadult development and high fecundity of very young adults. Thus, significant responses of marker loci to S selection might be uninformative from the point of view of detecting life-span QTL. On the other hand, any reduction in mean life span that was consistent among replicate S populations within a cross would most likely be due to negative genetic correlations between early-life fitness and life span (because of either pleiotropy or linkage). In which case, at least some of the markers that responded to S selection would be associated with life-span QTL. Almost all significant responses for X-linked markers occurred in cross 1. Significant S selection responses were observed for chromosome 2 and 3 markers in all three crosses. For chromosome 2 markers that showed significant S selection responses in the expected direction, there was a general consistency among crosses for markers located between map positions 49 and 71 (Table 2, Figure 1E). For chromosome 3, there was a similar consistency for markers located between positions 47 and 59 and for markers located at about map position 80-81 (Table 2, Figure 1F). These results were generally corroborated by the analyses of combined crosses, except for the region 47-59 on chromosome 3 (Table 3).

L and S selection response considered jointly:

We characterized the selection response of each marker locus as L type (significant increase in O allele frequency in L populations), S type (significant decrease in O allele frequency in S populations), or LS type (both L and S; Table 2). One difficulty with this categorization is that the response type might have changed with continued selection. For example, an S-type response could become an LS type if continued selection in the L lines caused O allele frequencies to eventually increase sufficiently. That said, the LS response indicates a negative genetic correlation between late- and early-life fitness that is localized in the region near the marker.

In 62 cases we had the necessary information to make categorizations (Table 2). We tested the null hypothesis that the numbers of the various types of selection responses (LS, L only, S only, and neither L nor S) could be due to chance. This is equivalent to the hypothesis that the loci that determined fitness in the L selection regime were independent of the loci affecting fitness in the S regime and that the two sets of loci were distributed independently of each other on the chromosomes. In fact, considering all three chromosomes together, the proportion of LS-type marker responses was very nearly that which would be expected by chance. Agreement between observation and expectation was similarly close for the other three response categories. These results suggest independence between loci with late-life and early-life fitness effects. In other words, genetic correlations are due to linkage. However, in this case, failure to reject the null hypothesis may be weak evidence in its favor. A similar result might be obtained if all loci had pleiotropic effects on late- and early-life fitness but the power to detect selection responses in the L and S treatments was rather low.

When we examined selection responses for individual chromosomes, however, some patterns did emerge. For chromosome 2, there was an excess of LS responses and a deficit of L-only and S-only responses. The deviation from expectation was significant (P < 0.05) by both χ² and Fisher's exact tests, although lack of independence between closely linked markers within crosses suggests caution in interpretation of results. If valid, however, this result indicates that marker loci that responded to L selection also tended to respond (in the opposite direction) to S selection. This result is consistent with antagonistic pleiotropy between late-life and early-life fitness effects (as opposed to linkage). For the X chromosome and chromosome 3, there was a trend toward a deficit of LS responses and an excess of L-only and S-only responses. The result was not statistically significant when the two chromosomes were combined (0.10 > P > 0.05), but is suggestive of the possibility that for the X chromosome and chromosome 3, genes affecting late- and early-life fitness tend to be in different chromosome regions.

The preceding analysis considered only those selection responses that were statistically significant in the expected direction. A more general analysis considers correlations between marker allele frequencies in the two treatments, regardless of whether the changes in allele frequencies were statistically significant (Table 4). Negative correlations are consistent with negative genetic correlations between late- and early-life fitness effects. For chromosome 2, such negative correlations were observed in crosses 2 and 3 and for all crosses combined. However, only the correlation for cross 2 was statistically significant. On the other hand, correlations for X-linked and chromosome 3 markers were consistently positive and significant in both cases when combined over crosses. One way such positive correlations could arise is if different chromosome regions responded to selection in the L and S treatments: for example, if markers that responded to selection in one treatment remained at a frequency of ∼0.5 in the other treatment. This interpretation is supported by the preceding analysis of significant selection responses. That is, there was a trend toward an excess of L-only and S-only selection responses for X-linked and chromosome 3 markers. A second way in which positive correlations can arise is if the selection response of a marker locus in one treatment is in the direction opposite to that expected. That might happen if the marker were close to a deleterious allele that became fixed by chance in one of the parental inbred lines used for a cross. We repeated the correlation analysis for each chromosome combined over crosses after eliminating the eight cases (seven markers) that responded significantly in the opposite direction (Table 2). Although all three correlations were still positive, none were statistically significant (Table 4).

TABLE 4.

Correlations of marker allele frequencies and QTL mapping bootstrap results

	Chromosome
Cross	X	2	3
A. Correlations between marker allele frequencies in S and L selection treatmentsa
1	0.9319 (5)	0.2840 (9)	0.5535 (10)
2	0.8186 (3)	−0.7217 (9)*	0.7419 (6)
3	0.0368 (5)	−0.2374 (7)	0.3979 (5)
All crosses	0.5627 (13)*	−0.1507 (25)	0.5892 (21)**
All crossesb	0.4700 (10)	0.2066 (22)	0.4054 (20)
B. Correlations between marker allele frequencies in L selection treatment and no. of bootstrap maximac
1	−0.9495 (5)	0.4282 (9)	−0.1268 (10)
2	−0.8642 (3)	0.5714 (9)	0.3350 (6)
3	−0.8554 (6)	0.7814 (8)*	0.0369 (5)
All crosses	−0.6315 (14)*	0.5446 (26)**	0.1007 (21)
C. Correlations between marker allele frequencies in S selection treatment and no. of bootstrap maximad
1	−0.9626 (5)	−0.5972 (9)	−0.0471 (10)
2	−0.4184 (3)	−0.6847 (9)*	0.1513 (6)
3	−0.3028 (5)	−0.3206 (7)	−0.1136 (6)
All crosses	−0.3756 (13)	−0.5802 (25)**	−0.0088 (22)

The number of marker loci used for each correlation is given in parentheses. Randomization was used to test for significance of correlations. For N ≥ 8, N = 7, and N = 6 the number of randomizations was 4999, 999, and 299, respectively. For N ≤ 5, no significance test was performed because the number of possible randomizations was too small.

^*P < 0.05,

^**P < 0.005.

^aCorrelations between mean O allele frequencies in S and L treatments.

^bMarkers that responded significantly to selection in the direction opposite to that expected were removed from the analysis (see text for explanation).

^cCorrelations between mean O allele frequencies in the L treatments and the number of statistically significant bootstrap maxima in Forbes et al. (2004). See the text for additional details about the calculation of the correlations.

^dCorrelations between mean O allele frequencies in the S treatments and the number of statistically significant bootstrap maxima in Forbes et al. (2004). See the text for additional details about the calculation of the correlations.

Comparison with QTL mapping results:

L populations:

Every life-span QTL identified by Forbes et al. (2004) could be associated with a significant marker response to L selection in our experiments, although not necessarily in the same cross(es) (Table 2). qtl4 of Forbes et al. provides one example of good correspondence between experiments. They detected qtl4 in all three crosses and placed it between map positions 59 and 73 on chromosome 2. We observed significant selection responses for markers at map positions 60 and 71 in all three crosses in our experiments. Given that a large fraction of the D. melanogaster genome is covered by the 10 QTL identified by Forbes et al. and that about half of our markers responded to L selection, substantial agreement between experiments might be expected by chance alone. However, markers that showed significant L selection responses were more likely to be located within a QTL region identified by Forbes et al. than markers that did not show a significant selection response. Considering all three crosses and all three chromosomes, there were 34 significant responses, of which 28 (82.4%) were for markers within QTL regions. On the other hand, there were 30 nonsignificant responses, of which 17 (56.7%) were for markers within QTL regions (P = 0.031, two-tailed Fisher's exact test). Considering just chromosomes 2 and 3, there were 28 significant marker responses, of which 26 (92.9%) were associated with QTL regions, and 20 nonsignificant responses, of which only 11 (55.0%) were associated with QTL regions (P = 0.004, two-tailed Fisher's exact test). When we tested results from two or three crosses in a combined analysis, significant L selection responses were seen for four consecutive markers between map positions 54.2 and 81 on chromosome 2 and for markers at positions 48.5 and 80.8 on chromosome 3 (Table 3). Those markers fall within the regions associated with qtl3, qtl4, qtl5, qtl9, and very nearly qtl8 and qtl10 of Forbes et al. (2004)(Table 3).

When we calculated correlations between marker allele frequencies in the L populations and the number of LR peaks from the bootstrapped QTL analysis (Forbes et al. 2004) some interesting patterns emerged (Table 4). For chromosome 2 combined over all three crosses and in cross 3 by itself, there was a significant positive correlation between the O marker allele frequency and the number of bootstrap peaks. These results suggest not only good correspondence between the life-span QTL (as detected in the recombination mapping experiments) and the selection responses in the L treatment, but also good correspondence within each cross. For chromosome 3, the correlation between marker allele frequencies and number of bootstrap peaks was low (Table 4). Finally, for the X chromosome, the correlation was significantly negative. Given that only one X-linked QTL was detected by Forbes et al.—and that in just one of six analyses and with additive effects opposite to those expected—it is not clear how to interpret this negative correlation. The overall picture, then, excepting the X chromosome, is of substantial agreement between the results of our L selection experiments and the QTL mapping results of Forbes et al.

S populations:

Every QTL of Forbes et al. (2004) could be associated with at least one significant marker response to S selection (Table 2). For chromosome 2, the correspondence between experiments was quite good at the level of individual crosses. In 11 cases we could compare the results between experiments (four chromosome 2 QTL by three crosses, less one case in which there was no marker locus within the QTL region in the selection experiment). Of those 11 cases, 9 agreed between experiments (P = 0.08, two-tailed Fisher's exact test). For example, a life-span QTL detected in a particular cross in the mapping experiment was associated with a significant S-selection response in the same cross. This result suggests not only good correspondence between the two sets of experiments for chromosome 2 loci, but also consistency with the idea of negative genetic correlations between late- and early-life fitness effects for chromosome 2 loci, in agreement with our joint analysis of L and S selection responses.

In contrast to the L selection response, there was no overall tendency for markers that were located within the confidence intervals for the QTL of Forbes et al. to respond to S selection when compared to markers that were not within the QTL confidence intervals. For example, considering all chromosomes and all crosses, 25 of 47 tests for markers located within life-span QTL regions responded significantly to S selection, whereas the comparable ratio for markers located outside life-span QTL was 10/20. These results are not surprising and suggest that at least some of the marker response to S selection was due to linkage only with loci that influenced early-life fitness and that did not have pleiotropic effects on life span. On the other hand, if we again restrict the analysis just to chromosome 2, 13 of 20 markers located within life-span QTL regions responded significantly to S selection, whereas only 2 of 8 markers located outside of QTL regions responded to S selection. Although this result is not significant (P = 0.096, Fisher's exact test), it is again suggestive of negative genetic correlations between late- and early-life fitness effects for at least some chromosome 2 genes.

Correlations between O marker allele frequencies in the S populations and the number of significant bootstrap maxima in the QTL mapping experiment are shown in Table 4. For chromosome 2, the correlations were consistently negative and significantly so for cross 2 and for all crosses combined. The negative sign of the correlations indicates that the frequency of the O marker alleles (derived from the long-lived ancestral populations) decreased in the S populations in regions of life-span QTL. It is good evidence for negative genetic correlations between late- and early-life fitness effects. The correlations for the other two chromosomes were not significant (Table 4).

DISCUSSION

Identification of life-span QTL regions:

These experiments demonstrate the utility of using selection experiments to identify chromosome regions that contain genes affecting late- and early-life fitness in D. melanogaster. The precision with which the number and location of fitness QTL were determined by this method is, however, relatively low. Greater precision would be possible with a denser marker map and additional generations of recombination before starting selection. Our greatest confidence about the location of life-span QTL regions comes from L selection responses that were consistent over more than one cross. Those regions were between recombination map positions 54 and 81 on chromosome 2 and near locations 48.5 and 81 on chromosome 3 (Table 3). Those regions correspond reasonably well to qtl3, qtl4, qtl8, qtl9, and qtl10 of Forbes et al. (2004) (Table 2). Other significant L selection responses should not be ignored, particularly when there is corroborating evidence from the recombination mapping experiments, as was the case most of the time (Table 2). On the basis of all the evidence from these selection experiments and the companion mapping experiments (Forbes et al. 2004), the most promising regions for future fine-scale mapping of life-span QTL appear to be between map positions 59 and 73 on chromosome 2 and between positions 38 and 62 and 71 and 80 on chromosome 3. Other very promising regions are between positions 45 and 59 on chromosome 2 and between 0 and 30 on chromosome 3. The regions between 45 and 59 on chromosome 2 and between 38 and 47 on chromosome 3 have strong support when results from other laboratories are also considered (Nuzhdin et al. 1997; Leips and Mackay 2000; Pasyukova et al. 2000; Vieira et al. 2000; Curtsinger and Khazaeli 2002; Luckinbill and Golenberg 2002; De Luca et al. 2003).

One confounding factor that affects interpretation of the L selection response is that the L selection procedure favored late-life fitness in general. Excepting long-term sperm storage by females, this was necessarily selection for longer life span in both sexes. However, other late life fitness components were certainly selected for, including late-life fertility. The genetic correlation between life span and later-life fecundity in females is often strongly positive (Service 2000), suggesting that much of the observed marker response to L selection was probably associated with loci that affect life span. Also, broad agreement between the L selection experiments and the longevity QTL mapping experiments (Forbes et al. 2004), as described above, argues that the marker selection responses in large part reflect association with life-span loci.

Life history trade-offs:

One important outcome of these selection experiments is that they provide clear evidence of life history trade-offs in the form of negative genetic correlations between late- and early-life fitness components. Antagonistic responses to selection for late- and early-life fitness (LS selection responses, Table 2) accounted for 38% of all significant marker responses to selection, and that proportion might increase with continued selection. In analyses that combined the results for all three crosses, antagonistic selection responses were observed for a pair of relatively closely linked markers on chromosome 2 and for two widely separated markers on chromosome 3 (Table 3). When all the markers on a chromosome were considered together, there was a significant negative allele frequency correlation between the L and S selection regimes for chromosome 2 markers in cross 2 (Table 4). Finally, for chromosome 2 over all three crosses, there was a significant negative correlation between the O marker allele frequency under S selection and the number of bootstrap maxima that supported a life-span QTL (Table 4). Another line of evidence for negative genetic correlations, in this case between longevity per se and early-life fitness, comes from the phenotypic responses to S selection. For cross 1, in which we measured the life span of the F₂ generation as well, the evidence suggests that the S selection regime resulted in a decrease in life span (Table 1). It is difficult to imagine that selection directly favored shorter life span. Rather, it is likely that the decrease in life span in the S populations was the result of a negative genetic correlation between life span and some component of early-life fitness that was favored under S selection.

These experiments do not allow us to distinguish clearly between antagonistic pleiotropy and linkage as causes of the negative genetic correlations between late- and early-life fitness that are revealed by the LS selection responses. However, some of our results are suggestive. We observed an excess of LS responses for chromosome 2 markers. That result is consistent with antagonistic pleiotropic effects of at least some fitness loci on chromosome 2. On the other hand, two other experiments have failed to provide extensive evidence for antagonistic pleiotropic effects of life-span QTL (Wayne et al. 2001; Curtsinger and Khazaeli 2002). One possibility to consider is that experiments of this sort may be biased toward finding antagonistic pleiotropy. The only QTL that we could detect were those for which the parental lines were fixed for alternative alleles. In the current context, that is most likely to be the case if the alleles have opposing fitness effects in the selection regimes used to produce the source B and O outbred populations (i.e., antagonistic pleiotropy). In the absence of such effects, detecting a QTL that increased late-life fitness under L selection, for example, would have required that the B inbred parental line have been fortuitously fixed for a QTL allele that was disadvantageous under L selection. Complementary fortuitous fixation at two linked QTL, one that responded to L selection and the other to S selection, could have produced negative genetic correlations by linkage disequilibrium. That, however, seems less likely than pleiotropy because it involves two chance events. Ultimately, differentiating between antagonistic pleiotropy and linkage would seem to require identifying the actual loci that affect life span, for example, and then demonstrating the pleiotropic effects, if any, of those loci.

Conclusions:

Our experiments suggest an explanation for conflicting experimental results regarding life history trade-offs in D. melanogaster. If our results give an accurate picture, they indicate that only a fraction of the loci that affect late- and early-life fitness are associated with negative genetic correlations. In a selection context, the antagonistic effects of such loci may be revealed. However, in a typical quantitative genetic analysis, such as a half-sib design, such negative correlations might be difficult to detect because the experiments reveal only the net effects of all loci affecting pairs of traits. Our data also suggest a reason for the sometimes conflicting results of apparently similar selection experiments. If only some fitness loci give rise to negative genetic correlations between late- and early-life fitness, then the different genetic stocks used for selection experiments might produce different results.

We believe that there is now a substantial body of experimental data upon which to base future studies of the genetics of life-span variation in D. melanogaster. These data include results from three independent sources of flies: (1) the pair of parental inbred lines used by the Mackay laboratory (Nuzhdin et al. 1997; Leips and Mackay 2000; Pasyukova et al. 2000; Vieira et al. 2000; Wayne et al. 2001; De Luca et al. 2003), (2) the inbred lines or their source laboratory populations used by the Luckinbill and Curtsinger laboratories (Curtsinger and Khazaeli 2002; Luckinbill and Golenberg 2002), and (3) the stocks used by us and by Forbes et al. (2004). The techniques used to identify life-span QTL include recombination mapping, deficiency complementation mapping, and, in this study, selection. Although most, if not all, studies identify some unique life-span QTL, there is also substantial agreement and overlap among QTL regions detected by the three laboratories. There appears to be a consensus that important life-span QTL are located in the centromeric region of chromosome 2 and on the left arm of chromosome 3. These should be productive areas for future investigations.