Estimating the Degree of Saturation in Mutant Screens

Abstract

Large-scale screens for loss-of-function mutants have played a significant role in recent advances in developmental biology and other fields. In such mutant screens, it is desirable to estimate the degree of “saturation” of the screen (i.e., what fraction of the possible target genes has been identified). We applied Bayesian and maximum-likelihood methods for estimating the number of loci remaining undetected in large-scale screens and produced credibility intervals to assess the uncertainty of these estimates. Since different loci may mutate to alleles with detectable phenotypes at different rates, we also incorporated variation in the degree of mutability among genes, using either gamma-distributed mutation rates or multiple discrete mutation rate classes. We examined eight published data sets from large-scale mutant screens and found that credibility intervals are much broader than implied by previous assumptions about the degree of saturation of screens. The likelihood methods presented here are a significantly better fit to data from published experiments than estimates based on the Poisson distribution, which implicitly assumes a single mutation rate for all loci. The results are reasonably robust to different models of variation in the mutability of genes. We tested our methods against mutant allele data from a region of the Drosophila melanogaster genome for which there is an independent genomics-based estimate of the number of undetected loci and found that the number of such loci falls within the predicted credibility interval for our models. The methods we have developed may also be useful for estimating the degree of saturation in other types of genetic screens in addition to classical screens for simple loss-of-function mutants, including genetic modifier screens and screens for protein-protein interactions using the yeast two-hybrid method.

ONE of the more useful pieces of information for determining the function of a gene and its encoded product is the loss-of-function mutant phenotype. The ground-breaking work of Nüsslein-Volhard and colleagues on Drosophila embryonic development (Nüsslein-Volhard and Wieschaus 1980; Jürgens et al. 1984; Nüsslein-Volhard et al. 1984; Wieschaus et al. 1984) was predicated on obtaining as complete a catalog as possible of the genes involved in the process of interest. Large-scale screening identified mutant lines with defects in embryogenesis, and these mutants were classified by morphological phenotype. Mutants with similar phenotypes were then tested for allelism. If this process is continued to saturation, then essentially all genetically detectable functions involved in a process should be identified.

This approach has the advantage of not depending on models or preconceptions about how the biological process of interest works. In many cases, classes of genes with similar loss-of-function phenotypes have been identified, defining specific developmental pathways that had not been previously anticipated. For example, the discovery of the segment polarity, pair-rule, and gap classes of mutants affecting Drosophila embryogenesis led to major advances in our understanding of metazoan development (Wilkins 1992). Similar intensive mutant screens have been carried out in a number of other organisms for a variety of pathways (Mayer et al. 1991; Haffter et al. 1996). This strategy of saturation mutagenesis has been central to the renaissance of developmental biology during the past two decades (Wilkins 1992, p. 13).

An important issue that arises in any saturation mutagenesis screen is the degree to which saturation has been achieved. Many attempts to estimate the fraction of loci missed in a mutant screen have started from the assumptions underlying the Poisson distribution. In this approach, the mean number of observed alleles per locus is used as an estimate of the rate parameter, λ, for a Poisson distribution, from which the zero-allele class (i.e., the fraction of loci remaining undetected) is calculated. Confidence intervals have not typically been calculated, in which case the accuracy of such estimates is difficult to assess. In some instances, new loci have later been detected beyond what was predicted by the apparent degree of saturation in the original screen. Many investigators have noted that the observed distribution of allele frequencies is a poor fit to a Poisson distribution, rendering such estimates suspect (Barrett 1980; Jürgens et al. 1984; Nüsslein-Volhard et al. 1984; Wieschaus et al. 1984; Haffter et al. 1996). The observed deviation from a Poisson distribution often takes the form of a large excess of loci represented by single alleles.

The Poisson approach to determining the degree of saturation assumes a single probability of recovering mutants that is constant across all genes. This assumption is unlikely to be true for real genes, and failure of this assumption may be a significant factor in underestimating the number of undiscovered genes. Mutations will not be recovered with equal frequency at all loci if, for example, differences in gene size or accessibility of chromatin to mutagens create different-sized target regions for mutations. Other factors that may affect observed mutation rates include differential stability of protein structural domains in response to amino acid substitutions (Nüsslein-Volhard and Wieschaus 1980) and rare phenotypes due to unusual alleles (hypermorphs, neomorphs, antimorphs, etc.). Haffter et al. (1996) pointed out that some genes may be underrepresented because the phenotypes produced by mutations in these genes are especially difficult to detect, leading to observer bias in the relative rates of discovery of new alleles.

In addition to developmental geneticists and other geneticists interested in functional problems, a second group of researchers has been interested in the problem of saturation mutagenesis. Throughout the 20th century, researchers attempted to estimate the total number of genes in Drosophila melanogaster from the degree of saturation in mutant screens (Judd et al. 1972; Hilliker et al. 1980). Because the degree of saturation was crucial to estimating gene number, substantial effort was applied to estimating this parameter. The inadequacy of the Poisson model was clearly recognized by these researchers (Barrett 1980; Lefevre and Watkins 1986). Also, Lefevre and Watkins (1986) showed that the gamma distribution, a two-parameter distribution that does not assume equimutability, gives a significantly better fit to mutagenesis data than does the Poisson, but they did not provide credibility or confidence intervals for their estimates. Although work on the gene number problem reached its apogee in the 1970s and early 1980s, the completion of the D. melanogaster genome sequence allows the results of these studies to be compared to more direct sequence-based estimates of gene number (Adams et al. 2000).

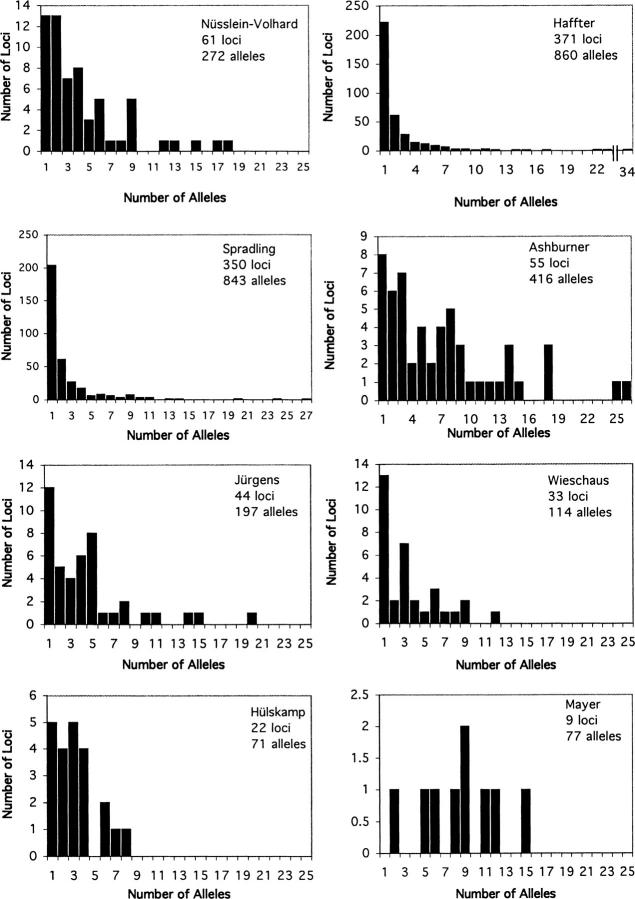
To determine the most appropriate statistical model for assessing saturation in mutagenesis screens, we analyzed data (Figure 1) from six published saturation mutagenesis studies drawn from the developmental genetics literature (Jürgens et al. 1984; Nüsslein-Volhard et al. 1984; Wieschaus et al. 1984; Mayer et al. 1991; Hülskamp et al. 1994; Haffter et al. 1996), from one study that identified P-element insertions in essential genes of D. melanogaster (Spradling et al. 1999), and from one study of phenotypically detectable mutations around the D. melanogaster Adh locus (Ashburner et al. 1999). We compared a Poisson substitution (single-mutation rate) model with a discrete multiple-mutation-rate class (mixture) model and a model with mutation rates continuously distributed as a gamma distribution. For the multiple-rate class model, we considered discrete numbers of rate classes both with and without flexible frequency parameters. The gamma distribution allowed us to account for a continuous range of mutabilities among genes, since the gamma distribution is flexible and allows for a wide range of mutation probabilities at different genes. We performed both maximum-likelihood (ML) and posterior probability (Bayesian) analyses to estimate model parameters and provide credibility intervals for the number of loci remaining undetected in large-scale screens. Support for different models was evaluated on the basis of the relative fit of the data under different models, considering both the classic nested-model analysis approach and the conceptually different and perhaps more logically consistent information-based approach (Adams et al. 2000). For readers interested in a detailed description of the statistical analysis, it is found in materials and methods; for those less interested in those details, we recommend skipping to results, where we reiterate the major conceptual points of the methods.

Figure 1.—

Distributions of number of loci with number of detection events (“alleles”) per locus. As with tables, the eight main data sets are identified by the first author of the study.

We find that the gamma-distributed mutation rate model generally gives a much better fit than the Poisson, but that for some data sets a multiple-rate class (mixture) model is equivalent to or preferred over the gamma model. The 95% credible intervals for estimates of the number of undiscovered loci are large under all models with variable rates, indicating that even in very large screens estimates of the degree of saturation are quite imprecise. In addition, we tested our models against a genomics-based estimate of the number of unmutated loci in a region of D. melanogaster chromosome arm 2L that is independent of the degree of allele saturation (Ashburner et al. 1999) and show that our estimate of the number of unidentified loci is in reasonably good agreement. The implications of these results for current genome-wide mutation studies and other types of mutant screens are discussed.

MATERIALS AND METHODS

Mutation frequencies in saturation mutagenesis experiments analyzed (Figure 1) were taken from studies on ethyl methanesulfonate (EMS)-induced zygotic mutations affecting the pattern of larval cuticle in D. melanogaster located on the second chromosome (Nüsslein-Volhard et al. 1984, data taken from their Table 3), chromosome 3 (Jürgens et al. 1984, data taken from their Table 2), and the X and fourth chromosomes (Wieschaus et al. 1984, data taken from their Table 3); a screen for ethylnitrosourea (ENU)-induced mutations involved in the development of Danio rerio (Haffter et al. 1996, data taken from their Table 4); a screen for EMS-induced mutants affecting trichome development of Arabidopsis thaliana (Hülskamp et al. 1994, data taken from their Table 1); a screen for EMS-induced embryo development mutants of A. thaliana (Mayer et al. 1991, data taken from their Table 1); a compilation of EMS-induced alleles in the Adh region of D. melanogaster chromosome arm 2L (Ashburner et al. 1999, data taken from their Table 1); and a large-scale screen to disrupt genes in D. melanogaster with P-element insertions (Spradling et al. 1999, data on confirmed mutations located within deficiencies on chromosome 2 taken from their Table 4). The data from Hülskamp et al. (1994) have been modified to take into account the demonstration that one of the kaktus alleles described in the study was later shown to be an allele of another locus, noek (Folkers et al. 1997). The Haffter et al. (1996) data set has one outlying locus with 34 alleles, and this locus was not included in the analyses to avoid biasing results, because the Poisson estimate is particularly sensitive to such outliers.

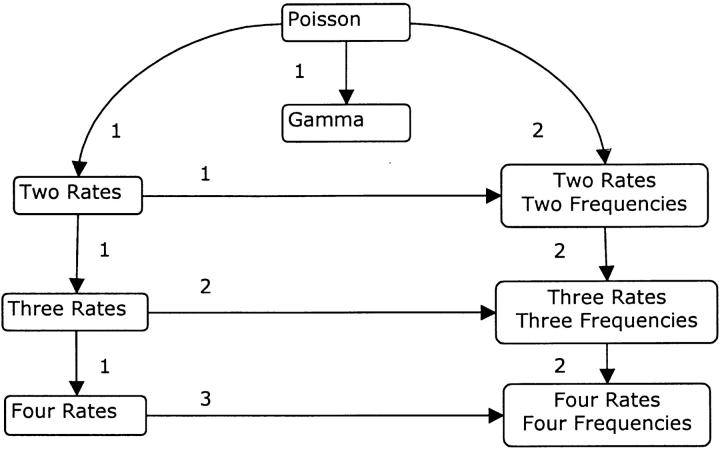
Poisson, multiple rates, and gamma distribution-based predictions for saturation mutagenesis experimental outcomes were obtained by maximizing the likelihood of model parameters. These include a rate parameter (λ) for the Poisson model, multiple rate parameters and sometimes frequency parameters for the multiple-rates model, and a scale (β) and shape parameter (α) for the gamma model. Likelihood, L, was calculated as the probability of the data, D, given a model, M, and its parameters, θ; that is, L = P(D|M, θ). Relative support for nested models was evaluated by comparing the difference in their log likelihoods; e.g., Δ ln L = ln [P(D|Gamma, α_MLE, β_MLE)] − ln [P(D|Poisson, λ_MLE)]. These comparisons are made using the maximum-likelihood values, and thus the parameter values used are the maximum-likelihood estimators (MLEs), the parameter values that have the highest probability of producing the observed data. Significance was determined by assuming that 2Δ ln L is distributed as χ²_v, the chi-square distribution, where v is the number of degrees of freedom, equal to the difference in free parameters between the models (Rice 1995). The nesting relationship of the models (Figure 2) allows for multiple comparisons between models, although the relationship between the gamma and the mixture models bears some explanation. The gamma model is not strictly nested within the mixture models, but in many situations the continuous gamma function can be well approximated with as few as four discrete rate categories (Yang 1993, 1994). Since the four-rate-class mixture model parameters could be adjusted to be exactly equal to such an approximation, a discrete gamma would be formally nested. Although the difference in likelihoods calculated using a continuous gamma or a discrete approximation will be small, the nested assumption and use of the chi-square distribution for probability estimation will lead to a slight bias toward not rejecting the gamma model. There is further concern in the opposite direction, though, in that mixture models can sometimes appear over-specified (McLachlan and Peel 2000), leading to a greater tendency to inappropriately accept them. An alternative approach to evaluating alternative models is Akaike's information-based approach (Akaike 1973; Burnham and Anderson 2002). With this approach, all models are viewed as being approximations to some unknown but presumably complicated true mechanism, and the best model is the one with minimal distance to the true mechanism, after correction for bias introduced by the number of parameters. The issue of nesting is not relevant to this philosophy, and we can view the model comparisons in this study as exploratory research to help guide future interpretation. We thus consider the Akaike information criterion (AIC), corrected for small data sets,

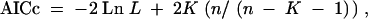1

where K is the number of parameters, and n is the number of loci. For easier interpretation, we present ΔAICc = AIC − AIC_min, where the minimum is among all alternative models for a data set. To better interpret the relative likelihood of different models we normalize the likelihoods to be a set of positive “Akaike weights” (Akaike 1978; Burnham and Anderson 2002), 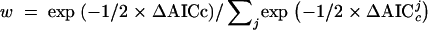, where the sum is over the AICc for all alternative models.

Figure 2.—

Relationships among models. Arrows are drawn pointing from simpler models to more complex models of which they are nested subsets. Numbers adjacent to arrows indicate the degrees of freedom separating the models. The models with higher numbers of rate classes become equal to the next lower number of rate-class models when two rate classes within them become equal. Variable-frequency rate-class models become equal to constant-frequency rate-class models when all frequencies equal 1/k, where k is the number of classes. The gamma model is equivalent to the Poisson model when α = ∞. Although the gamma model is not technically “nested” within the multiple-rate-class models, discrete approximations of the gamma model with the same number of rate categories would be nested.

For a particular model and a particular set of parameters, θ, the likelihood of observing the data obtained in the experiment was calculated as the multiplicative sum over the probabilities for each allele frequency, or

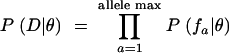2

For the Poisson model, 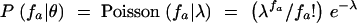, and these probabilities were obtained iteratively in the standard fashion, with

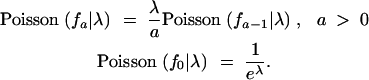3

For the multiple-rates model, the parameters are the rates for each of the k rate classes, λ₀, λ₁, … λ_k, and the frequencies each rate class, w₀, w₁, … w_k (variable frequencies model). The individual λ parameters for each rate class are Poisson rate parameters for loci in each class. To reduce the number of parameters, a simplified multiple-rate class model was also used in which the frequency of each rate class is fixed at 1/k. The number of rate classes, k, ranged from one (the Poisson model) to four.

The gamma distribution was also used to model the underlying mutabilities of different genes. Although the outcomes of the data (the observed allele counts, x) could also be modeled as a gamma distribution, this would not have any particular biological meaning; instead, if the underlying mutabilities are gamma distributed (gamma [α, β]), then the outcomes are distributed as a truncated negative binomial distribution (Lefevre and Watkins 1986; Bradlow et al. 2002), where the negative binomial distribution (NB) is given by

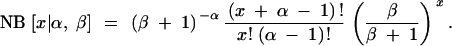4

Probabilities were obtained iteratively by noting that NB[1|α, β] = β(β + 1)^−(α+1)α, and NB[x + 1|α, β] = NB[x|α, β][(x + α)/(x + 1)][β/(β + 1)] (Lefevre and Watkins 1986). Truncated distributions for both Poisson and gamma distributions were obtained by dividing each probability estimate by 1 − Pr[0] to give the probability conditional on at least one mutant allele being recovered for each gene detected (that is, given that zero counts were not observed). We note that an accurate closed-form approximation of the posterior for NB distributions, written as a sum of polynomial terms, has recently been described and could lead to improvements in the speed of calculations (Bradlow et al. 2002). The calculations are already very brief on modern computers, however, so the effort to produce such analytic results was not expended.

A pragmatic and agnostic view of contrasting Bayesian and frequentist perspectives was taken, and so means for posterior probability distributions were also estimated, and 95% credible intervals for parameters inferred as the region excluding the 2.5% highest and 2.5% lowest values in the posterior distribution were estimated. The posterior probability distributions were estimated using a single-component Metropolis-Hastings implementation of Markov chain Monte Carlo (MCMC) methodology (Metropolis et al. 1953; Hastings 1970), where moves in the chain of parameter values X_t were proposed according to a proposal function q(X) and accepted according to probability

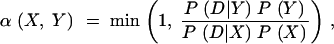5

where Y is the proposed set of parameter values for X_t+1, and P(D|X) is given by Equation 1. The relative priors, P(X), were uniformly 1.0 so that the posterior was equivalent to the likelihood function. Maximum parameter values were set at an arbitrarily large number (1000.0), but this maximum was never reached in the Markov chains (the minimum α value was set at 0.01, since smaller values lead to unreasonable expectations of ∼1.0 for the zero class). The proposal distribution for moves in the chain, q(X), was distributed as a uniform random variable from X_t − d to X_t + d, where X_t is the current value of the parameter being updated while other parameters remain unchanged, and d is constant. Negative proposal values were made positive. On the basis of preliminary runs, the constant, d, was usually set to a value of 0.1 for α, 0.5 for β and λ_k, and 0.05 for w_k. Run times and chain convergence were fast enough that a more sophisticated proposal distribution algorithm was unnecessary.

Chains were run for 100,000 iterations, and samples taken every 100 iterations. Means and credible intervals were calculated after removing the first m samples, where the burn-in time, m, was determined by visual evaluation of posterior values along with all parameter values to ensure that they had reached a consistent equilibrium. Generally, m was no larger than 4. The 95% credibility intervals for each parameter were calculated using upper and lower quantiles of the parameter. In addition to the parameters, we evaluated the statistic f₀, the probable frequency of genes that affect the trait having no observed mutations in the experiment. Maximum-likelihood values were determined from the most likely set of parameter values observed in the Markov chain.

RESULTS

The models:

Three different types of mutation-rate models were compared for each data set: a Poisson mutation model, a family of models that assume two or more discrete mutation rates, and a model assuming that mutation rates are gamma distributed. The Poisson model assumes that all genes have the same mutation rate and thus has only the single rate parameter, λ, that must be estimated. It should be noted that the observed mean number of alleles per locus resulting from the screen is not a valid estimate of λ, because it does not take the undetected loci into account in estimating the rate. This difficulty in estimating λ has occasionally been overlooked, although solutions are well known. The ML approach outlined here provides one way of estimating λ; alternatively, a standard correction can be applied (Barrett 1980).

The Poisson assumption of a single mutation rate is an obvious oversimplification, and it has been widely recognized that the number of alleles per locus rarely follows a Poisson distribution (Barrett 1980; Jürgens et al. 1984; Nüsslein-Volhard et al. 1984; Wieschaus et al. 1984; Haffter et al. 1996). This motivates our consideration of more complex mixture and gamma models. For the mixture models, each locus was still assumed to mutate randomly as described by a Poisson distribution, but there were k rate classes (where k = 2, 3, or 4) each with a separate λ rate parameter that estimates the mutability of the loci. Two types of multiple-rate models were considered for each value of k. The first was a model in which the frequency of loci in each rate class is fixed at ¹/_k. This allowed a minimal number of parameters to be estimated and thus had fewer degrees of freedom. These models are abbreviated as 2C, 3C, and 4C, depending on the number of rate classes (C). In the more flexible type of multiple-rate models, the frequencies of loci in each rate class (w) were also allowed to vary at the cost of an extra parameter (degree of freedom) per rate class. This latter approach is consistent with the idea that while the majority of mutations may be recovered at a single rate, there may be a few low-frequency “hot spots” of mutation and recovery with exceptionally high rates. These models are abbreviated as 2CVF, 3CVF, and 4CVF to stand for, e.g., two-rate class, variable frequency.

The gamma-distributed rates model also allows for rate variability, but unlike the mixture model, the rates are distributed nearly continuously rather than in only a few discrete categories. This model incorporates more flexibility and a certain amount of biological plausibility, in that the factors influencing mutation rate and mutant detection for each individual locus probably vary more widely than can be captured by the limited number of mutation rate classes that are tractable in the multiple-rate models. There is no intrinsic reason to assume that the mutation rates are limited to only a few discrete mutation rate classes. It is important to note that, as with the mixture models, the individual loci are still assumed to mutate via a random Poisson process; it is the mutation rates of the individual loci that are gamma distributed. The gamma distribution has two variable parameters to be estimated. The first of these, α, controls the shape of the distribution, and the second is the scale parameter, β, which does not affect the shape but rather the units of measurement. The gamma distribution makes relatively few assumptions about the way in which mutation rates are distributed, and depending on the value of α, it encompasses a wide variety of plausible mutation rate distributions. When α = 1, a gamma distribution of rates is identical to an exponential distribution of rates, and when α ≫ 1, the gamma distribution can give a reasonable approximation to a normal distribution of rates. As α approaches ∞, the gamma distribution approaches a normal distribution with infinitely small variance, thus converging on the Poisson single-rate model.

We compared models in two ways. The first method, nested model analysis, compares twice the difference in the natural log of maximum likelihoods between nested models, and probability values are based on the assumption that these values are distributed as chi-square under the null (nested) model. These probability values should not be overinterpreted, however, since there is no assurance that the chi-square assumption is correct, and there is in fact strong indication that it may be unwarranted in some of our comparisons (McLachlan and Peel 2000). They are included mostly for comparative purposes and because some readers may be more familiar with this approach. It is possible to obtain more accurate probability values using parametric bootstrapping (e.g., Pollock et al. 1999), but with the complex network of nesting relationships among models used in this study (Figure 2), it is not clear that a meaningful result will be obtained. Furthermore, the variation in credible intervals within the more complex models is much greater than the variation between models, making further simulation analysis of low value. The second method, the Akaike information criterion approach with Akaike weights, provides a satisfying alternative viewpoint that allows a joint interpretation of multiple models with nested and nonnested relationships (Burnham and Anderson 2002).

Application of models to analysis of the data of Nüsslein-Volhard et al. (1984):

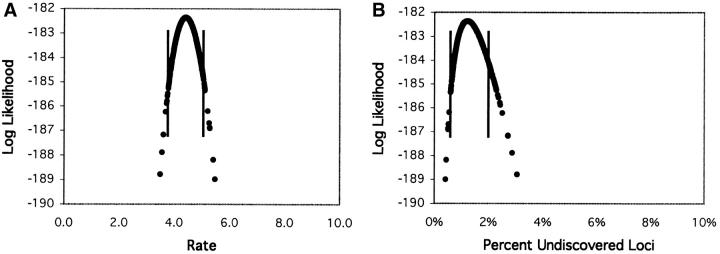
Perhaps the most well-known example of a saturation screen in the developmental literature is the screen for developmental patterning mutants on the second chromosome of D. melanogaster conducted by Nüsslein-Volhard and colleagues (Nüsslein-Volhard et al. 1984). Our analysis of this data set serves as an example of the application of the various models. For the Poisson model, the ML and Bayesian estimates of λ are both ∼4.4 alleles per locus (Table 1). These estimates were obtained using a MCMC strategy in which a chain randomly wandered the posterior probability space (in this case, equivalent to the likelihood surface). For this simple one-parameter model, the result is a simple curve (Figure 3), where the ML estimate is the maximum of the probability distribution, and the Bayesian estimate is the mean of the points in the distribution. Since points were sampled according to their posterior probability, the 95% credible interval is the interval that contains 95% of the points or, alternatively, the interval that excludes the smallest and largest 2.5% of points (Figure 3, vertical lines). For any value of λ the number of loci remaining undiscovered in the screen can be directly calculated, and thus ML, Bayesian, and C.I.'s for this statistic can also be evaluated. The fraction of undiscovered loci predicted under the Poisson model is ∼1%, with a range of 0.72–1.81% falling within the 95% credible interval (Figure 3B; Table 1, percentage undiscovered loci). Thus, the Poisson model suggests that most of the loci detectable in this screen have already been found.

TABLE 1.

Maximum-likelihood, Bayesian average, and Bayesian 95% C.I.'s for the Nüsslein-Volhard data set under the Poisson, gamma, and mixture models

			Estimate
Author	Model	Parameter	Maximum likelihood	Bayesian average	95% credible interval [lower, upper]
C. Nüsslein-Volhard	Poisson	Rate (λ)	4.40	4.47	[3.82, 4.86]
(Drosophila, 61 loci, 272 alleles)	Zero class	1.22%	1.14%	[0.72%, 1.81%]
Gamma	Shape (α)	0.91	0.88	[0.34, 1.77]
Scale (β)	3.72	3.88	[1.72, 7.05]
Rate (λ)	3.36	3.43	[1.80, 4.73]
Zero class	24.6%	23.0%	[9.60%, 41.8%]
2C	Rate 1 (λ1)	1.88	1.98	[1.12, 2.74]
Rate 2 (λ2)	8.26	8.22	[5.79, 11.83]
Zero class	7.64%	6.94%	[2.64%, 15.7%]
2CVF	Rate 1 (λ1)	2.48	2.50	[1.69, 3.28]
Freq 1	0.77	0.73	[0.52, 0.87]
Rate 2 (λ2)	10.39	10.54	[5.90, 13.04]
Zero class	6.49%	5.93%	[1.68%, 11.8%]
3C	Rate 1 (λ1)	1.48	1.50	[0.23, 2.98]
Rate 2 (λ2)	3.21	3.47	[1.93, 4.88]
Rate 3 (λ3)	9.81	10.44	6.08, 14.19]
Zero class	8.93%	8.60%	[2.15%, 23.9%]
3CVF	Rate 1 (λ1)	1.81	1.56	[0.10, 2.71]
Freq 1	0.62	0.25	[0.01, 0.70]
Rate 2 (λ2)	6.28	3.27	[1.88, 5.09]
Freq 2	0.31	0.35	[0.01, 0.78]
Rate 3 (λ3)	14.17	10.18	[5.17, 13.92]
Freq 3	0.08	0.35	[0.05, 0.51]
		Zero class	10.1%	7.22%	[2.61%, 18.3%]

Figure 3.—

Log-likelihood (natural log; ln L) values for sampled points in the Markov chain Monte Carlo simulation for the Nüsslein-Volhard data set under the Poisson model. Distributions are shown for (A) the rate (λ) and (B) the percentage of undiscovered loci (the fraction of all loci predicted to exist that was not detected in the experiment). The data shown are for 100,000 points from a chain sampled every 100 generations, with the first 50 points removed as “burn-in.” The bounds of the 95% credible regions are depicted with vertical lines, and the maximum-likelihood value is at the top of the curve.

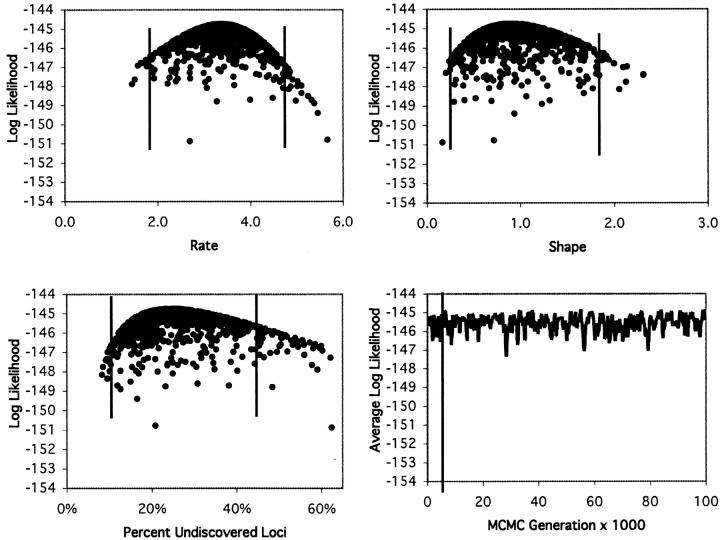
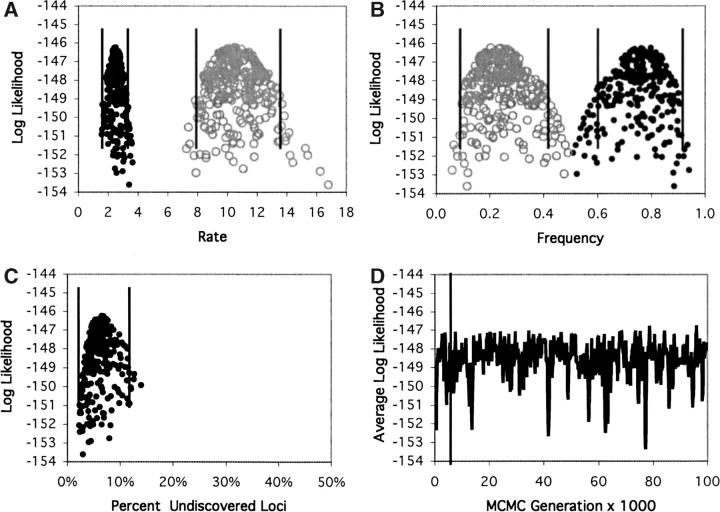
The results from analysis of models with variable mutabilities among loci show clearly that the Poisson assumption is not realistic. As noted by the original investigators, some loci appear to be much more mutable than others (Nüsslein-Volhard et al. 1984), and this is reflected in a difference in log likelihoods (ln L) of ∼37 between the Poisson model and the gamma model, with similar magnitudes of difference between the Poisson and the various mixture models (Table 2). This means that the gamma model is 2 × 10¹⁶ times more likely than the Poisson model (P ≪ 0.001) to explain the data. Since there are two parameters rather than one in the gamma model, the likelihood surface appears as a cloud of points rather than as a line when reduced to a two-dimensional graph (Figure 4). ML, Bayesian, and C.I. estimates were determined in the same way, however, and the percentages of undiscovered loci were calculated from the shape and scale parameters. To aid comparison with the Poisson model, we also estimated the mean rate (λ = α/β), and although the ML and Bayesian estimates (∼3.4) are slightly lower than those of the Poisson model, the 95% C.I. (1.80–4.73) contains the Poisson estimates (Table 1). For this slightly more complex model, we show the change in likelihood values over time to demonstrate that the average value is essentially constant after the initial burn-in phase, which is discarded, and that the different parts of the chain are relatively uncorrelated (Figure 4). Multiple independent runs of the chain confirmed that the chain had converged to equilibrium (data not shown). The most striking difference between the gamma and Poisson analyses is that the Poisson estimate of 1% undiscovered loci is not contained within the 95% C.I. (10–42%) of the gamma estimate (Table 1). Thus, the gamma model estimate suggests that saturation was not achieved in the original study and that up to one-third or more of the loci remain to be discovered. This means that with further mutagenesis, perhaps 50% more loci would be detected beyond those that have already been discovered.

TABLE 2.

Log maximum likelihood, 2Δ lnL, ΔAICc, and weight for all data sets and all models

	Modela (no. of parametersb)
Study	Poisson (1)	Gamma (2)	2C (2)	2CVF (3)	3C (3)	3CVF (5)	4C (4)	4CVF (7)
C. Nüsslein-Volhard
Ln L	−182.36	−144.75	−151.12	−146.18	−146.79	−143.97	−145.30	−143.93
2Δ ln L	76.86	1.63	14.37	4.49	5.72	0.07	2.74	0.00
ΔAICc	73.13	0.00	12.67	4.82	6.05	4.47	5.11	8.47
Weight	0.000	0.747	0.001	0.067	0.036	0.080	0.058	0.011
P. Haffter
Ln L	−772.88	−552.50	−620.40	−567.54	−586.37	−545.25	−572.52	−543.44
2Δ ln L	458.88	18.12	153.91	48.19	85.86	3.62	58.15	0.00
ΔAICc	447.24	8.48	144.27	40.56	78.23	0.00	52.52	0.42
Weight	0.000	0.008	0.000	0.000	0.000	0.548	0.000	0.444
A. C. Spradling
Ln L	−769.67	−536.41	−613.28	−552.08	−576.06	−529.51	−559.65	−524.88
2Δ ln L	489.57	23.05	176.80	54.39	102.35	9.26	69.55	0.00
ΔAICc	477.26	12.76	166.51	46.13	94.10	5.10	63.34	0.00
Weight	0.000	0.002	0.000	0.000	0.000	0.072	0.000	0.926
M. Ashburner
Ln L	−243.78	−162.47	−178.63	−175.68	−166.41	−163.19	−165.49	−161.40
2Δ ln L	164.77	2.15	34.47	28.58	10.02	3.59	8.19	0.00
ΔAICc	160.58	0.00	32.31	28.46	9.90	7.65	10.11	8.15
Weight	0.000	0.950	0.000	0.000	0.007	0.021	0.006	0.016
G. Jürgens
Ln L	−133.53	−104.55	−113.01	−107.28	−107.68	−102.29	−104.46	−102.37
2Δ ln L	62.46	4.51	21.44	9.98	10.77	0.00	4.34	0.14
ΔAICc	55.83	0.00	16.85	7.45	8.24	1.57	3.86	5.79
Weight	0.000	0.589	0.000	0.014	0.010	0.268	0.086	0.033
E. Wieschaus
Ln L	−81.08	−68.36	−68.40	−68.14	−66.36	−66.31	−66.50	−66.47
2Δ ln L	29.53	4.09	4.18	3.66	0.09	0.00	0.38	0.32
ΔAICc	25.31	2.01	2.02	3.57	0.00	4.12	2.37	8.49
Weight	0.000	0.156	0.155	0.072	0.426	0.054	0.131	0.006
M. Hülskamp
Ln L	−43.59	−42.77	−42.67	−42.66	−42.67	−42.66	−42.68	−42.69
2Δ ln L	1.85	0.21	0.02	0.00	0.02	0.01	0.04	0.06
ΔAICc	0.00	0.48	0.29	2.36	2.49	6.56	4.53	10.78
Weight	0.295	0.231	0.255	0.091	0.085	0.011	0.031	0.001
U. Mayer
Ln L	−25.37	−24.71	−24.69	−24.20	−24.45	−24.20	−24.74	−24.71
2Δ ln L	2.34	1.02	0.99	0.01	0.51	0.00	1.09	1.03
ΔAICc	0.00	0.97	0.96	2.15	2.65	6.58	5.45	12.10
Weight	0.340	0.209	0.210	0.116	0.090	0.013	0.022	0.001

^aThe preferred model (or models) for each data set is in italics, and the difference in log-likelihood values (the log of the likelihood ratio) from the most likely model is given on the subsequent line. Criteria for model choice are discussed in the text.

^bThe number of free parameters in the model.

Figure 4.—

Log-likelihood values for the Nüsslein-Volhard data set as in Figure 3, but for the gamma model. Distributions are shown for the rate and shape parameters and for the percentage of undiscovered loci. Also shown is the average log-likelihood over the course of the chain, with the vertical line representing the (probably unnecessary) burn-in cutoff at the 50th sample.

For the Nüsslein-Volhard et al. (1984) data set, all mixture models except the simplest [two rate classes of equal frequency (2C)] have maximum-log-likelihood values within 3 units of the gamma model (Table 2). The most preferred mixture model (based on Akaike weights; see materials and methods) is the 3CVF model, but the preference is not strong (see below). In Figure 5 we illustrate the analysis for the 2CVF model, in which both the mutation rates and the frequencies of the two rate classes must be estimated. As before, Figure 5D shows that the parameter space has been adequately sampled and likelihood values are no longer increasing. All of the multiple-rate models predict larger numbers of undiscovered loci than are predicted by the Poisson distribution; these predictions are much more similar to the predictions of the gamma-distributed rate model (Table 1). The 2CVF model illustrated in Figure 5 predicts a range of 3–16%, the 3C model predicts a higher range of 2–24%, and the most preferred and parameter-rich 3CVF model predicts a range of 3–18% (Table 1). Thus, while the gamma model is preferred over any of the multiple-rate models, the result with any of these models is essentially the same: perhaps up to 40% more loci remain to be discovered.

Figure 5.—

Log-likelihood values for the Nüsslein-Volhard data set as in Figure 3, but for the two-rate-class model with variable frequencies. Distributions are shown for (A) the rate and (B) frequency parameters, for (C) the percentage of undiscovered loci, and for (D) the likelihood over the course of the chain, as in Figure 4.

The most likely multiple-rate model is the 4CVF model (ln L = −143.93, Table 2), but with 7 d.f. (5 more than the gamma model and 4 more than the 2CVF and 3C models) it is less preferred than the other models. Although, strictly speaking, the gamma model is not nested within the four-rate, variable-frequency model, if one accepts the approximations and considerations discussed in materials and methods, the simpler gamma model would not be rejected because twice the Δ ln L between these models is well within the 95% region of a χ²₅ distribution. Similar arguments hold for the other mixture models. The alternative interpretation using the information criterion also indicates that the gamma model is preferable, since it has the lowest AICc value. The Akaike weights show that the majority of the weight of evidence favors the gamma model, which has a weight of 0.75, while the next closest model (3CVF) has a weight of only 0.08. The Akaike weights could be used to give a weighted estimate (Burnham and Anderson 2002), but it is clear enough that most reasonable models with variable mutabilities give the same result with regard to our concern here: saturation was not achieved.

Application of the models to other published data sets:

We applied the three types of models described above to seven more data sets from published mutant screens. Five of these screens come from the developmental genetics literature (Jürgens et al. 1984; Wieschaus et al. 1984; Mayer et al. 1991; Hülskamp et al. 1994; Haffter et al. 1996), one is concerned with saturation of a region around the D. melanogaster Adh gene for phenotypically detectable mutations (Ashburner et al. 1999), and one is concerned with saturating the D. melanogaster genome with P-element insertions (Spradling et al. 1999). Two of these mutation experiments included much larger numbers of detected loci than the data of Nüsslein-Volhard et al. (1984).

The largest data set that we analyzed is the screen by Haffter et al. (1996) for developmental mutants in the zebra fish D. rerio, which isolated 860 alleles representing 371 loci. For this data set, all six multirate models are substantially more likely than the Poisson to explain the data and have much lower ΔAICc (Table 2). The 3CVF model is the preferred model. It has the lowest AICc and Akaike weight (0.548), is a much better fit to the data than the Poisson model (Table 2; 2Δ ln L = 455.3; P < 0.001), and has a maximum likelihood slightly less than the 4CVF model (2Δ ln L = −3.62), a more complex model that requires two more free parameters than the 3CVF model and is thus not a significant improvement over 3CVF. The 3CVF model is significantly more likely (under the chi-square assumption) than any of its nested multirate models (Table 2; 2Δ ln L = 44.6 relative to the next-best 2CVF model). This interpretation is consistent with the information criterion approach, in which the best model among the multiple-rate class models is 3CVF with a weight of 0.548, followed by 4CVF with a weight of 0.444, while the gamma model has a weight of 0.008. The 3CVF model predicts that ∼45% of the loci have not been detected (ML estimate), with a 95% credible interval ranging from 34 to 53% (Table 3). In comparison, the comparatively unlikely Poisson model predicts that only 13% of the loci have not been detected, with a 95% credible interval ranging from 11 to 15% (Table 3). For this data set (and the next one), although it is not particularly likely, the gamma-distributed rates model predicts that 46–99% of the loci have not been discovered. This is accompanied by exceptionally small shape parameter estimates; in the absence of the zero class and a large number of loci observed only once (Figure 1), likelihoods are maximized by assuming that most loci were not observed. Although in the limit this is not reasonable, and may be modified by adjusting prior expectations (see discussion), it does indicate a finite possibility that the number of loci left to be discovered may be many times more than what was observed.

TABLE 3.

Maximum likelihood, Bayesian average, and Bayesian 95% C.I.'s for other data sets under the Poisson, gamma, and preferred mixture models

			Estimate
Author	Model	Parameter	Maximum likelihood	Bayesian average	95% credible interval [lower, upper]
P. Haffter	Poisson	Rate (λ)	2.01	2.00	[1.85, 2.17]
(Danio, 371 loci, 860 alleles)	Zero class	13.4%	13.5%	[11.4%, 15.4%]
Gamma	Shape (α)	0.01	0.05	[0.01, 0.70]
Scale (β)	3.42	3.13	[1.28, 3.99]
Rate (λ)	0.03	0.16	[0.03, 1.07]
Zero class	98.5%	93.2%	[46.2%, 98.6%]
3CVF	Rate 1 (λ1)	0.52	0.49	[0.00, 0.81]
Freq 1	0.76	0.75	[0.31, 0.82]
Rate 2 (λ2)	4.32	4.25	[0.78, 5.23]
Freq 2	0.21	0.22	[0.14, 0.37]
Rate 3 (λ3)	14.2	14.0	[4.92, 16.9]
Freq 3	0.03	0.04	[0.01, 0.24]
Zero class	45.3%	44.0%	[34.3%, 53.2%]
A. C. Spradling	Poisson	Rate (λ)	2.12	2.13	[1.95, 2.28]
(Drosophila, 350 loci, 843 alleles)	Zero class	12.0%	11.9%	[10.0%, 14.1%]
Gamma	Shape (α)	0.01	0.04	[0.01, 0.21]
Scale (β)	3.69	3.43	[1.71, 4.49]
Rate (λ)	0.04	0.15	[0.03, 0.61]
Zero class	98.5%	93.6%	[49.0%, 98.5%]
3CVF	Rate 1 (λ1)	0.74	0.62	[0.01, 0.89]
Freq 1	0.83	0.76	[0.31, 0.88]
Rate 2 (λ2)	6.41	4.90	[0.57, 7.37]
Freq 2	0.16	0.22	[0.08, 0.51]
Rate 3 (λ3)	23.1	15.3	[4.74, 19.7]
Freq 3	0.01	0.03	[0.00, 0.27]
Zero class	39.5%	39.9%	[32.4%, 48.1%]
M. Ashburner	Poisson	Rate (λ)	7.56	7.60	[6.99, 8.29]
(Drosophila, 55 loci, 416 alleles)	Zero class	0.05%	0.05%	[0.02%, 0.09%]
Gamma	Shape (α)	0.97	0.84	[0.41, 1.59]
Scale (β)	6.74	7.33	[4.22, 12.2]
Rate (λ)	6.52	6.22	[4.37, 8.13]
Zero class	13.8%	16.3%	[5.68%, 33.4%]
3CVF	Rate 1 (λ1)	2.08	2.05	[0.46, 3.25]
Freq 1	0.42	0.40	[0.05, 0.60]
Rate 2 (λ2)	8.64	8.10	[3.24, 11.1]
Freq 2	0.45	0.44	[0.30, 0.61]
Rate 3 (λ3)	21.9	22.1	[6.86, 31.2]
Freq 3	0.12	0.15	[0.02, 0.33]
Zero class	5.29%	5.34%	[1.34%, 15.6%]
G. Jürgens	Poisson	Rate (λ)	4.42	4.50	[3.95, 5.12]
(Drosophila, 44 loci, 197 alleles)	Zero class	1.20%	1.11%	[0.56%, 1.82%]
Gamma	Shape (α)	0.80	1.08	[0.477, 2.16]
Scale (β)	4.08	3.35	[1.75, 8.31]
Rate (λ)	3.25	3.73	[2.49, 5.07]
Zero class	27.4%	19.6%	[7.78%, 36.7%]
3CVF	Rate 1 (λ1)	0.31	1.85	[0.10, 3.20]
Freq 1	0.27	0.53	[0.24, 0.69]
Rate 2 (λ2)	4.23	5.37	[1.82, 8.88]
Freq 2	0.62	0.33	[0.08, 0.48]
Rate 3 (λ3)	13.7	13.5	[4.03, 21.3]
Freq 3	0.11	0.13	[0.02, 0.34]
Zero class	20.7%	8.66%	[1.68%, 30.5%]
E. Wieschaus	Poisson	Rate (λ)	3.33	3.28	[2.60, 4.00]
(Drosophila, 33 loci, 114 alleles)	Zero class	3.6%	3.75%	[1.67%, 5.6%]
Gamma	Shape (α)	0.54	0.80	[0.23, 1.84]
Scale (β)	3.60	3.11	[1.00, 6.50]
Rate (λ)	1.93	2.43	[1.11, 4.24]
Zero class	44.1%	32.4%	[11.2%, 61.0%]
3C	Rate 1 (λ1)	0.002	0.79	[0.01, 2.25]
Rate 2 (λ2)	2.80	3.20	[0.93, 5.85]
Rate 2 (λ2)	6.58	8.37	[3.45, 15.9]
Zero class	35.4%	16.6%	[3.92%, 35.5%]
M. Hülskamp	Poisson	Rate (λ)	3.08	3.06	[2.04, 4.13]
(Arabidopsis, 22 loci, 71 alleles)	Zero class	4.60%	4.68%	[1.57%, 10.5%]
Gamma	Shape (α)	5.00	1.59	[0.52, 2.30]
Scale (β)	0.58	1.61	[0.94, 4.70]
Rate (λ)	2.90	2.56	[1.42, 3.48]
Zero class	10.2%	22.0%	[12.2%, 40.9%]
2C	Rate 1 (λ1)	1.76	2.13	[0.29, 2.95]
Rate 2 (λ2)	4.29	4.84	[2.90, 10.50]
Zero class	9.3%	6.5%	[2.7%, 33.3%]
U. Mayer	Poisson	Rate (λ)	8.55	8.61	[6.57, 10.79]
(Arabidopsis, 9 loci, 77 alleles)	Zero class	0.02%	0.02%	[0.00%, 0.12%]
Gamma	Shape (α)	11.6	4.02	[1.30, 5.95]
Scale (β)	0.73	2.12	[1.27, 6.04]
Rate (λ)	8.54	8.83	[4.26, 12.3]
Zero class	0.17%	0.84%	[0.12%, 8.95%]
2C	Rate 1 (λ1)	6.01	6.73	[0.46, 11.50]
Rate 2 (λ2)	10.7	21.5	[7.35, 29.1]
		Zero class	0.12%	0.06%	[0.00%, 24.8%]

The other very large data set stems from an attempt to saturate the genome of D. melanogaster for P-element-induced lethal mutations (Spradling et al. 1999). We have examined these data for verified single P-element insertions located within deficiencies on chromosome 2, which included 843 alleles representing 350 loci. Once again, the gamma-rate model and the multiple-rate models all perform significantly better than the Poisson model (Table 1). The relative likelihoods are similar to the Haffter et al. (1996) data set, although in this case the 4CVF model is significantly better than the 3CVF model (2Δ ln L = 9.26; P < 0.01). The Akaike weight for the 4CVF model is 0.93, while that for the gamma is only 0.002. While the Poisson model predicts that ∼12% of all loci have not been detected, the 3CVF model predicts that 40% (95% credibility interval 32–48%) have not been detected (Table 3; 3CVF is shown for comparison to other data sets, but undetected loci predictions from 4CVF are similar).

Two other sets of mutagenesis data that detected a moderate number of loci, those of Ashburner et al. (1999) and Jürgens et al. (1984), showed patterns similar to that of Nüsslein-Volhard (Table 3). The Poisson model fits the data poorly compared to the other models, and the gamma-rate model is clearly preferred to the others. The Ashburner et al. (1999) data set, with 55 loci and 416 alleles, has an Akaike weight of 0.95 for the gamma model and weights of 0.007, 0.021, and 0.006 for the 3C, 3CVF, and 4C models, respectively. The Jürgens et al. (1984) data set, with 44 loci and only 197 alleles, produces an Akaike weight of only 0.589 for the gamma model, with most of the remaining weight distributed between the 4C and 3CVF models (Table 2). In both of these cases, the gamma-rate model and the best-fitting multiple-rate model predict that significantly more loci (up to one-third more) remain to be discovered than are predicted by the Poisson model, and the predictions of these two models are much more similar to each other than to the predictions of the Poisson model (Table 3). The estimates of the number of undiscovered loci under the Poisson model for the Ashburner and Jürgens data sets are 0.05 and 1.2%, respectively, while the gamma model estimates are 14 and 27%. These differences are similar in magnitude to the differences for the Nüsslein-Volhard data set, and if the gamma estimates are correct, then the Poisson is seriously underestimating the number of undiscovered loci that remain.

The three smallest mutagenesis experiments show a somewhat different pattern (Tables 2 and 3). For the data of Wieschaus et al. (1984), which included 114 alleles at 33 loci, the gamma model is significantly better than the Poisson model, but the 2C model is as likely as the gamma, with no difference in the number of parameters, and the 3C model is considerably more likely (Table 2). Although the more complex models are not better than the 3C model, the Akaike weight is only 0.43 for the 3C model. Most of the remaining weight is split between the gamma, 3C, and 4C models. Both the gamma model and the 3C model predict many more undetected loci than the Poisson model, and their predictions are similar to each other, although the gamma predicts somewhat more and has a broader range (Table 3). For the data of Hülskamp et al. (1994), with 71 alleles at 22 loci, both the gamma-rate model and the two-rate fixed-rate model are more likely than the Poisson, but not significantly so (Table 2). The Akaike weight for the Poisson model is 0.30, with most of the remaining weight split between the gamma and 2C models, but with a considerable amount of weight also on the 3C and 2CVF models. Variable-rate models (e.g., gamma and 2C) predict that more loci remain to be detected than are predicted by the Poisson (Table 3). The data of Mayer et al. (1991), a study that detected only 77 alleles at 9 loci due to the narrow range of phenotypes selected, show little difference in likelihood among all of the models (Table 2). Although in this case the Poisson model appears to be as good as any, and has an Akaike weight of 0.34, it estimates that ∼0.02% (95% C.I. 0.00–0.12%) of loci remain to be detected, while the gamma-rate model predicts that 0.2% of loci remain undetected (Table 3) and has a wide 95% C.I. of 0.1–9.0%. As with previous data sets, the gamma model is much more conservative than the Poisson in allowing for the possibility that more loci remain to be found.

DISCUSSION

For most of the data sets examined, the models incorporating multiple rates are a better fit to the data than the Poisson model, as expected. In many but not all cases, the nearly continuous gamma model approximation is preferable from both hierarchical model testing and information-based viewpoints. Models based on mixtures of Poisson distributions also usually performed well compared to the Poisson distribution; three cases (Spradling et al. 1999 and Haffter et al. 1996, the two biggest data sets, and Wieschaus et al. 1984, one of the smaller data sets) were mixture models preferable to the gamma model, and in one case (Mayer et al. 1991, again, one of the smaller data sets) the Poisson model was preferred. Perhaps the most significant result of our work is that the mixture models and the gamma model predicted much broader C.I.'s than the Poisson model, and the estimated number of undiscovered loci was generally considerably higher than that of the Poisson model. This indicates that for the mutagenesis experiments examined, many more loci may remain to be discovered than predicted by the Poisson model. Saturation in mutant screens is apparently much harder to achieve, and to demonstrate, than is generally appreciated. Thus, many mutagenesis studies are likely to have achieved much lower levels of saturation than previously assumed.

It is particularly notable that the probable distribution of undiscovered genes is very similar for the gamma model and the different mixture models. This means that even if we are unconvinced about the choice of gamma over a mixture model or the specific number and frequencies of rate classes, the prediction of undiscovered genes is robust to model variation. Although the creation of a small number of rate classes is conceptually simpler than a gamma distribution, a continuous distribution of rate classes is more biologically realistic since many of the factors affecting mutation rates per gene (e.g., frequencies, gene length, functional importance, and visibility of mutant phenotypes) are more likely to have a continuous rather than discrete distribution among different genes. In the two largest data sets, however, the gamma model, although not preferred, predicts that large numbers (up to 99%) of loci may remain to be discovered. Although this result is rather extreme and not particularly plausible, it is a warning that under rather simple scenarios we may predict that we have very little idea how many loci remain. This result could be modified by using other priors on the shape (or scale) parameter, and this would ideally be based on results from many studies. We were reluctant to introduce arbitrary informative priors prior to this initial study, but on the basis of the eight data sets analyzed here, α can have a broad range of values. The introduction of priors might of course broaden or narrow the credible intervals in any particular case, depending on how they are specified.

For three of our data sets, we were able to independently test the number of undiscovered loci relative to the model predictions. The clearest test involved the data of Ashburner et al. (1999). In this study on the genomics of the Adh region of D. melanogaster chromosome arm 2L, 55 loci detected by EMS mutagenesis were tabulated from the combined results of studies in this region over the years. An additional 18 loci were detected by other mutagens or by phenotypes due to homozygous deficiencies. These 18 loci represent 24.6% of the 73 total loci, just under the upper limit of 33.4% for the upper 95% C.I. for the gamma model (Table 3). It is possible that some of these loci could never be detected by EMS mutagenesis, but it seems plausible that many of them could have been isolated with this mutagen.

In the case of Nüsslein-Volhard et al. (1984), a number of loci with significant larval cuticle defects have been discovered since the initial study was carried out. These include split ends, oroshigane, Wnt oncogene analog 4, coracle, cyclope, takahe, and teashirt (FlyBase 2003). These 8 loci represent 11.6% of the 69 total loci (61 from Nüsslein-Volhard et al. 1984, plus the additional 8). This is at the low end of additional loci that are predicted by the gamma model (Table 1), which predicts a lower C.I. limit of 9.6%, or 7.3 new loci, although 8 new loci is well within the 95% C.I. of all of the multirate models (Table 1). The 8 new loci are a conservative estimate of the number of new loci; only loci with clear-cut larval cuticle phenotypes were included, and poorly described larval lethals were not considered. It is also possible that saturation still has not been achieved. For these reasons, the true total may be well within the gamma expectations.

Finally, Hülskamp et al. (1994) discovered 22 loci affecting trichome development in A. thaliana, which were estimated by them to represent >95% of detectable loci. Since this work, an additional 9 loci have been reported in the literature that theoretically could have been detected in the initial screen (Krishnakumar and Oppenheimer 1999; Luo and Oppenheimer 1999; Perazza et al. 1999; Walker et al. 2000). These 9 loci represent 29% of the total, which is within the upper 95% C.I. for the gamma and other multirate models (Table 3), but significantly more than the 2–11% predicted by the Poisson model.

These independent results, combined with the greater plausibility of the gamma model, suggest that the simplest and most conservative course of action in evaluating saturation mutagenesis screens is to assume a gamma distribution or mixture of Poissons rather than a Poisson distribution, even when the Poisson cannot be rejected on the basis of differences in likelihood. In other words, the gamma or mixture models are probably preferable null models, whereas use of the Poisson model is not well justified. The use of credible intervals in combination with the gamma and mixture models provides a statistically well-justified means to predict how much work may be needed to finish a mutagenesis analysis.

Our analyses cover multiple organisms (Drosophila, Danio, and Arabidopsis), multiple mutagens (EMS, ENU, and P elements), and data sets of various sizes. Our results suggest that the gamma model is a reasonable model for many of them. This distribution is flexible and allows for a wide range of mutation probabilities at different genes. Other mutagens, other traits, or other organisms may have different patterns, and mixture models are preferable in some cases, particularly for large data sets for which one observation per locus is much more frequent than any other allele count. The gamma-rates method should be useful for estimating the degree of saturation in many types of genetic screens in addition to classical screens for simple loss-of-function mutants, including genetic modifier screens and screens for protein-protein interactions using the yeast two-hybrid method. In other work, we have applied similar analyses toward predictions of the number of undiscovered species in an ecological/evolutionary discovery project on yeast species and found that a mixture model was preferable to the gamma model (S.-O. Suh, J. V. McHugh, D. D. Pollock and M. Blackwell, unpublished results). In that case, there appear to be distinct modes of species detectability. In comparison, the genetic data indicate that there are numerous highly mutable genes, but there is little evidence for strong modes of mutability or clusters of genes with similar high mutability rates. Instead, a distribution of gene mutabilities is evident, meaning that discrete hot spot mutability classes are not well supported.

A program for calculating maximum-likelihood estimates of the undiscovered class has been written in the C programming language and is available at www.biology.lsu.edu/webfac/dpollock/.