Gene Conversion and Crossing Over Along the 405-kb Left Arm of Saccharomyces cerevisiae Chromosome VII

Abstract

Gene conversions and crossing over were analyzed along 10 intervals in a 405-kb region comprising nearly all of the left arm of chromosome VII in Saccharomyces cerevisiae. Crossover interference was detected in all intervals as measured by a reduced number of nonparental ditypes. We have evaluated interference between crossovers in adjacent intervals by methods that retain the information contained in tetrads as opposed to single segregants. Interference was seen between intervals when the distance in the region adjacent to a crossover was <∼35 cM (90 kb). At the met13 locus, which exhibits ∼9% gene conversions, those gene conversions accompanied by crossing over exerted interference in exchanges in an adjacent interval, whereas met13 gene conversions without an accompanying exchange did not show interference. The pattern of exchanges along this chromosome arm can be represented by a counting model in which there are three nonexchange events between adjacent exchanges; however, maximum-likelihood analysis suggests that ∼8–12% of the crossovers on chromosome VII arise by a separate, noninterfering mechanism.

IN meiosis, recombinational repair of double-strand breaks (DSBs) that results in gene conversion is frequently accompanied by crossing over (Fogel and Hurst 1967), whereas an identical DSB is only rarely crossover associated in mitotic cells (Malkova et al. 1996). In mitotic cells, crossovers between homologous chromosomes may lead to disadvantageous loss of heterozygosity; but in meiosis, crossovers play an important role not only in promoting genetic diversity, but in ensuring proper chromosome segregation (reviewed by Roeder 1997; Zickler and Kleckner 1999; Walker and Hawley 2000).

Intimately connected to the problem of crossover control at a single locus is the phenomenon of crossover or chiasma interference, in which the proportion of closely spaced crossovers is lower than what would be expected from a random distribution. Interference is seen in multifactor crosses that produce fewer double recombinants than are expected on the assumption of independence of crossing over in two monitored intervals. Interference can also be measured by a lower-than-expected incidence of nonparental ditypes (i.e., four-strand double crossovers) within a single interval. In budding yeast, mutations such as zip1, msh4, or mlh1, which reduce crossing over, also appear to eliminate the constraints of interference (Ross-Macdonald and Roeder 1994; Sym and Roeder 1994; Khazanehdari and Borts 2000). In contrast, mus81 or mms4 mutations reduce exchanges without affecting interference (de los Santos et al. 2003). These observations support the idea that budding yeast have two pathways leading to crossovers, but only one of which imposes interference.

How one recombination event might influence another, at distances of tens of kilobases in yeast and much greater distances in flies and mammals, is not well understood. Various models have been proposed to explain interference, ranging from those in which the constraint is established at the time the DSB is first processed to those in which Holliday junction (HJ) resolvases themselves resolve a fixed number of intermediates as noncrossovers after having first resolved one intermediate as a crossover (King and Mortimer 1990; Foss et al. 1993; Zhao et al. 1995; Storlazzi et al. 1996; Kaback et al. 1999; Copenhaver et al. 2002; Fujitani et al. 2002). In “counting” models, the choice of which intermediates will be resolved as crossovers could occur within ordered clusters of recombination intermediates (Stahl et al. 2004, accompanying article, this issue). Models based on the relief of stress along the axis between homologous chromosomes (Storlazzi et al. 1995; Borner et al. 2004) may also have some aspects of counting, depending on the uniformity of stress along the chromosome axis. Counting models can account for the distribution of crossovers along chromosomes in Neurospora and Drosophila (Foss et al. 1993; McPeek and Speed 1995; Zhao et al. 1995; Copenhaver et al. 2002), with such models being somewhat more robust than models such as that of King and Mortimer (1990), which envision inhibitory signals spreading from the site of a crossover. A recent study of crossovers in tetrads from Arabidopsis concluded that the goodness of fit to a counting model was significantly improved by an additional assumption that there are in fact two types of crossovers, one with and one without interference. One set of exchanges may be related to the establishment of synapsis between homologs and be noninterfering, whereas later crossovers would obey the constraints of interference (Copenhaver et al. 2002). Similar considerations appear to apply to crossovers in humans (Housworth and Stahl 2003). Hence there would be a “sprinkling” of (perhaps) randomly distributed exchanges that would appear as closely spaced double crossovers in excess of the strict rules imposed by the various models.

The idea that the majority of noncrossovers might arise in a mechanistically different fashion from crossovers has its roots in studies of gene conversion by tetrad analysis in several fungi. Stadler (1959), studying Neurospora, first noted that only those gene conversions that were accompanied by crossing over caused crossover interference in adjacent intervals; that is, gene conversions accompanied by crossing over were associated with a reduction in additional crossovers in the next adjacent genetic interval, whereas gene conversions resolved as noncrossovers showed no interference. A similar conclusion was reached by Mortimer and Fogel (1974) for tetrads of Saccharomyces cerevisiae; however, their data are subject to criticism. Two different loci, arg4 and his1, served as the focus of their study. In the arg4 case, they considered a gene in which there were three heteroallelic markers. If, for example, only arg4-16 exhibited gene conversion, then two alleles within the same gene, arg4-17 and arg4-19 (3.3 and 0.2 cM away, respectively), were considered to be the flanking markers. If, however, arg4-16 and arg4-17 coconverted, then the flanking marker was considered to be thr1, 18 cM away. This shifting frame of reference makes it difficult to assess effects on recombination in still more distant intervals. Similarly, at the his1 locus, data for conversion of different alleles were combined with those from interallelic reciprocal recombination, where all markers segregated 2:2. These data contain several unexpected results. First, conversions of his1-2 not associated with exchange led to strong negative interference in the 2.5-cM arg4 to his1-1 interval (that is, a coefficient of coincidence of 3.3 rather than 1.0). There was no such effect on the opposite side, where the genetic distance to the flanking marker, arg6, was 11 cM and the adjacent interval (arg6-trp2) was 20 cM. In a similar fashion, conversions of his1-1 that were accompanied by crossing over nearly completely prevented crossing over in the adjacent his1-2 to arg6 interval (a coefficient of coincidence of 0.09); this value is much lower than most estimates of interference, where the coefficient of coincidence is between 0.5 and 0.2 (see below). No such strong interference was seen on the opposite side of his1-2, where the flanking markers are more distant; the coefficient of coincidence was not different from 1.0. The striking high negative interference in one case and unusually strong positive interference in another could be explained if there were not two recombination events, one a gene conversion within the first interval and the other a crossover in the adjacent interval, but rather a single recombination event in which his1-2 was converted, his1-1 was restored, and a crossover occurred between his1-1 and arg4. Such events are analogous to those seen among physical intermediates of recombination involving a marker that could not be readily mismatch corrected (Allers and Lichten 2001a,b).

To determine whether gene conversions without an associated crossing over in yeast are indeed different in their ability to exert interference from gene conversions with crossing over, we created a well-marked chromosome arm from which we could obtain detailed information about gene conversions, crossing over, and interference. We chose a 405-kb interval including most of the left arm of chromosome VII, which we divided into 10 intervals, using a set of auxotrophic and other markers isolated in the Y55 strain background (McCusker and Haber 1988b). Three drug-resistance markers and a nutritional marker (URA3) were introduced by gene targeting. One of these markers, met13-Y1E, shows a significant level of gene conversion, ∼9%, while three or more flanking markers on each side have 10-fold lower levels of non-Mendelian segregation. Thus few tetrads had to be eliminated because flanking markers were uninformative. From the analysis of >2500 tetrads we were able to establish that gene conversions with crossing over exhibit interference comparable to that seen in the analysis of intergenic crossing over. Gene conversions not associated with exchange did not perceptibly interfere with crossing over in adjacent intervals. In addition we present a description of crossing over along the entire chromosome arm, providing a large database that can be used to test various models of interference. We find that the fit of the counting model to the distribution of crossovers along this chromosome arm is improved by the addition of ∼8–12% of noninterfering exchanges.

MATERIALS AND METHODS

Strains:

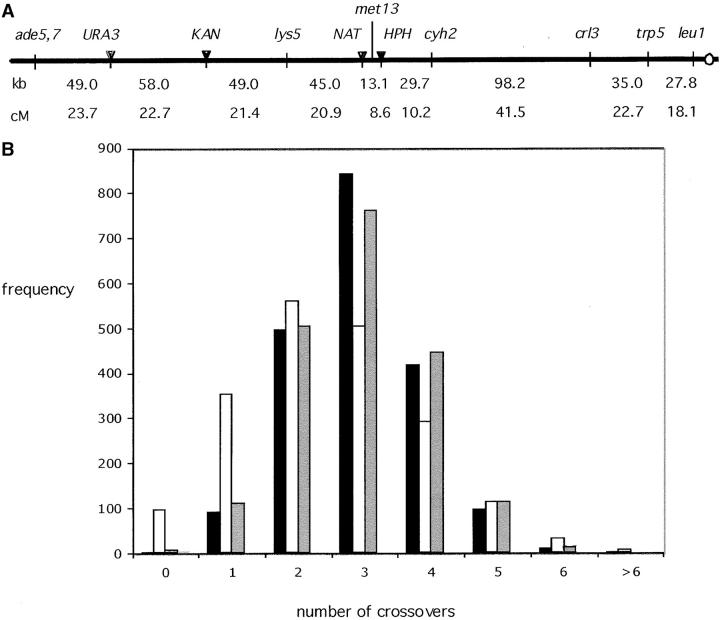
Diploid strain MAG100 was derived by a series of auxotrophic and drug-resistant mutations isolated in the homothallic Y55 strain background (McCusker and Haber 1988b). The alleles ade5-Y7, lys5-Y2, met13-Y1E, cyh2-Y1, trp5-Y1, and leu1-Y1 have been given Y prefixes to distinguish them from alleles in these genes isolated in other backgrounds. The temperature-sensitive mutation, crl3-2, was previously described (McCusker and Haber 1988a,b). Heterothallic (ho) haploid derivatives were constructed by knocking out the HO gene (ho::LEU2). Three drug-resistant markers were introduced by the methods of Wach et al. (1994) and Goldstein et al. (1999). The nourseothricin-resistance gene (NAT) was introduced into YGL131c, ∼6.6 kb distal to MET13. The hygromycin B-resistance (HPH) gene was inserted into ORF YGL121c, 6.5 kb proximal to MET13. The kanamycin-resistance (KAN) gene was inserted in an intergenic region located between nucleotides 166195 and 166294, based on the chromosome VII DNA sequence of S. cerevisiae posted at the Saccharomyces Genome Database (http://genome-www.stanford.edu/Saccharomyces/). The final strain, MAG100, shown in Figure 1, was constructed from two haploids of genotype MATa ura3-Y1 ade5-Y7 LYS5 MET13 HPH CYH2 crl3-2 trp5-Y1 leu1-Y1 and MATα ura3-Y1 ADE5 KAN lys5-Y2 NAT met13-Y1E cyh2-Y1 CRL3 TRP5 LEU1.

Figure 1.—

(A) Genetic and physical map of markers along the left arm of chromosome VII. In diploid MG100 (set II), the diploid did not contain the URA3 marker. Diploid YFS0407 (set I) contains both the URA3 marker and a BLE marker (not shown) that subdivides the cyh2-crl3 interval but was not used in the subsequent genetic analysis. (B) Expected vs. observed numbers of crossovers along the left arm of chromosome VII. The expected numbers of exchanges for the tetrads in set I were calculated from a Poisson distribution for each possible tetrad type, based on the average number of crossovers per tetrad (open bars), as described in materials and methods. The observed distribution is shown with solid bars. Also shown is the predicted distribution assuming the two-pathway model in which m = 3 and 8% of crossovers are noninterfering (shaded bars).

Subsequently, these haploid parents were modified to create diploid YFS0407. The long ade5-KAN region was subdivided by inserting URA3 in an intergenic region between CHC1 and POX1, deleting nt 107806 to 107906. Similarly, the long HPH-cyh2 interval was subdivided by insertion of the BLE (bleomycin-resistance) marker (Gatignol et al. 1987) in an intergenic region between GUP1 and SCY1 by deletion of the region of chromosome VII from nt 352596 to 352696. The MET13-containing haploid parent of diploid MAG100 was also crossed to an isogenic strain carrying the met13-5 allele (McCusker and Haber 1988b) to produce a haploid carrying the same markers but with met13-5 instead of MET13. When crossed to the original met13-1 parent, this yielded a new diploid heteroallelic for met13-1/met13-5.

Genetic analysis:

Diploids were grown in yeast extract-peptone-dextrose (YEPD) medium and sporulated at 30°, as described previously (McCusker and Haber 1988b). Tetrads were dissected on YEPD and germinated at 25° or 30°. Auxotrophic markers were scored by replica plating to standard nutritional drop-out media lacking one amino acid. The temperature-sensitive crl3-2 allele was scored by replica plating to YEPD plates subsequently incubated at 37°. Resistance to antibiotics was scored by replica plating to YEPD plates containing 10 mg/ml cycloheximide, 25 mg/ml nourseothricin, 300 μg/ml hygromycin B, or 300 μg/ml kanamycin.

Tetrad analysis and calculation of interference:

Tetrad data were analyzed using MacTetrad, version 6.9 written by Jonathan Greene, Warren Voth, and David Stillman. Map distances between markers were calculated by the formula of Perkins (1949), where map distance (in centimorgans) = 100([6NPD + (TT)]/[2 × [PD + NPD + TT]), where PD, NPD, and TT stand for parental ditype, nonparental ditype, and tetratype, respectively. Perkins's formula is valid in the absence of chromatid interference for intervals in which the number of exchanges greater than two is negligible. Interference was determined in two ways. First, interference within a single genetic interval was identified when the observed number of NPD tetrads was significantly lower than that expected on the basis of the formula 1/₂[1 − TT − (1 − (3TT/2)^2/3)] (Papazian 1952), where TT is the fraction of tetratype asci. Second, interference between crossovers in two intervals was determined by comparing the distribution of tetrad types (PD, NPD, and TT) in an adjacent interval for the case when the initial interval exhibited either a TT or NPD pattern (indicative of crossing over) or a PD pattern (taken as indicative of no crossing over). These two distributions were compared by chi-square (χ²) tests using the interactive chi-square site at http://faculty.vassar.edu/lowry/VassarStats.html. The crossover distribution was also evaluated by comparing the calculated map distances using the Stahl Lab Online Tools at http://groik.com/stahl/. Tetrads in which one of the markers had undergone gene conversion or postmeiotic segregation were excluded from these analyses. Because most markers, except MET13 and URA3, showed very low levels of gene conversion, this did not prove to be a problem.

To compare the distribution of crossovers among individual tetrads, tetrads were grouped by the number of apparent crossovers they contain. For example, a tetrad with six parental ditype intervals, one tetratype interval, and one nonparental ditype interval has three apparent crossovers. The maximum number of apparent crossovers observed in the data was seven. For each model, the probability of obtaining a tetrad with zero to six apparent crossovers was calculated using the Poisson distribution and the formula by Mather (1935); for the interference-only case we used the formulas of Bailey (1961) and Zhao et al. (1995). The probability distribution developed by Copenhaver et al. (2002) was used for the two-pathway model. The remaining probability for seven or more apparent crossovers was used for the last class. The expected number of tetrads in each class is just the total number of tetrads times the probability of the class. One sees a much better fit using a model that includes interference. The SAS codes used to conduct the statistical analyses assessing the two-pathway hypothesis for chiasma interference and assessing chromatid interference are available from E. A. Housworth upon request.

Maximum-likelihood analysis:

The method described in Copenhaver et al. (2002) was used to determine m, the fixed number of noncrossover events between nearest-neighbor crossovers, and p, the proportion of noninterfering crossover events.

RESULTS

Interference is observed in all intervals of the left arm of chromosome VII:

Two different diploids, MAG100 and YFS0407, were analyzed (Figure 1A). In MAG100 (set II), the 405-kb left arm of chromosome VII was subdivided into 9 intervals. In YFS0407 (set I) there were 11 intervals, created by the insertion of the URA3 and BLE genes, but difficulties in scoring the BLE marker led to a consideration of only 10 intervals. Set I includes 2076 complete tetrads; set II contains an additional 1451 tetrads. Overall, the results from the two diploids were quite similar (Table 1A), but there were some systematic differences that obliged us to treat the two data sets separately. The map lengths for the 9 elementary intervals in set II are all greater than those in set I, and for 4 of the intervals the differences are significant (Stahl Lab Online Tools). These intervals are lys5-NAT, HPH-cyh2, cyh2-crl3, and trp5-leu1. We do not know the origin of these differences, but suspects are the BLE and URA genes inserted in the set I diploid; there may also be differences in the way cells were grown and sporulated in the two laboratories that collected these sets of data.

TABLE 1.

Recombination in the left arm of chromosome VII

Set		ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
A. Crossovers in nine intervalsa
I	PD:TT:NPD	1082:827:14	1138:756:15	1234:780:5	1478:557:6	1724:332:0	1805:240:6	846:1168:40	1201:843:13	1520:539:4
cM	23.7 ± 0.8	22.2 ± 0.8	20.1 ± 0.6	14.5 ± 0.6	8.1 ± 0.4	6.7 ± 0.5	34.3 ± 1.0	22.4 ± 0.7	13.7 ± 0.6
II	PD:TT:NPD	366:980:77	866:539:11	882:526:11	1193:234:2	1160:269:4	492:887:50	842:568:13	941:481:6
cM	50.7 ± 1.7	21.4 ± 0.9	20.9 ± 0.9	8.6 ± 0.6	10.2 ± 0.7	41.5 ± 1.4	22.7 ± 1.0	18.1 ± 0.8
kb	49	58.3	49	45	13.1	29.7	98.2	35	27.8
Avg.	kb/cM,	2.1	2.6	2.4	2.5	1.6	3.5	2.6	1.6	1.7
ade5,7	URA3 (set I)	KAN	lys5	NAT	met13	HPH	cyh2	crl3	trp5	leu1
B. Conversion at eleven markersb
3:1	7/3	113	25/10	14/14	1/8	104/65	3/4	7/2	4/11	6/9	2/4
1:3	7/10	18	6/5	10/5	7/1	79/65	7/6	6/5	5/2	2/7	1/3
Frequency	0.008	0.063	0.013	0.012	0.005	0.089	0.006	0.006	0.006	0.007	0.003
Other (no.)	4:0 (1)	4:0 (6)	4:0 (1)	0:4 (2)	0:4 (2)	0:4 (1)	0:4 (1)	4:0 (2)	4:0 (2)	4:0 (1)
	0:4 (1)			0:4 (2)		4:0 (2)

^aTo determine the map length in each elementary interval along chromosome VII, 2076 four-spore tetrads (set I) and 1451 four-spore tetrads (set II) were scored. The centromere is to the right. Those tetrads exhibiting non-Mendelian segregation of either marker defining a given interval are not included. Map distances and standard errors in centimorgans (cM) were calculated with the aid of Stahl Lab Online Tools (http://groik.com/stahl/), on the basis of the formula cM = 100 × (TT + 6NPD)/2(PD + NPD + TT), which assumes that all intervals are subject to no more than two crossover events. Physical distances were determined from data in the Saccharomyces Genome Database (http://genome-www.stanford.edu/Saccharomyces/).

^bNon-Mendelian segregations observed in the 2076 analyzed tetrads of set I and the 1451 tetrads of set II (entered as set I/set II). For Frequency and for Other, data from the two sets are combined.

As shown in Table 1B, MET13 showed a substantial level of gene conversion (8.9%) whereas other markers experienced gene conversion at levels ranging from 1.3 to 0.3%, except for URA3 in set I, which had 6.3% gene conversion.

Generally, the map distances are consistent with those reported previously, as summarized in the chromosome VII genetic map of the Saccharomyces Genome Database. The overall genetic map, adding up each of the nine intervals, indicates that there were 3.31 crossovers/meiosis (165.7 cM for set I), or 2.44 kb/cM. For set II there were 3.88 crossovers/meiosis (194.1 cM), or 2.09 kb/cM. Compared to the physical distances of the intervals, we find that there are no exceptionally “hot” or “cold” intervals. The values ranged from 1.6 to 3.5 kb/cM (Table 1A).

All of the intervals examined showed significant crossover interference. In all but the two smallest intervals (NAT-MET13 and MET13-HPH), for which there were not enough data, this was evident from the reduced number of NPDs compared to the expected value, calculated from the equation of Papazian (1952). These data are shown in Table 2. The ratios of observed numbers of NPD to the expected value were generally between 0.1 and 0.33. Statistical uncertainties around the small numbers of NPDs observed for the HPH-cyh2 interval render the values for that interval unreliable.

TABLE 2.

Interference as judged by NPD ratios

Set	ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
I	0.21 ± 0.06	0.28 ± 0.07	0.09 ± 0.04	0.25 ± 0.10	0.0	1.57 ± 0.64	0.25 ± 0.04	0.21 ± 0.06	0.18 ± 0.09
II	0.52 ± 0.04		0.31 ± 0.09	0.33 ± 0.1	0.37 ± 0.26	0.55 ± 0.26	0.33 ± 0.05	0.32 ± 0.09	0.22 ± 0.09

The ratios observed NPD:expected NPD, with standard errors, were calculated with the aid of Stahl Lab Online Tools( http://groik.com/stahl/) according to the formula of Papazian (1952), for which ratios significantly less than unity demonstrate interference (see materials and methods).

Crossover interference can also be determined in a three- or four-factor cross by comparing the observed number of double crossovers to that expected on the assumption of no interference. We detected interference by first choosing an interval and identifying tetrads that were PD vs. those that contained a crossover (TT and NPD). Then, we compared the distributions of all tetrad types in an adjacent interval (PD, NPD, or TT) for those that were either noncrossovers or crossovers in the first interval . This approach retains the information contained in tetrads that is lost when the data are reduced to an analysis of single segregants. As an example, consider Table 3A, in which the interval under consideration is the centromere-adjacent trp5-leu1 region. We chose all tetrads in this interval in which there was evidence of crossing over (TT + NPD) and analyzed all of these tetrads for the distribution of tetrad types in each of the other intervals defined by adjacent markers (hereafter called elementary intervals). These results were compared with the distribution of tetrad types in the same intervals when there was no detected crossover event in the trp5-leu1 interval (PD). The significance of the difference in the distributions of tetrad types in adjacent intervals was then determined by contingency χ² tests. We also calculated the map distances for each of these cases, using Stahl Lab Online Tools, which test for the significance of differences between map lengths calculated from tetrad types. By the χ² test, the P-value in set I (0.034) suggests that interference extends into the cyh2-crl3 interval as well (Table 3A). This conclusion is supported by the observation that the difference in the calculated map lengths is also statistically significant for both data sets. For intervals further removed, interference was not detected.

TABLE 3.

Interference for nine intervals taken pairwise

Set		ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	NAT-HYG	HYG-cyh2	cyh2-crl3	crl3-trp5
A. trp5-leu1
I	TT + NPD	280:217:5 (24.6 ± 1.7)	319:180:3 (19.7 ± 1.4)	318:212:1 (20.5 ± 1.2)	398:137:1 (13.3 ± 1.1)	455:86:0 (8.0 ± 0.8)	467:70:3 (8.2 ± 1.2)	233:303:5 (30.8 ± 1.5)	473:69:0 (6.4 ± 0.7)
PD	792:607:9 (23.5 ± 0.9)	810:572:12 (23.1 ± 1.0)	909:562:4 (19.9 ± 0.7)	1070:417:5 (15.0 ± 0.7)	1258:244:0 (8.1 ± 0.5)	1372:168:3 (6.0 ± 0.5)	605:861:35 (35.7 ± 1.2)	727:773:13 (28.1 ± 0.9)
χ2P	0.72	0.10	0.51	0.28	0.92	0.15	0.09	<0.0001
Sig. SE (cM)	No	No	No	No	No	No	Yes	Yes
II	TT + NPD	130:323:22 (47.9 ± 2.7)		292:177:3 (20.7 ± 1.5)	294:177:2 (19.9 ± 1.4)	392:87:0 (9.1 ± 0.9)	379:102:2 (11.8 ± 1.3)	172:302:8 (36.3 ± 1.9)	395:85:3 (10.7 ± 1.4)
PD	230:641:55 (52.4 ± 2.2)		562:351:8 (21.7 ± 1.2)	575:340:9 (21.3 ± 1.2)	783:143:2 (8.4 ± 0.7)	764:162:2 (9.4 ± 0.8)	313:575:40 (43.9 ± 1.9)	441:482:10 (29.1 ± 1.2)
χ2P	0.40		0.87	0.54	0.25	0.09	0.03	<0.0001
Sig. SE (cM)	No		No	No	No	No	Yes	Yes
Set		ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-crl3	trp5-leu1
B. crl3-trp5
I	TT + NPD	446:344:7 (24.2 ± 1.3)	485:295:6 (21.1 ± 1.2)	504:326:3 (20.7 ± 1.0)	614:229:0 (13.6 ± 0.8)	712:137:0 (8.1 ± 0.6)	742:104:1 (6.5 ± 0.7)	465:376:11 (25.9 ± 1.4)	786:68:1 (4.3 ± 0.6)
PD	622:479:7 (23.5 ± 1.0)	644:454:9 (22.9 ± 1.1)	721:447:2 (19.6 ± 0.8)	848:325:6 (15.3 ± 0.9)	994:194:0 (8.2 ± 0.5)	1046:135:5 (7.0 ± 0.7)	375:789:29 (40.4 ± 1.4)	727:470:3 (20.3 ± 0.8)
χ2P	0.82	0.30	0.64	0.69	1.0	0.74	<0.0001	<0.0001
Sig. SE (cM)	No	No	No	No	No	No	Yes	Yes
II	TT + NPD	138:394:39 (55.0 ± 2.9)		354:212:4 (20.7 ± 1.4)	353:212:5 (21.2 ± 1.5)	474:96:1 (8.9 ± 0.9)	477:94:1 (8.7 ± 0.9)	266:300:11 (31.7 ± 1.9)	492:88:0 (7.6 ± 0.7)
PD	220:566:38 (48.2 ± 2.1)		499:312:7 (21.6 ± 1.2)	511:305:6 (20.7 ± 1.2)	696:134:1 (8.4 ± 0.7)	665:167:3 (11.1 ± 0.9)	223:579:38 (48.0 ± 2.0)	441:389:6 (25.4 ± 1.2)
χ2P	0.15		0.88	0.95	0.76	0.09	<0.0001	<0.0001
Sig. SE (cM)	No		No	No	No	No	Yes	Yes
Set		ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	crl3-trp5	trp5-leu1
C. cyh2-crl3
I	TT + NPD	617:492:5 (23.4 ± 0.9)	636:465:11 (23.9 ± 1.1)	742:443:1 (18.9 ± 0.7)	876:314:4 (14.2 ± 0.8)	1047:154:0 (6.4 ± 0.5)	1110:92:4 (4.8 ± 0.6)	818:382:4 (16.9 ± 0.8)	895:306:2 (13.2 ± 0.7)
PD	452:328:9 (24.2 ± 1.4)	495:281:4 (19.6 ± 1.1)	482:329:4 (21.7 ± 1.1)	585:239:2 (15.2 ± 0.9)	659:175:0 (10.5 ± 0.7)	687:148:2 (9.6 ± 0.8)	375:456:9 (30.4 ± 1.3)	605:231:2 (14.5 ± 0.9)
χ2P	0.13	0.02	0.13	0.23	<0.0001	<0.0001	<0.0001	0.30
Sig. SE (cM)	No	Yes (neg.)	Yes	No	Yes	Yes	Yes	No
II	TT + NPD	247:629:45 (48.8 ± 2.0)		578:328:9 (20.9 ± 1.2)	577:327:9 (20.9 ± 1.2)	782:140:2 (8.2 ± 0.7)	792:137:3 (8.3 ± 0.8)	617:300:11 (19.7 ± 1.3)	615:306:4 (17.8 ± 1.0)
PD	114:334:32 (54.8 ± 3.1)		276:201:2 (22.2 ± 1.4)	291:192:2 (21.0 ± 1.4)	395:89:0 (9.2 ± 0.9)	358:128:1 (13.8 ± 1.2)	223:264:2 (28.2 ± 1.4)	313:170:2 (18.8 ± 1.4)
χ2P	0.22		0.051	0.22	0.17	<0.0001	< 0.0001	0.50
Sig. SE (cM)	No		No	No	No	Yes	Yes	No
D. HPH-cyh2
I	TT + NPD	125:103:0 (22.6 ± 1.7)	142:82:3 (22.0 ± 2.7)	169:72:1 (16.1 ± 1.9)	195:49:0 (10.0 ± 1.3)	232:13:0 (2.7 ± 0.7)	150:91:5 (24.6 ± 3.0)	140:105:0 (21.4 ± 1.6)	171:73:0 (15.0 ± 1.5)
PD	944:715:13 (23.7 ± 0.9)	986:661:12 (22.1 ± 0.8)	1051:699:4 (20.6 ± 0.7)	1264:504:6 (15.2 ± 0.7)	1482:316:0 (8.8 ± 0.5)	687:1075:35 (35.8 ± 1.1)	1046:729:13 (22.6 ± 0.8)	1327:463:4 (13.6 ± 0.6)
χ2P	0.34	0.38	0.01	0.01	<0.0001	<0.0001	0.35	0.23
Sig. SE (cM)	No	No	Yes	Yes	Yes	Yes	No	No
II	TT + NPD	76:174:16 (50.6 ± 4.1)		152:113:3 (24.4 ± 2.3)	191:76:2 (16.4 ± 2.0)	245:25:1 (5.7 ± 1.4)	129:135:5 (30.7 ± 2.7)	170:94:1 (18.9 ± 1.8)	164:103:1 (20.3 ± 1.8)
PD	287:792:60 (50.6 ± 1.9)		701:421:8 (20.8 ± 1.0)	681:442:9 (21.9 ± 1.0)	943:206:1 (9.2 ± 0.6)	358:747:45 (44.2 ± 1.7)	665:466:11 (23.3 ± 1.1)	764:374:5 (17.7 ± 0.9)
χ2P	0.43		0.24	0.004	0.001	<0.0001	0.16	0.09
Sig. SE (cM)	No		No	Yes	Yes	Yes	Yes	No
Set		ade5,7-URA3	URA3-KAN	KAN-lys5	lys5-NAT	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
E. NAT-HPH
I	TT + NPD	168:140:4 (26.3 ± 2.3)	198:111:2 (19.8 ± 1.9)	224:99:1 (16.2 ± 1.6)	290:37:0 (5.7 ± 0.9)	316:11:2 (3.5 ± 1.4)	175:150:4 (26.4 ± 2.2)	194:135:2 (22.2 ± 1.8)	244:85:1 (13.8 ± 1.5)
PD	904:678:9 (23.0 ± 0.8)	931:636:13 (22.6 ± 0.9)	999:675:4 (20.8 ± 0.7)	1179:519:6 (16.3 ± 0.7)	1482:228:4 (7.4 ± 0.5)	659:1011:36 (36.0 ± 1.1)	994:701:11 (22.5 ± 0.8)	1258:452:3 (13.7 ± 0.6)
χ2P	0.26	0.29	0.002	<0.0001	<0.0001	<0.0001	0.99	0.92
Sig. SE (cM)	No	No	Yes	Yes	Yes	Yes	No	No
II	TT + NPD	65:156:12 (48.9 ± 4.1)		142:89:2 (21.7 ± 2.3)	197:36:2 (10.2 ± 2.1)	207:26:0 (5.6 ± 1.0)	89:129:13 (44.8 ± 4.4)	135:92:5 (26.3 ± 3.1)	145:85:2 (20.9 ± 2.3)
PD	296:810:64 (51.0 ± 1.9)		708:445:9 (21.5 ± 1.0)	680:485:9 (23.0 ± 1.0)	943:241:4 (11.2 ± 0.8)	395:746:36 (40.9 ± 1.5)	696:467:7 (21.8 ± 1.0)	783:388:4 (17.5 ± 0.8)
χ2P	0.71		0.99	<0.0001	0.001	0.03 (neg.)	0.06	0.25
Sig. SE (cM)	No		No	Yes	Yes	No	No	No
Set		ade5,7-URA3	URA3-KAN	KAN-lys5	NAT-HPH	HPH-cyh2	cyh2-crl3	crls3-trp5	trp5-leu1
F. lys5-NAT
I	TT + NPD	291:219:3 (23.1 ± 1.4)	321:187:4 (20.6 ± 1.5)	475:81:2 (8.3 ± 1.1)	525:37:0 (3.3 ± 0.5)	510:48:1 (4.8 ± 0.8)	241:306:12 (33.8 ± 2.0)	331:225:4 (22.2 ± 1.4)	422:137:1 (12.8 ± 1.0)
PD	776:591:10 (23.6 ± 0.9)	795:560:11 (22.9 ± 1.0)	754:697:3 (24.6 ± 0.7)	1179:290:0 (9.9 ± 0.5)	1264:191:4 (7.4 ± 0.6)	585:850:26 (34.4 ± 1.1)	848:607:7 (22.2 ± 0.8)	1070:395:3 (14.1 ± 0.7)
χ2P	0.94	0.21	<0.0001	<0.0001	0.006	0.36	0.72	0.28
Sig. SE (cM)	No	No	Yes	Yes	Yes	No	No	No
II	TT + NPD	125:372:30 (52.4 ± 2.8)		406:122:3 (13.2 ± 1.3)	494:36:2 (4.5 ± 1.0)	451:77:1 (7.8 ± 1.0)	194:319:17 (39.7 ± 2.3)	311:213:4 (22.4 ± 1.5)	349:177:2 (17.9 ± 1.3)
PD	231:590:46 (49.9 ± 2.1		452:414:8 (26.4 ± 1.2)	680:197:0 (11.2 ± 0.7)	681:188:3 (11.8 ± 0.9)	291:547:30 (41.9 ± 1.8)	511:344:9 (23.0 ± 1.3)	575:290:4 (18.1 ± 1.0)
χ2P	0.47		<0.0001	<0.0001	0.001	0.50	0.86	1.0
Sig. SE (cM)	No		Yes	Yes	Yes	No	No	No
G. KAN-lys5
I	TT + NPD	407:312:4 (23.2 ± 1.2)	521:203:3 (15.2 ± 1.1)	700:81:2 (5.9 ± 0.8)	679:100:0 (6.4 ± 0.6)	703:72:1 (5.0 ± 0.6)	333:428:16 (33.7 ± 1.6)	449:325:4 (22.4 ± 1.1)	566:213:0 (13.7 ± 0.8)
PD	648:490:8 (23.5 ± 1.0)	598:548:12 (26.8 ± 1.1)	809:767:9 (25.9 ± 0.8)	999:224:0 (9.2 ± 0.6)	1051:166:3 (7.5 ± 0.6)	482:720:22 (34.8 ± 1.2)	721:497:7 (22.0 ± 0.9)	909:315:3 (13.6 ± 0.7)
χ2P	0.92	<0.0001	<0.0001	0.002	0.004	0.25	0.86	0.51
Sig. SE (cM)	No	Yes	Yes	Yes	Yes	No	No	No
II	TT + NPD	173:350:23 (44.7 ± 2.5)		422:121:4 (13.3 ± 1.4)	454:91:0 (8.4 ± 0.8)	429:113:3 (12.0 ± 1.3)	203:319:18 (39.5 ± 2.3)	319:207:9 (24.4 ± 1.9)	359:178:2 (17.6 ± 1.3)
PD	186:619:53 (54.6 ± 2.3)		452:399:7 (25.7 + 1.2)	708:140:2 (8.9 ± 0.8)	701:151:1 (9.2 ± 0.7)	276:548:30 (42.6 ± 1.9)	499:350:4 (21.9 ± 1.1)	562:288:4 (18.3 ± 1.0)
χ2P	< 0.0001		<0.0001	1.0	0.12	0.13	0.06	0.81
Sig. SE (cM)	Yes		Yes	No	No	No	No	No
Set		ade5,7-URA3	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
H. URA3-KAN
I	TT + NPD	525:234:4 (16.9 ± 1.1)	560:204:2 (14.1 ± 1.0)	571:190:1 (12.9 ± 0.9)	649:113:0 (7.4 ± 0.6)	673:83:2 (6.3 ± 0.8)	285:461:15 (36.2 ± 1.6)	463:295:6 (21.7 ± 1.3)	584:182:1 (12.3 ± 0.9)
PD	541:580:9 (28.1 ± 1.0)	598:519:2 (23.7 ± 0.8)	795:316:5 (15.5 ± 0.9)	931:198:0 (8.8 ± 0.6)	986:139:3 (7.0 ± 0.7)	495:613:23 (33.2 ± 1.4)	644:479:6 (22.8 ± 1.0)	810:317:2 (14.6 ± 0.8)
χ2P	<0.0001	<0.0001	0.09	0.13	0.41	0.02	0.22	0.04
Sig. SE (cM)	Yes	Yes	Yes	No	No	No (neg.)	No	Yes
Set		KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-cl3	crl3-trp5	trp5-leu1
I. ade5,7-KAN
II	TT + NPD	672:365:8 (19.8 ± 1.1)	636:394:8 (21.3 ± 1.1)	874:168:0 (8.1 ± 0.6)	852:187:3 (9.8 ± 0.8)	366:639:35 (40.8 ± 1.7)	604:423:10 (23.3 ± 1.1)	696:340:5 (17.8 ± 1.0)
PD	186:170:3 (26.2 ± 1.9)	231:122:3 (19.7 ± 1.9)	296:63:2 (10.4 ± 1.5)	287:75:1 (11.2 ± 1.3)	114:233:14 (43.9 ± 3.0)	220:135:3 (21.4 ± 1.9)	230:129:1 (18.8 ± 1.5)
χ2P	0.0001	0.46	0.45	0.29	0.44	0.57	0.34
Sig. SE (cM)	Yes	No	No	No	No	No	No
Set		URA3-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-cl3	crl3-trp5	trp5-leu1
J. ade5,7-URA3
I	TT + NPD	589:233:4 (15.6 ± 1.0)	498:315:1 (19.7 ± 0.9)	601:222:0 (13.5 ± 0.8)	687:144:0 (8.7 ± 0.7)	728:100:3 (7.1 ± 0.8)	336:478:19 (35.5 ± 1.6)	485:348:3 (21.9 ± 1.0)	615:220:2 (13.9 ± 0.9)
PD	541:515:10 (27.0 ± 1.1)	648:404:3 (20.0 ± 0.9)	776:286:5 (14.8 ± 0.9)	904:168:0 (7.8 ± 0.6)	944:122:3 (6.6 ± 0.7)	452:599:18 (33.1 ± 1.3)	622:437:9 (23.0 ± 1.1)	792:278:2 (13.5 ± 0.8)
χ2P	<0.0001	1.0	0.92	0.37	0.69	0.49	0.41	0.89
	Sig. SE (cM)	Yes	No	No	No	No	No	No	No

This approach allowed us to examine the relatively small interval between NAT and HPH (ignoring what occurred at the MET13 locus between these two drug-resistance markers; Table 3E). A crossover between NAT and HPH caused interference in both adjacent intervals (lys5-NAT and HPH-cyh2). In set I, where map distances were somewhat shorter, we could see that interference also extended into the next two adjacent intervals (KAN-lys5 and cyh2-crl3). It could be that set II failed to detect interference simply because there are fewer tetrads. On the other hand, it could be because interference falls off with linkage map distance, not with physical distances.

In a similar fashion, we see that crossovers in each selected interval exert interference on the immediately adjacent intervals, but not necessarily over a longer distance. We summarize the genetic distance over which interference could be detected in Table 4, which shows the length of the intervals on either side of a selected interval, containing crossovers (TT or NPD), over which interference could be detected in at least one of the two sets of data. The extent, or reach, of interference to the left and to the right of each selected interval in which there was crossing over was calculated as the distance between the midpoint of the test interval and the midpoint of the most distant interval in which interference was seen, using set I data (Table 4). For 14 such cases, the mean length over which interference was detected was 30.8 ± 11.8 cM, corresponding to 78.6 ± 29.0 kb. These data include five instances in which interference extended beyond the last marker used in the analysis and thus the mean “reach” of interference will be somewhat larger. The longest genetic length over which interference was seen was 60.7 cM; the longest physical distance over which there was interference was 154.2 kb, about one-third of the chromosome arm. The shortest genetic distances over which interference was confined were 17.3 and 18.7 cM; in these two cases, interference did not extend another 21.2 or 20.5 cM (or another 53.7 or 64.0 kb), respectively.

TABLE 4.

Summary of interference measured between intervals

	ade5-KAN	KAN-lys5	lys5-NAT	NAT-HPH	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
cM (set I)	44.0	20.1	14.5	8.1	6.7	34.3	22.4	13.7
cM (set II)	50.7	21.4	21.0	8.6	10.2	41.5	22.7	18.1
kb	107.3	49	45	13.1	29.7	98.2	35	27.8
ade5-KAN	1, 2
KAN-lys5	1, 2	1, 2	1	1
lys5-NAT	1, 2	1, 2	1, 2
NAT-HPH	1	1	1, 2	1, 2	1
HPH-cyh2	1	1, 2	1, 2	1, 2	2
cyh2-crl3	1	1	1, 2	1, 2
crl3-trp5	1, 2	1, 2
trp5-leu1	1, 2	1, 2
Reach L   cM	≥32.1	17.3	≥60.7	36.0	27.9	28.4	46.4
kb	≥78.2	47.0	≥154.2	97.5	85.4	66.6	98.0
Reach R   cM	32.1	36.0	18.7	27.9	20.5	28.4	≥18.1
kb	78.2	97.5	50.5	85.4	64.0	66.6	≥31.4

Numerals 1 and 2 refer to data sets I and II, respectively. When both tests for interference were significant (see materials and methods), the numeral is shown in italics. Row headings correspond to Table 3, A–J, whereas the column headings correspond to the entries in Table 3. (The entries for ade5-KAN from set I do not appear in Table 3.) Reach L and Reach R indicate the distances over which interference was detected, by one or both tests in set I, to the left and right in the table. Distances were measured from the middle of the test interval to the middle of the most remote interval in which the interference was detected by one or both tests. The sporadic examples of significant positive interference, separated from the intervals showing interference around the selected interval, in Table 3, were not more frequent than expected by statistical fluctuation and were not entered in this table. Similar examples of apparent negative interference in Table 3, of comparable frequency, are not entered in this table.

Gene conversions without exchanges are noninterfering:

In some models of recombination, all gene conversions arise from a common process in which Holliday junctions are resolved. The act of resolving these intermediates might be the signal that is transmitted along the chromosome axis, resulting in interference. In this case, one might imagine that gene conversions without crossovers would be just as likely to interfere with adjacent crossover events as gene conversions that are accompanied by crossing over. If, however, gene conversions arising without an associated crossover occur by a mechanism that is distinct from one that leads to gene conversions with crossovers, then the two types of events might have quite different effects on interference.

Among 3527 tetrads pooled from set I and set II, there were 311 MET13 conversions that could be scored as crossovers or as noncrossovers for the flanking markers. In 145 of those tetrads (46.6%), the conversions were crossovers for NAT-HPH. The data in Table 5 demonstrate that the map length for the lys5-NAT interval, adjacent to the NAT-HPH interval, is significantly lower among crossover MET13 conversions than among noncrossovers. This difference could be due to positive interference between crossover MET13 conversions and crossing over in the neighboring interval, or it could be due to negative interference between noncrossover MET13 conversions and crossing over in the neighboring interval, as discussed in the Introduction. We can distinguish these by comparing the map distances in Table 5 with the corresponding map distances for the entire data set (average of sets I and II in Table 1). For the crossover MET13 conversions, that ratio is 0.39, indicative of positive interference. For the noncrossover MET13 conversions, the ratio is 1.03, a value that fails to support the observation of Mortimer and Fogel (1974) that suggested there is negative interference between noncrossover conversions and nearby crossing over. In the other adjacent interval (HPH-cyh2), we failed to see a significant difference in the frequencies of tetrad types or estimated map distances for the crossover vs. noncrossover MET13 conversions. However, we note that when all crossovers in the NAT-HPH interval were analyzed, there was clear interference in both lys5-NAT and HPH-cyh2 adjacent intervals (Tables 3 and 4).

TABLE 5.

Tetrad types for conversions atmet13

	ade5-KAN	KAN-lys5	lys5-NAT	HPH-cyh2	cyh2-crl3	crl3-trp5	trp5-leu1
Among 145   crossovers (cM)a	33:106:4 (45.5 ± 4.0)	103:40:0 (14.0 ± 1.9)	124:20:0 (6.9 ± 1.4)	132:11:1 (5.9 ± 2.3)	69:68:7 (38.2 ± 5.3)	81:64:0 (22.1 ± 2.1)	92:51:1 (19.8 ± 2.8)
Among 166   noncrossovers (cM)a	52:100:9 (47.8 ± 5.2)	105:55:0 (17.2 ± 1.9)	114:48:2 (18.3 ± 3.0)	143:22:1 (8.4 ± 2.2)	53:109:2 (36.9 ± 2.9)	98:65:1 (21.7 ± 2.6)	121:42:2 (16.4 ± 3.0)
χ2P	0.07	0.28	0.0009	0.18	0.0075	0.57	0.095
Significant SE (cM)b	No	No	Yes	No	No	No	No

^aCentimorgans were calculated as in Table 1.

^bSignificance of the difference between the estimated map lengths for the crossover and the noncrossover met13 conversions (see materials and methods).

Random-spore analysis of MET13 gene conversions:

It was possible that a larger number of MET13 gene conversions might increase the statistical significance of any interference in the HPH-cyh2 interval. To address this possibility, we crossed the MET13-containing haploid parent of diploid MAG100 with an isogenic strain carrying the met13-5 allele (J. McCusker and J. E. Haber, unpublished data), which recombines with met13-1 to produce MET13 prototrophs. The diploid was sporulated and asci were digested with 2% β-glucuronidase (Sigma, St. Louis) to produce random spores, which were plated on medium lacking methionine. A total of 945 MET13 spores were analyzed and scored for markers on chromosome VII as well as for mating type. All the spores were apparently haploid, on the basis of their ability to mate. There was an almost 1:1 ratio of spores that were ade5 vs. ADE5, as expected for a marker very far away on the same chromosome arm. Among the 945 MET13 spores, 466 (49.4%) were associated with a NAT-HPH crossover, in good agreement with the frequency of 46.6% obtained from dissected tetrads. Considering only the 479 noncrossover cases, 370 (77.2%) apparently involved gene conversion of met13-1 (linked to NAT) and the remainder were conversions of met13-5.

Among the MET13 random spores that were crossover associated, we found statistically significant interference in both the lys5-NAT and HPH-cyh2 intervals (Table 6). In contrast, there was no notable interference, either positive or negative, exerted by MET13 gene conversions that were not crossover associated. We also treated the complete tetrads of set II as if they were random spores, selecting all segregants that carried NAT and either did or did not carry HPH (the diploid MAG100 carries the same markers as the diploid used for random spore analysis). Here, too, we found that those unordered spores containing a NAT-HPH crossover exerted interference on both the lys5-NAT and HPH-cyh2 intervals. We therefore conclude that MET13 gene conversions, accompanied by a crossover between NAT and HPH, exert interference on both adjacent intervals.

TABLE 6.

Analysis of interference based on random spores

	Random spores		Individual spores from Set II tetrads
	Met+ spores that are NAT-hph noncrossovers	Met+ spores that are NAT-HPH crossovers (P < 0.0001)	Nonselected NAT-hph noncrossover spores	Nonselected NAT-HPH crossover spores (P = 0.0005)	Total NAT-hph and NAT-HPH spores
A. Crossing over in the lys5-NAT interval among individual sporesa
Crossovers	82	37	518	25	543
Noncrossovers	397	429	2063	212	2275
χ2P (interference)	0.29 (none)	<0.0001 (positive)	0.48 (none)	0.0012 (positive)
Random spores		Individual spores from Set II tetrads
	Met+ spores that are NAT-hph noncrossovers	Met+ spores that are NAT-HPH crossovers (P = 0.0015)	Nonselected NAT-hph noncrossover spores	Nonselected NAT-HPH crossover spores (P = 0.029)	Total NAT-hph and NAT-HPH spores
B. Crossing over in the HPH-cyh2 interval among individual sporesa
Crossovers	57	27	266	13	279
Noncrossovers	422	439	2346	222	2568
χ2P (interference)	0.18 (none)	0.007 (positive)	0.67 (none)	0.042 (positive)

The χ² P-values at the heads of columns 2 and 4 compare the crossovers in those columns to the noncrossovers in columns 1 and 3, respectively. The χ² P-values in the last rows of parts A and B compare the data in those columns with the total number of NAT-hph and NAT-HPH segregants in set II, treated as single spores. Random spores were obtained from a yeast diploid strain obtained by a cross between haploid strains isogenic to those used for tetrad analysis (Table 1, set II). The diploid used to generate Met⁺ random spores was derived from the haploids MATα lys5 NAT met13-1 cyh2 KAN and MATa ade5,7 leu1 HPH trp5 met13-5 crl3. The randomness of the spores was verified by monitoring phenotypes at both the ADE5,7 and the LEU1 loci (480 Ade⁻ and 465 Ade⁺; 434 Leu⁻ and 511 Leu⁺). Among Met⁺ spores, there were 466 crossovers (371 Nat⁻ Hph⁻ and 95 Nat⁺ Hph⁺) and 479 noncrossovers (370 Nat⁺ Hph⁻ and 109 Nat⁻ Hph⁺) for the flanking markers. The inequalities in both the crossover and noncrossover classes suggest that 78% of Met⁺ spores are the result of conversion of met13-1. This bias is expected from the sign and magnitude of the slope of the conversion gradient at the MET13 locus, where met13-5 is at the low-conversion end (J. McCusker and J. E. Haber, unpublished data).

^aA comparison of MET13 prototrophic random spores derived from a met13-1/met13-5 diploid (first two columns) with equivalent segregants obtained by treating the 1451 tetrads in set II as individual spores (last two columns). Only NAT-containing spores were counted so that crossover and noncrossover events were counted only once, to permit statistical comparisons with the random Met⁺ spore data.

Evidence for a class of noninterfering crossovers amid many interfering crossovers:

(Copenhaver et al. 2002) suggested that there may be two types of crossover events in meiosis, only one of which causes interference. In the absence of pairing sites that are seen in flies and worms (Hawley 1980; Rose et al. 1984; Villeneuve 1994; Dernburg et al. 1996; McKim et al. 1998), an initial set of DSB repair interactions between homologous chromosomes may be required to promote chromosome pairing and to permit subsequent recombination events between homologs. Stahl et al. (2004) have suggested that exchanges resulting from early DSB repair might not show interference. To examine this question, we first determined the pattern of recombination in each tetrad (available as supplementary data at http://www.genetics.org/supplemental/). We then applied the maximum-likelihood analysis approach presented by Copenhaver et al. (2002), based on the assumption that crossovers would be a mixture of those distributed by a mechanism imposing interference (the counting model), and the remainder distributed without interference.

A likelihood-ratio test was conducted to determine whether a model for crossing over that included two pathways, one subject to interference and one not subject to interference, fits the yeast tetrad data better than the model that includes only interference (see Copenhaver et al. 2002 for the mathematical details of the analysis). The yeast strains used in the Haber and Stahl labs differed, and the results for the analyses on the separate data sets are statistically significantly different. Thus, we consider the data sets individually. Further, since the mathematical model views gene conversions as point events that would not be observable, we threw out all tetrads with any markers that did not segregate 2:2. While it is also possible to view non-2:2 segregating markers as “missing data” and use all the tetrads in the analysis, the computation with missing data is much more complicated, mainly because the significance of the results must be computed via simulation. For the analysis, we used the markers ADE5, KAN, LYS5, NAT, HPH, CYH2, CRL3, TRP1, and LEU1 (i.e., we did not use the markers MET13 or URA3).

Prior to the analysis reported below, tetrads from set I that were determined to be highly unlikely under either the interference-only or two-pathway recombination models were reexamined genetically and all were determined to be misscored. These tetrads were then entered correctly and used in the analyses throughout the article. A rescoring of 200 randomly chosen tetrads gave an overall tetrad-scoring error rate of ∼2%. Not all misscored tetrads lead to aberrantly large likelihood-ratio values. However, a few do because misscoring can lead to tight double recombinants, which are more likely under the two-pathway model than the interference-only model of recombination. Thus, in the analysis below, we consider not only the results of the analysis of the data, which most likely contain some errors, but also how many tetrads of the sort that lend the greatest support to the two-pathway hypothesis we can discard from each data set and still retain statistical support for the two-pathway hypothesis. If the statistical support for the two-pathway hypothesis does not depend on only a few tetrads, then the results are more robust against data entry errors.

For the data of set I, the analysis is based on 1957 tetrads. The maximum-likelihood estimate of the interference parameter (which can be interpreted biologically as the number of noncrossover DSB repair events that are required to occur between crossovers) is m = 3. The maximum-likelihood estimate of the proportion of all crossovers that are in the interference-free pathway is p = 0.08. The two-pathway model fits significantly better than the interference-only model (significance <0.01 as determined through simulations). The support for the two-pathway hypothesis does not depend on only a few tetrads. If we throw out the top 1% of tetrads, which have the greatest likelihood ratio supporting the two-pathway hypothesis, the remaining tetrads still give statistically significant support to the two-pathway hypothesis (significance <0.05 as determined through simulations). That is, the support for the two-pathway hypothesis does not depend on only a few tetrads for which the likelihood ratio is aberrantly large. The predicted distribution of crossovers per tetrad for the two-pathway model is shown in Figure 1.

From the data of set II, based on the analysis of 1337 tetrads, we calculate that m = 3 and p = 0.12 (significance <0.01). For this analysis, we discarded not only the tetrads with gene conversions at any marker but also 8 tetrads that had adjacent NPDs. While not all adjacent nonparental ditypes are necessarily in error, a few of these are likely to be in error and those few greatly but erroneously increase the significance of the likelihood-ratio test conducted. Since we cannot verify these tetrads genetically, we conservatively chose to discard them. The strong statistical support for the two-pathway hypothesis remains even after we additionally throw out the top 4 remaining tetrads supporting the two-pathway hypothesis.

Thus from both sets of data, we estimate that, according to a counting model, there would be three intervening noncrossovers for each crossover. In addition, the best fit is achieved if there are an additional 8 and 12% of crossovers that are noninterfering.

Finally, both data sets were analyzed for chromatid interference, to ask if there was a bias in the proportions of double crossovers that occurred between two, three, and four chromatids. We used the method described by Zhao et al. (1995). Because their algorithm takes time that grows exponentially with the number of intervals considered, we broke the eight intervals into three groups of four intervals: the first four, the middle four, and the last four. While not ideal, this approach minimizes the number of separate analyses while being computationally tractable. There is no evidence of chromatid interference (P-value >0.10 in all cases), justifying our use of Perkins's and Papazian's equations for estimating map length and for detecting chiasma interference, respectively.

DISCUSSION

We have analyzed crossing over and interference along a 405-kb interval including nearly all of the left arm of chromosome VII. These data provide for the first time a sufficiently large set of tetrads from which it is possible to analyze the general distribution of crossovers and their relationship to gene conversion and interference. The intervals along this chromosome arm are relatively uniform, with no exceptionally hot or cold regions, unlike the well-studied chromosome III, where the number of kilobases per centimorgan can vary by more than fivefold for intervals of comparable distance to those studied here (Baudat and Nicolas 1997). Moreover, some intervals on chromosome III show little or no interference, whereas all intervals tested on chromosome VII show approximately a two- to threefold disparity in the observed and expected numbers of double crossovers. Evidence of a nonrandom distribution of crossovers is seen in Figure 1B, where the observed number of exchanges in set I is compared with that expected from a Poisson distribution of an average of 3.3 exchanges per chromosome arm. From these data we draw several important conclusions.

First, gene conversions that are not accompanied by crossing over are not interfering, whereas analogous gene conversions that are associated with a crossover impair crossing over in adjacent intervals. This observation confirms the conclusion made by Mortimer and Fogel (1974), but places the conclusion on a firm statistical footing. The lack of interference from noncrossover gene conversions suggests that the mechanism that leads to noncrossover outcomes may be fundamentally different from that producing crossovers. This conclusion supports the genetic and physical analyses of gene conversions (Porter et al. 1993; Gilbertson and Stahl 1996; Allers and Lichten 2001a,b), indicating that gene conversions without an associated exchange might arise by synthesis-dependent strand annealing rather than the cutting of double Holliday junctions (dHJs). In contrast, gene conversions with exchange appear to require cutting of a pair of Holliday junctions.

Second, gene conversions associated with crossing over cause interference similar to that caused by crossovers in the same interval that are not associated with gene conversion. It is likely, given the isogenic origin of the chromosomes used in these experiments, that there are few, if any, additional mismatches in these intervals other than those identified by mutations and the insertion of the heterologies of the drug-resistance markers. Hence, those intervals in which there is crossing over, but no detectable gene conversion, may not have experienced mismatch repair at all. If we remove from Table 3E the instances in which NAT-HPH crossovers were accompanied by a gene conversion of MET13 and examine only tetrads in which MET13 segregated 2:2, the distributions of tetrad types in the adjacent LYS5-NAT and HPH-CYH2 intervals are statistically indistinguishable from those seen in Table 5, examining only those tetrads that had a MET13 gene conversion. We conclude that crossover interference is apparently not detectably influenced by mismatch correction associated with gene conversions.

Third, we detected interference over distances varying from ∼20 cM to >40 cM (100 kb), which is about one-quarter of the total length of the chromosome arm. We cannot distinguish whether genetic or physical measures of distance best describe the attenuation of interference, because the ratio of centimorgan to kilobase does not vary considerably, although a previous analysis of data from Drosophila suggested that genetic distance rather than physical distance provides the better basis for analysis (Lande and Stahl 1993). There does not appear to be a correlation between the size of the selected interval undergoing a crossover and the extent of interference in adjacent regions.

Molecular mechanisms governing crossing over and interference:

The double-strand break repair (DSBR) model of Szostak et al. (1983) provided a robust framework for thinking about the molecular events leading to crossing over in meiosis.

A key feature of this model was the formation of dHJs. The existence of fully ligated dHJs was demonstrated in S. cerevisiae (Schwacha and Kleckner 1994, 1995). Implicit in the Szostak et al. model is that there should be two outcomes of a DSB repair event—gene conversions associated with crossing over and gene conversions without crossover—and that these two outcomes should appear simultaneously. It is also possible that DSBR can occur via dHJs that are not fully ligated (Cromie and Leach 2000). Such structures may not be stable even when DNA is treated with cross-linking agents. Unligated dHJs could be stabilized by the Msh4, Msh5, and Mlh1 proteins (reviewed by Stahl et al. 2004). Recently Osman et al. (2003) proposed that unligated strand-invasion intermediates arising early during strand exchange could be resolved to produce crossovers without generating stable dHJ intermediates.

Recently, investigations of meiosis in S. cerevisiae have suggested that the processes of gene conversion and crossing over are more complex, as there are several different mechanisms that may simultaneously or sequentially produce both noncrossover and crossover outcomes. For example, in an ndt80 mutant strain, where expression of later meiotic genes is prevented, noncrossovers were unperturbed but crossovers were greatly reduced and dHJs remained unresolved (Allers and Lichten 2001a,b). Moreover, during ectopic interhomolog meiotic recombination, noncrossover products appeared prior to crossovers in wild-type cells; in fact, noncrossovers appeared at the same time that dHJs could first be detected (Allers and Lichten 2001a,b). Taken together, these data provide evidence that there are at least two pathways of meiotic recombination, one that does not proceed through intermediates containing dHJs, producing noncrossovers, and a second process in which dHJs are formed, leading primarily, if not exclusively, to crossovers.

Noncrossover outcomes of gene conversion might frequently result from an alternative DSBR mechanism termed synthesis-dependent strand annealing (SDSA; Nasmyth 1982; McGill et al. 1990; Gloor et al. 1991; Pâques and Haber 1999; Allers and Lichten 2001b). SDSA mechanisms differ from the Szostak et al. (1983) model in that resolution of bimolecular intermediates does not involve cutting of dHJs, and the donor chromatid emerges from the interaction unaltered. Genetic evidence supporting such mechanisms has been found in both mitotic and meiotic cells (Nasmyth 1982; McGill et al. 1990; Gloor et al. 1991; Porter et al. 1993; Belmaaza and Chartrand 1994; Ferguson and Holloman 1996; Gilbertson and Stahl 1996; Pâques et al. 1998; Ira et al. 2003; Merker et al. 2003).

Moreover, in budding yeast meiosis, there appears to be more than one mechanism to generate crossovers. Mutations in S. cerevisiae that eliminate the synaptonemal complex proteins Zip1p, Zip2p, or Zip3p; the crossover control proteins Msh4p, Msh5p, or Mlh1p; the helicase Mer3p; and the exonuclease Exo1p all cause an approximately twofold decrease in crossing over, without any reduction in gene conversions per se and multiple mutants are similar to single mutants (Ross-Macdonald and Roeder 1994; Sym and Roeder 1994; Hollingsworth et al. 1995; Khazanehdari and Borts 2000; Kirkpatrick et al. 2000; Symington et al. 2000; Nakagawa and Kolodner 2002; Bishop and Zickler 2004; Borner et al. 2004). Without these so-called ZMM proteins (Borner et al. 2004), recombination intermediates that would normally become crossovers are apparently recovered as noncrossovers; and the remaining crossovers do not exhibit interference. Recently, de los Santos et al. (2003) have provided evidence for a second crossover-producing pathway, by demonstrating that Msh4/Msh5-independent crossovers in budding yeast meiosis depend on the Mus81-Mms4 endonuclease. The absence of Mus81-Mms4 does not affect interference.

Copenhaver et al. (2002) suggested that, in yeast, as well as mammals and green plants, there are two rounds of DSBR. The rationale for two different crossover pathways stems from the observation that, unlike worms and flies, S. cerevisiae apparently lacks meiotic chromosome pairing sites that can be used to bring homologous chromosomes into intimate alignment to promote meiotic recombination (Hawley 1980; Rose et al. 1984; Dernburg et al. 1996; Villeneuve 1994; McKim et al. 1998). In this view, one set of presumably early recombination events will be used for the purpose of synapsing homologous chromosomes and is not part of the subsequent, larger set of recombination events that are subject to interference. Stahl et al. (2004) have suggested that those organisms that rely on DSB repair rather than pairing sites for synapsis also have two different recombination machineries, one of which includes the Rad51p homolog Dmc1p plus two additional proteins, Mnd1p and Hop2p. This trio of proteins is lacking in flies and worms, which have pairing sites. The initial round of DSBR promotes synapsis; crossovers arising from those intermediates are independent of ZMM proteins and do not exhibit interference. A subsequent round of DSBR generates crossovers that are dependent on the ZMM proteins and display interference.

How interference is established among the different pathways leading to crossovers and noncrossovers is still unknown at the molecular level. Recently, several articles have appeared concerning how interference is imposed during meiotic recombination in budding yeast. An analysis of the effect of ZMM mutations on the formation of molecular intermediates and on crossing over has led to the conclusion that the decision whether a given recombination event will be resolved as a crossover occurs prior to the formation of stable strand exchange intermediates and independent of the formation of the synaptonemal complex (Borner et al. 2004). This conclusion is supported by the finding that Zip2 protein assembles at sites of synapsis in a nonrandom fashion even in the absence of the formation of the complete synaptonemal complex, and that Zip2 is preferentially associated with sites of crossing over (Borner et al. 2004; Fung et al. 2004). Zip2 is found at sites of DSBs in a rad50-S strain where the Spo11 protein that creates DSBs is not removed and the DSB ends are not resected (Chua and Roeder 1998); hence, at least in this pathological condition, Zip2 assembles quite early in the process of recombination. Moreover, Henderson and Keeney (2004) have found an apparent crossover homeostasis in a Spo11 mutant that reduces crossing over more than twofold, in that the number of Zip3 foci is not reduced. One interpretation of these results postulates that the designation of some sites to be preferentially resolved as crossovers may be related to changes in chromosome or chromatin structure early in the recombination process (Borner et al. 2004). Recently Stahl et al. (2004) extended the previous suggestion (Stahl 1993) that several DSBs may be assembled into clusters in which one of the DSBs is nonrandomly selected to be resolved as a crossover. This suggestion applies the ideas of a counting model to an earlier step in DSBR.

Analysis of interference by chi-square (counting) models:

We have analyzed these data in terms of a counting (chi-square) model, modified to allow for the sprinkling of a proportion of noninterfering crossovers that were engaged in the initial synapsis of homologs (Copenhaver et al. 2002; Stahl et al. 2004). As shown in Figure 1, this model provides a good description of the crossover distribution seen in S. cerevisiae as it does in other organisms (Copenhaver et al. 2002; Housworth and Stahl 2003). In budding yeast, crossovers leading to interference depend on Msh4, Zip1, and other ZMM proteins. The absence of one or more of these proteins reduces crossing over on average about two- to threefold; but in some intervals, the reduction is more severe. A prediction of the modified counting model is that, on chromosome VII's left arm, with only 8–12% noninterfering crossovers, the absence of Msh4 should reduce crossovers to this low value. Evidence presented in the accompanying article (Stahl et al. 2004) appears compatible with this conjecture, as a msh4 mutation reduces crossing over in the met13-cyh2 and cyh2-trp1 intervals to ∼20% of wild-type levels.

According to a counting model, if one selects noncrossovers in a particular interval, one should expect that the next adjacent interval would have a greater probability of an exchange than an interval selected at random, i.e., negative interference. In Table 6 we examined crossovers and noncrossovers obtained both from random spores and from tetrads. In both cases, spores with crossovers in the HPH-NAT interval showed clear positive interference; but spores without an exchange between HPH and NAT did not exhibit negative interference. The increase should be the difference between 1/m and 1/(m + 1), where m is the number of noncrossovers between consecutive crossovers. The absence of negative interference may be obscured by the large value of m and the presence of noninterfering crossovers distributed at random.

In considering whether the presence of some noninterfering crossovers can significantly improve a model for interference, we have focused our attention on the counting model for the following reasons: (1) The counting model provides a description of interference that is superior to those provided by other models of comparable, or less, simplicity (King and Mortimer 1990; McPeek and Speed 1995; Zhao et al. 1995; Broman and Weber 2000; Lin et al. 2001); (2) since the counting model has only one adjustable parameter (m, the number of failures between each pair of adjacent successes) the addition of another parameter (p, the fraction of noninterfering crossovers) results in a model that remains suitable for computerized analysis; (3) because the chi-square model is superior to that of King and Mortimer (1990) when no noninterfering crossovers are included, the King and Mortimer (1990) model is unlikely to be superior when such noninterfering crossovers are included in the analysis; and (4) the counting model is at present the only model in which the math and the biology have been shown to be quantitatively congruent [by demonstrating that the observed fraction of conversions accompanied by crossing over equals the fraction of “successes” implied by the best-fit value of m (Foss et al. 1993)].

The data set that we have created, with nine intervals over a 405-kb region of one chromosome, should also make it possible to test other conceptions of interference once mathematical models of alternative mechanisms are developed.