Co-infection Weakens Selection Against Epistatic Mutations in RNA Viruses

Abstract

Co-infection may be beneficial in large populations of viruses because it permits sexual exchange between viruses that is useful in combating the mutational load. This advantage of sex should be especially substantial when mutations interact through negative epistasis. In contrast, co-infection may be detrimental because it allows virus complementation, where inferior genotypes profit from superior virus products available within the cell. The RNA bacteriophage φ6 features a genome divided into three segments. Co-infection by multiple φ6 genotypes produces hybrids containing reassorted mixtures of the parental segments. We imposed a mutational load on φ6 populations by mixing the wild-type virus with three single mutants, each harboring a deleterious mutation on a different one of the three virus segments. We then contrasted the speed at which these epistatic mutations were removed from virus populations in the presence and absence of co-infection. If sex is a stronger force, we predicted that the load should be purged faster in the presence of co-infection. In contrast, if complementation is more important we hypothesized that mutations would be eliminated faster in the absence of co-infection. We found that the load was purged faster in the absence of co-infection, which suggests that the disadvantages of complementation can outweigh the benefits of sex, even in the presence of negative epistasis. We discuss our results in light of virus disease management and the evolutionary advantage of haploidy in biological populations.

WHEN multiple viruses infect a single cell, hybrid progeny can be produced that contain mixtures of genetic information found in the co-infecting parents. In many DNA and RNA viruses, the genetic exchange (sex) is achieved through recombination. But some RNA viruses feature genomes divided into segments (each containing different genes), where co-infection leads to hybrids featuring reassorted mixtures of the parental segments. Data suggest that reassortment readily occurs in natural populations of viruses; e.g., Influenza virus A possesses eight segments, and strains isolated from domestic pigs sometimes feature segment mixtures originating from human-, avian-, and swine-associated viruses (Gibbs et al. 2001; Olsen 2002; Steinhauer and Skehel 2002; Wuethrich 2003).

Sex may have evolved in viruses due to the general prediction that sexuality is favored because it reduces the frequency of suboptimal allele combinations and increases the frequency of superior combinations (Fisher 1930; Muller 1932; Crow and Kimura 1965; Felsenstein 1974). Sex can affect the distribution of genotype frequencies in a population if linkage disequilibrium exists between alleles at two or more loci, that is, if some combinations, such as AB and ab, are present in excess and others, such as Ab and aB, are deficient. Thus, in large finite populations experiencing linkage disequilibrium, sexuality can be favored over asexuality because it is more efficient at relieving the mutational load brought on by deleterious alleles. One key assumption of the classic models of sex (Fisher 1930; Muller 1932; Crow and Kimura 1965; Felsenstein 1974) is that the mutations eliminated by selection are unable to recur (see, e.g., Maynard-Smith 1968; Crow and Kimura 1969). However, sex can be advantageous under recurrent mutations if deleterious mutations are negatively epistatic or more harmful together than would be expected from their separate effects (Eshel and Feldman 1970). If harmful mutations act independently each additional mutation causes a comparable reduction in fitness, and log fitness decreases linearly with mutation number (i.e., log fitness is additive; Kondrashov 1993). But negative epistasis causes log fitness to decline more rapidly with increasing mutation number. In this case, sexuality is strongly favored over asexuality because sex creates mutational combinations of very low fitness that are more quickly eliminated by selection (Eshel and Feldman 1970; Kondrashov 1988). Thus, according to the classic prediction, co-infection may be beneficial in virus populations of large size because it allows sex to efficiently purge nonrecurrent deleterious mutations. This advantage of sex should be further pronounced if mutations interact through negative epistasis.

In contrast, co-infection may be detrimental to the evolution of virus populations because it allows for ecological interactions between viruses that can slow the elimination of deleterious mutations. The infection cycle of a lytic (lethal) RNA virus features three discrete stages: attachment of the virus and its entry into the host cell, replication of RNA and assembly of viral particles, and lysis (death) of the host cell causing release of virus progeny. During the replication stage, manufactured products diffuse within the cell to create a resource pool commonly available to all co-infecting genotypes. Representative products include replication enzymes and structural proteins such as those used to construct the capsid, which houses the viral RNA. The nature of the resource pool tends to prevent an individual virus from exclusive access to any products it contributes (Nee and Maynard-Smith 1990; Turner and Chao 1999, 2003; Nee 2000). As a consequence, inferior virus genotypes can potentially benefit from superior products circulating in the pool.

The intracellular interaction between an ordinary virus and a defective virus exemplifies a less-fit genotype that profits from co-infection. A defective virus lacks one or more protein-coding functions and thus cannot reproduce when infecting a cell on its own (fitness of zero). However, if the defective virus co-infects a cell with an ordinary virus the latter can provide the needed protein(s), allowing the defective virus to be represented in the progeny (fitness greater than zero; Kassanis and Nixon 1960; Roux et al. 1991; Frank 2003; Lopez-Ferber et al. 2003). This effect is generally known as complementation—the interaction between viral gene products or gene functions during co-infection that results in increased or decreased yield of the parental viruses (Mahy 2001). Thus, co-infection may weaken selection against deleterious alleles because complementation permits greater than expected representation of unfit genotypes in the virus progeny (Novella et al. 2004).

The RNA bacteriophage φ6 provides a powerful model to examine the evolutionary consequences of co-infection in RNA viruses (Chao et al. 1992, 1997; Turner and Chao 1998; Turner 2003). The φ6 genome is divided into three segments (Semancik et al. 1973), and a single phage contains all three segments (Day and Mindich 1980). Thus, a lone phage infecting a host cell reproduces clonally, but when multiple phage genotypes co-infect a cell they generate hybrid progeny through segment reassortment (Mindich et al. 1976; Turner et al. 1999). Because recombination between segments is rare or nonexistent in φ6 (Mindich et al. 1976), each segment can be treated as a single locus and the population genetics of the virus can be conveniently described using a simple three-locus model. Recent theoretical work has predicted the evolutionary importance of complementation in populations of RNA viruses (Frank 2001; Wilke and Novella 2003), but the phenomenon has not been extensively studied in phage φ6.

Here we examine the relative strengths of sex and complementation, in determining the outcome of co-infection in a segmented RNA virus. To do so, we contrasted the ability for co-infecting and clonal populations of phage φ6 to purge the fitness load created by a set of deleterious mutations of known epistatic effect. The short duration of our experiments minimized mutational recurrence as an important factor, similar to the classic models. If sex is a stronger force, we predicted that the load should be purged faster in the presence of co-infection. In contrast, if complementation is more important we hypothesized that mutations would be eliminated faster in the absence of co-infection. Our results show that harmful mutations are removed more quickly in the absence of co-infection, demonstrating that the disadvantages of complementation can outweigh the advantages of sex in eliminating deleterious mutations. In turn, our observations suggest that co-infection did not evolve to combat the mutational load in segmented virus populations of large size.

MATERIALS AND METHODS

Bacteria and viruses:

Phages and bacteria were cultured at 25° in Luria-Bertani broth at pH 7.5 (LC medium). Overnight cultures of bacteria were grown from a single colony placed in 10 ml LC medium, with shaking incubation (120 rpm). Pseudomonas syringae pathovar phaseolicola was purchased from American Type Culture Collection (ATCC; no. 21781). L. Mindich (Public Health Research Institute, Newark, NJ) kindly provided two additional hosts: P. pseudoalcaligenes East River isolate A (ERA) and LM1034, P. phaseolicola with plasmid pLM746 containing the β-subunit of the Escherichia coli β-galactosidase gene. Viruses were grown on lawns made from overnight bacterial cultures. Agar concentrations in plates were 1.5 and 0.7% for bottom and top LC agar, respectively. Plates contained 3 ml of top agar and a 200-μl bacterial lawn. Bacterial stocks were stored in 4:6 glycerol/LC (v/v) at −80°.

Viruses (Table 1) were derived from a single clone of wild-type (wt) phage φ6 (Vidaver et al. 1973). We isolated three mutants of φ6, each harboring a deleterious mutation on a different one of the three segments. φPT88 features X, the α-subunit of the E. coli β-galactosidase gene inserted in the large (L) segment; X-marked phages form blue plaques on LM1034 lawns in the presence of X-gal (0.4% w/v; Onodera et al. 1993; Turner et al. 1999). φPT87 features h, a spontaneous host-range mutation on the medium (M) segment; h-marked phages form clear plaques on lawns containing a mixture of P. phaseolicola and P. pseudoalcaligenes ERA (200:1 ratio), whereas ordinary phages form turbid plaques because they do not kill the latter host (Chao et al. 1992). φPT313 features ts, a spontaneous temperature-sensitive mutation on the small (S) segment that prevents virus replication at 29° (Mindich et al. 1976). Mutational revertants occur very rarely, allowing effects of reversion to be ignored in our experiments. Unless otherwise indicated, phage lysates were prepared by growing viruses on a P. phaseolicola lawn for 24 hr; plaques were then collected and filtered (0.22-μm filter, Durapore; Millipore, Bedford, MA) to remove bacteria. Phage lysates were stored at −20° in 4:6 glycerol/LC (v/v).

TABLE 1.

Fitness loads associated with virus mutants

				Multiplicative model
Virus	Description	n	Log10 Wa (±SE)	Expected Log10W	Deviationb
wt φ6	Wild-type φ6 (+/+/+)	0
PT88	β-gal mutant (X/+/+)	6	−0.49*** (± 0.15)	NAc	NA
PT87	Host-range mutant (+/h/+)	6	−0.13* (± 0.09)	NA	NA
PT313	Temperature-sensitive mutant (+/+/ts)	3	−0.21* (± 0.03)	NA	NA
PT85	L and M marked hybrid (X/h/+)	9	−0.69*** (± 0.21)	−0.62	−0.07 (NS)
PT86	L and S marked hybrid (X/+/ts)	6	−3.69*** (± 0.78)	−0.70	−2.99***
PT314	M and S marked hybrid (+/h/ts)	3	−0.38** (± 0.17)	−0.34	−0.06 (NS)
PT20	Triply marked hybrid (X/h/ts)	3	−4.09*** (± 0.12)	−0.84	−3.25 (NT)

^aRaw means (±SE); asterisks denote t-tests (n − 1 d.f.) for difference of log₁₀ W from zero. *P < 0.05, **P < 0.01, ***P < 0.001.

^bApproximate F-tests (d.f. = 1, 32) from three-way factorial ANCOVA performed using SAS mixed procedure, testing for epistatic interactions between mutations. ***P < 0.001, not significant (NS); P > 0.05, not tested (NT).

^cNA, not applicable.

Phage crosses:

To cross viruses, two phage strains were mixed (each at a final concentration of 5 × 10⁸/ml) and allowed to adsorb to exponentially growing P. phaseolicola (at a final concentration of 2 × 10⁸/ml) for 40 min in a static incubator. Approximately 2.5 × 10³ infected cells were then plated with top agar on a P. phaseolicola lawn and incubated overnight. Resulting plaques were harvested and filtered to obtain a lysate featuring hybrid reassortants.

Experimental treatments:

Experimental treatments were modifications of classic single-burst assays (Stent 1963). We prepared high-titer lysates of a single clone of wt φ6 and each of the three mutants; these were then combined to obtain a mixture of the four genotypes in a 1:1:1:1 ratio. The mixture was used to found three replicate populations in each of two treatments: a high-multiplicity treatment combined 4 × 10⁸ viruses with 2 × 10⁸ exponentially growing P. phaseolicola cells to obtain a multiplicity-of-infection (MOI; ratio of phages to bacterial cells) of 2, whereas a low-multiplicity treatment used 2 × 10⁴ viruses to achieve MOI = 0.0001. Volume of treatment populations was increased to 1 ml using LC broth, and these were then incubated at 25° for 180 min to allow a single infection (burst), followed by 5 min on ice. A 500-μl sample of each mixture was filtered to acquire a lysate containing the virus progeny of the initial bursts and then diluted onto a P. phaseolicola lawn to obtain ∼400 plaques per plate. Because each plaque contains ∼10⁶ virus particles, population size expands to ∼4 × 10⁸ viruses in each propagation cycle; however, the effective population size is much closer to the harmonic mean, a value dominated by bottleneck size. Propagation cycle was completed by harvesting the plaques and titering the resulting lysate on P. phaseolicola; each cycle consisted of five generations of virus evolution (one in the tube plus four on the plate). Titered lysates were used to initiate the next propagation cycle, and the experiment consisted of up to nine cycles (45 generations). Because the P. phaseolicola hosts were grown daily from frozen stock, this prevented bacteria/phage coevolution (e.g., evolution of phage resistance). Samples of population lysates were stored in a −20° freezer for future study. We tracked loss through time of X and h mutants in treatment populations using selective plates; tracking ts is considerably more difficult because it confers lack of growth at 29°, a trait visible only when plaques are individually picked onto selective plates. Frequencies of X and h mutants were monitored by plaquing ∼100 viruses per population, every five generations.

Assuming Poisson sampling (Sokal and Rohlf 1981), the proportion of cells infected with 0, 1, and 2 phages is, respectively, P(0) = e^−MOI, P(1) = (e^−MOI × MOI)/1, and P(≥2) = 1 − P(0) − P(1). Thus, only P(≥2)/(1 − P(0)) or 0.005% of all infected cells are expected to contain two or more viruses at MOI of 0.0001, and clonal infections predominate. Similarly, 69% of infected cells are predicted to be multiply infected at MOI = 2, and co-infection predominates. There is a limit to co-infection in φ6, where regardless of MOI only two viruses (on average) are able to enter the cell (Olkkonen and Bamford 1989; Turner et al. 1999). Therefore, the limit causes the Poisson to overestimate the actual probabilities of uninfected cells, particularly at high MOI.

Paired-growth fitness assays:

After the method of Chao (1990), fitness was measured by comparing the growth rate of a test phage relative to that of wt φ6, or φ6 bearing an h marker (φ6h). The ratio of test phage to φ6 (or φ6h) in the starting mixture (R₀) and in the harvested lysate (R₁) was estimated by plaques formed on selective plates, where competitors are distinguished by plaque morphology (see above). Fitness (W) in paired-growth experiments is defined as W = R₁/R₀. Preliminary assays showed the h marker carries a 5% fitness cost (data not shown); measurements relative to φ6h reported below are adjusted to reflect the cost.

Statistical analyses:

We tested whether each mutant genotype differed in log₁₀ fitness relative to wt φ6 using t-tests. We then used a mixed-linear model with presence or absence of each of the mutations included as fixed factors and the replicate included as a random covariate. This model detects epistasis because the two-way interaction term tests whether the double mutants have fitness different from that expected on the basis of linearity on the log scale (i.e., difference from multiplicativity). The three-way interaction could not be tested due to the absence of a fitness estimate relative to the wild type for a genotype bearing no mutations.

We analyzed whether MOI affects the loss of deleterious alleles using a mixed-general-linear model to test the dependence of mutation (marker) frequency in the population as a function of MOI treatment. This model contained MOI (low vs. high) and generation (continuous) as fixed factors. Population nested within MOI and its interaction with generation were included as random factors. The analysis used square-root-transformed data of marker frequencies to improve normality. Two additional experiments focused on decline of the X at low and high MOI in a single generation under two different starting frequencies. These were analyzed as described above, except generation was treated as a categorical variable.

All mixed models were constructed using the SAS mixed procedure using SAS software release 8.2 (SAS Institute 2002), and in all, the denominator degrees of freedom for F-tests of fixed effects were estimated using the Satterthwaite approximation.

RESULTS

Fitness effects of deleterious mutations and evidence for negative epistasis:

To examine the fitness load associated with deleterious mutations X, h, and ts, we isolated three mutants of φ6, each harboring a deleterious mutation on a different one of the three virus segments (Table 1). We then conducted phage crosses to obtain hybrids bearing two and three deleterious mutations per genome. Paired-growth assays were used to estimate the mean log₁₀ fitness (log₁₀ W) of each mutant relative to wt φ6 on P. phaseolicola. Table 1 lists the raw means and standard errors of log₁₀ W for each mutant; statistical analyses showed that in every case the mean fitnesses of the single, double, and triple mutants were significantly less than that of the unmarked wild-type virus. Using these data we calculated the expected log₁₀ W for hybrids bearing two mutations, assuming that the fitness effect of each mutation was independent. We also compared the observed fitness values of genotypes carrying double mutations with those expected under multiplicativity. Results (Table 1) showed that when the X or ts mutation was combined with the h mutation, log₁₀ W of the double mutant was approximately the addition of the individual deleterious effects. In contrast, when X and ts were present in the same genome, log₁₀ W of the mutational combination was significantly less than that predicted under multiplicativity, indicating negative epistasis (Table 1). The triple mutant presented the lowest fitness of all mutational combinations, but we could not test whether this result was also due to negative epistasis (see materials and methods). Thus, the deleterious mutations alone and in combination impose a fitness load in populations of φ6, and epistasis sometimes governs this outcome.

Simulation predicting sex is advantageous in purging the mutational load:

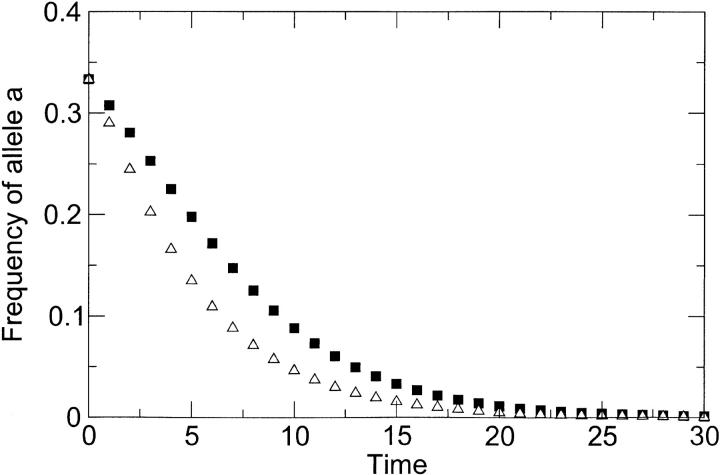
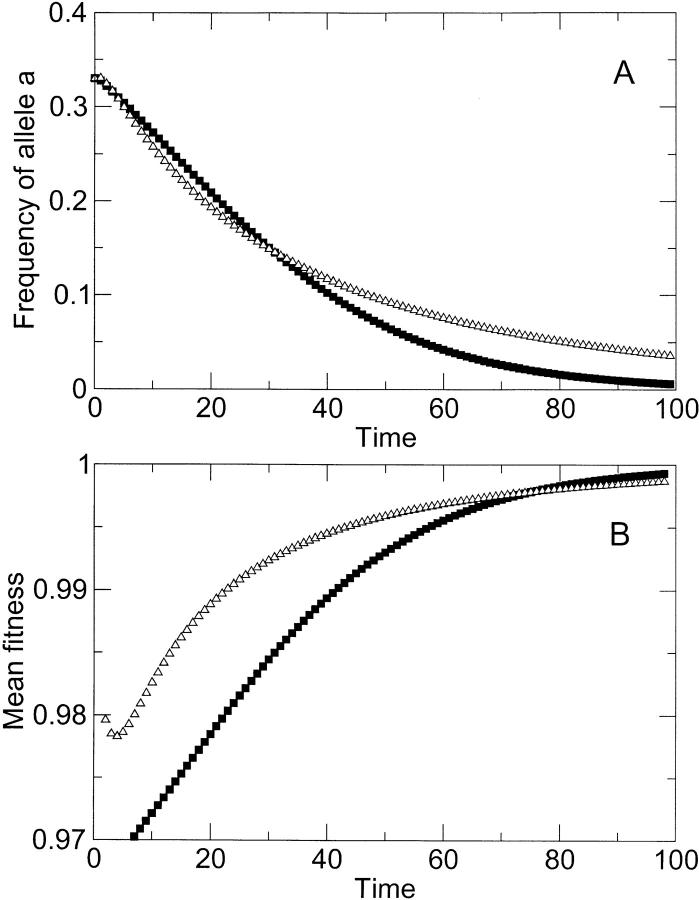
We carried out numerical simulations in a simple two-locus model to verify the expectation from classical work (Fisher 1930; Muller 1932; Crow and Kimura 1965) that sex results in accelerated elimination of deleterious mutations (details are given in appendix A). Evolving populations begin with a substantial mutational load, because nonmutated (wild-type) genotypes are a minority in a population composed mostly of less-fit mutants. As in the classic models (Fisher 1930; Muller 1932; Crow and Kimura 1965), we include the simple assumption that mutations do not recur. Thus, the model is intended to contrast the approach of sexual and asexual populations to a known equilibrium, where the wild type fixes in the population. Figure 1 shows that the mutants disappear faster in a sexual population than in an asexual population. Here, the figure shows epistatic interactions among deleterious mutations, but results are qualitatively similar when interactions are multiplicative (data not shown).

Figure 1.—

Loss of allele a (that is, mutants aB and ab) as a function of time (in generations), as predicted by the classic reassortment model of appendix A. Squares correspond to the case of selection only (that is, absence of co-infection), and triangles correspond to the case of alternating reassortment and selection (presence of co-infection). Initial frequencies of genotypes AB, aB, and Ab were 1:1:1. Deleterious effects were s_a = s_b = 0.2, and s_ab = 0.5. The model predicts faster loss of deleterious alleles in the presence of co-infection.

Disadvantage of co-infection in purging the mutational load in experimental populations:

To test the effect of MOI treatment on the ability of virus populations to combat the mutational load and the prediction that sex allows mutations to be purged faster in evolving populations (Figure 1), we created virus populations in complete linkage disequilibrium by mixing a minority of wt φ6 with a majority of the three single mutants (X/+/+, +/h/+, +/+/ts) in equal proportion.

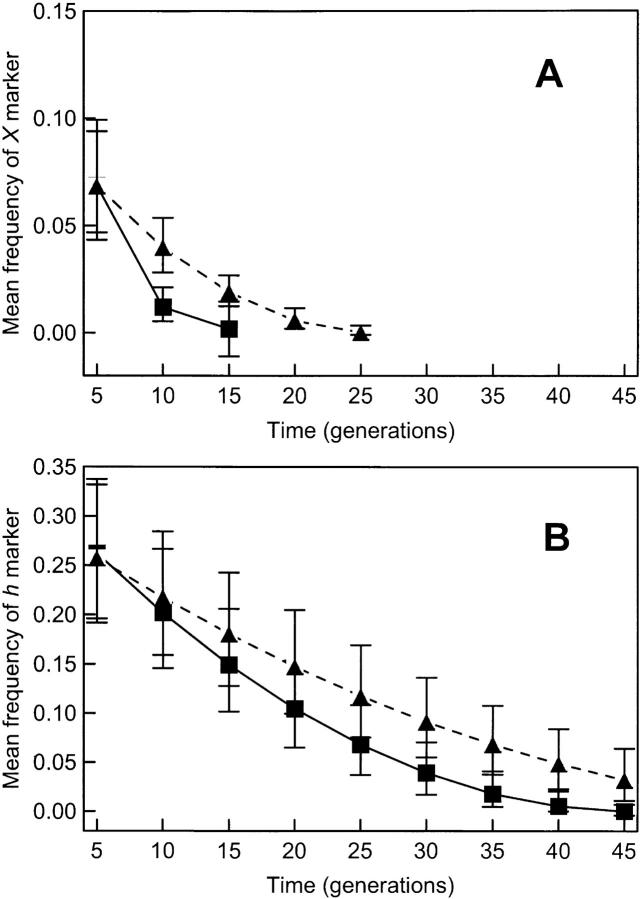
We found that the square root of the frequency of X declines linearly with increasing generation number. The X mutation was detectable until generation 15 in all three populations in the low-MOI treatment, after which its frequency dropped below the limit of detection (Figure 2A). In contrast, in the high-MOI populations X was detectable until generation 25. This result is reflected in a significantly faster rate of loss for X in the low-MOI treatment relative to the high-MOI treatment (generation × MOI interaction, F_(1,19) = 14.76, P = 0.0011).

Figure 2.—

Loss through time of virus mutants in populations propagated in the presence and absence of co-infection. Each point is the back-transformed least-squares mean frequency (±95% C.I.) of marked viruses in three replicate populations evolved at MOI = 2 (triangles) or MOI = 0.0001 (squares). Populations started with wt φ6-, X-, h-, and ts-marked viruses at an initial ratio of ∼1:1:1:1. (A) Trajectory for X mutants; (B) trajectory for h mutants. In all cases mutations disappear faster in the absence of co-infection.

Similarly, we observed that the square root of the frequency of h also declines linearly with increasing generation number. The h mutation could not be detected at generation 45 in the low-MOI treatments, whereas it was still present (mean frequency of 0.04) in the high-MOI populations until generation 45 when the experiment was terminated (Figure 2B). This difference resulted in a significantly faster rate of loss in the low-MOI populations relative to their high-MOI counterparts (generation × MOI interaction, F_(1,34) = 8.53, P = 0.0062). From these and the above data we concluded that the mutational load was purged faster in the absence of co-infection.

Demonstrating the importance of virus complementation:

We observed that deleterious mutations disappeared faster in the absence of co-infection. One explanation is that selection against deleterious mutations is weaker with co-infection, because it allows complementation to outweigh any potential selective advantage due to sex. To examine the importance of complementation, we used two approaches. First, we examined experimentally whether co-infection affects the strength of selection against one of the deleterious mutations, tracked over the course of a single virus generation. Second, we analyzed a more realistic theoretical model that incorporates the effects of complementation and compares its effects relative to reassortment.

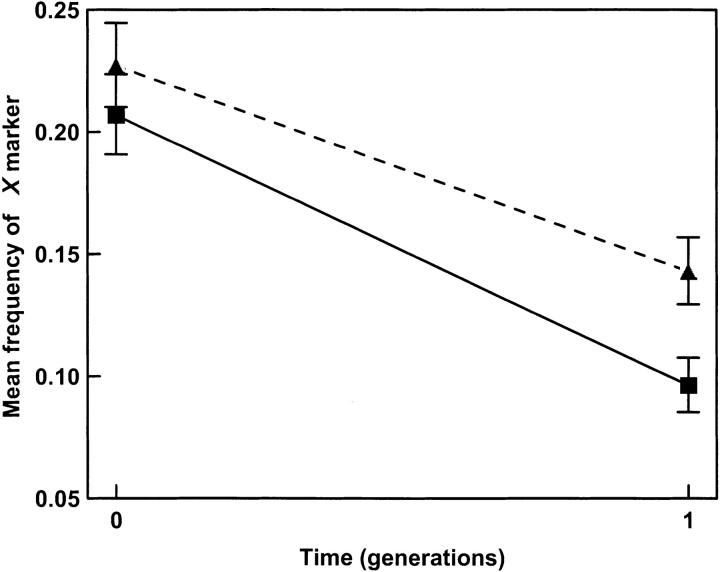
To examine the effect of complementation experimentally, we mixed wild-type and X-marked mutants at high and low MOI and tracked their relative frequencies in single-burst assays. High MOI in these assays was MOI = 5 because this MOI allowed a very high percentage of cells to be multiply infected (∼96.6% according to the Poisson distribution), creating a better signal for our measurements. If sex is more important, the frequency of mutants in the first generation should be lowest in the presence of co-infection. In contrast, if complementation is a stronger force, the mutant frequency should be lowest in the absence of co-infection.

The first of two experiments mixed wt and a majority of the three single mutants (X/+/+, +/h/+, and +/+/ts) in equal proportion, at low and high MOI. The mean (n = 12) initial frequency of X-marked genotypes in these assays was 0.217 ± 0.023 (SD) at the start of the infection cycle. This value did not differ statistically between the two treatments (independent samples t-test: t = 1.56, d.f. = 10, P = 0.150). As expected the X mutants decreased in frequency in all test populations due to the cost of the marker, but the change was more pronounced in the low-MOI populations where co-infection was generally absent (Figure 3). The significantly greater loss of the X marker at low MOI relative to high MOI suggests that X mutants are at lower frequency among progeny viruses in the low-MOI treatment relative to the high-MOI treatment (generation × MOI interaction, F_(1,10) = 12.16, P = 0.0059). A second experiment mixed wt and a single mutant virus (X/+/+) at an initial ratio of 1:1 at both low and high MOI. Although the second experiment does not contrast opposing strengths of complementation and reassortment, it is useful for accurately examining the effects of complementation in isolation. Mean (n = 6) initial frequency of X mutants was 0.474 ± 0.034 (SD) at the start of the infection cycle, and this value did not differ statistically according to treatment (t = 0.901, d.f. = 4, P = 0.418). Once again, the X mutants decreased faster at low MOI (data not shown), reflected by significantly reduced frequency of the mutants in the virus progeny at low MOI relative to high MOI (generation × MOI interaction, F_(1,8) = 59.72, P < 0.0001). The combined assays strongly suggested that the detrimental effects of complementation can be substantial and could outweigh any positive effects for sex to eliminate deleterious mutations in co-infecting virus populations.

Figure 3.—

Loss of X mutants during a single generation in populations propagated in the presence and absence of co-infection. Each point is the back-transformed least-squares mean frequency (±95% C.I.) of three replicate populations evolved at MOI = 5 (triangles) or MOI = 0.001 (squares). Populations were initially composed of wt virus and three single mutants (X/+/+, +/h/+, and +/+/ts) in equal proportion. Data show stronger selection against mutants in the absence of co-infection.

More realistic model shows that complementation can slow down the purging of the mutational load:

We have studied a more realistic model of reassortment that takes complementation dynamics into account. Our simple model is only of limited applicability to virus populations, because it assumes (in line with the classic models; Fisher 1930; Muller 1932; Crow and Kimura 1965) that reassortment happens in a separate step before selection. In reality, viruses reassort while they co-infect a cell, and the selection pressure a particular mutant experiences is strongly dependent on the other co-infecting mutants. The co-infecting mutants can complement each other's gene products, with the result that a deleterious mutant may experience a reduced selective disadvantage or none at all when co-infecting with the wild type (Novella et al. 2004). In our more realistic model, we assume that replication and reassortment happen at the same time. Further, we assume that the deleterious alleles are fully recessive, such that the presence of a wildtype allele eliminates the deleterious fitness effects of all co-infecting deleterious alleles. Our model is based on a model employed successfully by Turner et al. (1999) to study the limit of co-infection in φ6. We limit the number of co-infecting virions to at most two per cell, a number that is consistent with experimentally observed limits of co-infection in φ6 (Olkkonen and Bamford 1989; Turner et al. 1999). The details of the model are given in appendix B.

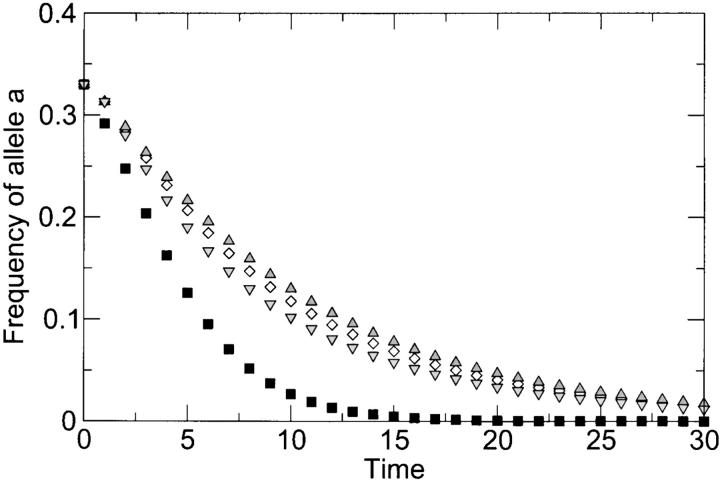
While the classical model of separate reassortment and selection predicts that recombination always purges deleterious mutations faster, as long as the double mutant is more deleterious than at least one of the single mutants (appendix A), the results are not as clear-cut for the more realistic complementation model. We have found that the deleterious effects of the single mutants play an important role in the dynamics of the system. If the single mutants are strongly deleterious, then a population in which co-infection is common will purge the mutants slower than one in which co-infection is rare (Figure 4). The degree of epistasis, that is, whether the double mutant is more or less deleterious than the combined effect of the single mutants, has little effect on this result (Figure 4). On the other hand, if the single mutants are only weakly deleterious, then the abundance level of the mutants plays a role as well. If the mutants are abundant, then they are purged faster from a population with frequent co-infection, but if they are rare, then they are purged faster from a population without frequent co-infection (Figure 5A). More generally, regardless of how weakly deleterious the mutants are, if their abundance is sufficiently low, then they are purged faster from a population in which co-infection is rare.

Figure 4.—

Loss of allele a as a function of time (in generations), as predicted by the more realistic reassortment model of appendix B. Squares correspond to the case with no co-infection (r = 0), and all other points correspond to the case of frequent co-infection (r = 0.69, equivalent to an MOI of 2) and various levels of epistasis. Initial frequencies of genotypes AB, aB, and Ab were 1:1:1. Deleterious effects were s_a = s_b = 0.3 and s_ab = 0.51 (diamonds, no epistasis), s_ab = 0.3 (upward-facing triangles, extreme case of positive epistasis), and s_ab = 1.0 (downward-facing triangles, extreme case of negative epistasis). The curve for r = 0 is independent of s_ab (and thus of the level of epistasis) because the double mutant is absent from the initial population and cannot be generated later on. The model predicts faster loss of deleterious alleles in the absence of co-infection.

Figure 5.—

(A) Loss of allele a as a function of time (in generations), as predicted by the model of appendix B. Squares correspond to the case with no co-infection (r = 0), and triangles correspond to the case of frequent co-infection (r = 0.69, equivalent to an MOI of 2). In contrast to the case of Figure 4, single mutants were only slightly deleterious. (Deleterious effects were s_a = s_b = 0.05, s_ab = 0.3; initial frequencies of genotypes were as in Figure 4.) The model predicts slower loss of abundant and faster loss of rare slightly deleterious alleles in the presence of co-infection. (B) Mean population fitness (per infected cell) in the simulations displayed in A (squares correspond to r = 0, and triangles correspond to r = 0.69).

So far in our simulations, we have focused on which population clears deleterious mutants more efficiently. However, in terms of evolutionary success, the mean fitness of the population can be a more important quantity. In a situation in which a co-infecting population directly competes with another population that does not co-infect, the population that produces less offspring (i.e., has lower fitness) will have a disadvantage, regardless of the amount of deleterious mutations that it carries. For co-infecting populations, there are two ways to measure mean fitness, one based on the mean number of offspring virions per infecting virion and one based on the mean number of offspring virions per infected cell. Both definitions can be useful, depending on the particular circumstances. If virions are abundant and susceptible cells are rare, it makes more sense to consider the amount of offspring virions produced per infected cell, but the opposite is true if virions are rare and susceptible cells are abundant. We found that if we measure mean fitness per infecting virion, then the co-infecting populations have essentially always a fitness disadvantage, unless strongly deleterious mutants are very abundant. The situation is more complicated if we measure mean fitness per infected cell. For this measure, the co-infecting populations have a higher mean fitness than populations without co-infection if the deleterious mutants are abundant (Figure 5B) and have a lower mean fitness if the deleterious mutants are rare (Figure 5B). That is, the conditions under which the coinfecting population has higher fitness coincide approximately with the conditions under which the co-infecting population clears mutants less efficiently. However, for moderately abundant deleterious mutants, the situation can be reversed (see time steps 30–70 in Figure 5B).

DISCUSSION

Theoretical explanations for the widespread occurrence and maintenance of sex often hinge on its advantage in eliminating the fitness load created by deleterious mutations, especially in the presence of negative epistasis (Kondrashov 1988). The classic argument predicts that sex is favorable in combating the mutational load in evolving populations, as long as linkage disequilibrium exists (i.e., some haplotypes are more common than expected) and mutations cannot recur (Fisher 1930; Muller 1932; Crow and Kimura 1965). We directly tested the classic prediction using the segmented RNA phage φ6 and a group of mutations of known epistatic effect. Co-infection allows φ6 to experience sex, where mutations may be more efficiently eliminated. Contrary to the classic prediction, we found that deleterious mutations in large populations of phage φ6 are removed faster in the absence of co-infection.

These data can be explained by complementation, which occurs passively between co-infecting viruses. Complementation allows less-fit genotypes to benefit by using superior products generated by co-infecting viruses of high fitness. This phenomenon is suggested to explain the unexpectedly high frequencies of low-fitness mutants in viral populations (Wilke and Novella 2003), the maintenance of transmission in nontransmissible plant viruses (for review, see Froissart et al. 2002), and the lack of viral clearance following infection by human immunodeficiency virus (HIV)-1 (Lawson et al. 2002). Also, complementation allows defective viruses to persist despite their requirement for essential gene products provided by ordinary co-infecting viruses (Steinhauer et al. 1989; Roux et al. 1991; Moreno et al. 1997; Frank 2003; Lopez-Ferber et al. 2003) and permits the evolution of multipartite viruses that feature genomic segments that are packaged into separate virus particles (Knipe and Howley 2001). Our observations indicate that complementation can be a more potent population-level force than sex in determining the outcome of virus co-infection.

In our detailed complementation model, we assume that two alleles that co-infect the same cell have equal chances to be incorporated into offspring virions. While this assumption is reasonable, it need not be correct in all cases. For example, an RNA virus segment from which a gene has been deleted can be replicated faster because of its reduced size and will therefore be present in a larger fraction of offspring virions than a co-infecting wild-type segment. (This situation is typical for defective viruses that lack certain essential genes.) It is straightforward to extend the present model to include these differences in intracellular replication efficiency, as discussed by Turner et al. (1999). The main effects caused by differences in intracellular replication efficiency are clear. If a deleterious mutant has higher intracellular replication efficiency than the wild type, then it profits even more from co-infection with the wild type than it would if both had equal intracellular replication efficiency. Thus, co-infecting populations will purge such mutants even less efficiently. On the other hand, if a deleterious mutant has lower intracellular replication efficiency than the wild type, then a co-infecting population will purge such mutants either faster or slower than a population without co-infection. Which of the two possibilities takes place will depend on the exact magnitude of the difference in intracellular replication efficiency and whether the mutant has some other defects that can be complemented by wild-type genes.

Our complementation model is similar to one recently presented by Bretscher et al. (2004) in the context of the evolution of drug resistance in HIV. The main difference between their model and our model is that Bretscher et al. studied mutation-selection balance under recurrent mutations, while we focused on the speed at which deleterious mutations are purged from a population. The differences between Bretscher et al.'s results and our results mirror the case of classical recombination models that we discussed in the Introduction: Bretscher et al. found that the sign of epistasis determines whether recombination increases or decreases the equilibrium frequency of mutants, whereas we found here that epistasis has only a minor effect on the speed at which mutants are purged from a reassorting population.

Below we discuss the relevance of our results for the evolution of intracellular interactions in phage φ6, the proposed selective advantage of haploids over diploids, effects of complementation in virus disease management, and the evolution of virus segmentation and co-infection.

Mechanisms for complementation and their evolution:

We can suggest at least two (not mutually exclusive) mechanisms that allow complementation to benefit inferior mutants in phage φ6. First, there may be an advantage in the rate of RNA replication experienced by mutant genotypes during co-infection, relative to the rate that occurs during clonal infections. That is, RNA replication of a deleterious mutant may be enhanced because it encounters the superior RNA polymerase that is generated by the wild-type genotype and that is freely circulating in the intracellular resource pool. Second, the rate of encapsidation of deleterious mutants may be increased during co-infection. During virus reproduction empty virus capsids (protein shells that house the RNA) are generated, and replicated segments enter the capsid in an ordered fashion (Qiao et al. 1997). Wild-type viruses might produce abundant capsid proteins that are freely obtainable from the resource pool, and these could allow the less-fit mutants to be encapsidated at a higher rate than occurs during clonal infections. Further work is needed to distinguish between these and other potential mechanistic explanations for our data.

Our results not only reveal a fundamentally important aspect of phage φ6 biology, but also may further explain our earlier results for the evolution of reduced fitness in φ6 populations evolved under high rates of co-infection (Turner and Chao 1998, 1999, 2003). We previously observed that viruses propagated on P. phaseolicola for hundreds of generations at high MOI evolved traits that were specific only for co-infection and that led to poor performance during clonal infections; one interpretation is that the evolved viruses are selfish genotypes (cheaters) that gain a large competitive advantage by sequestering intracellular viral products (Turner and Chao 1998). Although the selfish phages could outcompete their wild-type φ6 ancestor in environments allowing frequent co-infection, the fixation of these cheaters caused overall fitness of the population to decline due to the inherent cost of being a cheater (Turner and Chao 1999). These data conform to the expectation of evolution of lowered fitness in a population of selfish individuals as predicted by the prisoner's dilemma of game theory (Maynard Smith 1982; Turner and Chao 1999). Thus, the evolution of virus cheaters at high MOI may be due to strong selection for genotypes that adapt to environments containing frequent co-infection, by specializing in traits relating to complementation. However, this idea assumes that complementation is not entirely passive and thus can be improved through selection.

Evolution of ploidy:

Our data also pertain to the evolution of ploidy in biological populations. Diploid organisms carry one set of chromosomes from their mother and a second set from their father. Viruses are strictly haploid; phage φ6 carries one set of “chromosomes” (segments) and thus only one set of genes. But other studies have usefully compared genetic processes operating in haploids and diploids (e.g., Long and Michod 1995). Diploidy and complementation are similar because both mechanisms permit the masking of deleterious recessive alleles; it is suggested that this dominance phenomenon can be sufficient to provide a selective advantage for diploids over haploids (Kondrashov and Crow 1991; Perrot et al. 1991; Otto and Goldstein 1992). However, our results suggest a difficulty for complementation to evolve in φ6 populations because it slows the elimination of deleterious mutations. One possibility is that complementation evolves because it provides a short-term advantage where (at least some) dominance by higher-fitness alleles allows greater overall productivity of the virus population; Perrot et al. (1991) similarly showed that diploidy can evolve despite a fitness disadvantage relative to haploidy when the population reaches equilibrium. Thus, complementation might permit a co-infecting population to grow faster in the first few generations than a similar clonal population, even though the fraction of low-fitness mutants would be larger. Our simulations show some support for this idea, but the relative fitness of co-infecting and clonal populations does not follow a clear pattern. The idea could be tested more thoroughly with further simulations and experiments examining deleterious mutations and population growth dynamics in co-infecting vs. clonal populations of phage φ6. Another intriguing possibility for future study is to examine the fate of deleterious mutants of φ6 during co-infection with ordinary φ6 (as studied here) vs. co-infection with a distant virus relative of φ6 that is unable to complement the harmful mutation(s) (Mindich et al. 1999).

It is also argued that diploidy may be favored because it doubles the copy number of each gene, thus increasing the rate at which adaptive mutations are produced (Paquin and Adams 1983; Kondrashov and Crow 1991; Orr and Otto 1994). However, others have highlighted that there may be a cost of producing double the amount of DNA, which might override this potential benefit to diploids (Long and Michod 1995). These hypotheses are not overly relevant to the evolution of complementation in φ6 because the virus produces a finite number of progeny per infected cell whether or not co-infection occurs; that is, two co-infecting viruses do not generate twice the number of offspring relative to a clonal infection (Turner et al. 1999). Haploidy is very common in biological populations, and it is suggested that haploidy can be advantaged over diploidy in terms of the fixation time for adaptive mutations that are not dominant and that arise in populations of large size (Orr and Otto 1994; Greig and Travisano 2003; Zeyl et al. 2003). The reason for the advantage is that these mutations confer larger selective benefits on haploids than on diploid heterozygotes. In this work we do not consider complementation and the fate of beneficial alleles, but the phenomenon warrants future study.

Complementation and disease management:

There are broad implications of our results, especially in terms of virus disease management. Antiviral drugs are increasingly used to combat pathogenic RNA viruses of humans and domesticated animals. A common assumption is that pathogenic viruses, such as human HIV, are likely to experience reduced growth (i.e., a fitness cost) when they acquire resistance to an antiviral drug. In turn, this should prevent widespread proliferation of resistant virus genotypes because they are assumed to be competitively inferior to susceptible virus genotypes. Thus, the hope is that the antiviral drugs would be long-term effective in combating virus disease. Our data suggest that deleterious mutations (such as resistance alleles) can experience weak selection in virus systems if the environment allows for moderate levels of co-infection and the occurrence of complementation. Similarly, our results hint that complementation might allow competitively inferior viruses to persist within the host long enough for acquisition of compensatory mutations that lead to increased fitness. Thus, it becomes important to closely examine the clinical practice of using antiviral drugs to combat pathogenic viruses, especially in relation to the viral titers within the host. That is, the greater the overall density of viruses in the host, the greater the likelihood that viruses will experience co-infection and complementation in cells or tissues supporting the disease. For these reasons, we caution that passive complementation between ordinary and resistant virus genotypes might oppose selection against resistant strains in between rounds of antiviral therapy since co-infection can occur often within tissues of an infected host (R. Froissart, D. Roze, M. Uzest, L. Galibert, S. Blanc et al., unpublished results; Jung et al. 2002).

Evolution of segmentation and co-infection:

Segmentation of the RNA genome is a feature shared by a variety of animal, plant, and bacterial viruses. Different hypotheses have been proposed to explain this genome organization. One possibility is that segmentation evolved to promote more efficient packaging of the RNA genome (Qiao et al. 2000). Alternatively, segmentation may have arisen as an adaptation to promote genetic exchange (Chao 1988, 1994; Nee 1989), as similarly hypothesized for the evolution of recombination in eukaryotes (Chao 1994). However, for reassortment (or any other intracellular viral process) to confer a potential benefit, segmented viruses must experience co-infection. As in our study, it therefore becomes essential to contrast virus evolution in co-infecting vs. clonal populations, where reassortment is one of the many properties that may distinguish these environments.

Several studies have concerned the evolutionary consequences of co-infection in φ6. Chao et al. (1992)(1997) demonstrated that co-infection is beneficial in combating the effects of Muller's ratchet, the fixation of deleterious mutations in small populations subjected to intensified genetic drift; co-infection permits reassortment where mutated viruses can produce more-fit offspring bearing fewer deleterious mutations. In contrast, Turner and Chao (1998)(1999, 2003) and our data demonstrate the negative effects of co-infection in large populations of phage φ6. The latter results include the fitness reduction brought on by strong intrahost competition between viruses, the potential for evolution of selfish genotypes that reduce mean population fitness, and (here) the ability for co-infection to weaken selection against deleterious mutations. Taken together, these studies suggest that frequent co-infection can be a net disadvantage in φ6 populations of large size, despite potentially positive effects for sex to eliminate deleterious mutations through segment reassortment. It is unknown whether φ6 particles have absolute control over the number of viruses that enter a cell, but elsewhere we examine the limit to co-infection in the virus and suggest the mechanism is at least partially virus determined (Olkkonen and Bamford 1989; Turner et al. 1999). Further theoretical and empirical studies in φ6 are needed to resolve whether short-term advantages of co-infection are sufficient to promote the evolution of multiple infections.

APPENDIX A:

CLASSICAL REASSORTMENT MODEL

For completeness, here we outline a two-locus model that corresponds to the classic work on the evolution of sex as studied by Fisher (1930), Muller (1932), Crow and Kimura (1965), and Felsenstein (1974).

Consider two loci, each of which can exist in two allelic states. Let AB denote the wild type, and let s_a be the selective disadvantage of the aB genotype, s_b be the selective disadvantage of the Ab genotype, and s_ab be the selective disadvantage of the ab genotype. After one round of selection, the concentrations x_AB, x_aB, x_Ab, x_ab of the four genotypes change to

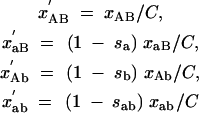A1

(primed quantities indicate concentrations after selection), with C = x_AB + (1 − s_a)x_aB + (1 − s_b)x_Ab + (1 − s_ab)x_ab. Under random reassortment, the concentrations change to

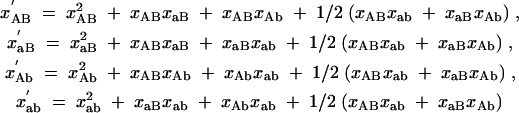A2

We disregard mutations, as they are not relevant in the current experimental setup.

For the asexual populations, one experimental passage corresponds then to a single round of selection. For the reassorting populations, one passage corresponds to one round of reassortment followed by one round of selection. We assume that the populations are inoculated with equal frequencies of the AB, aB, and Ab genotypes. Over time, the populations lose the mutant genotypes, until the AB genotype has taken over the whole population. Figure 1 shows that the mutant genotypes disappear faster in a reassorting population than in an asexual population. We find numerically that reassorting populations have this advantage whenever either s_a or s_b (or both) are smaller than s_ab, such that the double mutant is more deleterious than at least one of the single mutants.

APPENDIX B:

MODEL OF COMBINED REPLICATION AND REASSORTMENT

The model presented in appendix A does not correspond to the reality of virus replication: the model separates the two processes of reassortment and replication, whereas in reality viruses reassort and replicate at the same time while they co-infect cells. We therefore introduce a new model in which reassortment and replication are not separated. Our model is based on the model of φ6 reassortment presented in Turner et al. (1999). However, we make the simplifying assumption that co-infection is limited to at most two virions per cell (N = 2 in the terminology of Turner et al. 1999). We make this assumption because experimental evidence strongly supports a limit to co-infection of between two and three phages per cell in φ6 (Olkkonen and Bamford 1989; Turner et al. 1999). Our model is also similar to a recent model on recombination in HIV (Bretscher et al. 2004), but differs from this model in that we do not consider recurrent mutations and in details of how fitness is calculated for co-infecting viruses.

We again consider two loci, as in appendix A, and denote the respective selective disadvantages of the two single mutants and the double mutant by s_a, s_b, and s_ab. Under co-infection, we assume that the best combination of genes in the cell determines the amount of virions produced by that cell (that is, the deleterious alleles are fully recessive). Thus, a cell infected by an aB and an Ab virion produces as many virions as a cell infected by wild-type AB, while a cell infected by an Ab and an ab virion produces as many virions as a cell infected by an Ab virion alone, that is, 1 − s_b fewer virions than a cell infected by the wild type. Further, we assume that there are no intracellular differences in replication efficiency for the different alleles, so that, for example, a cell that is infected with both the a and the A allele produces virions that have equal probabilities to carry either allele. We denote the fraction of cells that are double-infected by r. The parameter r is related to the MOI via r = P(≥2)/(1 − P(0)), as explained in Experimental treatments in materials and methods.

Equations B1 define how the concentrations x_AB, x_aB, x_Ab, and x_ab change after one passage,

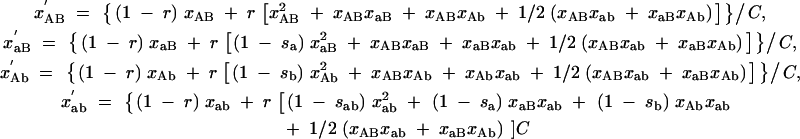B1

(primed quantities denote concentrations after the passage), with

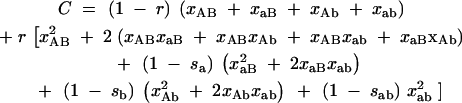B2

The parameter C can be interpreted as the mean fitness of the population, measured in units of the fitness of a wild-type virion.