Linkage Disequilibrium Mapping of Yield and Yield Stability in Modern Spring Barley Cultivars

Abstract

Associations between markers and complex quantitative traits were investigated in a collection of 146 modern two-row spring barley cultivars, representing the current commercial germ plasm in Europe. Using 236 AFLP markers, associations between markers were found for markers as far apart as 10 cM. Subsequently, for the 146 cultivars the complex traits mean yield, adaptability (Finlay-Wilkinson slope), and stability (deviations from regression) were estimated from the analysis of variety trial data. Regression of those traits on individual marker data disclosed marker-trait associations for mean yield and yield stability. Support for identified associations was obtained from association profiles, i.e., from plots of P-values against chromosome positions. In addition, many of the associated markers were located in regions where earlier QTL were found for yield and yield components. To study the oligogenic genetic base of the traits in more detail, multiple linear regression of the traits on markers was carried out, using stepwise selection. By this procedure, 18–20 markers that accounted for 40–58% of the variation were selected. Our results indicate that association mapping approaches can be a viable alternative to classical QTL approaches based on crosses between inbred lines, especially for complex traits with costly measurements.

THE genetic dissection of complex traits still presents a challenge. The oligo/polygenic character of complex traits, combined with interactions between loci, makes the task a priori difficult and intricate. In addition, environmental factors trigger and modify gene actions and thereby further complicate the analysis. Yield is the classical example of a complex trait. Yield fluctuations in relation to environmental factors are often described in terms of adaptability and stability. The latter can be considered to constitute complex traits on their own. Parameters quantifying adaptability and stability require observations across a range of environments for their estimation. The parameters are typically defined in terms of linear and quadratic functions of the genotype by environment (GE) interaction (Lin et al. 1986).

Adaptability has been studied from several perspectives, manifested by special conferences of breeders and geneticists (Tigerstedt 1997) and physiologists (Thomas and Farrar 1997). Geneticists incline to explanations in terms of favorable epistatic combinations of alleles (Allard 1997). Physiologists focus on the stress response and developmental genes involved. Forster et al. (2000) stated that developmental genes have strong pleiotropic effects on a number of performance traits in barley, but Cattivelli et al. (2002) concluded that little is known about the regulatory mechanisms controlling stress responses, mainly because all stress responses involve many genes.

The polygenic basis of complex traits has consequences for the application of quantitative trait locus (QTL) mapping methodology, as many markers that are associated with the trait need to be identified. Typically, for QTL mapping, a cross between two inbred lines is made and the cosegregation of alleles of mapped marker loci and phenotypic traits allows the identification of linked markers. For complex traits with GE interaction, this approach implies large-scale testing of special mapping populations across a range of environments. Several researchers have conducted such multi-environment trials for various traits in different plant species, e.g., drought resistance in cotton (Saranga et al. 2001), photoperiod plasticity in Arabidopsis (Ungerer et al. 2003), growth and yield in rice (Hittalmani et al. 2003), and yield in barley (Romagosa et al. 1996; Teulat et al. 2001; Voltas et al. 2001). They all succeeded in identifying loci that interacted with the environment, so-called stability loci. Some loci for stability colocalized with loci for the mean expression of the trait, while others appeared at positions where no QTL for the mean expression were found. This finding leaves inconclusive the debate about the genetic base of stability raised in the evolutionary biology literature. Two types of genetic control for stability were described by Via et al. (1995). In the allelic sensitivity model, the constitutive gene is itself regulated in direct response to the environment, whereas in the gene regulation model one or more regulatory loci are under the direct influence of the environment and the constitutive genes are switched on and off by the regulatory gene(s). Colocalization of QTL exhibiting GE interaction and QTL for stability parameters would point in the direction of allelic sensitivity models. QTL for stability parameters appearing elsewhere than the QTL for the trait itself would indicate a regulatory gene model.

In this article we explore the possibilities of mapping traits in a collection of modern cultivars, instead of in a segregating population derived from a biparental cross. We looked at methodology that has become popular in human genetics under names such as association mapping and linkage disequilibrium (LD) mapping. The success of LD mapping is obvious from the series of disease genes that have been fine mapped. For a review, see Cardon and Bell (2001). Therefore, quantitative geneticists working in crop plants have started to adapt the methodology to their situation (e.g., Jannink and Walsh 2002; see Gaut and Long 2003 for a review of LD in crop plants).

In the plant breeding context, LD mapping has several advantages over classical linkage analysis using segregating populations. First, broader genetic variation in a more representative genetic background can be included in the analyses. Second, LD mapping may attain a higher resolution. Third, multi-trial phenotypic data stored in databases can be linked to marker characterizations of the involved cultivars. Especially the latter advantage is important when evaluation of the trait is time and money consuming, as is the case with mean yield, adaptability, and stability.

A genome-wide LD scan requires many markers, the number depending on the level of LD. In sugar beet, LD extended up to 3 cM (Kraft et al. 2000), while in some Arabidopsis populations LD exceeded even 50 cM (Nordborg et al. 2002). In contrast, in maize LD diminished already after 2000 bp (Remington et al. 2001). As no data are known for barley, a first objective of our research was to obtain an estimate of the level of LD in barley. Our germ plasm consisted of 146 modern two-row European spring barley cultivars. They were homozygous, diploid lines, created by inbreeding or by doubling haploids. As the cultivars were grown all over northwest Europe during the last decade, including the United Kingdom, France, Germany, Sweden, Denmark, and The Netherlands, they were therefore representative for a large part of the European germ plasm.

The main objective of this article was the detection of associations between marker alleles and the quantitative traits mean yield, yield adaptability, and yield stability in a set of modern spring barley cultivars. Yield adaptability was defined as the slope of the regression of yield for an individual cultivar on the mean yield (over all cultivars) across environments (Finlay and Wilkinson 1963). Yield stability was defined as the mean square of deviations from the Finlay-Wilkinson line (Eberhart and Russell 1966). We used data from the official Danish barley variety trials for the national and recommended lists from 1993 to 2000. Although many QTL have been found for yield (see for an overview http://barleyworld.org/NABGMP/qtlsum.htm), only a few have been reported for yield adaptability and yield stability (Voltas et al. 2001; Malosetti et al. 2004). Yield stability is considered an important attribute of good cultivars, but selection for yield stability is too time and money consuming to be carried out routinely.

Earlier attempts for establishing association between traits and markers across germ-plasm collections concerned oat, rice, maize, sea beet, and barley. In oat, Beer et al. (1997) found associations between markers and 13 quantitative traits in a set of 64 landraces and cultivars. In rice, Virk et al. (1996) predicted the value for 6 traits using multiple linear regression. In maize, Thornsberry et al. (2001) found associations between Dwarf8 polymorphisms and flowering time. In sea beet, Hansen et al. (2001) mapped the bolting gene, using AFLP markers in four populations. In barley, Igartua et al. (1999) concluded that marker-trait associations for heading date, found in mapping populations, were, to some extent, maintained in 32 cultivars. Ivandic et al. (2003) found association between markers and the traits of water-stress tolerance (chromosome 4H) and powdery mildew resistance in 52 wild barley lines. Chromosome 4H is, according to Forster et al. (2000), known for many loci involving abiotic stress tolerance, including salt tolerance, water use efficiency, and adaptation to drought environments.

This article is, to the best of our knowledge, the first publication on the extent of LD in a large collection of commercial barley cultivars and on the usage of LD to explore the genome for markers linked to complex traits such as mean yield and yield stability.

MATERIALS AND METHODS

Plant material and quantitative traits:

Yield data of 146 modern European two-row spring barley cultivars were obtained from the official Danish variety trials over the period 1993–2000. Each year new cultivars were added to the trials, while others were discarded. The number of cultivars tested per year varied between 49 and 66. The number of locations at which a cultivar was tested varied between the years: 15 for 1993, 13 for 1994, and 5 for 1995–2000. Cultivars were tested in varying numbers of environments (year by location combinations) with a minimum of 5, a maximum of 50, and an average of 15 environments per cultivar. Each trial consisted of two replicates. More details can be found at http://www.planteinfo.dk.

The yield trials were either treated or not treated with chemicals to control leaf diseases. For treated and untreated trials, Finlay-Wilkinson regression coefficients were estimated as a measure for yield adaptability (b_i; Finlay and Wilkinson 1963). As a measure for yield stability, mean squared deviations from regressions were estimated (s_i²; Eberhart and Russell 1966). Both statistics were based on the regressions of yields for individual genotypes in a trial on an environmental index, the latter supposed to express the general growing conditions in the trial. We estimated the environmental index by the environmental effects obtained from the fit of an additive model (phenotype = genotype + environment). Values of s_i² were log transformed for subsequent analyses. Yield, stability, and adaptability will be called YLD, STAB, and ADAP, respectively, with subscript tr or untr referring to treated and untreated trials, respectively.

AFLP markers:

The testing authorities supplied us with seed of all the cultivars tested in 1999. For cultivars not tested in 1999, seed was provided by the original breeders. Collection of DNA from leaf tissue and AFLP analysis were done as described by Qi and Lindhout (1997). Fourteen primer combinations were employed: E33M54, E35M48, E35M54, E35M55, E35M61, E37M33, E38M50, E38M54, E38M55, E39M61, E42M32, E42M48, E45M49, and E45M55. Individual markers were identified following the profiles of Qi and Lindhout (1997)(also see http://wheat.pw.usda.gov/ggpages/Qi/). Markers were scored for presence (1) or absence (0) of a band. When two markers were very closely linked, or when they were allelic, the marker with most missing values was discarded. In total 286 polymorphic markers were scored within this germ plasm. For analyses, 236 markers with band frequencies between 5 and 95% were used.

Map position based on an integrated map:

Map positions of markers were derived from an integrated map using three segregating populations: (1) L94 × Vada, 568 markers (Qi and Lindhout 1997); (2) Apex × Prisma, 252 markers (Yin et al. 1999); and (3) GEI119 × Gunhild, 137 markers (Koorevaar 1997). The integrated map was constructed with the software package JoinMap (Van Ooijen and Voorrips 2001). The assumption was made that AFLP markers with equal gel mobility were identical (Rouppe van der Voort et al. 1997; Waugh et al. 1997). The role of the integrated map is critical in our study. Every genetic map created with real life data, and therefore probably including scoring and other errors, will give rise to some mistakes in the order of the marker loci. The integration of three different maps into one is another source of errors. For that reason, the AFLP data were checked with great care, and any suspicious marker was removed. Furthermore, we carried out an extra control measure in the form of reference gels, including all markers and all parental lines, to double-check gel mobility and to minimize erroneous equal labeling of markers.

The number of markers common to two or three populations was 89, varying from 8 on chromosome 1 to 18 on chromosome 7. To constrain the number of possible map orders, five loci per chromosome provided a “skeleton map” (fixed order) to which other markers were added. The fixed-order loci were chosen to cover well the chromosomes from the map of Qi et al. (1998). The latter map was aligned to the RFLP map of the Proctor × Nudinka population (Becker et al. 1995).

Goodness of fit of proposed marker orders and positions on chromosomes were tested by a statistic that measured the overall discrepancy between map distances based on “direct” estimates of recombination frequencies between individual markers on the one hand and the fitted map distances based on all available pairwise recombination frequencies on the other hand (Stam 1993). This statistic approximately follows a chi-square distribution under the null hypothesis of a correct order of the markers on the map, with degrees of freedom equal to the total number of pairwise distances minus the number of adjacent pairs of markers on the chromosomes.

Population structure:

To investigate possible structure in the set of cultivars, various analyses were performed. First, an agglomerative hierarchical cluster analysis was performed on band incidence. As the measure for proximity, the Jaccard coefficient was chosen, while for the cluster algorithm average linkage, also known as UPGMA, was used (Gordon 1981). Second, a correspondence analysis was applied to the cultivar by marker matrix of band incidences (Greenacre 1984) and the plot of cultivar scores on the first two axes was used to investigate population structure. Finally, a Bayesian-model-based clustering was performed as described by Pritchard et al. (2000). The basis of this clustering method is the allocation of individual genotypes to groups in such a way that Hardy-Weinberg equilibrium and linkage equilibrium are valid within clusters, whereas these forms of equilibrium are absent between clusters. As we worked with homozygous lines, we adapted the method to our situation by using the method to detect exclusively association between marker loci while ignoring the within-marker locus situation. The analysis was applied once to the complete set of all markers and once to a set of moderately independent markers.

Linkage disequilibrium:

A commonly used measure for quantifying and comparing LD in the context of LD mapping is the squared correlation coefficient r² between pairs of biallelic markers (Pritchard and Przeworski 2001). We have calculated r² between all pairs of loci and plotted it against the genetic distance in centimorgans to determine the map distance across which LD can occur within our set of cultivars.

Marker-trait associations:

Pearson correlation coefficients were calculated among the traits YLD, ADAP, and STAB (treated and untreated), on the one hand, and band incidences for markers on the other hand. This is effectively equivalent to t-tests using marker incidence as a grouping variable. The test statistic for Pearson correlations, t* = r (n − 2)^1/2/(1 − r²)^1/2, with r the correlation and n the number of observations, follows a t_(n−2) distribution under the null hypothesis. To control for multiple testing, we tested at a false discovery rate (FDR) of 0.20 (Benjamini and Hochberg 1995). The false discovery rate, q*, is defined as the expected proportion of true null hypotheses within the class of rejected null hypotheses. In practice, the procedure works as follows. Let H₍₁₎, H₍₂₎, … , H_(m) represent a series of hypotheses sorted by increasing P-value, P₍₁₎, P₍₂₎, … , P_(m), so that P₍₁₎ ≤ P₍₂₎ ≤ … ≤ P_(m). Then the hypotheses H₍₁₎, H₍₂₎, … , H_(k) are rejected, where k is the largest i for which P_(i) ≤ (q* i)/m. In analogy to LOD profiles in QTL testing, association profiles were created by plotting P-values for marker-trait correlations against chromosome position. Association profiles graphically display the LD region around an associated marker and can help in the assessment of the “credibility” of a marker-trait association. To verify the relevance of our marker-trait associations, we checked the literature for QTL in the regions near markers with significant trait association.

In addition to studying marginal marker-trait associations, i.e., correlations between markers and traits without correction for associations with other markers (cf. simple interval mapping), YLD, ADAP, and STAB were regressed on markers using multiple linear regression (cf. composite interval mapping) in an attempt to investigate conditional marker-trait associations. The final objective of this exercise was to obtain an estimate of the minimum and maximum theoretical trait values achievable by selective choice of marker alleles. Two methods for model construction were used. First, a stepwise regression procedure (Montgomery and Peck 1982) with an F-value for entering the regression model, F_in, of 4 and an F-value for dropping out of the model, F_out, of 1 was used. The marker set for model building was the full set of markers. In this way a model with a good combination of markers out of the complete set of markers was selected. Second, a regression model was constructed on the basis of the subset of markers that had significant correlation on an individual basis with the trait. In this second model, we used a combination of the individually best markers to predict the response, no selection was applied any more. The differences in predictions from both models illustrate the necessity of accounting for correlations between markers. We chose as goodness-of-fit statistics the amount of explained variation adjusted for the number of regressors (R²_adj; Montgomery and Peck 1982).

RESULTS

Yield, stability, and adaptability:

Table 1 presents several statistics concerning YLD, ADAP, and STAB. Mean YLD_tr was higher than YLD_untr, as expected. The correlation between the treated and untreated versions of YLD, ADAP, and STAB was highly significant. YLD was weakly negatively correlated with STAB, treated and untreated.

TABLE 1.

Descriptive statistics for yield, adaptability, and stability

	YLD (kg/ha)		ADAP (bi)		STAB lns2i
	Treated	Untreated	Treated	Untreated	Treated	Untreated
Average	5779.3	5367.9	1.001	0.9978	1.8639	1.6041
Minimum	4841.0	4123.6	0.713	0.595	−1.8363	−3.5166
Maximum	6377.1	6037.9	1.490	1.254	4.0054	3.5825
Variance	2.7046	3.835	0.1061	0.0978	0.8192	0.8426
Correlations
YLDtr
YLDuntr	0.90***
ADAPtr	−0.06	−0.08
ADAPuntr	−0.11	−0.19	0.76***
STABtr	−0.25*	−0.34***	0.15	0.15
STABuntr	−0.29**	−0.45***	0.02	0.06	0.60***

Descriptive statistics for yield (YLD), adaptability (ADAP), and stability (STAB). The yield trials were either treated (tr) or not treated (untr) with chemicals to control leaf diseases.

^*P < 0.01,

^**P < 0.001,

^***P < 0.0001.

Integrated map and map position:

The final integrated map, based on three crossing populations, consisted of 811 AFLP markers on a genome of 1052 cM (Kosambi mapping function) with eight gaps >10 cM and one gap >20 cM (data not shown). The quality of the integrated map was good, considering the low values for the goodness-of-fit statistics for map order across the chromosomes (see materials and methods). Of the 236 markers that were found to be polymorphic across the cultivars, 123 appeared also on the integrated map of the crossing populations. The other 113 markers were not mapped, because they were apparently present or absent in both parents of the populations. Coverage figures for the 123 mapped markers showed 12 gaps between 10 and 20 cM, 6 gaps between 20 and 30 cM, and 7 gaps of >30 cM. However, some of the 113 unmapped loci may be located inside those gaps.

Population structure:

The 236 AFLP markers allowed unique identification of each cultivar. To investigate population structure, which could cause associations in the absence of linkage, we performed three types of analysis. A hierarchical cluster analysis with proximity defined by Jaccard coefficients and average linkage as clustering algorithm produced a dendrogram that hinted at the existence of two subgroups. Correspondence analysis confirmed this split in the germ plasm (Figure 1). The split could not be explained by geographic arguments or by a separation of fodder and malting barleys. Various analyses using the Bayesian clustering methodology described in Pritchard et al. (2000) did not provide information on possible population structure. The posterior probabilities for the numbers of clusters either remained about constant or kept steadily increasing with the number of clusters without individual varieties being allocated clearly to specific clusters. In both cases we concluded for absence of population structure.

Figure 1.—

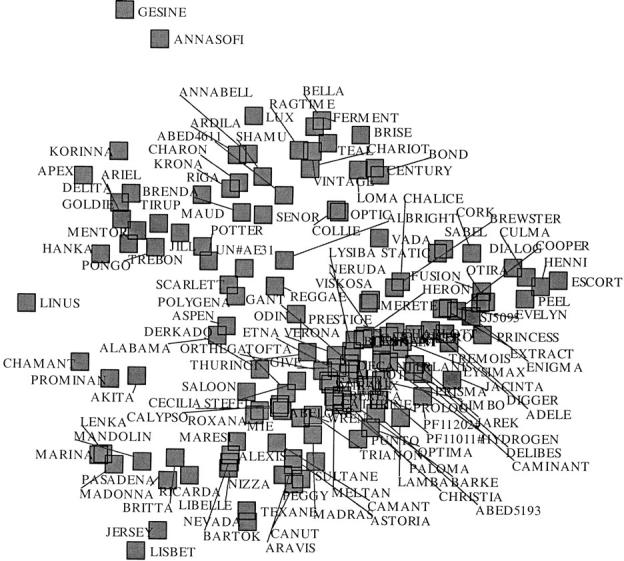
Correspondence analysis plot for 146 modern barley cultivars based on 236 AFLP markers. The germ plasm roughly falls apart in the subgroups at the top left and the bottom right in the plot.

Linkage disequilibrium:

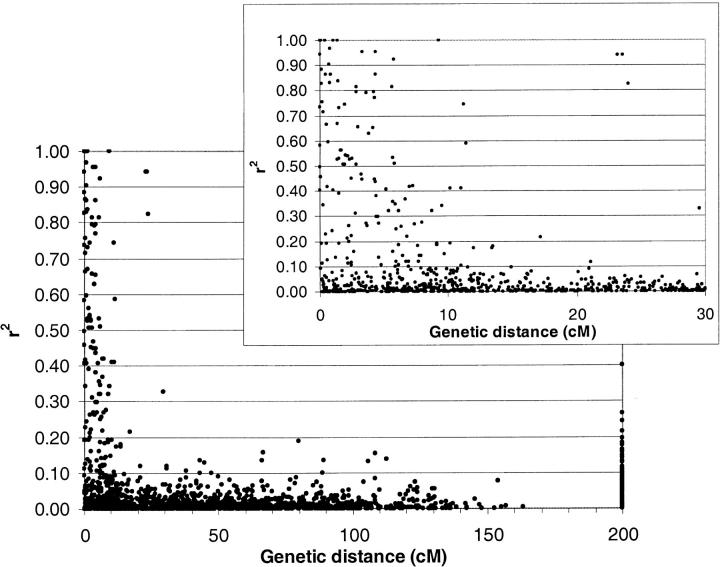
Figure 2 gives LD as a function of genetic distance. LD was very common for distances <10 cM. Occasionally, LD occurred between loci farther apart. The r² between unlinked loci on different chromosomes was always <0.28, except for two markers on chromosomes 3 and 5, which had an r² of 0.40. These two markers also exhibited markedly different band frequencies between the two subgroups found by the cluster and correspondence analysis. In contrast to a priori expectation, some marker pairs that were close together on the integrated map were not correlated across the cultivars and so were in linkage equilibrium (LE). To check whether this unexpected apparent LE could be explained by misplaced markers due to the integration of maps from different mapping populations, we investigated the closely linked marker pairs in more detail. There were in total 53 marker pairs with distance <1 cM, of which 32 had a significant correlation (P < 0.01), while 19 pairs were not significantly correlated (P > 0.01) and thus in LE. Of the 19 pairs in LE, 13 contained two markers that were mapped using different populations, while 6 pairs consisted of two markers that were mapped in the same population. The three loci pairs in LE with the shortest distance between them (<0.06 cM) were all mapped in the L94 × Vada population. This shows that the map integration in itself could not be the only explanation for apparent LE on short distances.

Figure 2.—

Linkage disequilibrium (r²) as a function of genetic distance for 123 AFLP loci on the barley genome. LD has been determined with 146 modern barley cultivars; the genetic distance has been determined with an integrated map from three segregating populations. A genetic distance of 200 cM was chosen to represent unlinked loci on different chromosomes. The inset provides an enhanced view of LD decay.

Association:

Table 2 gives an overview of markers with their genome positions and correlations with traits. For the correlations, P-values and q* values of the FDR analysis are presented. All markers with q* ≤ 0.20 belong to a group for which the proportion of false positives is no greater than 0.20. Only markers with a P < 0.01 for at least one of the traits are shown.

TABLE 2.

Correlation of AFLP markers with yield, adaptability, and stability

			Yield						Adaptability (bi)						Stability lns2i
Treated			Untreated			Treated			Untreated			Treated			Untreated
AFLP	Chromosome	Position (cM)	r	P	q*	r	P	q*	r	P	q*	r	P	q*	r	P	q*	r	P	q*
E38M55-205	1	95.9	0.02	0.04	−0.24	*	−0.18	0.06	0.07
E38M50-119	1	105.8	−0.10	−0.08	0.24	**	0.19	0.06	−0.12
E42M48-270	2	6.7	0.13	0.15	−0.13	−0.16	−0.23	*	q	−0.06
E35M54-412	2	33.7	−0.21	−0.28	***	q	−0.18	−0.08	0.15	0.21
E45M55-086	2	36.2	0.08	0.12	−0.06	−0.13	−0.26	**	q	−0.15
E42M32-333	2	94.5	−0.21	−0.22	*	q	−0.05	−0.03	−0.10	−0.05
E35M48-250	3	19.5	−0.29	***	q	−0.29	***	q	−0.04	−0.06	0.10	0.14
E45M55-142	4	45.8	0.10	0.16	0.05	0.05	−0.26	**	q	−0.22
E33M54-282	4	47.8	−0.18	−0.25	*	q	−0.05	−0.02	0.15	0.21
E42M48-139	4	48.3	0.10	0.12	−0.06	0.07	−0.22	*	−0.12
E45M55-212	4	86.1	−0.22	*	−0.21	q	0.15	0.08	0.03	0.05
E35M55-262	4	105.0	−0.14	−0.16	−0.13	−0.17	0.30	***	q	0.16
E37M33-083	5	129.5	−0.17	−0.22	*	q	0.14	0.04	0.12	0.04
E42M48-103	6	35.1	0.20	0.20	−0.04	−0.05	−0.32	***	q	−0.15
E38M55-114	7	0.0	0.27	**	q	0.28	**	q	−0.06	−0.09	−0.06	−0.09
E38M54-247	7	7.4	0.30	***	q	0.34	****	q	−0.06	−0.05	−0.11	−0.04
E38M50-385	7	28.5	−0.15	−0.23	*	q	−0.17	−0.04	0.12	0.15
E38M50-355	7	32.4	0.24	*	0.31	***	q	−0.06	−0.12	−0.21	−0.24
E35M48-380	Unmapped	−0.27	**	q	−0.25	**	q	−0.20	−0.12	0.15	0.22	*
E35M54-069	Unmapped	0.19	0.25	**	q	0.17	0.03	−0.17	−0.22	*
E35M61-106	Unmapped	−0.22	−0.23	q	−0.22	−0.19	0.14	0.25	*
E38M50-382	Unmapped	0.24	*	0.19	0.00	0.02	−0.05	−0.04
E38M50-388	Unmapped	−0.07	−0.10	0.16	0.26	*	0.03	0.09
E38M50-390	Unmapped	0.21	0.28	***	q	0.07	−0.04	−0.25	**	q	−0.26	**
E38M55-110	Unmapped	−0.08	−0.08	0.23	*	0.15	0.00	0.00
E42M32-187	Unmapped	0.20	0.26	**	q	0.15	0.02	−0.24	**	q	−0.22
E42M32-271	Unmapped		−0.07			−0.05			0.02			0.12			−0.33	****	q	−0.25	**

Only AFLP markers with a significant marker-trait correlation are given (P < 0.01). A q indicates that the false discovery rate control value calculated according to Benjamini and Hochberg (1995) is <0.20; see materials and methods. The position on the chromosome is given in centimorgans from the top of the short arm.

^*P < 0.01,

^**P < 0.005,

^***P < 0.001,

^****P < 0.0001.

Taking q* ≤ 0.20 as the threshold, 4 markers could be identified for YLD_tr, 15 markers for YLD_untr, and 8 markers for STAB_tr. No markers with significant association for STAB_untr and ADAP_tr/untr were found at q* ≤ 0.20. The most significantly correlated markers for YLD_tr/untr were located at the top of chromosome 7 (7.4 cM) and chromosome 3 (19.5 cM). The most significant correlations for STAB_tr were for a marker with unknown position and for markers on chromosomes 4 and 6. In general, markers were correlated with only one of the traits. Two unmapped markers formed an exception as they were correlated with both YLD and STAB. As none of the markers found associated with a trait differed in allele frequency between the two subgroups of cultivars identified by the cluster analysis and the correspondence analysis, we concluded that the associations were not caused by substructure in the germ plasm.

In Figure 3 the P-value of the correlation is given as a function of map position for a selection of trait-chromosome combinations. For YLD_untr a peak appeared on chromosome 2 at 34 cM with a rapid decline at 5 cM before the peak and 1 cM after the peak. The same peak showed up in the YLD_tr graph, but with a lower magnitude. For both YLD_tr and YLD_untr, peaks appeared on chromosome 3 at 20 cM. No mapped markers were located before this peak, and the markers shortly beyond this peak showed a fast decrease in correlation, suggesting LD across a short distance. On chromosome 7 (5H), there were peaks at 7 and at 32 cM. The first peak at 7 cM was preceded by a significant correlation at 0 cM, suggesting LD over a distance of at least 7 cM. The second peak at 32 cM decayed already 1 cM before and 2 cM after the peak.

Figure 3.—

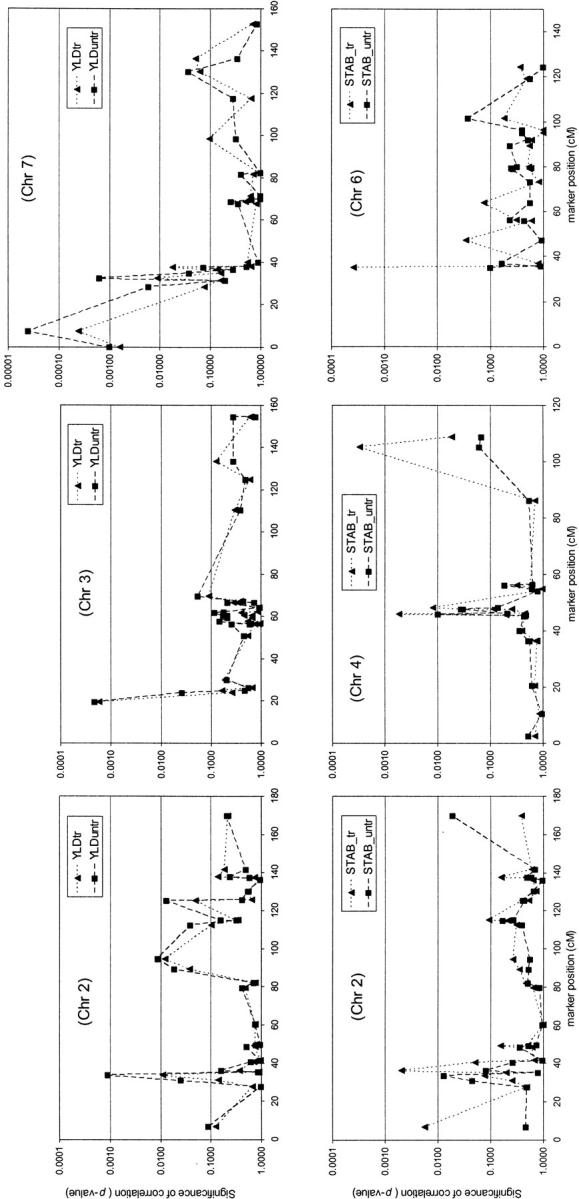
Association profiles showing the P-values of correlation between marker and trait against the position of the marker on the chromosome. (Top) Yield on chromosomes 2, 3, and 7. (Bottom) Yield stability on chromosomes 2, 4, and 6.

For STAB_tr, peaks were found at chromosomes 2, 4, and 6. All peaks faded rapidly. On chromosome 4 at 46 cM, the graph jumped up and down in the 46–48 cM area. After the first peak at 46 cM, a drop followed and then a second (smaller) peak followed at 48 cM.

In Table 3 an overview is given of the trait-associated markers, their map position, and related QTL found in the same region by other authors. All of our YLD-associated markers and three of the STAB-associated markers were found in a region where at least once before a yield QTL has been reported. In addition, two of the three STAB-associated markers also coincided with a region known to exhibit QTL × E interaction (Voltas et al. 2001; Malosetti et al. 2004).

TABLE 3.

Trait-associated markers and QTL reported in literature in the same region

Associated in this research			Reported in literature
Chromosome	Position (cM)	Associated with	Bin	QTL for	Population	Author
2	33.7	YLDtr/untr	3–4	Yield	Steptoe/Morex	Hayes et al. (1993)
2	94.5	YLDuntr	10	Yield	Steptoe/Morex	Hayes et al. (1993)
3	19.5	YLDtr/untr	3	Yield	Blenheim/Kym	Bezant et al. (1997)
4	47.8	YLDuntr	5	Yield	Harrington/Morex	Marquez-Cedillo et al. (2000)
4	86.1	YLDuntr	8–10	Yield	Harrington/TR306	Tinker et al. (1996)
5	129.5	YLDuntr	12–13	Yield	Harrington/Morex	Marquez-Cedillo et al. (2000)
7	0/7.4	YLDtr/untr	1–2	Yield	Blenheim/Kym	Bezant et al. (1997)
Yield	Apex/Prisma	M. Jarso (unpublished results)
7	28.5/32.4	YLDtr/untr	3	Yield	Harrington/TR306	Tinker et al. (1996)
2	6.7	STABtr	1	—	—
2	36.2	STABtr	3–4	Yield	Steptoe/Morex	Hayes et al. (1993)
G × E	Steptoe/Morex	Voltas et al. (2001);   Malosetti et al. (2004)
4	45.8	STABtr	5	Yield	Harrington/Morex	Marquez-Cedillo et al. (2000)
4	105.0	STABtr	11	Yield	Steptoe/Morex	Hayes et al. (1993)
G × E	Steptoe/Morex	Voltas et al. (2001)
Stress-response	Several	Forster et al. (2000)
6	35.1	STABtr	3–4		—	—

Significant marker-trait associations, marked with q in Table 2, linked to QTL reported in literature. The traits were yield (YLD) and yield stability (STAB). The yield trials were either treated (tr) or not treated (untr) with chemicals to control leaf diseases. The Bin positions were determined using the Bin maps available at http://www.barleyworld.org, where an overview of known QTL also can be found. The position on the chromosome is given in centimorgans from the top of the short arm.

Multiple linear regression:

Using all 236 markers, mapped and unmapped, we tried to describe variation in YLD, ADAP, and STAB by a linear regression model including marker predictors. Stepwise regression resulted in regression models containing 18–20 markers (Table 4). The R²_adj, adjusted for the number of predictors in the model, was 55/56% for YLD_tr/untr, 45/40% for ADAP_tr/untr, and 56/58% for STAB_tr/untr. Therefore a large amount of the variation of these traits could be described by regression on markers (band incidence). By choosing the adequate marker profile, i.e., by creating a hypothetical marker genotype, the regression models could be used to predict minimum and maximum theoretical trait values. For YLD_tr, the minimum and maximum value were 3631 and 7804 kg/ha, respectively. This is much less and much more, respectively, than the realized minimum and maximum of 5779 and 6377 kg/ha. So, if a genotype with all the favorable alleles for the selected set of markers could be created, this genotype would theoretically yield 7804 kg/ha. A similar transgression can be observed for the other traits.

TABLE 4.

Predicting phenotypes with multiple linear regression analysis

				Realized			Predicted with selection
Trait	Selection of markers	No. of selected markers	R2adj (%)	Mean	Min	Max	Min	Max
YLDtr	Stepwise	19	54.5	5779	4841	6377	3631 ± 330a	7804 ± 305
P < 0.05	29	32.9	4782 ± 418	6603 ± 401
P < 0.01	7	25.8	5414 ± 65	6155 ± 66
q* < 0.20	4	21.7	5588 ± 37	6143 ± 67
YLDuntr	Stepwise	18	56.4	5368	4124	6038	2494 ± 343	7117 ± 159
P < 0.05	35	40.2	3944 ± 299	6967 ± 318
P < 0.01	13	29.9	4400 ± 209	6309 ± 207
q* < 0.20	19	34.0	4395 ± 221	6131 ± 219
ADAPtr	Stepwise	18	44.9	1.00	0.60	1.25	0.41 ± 0.08	1.70 ± 0.08
P < 0.05	25	17.4	0.76 ± 0.07	1.27 ± 0.08
P < 0.01	3	10.9	0.91 ± 0.02	1.05 ± 0.01
q* < 0.20	0	NA	NA	NA
ADAPuntr	Stepwise	18	40.3	1.00	0.71	1.49	0.55 ± 0.06	1.68 ± 0.08
P < 0.05	14	21.3	0.84 ± 0.03	1.30 ± 0.05
P < 0.01	1	1.8	0.99 ± 0.01	1.05 ± 0.03
q* < 0.20	0	NA	NA	NA
STABtr	Stepwise	18	55.7	1.60	−3.52	3.58	−6.29 ± 0.72	9.10 ± 0.87
P < 0.05	21	25.7	−2.19 ± 0.74	3.81 ± 0.73
P < 0.01	9	22.7	−0.76 ± 0.46	2.40 ± 0.37
q* < 0.20	8	23.2	−0.69 ± 0.42	2.29 ± 0.23
STABuntr	Stepwise	20	57.5	1.86	−1.84	4.00	−7.27 ± 0.80	9.55 ± 0.80
P < 0.05	18	18.2	−0.68 ± 0.60	3.27 ± 0.57
P < 0.01	5	13.2	0.71 ± 0.40	2.01 ± 0.27
	q* < 0.20	0	NA				NA	NA

Predicting YLD, ADAP, and STAB with a subset of markers. The subset was chosen either using stepwise regression starting with the full set or on the basis of the significance of correlation of the markers with the trait of interest. R²_adj is the adjusted R². Realized mean, min(imum), and max(imum) values are given for comparison. Predicted min and max values were calculated using the regression model with the least/most favorable allele configuration. Yield is in kilograms per hectare. NA, not available.

^a± standard error.

Performing the regression with the subset of only those markers that showed significant marker-trait correlations on an individual basis, and so without further selection by a regression subset procedure, led in all cases to a lower R²_adj. In addition, predicted minimum and maximum values were less extreme, and in most cases did not exceed realized minima and maxima.

The final sets of markers selected by the two different strategies contained only a very modest overlap. Across the six traits under study, the maximum observed overlap amounted to five markers, roughly a quarter of the selected set by stepwise regression.

DISCUSSION

The main findings for the collection of barley cultivars that we studied are: (1) LD was extended to as far as 10 cM distance, (2) markers were associated with the traits of yield and yield stability, and (3) the markers could be useful for selection.

LD:

LD stretched over a distance of at least 10 cM. It is difficult to give the number of markers needed for a genome-wide scan, because LD varies over the genome in relation to, among other factors, varying recombination rate and selection. Contrary to expectation, we also found LE between some closely linked markers. The same observation on LD at larger distances and LE at short distances was found in Arabidopsis (Nordborg et al. 2002).

In comparison to other species, an LD interval up to 10 cM is large. Only in Arabidopsis populations were larger distances found (>50 cM), but this was in populations founded by only a few genotypes and after extreme inbreeding (Nordborg et al. 2002). In sugar beet lines, LD was <3 cM (Kraft et al. 2000) and in maize LD diminished over a distance of 2000 bp (Remington et al. 2001). Many factors influence LD (see Ardlie et al. 2002), but the most probable cause for the high level of LD in barley is the fact that it is an inbreeder. In addition, the current population of cultivars descended from a limited number of founding types (Russell et al. 2000) in which some haplotypes were lost and others were preserved, which will have increased LD. Finally, selection can increase LD, for instance, by a hitchhiking effect, in which the alleles at flanking loci of a locus under selection can be rapidly swept to high frequency or fixation.

A major complication in LD studies like the one undertaken in this article is the appearance of false-positive marker-trait associations due to population structure. Bayesian cluster analysis following Pritchard et al. (2000) gave no clue to the existence of such structure. A hierarchical cluster analysis and correspondence analysis did point to the existence of two subpopulations. However, fortunately, no trait-associated markers were in the set of markers discriminating between the two subpopulations, so we concluded that identified marker-trait associations were not a consequence of population structure, but very probably were indeed caused by linkage.

Association:

Association between markers and traits (YLD, ADAP, and STAB) was examined in three ways: (1) significance of marker-trait correlations, (2) LD profiles over chromosomes (P-values against chromosome position), and (3) marker-trait associations found in other (QTL) studies.

Establishing a significance threshold for marker-trait associations is critical. In genome-wide LD mapping, many markers are tested simultaneously, and some correction for multiplicity of testing is required. Well-known approaches include Bonferroni-like procedures (e.g., Holm 1979) and permutation tests (Churchill and Doerge 1994). Both kinds of approaches aim at controlling the type I error; that is, the probability of obtaining any false positive should be below a specified level, usually 0.05. As a result, the power (or the proportion of correctly identified positives) of these approaches can become very low. Holland and Copenhaver (1987) improved the Holm method with respect to power, but it remained conservative with impaired power. Instead of controlling the type I error, Benjamini and Hochberg (1995) advocated the control of the so-called FDR. FDR was defined as the expected proportion of true null hypotheses within the class of rejected null hypotheses. The multiplicity control in FDR is directed at not surpassing a particular percentage of false positives (wrongly rejected null hypotheses, marker-trait associations that “in reality” do not exist) within the set of identified positives. We argue that for our purposes—an exploratory genome-wide LD scan—an FDR control for multiplicity is more appropriate than a type I control. Identification of associated markers in LD mapping could be followed by the creation of a segregating population, polymorphic for the involved loci, in which the association is confirmed or refuted. In a similar vein, Weller et al. (1998) demonstrated the utility of an FDR approach in the genetic dissection of complex traits.

In any LD mapping, it will be informative to examine the flanking markers of trait-associated markers. A chromosome-wide association profile containing a trait-associated marker will show whether the associated marker stands out or whether a smooth rise and fall appears before and after the marker. The latter pattern might point to real association, although it still remains possible that LD extends over such a short distance that a ragged profile appears. Therefore, a smooth association profile confers confidence with respect to the identified marker-trait association, but a ragged profile does not necessarily invalidate a found association.

Another kind of confirmation for identified associations came from reported QTL from linkage analysis studies. All of the YLD-associated markers coincided with earlier reported yield QTL. Most of the earlier reported QTL were found in crosses within North American germ plasm, while we used only European material. This suggests that, at least for yield, the North American germ plasm genotypically resembles the European germ plasm. An explanation might be that North American cultivars and European cultivars have common ancestors. Support for this hypothesis is given by Fischbeck (2003), where it is stated that barley seeds were introduced to North America from many countries, especially from Central, Northern, and Eastern Europe.

Furthermore, three of the STAB-associated markers were located in a region of known yield QTL, and two of those three (on chromosomes 2 and 4) also coincided with a region earlier found to exhibit QTL × E interaction (Table 3). In addition, the STAB-associated marker on chromosome 4 is located in the region where several stress-responsive genes have been found (Forster et al. 2000).

The question on the feasibility of selection on stability is an old one. Heritability for stability measures is generally low (Becker and Leon 1988; Leon and Becker 1988; Lin and Binns 1991; Sneller et al. 1997). We have found markers associated with stability, but we do not know the nature of the genes linked to these markers. Three of five of the STAB-associated markers were in a region where yield QTL also have been found, suggesting the presence of environmentally affected yield QTL. The other two STAB-associated markers were in a region where so far no yield or yield-related QTL were reported, suggesting environmentally affected regulatory genes. However, if yield QTL were present at those locations, their irregular expression might be the reason for their nonidentification so far.

Multiple linear regression:

The question of whether markers could be useful for predicting phenotypic responses was answered with multiple linear regression, explaining traits by band incidence of markers. When subsets of 18–20 markers were selected from the total set of markers using stepwise regression, between 40 and 58% of the variation could be explained. We predicted the theoretical minimum and maximum for all traits according to the final regression model by choosing the favorable alleles (1 or 0, depending on the sign of the effect) for the selected markers. The predicted minimum and maximum values were far beyond the observed minimum and maximum values. This could be explained by the absence of genotypes with exclusively (un)favorable alleles, but also by the fact that accumulating alleles almost always result in a lower effect than one might expect on the basis of adding up the effects of all the alleles. Nevertheless, selection on the basis of these markers might result in genotypes with superior yield and/or stability potential.

The marker-trait assocation models were fitted by regression under the assumption that individual varieties represented independent units. Of course, this assumption will have been violated by pedigree relations between the varieties. At first sight it may seem attractive to take account of these pedigree relations by inclusion of a relationship matrix in a mixed-model analysis of the same data. However, several considerations have prevented us from changing from a standard regression model to a mixed-model analysis. First, the pedigree information for collections of varieties as included in the present study typically is very incomplete. Second, the use of a relationship matrix is a logical consequence of the use of polygenic models for quantitative traits, but its use in oligogenic QTL models is far less natural. The estimator of the genetic correlation between genotypes in a polygenic model is a function of the expected identity by descent across the whole of the genome. However, in an oligogenic QTL model, the use of the expected identity by descent across the whole genome in the estimation of genetic correlations becomes questionable. In the latter case, the use of local identity-by-descent relations on the positions of the QTL would seem more appropriate. These local identity-by-descent measures may be estimated from the allele composition of trait-associated markers as described by Milligan (2003). The reliability of such estimates is still a matter of discussion and for that reason we preferred to use equally weighted independent varieties above disputably weighted and correlated varieties.

It may be contested that linkage will preclude the attainment of optimal allele configurations. However, closely linked markers were very seldom included in the stepwise regression models, because of the nature of this subset selection procedure. The predictions from the final stepwise regression models were thus supposed to represent a reasonably optimal combination of alleles on different loci. In contrast, the regression model based on the set of markers that were individually highly correlated with the trait did not take into account linkage relations between loci. Therefore, with this model, far less extreme minimum and maximum responses were obtained.

In conclusion, LD mapping seems to have clear potential for improving barley, especially for complex traits, like yield and yield stability, for which measurements are costly and time consuming. Combining existing phenotypic variety trial data and genotypic marker characterizations within an LD approach may prove to be highly profitable.