The Changing Tails of a Novel Short Interspersed Element in Aedes aegypti

Abstract

A novel family of tRNA-related SINEs named gecko was discovered in the yellow fever mosquito, Aedes aegypti. Approximately 7200 copies of gecko were distributed in the A. aegypti genome with a significant bias toward A + T-rich regions. The 3′ end of gecko is similar in sequence and identical in secondary structure to the 3′ end of MosquI, a non-LTR retrotransposon in A. aegypti. Nine conserved substitutions and a deletion separate gecko into two groups. Group I includes all gecko that end with poly(dA) and a copy that ends with AGAT repeats. Group II comprises gecko elements that end with CCAA or CAAT repeats. Members within each group cannot be differentiated when the 3′ repeats are excluded in phylogenetic and sequence analyses, suggesting that the alterations of 3′ tails are recent. Imperfect poly(dA) tail was recorded in group I and partial replication of the 3′ tandem repeats was frequently observed in group II. Genomic evidence underscores the importance of slippage retrotransposition in the alteration and expansion of the tandem repeat during the evolution of gecko sequences, although we do not rule out postinsertion mechanisms that were previously invoked to explain the evolution of Alu-associated microsatellites. We propose that the 3′ tandem repeats and the poly(dA) tail may be generated by similar mechanisms during retrotransposition of both SINEs and non-LTR retrotransposons and thus the distinction between poly(dA) retrotransposons such as L1 and non-poly(dA) retrotransposons such as I factor may not be informative.

TRANSPOSABLE elements (TEs) can be categorized as RNA-mediated or DNA-mediated elements according to their transposition mechanisms (Finnegan 1992). The transposition of RNA-mediated TEs involves a reverse transcription step, which generates cDNA from RNA molecules (Eickbush and Malik 2002). The cDNA molecules are integrated in the genome, allowing replicative amplification. RNA-mediated TEs include long terminal repeat (LTR) retrotransposons, non-LTR retrotransposons, and short interspersed elements (SINEs). SINEs are generally between 100 and 500 bp long. SINE transcription is directed from Pol III promoters that are similar to those found in small RNA genes. SINEs can be further divided into three groups on the basis of the similarities of their 5′ sequences to different types of small RNA genes. Elements such as the primate Alu family share sequence similarities with 7SL RNA (Jurka 1995) while most other SINEs belong to a different group that share sequence similarities to tRNA molecules (Adams et al. 1986; Okada 1991; Tu 1999). Recently, a new group of SINEs named SINE3, which shares similarities to 5S rRNA, has been discovered in the zebrafish genome (Kapitonov and Jurka 2003).

Unlike LTR and non-LTR retrotransposons, SINEs do not have any coding potential and thus it has been proposed that SINEs are replicated by “borrowing” the retrotransposition machinery from autonomous non-LTR retrotransposons and that this process may be facilitated by the presence of similar sequences or structures at the 3′ ends of a SINE and its “partner” non-LTR retrotransposon (Ohshima et al. 1996; Okada and Hamada 1997; Kajikawa and Okada 2002). Experimental support for this hypothesis has been recently reported. An eel SINE, UnaSINE1, shares similar 3′ sequences and TGTAA tandem repeats with an eel non-LTR retrotransposon, UnaL2. UnaL2 was able to mobilize UnaSINE1 during a retrotransposition assay performed in human HeLa cells (Kajikawa and Okada 2002). It was hypothesized that UnaL2 and UnaSINE1 retrotranspose through a slippage mechanism similar to that of telomerase, which can generate tandem repeats (Chaboissier et al. 2000; Kajikawa and Okada 2002). Alu, a human SINE, was also shown to transpose by a non-LTR retrotransposon-mediated mechanism using marked Alu sequences in HeLa cells (Dewannieux et al. 2003). The non-LTR retrotransposon in this case is the human L1 element. The change of the length of the terminal poly(dA) tract in the marked Alu is thought to result from slippage reverse transcription (Dewannieux et al. 2003). It was also shown that mutations introduced in the poly(dA) tails of Alu provide a source for the genesis of primate microsatellites, which may involve postinsertion mechanisms (Arcot et al. 1995).

Only a small number of SINEs have been described in insects and they all belong to the tRNA-related group (Adams et al. 1986; Tu 1999; Feschotte et al. 2001; reviewed in Tu 2004). Here we report the discovery and characterization of a unique family of tRNA-related SINEs named gecko in the yellow fever mosquito, Aedes aegypti. The 3′ region of gecko was similar to the 3′ region of MosquI, a non-LTR retrotransposon in A. aegypti. We describe natural alterations between 3′ tandem repeats and the poly(dA) tail in gecko. We propose that the 3′ tandem repeats and poly(dA) tails may be generated by similar mechanisms during retrotransposition and our data provide unique genomic and evolutionary support for the slippage retrotransposition model.

MATERIALS AND METHODS

Database search and computer-aided analysis of large-output files:

Database search was performed using BLAST (Altschul et al. 1997). In addition to the nonredundant GenBank database and the NCBI EST database, two A. aegypti databases were also used. The first is an A. aegypti BAC-end database that contains 117,953 BAC-end sequences, which are part of the NCBI genome survey sequence (GSS) database. The second is an A. aegypti EST database from The Institute for Genomic Research (TIGR; http://www.tigr.org/tdb/e2k1/aabe/). In addition to web-based searches, we also downloaded the two A. aegypti databases for searches on a Dell 530 Linux workstation, which is equipped with twin 2.0 GHz processors, 1.5 Gb RAM, and 80 Gb hard drive. Subsequent analyses of the BLAST output were all performed on this Linux workstation. We used two C programs, TEpost and FromTEpost (Biedler and Tu 2003), to analyze BLAST output and retrieve hits plus flanking sequences. Both programs are available for download from our webpage (http://jaketu.biochem.vt.edu). TEpost uses a BLAST output file as input and produces an output file listing each BLAST hit in a row along with several characteristics associated with that hit. Due to the nature of BLAST and the presence of insertions/deletions or other chromosomal rearrangements, BLAST hits corresponding to one TE copy can be reported as multiple hits and can result in an overestimation of number of copies. A gap-length parameter was added to reduce this occurrence by grouping fragmented hits associated with one TE copy as a single match (Biedler and Tu 2003). From TEpost uses TEpost files as input to produce FASTA sequence files of the recorded hits. Flanking sequences are included if the output file is used as input for subsequent programs such as SINEDR (see below), which identifies tandem repeats and target-site duplications. The flanking sequences of confirmed gecko copies were used to search the A. aegypti BAC-end database to identify evidence of gecko insertions that resulted in target duplications. In addition, ATcontent (Tu 2001a) was used to calculate A + T contents of a large number of sequences in the FASTA format.

SINEDR and CountTR:

SINEDR is a C program that searches a sequence database for SINE elements that are flanked by direct repeat, or target-site, duplication (TSD). The input file is a sequence database in FASTA format. The program initiates the search by identifying user-specified simple repeats typically found at the 3′ end of SINEs. Users also provide specifications of the number of times the unit is repeated in tandem. The program then detects direct repeat sequences with the 3′ direct repeat starting at the end of the tandem repeat and the 5′ direct repeat within user-specified distance, which is normally a few hundred bases. Users also specify the minimum and maximum length of the direct repeat and the number of mismatches allowed between the two sides of the direct repeat. An additional parameter is built in to allow offset between the end of the tandem repeat and the beginning of the 3′ direct repeat (or 3′ TSD). Allowing offset is important for the discovery of SINE copies that have imperfect tandem repeats. A series of output files are presented, including files for all copies of putative SINEs, their direct repeats, and SINE plus flanking sequences. In this study, our input file for the SINEDR search was a subdatabase that includes all gecko sequences identified in the BLAST search of an A. aegypti BAC-end database described above using a 1e-4 cutoff. Matches with gecko on minus strands were reversed and then combined with matches on the positive strands. Our specification for the 3′ tandem repeats was either 8 base homo poly(dA) or two units of the 4-bp tandem repeat. We required the TSD to be between 7 and 35 bp and allowed no mismatch. Up to 4 bp of offset was allowed. The distance between the two halves of the direct repeat is set between 30 and 350 bp. Manual inspection was performed to remove a small number of false positives. This version of SINEDR is designed to assist the analysis of the thousands of copies of a known SINE by focusing on copies that have reasonable 3′ sequences and that are flanked by direct repeat. It is not intended to uncover new SINEs with unique tandem repeats although it can perform such a function. CountTR is a C program that counts the number of tandem repeats in FASTA formatted sequences in a database. Users specify the unit of tandem repeats and the output is a tab-delimited file reporting the number of single, double, triple, quadruple (and so on) repeats found in each sequence. Both programs are available from the authors upon request.

Pairwise and multiple sequence comparisons and secondary structure prediction:

Several GCG programs (Accelrys, San Diego) were used for sequence analysis. These include Gap and Bestfit for pairwise comparison, Pileup for multiple sequence alignment, and Pretty for consensus construction. Unless otherwise specified, the gap weight was 3 and gap-length weight was 0 in Pileup analyses. Multiple sequence alignments were also obtained using ClustalX v1.81 (Thompson et al. 1997). Parameters used for ClustalX alignments were pairwise gap penalty, (open = 30, extension = 0.8) and multiple gap penalty (open = 10, extension = 0.25). Both Mfold of GCG and GeneQuest of Lasergene (DNASTAR, Madison, WI) were used to predict secondary structures.

Phylogenetic inference and calculation of sequence divergence:

Phylogenetic analyses were performed using multiple sequence alignments of full-length gecko sequences that are flanked by TSDs although TSDs were not included in the alignment. These alignments were obtained using ClustalX as described above. All phylogenetic analyses were performed with PAUP v4.0b10 (Swofford 2002). Both neighbor-joining and minimum evolution trees were constructed. Five hundred bootstrap replicates were used to assess the confidence in the groupings. Maximum-parsimony analysis was also attempted. However, no results were produced due to the large number of trees that require extensive computer memory. Pairwise sequence divergence was also calculated using PAUP v4.0b10 (Swofford 2002).

Estimation of copy numbers:

The copy number of gecko in A. aegypti was calculated according to the total number of gecko elements in the database and the percentage of coverage of the A. aegypti database. The number of gecko in the database was estimated on the basis of a BLASTN search at a cutoff of e-4 using a consensus that was derived from >60 full-length copies as the query. There are 117,793 sequences in the BAC-end sequence database, which cover ∼9% of the genome. Nonredundant sequences cover ∼8.2% of the genome. The size of the A. aegypti haploid genome is ∼800 Mbp (Rai and Black 1999). The following formula was used: copy no. = (no. in database)/genome coverage of the database.

The 8.2% value was used when redundant gecko copies could be removed from our analysis. In cases where redundancy was not removed from analysis of gecko copies, the 9% value was used in the estimation.

Statistical analysis:

The two-sample Mann-Whitney test was used for the nonparametric comparison between medians of different data sets. For parametric analyses of the means, either a pooled-variance t-test or a “Welch's approximate t-test” was used on the basis of the result of an F-test (α = 0.05), which estimates the probability of equal variance between two data populations (Zar 1996). All statistical tests and calculations were performed using MINITAB version 10.5 (MINITAB, State College, PA).

RESULTS

A. aegypti gecko elements are a novel family of highly reiterated and tRNA-related SINEs that have at least four types of 3′ termini:

gecko was first discovered as a repeat element during our analysis of the BAC-end sequences from A. aegypti (GSS database, NCBI), which cover ∼9% of the genome. There are 647 copies of gecko in the database, indicating that ∼7200 copies of gecko are in the A. aegypti genome (Table 1). We used both multiple sequence alignments and the TSD-finding computer program SINEDR to define the boundaries of full-length gecko elements and to identify their TSDs. There are at least four types of gecko sequences, each with a distinct 3′ terminus. Figure 1, A–C, shows three separate multiple sequence alignments of gecko elements that end with a poly(dA) tract, CCAA tandem repeats, or CAAT tandem repeats, respectively. There is also one copy of gecko in the database that ends with an AGAT tandem repeat. The consensus of the four types of gecko elements (Figure 1D) is ∼185 bp long, not counting the variable repeats at the 3′ end. Evidence of insertion that resulted in TSDs has been found for gecko elements that end with the poly(dA), the CCAA, or the CAAT repeats (Figure 2, A–C). No such evidence is available for the AGAT gecko because there is only one AGAT gecko that has TSDs. Several features indicate that gecko is a novel family of SINEs. These features include small size, TSDs with variable sequence and length, imprecise 5′ ends, and a poly(dA) tract or tandem repeat at the 3′ end. Moreover, the 5′ region of gecko contains sequences similar to the A and B boxes of Pol III promoters that are conserved among tRNA molecules, suggesting that gecko is a tRNA-related SINE (Figure 3A).

TABLE 1.

Copy-number estimation ofgecko inA. aegypti

Groupings	No. in database	No. in genome	Intragroup identity (%)d
Full-length with TSDa	93	1130	ND
Poly(dA)	62	750	94.4 ± 3.2
(CCAA)n	23	280	98.2 ± 1.1
(CAAT)n	7	∼90	93.2 ± 6.9 (98.0 ± 1.0)e
(AGAT)n	1	∼10c	NA
All full-length copiesb	262	2900	ND
All gecko copiesb	647	7200	ND

^aFull length is defined as ≥170 bp. Only copies with perfect tandem repeats or poly(A) tract were included. Redundant copies were removed. Therefore, copy number was estimated assuming 8.2% coverage of the genome by nonredundant BAC-end sequences.

^bRedundant copies were not removed. Therefore, copy number was estimated assuming 9% coverage of the genome by the total BAC-end sequences.

^cThe estimation is based on one copy, which is subject to large variation.

^dAverage percentage of identity and standard deviation of all pairwise comparisons.

^eThe numbers in parentheses were calculated after removing one divergent copy.

Figure 1.—

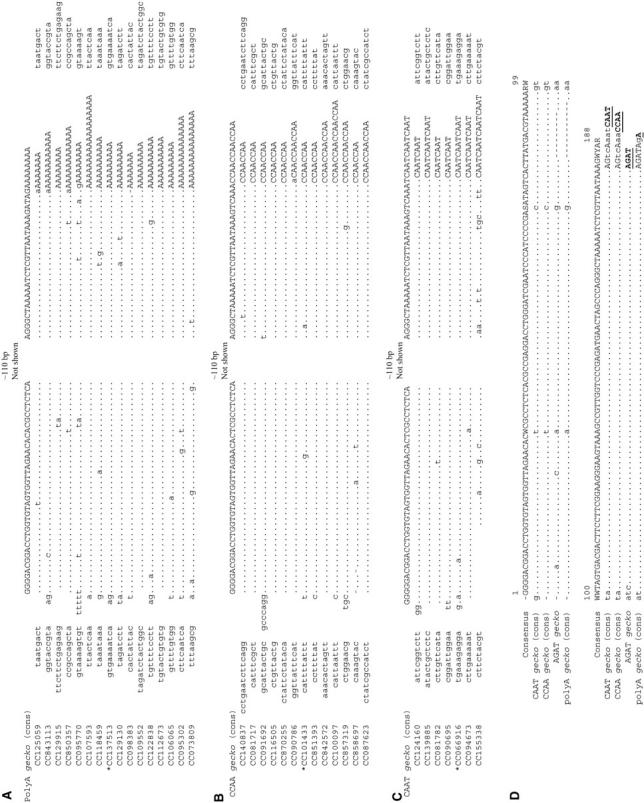
Multiple sequence alignment of representative gecko elements that end with a poly(dA) tract (A), CCAA repeat (B), and CAAT repeat (C). In A and B, only a sample of randomly selected full-length copies are shown. Sequences were aligned using Pileup of GCG (gap weight = 3 and gap-length weight = 0). Each consensus shown at the top of each alignment was created using Pretty of GCG by simple majority rule. Dots indicate bases that are identical to the consensus. Lowercase letters in the gecko alignment indicate sequence variation. Target-site duplications are shown flanking the alignments. Asterisks indicate copies shown in Figure 2 as evidence for past mobility. (D) Comparison between the consensus of poly(dA) gecko, CCAA gecko, CAAT gecko, and a gecko copy that ends with AGAT repeats. The tandem repeat units at the 3′ termini are underlined and in boldface type.

Figure 2.—

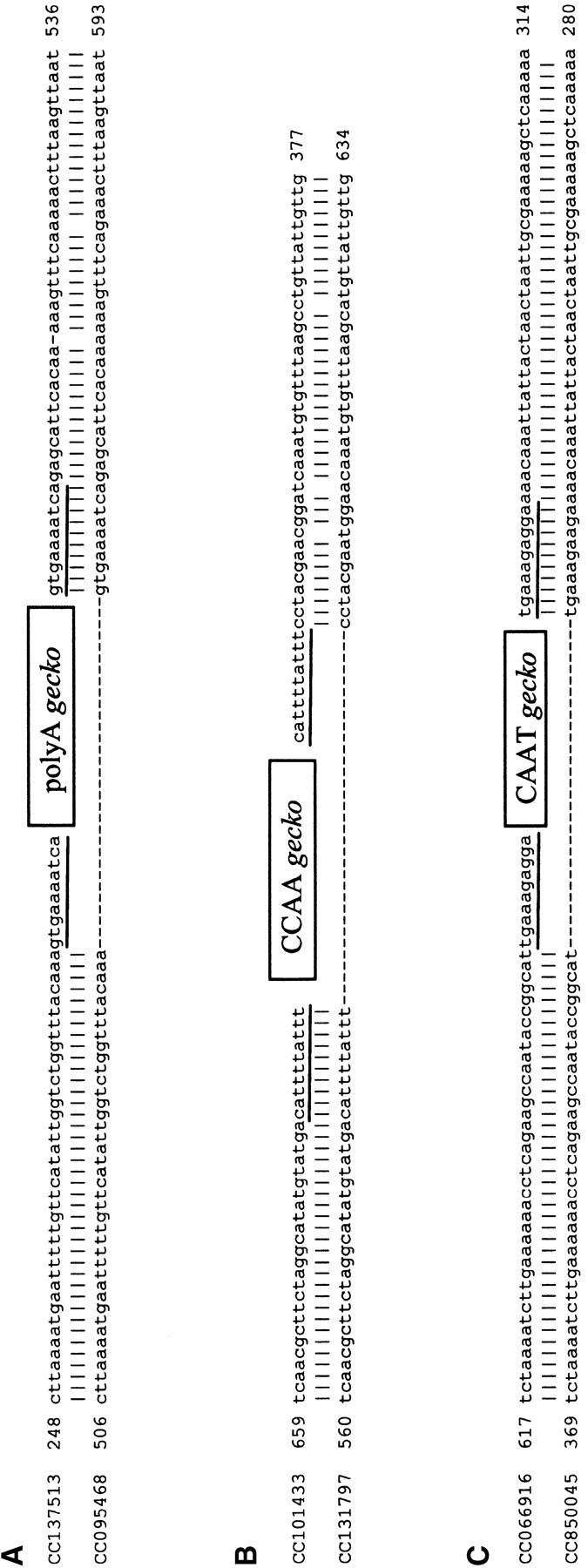
Examples of past mobility of three types of gecko elements. Sequences at the top contain the gecko insertion as indicated by the box and target-site duplications as indicated by the underlining. Evidence of gecko insertion was identified using sequences flanking confirmed gecko copies to search the A. aegypti BAC-end database.

Figure 3.—

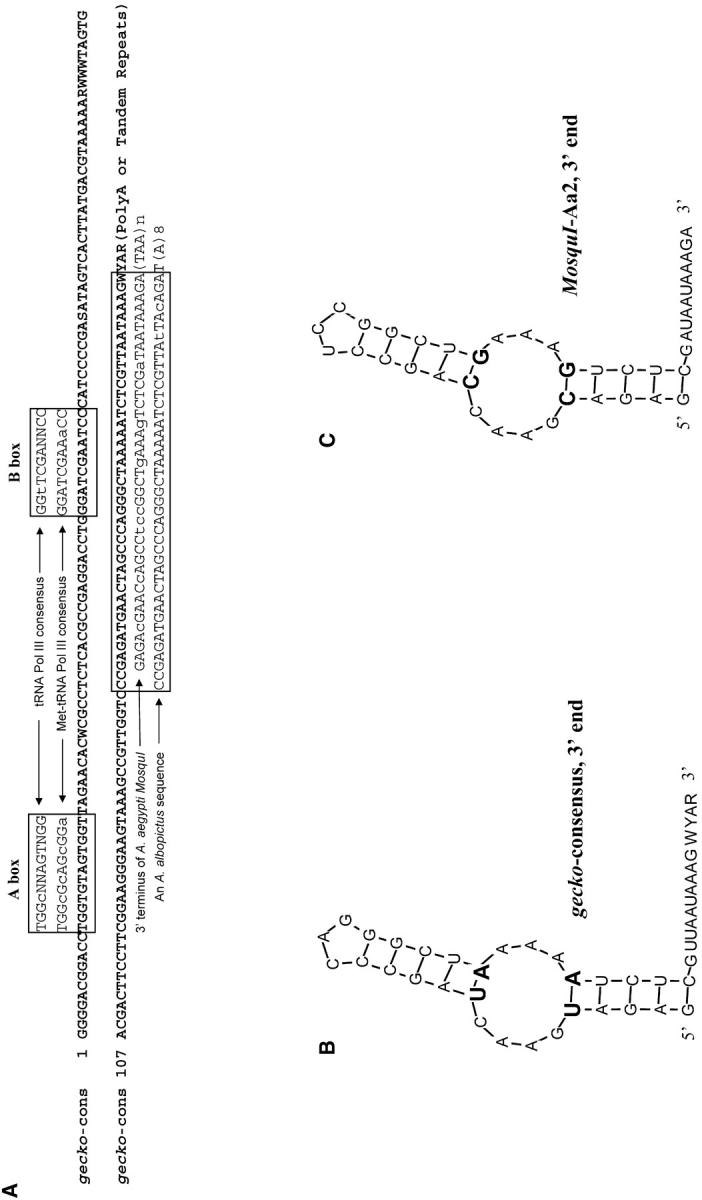
(A) Consensus of A. aegypti gecko and its features. 5′ gecko sequences were aligned to the A and B boxes of polymerase III promoters that are derived from the consensus sequences of tRNA Pol III and Met-tRNA Pol III (Deininger 1989). Thirty-three base pairs of the 41-bp fragment at the 3′ end of gecko are identical to the 3′ terminus of MosquI, a non-LTR retrotransposon in A. aegypti (Tu and Hill 1999). Forty-two base pairs of the 44-bp fragment at the 3′ end of gecko are identical to an uncharacterized sequence in A. albopictus (GenBank AF144549). Uppercase letters indicate conservation between gecko and the aligned sequences. Lowercase letters indicate variations. Twenty base pairs of a 21-bp region near the 5′ end of gecko (nucleotides 25–45 in the consensus) is identical to the reverse strand of a yeast tRNA sequence (Suzuki et al. 1994), which is not shown. (B) Predicted secondary structure of the 3′ end of the gecko consensus as shown in Figure 1D. (C) Predicted secondary structure of the 3′ end of MosquI-Aa2, a full-length copy of a non-LTR retrotransposon in A. aegypti. (B and C) Structures predicted using the GeneQuest program of Lasergene. Mfold of GCG was also used, which gave similar structural predictions. The two pairs of complementary changes between structures in B and C are in boldface type and a larger type size.

Subdivisions of gecko and their relative abundance:

To investigate the structural features and subdivisions of the gecko element, we focused on full-length gecko elements that are flanked by target-site duplications. As shown in Table 1, after removing redundant copies, 93 gecko are flanked by perfect TSDs and are 170 bp or longer, which we consider full-length or nearly full-length. Of the 93 gecko elements, 62 contain poly(dA) tract at their 3′ end. Twenty-three copies end with CCAA tandem repeats and 7 end with CAAT tandem repeats. Also, one copy ends with AGAT tandem repeats. The corresponding genomic copy numbers of full-length gecko elements in these different categories are also shown in Table 1. We performed phylogenetic analysis on all 93 full-length gecko elements using neighbor joining and minimum evolution algorithms. When the variable 3′ terminal repeats were included, poly(dA) gecko elements and the single AGAT gecko were in one group (group I) while CCAA gecko and CAAT gecko formed group II (data not shown). When the 3′ repeat was excluded from the analysis, groups I and II were still supported. In both cases, the bootstrap values for the two groupings were weak (51%). With the exception of a divergent CAAT gecko element, CAAT and CCAA elements form their own subgroups only when the variable 3′ repeat region is included. Groups I and II described above are supported by comparisons of the consensus and representative sequences of these four types of gecko elements, as shown in Figure 1D. There are nine conserved substitutions in the consensus sequences that divide gecko into two groups, which is consistent with the phylogenetic grouping. We also determined the level of sequence divergence within each type of gecko element. As shown in Table 1, the average levels of sequence identities are 94.4% (±3.2%) among poly(dA) gecko elements, 93.2% (±6.9%) among CAAT gecko elements, and 98.2% (±1.1%) among CCAA gecko elements.

The 3′ repeats of gecko:

To investigate the 3′ termini of gecko elements in detail, we expanded our analysis to include both full-length and 5′ truncated gecko copies that may or may not end with a perfect tandem repeat or a perfect poly(dA) tract, as long as they are flanked by TSDs. When we set the parameters of the SINEDR program to require two or more tandem repeats or eight or more deoxyadenosines at the 3′ region but allowed the terminal 1–4 bases to deviate from the repeat unit or the poly(dA) tract, we identified 177 copies of gecko elements. After removing redundant copies and copies with misplaced TSDs, there are a total of 144 copies. Among these are 87 poly(dA) gecko, 1 AGAT gecko, 44 CCAA gecko, and 12 CAAT gecko. There are 74 poly(dA) gecko elements that end with a perfect poly(dA) tract and 13 that end with other bases. In the case of group II gecko elements that end with CCAA or CAAT tandem repeats, we observed many cases of partial replication of the repeat unit at their 3′ termini. All but one of the imperfect 3′ termini are partial extensions of the repeat unit. We summarized in Table 2 the number of copies with a complete repeat unit and the number of copies with up to a 3-bp extension. Two sets of numbers are given in Table 2. The first set reflects the maximum length of TSDs and the second set, which is in parentheses, reflects the maximum length of the 3′ extension. In either case, a significant number of gecko end with 1- to 3-bp extensions of the CCAA or CAAT repeat unit.

TABLE 2.

The 3′ repeats of CCAAgecko and CAATgecko inA. aegypti

	gecko group
3′ repeats	CCAA gecko	CAAT gecko
gecko copies with TSDsa
Complete repeat: (CCAA)n or (CAAT)n	31 (11d)	8 (4)
Repeat plus 1- to 3-bp extensionb	13 (33)	4 (8)
All gecko copies, with or without TSDsc
(CCAA)2 or (CAAT)2	56	18
(CCAA)3 or (CAAT)3	22	10
(CCAA)4 or (CAAT)4	4	3

^aThe two rows below count the number of gecko that end with complete repeat units vs. the number of gecko that end with a 1- to 3-bp extension of the repeat units. Only copies with TSDs are considered here because it is difficult to determine the end of gecko without TSDs. In cases where gecko ends with imperfect tandem repeats, it is sometimes difficult to determine where the gecko ends and where the TSDs begin. Therefore, two sets of numbers are given. The first set reflects the maximum length of TSDs. The second set, which is in parentheses, reflects the maximum length of the 3′ extension.

^bThese are copies that end with (CCAA)_nC, (CCAA)_nCC, (CCAA)_nCCA, (CAAT)_nC, (CAAT)_nCA, or (CAAT)_nCAA.

^cThe three rows below count the numbers of gecko that end with two, three, or four repeat units. No gecko ends with more than four repeat units. All gecko copies are considered with or without TSDs. Only a complete 4-bp unit is counted. For example, (CCAA)₂CC is counted as two repeat units. There are no other CCAA or CAAT tandem repeats in gecko in addition to the repeats at the 3′ termini. The above statement was confirmed by examining consensus sequences and a number of individual gecko copies.

^dThere is one case in which the 3′ end is CCAAACCAA instead of (CCAA)_n.

To determine the variation in the number of 3′ repeats, all nonredundant gecko copies regardless of length and TSDs were surveyed using CountTR (Table 2). Fifty-six gecko end with the doublet (CCAA)₂, 22 with (CCAA)₃, and 4 with (CCAA)₄. Eighteen gecko end with (CAAT)₂, 10 end with (CAAT)₃, and 3 with (CAAT)₄. No gecko ends with more than four repeat units. To compare the relative frequency of these gecko-associated repeats with the relative frequency of the same repeats in the rest of the genome, we surveyed the nonredundant A. aegypti BAC-end database to count all CCAA and CAAT tandem repeats. For example, to count the number of (CCAA)₂ in genomic regions not occupied by gecko, we included the number of (CCAA)₂ as well as the number of (TTGG)₂ and deducted the number of (CCAA)₂ that is associated with gecko. We used the same method to count the number of CAAT repeats in genomic regions not occupied by gecko. Please note that all gecko had been appropriately oriented. Taking together, the non-gecko portion of the BAC-end sequences contain 5297 (CCAA)₂, 102 (CCAA)₃, and 12 (CCAA)_≥4, as well as 6581 (CAAT)₂, 101 (CAAT)₃, and 12 (CAAT)_≥4. We calculated the percentage of CCAA or CAAT gecko that end with three or more repeat units because there is a large enough sample size. Thirty-two percent of CCAA gecko end with (CCAA)_≥3 although the percentage of (CCAA)_≥3 among non-gecko CCAA tandem repeats is only 2.1%. Similarly, 42% of CAAT gecko end with (CAAT)_≥3 although the percentage of (CAAT)_≥3 among non-gecko CAAT tandem repeats is <1.7%. As discussed later, the differences in the relative frequency between gecko-associated repeats and the repeats in the rest of the genome may help illuminate how gecko-associated repeats arose. Moreover, (CCAA)_≥3 and (CAAT)_≥3 that are at the 3′ end of gecko represent a large fraction of the total such repeats in the genome, 18.6 and 10.3%, respectively, although both types of gecko occupy <0.05% of the genome. Therefore gecko appears to be a significant source of certain microsatellites in A. aegypti. It should be noted that microsatellites are thought not to be abundant in A. aegypti (Fagerberg et al. 2001).

The 3′ region of gecko is similar in sequence and structure to the 3′ end of MosquI, a non-LTR retrotransposon in A. aegypti:

MosquI is a potentially autonomous non-LTR retrotransposon in A. aegypti (Tu and Hill 1999). As shown in Figure 3A, 33 bp of the 41-bp fragment near the 3′ end of the gecko consensus are identical to the 3′ terminus of MosquI-Aa2, a full-length copy of MosquI. Moreover, the predicted secondary structures of the 3′ regions of the two retro-elements are identical (Figure 3, B and C). The eight base differences between the two sequences include two pairs of complementary changes in the base-paired stem that do not change the structure, three bases in the unpaired tip, and one base outside of the stem-loop structure. As described above, gecko has four types of “tail,” a poly(dA) tract and three types of tandem repeats. However, these repeat sequences are all different from the TAA tandem repeats at the 3′ end of MosquI. During a BLAST search of the NCBI nonredundant nucleotide database, a match to gecko was identified in A. albopictus, a species in the same subgenus as A. aegypti. The match was to a fragment in an intron of the A. albopictus ribosomal protein gene rpl34 (GenBank accession AF144549). The match is limited to the 3′ end of gecko, which extends 2 bp beyond the 5′ of the match between gecko and MosquI (Figure 3A).

Distribution of gecko is biased and gecko sequences are found in ESTs:

The average A + T content of the A. aegypti genome is 62.0 ± 0.3% (mean ±SEM), which was estimated on the basis of the A + T content of 400 random samples from the BAC-end sequences. Although the average A + T content of the 144 gecko elements (52.1 ± 0.3%) is significantly less than the genome average (P < 0.001), their TSDs (66.1 ± 1.3%) and flanking sequences (64.5 ± 0.5%) are significantly more A + T-rich (P < 0.01 and P < 0.002, respectively). We did not detect any significant difference between the different gecko groups with regard to the A + T content of their flanking sequences. When the gecko consensus sequence is used as a query to search both the NCBI EST database and the TIGR A. aegypti cDNA database (http://www.tigr.org/tdb/e2k1/aabe/), six matches that have e-values better than the 1e-5 cutoff were found. One EST from an A. aegypti antennal cDNA library (BM144167) showed 93% identity to the full-length gecko sequence. The other five are matches to TIGR cDNA sequences (TIGR identification nos. allcDNA_2176, 3605, 9602, 10056, and 11637), with identities ranging from 67 to 88%.

DISCUSSION

Is MosquI the “partner” of gecko?

There is strong experimental support for the hypothesis that SINE retrotransposition relies on the machinery provided in trans by a “partner” non-LTR retrotransposon (Kajikawa and Okada 2002; Dewannieux et al. 2003). It is proposed that SINE transcripts are recognized by the retrotransposition machinery of their partner non-LTR retrotransposon through shared sequences or structures at their 3′ termini. On the basis of the fact that the 3′ regions of gecko and MosquI are similar in sequence and identical in secondary structure (Figure 3), we hypothesize that MosquI is the non-LTR retrotransposon “partner” of gecko. MosquI is a potentially autonomous non-LTR retrotransposon in A. aegypti that is related to the Drosophila I factor (Tu and Hill 1999). The 3′ repeats of gecko are different from the TAA tandem repeats at the 3′ end of MosquI. Such a difference is consistent with the ever-changing nature of the 3′ repeats in the gecko family. It is also consistent with the fact that the TAA repeats of the Drosophila I factor are not absolutely required for retrotransposition (Chaboissier et al. 2000) although the UAA repeats are essential for the precise initiation of the reverse transcription of the I factor (Chambeyron et al. 2002). Moreover, it has been shown that although the 3′ tandem repeats are required for retrotransposition of the eel element UnaL2, the actual sequence of the repeat unit is not as important (Kajikawa and Okada 2002). If we accept the MosquI-gecko partnership hypothesis, one interesting question to consider is the copy-number difference between MosquI, which comprises 14 full-length and truncated copies, and gecko, which comprises ∼7000 copies. Cis-preference of retrotransposition has been shown for both human L1 and Drosophila I factor (Chambeyron et al. 2002; Dewannieux et al. 2003). There may be two mechanisms that can result in a high copy number of gecko despite the possible cis-preference of its partner non-LTR retrotransposons. The first is a possible competitive access of gecko RNA to ribosomes that may balance against the cis-preference. A 21-bp fragment in the 5′ region of gecko is 95% identical to the reverse strand of the TψC region of a yeast tRNA sequence (Suzuki et al. 1994; see Figure 3 legend). The TψC loop is recognized by ribosomes for tRNA binding. The second mechanism could involve a lesser degree of selection pressure on short elements than its non-LTR partner, presumably because small-size SINEs are less efficient substrates for homologous recombination or because their impact on neighboring genes may be less severe (Petrov et al. 2003). It should be noted that we cannot rule out the possibility that there are other non-LTR retrotransposons in A. aegypti that have contributed to the mobility of gecko. We have also found a sequence that matches the 3′ region of gecko in an intron of a ribosomal protein gene in the related mosquito A. albopictus. The match is limited to the 3′ region and is only 2 bases apart from the match between gecko and MosquI (Figure 3A). It is possible that the 3′ sequence defined by the similarity among gecko, MosquI, and the A. albopictus element is a reverse transcriptase recognition signal (Tu 2001b) that is shared between these sequences in the two closely related species.

Natural alteration of the 3′ repeat units in the gecko family: Slippage retrotransposition or postintegration mechanisms?

We have shown in this study that alterations of 3′ repeats have occurred during evolution among closely related gecko elements, some of which are indistinguishable if not for their distinct 3′ repeats, thus suggesting that these 3′ changes are recent. Primate Alu sequences have been previously shown to be associated with microsatellite repeats (e.g., Arcot et al. 1995; Jurka and Pethiyagoda 1995). Arcot et al. (1995) suggest that mutations introduced during reverse transcription or after insertion are followed by expansion/contraction of the changed sequences, which subsequently give rise to Alu-associated microsatellites through a process involving replication slippage and/or recombination. On the other hand, a slippage retrotransposition hypothesis has been invoked to explain the change in the length of the terminal poly(dA) in retrotransposed copies of an engineered Alu (Dewannieux et al. 2003). The same hypothesis is used to explain the alterations of 3′ repeats during retrotransposition from marked constructs of the Drosophila I factor (Chaboissier et al. 2000) and the eel UnaL2 (Kajikawa and Okada 2002). According to the slippage retrotransposition model, 3′ sequences in the transcript may be used as template for multiple rounds of reverse transcription during the initial phase of retrotransposition that may involve RNA template slippage. Such a process can potentially expand the number of repeats and introduce mutations (Kajikawa and Okada 2002). Here we argue that the slippage retrotransposition model can better explain the evolution of the variable tandem repeats in gecko although we do not rule out the involvement of postintegration events especially in the initial changes of the 3′ sequences. Our conclusion is based on a synthesis of recent data as well as new information from observations of gecko elements. When Lai and Sun (2003) analyzed microsatellite mutation rates in the entire human genome, which are the results of mostly replication slippage and possibly some recombination events, they confirmed the existence of a size threshold for microsatellite mutation, which is four repeat units at the minimum for di-, tri-, or tetranucleotides. If such a threshold is applicable in A. aegypti, few gecko meet the minimum and none exceeds the threshold. Nonetheless, 32% of the CCAA gecko and 42% of the CAAT gecko end with three or more repeat units (Table 2), which is in contrast to the fact that only 2.1% of the CCAA repeats and 1.7% of the CAAT repeats contain three or more repeat units in the rest of the A. aegypti genome. If we set aside the threshold issue and assume postintegration replication slippage or recombination as major mechanisms for the evolution of repeats in the 3′ repeats of gecko, we would not be able to explain the higher percentage of long repeats (three or more units) in gecko compared to that of the same tandem repeats in the rest of the genome because such postintegration mechanisms should have affected the same tandem repeats in a similar manner. Thus with the possibility of more than one round of reverse transcription of the repeat unit during RNA template slippage, the slippage retrotransposition model offers an attractive alternative. A mutated repeat unit can be amplified in this way to create an efficient substrate for postintegration mechanisms without requiring the same mutation to occur in multiple units by chance. A few other observations are also consistent with the slippage retrotransposition model. Luan and Eickbush (1995) showed that additional nucleotides were added to the target DNA during retrotransposition of the non-LTR retrotransposon R2 and the 3′ terminal sequence in the transcript of R2 was used as template for the genomic addition. The frequent partial replication of the 3′ repeats in gecko elements (Table 2) also offers support for the slippage retrotransposition model. In the case of gecko, the slippage may provide a mechanism for the reverse transcriptase to pass the stem-loop structure and thus complete reverse transcription as suggested by Kajikawa and Okada (2002). It is interesting that the sequences 5′ to the repeat units in group II gecko are similar to their repeat units (Figure 1D, CAAAT for CAAT gecko and CAAA for CCAA gecko). It is not yet clear whether these changes at the immediate 5′ of the repeat units have contributed to the alteration of the repeat units or are the results of the alteration of the repeat units. In summary, genomic evidence suggests that slippage retrotransposition is important for the alteration and expansion of the repeat during the evolution of gecko sequences. Our genomic analysis has provided a new perspective in support of the slippage retrotransposition model and suggests that the model is applicable to both SINEs and non-LTRs. The slippage retrotransposition model and the postintegration model are not mutually exclusive, although the former emphasizes the contribution by slippage reverse transcription to both the initial alteration and expansion of the repeat unit. Postintegration mutation can change the 3′ sequences in the transcript that serves as the template for slippage retrotransposition. The microsatellite slippage mechanism could also very well be involved once the threshold size is reached, which appears to be the case for the long (CA)_n microsatellites associated with Alu (Arcot et al. 1995).

A common mechanism producing the poly(dA) tract and 3′ tandem repeats?

We have shown that a given gecko element may exist as either a poly(dA) element or an element with different types of 3′ tandem repeats. Given the fact that gecko is a tRNA-related SINE that is transcribed from a Pol III promoter, its poly(dA) tract is most likely generated during the slippage reverse transcription rather than during polyadenylation. Therefore either a poly(dA) tract or 3′ tandem repeats may be generated by target primed reverse transcription (TPRT) as part of the evolutionary process of closely related members of the same SINE family. The conversion from tandem repeats to poly(dA) tail or vice versa can be achieved by changes in the 3′ sequence of the transcript that is used as template for the slippage TPRT. The initial change in the 3′ sequence may result from the error-prone nature of the slippage reverse transcription or from postinsertion mutation. Given the generally higher level of divergence between full-length poly(dA) gecko elements than between full-length CCAA and CAAT gecko elements (with the exception of one copy), it is possible that the poly(dA) gecko is the ancestral form that gave rise to the group II gecko, which end with tandem repeats.

Can our conclusion from analysis of gecko be applied to SINEs and non-LTRs in general? With respect to 3′ termini, non-LTR retrotransposons are classified as poly(dA) elements such as human L1 or elements with 3′ tandem repeats such as the Drosophila I factor (Bucheton et al. 2002). Boeke (2003) further divides the later group into poly(dA)-related repeats such as TAA or repeats unrelated to poly(dA). Data presented in this study and previous work question the significance of the above classification. As described earlier, non-poly(dA) retrotransposons can produce copies with a poly(dA) tract when modifications are made at the 3′ end (Luan and Eickbush 1995; Chaboissier et al. 2000). Moreover, several features of L1, the most extensively studied poly(dA) element, suggest that its poly(dA) tract may also be derived from the TPRT process. The AATAAA polyadenylation signal of human L1 is immediately followed by the poly(dA) tract, which is inconsistent with poly(A) addition that normally occurs 10–30 nucleotides downstream of the AAUAAA signal (Ostertag and Kazazian 2001). A subset of the human L1 ends with TAAA or GAAA tandem repeats in place of poly(dA) (Szak et al. 2002), which suggests an origin from slippage TPRT and further highlights the artificial nature of the classification of poly(dA) vs. tandem repeat elements. We cannot rule out the possibility that the poly(A) tail added in the transcript during polyadenylation is to some extent involved in generating the genomic poly(dA) tract, considering the relatively long length (10–85 bp) of the poly(dA) tracts in L1 (Ostertag and Kazazian 2001; Szak et al. 2002). However, the long poly(dA) could be simply generated by multiple slippage reverse transcription of a short poly(A) unit during TPRT. In fact, the GAAA tandem repeats in some L1 elements can be up to 198 bp long (Szak et al. 2002). In summary, the 3′ tandem repeats and the poly(dA) tract may be generated by similar mechanisms during retrotransposition of non-LTRs as well as SINEs. Thus the distinction between poly(dA) and non-poly(dA) elements may not be informative with regard to their origin and evolutionary relationship. The hypothesis described here also suggests a possible separation between polyadenylation and the presence of the genomic poly(dA) tract in some non-LTR retrotransposons, which explains the well-documented disconnect between polyadenylation signal and the presence of poly(dA) in non-LTR retrotransposons (Bensaadi-Merchermek et al. 1997; Eickbush and Malik 2002; Biedler and Tu 2003).