Intragenic Spatial Patterns of Codon Usage Bias in Prokaryotic and Eukaryotic Genomes

Abstract

To study the roles of translational accuracy, translational efficiency, and the Hill-Robertson effect in codon usage bias, we studied the intragenic spatial distribution of synonymous codon usage bias in four prokaryotic (Escherichia coli, Bacillus subtilis, Sulfolobus tokodaii, and Thermotoga maritima) and two eukaryotic (Saccharomyces cerevisiae and Drosophila melanogaster) genomes. We generated supersequences at each codon position across genes in a genome and computed the overall bias at each codon position. By quantitatively evaluating the trend of spatial patterns using isotonic regression, we show that in yeast and prokaryotic genomes, codon usage bias increases along translational direction, which is consistent with purifying selection against nonsense errors. Fruit fly genes show a nearly symmetric M-shaped spatial pattern of codon usage bias, with less bias in the middle and both ends. The low codon usage bias in the middle region is best explained by interference (the Hill-Robertson effect) between selections at different codon positions. In both yeast and fruit fly, spatial patterns of codon usage bias are characteristically different from patterns of GC-content variations. Effect of expression level on the strength of codon usage bias is more conspicuous than its effect on the shape of the spatial distribution.

CODON usage bias refers to the nonrandom usage of synonymous codons. Frequently used codons are often termed optimal or major codons, whereas less frequently used ones are termed nonoptimal or minor codons. Nonoptimal codons usually correspond to less abundant tRNAs than optimal codons do (Ikemura 1981, 1982, 1985; Bulmer 1987; Akashi 2001) and the translational machinery is more likely to stall there (Kurland 1992). These processing errors, termed premature termination or nonsense errors, can occur at comparable levels to misincorporation or missense errors, during the elongation stage of translation (Kurland 1992). Therefore, purifying selection is expected to increase in intensity as peptide elongation proceeds (Eyre-Walker 1996b; Akashi 2001) and should lead to gradual increase in codon usage bias along a gene (Eyre-Walker 1996b). In addition, optimal codons may be selected for translational efficiency and so are more frequently used in highly expressed genes (Sharp and Li 1986; Shields and Sharp 1987; Sharp et al. 1993; Hartl et al. 1994; Moriyama and Powell 1997; Akashi 2001; Carlini and Stephan 2003). Therefore, codon usage bias may be accounted for by negative selection against nonoptimal codons and positive selection for optimal codons. Neither selection against missense errors nor selection for translational efficiency is expected to be position dependent within genes, whereas selection against nonsense errors is expected to leave an incremental pattern of codon bias along translational direction within genes (Eyre-Walker 1996b).

Recombination is another important but often controversial factor that affects codon usage bias. Selection at one locus can interfere with selection at another locus, known as the Hill-Robertson effect (Hill and Robertson 1966). Negative selection against nonoptimal codons and positive selection for optimal codons are both likely to be weak (Hartl et al. 1994; Akashi 1995; Akashi and Schaeffer 1997; Kliman 1999; Maside et al. 2004). Nevertheless, selection at one codon position within a gene can interfere with selection at other codon positions in the gene if they are tightly linked (Li 1987; McVean and Charlesworth 2000; Comeron and Kreitman 2002). As a result, recombination is expected to increase the selection efficacy on codon usage bias. Several studies have observed a positive correlation between recombination rate and codon usage bias (Kliman and Hey 1993, 2003; Comeron et al. 1999; Betancourt and Presgraves 2002; Comeron and Kreitman 2002; Hey and Kliman 2002). However, there have also been observations suggesting that the Hill-Robertson effect has a minor influence on codon usage bias and is overwhelmed by the mutation pressure associated with recombination (Marais et al. 2001, 2003). The controversy around the Hill-Robertson effect on codon bias is due partially to the uncertainty in the recombination rate estimation (Kliman and Hey 2003; Marais et al. 2003). This uncertainty may be mitigated by studying the intragenic pattern of codon usage bias because intragenic variation of recombination rate is unlikely to be as extensive as intergenic variation. Comeron and Kreitman proposed that the Hill-Robertson effect should yield a distinctive intragenic spatial pattern of codon usage bias, with low bias in the middle but high bias near the ends (Comeron and Kreitman 2002). In the fruit fly genome, these authors showed that codon usage bias was indeed lower in the middle segment of long exons, and centrally located introns were found to mitigate the interference effect.

In short, the intragenic spatial distribution pattern of synonymous codon usage bias (spatial codon usage bias, for simplicity) may bear the signatures of selection against nonsense errors and the Hill-Robertson effect. This spatial bias pattern and other spatial patterns (such as substitution rate and GC-content variation) are important in molecular evolution and evolutionary genomics (Bulmer 1991; McVean and Charlesworth 2000; Comeron and Kreitman 2002; Marais and Charlesworth 2003).

Spatial codon usage bias was first addressed in Escherichia coli genes (Bulmer 1988; Chen and Inouye 1990, 1994; Eyre-Walker and Bulmer 1993; Eyre-Walker 1996a). Due to the nonlinear nature of the spatial patterns, most studies detected statistically significant changes only in regions near the start codons. Many studies also focused on the preferential usage of nonoptimal codons in the initial regions (Burns and Beacham 1985; Chen and Inouye 1990; Ohno et al. 2001). A more sophisticated statistical method, such as isotonic regression, that can detect the trend of codon usage bias in the full length should be used. Isotonic regression refers to the test of an alternative hypothesis with ordered expectations (Robertson et al. 1988; Sokal and Rohlf 1995; Wu et al. 2001). It is a very powerful method to test the existence of a monotonic trend in nonlinear data structure. For example, it has been successfully used in a global-warming study (Wu et al. 2001).

In eukaryotic genomes, spatial codon usage bias has received less attention (Bulmer 1988; Kliman and Eyre-Walker 1998; Comeron and Kreitman 2002). Consequently, it is unclear as to the relative importance of selection against nonsense errors, selection against missense errors, and selection for translational efficiency. It is even controversial whether linked weak selection has a discernable effect on codon bias (Kliman and Hey 1993, 2003; Comeron et al. 1999; McVean and Charlesworth 2000; Marais et al. 2001, 2003; Comeron and Kreitman 2002; Hey and Kliman 2002; Marais and Piganeau 2002; Kliman et al. 2003). To address these issues, we present a systematic study of the intragenic spatial codon usage bias in both prokaryotic and eukaryotic genomes.

Codon usage bias may also be influenced by the interaction of mutation, selection, and random drift (Bulmer 1987, 1991; Shields and Sharp 1987; Sharp et al. 1993; Kliman and Hey 1994; Eyre-Walker and Bulmer 1995; Akashi 1997; Akashi et al. 1998; Rand and Kann 1998); effective population size (Li 1987; Bulmer 1991; Berg 1996); evolutionary history (Begun 2001); biased gene conversion (Galtier et al. 2001; Birdsell 2002; Galtier 2003; Marais 2003); mRNA secondary structure (Eyre-Walker and Bulmer 1993; Hartl et al. 1994; Antezana and Kreitman 1999; Chen et al. 1999; Carlini et al. 2001); translational initiation (Sakai et al. 2001; Stenstrom et al. 2001; Niimura et al. 2003); and many other factors (Fitch 1980; Modiano et al. 1981; Bulmer 1990; Berg 1996; McVean and Hurst 2000; Plotkin and Dushoff 2003). These confounding factors make codon usage bias a difficult subject to study. Here, we focus on the intragenic spatial codon usage bias and study the relative strength of codon usage bias along the open reading frame. This approach enables us to detect the expected signatures of selection against nonsense errors and the Hill-Robertson effect.

MATERIALS AND METHODS

Genomic data:

We parsed out 5366 reliable ORFs from a version of the Saccharomyces cerevisiae genome downloaded from the Saccharomyces Genome Database website on July 11, 2003. The annotations of these 5366 ORFs have been confirmed by a comparative genome analysis (Kellis et al. 2003). We excluded ORFs that were either questionable or with uncertain annotations.

The release 3.1 version of the Drosophila melanogaster genome was downloaded from Flybase on March 20, 2003. We parsed out 10,617 ORFs with a single splicing isoform and restricted our analysis in these genes because genes with multiple splicing isoforms are more likely to be misannotated. From these single splicing isoforms, we parsed out 2171 intronless genes and 2049 genes with two coding exons.

The GenBank accession numbers for the prokaryotic genomes are E. coli K12, U00096; Bacillus subtilis, AL009126; Sulfolobus tokodaii, NC_003106; and Thermotoga maritima, AE000512. In all genomes studied, we restricted our analysis to ORFs >150 codons because short genes do not have enough codons for their overall pattern to be evaluated.

Gene expression data:

Gene expression levels in S. cerevisiae were generated by the Young lab at Massachusetts Institute of Technology (http://web.wi.mit.edu/young/pub/data/orf_transcriptome.txt) (Holstege et al. 1998). Gene expression levels in D. melanogaster were generated by the Reichert lab at the University of Basel. The Omnibus accession numbers are GPL70, GSM1359, GSM1360, GSM1361, and GSM1362 (Montalta-He et al. 2002).

Isotonic regression:

Isotonic regression is a method for fitting data to order constraints (Robertson et al. 1988; Wu et al. 2001). “Isotonic” means “order preserving.” This nonparametric method is a very powerful way to test the existence of a monotonic trend under a nonlinear model. Suppose that we observe a sequence of random values, X_i, under the model X_i = μ_i + σε_i, 1 ≤ i ≤ n, where ε_i are independent standard normal random variables and σ > 0 is the standard deviation. We want to test the null hypothesis H₀: μ₁ = μ₂ … = μ_n (constant) vs. the alternative hypothesis H_A: μ₁ ≤ μ₂ … ≤ μ_n with at least one i such that μ_i < μ_i+1 (a monotonic increasing trend). To define the isotonic test, assume at the outset that σ is known. The following likelihood-based test is proposed by Wu et al. (2001),

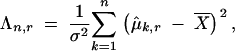1

where 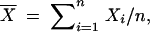r is a penalty factor that is defined later, and μ̂_k,r is the estimated trend

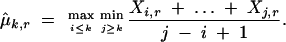2

Here 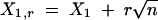, , 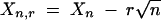and X_i,r = X_i for 2 ≤ i ≤ n − 1. The estimated trend (Equation 2) is nondecreasing in k. Under the requirement r > 0, μ̂_1,r and μ̂_n,r are consistent estimators of μ₁ and μ_n (Wu et al. 2001); for r = 0, μ̂_1,0 and μ̂_n,0 will be biased. To implement the test statistic (Equation 1), we estimate σ² by 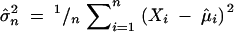and let r = cσ_n, where c > 0 is the penalty term. Cutoff values of Λ_n,r are given in Table 1 in Wu et al. (2001). For example, for c = 0.1 and n = 100, the cutoff values of Λ_n,r are 7.7 and 11.58 at the 5 and 1% levels, respectively. Simulations and several applications showed that such a test has very good power (Wu et al. 2001). The magnitude of Λ_n,r indicates the significance of the presence of a trend. Intuitively, the larger the Λ_n,r, the stronger the monotonic trend.

TABLE 1.

Monotonic trend of intragenic spatial codon usage bias along the translational direction

		First half			Second half
Species	Lc	λ of N̂c	λ of N̂′c	Codon bias trend along translational direction	λ of N̂c	λ of N̂′c	Codon bias trend along translational direction
E. coli	185	21.8***	19.8***	Increase	0.6	0.1	Plateau
[+25, −25]	255	22.6***	23.5***	Increase	1.5	1.3	Plateau
325	58.3***	41.7***	Increase	14.1***	15.4***	Plateau, decrease
420	76.1***	69.4***	Increase	7.8*	7.7*	Plateau, decrease
675	243.8***	243.5***	Increase	34.1***	31.3***	Plateau, decrease
B. subtilis	175	1.7	8.9**	Increase	8.2**	3.8	Plateau
[+25, −25]	230	0.0	0.3	Plateau	0.1	0.0	Plateau
285	9.5**	9.3**	Increase	4.9	5.3	Plateau
345	0.1	2.3	Plateau	1.4	0.1	Plateau
430	2.1	9.7**	Increase	0.2	1.2	Plateau
710	36.9***	49.0***	Increase	4.8	8.2*	Decrease
T. maritima	200	18.4***	16.4***	Increase	8.9**	6.9	Plateau
[+25, −25]	285	3.9	8.8**	Increase	0.2	3.1	Plateau
375	7.0	5.0	Plateau	11.1**	12.2***	Decrease
610	30.7***	24.7***	Increase	1.1	0.4	Plateau
S. tokodaii	185	5.1	10.0**	Increase	6.5	9.0**	Increase, decrease
[+25, −25]	255	0.6	0.0	Plateau	0.0	1.1	Plateau
350	0.1	7.2*	Increase	1.8	3.1	Plateau
570	7.8*	8.2**	Increase	4.2	12.1**	Plateau, decrease
S. cerevisiae	205	2.4	3.4	Plateau	12.6***	21.8***	Increase
[+25, −25]	300	23.2***	22.1***	Increase	12.7***	25.3***	Increase
400	32.5***	8.1*	Increase	4.9	22.3***	Increase
515	46.0***	8.5**	Increase	2.7	12.2***	Increase
680	114.3***	1.8	Plateau	0.0 (12.7***)	4.6 (1.0)	Plateau
1175	289.6***	20.3***	Increase	0.0 (68.5***)	0.1 (43.8***)	(Decrease)
D. melanogaster	180	NA	NA	NA	NA	NA	NA
[+110, −110]	240	5.7	1.0	Plateau	2.2	1.1	Plateau
305	5.8	8.4**	Decrease	4.4	8.1**	Increase
380	15.4***	14.6***	Decrease	26.3***	27.0***	Increase
460	22.9***	13.3***	Decrease	3.1	2.5	Plateau
565	1.5	1.0	Plateau	4.9	0.5	Plateau
745	87.9***	55.4***	Decrease	10.1**	2.3	Plateau
	1515	262.7***	135.6***	Decrease	126.8***	39.3***	Increase

Significance at 0.01 (***), 0.05 (**), and nearly 0.05 (*) levels is shown. λ, the test statistic of isotonic regression. In parentheses are the λ values and spatial bias patterns for the opposite trends, because isotonic regression detects only a monotonic trend. L_c, average gene length measured in the number of codons. Genes are grouped into equal intervals by their lengths. In parentheses are the Λ values calculated for the first halves and second halves excluding only the start and stop codons. In brackets are the ranges in which isotonic regression is applied. The bias trend of the significant patterns is interpreted on the basis of only the N̂^′_c results, although N̂_c and N̂^′_c often give similar interpretations. Additionally, when the increasing or decreasing pattern is significant in the first half, the nonsignificant pattern in the second half is interpreted as “plateau.” When a regression plot shows that significant changes in second half are near only the 3′ end, the trends are interpreted as “plateau, increasing” or “plateau, decreasing” accordingly. In the L_c = 185 interval for S. tokodaii, the trend in the second half increases and then decreases. Penalty factor c = 0.1 for isotonic regression. NA, not applicable.

In practice, to test a decreasing trend in a series of observations, we simply flip the sign of the data and test the monotonic increasing trend. Because the spatial patterns studied here are very noisy, we applied this regression at different ranges to ensure that the significance of a trend is stable.

Supersequences across codon positions:

To examine the global spatial codon usage bias in a group of genes, we generated supersequences for each codon position across all the genes in this group (Figure 1). We used the start codon as the reference for supersequences along the translational direction (forward) and the stop codon as the reference for supersequences in the opposite direction (backward). We use forward and backward supersequences to study the first half and the second half of genes separately. The modified effective number of codons (N̂^′_c; Novembre 2002) for each supersequence describes the overall codon usage bias at the codon position specified by the supersequence. The statistic N̂^′_c is a generalized form of the effective number of codons N̂_c (Wright 1990) and accounts for the background nucleotide composition. We use the supersequence from the first and the second base to estimate the background nucleotide composition during the N̂^′_c calculation. By studying the first half and the second half in opposite directions, this method is more sensitive to variations at codon positions than sliding-window methods are. For comparison, we calculated both the original effective number of codons, N̂_c, and the modified version, N̂^′_c.

Figure 1.—

Supersequences at each codon position across genes. (A) First half in translational direction (forward); (B) second half opposite to translational direction (backward). Each bar () represents a codon position. Vertical arrows represent supersequences.

When using this supersequence method to analyze the intragenic spatial pattern in an entire genome, extreme length variation between genes can complicate the spatial pattern. We therefore group genes in a genome into equal intervals by gene length. Genes in each group have comparable lengths. The average length of each group divided by two is the length of the forward and backward supersequences. The minimum number of genes in each interval (group) is 200. This ensures that each supersequence by position has at least 200 codons. Simulation shows that the effective number of codons is more accurate as a proxy for codon usage bias when gene length is >200 codons (Wright 1990).

This supersequence approach is also adopted to study the intragenic GC-content variation and the ratio of A/T-ending vs. G/C-ending major codons for Isoleucine, Valanine, and Alanine in yeast genes. The A/T-ending major codons are ATT, GTT, and GCT. The G/C-ending major codons are ATC, GTC, and GCC (Akashi 2003).

Implementation:

Parsing of ORFs and sequence manipulations were coded in PERL. The modified effective number of codons N̂^′_c was calculated using the program ENCprime (Novembre 2002). The effective number of codons (N̂_c) was calculated using both ENCprime and the program CHIPS from the EMBOSS package (http://www.hgmp.mrc.ac.uk/Software/EMBOSS/) (Wright 1990; Rice et al. 2000). The R statistical package (http://www.r-project.org/) was used for statistical analysis and plots (Ripley 2001).

Key PERL and R scripts are available at the Li lab website (http://pondside.uchicago.edu/lilab/research.html). All programs are tested only in a Red Hat Linux platform. The most recent versions of programs related to this work are also available upon request from H. Qin (hong_qin@urmc.rochester.edu).

RESULTS

Intragenic spatial codon usage bias in prokaryotic genomes:

We chose to study three bacterial genomes, E. coli, B. subtilis, and T. maritima, and one archaeal genome, S. tokodaii. In each genome, we grouped genes into equal groups (bins) by gene length. This grouping is necessary because large gene-length variation can obscure the global pattern generated by our supersequence method. We chose N̂^′_c as the measure of codon usage bias because it is insensitive to gene length (Wright 1990; Comeron and Aguade 1998) and because it takes account of background nucleotide composition variation (Novembre 2002). N̂^′_c is a generalized form of the effective number of codons, N̂_c, which is a measure of the departure from equal usage of synonymous codons (Wright 1990). A large N̂^′_c or N̂_c value indicates weak bias, whereas a small value indicates strong bias. The maximal value of N̂^′_c or N̂_c is 61, indicating equal usage of codons, i.e., no codon bias. For a gene with all 20 kinds of amino acids and with the strongest codon usage bias, its N̂^′_c or N̂_c value is 20.

We then generated supersequences for each length group, both along and opposite to the translational direction, using the start and stop codons as references, respectively (start and stop codons are excluded in plots and isotonic regression). At each codon position, the first and second bases are chosen to generate a supersequence to estimate the background nucleotide composition in the calculation of N̂^′_c. The N̂^′_c of each supersequence is plotted against its codon position (Figure 2). Because a small N̂^′_c value indicates strong codon usage bias, we inverted the N̂^′_c axis in the plot. Forward and backward plots are put side-by-side to represent the full-length spatial codon usage bias. For comparison, we always calculated both N̂^′_c and N̂_c to check the consistency of spatial patterns.

Figure 2.—

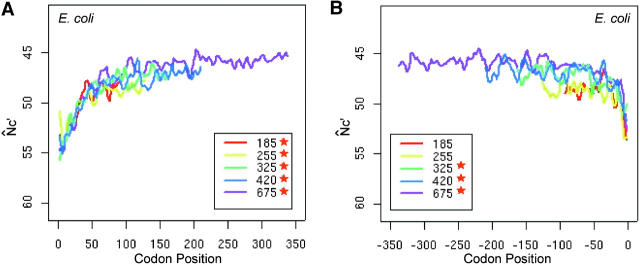
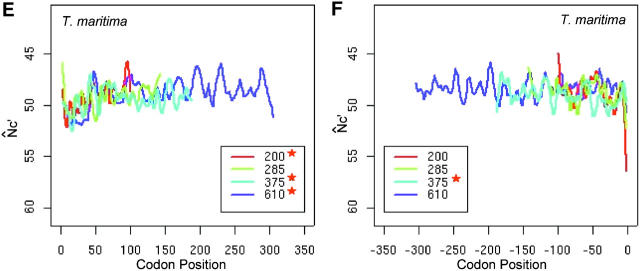
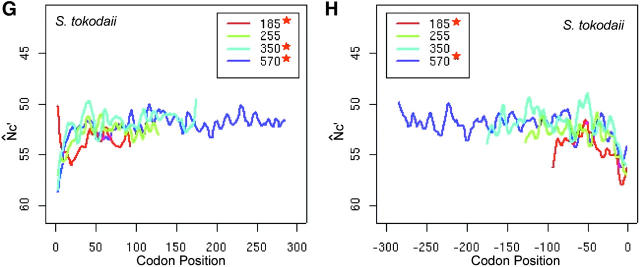
Intragenic spatial codon usage bias in prokaryotic genomes, Escherichia coli K12 (A and B), Bacillus subtilis (C and D), Thermotoga maritima (E and F), and Sulfolobus tokodaii (G and H). Asterisks in the insets indicate trends are significant by isotonic regression (see Table 1). N̂^′_c is plotted in the vertically inverted direction because a large value represents weak bias. Both the start and stop codons are excluded in the plots. For visual presentation, plots were smoothed by a locally weighted regression in a sliding window of 10 codons; however, the isotonic regression was applied to the original data. Genes were grouped into intervals with approximately equal numbers of genes by their length measured in the number of codons. The average length of each interval is given in the insets. The plot of each length interval is color coded.

The intragenic spatial codon usage bias in E. coli (Figure 2, A and B) shows that codon usage bias gradually increases, plateaus, and then deceases sharply starting at ∼50 codons from the stop codon. The pattern is consistent with previous reports in E. coli (Bulmer 1988; Eyre-Walker and Bulmer 1993; Eyre-Walker 1996a). The increasing trend of codon usage bias from approximately the 25th codon up to the middle section is also visible in previous reports, although the authors drew attention mainly to the initial regions (Bulmer 1988; Eyre-Walker and Bulmer 1993).

To detect weak evolutionary forces in the N̂^′_c vs. codon position plot, which has large fluctuations, we applied an isotonic regression analysis to the first halves beyond the first 25 codons and the second halves before the last 25 codons. The adopted isotonic regression method uses a penalty factor to generate an unbiased test statistic, Λ (see materials and methods). The critical value of Λ is used to distinguish between a null hypothesis H₀: μ₁ = μ₂ … = μ_n (constant) and the alternative hypothesis H_A: μ₁ ≤ μ₂ … ≤ μ_n for an increasing trend.

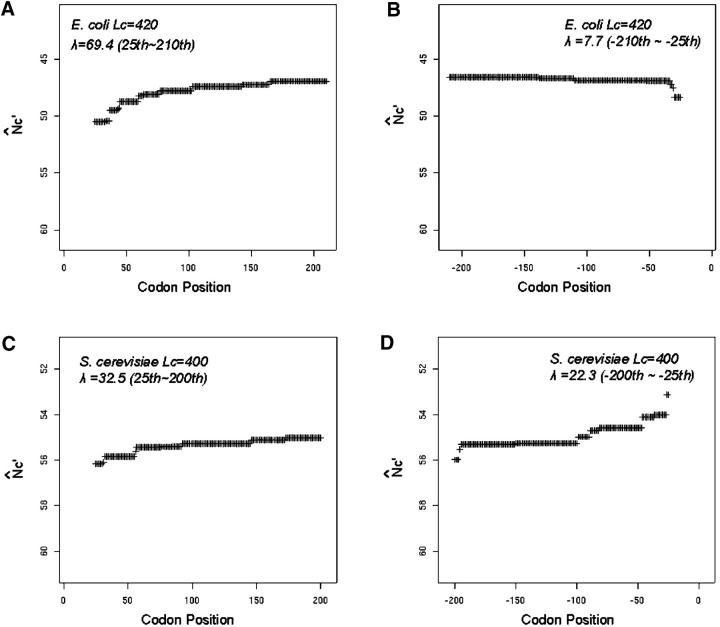
We calculated Λ for the first half and the second half of the coding sequences separately (Table 1). The critical value of the test statistic Λ at the 1% significance level is in the range of (12, 13) for sample sizes ranging from 100 to 1000 codons and penalty factor c = 0.1. The gradual increasing trend from the 25th to the 200th codon is indeed significant at the 1% level for all five length groups of genes in E. coli. The gradual increasing and then plateau trend of codon usage bias can be intuitively understood from the plot of the regression mean (expected N̂^′_c) vs. codon position (for example, Figure 3, A and B). The plateau of this increasing trend is confirmed by the insignificant Λ values in the second halves and can be seen from the regression plot (Figure 3, A and B).

Figure 3.—

Trend of spatial codon usage bias as shown by the expected N̂^′_c values from isotonic regression. Both the start and stop codons are excluded in the analysis. Side-by-side plots of expected N̂^′_c+ vs. codon positions for the first halves and second halves are presented along the translational direction. L_c is the gene length measured in the number of codons. Λ is the test statistic of isotonic regression. Two examples are presented, the L_c = 420 interval in the E. coli genome (A and B) and the L_c = 400 interval in the S. cerevisiae genome (C and D). In E. coli, the isotonic regression is applied to codon positions beyond the first 25 and before the last 25 codons. In S. cerevisiae, regression is applied to codon positions beyond the first 20 and before the last 20 codons.

Although the increasing trend of codon bias is consistent with purifying selection against nonsense errors, it may also be accounted for by changing selection pressure for mRNA structure after the initiation stage (Eyre-Walker and Bulmer 1993). To further explore the possible mechanism behind the gradually increasing codon usage bias from about the 25th to the 200th codon position, we chose to study the intragenic spatial patterns in B. subtilis (Figure 2, C and D), T. maritima (Figure 2, E and F), and S. tokodaii (Figure 2, G and H).

In B. subtilis, codon usage bias decreases near the start, but gradually increases along the translational direction, and then plateaus toward the end. In T. maritima, codon usage bias gradually increases up to the 150th codon position, plateaus, and then drops near the 3′ end. The codon usage bias in S. tokodaii follows a pattern similar to that in T. maritima. The codon usage bias pattern is also variable near the initiation regions in both T. maritima and S. tokodaii. Thus, in the four prokaryotic genomes examined, the spatial pattern is variable near the initiation region, but consistently increases gradually from about the 25th to the 200th codon. Therefore, different evolutionary forces must predominate in the initial region and in the central segments of genes, respectively. We argue that the gradual increasing codon usage bias is due to stronger purifying selection to eliminate errors with higher costs in late elongation steps (Bulmer 1988; Kurland 1992; Eyre-Walker and Bulmer 1993).

Both N̂^′_c and N̂_c give similar spatial patterns for the four prokaryotic genomes examined. The absolute values of N̂^′_c can differ by as much as 10 from the values of N̂_c in S. tokodaii, yet their spatial patterns are largely unchanged, as supported by results from isotonic regressions (Table 1). The differences between N̂^′_c and N̂_c values do affect the significance evaluation, because large differences are usually more easily detected than small ones for a given sample size. Because N̂^′_c takes nucleotide composition into account, we use Λ from N̂^′_c values to evaluate the significance of a bias trend. Notably, in both E. coli and B. subtilis, the gradual increasing trends are more conspicuous in longer genes than in shorter genes.

Intragenic spatial codon usage bias in the S. cerevisiae genome:

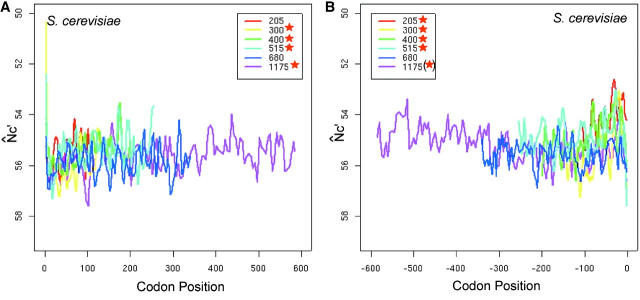
The spatial codon usage bias pattern in S. cerevisiae resembles that of prokaryotic genomes, but the gradual increasing trend is discernable even in the second half of yeast genes (Figure 4, A and B). In L_c ≈ 300, 400, and 515 length intervals (L_c is the number of codons in a gene), the N̂^′_c plot drops near the start codon, increases along the translational direction from about the 25th to the 200th codons, plateaus for ∼100 codons, and then gradually increases again up to the −25th codons, and finally drops near the end (Figure 3, C and D; Figure 4, A and B). The increasing trend in the second half is consistent in genes <600 codons and is significant by isotonic regression (Table 1 and Figure 3, C and D). The increasing trend from the +25th to the +400th is also significant in the L_c ≈ 1175 interval, but the second half shows an opposite trend as compared to shorter length intervals.

Figure 4.—

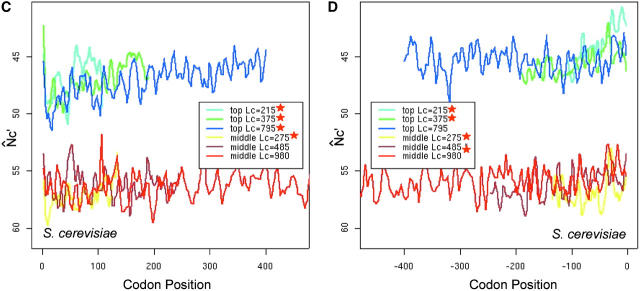
Incremental pattern of intragenic spatial codon usage bias in S. cerevisiae (A and B) and the effect of expression on the pattern (C and D). The N̂^′_c value is plotted in the inverted direction. Both the start and stop codons are excluded in the plots. Plots are smoothed by a locally weighted regression in a sliding window of 10 codons (the isotonic regression was applied to the unsmoothed data). Asterisks in the inset indicate significant trends by isotonic regression (see Tables 1 and 2). The asterisk in parentheses indicates a significant trend opposite to other groups. In C and D, genes are grouped into top 20%, middle 20%, and bottom 20% by their expression levels measured by Affymetrix DNA microarrays. Genes are then divided into three equal intervals by gene length (L_c). Each group is labeled by its expression level and average gene length. The bottom 20% in yeast shows a flat pattern and is omitted for clarity.

The N̂_c analysis in yeast shows a similar increasing trend of bias along translational direction from the +25th to the +400th codon (plots are not shown, but isotonic regression results are given in Table 1). The N̂^′_c plots are usually noisier than the N̂_c plots, maybe because more parameters have to be estimated in the N̂^′_c plots than in the N̂_c plots.

We then studied the effect of gene expression on the spatial pattern (Figure 4, C and D; Table 2). Holstege et al. (1998) estimated the number of mRNA molecules of each yeast gene in a single wild-type haploid cell using high-density oligonucleotide arrays. The estimation is conducted for cells grown to the midlog phase in rich media and has been shown to be informative in codon usage analysis (Akashi 2003). We picked genes from the top 20%, the middle 20%, and the bottom 20% by the transcript abundance and compared their spatial bias patterns. There is clearly a shift of the spatial patterns between the top and middle 20% expression levels. The spatial patterns are mostly flat in the bottom 20% expression level, indicating that intragenic spatial codon usage bias is dependent upon expression level. The increasing trends in short genes are comparable in top and middle expression levels, indicating that changes of spatial patterns can be decoupled from changes of expression levels.

TABLE 2.

Effect of gene expression level on the intragenic spatial pattern of codon bias in yeast

		First half			Second half
Expression level	Lc	λ of N̂c	λ of N̂′c	Codon bias trend along translational direction	λ of N̂c	λ of N̂′c	Codon bias trend along translational direction
Top 20%	215	3.3	10.9**	Increase	15.4***	26.5***	Increase
375	72.3***	35.9***	Increase	2.9	14.3***	Increase
795	83.4***	32.5***	Increase	1.2	4.0	Plateau
Middle 20%	275	9.5	10.4**	Increase	9.9**	24.5***	Increase
485	10.9**	4.0	Plateau	7.8	14.8***	Increase
980	39.7***	1.4	Plateau	0.8	6.5	Plateau
Bottom 20%	270	2.7	1.4	Plateau	4.2	2.4	Plateau
500	8.2	1.1	Plateau	3.2	6.1	Plateau
	930	74.1***	4.6	Plateau	0.4	0.6	Plateau

Significance at 0.01 (***) and 0.05 levels (**) is shown. λ, the test statistic of isotonic regression. L_c, average gene length measured in the number of codons. In each expression level, genes are grouped into equal intervals by their lengths. The trend is analyzed after the first 25 codons and before the last 25 codons. The bias trend of the significant patterns is interpreted on the basis of only the N̂^′_c results. Penalty factor c = 0.1 for isotonic regression.

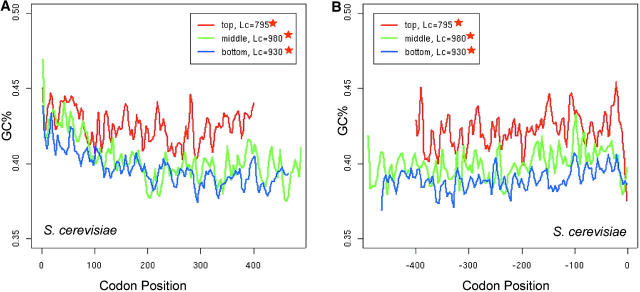
Because nonselective forces are often correlated with changes of GC content (Marais 2003), we investigated the intragenic spatial pattern of GC content using the first and second base of each codon position. Although N̂^′_c has taken the background nucleotide composition into account, investigation of nonselective forces can help us to better understand the observed incremental pattern of codon bias. The intragenic spatial pattern of GC-content variation is also dependent upon expression levels (Figure 5, A and B). The spatial pattern appears to be U-shaped in lowly expressed genes, but the U-shape is less conspicuous in highly expressed genes, which is supported by isotonic regression (Table 3). The overall GC content is higher in highly expressed genes than in lowly expressed ones. Notably, the U-shaped spatial pattern of GC-content variation is more or less symmetric, whereas the incremental shape of the codon bias is asymmetric.

Figure 5.—

Intragenic spatial pattern of GC content in S. cerevisiae and the effect of expression on the pattern. Both the start and stop codons are excluded in the plots. Plots are smoothed by a locally weighted regression in a sliding window of 10 codons. Asterisks in the insets indicate significant trends by isotonic regression (see Table 3). Genes are grouped in the same way as in Figure 4, C and D.

TABLE 3.

Intragenic spatial pattern of GC content inS. cerevisiae

		First half		Second half
Expression level	Lc	λ of GC%	Trend along translational direction	λ of GC%	Trend along translational direction
Top 20%	215	12.1***	Decrease	4.3	Plateau
375	6.7	Plateau	6.2	Plateau
795	11.1**	Decrease	9.3**	Increase
Middle 20%	275	3.5	Plateau	3.9	Plateau
485	12.3***	Decrease	7.9	Plateau
980	83.1***	Decrease	27.1***	Increase
Bottom 20%	270	9.1**	Decrease	6.5	Plateau
500	35.9***	Decrease	6.2	Plateau
	930	108.5***	Decrease	20.2***	Increase

Significance at 0.01 (***) and 0.05 levels (**) is shown. λ, the test statistic of isotonic regression. L_c, average gene length measured in the number of codons. In each expression level, genes are grouped into equal intervals by their lengths. The trend is analyzed after the first 25 codons and before the last 25 codons. Penalty factor c = 0.1 for isotonic regression.

To further test the role of GC-content variation, we calculated the ratio of A/T-ending major codon number vs. G/C-ending major codon number for Isoleucine, Valanine, and Alanine. In yeast, these three codon families contain two major codons, one with A/T ending and another with G/C ending (Akashi 2003). We calculated the intragenic spatial distribution of this ratio in genes grouped by expression levels. The spatial pattern of this ratio appears to be flat in all groups of genes (data not shown). When applying isotonic regression at different ranges, no stable significant regression score was found.

Intragenic spatial codon usage bias in the D. melanogaster genome:

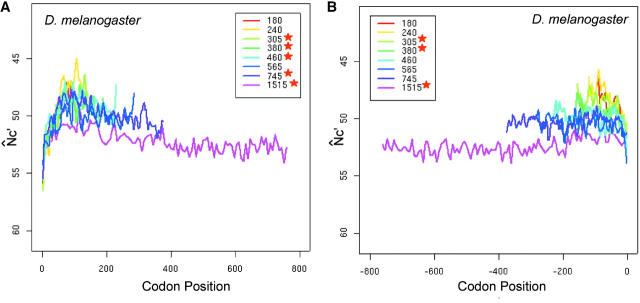
D. melanogaster is of particular interest to us because its codon usage bias was suggested to be nonuniformly influenced by the Hill-Robertson effect (Comeron and Kreitman 2002). Indeed, D. melanogaster reveals a distinctive M-shaped global spatial codon usage bias (Figure 6, A and B), with less bias in the middle and at both ends. The low codon usage bias in the middle is statistically significant, confirmed by the decreasing trend in the first halves and the increasing trend in the second halves of genes shown by isotonic regression in the central segments (Table 1). The plots of longer genes are often below the plots of shorter genes, especially in the middle section, indicating that overall codon usage bias of longer genes tends to be weaker than that of shorter genes. The N̂_c analysis in D. melanogaster gives the same M-shaped global spatial pattern as does the N̂^′_c analysis (plots are not shown, but isotonic regression results are given in Table 1).

Figure 6.—

The M-shaped pattern of the intragenic spatial codon usage bias in D. melanogaster (A and B) and the effect of expression level on the pattern (C and D). The N̂^′_c value is plotted in the inverted direction. Asterisks in A and B indicate significant trends in the middle section by isotonic regression (see Table 1). Plots are smoothed by a locally weighted regression in a sliding window of 10 codons (the isotonic regression was applied to the unsmoothed data). Genes are grouped by gene length. Each group contains similar numbers of genes and is labeled by its average gene length (L_c). Plot of each length interval is color coded.

Next, we investigated the effect of expression level on the M-shaped spatial pattern. Montalta-He et al. (2002) provided four independent measurements of gene expression level in wild-type D. melanogaster, using high-density oligonucleotide arrays. We used the averaged intensity value of these four independent hybridizations as our estimate of expression level for each gene. We obtained expression measurements from Montalta-He et al.'s experiments for over 7300 single-isoform ORFs (Release 3.1). We then picked genes from the top 20% and bottom 20% of the distribution at expression levels and compared their spatial codon usage bias (Figure 6, C and D). The plots are noisier than the whole-genome plots due to the smaller data sets here. Nevertheless, expression level shifts only the spatial bias pattern without dramatically altering the M-shape.

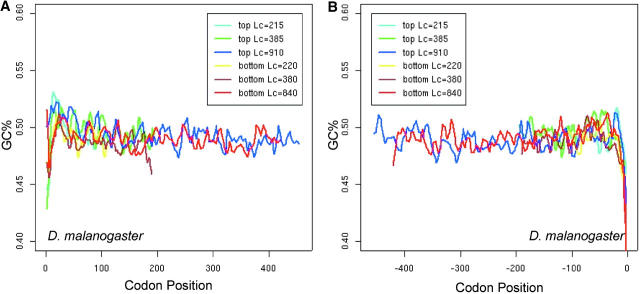
We then revealed the intragenic GC-content variation using the first and second base of each codon position (Figure 7, A and B). The overall pattern of intragenic GC-content variation is also M-shaped; however, the sharp variations are located mostly within the first and last 50 bp. In contrast, the pattern of codon bias peaks around +100 bp and −100 bp (Figure 6).

Figure 7.—

The intragenic spatial pattern of GC-content variation in D. melanogaster. GC content is estimated using the first and second base of each codon position. Genes are first partitioned by expression level as in Figure 6, C and D, and then grouped by gene length measured in the number of codons (L_c).

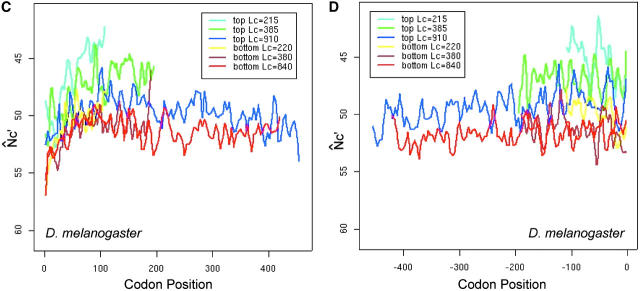
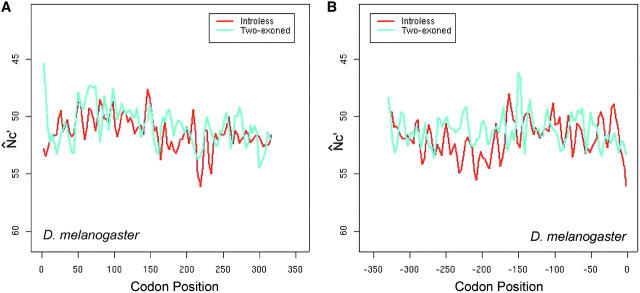
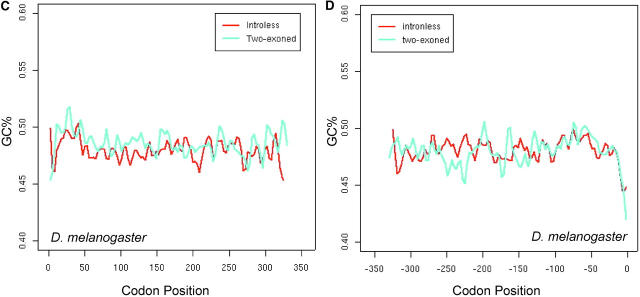
The presence of introns is expected to mitigate the effect of interference (Comeron and Kreitman 2002), so we compared the spatial patterns N̂^′_c in intronless and two-exon genes. In long genes (average length >500 to ∼600 bp), the M-shaped spatial pattern of intronless genes appears to be more conspicuous than that of two-exon ones, in the sense that the latter is more flat (Figure 8, A and B). In the middle section (from +200th to −200th), N̂^′_c is significantly higher in intronless genes than in two-exon genes (t-test, P-value = 0.01), indicating the significantly lower codon bias in the middle section of intronless genes. For comparison, we calculated the intragenic pattern of GC content variation in the two groups of genes (Figure 8, C and D). In the middle section, GC variation between the two gene groups is not significantly different by t-test.

Figure 8.—

The effect of introns on the intragenic spatial patterns of codon usage bias (A and B) and GC-content variation (C and D) in D. melanogaster. Only the longest groups of genes are presented. Equal numbers of intronless and two-exon genes are used to ensure appropriate comparisons.

DISCUSSION

Variation of codon usage bias near the start and stop codons:

In most genomes, we observed sharp variations near the start and stop codons. In addition to the weakened elongation-related selection (Eyre-Walker and Bulmer 1993), several other possibilities may account for the variation of codon bias near the start and stop codons. First, the ends of ORFs are more likely to be misannotated, especially in the yeast and fruit fly genomes. We hope to have mitigated this possibility in yeast to some extent by excluding ORFs with uncertain annotations. A recent comparative analysis of several yeast genomes proposed to change the annotations of ∼500 yeast ORFs (Kellis et al. 2003). For simplicity, we excluded these questioned ORFs from the downloaded S. cerevisiae genome. The starting ATG codons in the prokaryotic genomes can be identified with high confidence by the presence of an upstream Shine-Dalgarno sequence (Saito and Tomita 1999; Sakai et al. 2001). Therefore, it is unlikely that the codon usage bias variation near the initiation ATG in the prokaryotic genomes is due to misannotations. There is evidence that the occurrence of ATG in the 5′-UTR is highly suppressed in the eukaryotic genomes (Saito and Tomita 1999), which indicates that the initiation codon ATG is less likely to be misannotated than the stop codon.

Second, the ends of ORFs are evolutionarily more variable than the middle section of the coding sequence. The possibility is supported by the comparison of several yeast genomes (Kellis et al. 2003). The S. cerevisiae genome contains ∼250 ORFs that show variable stop codon positions in other sensu stricto yeast genomes, suggesting that coding regions near the stop codon are indeed evolutionarily variable (Kellis et al. 2003).

Third, the base composition near both ends is different from that in the middle section of the reading frame. The modified effective number of codons, N̂^′_c, takes the background nucleotide composition into account. In practice, it is hard to find a “perfect” background sequence. We estimate the background nucleotide composition by using the first and second bases in a given codon position to generate supersequences. This may not be a good choice, because nonsynonymous sites show a weaker correlation with GC content than synonymous sites in prokaryotic genomes (Lobry 1997; Singer and Hickey 2000). In E. coli, base composition is variable in the first 15–20 codons, but this variation disappears after the first 20 codons (Eyre-Walker and Bulmer 1993). However, the consistent trend of both N̂^′_c and N̂_c after the initial region in four prokaryotic genomes begs a common explanation other than base composition variation. Further analysis will be needed to better understand the nature of the codon usage bias variation in regions near the start and stop codons.

The incremental pattern of intragenic spatial codon usage bias in yeast and prokaryotic genomes:

Both nonselective forces and selective forces have been argued to shape the codon usage bias in yeast (for reviews see Akashi 2001 and Marais 2003). Here, we show that codon usage bias and GC-content variation follow characteristically different spatial patterns within yeast genes. The incremental spatial pattern of codon usage bias is asymmetric and is stronger in highly expressed genes (Figure 4, C and D). The spatial pattern of GC-content variation is more or less a symmetric U-shape and is stronger in lowly expressed genes (Figure 5, A and B).

Various arguments can explain this incremental pattern of codon usage bias. One argument is the 5′-3′ polarity in gene conversion (Schultes and Szostak 1990; Nicolas and Petes 1994; Nicolas 1998). This polarity in conjunction with biased repair toward GC (Marais 2003) would then explain the incremental spatial pattern of codon bias in yeast. The intragenic spatial pattern of GC-content variation shows a moderate feature of polarity, but its overall pattern is largely symmetric. This pattern indeed suggests the role of recombination, but its characteristics are in discordance with the incremental nature of the spatial codon pattern in yeast. Using the ratio of A/T-ending vs. G/C-ending major codon numbers of Isoleucine, Valanine, and Alanine, we did not detect significant influence of GC-content variance on intragenic codon bias, although this negative result may be due to the weak power of this method. Furthermore, because GC-content variations are also influenced by gene expression levels in yeast, association with GC-content variation is not a good indicator for either selective or nonselective forces in this organism. It is also not obvious why biased gene conversion ought to be correlated with gene expression levels. Finally, nucleotide composition variation is corrected in the calculation of pattern of codon usage bias. Hence, the strength of codon bias variation is much stronger than the expected variation exclusively contributed by nucleotide composition variation.

Selection against nonsense errors is another argument to explain this kind of position-dependent effect, because costs for errors are higher in late elongation steps (Kurland 1992; Akashi 2001). This straightforward argument is favored by us on grounds of parsimony. Both selection against misincorporation and selection for translation efficiency are expected to be position independent (or gene-length independent) and have to be ruled out.

In E. coli and B. subtilis, the incremental pattern is stronger in longer genes than in shorter genes. It is known that codon usage bias is positively correlated with gene length in E. coli (Eyre-Walker 1996b; Moriyama and Powell 1998). Stronger spatial bias in longer genes would then explain the observed positive correlation between codon usage bias and gene length (Eyre-Walker 1996b; Moriyama and Powell 1998). In other words, the biased spatial pattern reflects the overall biased usage of synonymous codons in these genomes. Interestingly, the incremental pattern in E. coli was attributed to nonselective factors (Eyre-Walker and Bulmer 1993; Eyre-Walker 1996a), but positive association between gene length and codon bias was proposed to be due to selection against nonsense errors (Eyre-Walker 1996a). We argue that purifying selection against nonsense errors is a consistent explanation for both the incremental spatial pattern and the association between codon usage bias and gene length.

Although purifying selection against nonsense errors is our best argument so far, we do not exclude the possibilities of other factors, such as constraints at the protein conformation level.

The M-shaped intragenic spatial codon usage bias in the D. melanogaster genome:

The M-shaped intragenic pattern of codon usage bias has taken into account the M-shaped GC-content variation. The spatial pattern of codon bias is influenced by expression levels and peaks around the +100th codon position in the 5′ region and broadly around the −100th in the 3′ region (Figure 6, C and D), whereas the spatial pattern of GC-content variation appears to be insensitive to changes of expression levels and peaks at +50th and −50th codon positions (Figure 7, A and B). The presence of introns significantly influences the pattern of codon usage bias but not the pattern of GC-content variation.

In D. melanogaster, GC-biased mutation and/or GC-biased gene conversion has been postulated to contribute to codon usage bias differences between genes, i.e., the intergenic pattern (Marais et al. 2001, 2003; Marais 2003; but see also Betancourt and Presgraves 2002; Hey and Kliman 2002). On the basis of this argument, the M-shaped pattern of GC-content variation would suggest intragenic variation of recombination rate. Hence, the spatial pattern of codon usage bias reflects the pattern of recombination rate variation. However, this argument would ignore the correction of GC background in the calculation of codon usage bias. In addition, the spatial pattern of GC-content variation is characteristically distinct from the spatial pattern of codon usage bias.

Under the Hill-Robertson interference model, Comeron and Kreitman proposed that more sites are linked in the middle section of genes than in other regions of genes, thereby resulting in stronger interference in the middle section (Comeron and Kreitman 2002). This argument is more straightforward than the GC-content version and is further supported by the comparison between intronless and two-exon genes. It should be noted that the Hill-Robertson effect alone should give a U-shaped pattern. The M-shape hence indicates the presence of other factors. It is interesting that the M-shaped spatial bias peaks around +100th (forward) and broadly around −100th codon positions (backward). This may be informative about the interaction of the weak selection for codon usage bias, mutation rate, and recombination rate.

Besides the assumed weak selection on synonymous codon usage, there is the alternative argument of strong selection. As Fay and Wu showed, strong selection and hitchhiking can occur in a ∼350-bp region, short enough to influence intragenic distribution of codon usage bias (Fay and Wu 2000). The key difference between the strong- and weak-selection models is the number of sites involved in the formation of the M-shape. Strong-selection models typically imply selection at a single site, whereas weak-selection and interference models require multiple sites. We think that the gradual decreasing trend toward the middle section is more consistent with weak selection at multiple sites.

As with yeast, it is very difficult to distinguish selective vs. nonselective forces in fruit fly genes (Duret 2002). Although we think that the Hill-Robertson interference is the most parsimonious argument, the question is still open and more studies are needed. A genome-scale comparison of gene structures and intragenic spatial patterns of codon usage bias between D. melanogaster and D. pseudoobscura may be informative for this subject.

Why is there lack of interference in yeast and prokaryotic genes?

It is perplexing that there is no detectable signature of the Hill-Robertson effect in yeast and its spatial codon usage bias resembles that of prokaryotes. Although recombination during sexual reproduction occurs at a much higher rate in the yeast genome than in the fruit fly genome in the laboratory (Cherry et al. 1997; Gerton et al. 2000), sexual reproduction of yeast may occur rarely in nature (Jensen et al. 2001; Winzeler et al. 2003). Simulation showed that the intragenic spatial pattern of codon usage bias is insignificant when recombination is low (Comeron and Kreitman 2002; J. M. Comeron, unpublished data). At the extreme case of no recombination, the Hill-Robertson effect will be the same at every position of the sequence and will thus produce no signature on the spatial pattern of codon usage bias. Hence, a very low effective recombination rate may account for the absence of a signature of the Hill-Robertson effect on the spatial pattern of codon usage bias in yeast and prokaryotes.

On the other hand, the effective recombination rate of yeast may be indeed much higher in yeast than in fruit fly, which can also explain the discrepancy between these two species. The uncertainty on this issue highlights the importance of studying the polymorphic variations in natural isolates of yeast.

The effect of expression levels on intragenic spatial codon usage bias:

The positive correlation between codon usage bias and expression levels is often attributed to selection for translational efficiency (Gouy and Gautier 1982; Sharp and Li 1986; Duret and Mouchiroud 1999; Akashi 2001; Carlini and Stephan 2003). Selection against nonsense errors is largely suggested by the positive correlation between codon usage bias and gene length in some genomes (Moriyama and Powell 1998; Coghlan and Wolfe 2000). Selection against missense errors is based on the positive correlation between codon usage bias and conservation of amino acids (Akashi 1994). The selection effect for translational efficiency and against missense errors on the spatial pattern of codon bias is expected to be uniform, whereas the selection effect against nonsense errors is expected to be incremental along the translational direction, i.e., asymmetric. Hence, studying the intragenic spatial pattern of codon bias can dissect the roles of these evolutionary forces. If an asymmetric spatial pattern is observed, it is unlikely to be the result of a process with a uniform spatial effect.

By choosing appropriate expression levels, we show that expression levels significantly affect the overall codon usage bias in both yeast and fruit fly genes, but to a lesser extent on the intragenic spatial pattern of codon usage bias. Therefore, we argue that selection for translational efficiency significantly affects the overall codon usage bias, i.e., the average, whereas purifying selection against nonsense errors and the Hill-Robertson effect greatly influences the shape of the spatial codon usage bias, i.e., the spatial distribution.

Final remarks:

Compared with some previous methods in analyzing patterns of codon usage bias (Bulmer 1988; Hartl et al. 1994; Eyre-Walker 1996b; Comeron et al. 1999; Comeron and Kreitman 2002; Kliman et al. 2003), our method is more sensitive for addressing variations by positions and identifying the trend of changes in spatial patterns. This enables us to distinguish the subtle signatures of various evolutionary forces. The gradually increasing spatial bias pattern in S. cerevisiae and prokaryotic genomes suggests purifying selection against nonsense errors. The M-shaped global spatial codon usage bias confirms the low codon usage bias in the middle of genes in D. melanogaster, which may be best explained by the interference of weak selections (Comeron and Kreitman 2002). Selection for translational efficiency mainly affects the overall codon usage bias, whereas selection against nonsense errors and Hill-Robertson interference leave discernable signatures in the intragenic spatial pattern. Therefore, our analysis suggests two types of selective process on codon bias: One is the optimization of the biochemical process of translation, and the other is the subtle process due to evolutionary mechanisms and is best understood from theory of population genetics. The first is common to most species. The second, acting upon the first type of selection, is expected to differ among species because it is sensitive to the effective population size and the evolutionary history of each species. Hence, further analysis of global spatial codon usage bias in other genomes may help us better understand the evolution of codon usage in those species.