The Probability and Chromosomal Extent of trans-specific Polymorphism

Abstract

Balancing selection may result in trans-specific polymorphism: the maintenance of allelic classes that transcend species boundaries by virtue of being more ancient than the species themselves. At the selected site, gene genealogies are expected not to reflect the species tree. Because of linkage, the same will be true for part of the surrounding chromosomal region. Here we obtain various approximations for the distribution of the length of this region and discuss the practical implications of our results. Our main finding is that the trans-specific region surrounding a single-locus balanced polymorphism is expected to be quite short, probably too short to be readily detectable. Thus lack of obvious trans-specific polymorphism should not be taken as evidence against balancing selection. When trans-specific polymorphism is obvious, on the other hand, it may be reasonable to argue that selection must be acting on multiple sites or that recombination is suppressed in the surrounding region.

MOST species appear to be monophyletic for most of their genomes. That is, most sites in most genomes have the property that, with respect to that site, all homologous chromosomes in one species are more closely related to each other than they are to any homologous chromosome from another species. This behavior is expected from standard population genetics theory, as long as the species became reproductively isolated sufficiently long ago (see, for example, Hudson and Coyne 2002; Rosenberg 2002). However, exceptions are expected when balancing selection has maintained two or more alleles since the time of speciation. When this occurs, an allele sampled from a particular species may well be more closely related to members of the same functional allelic class in related species than to members of different allelic classes in the same species. This is referred to as trans-specific polymorphism (Klein 1980).

A few clear cases of trans-specific polymorphism have been found, in particular, in the MHC (e.g., Figueroa et al. 1988) and plant self-incompatibility loci (e.g., Ioerger et al. 1990). At the same time, studies of sequence variability in several genes that might a priori be considered good candidates for trans-specific polymorphism have failed to find strong evidence for this hypothesis. Examples include the primate ABO blood group system (Saitou and Yamamoto 1997) and red/green color vision polymorphism in New World monkeys and lemurs (Boissinot et al. 1998; Tan and Li 1999). In these cases, are the functionally similar alleles in different species examples of trans-specific polymorphism, or are they due to convergent evolution? The purpose of this article is to develop a modeling framework that allows us to address these questions. We focus in particular on our ability to detect trans-specific polymorphism when it exists and how this is determined by the length of the chromosomal region that is affected by the presence of a trans-specific polymorphism.

Throughout, we discuss relatedness in the genealogical sense, i.e., with reference to “descent” rather than to allelic “state.” Thus, when we say that two homologous copies of a site (or locus or nonrecombining sequence) are more closely related to each other than to a third copy, we mean that the most recent common ancestor (MRCA) of these two is more recent than the MRCA of either of them and the third copy. This does not necessarily mean that the two copies are more similar to each other than either is to the third copy (although if they are not, we would typically not be able to infer the true relationship).

BASIC MODEL

We are interested in the following scenario. An ancestral species/population splits into two τ units of time ago. For simplicity, both descendant populations are assumed to be of the same size as the original one. All populations evolve according to a standard neutral model, the coalescent approximation is employed, and time is measured in units of the effective number of homologous chromosomes in each of the current populations. We consider both selective neutrality and various forms of balancing selection.

We consider the following questions for samples of homologous sequence taken from the two species:

• What is the probability that the genealogy of a particular site does not reflect the species tree, i.e., that the samples from the two species are not both monophyletic? We refer to sites with this property as trans-specific.

• Given that a particular site (or sites) is (or are) trans-specific, what is the probability that a linked site is also trans-specific?

• Given that a particular site (or sites) is (or are) trans-specific, what is the distribution of the length of the chromosomal region for which this remains true?

PROBABILITY OF TRANS-SPECIFICITY

Consider a sample of n₁ homologous copies of a site from species 1 and n₂ from species 2. The number of ancestral lineages decreases back in time according to a death process. The probability of trans-specificity may be calculated by first conditioning on the number of surviving lineages in each species at the time of speciation, τ, and then calculating the probability that these lineages coalesce in the ancestral species in a trans-specific manner. Assuming neutrality, the numbers of surviving lineages in each species at τ are independent, identically distributed random variables whose distribution is given by Tavaré (1984), and the conditional probability of trans-specificity can be found using the results of Saunders et al. (1984). The expression for the total probability can easily be evaluated numerically: see Nordborg (2001), for example. Numerous treatments of the probability of trans-specificity exist (e.g., Pamilo and Nei 1988; Takahata 1989; Hey 1994; Hudson and Coyne 2002; Rosenberg 2002); our main purpose here is to introduce the basic concepts and to enable comparisons with later results.

Trans-specificity is impossible unless there are at least three ancestral lineages at the time of speciation. If there are two lineages in one species and one in the other, then the probability of trans-specificity is 2/3 (trans-specificity is avoided if and only if the two lineages from the same species coalesce with each other; this happens in one out of three equally likely topologies). The probability of trans-specificity is higher if there are more than three ancestral lineages. Thus the probability of trans-specificity is at least 2/3 given that there are at least three lineages at the time of speciation. The probability that there are at least three lineages at the time of speciation, on the other hand, decreases sharply with τ and can be vanishingly small. The probability of trans-specificity is thus mainly determined by this latter probability.

To put this into context, consider a sample of size two. The probability that the MRCA of the sample predates speciation is e^−τ. Let T be the time until the MRCA for two genes, and note that under our model, E[T] = 1 for two genes sampled from the same species, whereas E[T] = τ + 1 for two genes sampled from different species. Since the average number of pairwise differences between sequences is proportional to pairwise coalescence times under neutrality, an estimate of τ can be obtained as the ratio of the average number of pairwise differences between and within species, −1. For example, if, on average, humans and chimps are at most 99% identical, and humans and humans are at least 99.9% identical, then τ ≥ 10⁻²/10⁻³ – 1 = 9. Let us say τ = 8 to be on the safe side. Then the probability that the MRCA of a sample from humans predates speciation from chimps would be e⁻⁸ = 3.3 × 10⁻⁴ (and probably much smaller).

This is a small number, but the genome is large. If there are G sites in the genome, then we expect Ge^−τ to have MRCAs that predate speciation. If we consider the whole population rather than just two copies of the genome, the expected number of sites with MRCAs that predate speciation increases about threefold: the time until there are two ancestral lineages is ∼1, so the expected number of sites is ∼ Ge^−(τ−1) ≈ 3Ge^−τ. For the ranges of τ we are interested in, qualitative conclusions are unaffected by sample size. For simplicity, we therefore discuss mainly samples of size two throughout this article.

The probability of trans-specificity for a site depends on whether the site is polymorphic or not. The calculations above assumed no knowledge of allelic state. What is the probability that T > τ for a polymorphic locus A, i.e., for a sample of two different alleles? We consider the process that keeps track of the number of ancestral lineages in each of the two allelic classes. Denote the state of the process at time t by X_t = (i, j), where i is the number of lineages in the first allelic class, and j is the number of lineages in the second allelic class. The probability we seek is

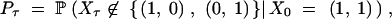which we write as P_τ = Q_τ/Q₀, with

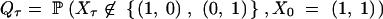We consider two cases: unidirectional mutation and bidirectional mutation. For the case of unidirectional mutation, assume that allele A₁ mutates into A₂ at rate θ/2 and that further mutation in A₂ does not change the allelic state (we think of A₂ as a loss-of-function allele: this case is motivated by the observation that many examples of balancing selection appear to involve such mutations). Using standard population genetics theory (Hudson 1990), we find

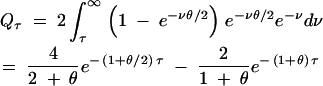and

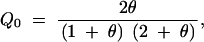so that

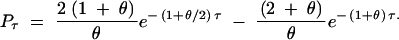For the case of bidirectional mutation, assume that alleles A₁ and A₂ mutate back and forth at rate θ/2. Here we find

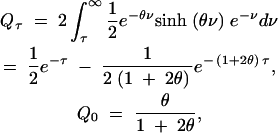and

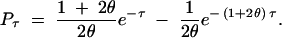These results make intuitive sense: for small θ, P_τ ≈ (1 + τ)e^−τ in both cases. The probability of trans-specificity conditional on polymorphism is higher than the unconditional probability because the fact that a (rare) mutation must have occurred automatically pushes the time to the MRCA further back in time. For large θ, P_τ ≈ 0 with unidirectional mutation and P_τ ≈ e^−τ with bidirectional mutation. In the former case, the MRCA must be recent or all A₁ would have mutated to A₂, whereas in the latter case, mutations occur so frequently that the allelic states tell us nothing about the age of the MRCA.

The main conclusion from the above discussion, however, is that no matter which model is used, the probability of trans-specificity under neutrality is always very low for large τ (for recent attempts to estimate it directly, see Chen and Li 2001; O'hUigin et al. 2002). In contrast, if some form of balancing selection is acting, trans-specificity becomes highly probable. Selected alleles will of course also be lost through genetic drift, but this occurs over entirely different timescales (Takahata 1990; Vekemans and Slatkin 1994), and it is easy to imagine strengths of selection that make loss of polymorphism during speciation unlikely even if one believes that speciation is accompanied by genetic bottlenecks (Vincek et al. 1997). Trans-specificity may therefore, in and of itself, be viewed as evidence for a history of balancing selection. But how do we detect trans-specificity? To consider the traces of trans-specificity in sequence data, we need to know something about its chromosomal extent. This is the topic of the following sections.

THE EXTENT OF TRANS-SPECIFICITY

What is the probability that a locus is trans-specific given that it is linked to a locus that is trans-specific? Let the recombination rate between the two loci be ρ/2, where ρ = 4Nr, N is the effective population size, and r is the recombination fraction, and consider a sample of size two. The site is trans-specific if no recombination occurs before coalescence at the other site. The probability of this is

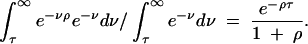1

If, as suggested above, τ ≈ 8 for humans and chimps, and ρ per site is 5 × 10⁻⁴ (Przeworski et al. 2000; Pritchard and Przeworski 2001; Innan et al. 2003), then the probability is >60% for sites separated by 100 bp, but it decreases rapidly to 1% for 1 kb. Linkage to a trans-specific site increases the probability of trans-specificity for tighly linked sites dramatically, but we should not expect large chromosomal regions to be trans-specific (at least not due to linkage).

The probability just derived is an underestimate: the focal site can of course be trans-specific without being identical by descent (with respect to recombination) to the conditional one. Most importantly, whereas two lineages linked to a trans-specific site cannot coalesce before τ without at least one recombination, a single recombination does not allow them to coalesce unless it occurs between descendants of different trans-specific lineages (“moving” the two lineages into the same trans-specific lineage). The probability of this depends on the frequency of descendants of each trans-specific lineage in every generation back to τ.

To take this into account, we consider the model of balancing selection first described by Hudson and Kaplan (1988) and extended by Nordborg and Innan (2003). Imagine that some form of strong balancing selection maintains two alleles, A₁ and A₂, at a locus. Selection is strong enough to maintain the alleles at frequencies x and 1 − x, respectively. The recombination rate between the locus under selection and the locus of interest is ρ/2, as before. Depending on the allelic state at the former locus, each haplotype belongs to one of two allelic classes. The state of a sample of size two from the focal locus can be described by (z₁, z₂), where z_i denotes the number of lineages belonging to the A_i allelic class. The ancestry of the sample can be described by the Markov process z = (z₁, z₂) with states (1, 1), (2, 0), (0, 2), (1, 0), (0, 1). Let i = 1, 2, 3, 4, 5 refer to these states in the order given. The rate matrix Q = {q_ij}_i,j of z is

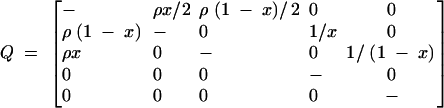with diagonal elements given by q_ii = −∑_jq_ij. The states (1, 0) and (0, 1) are absorbing, and the process starts in (1, 1).

Probability of trans-specificity:

We are interested in P_τ(ρ, x), the probability that two lineages that start in (1, 1) are still distinct at the time of speciation. An exact solution can be found using standard methods. For x = 1/₂ we find

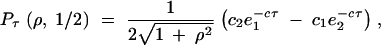2

where 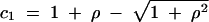and 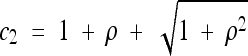. The solution for general x is highly intractable, but it can be shown that lim_ρ→∞P_τ(ρ, x) = e^−τ, in agreement with Equation 2 and with our intuition for unlinked loci.

Several approximations are possible for ρ ≈ 0. We consider two: the first is the best one we found; the second, the simplest.

Approximation 1:

The first approximation is obtained by modifying the rate matrix Q so that the recombination rate is set to zero once the process has left (1, 1). This prevents the process from reentering (1, 1), which simplifies calculations considerably. It is readily verified that this modified process corresponds to the original one in the limit x → 0 or x → 1, so the approximation is exact for these cases. Using the modified matrix, we find

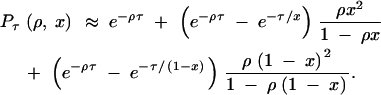3

Approximation 2:

Assume that the lineages stay distinct if and only if no recombination occurs. This yields

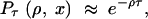4

which should be compared to Equation 1.

Equations 2–4 give the probability that two lineages linked to different alleles in a balanced polymorphism stay distinct until speciation. If this happens, trans-specificity is highly probable for the range of parameters in which we are interested (ρ ≈ 0, τ ≫ 1): one of the two lineages is likely to coalesce with lineages within the same allelic class from the other species long before a recombination event occurs. Equations 2–4 can thus be seen as approximations of the same probability as Equation 1.

Returning to our human-chimp example, and assuming x = 1/₂, we find that Equations 2–4 give probabilities of trans-specificity of 69, 69, and 67%, respectively, for sites separated by 100 bp; and 6, 2, and 2%, respectively, for sites separated by 1 kb. As predicted, Equation 1 underestimates the probability of trans-specificity; however, the results are qualitatively similar. It can be shown that the probability is increased further when x ≠ ¹/₂: intuitively, this is because the probability of recombination between the allelic classes is maximized when allele frequencies are even. With x = 0.01, Equation 3 gives 70 and 4%, respectively, in the above two cases.

Length of trans-specificity:

Let L_τ(ρ, x) be the length of the region on one side of the site under selection where two haplotypes from different allelic classes still have distinct lineages at time τ. L_τ(ρ, x) is possibly the total length of a number of disjoint intervals. We have 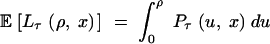. From this, and by considering the properties of P_τ, it follows that for arbitrary 0 < x < 1,

5

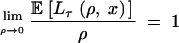6

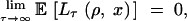7

and

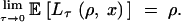8

These equations are useful for evaluating approximations to E[L_τ(ρ, x)], the exact value of which is not known for any x. The two approximations introduced above can be applied, however.

Approximation 1:

The density of L_τ(ρ, x) can be approximated by

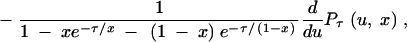where P_τ(u, x) is given by Equation 3, but the expectation cannot be obtained analytically. We refer to this expectation as E₁[L_τ(ρ, x)]. Equations 6–8 hold for E₁[L_τ(ρ, x)], but Equation 5 does not. Instead we have

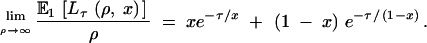Note that Equation 5 holds if x ≈ 0 or x ≈ 1.

Approximation 2:

L_τ(ρ, x) is approximately exponential with intensity τ, Exp(τ), truncated at ρ, and the expectation is

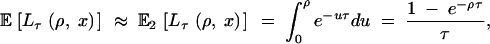where P_τ(u, x) is given by Equation 4. Equations 6–8 hold for E₂[L_τ(ρ, x)], but instead of Equation 5 we have .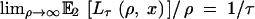

Approximation 3:

A third approximation comes from the expected coalescence time for a linked locus. As is discussed further below, this is ∼1 + 1/ρ if τ is large. Solving τ = 1 + 1/E[L_τ(ρ, x)] gives the estimate E₃[L_τ(ρ, x)] = 1/(τ − 1), which should be truncated at ρ if greater than ρ.

Table 1 shows how these approximations perform for a range of parameters. It can be seen that E[L_τ(ρ, x)] > E₁[L_τ(ρ, x)] > E₂[L_τ(ρ, x)] (this can be proved for all r and x). E₃[L_τ(ρ, x)] works surprisingly well as long as ρ > 1/(τ − 1). The approximations can be extended to handle both sides of the balanced polymorphism simply by assuming independence of recombination on each side and multiplying by two.

TABLE 1.

The performance of approximations for E[L_τ(ρ,x)]

	ρ =
	0.1	1	10	100	1000
τ = 5
E[Lτ(ρ, x)]	0.081	0.271	0.410	1.07	7.18
E1[Lτ(ρ, x)]	0.081	0.223	0.227	0.231	0.272
E2[Lτ(ρ, x)]	0.079	0.199	0.200	0.200	0.200
E3[Lτ(ρ, x)]	0.100	0.250	0.250	0.250	0.250
τ = 10
E[Lτ(ρ, x)]	0.065	0.120	0.123	0.128	0.169
E1[Lτ(ρ, x)]	0.065	0.106	0.106	0.106	0.106
E2[Lτ(ρ, x)]	0.063	0.100	0.100	0.100	0.100
E3[Lτ(ρ, x)]	0.100	0.111	0.111	0.111	0.111
τ = 25
E[Lτ(ρ, x)]	0.038	0.043	0.043	0.043	0.043
E1[Lτ(ρ, x)]	0.037	0.041	0.041	0.041	0.041
E2[Lτ(ρ, x)]	0.037	0.040	0.040	0.040	0.040
E3[Lτ(ρ, x)]	0.042	0.042	0.042	0.042	0.042

All calculations were made at x = ¹/₂, where E[L_τ(ρ, x)] can be calculated numerically. Note that ρ can be thought of either in terms of the (scaled) genetic length of the fragment or as a physical length (given assumptions about the recombination rate per base pair).

How should we interpret these results? Note that the expected length decreases with τ in Table 1. This is in agreement with Equation 7 and is perfectly intuitive: larger τ means more time for recombination to decrease the size of the trans-specific segment. However, we also see that E[L_τ(ρ, x)] increases with ρ, in particular for τ = 5. This may seem paradoxical: if we imagine that the recombination rate per base pair is constant, then increasing ρ simply corresponds to looking at a larger section of the genome. The length of the trans-specific segment surrounding a balanced polymorphism should not depend on how large a section of the genome we look at (unless, of course, we are looking at a region that is too small to contain the entire trans-specific segment, but this hardly explains the difference between ρ = 100 and ρ = 1000). The reason for the increase is that L_τ(ρ, x) includes trans-specific regions that have nothing to do with the trans-specific polymorphism. As noted earlier, there is a small but positive probability that any site is trans-specific. The more of the genome we look at, the more of these we will encounter. The intuitive interpretation of Equation 5 is that, for sufficiently large regions, the fraction of the genome that has not coalesced by τ is simply e^−τ, which is the probability that a particular site has not coalesced by τ. The case τ = 5, ρ = 1000 is approaching this limit: 7.18 × 10⁻³ ≈ e⁻⁵ = 6.74 × 10⁻³. Thus, in this case, most of the fragments that have not coalesced by τ are not associated with the balanced polymorphism. These fragments may or may not be trans-specific (the probability for each fragment is ∼2/3), whereas the fragments that are linked to the balanced polymorphism are almost certain to be trans-specific. For τ = 5, the various approximations give a much better idea of the length of the trans-specific fragment that is associated with the balanced polymorphism than does the exact calculation. For approximations 1 and 2 this is not surprising, given that they are defined in terms of a region contiguous with the selected site. For larger values of τ, all expectations agree because the probability of noncoalescence that is not due to linkage to the balanced polymorphism is negligible. A slight increase is seen between ρ = 0.1 and ρ = 1: this is due to the former region being too small to contain the trans-specific region with sufficiently high probability.

Simulation results:

The process described here can be simulated, for example, using the algorithm described by Nordborg and Innan (2003). One simply simulates two independent realizations of balancing selection for time τ and then merges the states of the two processes and continues the simulation until all fragments have reached their MRCA.

We used simulations to investigate how well our analytical results concerning E[L_τ(ρ, x)] predict the actual length of trans-specificity. Recall that L_τ(ρ, x) is the length of the region on one side of the site of selection where two haplotypes belonging to different allelic classes in a single species still have distinct lineages at the time of speciation, τ. To obtain the length that is trans-specific in samples, we have to consider L_τ(ρ, x) on both sides of the polymorphism, L_τ(ρ, x) in each species, the probability that lineages distinct at speciation actually coalesce in a trans-specific manner, and samples >2.

By assuming that the lengths of either side are independent, noting that the lengths in different species are independent, and ignoring the final two issues (i.e., we assume that lineages belonging to different allelic classes at speciation will almost always coalesce in a trans-specific manner and that samples >2 will have coalesced to 2 long before speciation for the parameters of interest here), we obtain the following approximation for the expected length of trans-specificity in a region of length ρ surrounding a balanced polymorphism in a pair of species:

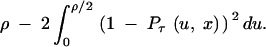9

Table 2 illustrates the performance of this approximation for various parameter values and sample sizes. In agreement with the argument just given, the expected length of trans-specificity increases only weakly with sample size. In general, the approximation is quite good, although it overestimates the length slightly. Whether this is due to nonindependence between the two sides or due to some distinct lineages not coalescing in a trans-specific manner is not clear.

TABLE 2.

The performance of E[L_τ(ρ,x)] as an approximation for the expected length oftrans-specificity

	ρ =
	0.1	1	10
τ = 5
Approximation	0.099	0.633	1.178
n = 4	0.096 (0.009)	0.563 (0.219)	0.983 (0.516)
n = 8	0.096 (0.010)	0.595 (0.214)	1.190 (0.603)
n = 12	0.096 (0.010)	0.603 (0.211)	1.276 (0.642)
n = 16	0.096 (0.010)	0.610 (0.215)	1.336 (0.668)
n = 20	0.096 (0.010)	0.614 (0.215)	1.361 (0.679)
τ = 10
Approximation	0.095	0.349	0.378
n = 4	0.092 (0.014)	0.306 (0.162)	0.330 (0.188)
n = 8	0.091 (0.015)	0.322 (0.170)	0.358 (0.206)
n = 12	0.091 (0.014)	0.321 (0.167)	0.365 (0.204)
n = 16	0.091 (0.014)	0.327 (0.165)	0.373 (0.211)
n = 20	0.091 (0.015)	0.331 (0.169)	0.370 (0.205)
τ = 25
Approximation	0.079	0.129	0.129
n = 4	0.075 (0.021)	0.103 (0.070)	0.106 (0.068)
n = 8	0.073 (0.021)	0.102 (0.070)	0.109 (0.070)
n = 12	0.073 (0.021)	0.103 (0.069)	0.108 (0.070)
n = 16	0.074 (0.021)	0.104 (0.071)	0.110 (0.071)
n = 20	0.073 (0.021)	0.104 (0.071)	0.110 (0.071)

All calculations were made at x = ¹/₂, where approximation (9) can be calculated numerically. Mutation between the two allelic classes was symmetric at rate 0.01 (except for ρ = 0.1, when a rate of 0.001 was used). Samples were evenly distributed among species and allelic classes; i.e., n = 16 means four in each allelic class in each of two species. Estimates are based on 5000 simulations; numbers in parentheses are standard deviations.

The pattern around a particular site:

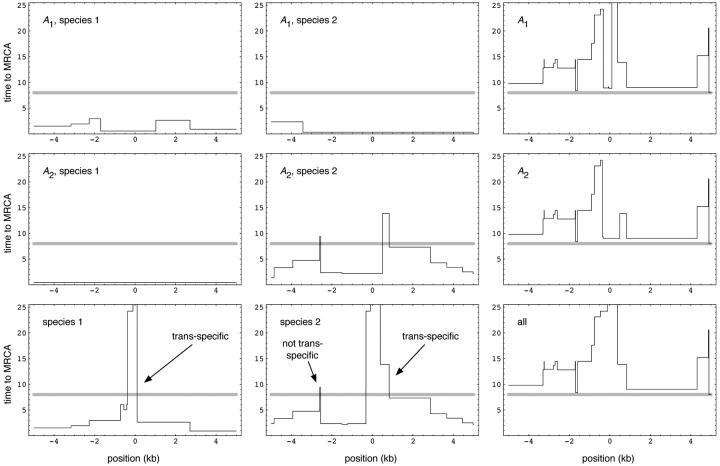
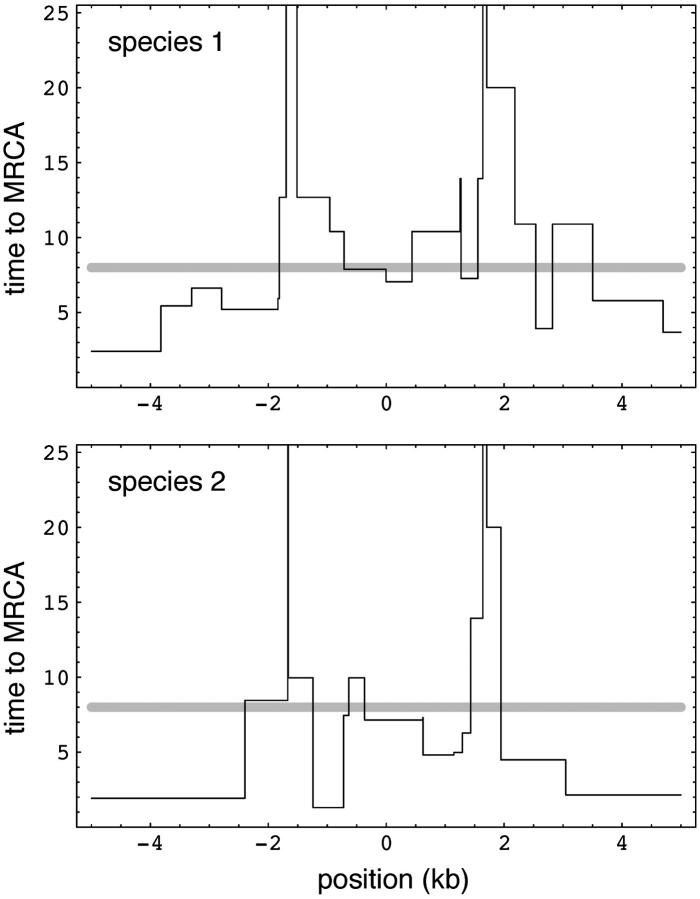
The results in Table 2 are averages over thousands of realizations. While these results are helpful in understanding the behavior of the process, data are likely to come from a single locus or a small number of loci. Expected values are not sufficient to interpret such data. By studying individual realizations of the process, we can get some idea of how variable it is and what real data might look like. Figure 1 summarizes the results of a single realization that used the human-chimp parameters, by plotting the time to the MRCA along a 10-kb region. The different plots show the coalescence time for different samples. Note that all members of the same allelic class that were sampled within the same species typically coalesce much more recently than speciation. This behavior should be contrasted with samples that include members of different allelic classes: regions closely linked to the balanced polymorphism typically coalesce much further back in time, leading to regional trans-specificity. Members of the same allelic class sampled from different species can of course coalesce only in the ancestral species, but they do so much faster than do members of different allelic classes. Note that the pattern is highly variable and that it is sometimes possible for members of the same allelic class to have a MRCA that is older than speciation (Figure 1, center). As discussed above, lineages that are older than speciation need not be trans-specific.

Figure 1.—

Summary of a single realization of the single-locus trans-specific balanced polymorphism. Five lineages were sampled in each allelic class in each species, for a total of 20. Each plot shows the time to MRCA for a subset of the sample. The selected locus was located in the center of the region. Mutation at this locus was symmetric at rate 0.01. Other parameters used were ρ = 5 (note that in this and subsequent figures, ρ refers to the total length of the region containing the selected site or sites), x = 0.5, and τ = 8 (marked by a shaded line).

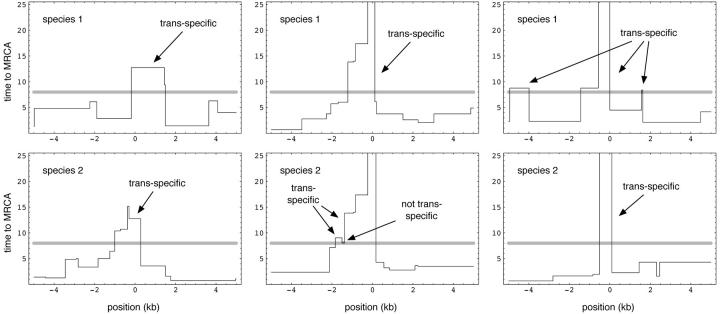
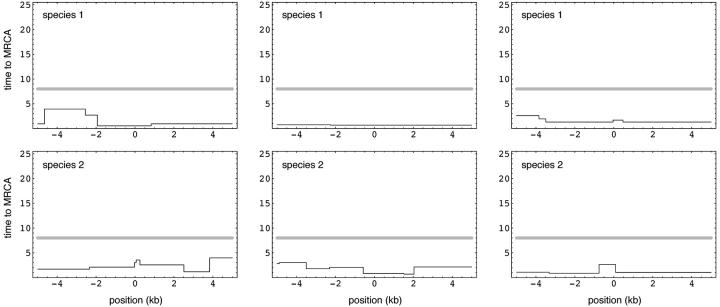
Figure 2 shows the time to MRCA for within-species samples in three more realizations. The expected length of the trans-specific region is on the order of 0.5–1 kb for these parameters. Note that trans-specific regions may often be disjoint from the region surrounding the balanced polymorphism. These additional regions are nonetheless caused by linkage to the balanced polymorphism: as we have discussed, trans-specificity in the absence of balancing selection is highly unlikely. The behavior in the absence of balancing selection is completely different, as is illustrated in Figure 3.

Figure 2.—

Three further examples of the process used in Figure 1. The parameters are the same, and each column represents one realization.

Figure 3.—

Three examples of the process used in Figures 1 and 2, but without balancing selection. Instead, 10 neutral lineages were sampled from each species.

In summary, the four realizations shown in Figures 1 and 2 illustrate the enormous variability of the process and thus the danger of relying on expected values when analyzing data. While the genealogy surrounding a trans-specific polymorphism is in general expected to be quite different from what is expected in the absence of balancing selection (Figure 3), the variability between different trans-specific cases is striking. Not only does the length and genealogical depth of the trans-specific region vary between realizations, but also it is the case that trans-specific regions may not be centered on, or even contain, the site under selection. Furthermore, peaks of polymorphism may sometimes occur within allelic classes in a single species.

Two selected loci:

Our model can easily be extended to two or more selected sites, using the approach described in Nordborg and Innan (2003). This is of relevance because balancing selection may well act to maintain complex alleles that are distinguished by more than a single functionally important mutation (the MHC is a case in point). While it is perfectly possible under this model to obtain analytical results analogous to those presented for the single-locus model, they are too complicated to be useful except in very special cases. In particular, because coalescence between allelic classes in the two-locus model must often involve more than a single recombination event (e.g., for a site located between the selected loci sampled in A₁B₁ and A₂B₂), the simple approximations used above do not apply.

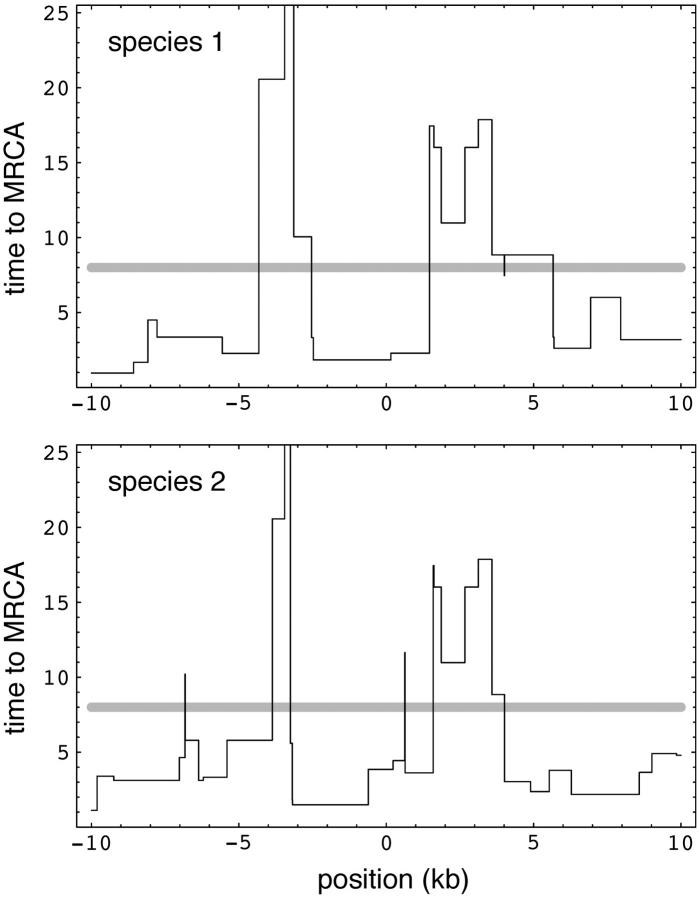
Because of this, and also due to space limitations, we content ourselves with showing simulation results that illustrate the main points. Figure 4 shows a straightforward extension of the other examples to two loci. As we would expect, there are now regions of trans-specificity around each selected site. In addition, the variance in time to MRCA in the general region has clearly increased due to the very complex history of recombination among the four haplotypic classes.

Figure 4.—

A realization of a model of two-locus balanced polymorphism. The selected sites were located one-third and two-thirds of the distance from the left side of the plot, respectively (i.e., at ±3.33 kb). The frequencies of all four haplotypic classes were taken to be the same, 0.25, and ρ = 10 for the region. Two lineages were sampled in each of the four classes, for a total of eight lineages per species. In this plot, all regions with a MRCA older than speciation were trans-specific.

Figure 5 illustrates what happens when the sites are closer to each other. In this case, there are two sites in a 10-kb region, rather than one (as in the other cases). Note that there is a tendency for much of the region between the two loci to be trans-specific. Clearly, extensive trans-specificity is expected in a region where multiple closely linked sites are subject to balancing selection. It should be noted that this in no way relies on epistatic interaction between the selected sites.

Figure 5.—

Another realization of the model used in Figure 4, but with ρ = 5. Again, all regions with a MRCA older than speciation were trans-specific.

DETECTING TRANS-SPECIFICITY

We have shown the extent of trans-specificity around a trans-specific polymorphism maintained by balancing selection is likely to be quite small and therefore probably difficult to detect. To explore this further, we considered the power of simple phylogenetic methods to detect trans-specific polymorphism. We simulated large numbers of data sets using the model above and then used a simple phylogenetic reconstruction method to determine what fraction of these data sets supported a trans-specific relationship.

Table 3 shows the results of this study. It is clear that power decreases rapidly with recombination, as would be expected. It also decreases with increased mutation rate. This may seem counterintuitive given that more polymorphism should provide more information about the underlying genealogy. However, more mutation also means increased probability of repeat mutation, i.e., more noise from the point of view of phylogenetic reconstruction.

TABLE 3.

The probability thattrans-specificity is apparent using phylogenetic methods

	ρ =
	0.1	1	2	5	10
Finite sites model
θ = 0.1	0.796	0.369	0.224	NA	NA
θ = 1	0.832	0.414	0.164	0.017	0.002
θ = 10	0.833	0.397	0.081	0.000	0.000
Finite synonymous sites model
θ = 0.1	0.801	0.400	0.194	NA	NA
θ = 1	0.839	0.365	0.148	0.008	0.001
θ = 10	0.840	0.264	0.026	0.000	0.000

Power was estimated using 1000 replicates for each parameter combination. The selected polymorphism was located in the center of the region, and mutation between allelic classes occurred with symmetric rate 0.01. Other parameters used were x = 0.5, τ = 8, and n = 4 (cf. Table 2). Neutral mutations were added according to a simple Jukes-Cantor substitution model (Jukes and Cantor 1969) using a method similar to the one used by Schierup and Hein (2000). The simulated region was assumed to correspond to 1 kb, but in the “finite synonymous site” model, only one-third of all sites were allowed to vary. Mutations were added according to the rates in the table, but data sets with less than three segregating sites were not used as they provide too little information for phylogenetic methods. We used PHYLIP for phylogenetic reconstruction. Each data set was run through seqboot (to generate 1000 bootstrap data sets), dnadist, neighbor, and finally consense to generate a consensus tree. If the final tree showed a trans-specific topology with a bootstrap support of >70% for the terminal branches, the data set was said to support trans-specificity.

The region used in our study was too small to explore the effects of using different window sizes when searching for trans-specificity. This will clearly influence power: the window size used must be large enough to obtain statistical significance, yet not so large as to drown out any unusual pattern in the surrounding neutral “noise.” The problem is analogous to detecting balancing selection within species (Nordborg and Innan 2003).

DISCUSSION

We have described how the structured ancestral recombination graph (Nordborg and Innan 2003) can be used to model trans-specific polymorphism. We show that trans-specific balancing selection will lead to a distinctive (and highly complex) local distortion in the genealogical graph, but that the extent of the region affected is expected to be quite small. The main implication of these results is that we should not necessarily expect to be able to detect trans-specific polymorphism by simply applying phylogenetic tree-building algorithms to genes or parts of genes: the trans-specific region may be too small. To the problem of the size of the region should be added that any region that is in fact trans-specific is likely to have a very distant MRCA indeed. The time axis in the figures used in this article was cut off at 25 to show detail: in most cases, the time to the MRCA for the trans-specific region was several hundred. With such distances, repeated mutation events may start to interfere with the phylogenetic signal by causing homoplasy. It should also be noted that gene conversion may well make the affected region even smaller (Andolfatto and Nordborg 1998; Wiuf and Hein 2000). Finally, it cannot be emphasized enough that the model of recombination used is simplistic and unlikely to be accurate for the short chromosomal distances that are relevant here (Nordborg 2000). In terms of robustness of our predictions, uncertainty about the local recombination process is likely to be far more important than uncertainty about speciation and selection.

Nonetheless, the basic conclusion that regions of trans-specificity are likely to be quite short seems hard to avoid. Suitable data for testing our predictions are available in primates, for the ABO system (Saitou and Yamamoto 1997) and for color vision genes (Shyue et al. 1995, 1998; Boissinot et al. 1998). Table 4 shows our rough estimates of the extent of trans-specificity surrounding putatively selected sites in these data. The extent of trans-specificity, if that is what it is, seems to be at most a few hundred base pairs.

TABLE 4.

The extent oftrans-specificity in data

Selected codon	Direction	Lmin	Lmax
ABO: human/chimp
156 (010)	3′	0	46
Opsin: saki/howler
180 (010)	5′	0	31
229 (100)–233 (100)	5′	0	12
3′	0	54
277 (010)–285 (100)	5′	0	93
3′	0	199
Opsin: capuchin/squirrel
180 (010)	5′	0	97
3′	>20	?
229 (100)–233 (100)	5′	0	12
3′	54	130
275 (100)–276 (101)–277     (010)–285 (100)	5′	22	181
Opsin: tamarin/marmoset
180 (010)	5′	22	181
229 (100)–233 (100)	5′	2	67
3′	0	62
275 (100)–285 (010)	5′	0	181

The position of the trans-specific site in each selected codon is given by the three numbers in parentheses: 1 represents the trans-specific site. L_min is the distance, in base pairs, to the last putatively nonselected trans-specific polymorphism from the selected sites in the given direction. L_max is similarly the distance to the first fixed difference between the species. Data are from Saitou and Yamamoto (1997), Shyue et al. (1995)(1998), and Boissinot et al. (1998).

In summary, we should not expect trans-specific balanced polymorphism to be easy to detect, at least not by looking simply for trans-specific regions. As a consequence, failure to detect such regions should not be taken as evidence against trans-specific balancing selection. On the other hand, when trans-specific regions are detected, there is good reason to suspect balancing selection and possibly also a local reduction in the rate of recombination or multiple selected sites. Both will tend to increase the length of trans-specific regions.