Genome Scanning for Interspecific Differentiation Between Two Closely Related Oak Species [Quercus robur L. and Q. petraea (Matt.) Liebl.]

Abstract

Interspecific differentiation values (G_ST) between two closely related oak species (Quercus petraea and Q. robur) were compiled across different studies with the aim to explore the distribution of differentiation at the genome level. The study was based on a total set of 389 markers (isozymes, AFLPs, SCARs, microsatellites, and SNPs) for which allelic frequencies were estimated in pairs of populations sampled throughout the sympatric distribution of the two species. The overall distribution of G_ST values followed an L-shaped curve with most markers exhibiting low species differentiation (G_ST < 0.01) and only a few loci reaching >10% levels. Twelve percent of the loci exhibited significant G_ST deviations to neutral expectations, suggesting that selection contributed to species divergence. Coding regions expressed higher differentiation than noncoding regions. Among the 389 markers, 158 could be mapped on the 12 linkage groups of the existing Q. robur genetic map. Outlier loci with large G_ST values were distributed over 9 linkage groups. One cluster of three outlier loci was found within 0.51 cM; but significant autocorrelation of G_ST was observed at distances <2 cM. The size and distribution of genomic regions involved in species divergence are discussed in reference to hitchhiking effects and disruptive selection.

UNDERSTANDING speciation remains one of the fundamental problems in biology. The predominant view is that new species arise most often in allopatry where geographically isolated populations of the same ancestral species diverge progressively (Mayr 1963). However, this view has been challenged by both empirical results and theoretical investigations. Indeed, sympatric speciation events have been observed in controlled experiments (Rice and Hostert 1993; Rundle 2002), under natural conditions (Schliewen et al. 2001), and also demonstrated by simulation models (Dieckmann and Doebeli 1999; Kondrashov and Kondrashov 1999). In the simplest scenario, sympatric speciation occurs when disruptive selection favors two extreme phenotypes. Accordingly, the intermediary individuals that are less adapted are eliminated and progressively reproductive isolation is established between the two extreme phenotypes.

With the big advances in genetic and molecular analysis in the last decade the main issue has now moved to the divergence between species at the genome level. In his view of speciation, Wu (2001) presents genes as the units of species differentiation. This opinion contradicts the biological species concept (Mayr 1963), which assumes a highly coadaptive genetic architecture leading to whole-genome isolation. In Wu's model, the maintenance of two sympatric and interfertile species will translate at the genome level to a mosaic of impermeable and permeable regions to gene flow. Impermeable regions accumulate divergence in response to selection whereas permeable regions share introgressed genes that decrease differentiation in these regions. Genomic differentiation between closely related species has been investigated by comparing positions of markers on genetic maps of the parental species and their hybrids (Rieseberg et al. 2000) and analyzing the distribution of quantitative trait loci (QTL) of traits exhibiting interspecific phenotypic differentiation (Orr 2001).

The two predominant European oaks, pedunculate (Quercus robur L.) and sessile oak [Q. petraea (Matt.) Liebl.], are an interesting model to study interspecific differentiation at a genome level. The two species are interfertile and cohabit in most European forests despite their soil preferences. Q. robur is more frequent on soils with high nutrient availability and Q. petraea occupies drier sites (Lévy et al. 1992). However, in most situations the two species cohabit in the same stands along a gradient of water availability and soil fertility. Thanks also to the extensive pollen flow (Streiff et al. 1998), natural hybridization between both species is quite frequent (Bacilieri et al. 1996). In spite of interspecific gene flow, strong phenotypic differences are maintained for leaf morphological and ecophysiological traits (Kremer et al. 2002). A recent study indicated that QTL controlling leaf morphology were distributed all over the genome with, however, two clusters on two linkage groups (Saintagne et al. 2004). These phenotypic differences contradict earlier reports based on molecular data. With only a few exceptions (Gömöry et al. 2001) all genetic surveys conducted with different markers indicated extremely low species differentiation (Petit and Kremer 1993; Barreneche et al. 1996; Coart et al. 2002; Mariette et al. 2002). The genetic homogeneity between the two species was well illustrated in the study of Bodénès et al. (1997a), where among 2800 RAPD fragments only 2% displayed a significant allelic frequency difference. Rare outlier markers exhibiting large species differences were found for isozymes by Gömöry (2000), for sequence-characterized amplified regions (SCARs; Paran and Michelmore 1993) by Bodénès et al. (1997b), and for amplified fragment length polymorphisms (AFLPs; Vos et al. 1995) by Coart et al. (2002) and Mariette et al. (2002).

Scanning the genome for genetic diversity has been suggested as a method to detect molecular signatures of natural selection and has actually been implemented in Drosophila (Hamblin and Aquadro 1999), in goatgrasses (Dvorak et al. 1998), in maize (Tenaillon et al. 2001), in sorghum (Draye et al. 2001), and in tomato (Stephan and Langley 1998). The rationale of the method is based on the observation that a beneficial mutation in a coding region of the genomes leads to a selection sweep at the selected locus and the sweep extends to the flanking regions due to linkage (Schlötterer 2003). We extended here the concept of genomic scanning to genetic differentiation, as was recently implemented in humans (Akey et al. 2002). The reason is that for an outcrossing species, gametic disequilibrium is more pronounced at an interpopulational level than at the within-population level, the latter being constantly eroded by recombination due to random mating (Le Corre and Kremer 2003). As species differences between the two sympatric Q. petraea and Q. robur are suspected to be generated by divergent selection (Petit et al. 2003), species differentiation can actually be analyzed in a similar way to population divergence due to diversifying selection toward different optima (Le Corre and Kremer 2003). These authors found that population differentiation due to diversifying selection creates large between-population disequilibria between loci involved in traits submitted to selection, whether these loci are linked or not. Hence we would expect that a systematic scanning of the genome for interspecific differentiation would decipher the “molecular architecture” of species divergence. In this study we assembled results from previous genetic surveys conducted in these two oak species during the past 10 years, with various marker techniques. We completed these surveys by additional molecular screening to obtain a large data set of interspecific differentiation between the two species (interspecific G_ST values; Nei 1987). These G_ST values were then plotted along the linkage groups of an oak genetic map (Barreneche et al. 1998). The aim of this study was, by combining population and mapping studies, to describe the genomic arrangement of species differentiation between the two closely related oak species, Q. petraea and Q. robur.

MATERIALS AND METHODS

Mapping population:

The mapping pedigree is a F₁ full-sib cross of Q. robur (3PxA4) composed of 278 full-sibs. The male parent originated from Arcachon (latitude 44.40N, longitude 1.11W) and the female parent was located at the Forestry Research Station of Pierroton (latitude 44.44N, longitude 0.46W).

A subset of 94 full-sibs was used for the construction of a Q. robur genetic map (Barreneche et al. 1998) and the entire set (278) was used to build a framework map for the QTL mapping (Saintagne et al. 2004).

Sampling of natural populations and markers:

Genetic differentiation between Q. petraea and Q. robur was estimated in three genetic surveys that were conducted with different genetic markers during the past 10 years (Table 2). Allele frequencies were assessed in populations of each species that were clustered in pairs throughout the natural range of the two species. The sampling procedure (the location and composition of pairs) and the markers used varied among the three surveys.

1. The first survey was based on isozymes (Zanetto et al. 1994) and comprised seven pairs of populations.

2. The second survey was conducted with SCARs and comprised 8 pairs of populations (Bodénès et al. 1997b). Five pairs of populations of the second survey were also used for a microsatellite diversity analysis (Muir et al. 2000).

3. The third survey was conducted with microsatellites, AFLPs, and single-nucleotide polymorphisms (SNPs) and comprised 10 pairs of populations. Seven pairs of populations were already analyzed by Mariette et al. (2002) to estimate genetic diversity and differentiation for six microsatellites and for four PstI-MseI primer-enzyme AFLP combinations. For this study the sampling was extended to the 10 pairs and the molecular analyses were done with AFLPs (eight EcoRI-MseI and three PstI-MseI primer enzyme combinations), additional microsatellites, and SNPs (Tables 1 and 3).

TABLE 2.

Sample sizes and distribution of populations and species

Marker type (no. of loci)	No. of pairs	Average sample size (no. trees/species/pair)	No. of trees/ species	Geographic distribution of pairs	Reference
Isozymes (12)	7	120	840	Range wide	Zanetto et al. (1994)
SCARs (13)	8	45	360	Range wide	Bodénès et al. (1997b)
Microsatellites (2)	5	16	80	Western part	Muir et al. (2000)
Microsatellites (6)	7	170	1190	Western part	Mariette et al. (2002)
Microsatellites (30)	10	5	50	Western part	This study
SNPs (23)	10	10	100	Western part	I. Porth, C. Scotti-Saintagne,   A. Kremer, P. Schuster,   E. Heberle-Bors and K. Burg   (unpublished results)
AFLPs (107)	7	45	345	Western part	Mariette et al. (2002)
AFLPs (196)	10	10	100	Western part	This study

TABLE 1.

Location and composition of stands used in the third genetic survey

Country	Name	Composition	No. of trees genotyped/species
France	Petite Charnie	Q. petraea and Q. robur	10
The Netherlands	De Meinweg	Q. petraea and Q. robur	10
Spain	Arlaban	Q. petraea and Q. robur	10
United Kingdom	Dalkeith	Q. petraea and Q. robur	10
Austria	Sigmundsherdberg	Q. petraea and Q. robur	10
United Kingdom	Roudsea Wood	Q. petraea and Q. robur	10
Switzerland	Büren	Q. petraea and Q. robur	10
Germany	Escherode	Q. petraea and Q. robur	10
Hungary	Sopron	Q. petraea and Q. robur	10
Denmark/Sweden	Hald Ege/Gysingea	Q. petraea/Q. robur	10/10

^aHald Ege is a pure Q. petraea stand and Gysinge is a pure Q. robur stand.

In the first two surveys, acorns were collected in reportedly pure stands of Q. petraea and Q. robur that were separated by <150 km within each pair (except one pair in Scandinavia, where the two stands were ∼500 km apart). Acorns were sown in the nursery, and isozymes or DNA were extracted from tissues collected on the seedlings. In the third survey, the data originated from adult trees sampled in the forest and not from their offspring raised in the nursery. Populations were also sampled in pairs and a pair consisted of a continuous stand comprising the two species (Mariette et al. 2002). However, for one pair (Scandinavia) the two stands were geographically distant (Table 1). A multivariate analysis of leaf morphology permitted us to assign the species name to each tree and trees with intermediate morphology were excluded from the sample (Kremer et al. 2002).

Molecular analysis:

Details of the protocols for the molecular analysis are given in the different references of the previous articles (Table 2). We give here only the protocols for the molecular analyses realized to obtain the unpublished third survey data. The protocol to analyze PstI/MseI combinations of AFLPs in oaks was described in Gerber et al. (2000). For this study we extended the protocol to EcoRI/MseI combinations with no major modification. The 50- to 700-bp sizing standard marker (LI-COR, Biotechnology Division) was employed to determine the size of fragments and the Saga LI-COR software was used for scoring the AFLP fragments. The development of the 38 microsatellites was described in Steinkellner et al. (1997) and in Kampfer et al. (1998). Protocols for amplification and separation of microsatellites were described in Streiff et al. (1998). Thirty-eight SNPs were developed from 14 expressed sequence tags (ESTs) differentially expressed between the two species in response to an osmotic stress as described by I. Porth, C. Scotti-Saintagne, A. Kremer, P. Schuster, E. Heberle-Bors and K. Burg (unpublished results). Among the 38 SNPs, 23 were scored in the natural populations for estimating G_ST, among which 3 were also mapped in the segregating full-sib family (Table 3).

TABLE 3.

Number of markers used for estimatingG_ST and for mapping purposes

Markers	No. of markers with GST value	No. of outlier markers (%)a	No. of markers with GST values and mapped
EcoRI/MseI-AFLPs	167	13 (8)	77
PstI/MseI-AFLPs	136	14 (10)	29
Microsatellites	38	5 (13)	37
SNPs	23	5 (22)	3
SCARs	13	7 (53)	6
Isozymes	12	3 (25)	6
Total no.	389	47 (12)	158

^aOutlier loci were identified according to Beaumont and Nichols (1996)(see text).

Estimation of the interspecific genetic differentiation:

For all types of markers (dominant and codominant) the genetic differentiation between sessile and pedunculate oak populations was estimated by Nei's coefficient of genetic differentiation, G_ST (Nei 1987). The data were bulked over all populations within a given species to obtain allelic frequencies for each species. The species sample size on which the allele frequencies were calculated varied between 50 and 1190 per species (Table 2).

Dominant markers:

For estimating genetic differentiation at a single locus for AFLP markers, the allele frequency of the null allele was derived from the frequency of phenotypes that did not exhibit a band by using a second-order Taylor expansion (Mariette et al. 2001). To avoid biases due to the low frequency of null alleles and low sample sizes, the calculation of G_ST was restricted to the fragments with an observed frequency <1–3/n_i [n_i is the sample size of species i following Lynch and Milligan's (LM) recommendation (Lynch and Milligan 1994)]. Chi-square tests based on the presence and absence of bands and not on the alleles controlling the expression of bands were used to test for frequency differences between the two species. The analysis was performed by using the HAPDOM computer program (Antoine Kremer, INRA- UMR BIOGECO, Cestas, France). In total G_ST values were computed on 167 EcoRI/MseI-AFLP markers and 136 PstI/MseI-AFLP markers (Table 3).

Codominant markers:

For all isozymes (Zanetto et al. 1994), SCARs (Bodénès et al. 1997b), microsatellites (Muir et al. 2000; Mariette et al. 2002; this study), and SNPs (I. Porth, C. Scotti-Saintagne, A. Kremer, P. Schuster, E. Heberle-Bors and K. Burg, unpublished results), interspecific G_ST values were estimated following Nei (1987)(p. 191).

Statistical tests for species differentiation were done by using two methods depending on the markers and the data sets. For large sample sizes of codominant markers (isozymes, SCARs, and microsatellites analyzed by Mariette et al. 2002) chi-square and G-tests were used for testing allele frequency differences. For the remaining microsatellites (Muir et al. 2000 and this study) and SNPs, the species differentiation was tested by permuting genotypes among the two species.

Finally, the overall survey of interspecific differentiation was based on 389 markers, combining dominant and codominant markers (Table 3). We compared the distribution of the G_ST values over all loci to their expectation under the neutral assumption. Beaumont and Nichols (1996) have shown that the distribution F_ST as a function of heterozygosity in the context of an island model is quite robust to a wide range of conditions (population structure, demographic structure, mutations level). We applied this method (with the infinite allele model) to identify markers deviating from the null hypothesis of neutral evolution. All G_ST's were first transformed to F_ST values by using the Cockerham and Weir (1987) transformation [F_ST = nG_ST/(G_ST + n − 1), where n is the number of populations] and F_ST's were plotted as a function of expected heterozygosities. The analysis was done in a two-step procedure. The first envelope of neutral expectation was based on the overall mean value of F_ST. Markers with F_ST values outside the 95% envelope (corresponding to the null hypothesis) were then removed and a new analysis was done on the basis of the mean value of F_ST. Markers with F_ST values outside the 95% envelope after the second analysis were considered as outliers. Calculations were done using the Fdist2 program (Beaumont and Nichols 1996).

Linkage map for G_ST mapping and distribution of markers along the linkage groups:

We constructed a particular genetic map dedicated to our objective. This map, called “G_ST map,” was assembled by using marker locations from two previous maps built with the same pedigree: (1) the saturated map of Q. robur (Barreneche et al. 1998) that was constructed with a sample of 94 individuals from the full-sib family, which in its last updated version comprised >600 markers, and (2) the “QTL map” (Saintagne et al. 2004) based on all 278 offspring, which comprised only 128 markers. The density of markers was higher in the former than in the latter map; however, the precision of marker location was better in the latter than in the former because of the differences in sample size. And last, markers that were polymorphic in natural populations, for which G_ST values were available, could not be mapped when they were not variable between the two parents of the mapping pedigree. To cope with these constraints, we constructed the so-called G_ST map with the main aim to locate as precisely as possible the different markers and to map as many as possible markers for which G_ST values were available.

The G_ST map was constructed in two steps. The first step consisted of constructing a map comprising the markers scored on the 278 full-sibs, e.g., having the most precise location. The construction was done according to the pseudo-testcross strategy (Grattapaglia et al. 1995). Analysis of linkage among loci was carried out with JOINMAP version 3.0 (van Ooijen and Voorrips 1993) using the LOD grouping command (LOD ≥ 4) and the calculate map command (LOD > 3, REC < 0.4) by performing a ripple each time after adding one locus. The consensus map between the two parents was built by using codominant markers and the dominant markers displaying a 3:1 segregation type as bridge markers. Before applying the map integration command (LOD > 3, REC < 0.4) differences in recombination rates between linked loci were tested using a standard G²-statistic. When the test was significant (P < 0.01), markers were not used as bridge markers. The second step consisted of adding all other markers, which were scored on only 94 offspring. The addition of new markers was done by maintaining the order of the markers genotyped on 278 individuals (fixed-order option of Joinmap). The map integration was performed with the same previous options (LOD > 3, REC < 0.4). Markers in conflict with the fixed order were removed.

The final G_ST map comprised in total 527 markers distributed on 980 cM, with one marker on average every 1.8 cM. Among the 527 markers, 158 were characterized for their G_ST values (Table 3), and only these markers are represented in Figure 4. Before plotting the G_ST values along the linkage groups, we checked the distribution of the markers used for the construction of the map. The distribution of markers was compared to the null hypothesis of random distribution. If the genome is subdivided in N intervals, in the case of random distribution of markers, the number of markers per interval would follow a Poisson distribution of mean μ. If the average number of random occurrences per interval is μ, then the probability that x markers are within a given interval is

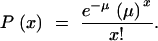Figure 4.—

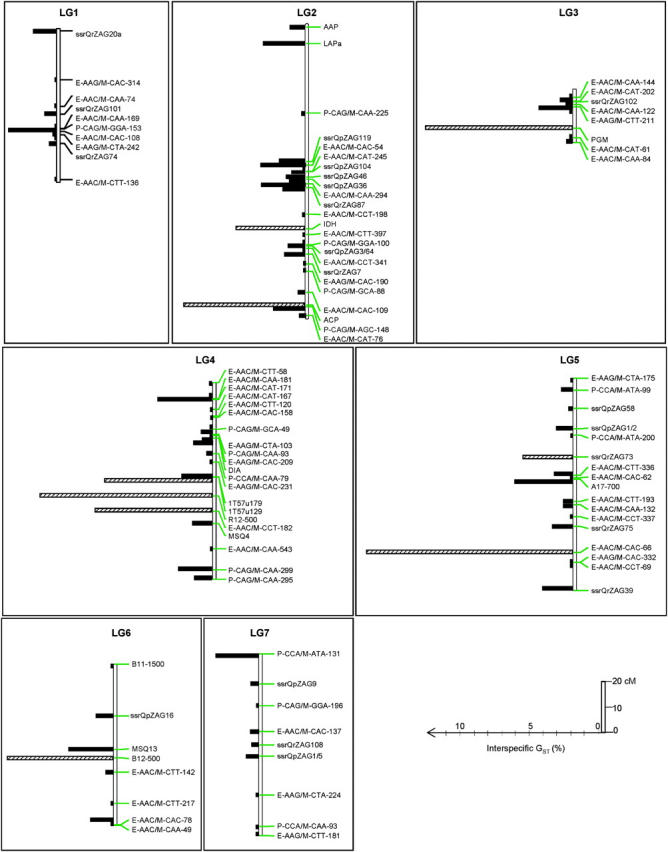
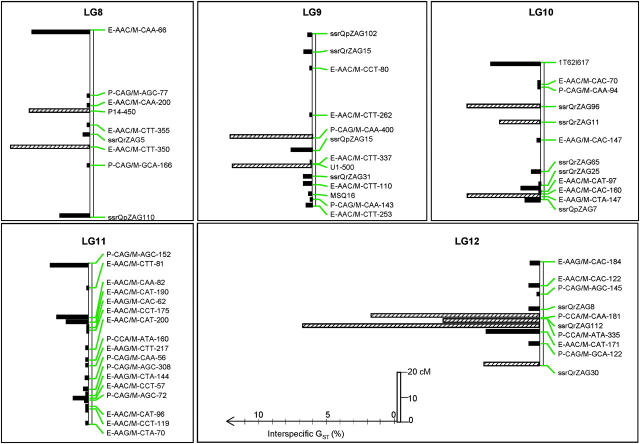
Distribution of G_ST values along the linkage groups. Markers without G_ST values are not indicated on the map, but were used for the map construction. Markers with hatched bars are outlier loci with large G_ST values (according to Beaumont and Nichols 1996) P, PstI/MseI-AFLP marker; E, EcoRI/MseI-AFLP marker; MSQ, microsatellite Quercus; ssr, single-sequence repeat; microsatellite markers; 1T, 2T, SNPs; A17-700, B11-1500, B12-500, P14-450, R12-500, U1-500, SCARs; IDH, ACP, PGM, DIA, LAPa, AAP, isozymes.

We compared the distribution of markers to the Poisson distribution by using a G-test of goodness of fit. The comparison to the Poisson distribution was done by subdividing the linkage group in intervals of 2 cM. The size of the interval was a compromise between the density of markers available on the map and the precision of the marker position.

Distribution of interspecific G_ST values along the linkage groups:

As one of the goals of this study was to investigate the distribution of interspecific differentiation we plotted G_ST values along the linkage groups.

We used Moran's index, or the spatial autocorrelation (Sokal and Oden 1978), to check for correlation between G_ST values between two markers separated by a given genetic distance on the linkage groups. The correlation between G_ST values of two markers separated by distance q can be written as

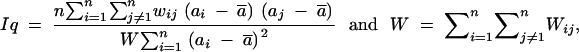with n the total number of markers; W_ij = 1 if markers i and j are within distance class q and is set to 0 when the two markers are not within the distance class q.

The a values represent the level of interspecific genetic differentiation of the marker (G_ST) and 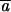is the mean of the a_i when all the n markers are considered.

Observed I values were compared to the null hypothesis of random distribution of G_ST values by using a permutation test. G_ST values were reshuffled among markers by keeping the marker position constant. Ten thousand permutations were used to construct the distribution corresponding to the null hypothesis using the SPAGeDI program (Hardy and Vekemans 2002).

RESULTS

Overall distribution of markers and G_ST values in the genome:

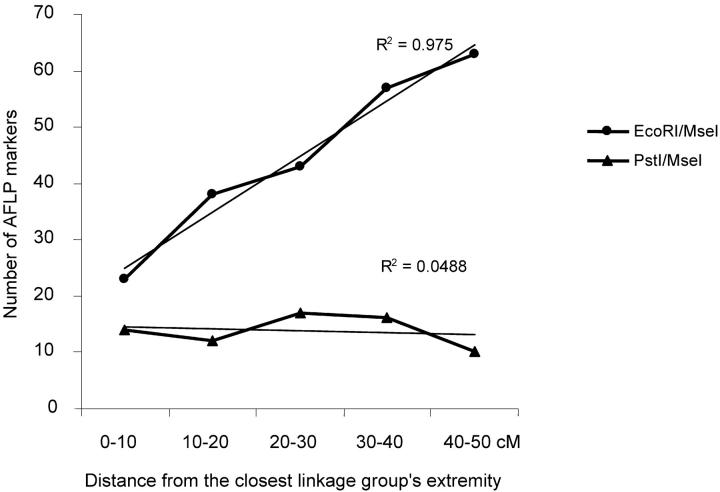
We compared the distribution of G_ST values estimated for AFLPs and microsatellites. In addition, the AFLP markers could be subdivided in two different classes: fragments digested by EcoRI/MseI and by PstI/MseI enzymes. EcoRI and PstI differed in their ability to cut restriction sites containing methylated cytosine. PstI (5′ CTGCAG 3′) is greatly inhibited by C methylation whereas EcoRI (5′ GAATTC 3′) is relatively insensitive to C methylation. The distribution of distances to the linkage group ends was different for both types of AFLPs. PstI/MseI markers were uniformly distributed (chi-square test nonsignificant), while EcoRI/MseI markers were preferentially located in the internal parts of the linkage groups (Figure 1; chi-square test significant, P = 0.0002).

Figure 1.—

Variation of the number of EcoRI/MseI and PstI/MseI markers according to their position within the linkage groups.The x-axis indicates the distance from the markers to their closest linkage group extremity. Markers were grouped into 10-cM distance classes. The y-axis indicates the number of markers corresponding to each distance class. The length of all linkage groups was standardized to 100 cM and marker positions were recalculated by interpolation.

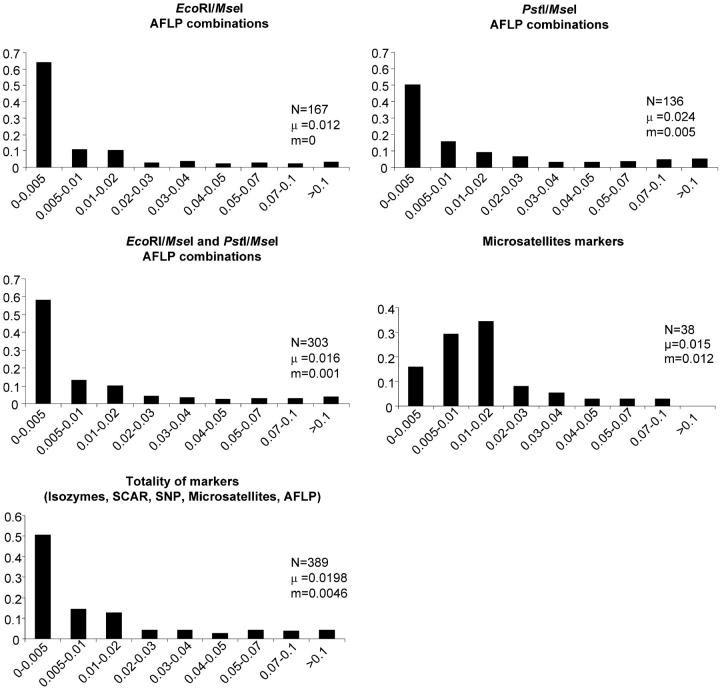
The interspecific G_ST values of the EcoRI/MseI and PstI/MseI-AFLP markers followed an L-curve distribution (Figure 2), with numerous loci displaying a low G_ST value and a few markers displaying larger values. The two distributions are not significantly different when compared by Fisher's exact test (P = 0.245). However, the mean G_ST value of PstI/MseI-AFLP markers is twofold larger than the mean value of EcoRI/MseI markers (Figure 2, 0.024 for PstI/MseI vs. 0.016 for EcoRI/MseI). Medians of the G_ST values of the two distributions were significantly different when compared with the nonparametric Wilcoxon test (W = 22,913, P = 0.0031).

Figure 2.—

Distribution of the G_ST values according to the marker types. G_ST values were arranged in different classes on the x-axis, and proportion of markers is on the y-axis. N, number of markers; μ, mean of the G_ST values; m, median of the G_ST values.

The distribution of the microsatellite marker G_ST values differed from the distribution of the AFLP markers as shown by Fisher's exact test (P < 0.0002). Compared to the AFLP markers, microsatellites displayed larger differentiation: 55% of the G_ST values were >1%, whereas only 29% of the AFLP markers were in this category. The mean of the G_ST values for microsatellites was closer to values obtained for PstI/MseI-AFLP markers, with, however, different medians as shown by the Wilcoxon test (W = 4106.5; P = 0.0044).

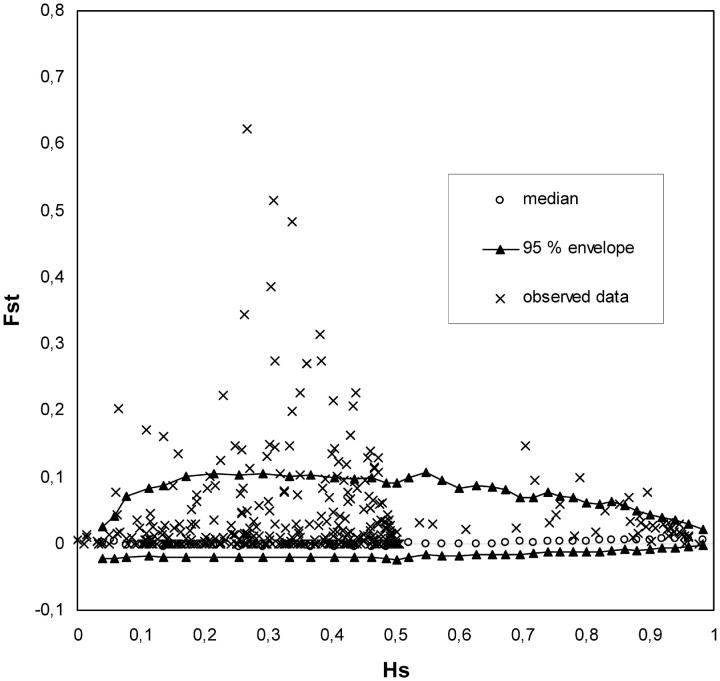
The distribution of G_ST values was compared to the neutral expectation by using the method of Beaumont and Nichols (1996). The overall mean F_ST value (0.0357) over the 389 markers was used to construct the expected distribution of F_ST in an infinite allele model. Thirty-six markers exhibited F_ST exceeding 95% of the null distribution. These markers were removed and a second analysis was done (mean F_ST value = 0.0176). In total, 47 markers fell outside the 0.95 envelope corresponding to the neutral expectation (Figure 3 and Table 3). There were differences in the proportion of outlier markers according to marker types (Table 3), with SNPs, SCARs, and isozymes exhibiting a larger proportion of outlier loci than AFLPs and microsatellites.

Figure 3.—

Distribution of F_ST values as a function of heterozygosity (H_S). The envelope of values corresponding to neutral expectations (with F_ST = 0.0176) with the infinite allele model was constructed according to Beaumont and Nichols (1996).

Distribution of G_ST values along linkage groups:

The consensus map contained 527 markers from which 158 were characterized for their G_ST values (Table 3 and Figure 4). The map covered 980 cM with on average one marker every 1.8 cM, which corresponded to 82% of the estimated genome size (Barreneche et al. 1998).

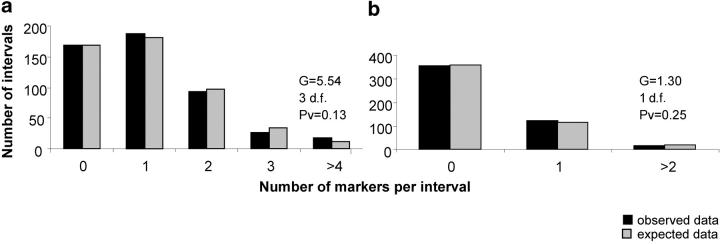
The distribution of the 527 markers used for constructing the G_ST map was random as shown by a nonsignificant G-test (G = 5.54, 3 d.f., P = 0.13; see Figure 5a), when the distribution of the number of markers per interval was compared to the Poisson distribution (see materials and methods). Similarly, when we considered the subset of 158 markers with a known G_ST value that were mapped, the distribution was random as shown by a nonsignificant G-test (G = 0.52, 1 d.f., P = 0.47; see Figure 5b).

Figure 5.—

Observed and expected distribution of the markers in the genome. (a) Distribution of the total number of mapped markers (527) in the genome. (b) Distribution of the mapped markers with a known G_ST value (158) in the genome.

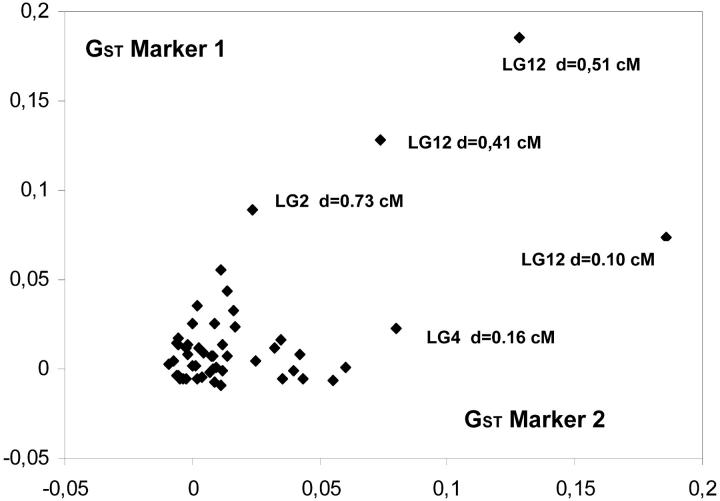
Unfortunately only 20 outlier loci among the 47 identified by the Beaumont and Nichols test were polymorphic in the mapping pedigree and could be mapped. They were distributed over nine linkage groups (Figure 4). G_ST values were not randomly distributed along the linkage groups as shown by the spatial autocorrelation (Figure 6). Significant autocorrelations were observed for the first distance class. Indeed, pairs of markers separated by <2 cM exhibited significant correlation of their G_ST values (P = 0.003). The distance of 2 cM should be considered as an upper limit of the width for correlated differentiation as the number of markers (with known G_ST values) was too low to estimate autocorrelation in smaller intervals. The significant autocorrelation at distances <2 cM was mostly generated by one cluster of outlier loci located on linkage group 12 (Figure 7). Fifty pairs of markers were separated by <2 cM (Figure 7), but 3 pairs assembled markers with outlier loci that were all located on one cluster (linkage group 12), within <0.51 cM (Figures 4 and 7). Interestingly this cluster comprises two different marker types (one microsatellite ssrQrZAG112 and two PstI/MseI-AFLP markers, P-CCA/M-CAA-181 and P-CCA/M-ATA-335). Groupings of markers with large G_ST values occurred also on linkage groups 2 and 4 (Figures 4 and 7).

Figure 6.—

Autocorrelation (I) of G_ST values as a function of genetic distance. The x-axis indicates the classes of distance between pairs of markers (in centimorgans). The y-axis indicates Moran's index (I).

Figure 7.—

Covariation of G_ST values for pairs of markers separated by <2 cM. Annotations are given for all pairs composing at least one outlier locus (according to Beaumont and Nichols 1996). The annotation includes the linkage group (LG) and the distance (d, in centimorgans) separating the two markers. The three pairs on LG12 comprise three markers located within <0.51 cM (see text and Figure 4).

DISCUSSION

Genome-wide distribution of interspecific differentiation:

Our results clearly confirmed earlier reports that the genomes of these two closely related oak species are extremely permeable. An important body of results shows that various genetic markers exhibit low species differentiation (Bodénès et al. 1997a; Mariette et al. 2002). However, most of these studies were restricted to a low number of loci, and the limited sampling in the genome did not allow us to identify those genomic regions that are less permeable. Our study based on 389 markers clearly showed that the distribution of species differentiation follows an L-shaped curve, with only a few markers exhibiting large species differentiation. Earlier random amplification of the oak genome suggested that markers that differentiate the two species are likely to be present in extremely small numbers (Bodénès et al. 1997a). To our knowledge there are only two reported studies on genome-wide distribution of G_ST values. Mariette et al. (2002) in addition to interspecific values also provided distributions for intraspecific G_ST values in both oak species separately. The L distribution was confirmed at both levels, but the distribution of interspecific G_ST was much more skewed than the distribution of the intraspecific G_ST. In humans, a clear L-shaped distribution was also found in a large-scale study based on 26,530 SNPs, but again skewness was less pronounced than in our case at the interspecific level (Akey et al. 2002). These differences may indicate that the genomic regions contributing to interspecific divergence are fewer than those for intraspecific divergence. Despite the evolutionary stochastic variance of G_ST of neutral markers (Robertson 1975), we found that 12% of the markers exhibited G_ST values that were not compatible with the neutral expectation according to the Beaumont and Nichols test (Beaumont and Nichols 1996). This number may be even larger because in multilocus systems genes showing low G_ST values may also be responding to selection. In a recent article, Le Corre and Kremer (2003) used simulations to monitor the evolution of G_ST of genes contributing to a quantitative trait undergoing diversifying selection in a set of populations. The results indicated that only a reduced number of genes contributing to a trait will actually behave as outliers, whereas others will behave as neutral markers despite their contribution to the trait submitted to selection. As a conclusion, the overall distribution of G_ST values (Figure 2) is most likely composed of a mixture of two partially overlapping distributions corresponding to markers undergoing selection and neutral markers. Because of their partial overlap, inferences about their response to selection can be made only for markers with extreme G_ST values (outliers). The distribution of microsatellites does not fit to this general L shape, but this may be attributed merely to the way microsatellites were developed. Only those microsatellite motifs that exhibited allelic polymorphism were actually used as genetic markers, whereas many others were discarded when molecular libraries were screened simply because they were not polymorphic (Steinkellner et al. 1997). Hence the distribution in Figure 2 is truncated due to the molecular screening procedure that was applied during the development of microsatellite markers. AFLPs did not undergo this screening procedure although they were partly pruned by applying the Lynch and Milligan (1994) restriction. However, there was a difference in the level of interspecific differentiation detected by two different AFLP markers. The mean G_ST value for PstI/MseI-AFLP markers was twofold larger than that for EcoRI/MseI-AFLP markers. These differences could be due to the sensitivity to cytosine methylation of the PstI restriction enzyme. Different studies show that markers generated by EcoRI/MseI and PstI/MseI enzyme combinations are differently distributed in the genome. EcoRI/MseI markers are preferentially localized in centromeric regions whereas PstI/MseI markers are localized in the hypomethylated noncentromeric regions of the chromosome (Castiglioni et al. 1999; Young et al. 1999), as confirmed also in our study (Figure 1). Yet, the DNA methylation has an essential regulatory gene expression function. It provides a mechanism to turn off permanently the transcription of genes whose activity is not required in a particular cell type. This stable silencing of a large fraction of the genome would allow the transcriptional machinery to focus on those genes that are essential for the expression and the maintenance of the differentiated phenotypes (Kass et al. 1997). Hence PstI cuts preferentially in the coding regions that are expressed, whereas the EcoRI restriction enzyme cuts rather randomly in the genome. Interestingly our results indicated that fragments digested by PstI exhibited larger species differentiation than fragments digested by EcoRI, suggesting that species differentiation would preferentially be located in nonneutral regions of the genome. The proportion of outlier loci, e.g., markers with large G_ST values, was also different according to marker types (Table 3). It was much lower in markers located in anonymous regions (AFLPs and microsatellites) than in markers located in genes or nonanonymous regions (isozymes, SNPs, and SCARs). These results also contribute to the conclusion that species divergence between Q. petraea and Q. robur resides mostly in functional regions of the genome.

Distribution of interspecific differentiation along linkage groups:

Interspecific differentiation between the two species was widely distributed throughout the genome as markers with large G_ST values were present at various locations on all linkage groups (Figure 4). Here we identified 47 outlier loci (12%) among which only 20 could be positioned on the genetic map. Their location over nine different linkage groups indicated that selection acting toward species divergence is widespread in the genome. To our knowledge this is the first systematic genome scan available for species differentiation. Interestingly our results confirmed those observed by a different approach, where QTL involved in phenotypic discriminant characters were also distributed over all the linkage groups (Saintagne et al. 2004). Wide distribution of large G_ST values was also observed in humans, when intraspecific differentiation was calculated among African-American, East Asian, and European-American populations (Akey et al. 2002). Besides their broad distribution, high G_ST values were clustered at short genetic distances in a few hot spots, which are well illustrated on three linkage groups (LG12, LG2, and LG4). In one of these spots (LG12) three outlier loci concentrated within <0.51 cM. As shown by the Beaumont and Nichols (1996) test, differentiation within this spot deviates from neutral expectation and the size of the spot is most likely caused by hitchhiking effects due to selection. Hitchhiking effects result from the linkage disequilibrium near the selected locus (Andolfatto 2001). Our results suggested that selection is most likely involved in species divergence. Directional selection within population (within species in our case) is known to create a local reduction of within-population diversity, called selective sweep (Kaplan et al. 1989). When acting in opposing directions in two different species, disruptive selection toward different optima will contribute to decreasing the within-species diversity at the target locus and to increasing species divergence. Hence disruptive selection will actually increase differentiation at the target locus and in adjacent regions as a result of hitchhiking. In oak species, the physical size of the hitchhiked region for interspecific differentiation is <2 cM on the basis of autocorrelation analysis (Figure 6). This is much larger than in humans. Akey et al. (2002) found that correlations between G_ST values of adjacent SNPs were significant when SNPs were separated by <200 kb, which translates into a genetic distance close to 0.2 cM. Discrepancy between these values may be due to the difference in the strength of selection responsible for species and population differentiation. The size of a hitchhiked region depends on the ratio of the selective advantage of the favored alleles to the recombination fraction (Andolfatto 2001). As already indicated the skewness of the overall L distribution of G_ST is much more pronounced, even in oaks (Mariette et al. 2002), for inter- than for intraspecific differentiation, suggesting a difference in the strength of selection. Interestingly, in humans the size of the hitchhiked region for population differentiation (200 kb; Akey et al. 2002) is much larger than the size of linkage disequilibrium (LD) within populations. Consensual reported values of LD vary between 10 and 30 kb (Ardlie et al. 2002), suggesting that differentiation may be a more powerful tool than within-population diversity for detecting selection signatures in populations. LDs in outcrossing plants, mainly maize, are significant at much lower distances (up to a few kilobases) and would indicate a much narrower hitchhiking window (Flint-Garcia et al. 2003). The 2-cM size of the hitchhiked region in our study is an overall estimate that may vary from region to region. Autocorrelation analysis assumes that the strength of the processes leading to the spatial distribution is stationary, meaning in our case that the strength of selection would have the same magnitude at all hitchhiked regions. No argument supports this assumption. The results as shown in Figure 4 actually indicate different sizes. Linkage groups 2 and 4 exhibit regions extending over 4 cM, whereas LG12 exhibits narrow regions. The 2-cM size of the hitchhiked region is also an upper limit. Because the overall number of markers was not large enough we were not able to calculate correlations between adjacent G_ST's at smaller distances. It is highly likely that these correlations would actually increase at smaller distances. At this stage, with the existing sampling of markers, we were not able to monitor the decay of differentiation within the hitchhiked region. In combination with the QTL detection of discriminant phenotypic traits, this study will help to locate genes that may be responsible for species differentiation. Ongoing investigations based on gene expression studies will help to identify candidate genes that will be further mapped on the oak genetic maps. Their colocalization with high-G_ST regions will provide a piece of evidence for their involvement in species differentiation.