Abstract
The orientations of the semicircular canals determines the response of the canals to head rotations and, in turn, the brain’s ability to interpret those motions. The geometry of chinchillas’ semicircular canals has never been reported.
Volumetric representations of three chinchilla skulls were generated using a microCT scanner. The centroids of each semicircular canal lumen were identified as they passed through the image slices and were regressed to a plane. Unit vectors normal to the plane representing canal orientations were used to calculate angles between canal pairs. Pitch and roll maneuvers required to bring any canal into the horizontal plane for physiologic investigation were calculated.
The semicircular canals of the chinchilla were found to be relatively planar. The horizontal canal was found to be oriented 55.0° anteriorly upward. Pairs of ipsilateral chinchilla canals were not orthogonal and contralateral synergistic pairs were not parallel. Despite this arrangement, the canal plane unit normal vectors were organized to respond with approximately equal overall sensitivity to rotations in any direction. The nonorthogonal chinchilla labyrinth may provide an opportunity to determine whether the frame of reference used by the central vestibular and oculomotor system is based on directions of afferent maximum sensitivity or prime directions.
Keywords: vestibular, vestibulo-ocular reflex, anatomy, chinchilla
INTRODUCTION
The semicircular canals are responsible for measuring angular acceleration of the head. Physiologic study of semicircular canal function requires accurate positioning of the head to bring a particular canal into the plane of rotation. The orientation of the plane in which each canal lies has been determined geometrically from the shape of the labyrinth in many species, including toadfish (Ghanem et al., 1998), turtle (Brichta et al., 1988), pigeon (Dickman, 1996), guinea pig (Curthoys et al., 1975), rabbit (Ezure et al., 1984; Mazza et al., 1984), cat (Blanks et al., 1972; Ezure et al., 1984), monkey (Blanks et al., 1985; Reisine et al., 1988), and human (Blanks et al., 1975a; Spoor et al., 1998; Takagi et al., 1988; Takagi et al., 1989).
Several studies have used the chinchilla as a model animal for investigations of semicircular canal function, although the planar geometry of their semicircular canals has not been previously reported. An anatomic and neurophysiologic study in chinchilla first described the existence of a separate group of irregular afferent fibers in mammals, the “low-gain” irregular fibers, that terminated exclusively in calyceal endings in the vestibular periphery and that responded with a particularly low sensitivity to 2 Hz head rotations (Baird et al., 1988). More recent work studying afferents responding to rotations up to 20 Hz indicated that the responses of all afferents form a continuum from relatively tonically responding regular afferents, to more dynamically responding “high-gain” irregular afferents, to the most dynamic “low-gain” vestibular afferents (Hullar et al., 1999; Hullar et al., 2005). Chinchillas remain a species of choice for investigating hypotheses such as the possible importance of “low-gain” irregular fibers for sensing the onset of motion (Hullar et al., 2000; Lewis et al., 1994), the responses of semicircular canal afferents in a model of anterior canal dehiscence (Carey et al., 2004), and responses following intratympanic gentamicin administration (Hirvonen et al., 2005). The chinchilla is also a model species for a vestibular prosthesis (Della Santina et al., 2004).
Previous studies of the vestibular labyrinth have shown significant departures from orthogonality among the planes of the semicircular canals in several species (Blanks et al., 1975a; Curthoys et al., 1975; Dickman, 1996; Ezure et al., 1984; Ghanem et al., 1998). A consequence of this geometry is that a rotation in the plane of maximal sensitivity for one canal stimulates one or both of its sister canals. The vector of rotation of a canal that does not stimulate its sister canals has been termed the canal’s “prime direction.” Any rotation of the head can be represented by simple addition of the “prime direction” vectors normal to each null plane, resulting in potential computational advantages for the organism (Rabbitt 1999). The use of this coordinate frame by the oculomotor system is suggested by the finding that the pulling directions of the extraocular muscles of rhesus monkeys align more closely with their canals’ prime directions than with their maximal afferent response directions (Haque et al., 2003). However, because the two reference frames align closely in this species due to the relative orthogonality of its semicircular canals (Blanks et al., 1985; Reisine et al., 1988), this hypothesis is difficult to test. If chinchilla semicircular canals are less orthogonal than rhesus monkeys, they may offer a better opportunity to test the hypothesis that the central vestibular and oculomotor systems use prime directions to encode vestibular signals.
Any non-orthogonality in the canal orientations of the chinchilla labyrinth may also indicate that chinchillas are more sensitive to rotations in particular directions than others. In the rabbit (Mazza et al., 1984) and turtle (Brichta et al., 1988), the orientation of the canals has been used to suggest that the animal is more sensitive to roll than pitch or yaw of the head. This may allow the animal to be more sensitive to common movements and less sensitive to less frequently encountered inputs to the vestibular system. The nonorthogonality described in rabbits suggests that related species such as chinchillas may also be oriented to encode head rotations in particular directions with enhanced sensitivity. Precise knowledge of the orientation of chinchilla semicircular canals, combined with previous reports describing the responses of chinchilla afferents to head rotations (Baird et al., 1988; Hullar et al., 1999; Hullar et al., 2005) will allow a more complete picture of the actual afferent signal reaching the central vestibular system in response to any particular head rotation.
Despite the ongoing interest in the responses of the chinchilla semicircular canals to rotational stimulation, the anatomic canal planes of these animals have not yet been described. The geometry of the semicircular canals has been measured previously using a micromanipulator-held needle in a stereotaxic frame (Blanks et al., 1989; Blanks et al., 1985; Brichta et al., 1988; Curthoys et al., 1975; Ezure et al., 1984; Haque et al., 2003; Mazza et al., 1984) and histologic techniques (Ghanem et al., 1998). High-voltage computerized tomography scanning, or microCT, is a novel alternative technique for investigating the geometry of the vestibular labyrinth that allows accurate acquisition of data from bony specimens. It is relatively immune to errors of measurement and registration that are of concern in other techniques and allows rapid acquisition of data. Here we report the use of this imaging modality to determine the geometry of the semicircular canals of the chinchilla bony labyrinth.
METHODS
All experiments described in this paper were performed with the approval of of the Washington University School of Medicine Animal Studies Committee. The soft tissue from the skulls of three previously euthanized adult animals was manually removed and the skull was air-dried. No changes in skull anatomy were noted during the drying process, as the suture lines of the skull were fused in the adult animals used here. The skulls were then scanned in a microCT scanner (micro40, Scanco, Bassersdorf, Switzerland), producing a three-dimensional image set with isotropic voxels defined by the scanner hardware and software to be 36 microns per side. Accuracy of the voxel dimensions was confirmed by measuring the dimensions of the skulls using a micrometer and comparing to the same dimensions determined from counting voxels. Images were analyzed using software custom-written in Matlab (www.themathworks.com, Natick, MA).
Each semicircular canal was identified as it passed through the image slices generated by the scanner and the centroid of each bony canal’s lumen was determined using software custom-written in MATLAB (Fig. 1A–C). Each canal was traced from the ampullated end through the length of the canal until it re-entered the vestibule. The common crus was included in tracings of the anterior and posterior canals. Several landmarks can be used to define a standard stereotaxic coordinate system in rodents. The lines connecting the external auditory meati and the line connecting the bregma and lambda horizontal have been proposed to define the transverse and sagittal orientations of such a frame (Slotnick et al., 1975). Also widely used in rodent species is a coordinate system based on a horizontal plane defined by rotating the skull until a particular vertical distance separates the midpoints of the external auditory canals and the midline point at which the posterior edge of the incisors enters the maxilla (De Groot, 1959; Hoffman et al., 1968; König et al., 1963; Paxinos et al., 1998). The coordinate system used here relies on a third system whose horizontal plane is defined by the centers of the meati of the left and right external auditory canals and the point where the posterior edges of the incisors met and entered the maxillary bone, as suggested previously for rodents such as the guinea pig (Curthoys et al., 1975) and rat (Sherwood et al., 1970). The sagittal plane was perpendicular to the horizontal plane and intersected it along a line connecting the incisor landmark and the midpoint of the interaural line.
Fig. 1.
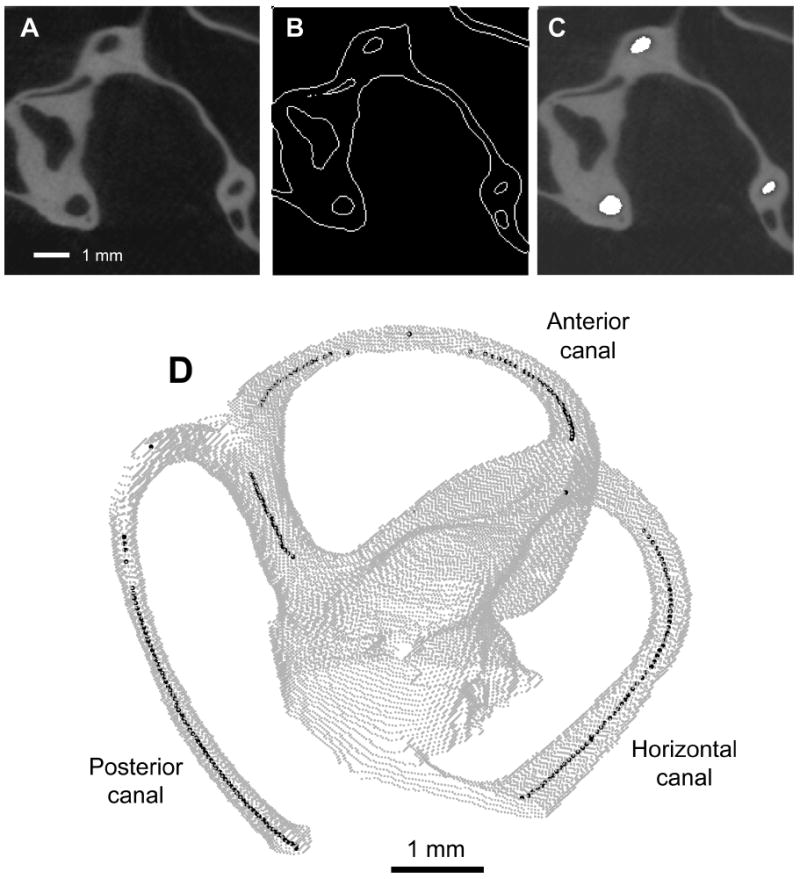
Canal planes determined using microCT technique. A: Raw microCT image of a portion of the chinchilla labyrinth in the axial plane, with semicircular canals and surrounding structures dark and neighboring bone bright. B: Bony edges of the same image have been determined and are represented by white lines. C: The areas representing the lumen of each semicircular canal have been determined and are filled in white. D: The outlines of the semicircular canals and nearby labyrinth from all the images in a data set are assembled here into a single volume (gray) with the centroids of each canal’s lumen represented by a black dot. In cases where the microCT image plane was tangent to the canal or when digitizing the bifurcation of the common crus, a reliable centroid could not be identified. These areas are represented by gaps in the line of black dots.
All data points were rotated by multiplying them by a series of rotation matrices calculated to orient the centers of the meati of the left and right external auditory canals and the point where the posterior edges of the incisors met and entered the maxillary bone to the desired horizontal plane. In its final orientation, the skull faced in the direction of the x axis of a right-handed coordinate frame, with the y axis facing out the animal’s left ear and the z axis out the dorsum of the skull. The origin of the coordinate frame was at the center of the interaural line. The anatomic plane of each canal was determined using a least-squared fit of a flat plane to the set of the canal’s centroids. Unit vectors normal to each canal’s anatomic plane were used to describe the axis of rotation orthogonal to the canal plane. The canal plane’s direction normals represented the axis of rotation of the canal, with the polarity of each vector assigned so that an excitatory rotation of the canal and the positive direction of the vector corresponded via the right-hand rule as described previously (Ezure et al., 1984).
The nonorthogonal orientation of the semicircular canals in the rabbit (Mazza et al., 1984) and turtle (Brichta et al., 1988) has been previously suggested to contribute to heightened sensitivity of the canals to rotations in particular directions. To determine the overall sensitivity of the chinchilla vestibular system to rotations in any direction, a set of vectors were projected at one degree intervals from the origin to a unit sphere whose center corresponded to the origin of the coordinate axis frame of reference. Each vector corresponded via the right-hand rule to a rotation of the head and was projected onto each semicircular canal’s direction normal vector using the dot product of the two unit vectors. Because canal afferents in chinchillas have been shown to respond linearly to moderate rotations (Baird et al., 1988; Hullar et al., 1999; Hullar et al., 2005) the rotation vectors were also projected onto the inverse of each canal’s direction vector to represent the same canal’s response to inhibitory rotations. The projections of each rotation vector onto each of the resulting twelve canal vectors was summed. The length of the resulting vector was represented by a value placed at the point where the rotation vector intersected the surface of the unit sphere. A surface was fitted to the resulting points, representing the labyrinth’s overall sensitivity to rotations in any direction.
RESULTS
Points defining each canal spanned an arc of 177.3 ± 2.5 deg (mean ± standard deviation) for the anterior canal, 156.4 ± 8.7 deg for the horizontal canal, and 174.9 ± 2.2 deg for the posterior canal. Fig. 1D shows the relationship among the digitized points for the semicircular canals of one labyrinth. Planarity was measured by calculating the angular deviation between the most extreme points below and above the plane of the canal through the canal’s center. Points defining the anterior canals subtended an angle of 9.0 ± 1.4 degrees, points defining the horizontal canals subtended an angle of 9.0 ± 1.8 degrees, and points defining the posterior canals subtended an angle of 10.3 ± 1.5 degrees. The radius of curvature of the canals was 2.365 ± 0.108 mm for the anterior canals, 1.750 ± 0.176 mm for the horizontal canals, and 1.609 ± 0.108 mm for the posterior canals, with the anterior canal significantly larger than the other two (p<0.01). This is consistent with previous observations that the anterior canal tends to be larger than the others (Gray, 1907–1908). The average positions of the centers of curvature of each canal are shown in Table 1, with the origin defined as the midpoint of the interaural line. The average orientation of the canal plane normal directions are shown in Table 2, with the polarity of the vector determined from the direction of excitatory rotation of the canal using the right-hand rule. Fig. 2 shows the canal plane direction normals as solid lines. Analysis of the animals’ six horizontal canals indicated that their anterior ends were pitched 55.0 ± 6.5 (range: 49.5–63.9) degrees above the reference horizontal plane used here. The lateral edges of the horizontal canals were tilted down 14.0 ± 6.7 (range: 4.3–22.7) degrees below the horizontal plane, and the anterior edge of the anterior canals were rotated 33.9 ± 1.9 (range: 31.7–36.1) degrees away from the sagittal plane. In chinchillas, the horizontal plane defined by the line connecting the bregma and lambda was found to be pitched 24.7 ± 1.1 degrees nose up from the horizontal plane used here. A second alternative horizontal plane, calculated by rotating the skull until a particular vertical distance separates the midpoints of the external auditory canals and the midline point at which the posterior edge of the incisors enters the maxilla, differs from the standard plane used here by the arcsine of the vertical displacement desired divided by the distance from midpoint of interaural line to incisors, which in our sample was found to be 53.8 mm (sd ± 0.5 mm).
Table 1.
Position of canal centers relative to the origin (defined as the midpoint of the interaural line), in mm. (Values given as mean ± standard deviation)
| X | Y | Z | |
|---|---|---|---|
| Left HC | −0.512 ± 0.281 | 8.219 ± 0.234 | −5.188 ± 0.172 |
| Left AC | −0.747 ± 0.164 | 7.172 ± 0.352 | −3.444 ± 0.298 |
| Left PC | −1.795 ± 0.108 | 6.583 ± 0.239 | −5.841 ± 0.341 |
| Right HC | −0.388 ± 0.131 | −8.202 ± 0.207 | −5.387 ± 0.323 |
| Right AC | −0.709 ± 0.132 | −7.186 ± 0.136 | −3.563 ± 0.424 |
| Right PC | −1.763 ± 0.115 | −6.578 ± 0.157 | −5.954 ± 0.500 |
HC, horizontal canal; AC, anterior canal; PC, posterior canal.
Table 2.
Orientation of average unit-length canal plane direction normal vectors. (Values given as mean ± standard deviation).
| X | Y | Z | |
|---|---|---|---|
| Left HC | −0.799 ± 0.082 | 0.156 ± 0.087 | 0.565 ± 0.117 |
| Left AC | −0.491 ± 0.037 | 0.729 ± 0.007 | −0.476 ± 0.030 |
| Left PC | −0.322 ± 0.066 | −0.673 ± 0.014 | −0.662 ± 0.030 |
| Right HC | 0.810 ± 0.063 | 0.096 ± 0.134 | −0.560 ± 0.094 |
| Right AC | 0.488 ± 0.035 | 0.727 ± 0.022 | 0.480 ± 0.050 |
| Right PC | 0.311 ± 0.062 | −0.675 ± 0.050 | 0.665 ± 0.025 |
HC, horizontal canal; AC, anterior canal; PC, posterior canal.
Fig. 2.
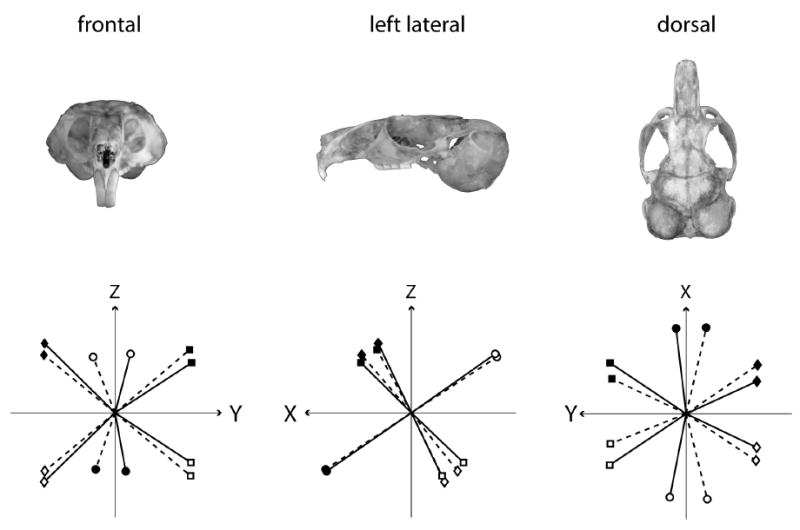
Canal rotation vectors, viewed looking from positive values of each axis toward the origin. Top row indicates direction of view relative to the head. Canal plane normal directions, solid lines; prime directions, dotted lines. Horizontal canals, circles; anterior canals, squares; posterior canals, diamonds. Left side, open symbols; right side, solid symbols. Polarity of each vector assigned so that an excitatory rotation of the canal and the positive direction of the vector corresponds via the right-hand rule.
Angles between pairs of ipsilateral canals and between pairs of contralateral synergistic canals, calculated as the arccosine of the dot product of the canal plane direction normals, are shown in Table 3. The anterior-posterior canal pairs were nearly orthogonal on both the left and right sides, the horizontal-posterior canal pairs formed an angle greater than 100 degrees bilaterally, and the horizontal-anterior canal pairs formed an angle less than 79 degrees bilaterally. Synergistic canal pairs were found not to be parallel, with the angles between synergistic canals approximately 165 degrees for all three canal pairs. The orientations of the canals can be used to determine how to rotate an animal from the reference horizontal position so that any particular semicircular canal is oriented in the earth horizontal plane for physiologic testing. The rotation angles to accomplish these maneuvers, in order of pitch then roll, are shown in Table 4.
Table 3.
Angles, in degrees, between ipsilateral canal pairs and synergistic canal pairs determined from the arccosine of the dot product of the unit normal vectors in Table 2. (Values given as mean ± standard deviation)
| Left HC vs AC | 76.3 ± 2.7 |
| Left HC vs PC | 103.0 ± 5.7 |
| Left PC vs AC | 90.9 ± 1.7 |
| Right HC vs AC | 78.7 ± 5.7 |
| Right HC vs PC | 101.0 ± 6.9 |
| Right PC vs AC | 91.0 ± 2.3 |
| HC-HC | 165.4 ± 12.0 |
| RALP | 165.2 ± 0.3 |
| LARP | 164.4 ± 1.3 |
HC, horizontal canal; AC, anterior canal; PC, posterior canal; HC-HC, angle between contralateral horizontal canals; RALP; angle between right anterior and left posterior canals; LARP, angle between left anterior and right posterior canals.
Table 4.
Magnitude of pitch and roll rotations, in degrees, required to bring each semicircular canal into an earth-horizontal plane.
| Canal | Pitch | Direction | Roll | Direction |
|---|---|---|---|---|
| Left HC | 54.7 | ND | 9.1 | RED |
| Left AC | 45.9 | NU | 46.8 | LED |
| Left PC | 25.9 | NU | 42.4 | RED |
| Right HC | 55.3 | ND | 5.57 | LED |
| Right AC | 45.5 | NU | 46.7 | RED |
| Right PC | 25.1 | NU | 42.6 | LED |
HC, horizontal canal; AC, anterior canal; PC, posterior canal; ND = pitch nose down, NU = pitch nose up, RED = roll right ear down, LED = roll left ear down
Data shown in Fig. 3 represent the overall sensitivity of the chinchilla vestibular system to rotations in any direction in comparison to a similar representation of the guinea pig and rabbit vestibular system based on previously published data (Curthoys et al., 1975; Mazza et al., 1984). The response in any given direction of rotation is given as a percentage of the maximum response overall. Despite the canals’ nonorthogonality, the minimal response of the chinchilla labyrinth in any direction is within 95% of the maximal response while the same technique reveals that the guinea pig rabbit is approximately half as sensitive to pitch rotations as to roll rotations of the head.
Fig. 3.
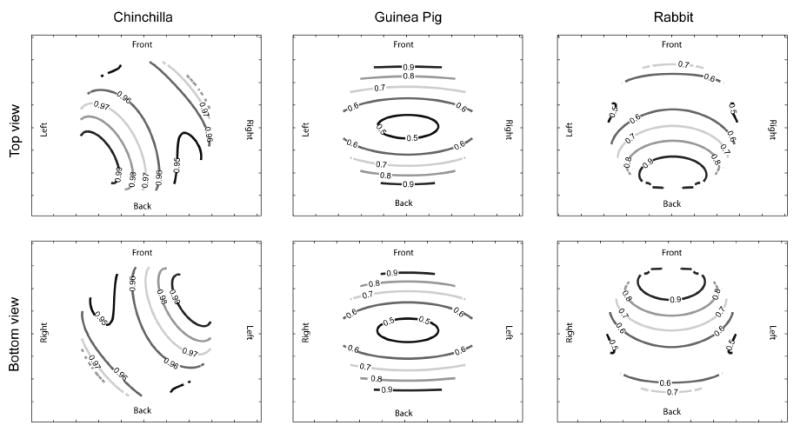
Relative response of vestibular labyrinth to rotations. The response of the labyrinth to a rotation in any direction (represented by a unit vector projecting from the origin to the surface of the unit sphere) is represented by the value at the point where the rotation vector intersects a unit sphere. All numbers normalized to be a percentage of the labyrinth’s maximal response. Top row, looking down onto unit sphere from above; bottom row, looking up at unit sphere from below. Left column, responsiveness of chinchilla labyrinth; middle column, responsiveness of guinea pig labyrinth derived from Curthoys (1975); right column, responsiveness of rabbit labyrinth derived from Mazza and Winterson (1984), Despite the nonorthogonality of the chinchilla canals, it is relatively evenly responsive to rotations in all directions while the guinea pig and rabbit are much more sensitive to roll rotations than pitch or yaw rotations.
The estimated prime directions of the chinchilla semicircular canals were obtained by calculating the cross product of each canal’s two ipsilateral sister canals, with the results shown in Table 5. Reflecting the nonorthogonality of the chinchilla’s semicircular canals, the prime directions differ from the axes of rotation of maximum sensitivity by 11.2–22.2 degrees. Prime directions were also not orthogonal, with the horizontal-anterior canal pairs forming acute angles and horizontal-posterior canal pairs forming obtuse angles as shown in Table 6. Analogous to Table 3, Table 7 shows reorientations for vertically positioning the prime direction of each chinchilla canal to allow physiologic study without stimulating its ipsilateral sister canals.
Table 5.
Orientation of average prime direction unit vectors. Angles between prime directions and canal plane direction normals determined from the arccosine of the dot product of the unit vectors in Tables 1 and 4. (Values given as mean ± standard deviation)
| Prime directions | Angle between canal plane normal directions and prime directions | |||
|---|---|---|---|---|
| X | Y | Z | ||
| Left HC | −0.818 ± 0.030 | −0.202 ± 0.043 | 0.535 ± 0.046 | 21.2 ± 4.0 |
| Left AC | −0.287 ± 0.070 | 0.724 ± 0.019 | −0.604 ± 0.050 | 16.6 ± 2.2 |
| Left PC | −0.447 ± 0.125 | −0.666 ± 0.018 | −0.557 ± 0.104 | 15.0 ± 5.9 |
| Right HC | 0.817 ± 0.027 | −0.191 ± 0.032 | −0.541 ± 0.031 | 17.4 ± 6.1 |
| Right AC | 0.335 ± 0.119 | 0.709 ± 0.019 | 0.604 ± 0.074 | 13.3 ± 2.5 |
| Right PC | 0.468 ± 0.075 | −0.682 ± 0.028 | 0.554 ± 0.088 | 11.2 ± 6.9 |
HC, horizontal canal; AC, anterior canal; PC, posterior canal.
Table 6.
Angles between ipsilateral canal pairs and synergistic canal pairs determined from the arccosine of the dot product of the unit prime directions shown in Table 4. (Values given as mean ± standard deviation)
| Left HC vs AC | 103.6 ± 3.0 |
| Left HC vs PC | 78.2 ± 6.5 |
| Left PC vs AC | 91.2 ± 1.7 |
| Right HC vs AC | 101.0 ± 6.1 |
| Right HC vs PC | 77.7 ± 5.6 |
| Right PC vs AC | 89.6 ± 3.2 |
| HC-HC | 157.2 ± 4.3 |
| RALP | 163.2 ± 6.5 |
| LARP | 164.4 ± 4.5 |
HC, horizontal canal; AC, anterior canal; PC, posterior canal; HC-HC, angle between contralateral horizontal canals; RALP; angle between right anterior and left posterior canals; LARP, angle between left anterior and right posterior canals.
Table 7.
Magnitude of pitch and roll rotations, in degrees, required to bring each average semicircular canal’s prime direction into an earth-vertical plane so that canal’s sister canals will not be stimulated by an earth-horizontal rotation.
| Canal | Pitch | Direction | Roll | Direction |
|---|---|---|---|---|
| Left HC | 56.8 | ND | 11.7 | LED |
| Left AC | 25.4 | NU | 47.3 | LED |
| Left PC | 38.7 | NU | 43.0 | RED |
| Right HC | 56.5 | ND | 11.0 | RED |
| Right AC | 29.0 | NU | 45.7 | RED |
| Right PC | 40.2 | NU | 43.2 | LED |
HC, horizontal canal; AC, anterior canal; PC, posterior canal; ND = pitch nose down, NU = pitch nose up, RED = roll right ear down, LED = roll left ear down
DISCUSSION
Using microCT scanning, the geometry of the chinchilla semicircular canals was determined. All canals were relatively planar. The orientation of the horizontal canal relative to the horizontal plane was similar to that described in a related species, the guinea pig. Ipsilateral sister canals were found to vary by up to 13.7 degrees from orthogonal. Synergistic canal pairs were found to vary by up to 15.6 degrees from parallel. Despite this geometry, the chinchilla was found to be relatively evenly sensitive to rotations in all directions. Prime directions differed from canal normal directions by up to 21.2 degrees. The geometric relationships described here will facilitate further experiments regarding the physiology of the peripheral and central vestibular system of mammals.
Shape of individual canals
The planarity of the chinchilla canal was measured by calculating the sum of the angular deviation between the most extreme points below and above the plane of the canal, as suggested previously (Blanks et al., 1985). All canals had approximately the same deviation from planarity of approximately 10 degrees. This is in the same range as squirrel monkey and rhesus, although the anterior canals in these species appeared to be slightly more nonplanar than their sister canals (Blanks et al., 1985). The chinchilla canals appear to be significantly closer to planar than some comparison species, such as pigeon (Dickman, 1996; Landolt et al., 1975) and toadfish (Ghanem et al., 1998) where large deviations from planarity have been noted.
The radius of curvature of the chinchilla semicircular canals have been previously determined to be 2.130 ± 0.168 mm for the anterior canal, 1.90 ± 0.015 for the horizontal canal, and 2.040 ± 0.306 mm for the posterior canal using histologic techniques (Ramprashad et al., 1984) These data agree well with the values reported here for the anterior and lateral canals, although the posterior canal radius reported here is somewhat smaller than previously described. The anterior canal is larger than the others in both studies, consistent with the relationship found in other species including pigeon (Landolt et al., 1975), bat (Ramprashad et al., 1980), guinea pig, squirrel and rhesus monkey (Blanks et al., 1985), and man (Curthoys et al., 1977). In pigeon, the gain of anterior canal afferents has been shown to be higher than those of other canals (Dickman, 1996) and in cat, the sensitivity of the canals has been shown to correlate to their radius of curvature, with the most sensitive anterior canal being the largest and the least sensitive horizontal canal the smallest (Blanks et al., 1975b; Curthoys et al., 1977). A similar comparison has not been reported for chinchillas. A biophysical model of the labyrinth indicates that the sensitivity of a particular canal is related to the square of its radius of curvature (Rabbitt et al., 2004). The chinchilla anterior canal, therefore, would be expected to have a gain approximately twice that of the horizontal and posterior canals. The functional advantage of a relatively larger anterior canal, if any, remains to be determined.
Angles between canals and sensitivity to rotations
The horizontal canal was found to be oriented anteriorly upward by 55.0 degrees relative to the horizontal plane used here. This corresponds well with the value of 48 degrees found previously in a closely related species, the guinea pig (Curthoys et al., 1975). Angles between ipsilateral sister pairs of chinchilla semicircular canals average 8.5 ± 5.9 degrees, or slightly closer to orthogonal than those previously reported in the related guinea pig where angles between canals measured an average of 17.7 ± 12.8 degrees (Curthoys et al., 1975). Synergistic canal pairs in chinchilla varied from parallel by 14.6–15.6 degrees. This range approximates the average value reported for several other species including pigeon (Dickman, 1996), rabbit and cat (Ezure et al., 1984), and squirrel monkey (Blanks et al., 1985) but is somewhat less than other species such as toadfish (Ghanem et al., 1998), guinea pig (Curthoys et al., 1975), and human (Blanks et al., 1975a). Although in the rhesus monkey, horizontal canal pairs aligned significantly closer to parallel than the left anterior-right posterior and right anterior-left posterior synergistic pairs (Blanks et al., 1985), no such preference was noted in the chinchilla or in other lateral-eyed animals such as toadfish (Ghanem et al., 1998) and guinea pig (Curthoys et al., 1975) or frontal-eyed animals such as squirrel monkey (Blanks et al., 1985). The development of precisely parallel synergistic canal pairs may therefore not be required for accurate oculomotor function.
A set of three canals that is non-orthogonal will be most sensitive to rotations in the average plane of the canals and less sensitive to rotations in other directions, potentially increasing the signal to noise ratio of the vestibular periphery to rotations in certain favored directions but decreasing it in others, as has been previously suggested in the rabbit (Mazza et al., 1984) and turtle (Brichta et al., 1988). Although the chinchilla semicircular canals are non-orthogonal, Fig. 3 demonstrates that the chinchilla is nearly equally sensitive to rotations in all directions (assuming equal sensitivity of all canals). This is quite distinct from guinea pig and rabbit, small mammals of comparable size whose canal orientations suggest that they may be significantly more sensitive to head rotations in certain directions than in others. The geometric relationship of the semicircular canals of a wider variety of species remains to be explored.
Prime directions differ significantly from geometric canal directions
A canal’s prime direction is defined by the axis of rotation about which its two sister canals are not stimulated. Rabbitt (1999) has suggested that it may be computationally advantageous to an animal to code head rotations in the frame of reference of prime vectors rather than normal canal plane directions or the closely related directions of rotation generating maximum afferent sensitivity. As Haque et al. (2003) have pointed out, this hypothesis is difficult to test in primates with nearly orthogonal canal orientations as in those cases the prime directions are almost identical to the normal canal plane vectors derived from the canal’s anatomy. The non-orthogonal geometry of the canal planes of the chinchilla, however, determines that its prime directions vary by up to 21.2 degrees from normal canal plane directions. The findings presented here indicate that the chinchilla may be an attractive animal to determine if normal canal plane directions or prime directions serve as the organizing geometric basis for central vestibular processing.
Relationship of the canal planes to physiologic planes
Variability in the orientation of canal planes among animals may make reliable positioning of an animal for physiologic experimentation difficult (Reisine et al., 1988). Each labyrinth may develop in a slightly different orientation in the skull and the canals forming that labyrinth may develop slightly differently relative to each other. In the sample presented here, the range of angles over which the horizontal was pitched up anteriorly was 14.4 degrees, the range over which the lateral edge of the horizontal canal was tilted down was 18.4 degrees, and the range over which the anterior edge of the anterior canal was rotated laterally from the sagittal plane was 4.4 degrees. Within each labyrinth, the standard deviations of the angles between ipsilateral sister canals was 6.9 degrees or less, indicating little variation among individuals. These ranges provide an estimate of the error that may be encountered when positioning a particular animal according to the average values presented here and suggest that accurate interpretation of physiologic findings may require postmortem anatomic analysis in some cases.
Another source of error in using average values for canal planes when positioning animals for physiologic testing is the difference in orientation between anatomic canal planes and planes of maximal afferent sensitivity due to effects such as differences between the shape of each canal’s bony canal and membranous duct, departures from a toroidal shape, nonplanarity, and fluid coupling among the canals during particular stimulus conditions (Oman et al., 1987). However, planes of maximal semicircular canal afferent sensitivity have been shown to lie close to the anatomically determined canal plane in several animals including cat, where the maximum difference was less than 11 degrees (Estes et al., 1975) and rhesus where the maximum difference was less than 12 degrees (Reisine et al., 1988). In the pigeon, the difference was 8–10 degrees for the horizontal and posterior canals; although the anterior canal is nonplanar in this species, its afferents’ plane of greatest sensitivity corresponded to a weighted average of the canal’s dihedral planes (Dickman, 1996). The canal planes described here are therefore likely to fall close to the actual planes of maximal afferent sensitivity and may be used for physiologic positioning, although this remains to be verified with afferent recordings.
Acknowledgments
The authors wish to acknowledge funding support from Washington University’s Hoopes Undergraduate Research Fund (CDW), the McDonnell Center for Higher Brain Function (TEH), and the National Institutes of Health NIDCD K08-DC006869 (TEH). We also thank Brian Uthgenannt for invaluable technical help scanning the specimens.
References
- Baird RA, Desmadryl G, Fernandez C, Goldberg JM. The vestibular nerve of the chinchilla. II Relation between afferent response properties and peripheral innervation patterns in the semicircular canals. J Neurophysiol. 1988;60:182–203. doi: 10.1152/jn.1988.60.1.182. [DOI] [PubMed] [Google Scholar]
- Blanks RH, Torigoe Y. Orientation of the semicircular canals in rat. Brain Res. 1989;487:278–87. doi: 10.1016/0006-8993(89)90832-9. [DOI] [PubMed] [Google Scholar]
- Blanks RH, Curthoys IS, Markham CH. Planar relationships of semicircular canals in the cat. Am J Physiol. 1972;223:55–62. doi: 10.1152/ajplegacy.1972.223.1.55. [DOI] [PubMed] [Google Scholar]
- Blanks RHI, Curthoys IS, Markham CH. Planar relationships of the semicircular canals in man. Acta Otolaryngol (Stockh) 1975a;80:185–196. doi: 10.3109/00016487509121318. [DOI] [PubMed] [Google Scholar]
- Blanks RHI, Estes MS, Markham CH. Physiologic characteristics of vestibular first order canal neurons in the cat. II Response to constant angular acceleration. J Neurophysiol. 1975b;38:1250–1268. doi: 10.1152/jn.1975.38.5.1250. [DOI] [PubMed] [Google Scholar]
- Blanks RHI, Curthoys IS, Bennett ML, Markham CH. Planar relationships of the semicircular canals in rhesus and squirrel monkeys. Brain Res. 1985;340:315–324. doi: 10.1016/0006-8993(85)90928-x. [DOI] [PubMed] [Google Scholar]
- Brichta AM, Acuna DL, Peterson EH. Planar relations of semicircular canals in awake, resting turtles, Pseudemys scripta. Brain Behav Evol. 1988;32:236–45. doi: 10.1159/000116551. [DOI] [PubMed] [Google Scholar]
- Carey JP, Hirvonen TP, Hullar TE, Minor LB. Acoustic responses of vestibular afferents in a model of superior canal dehiscence. Otol Neurotol. 2004;25:345–52. doi: 10.1097/00129492-200405000-00024. [DOI] [PubMed] [Google Scholar]
- Curthoys IS, Markham CH, Curthoys EJ. Semicircular duct and ampulla dimensions in cat, guinea pig and man. J Morphol. 1977;151:17–34. doi: 10.1002/jmor.1051510103. [DOI] [PubMed] [Google Scholar]
- Curthoys IS, Curthoys EJ, Blanks RH, Markham CH. The orientation of the semicircular canals in the guinea pig. Acta Otolaryngol. 1975;80:197–205. doi: 10.3109/00016487509121319. [DOI] [PubMed] [Google Scholar]
- De Groot, J. 1959. The rat forebrain in stereotaxic coordinates Noord-Hollandsche Uitg. Mij., Amsterdam.
- Della Santina CC, Migliaccio AA, Minor LB. Vestibulo-ocular reflex of chinchilla during head rotation and functional electrical stimulation. J Vest Res. 2004;14:98. [Google Scholar]
- Dickman JD. Spatial orientation of semicircular canals and afferent sensitivity vectors in pigeons. Exp Brain Res. 1996;111:8–20. doi: 10.1007/BF00229550. [DOI] [PubMed] [Google Scholar]
- Estes MS, Blanks RH, Markham CH. Physiologic characteristics of vestibular first-order canal neurons in the cat. I Response plane determination and resting discharge characteristics. J Neurophysiol. 1975;38:1232–49. doi: 10.1152/jn.1975.38.5.1232. [DOI] [PubMed] [Google Scholar]
- Ezure K, Graf W. A quantitative analysis of the spatial organization of the vestibulo-ocular reflexes in lateral- and frontal-eyed animals. I Orientation of semicircular canals and extraocular muscles. Neuroscience. 1984;12:85–93. doi: 10.1016/0306-4522(84)90140-4. [DOI] [PubMed] [Google Scholar]
- Ghanem T, Rabbitt RD, Tresco PA. Three-dimensional reconstruction of the membranous vestibular labyrinth in the toadfish, Opsanus tau. Hear Res. 1998;124:27–43. doi: 10.1016/s0378-5955(98)00108-7. [DOI] [PubMed] [Google Scholar]
- Gray, A.A. 1907–1908. The Labyrinth of Animals Churchill, London.
- Haque A, Angelaki DE, Dickman JD. Spatial tuning and dynamics of vestibular semicircular canal afferents in rhesus monkeys. Exp Brain Res. 2003;155:81–90. doi: 10.1007/s00221-003-1693-0. [DOI] [PubMed] [Google Scholar]
- Hirvonen TP, Minor LB, Hullar TE, Carey JP. Effects of intratympanic gentamicin on vestibular afferents and hair cells in the chinchilla. J Neurophysiol. 2005;93:643–55. doi: 10.1152/jn.00160.2004. [DOI] [PubMed] [Google Scholar]
- Hoffman, R., Robinson, P., Magalhaes, H. 1968. The golden hamster; its biology and use in medical research Iowa State University Press, Ames, IA.
- Hullar TE, Minor LB. High-frequency dynamics of regularly discharging canal afferents provide a linear signal for angular vestibuloocular reflexes. JNeurophysiol. 1999;82:2000–2005. doi: 10.1152/jn.1999.82.4.2000. [DOI] [PubMed] [Google Scholar]
- Hullar, T.E., Carey, J.P., Minor, L.B. 2000. Short-latency responses of the VOR are likely to be driven by high-gain irregularly discharging afferents. Abstr ARO Midwinter Meeting.
- Hullar TE, Della Santina CC, Hirvonen TP, Lasker DM, Carey JP, Minor LB. Responses of irregularly discharging chinchilla semicircular canal vestibular-nerve afferents during high-frequency head rotations. J Neurophysiol. 2005;93:2777–2786. doi: 10.1152/jn.01002.2004. [DOI] [PubMed] [Google Scholar]
- König, J., Klippel, R. 1963. The rat brain, a stereotaxic atlas of the forebrain and lower parts of the brain stem Williams and Wilkins, Baltimore.
- Landolt JP, Correia MJ, Young ER, Cardin RP, Sweet RC. A scanning electron microscopic study of the morphology and geometry of neural surfaces and structures associated with the vestibular apparatus of the pigeon. J Comp Neurol. 1975;159:257–87. doi: 10.1002/cne.901590207. [DOI] [PubMed] [Google Scholar]
- Lewis ER, Parnas BR. Theoretical bases of short-latency spike volleys in the peripheral vestibular system. J Vestib Res. 1994;4:189–202. [PubMed] [Google Scholar]
- Mazza D, Winterson B. Semicircular canal orientation in the adult resting rabbit. Acta Otolaryngol. 1984;98:472–480. doi: 10.3109/00016488409107588. [DOI] [PubMed] [Google Scholar]
- Oman CM, Marcus EN, Curthoys IS. The influence of semicircular canal morphology on endolymph flow dynamics. Acta Otolaryngol (Stockh) 1987;103:1–13. doi: 10.3109/00016488709134691. [DOI] [PubMed] [Google Scholar]
- Paxinos, G., Watson, C. 1998. The rat brain in stereotaxic coordinates Academic Press, San Diego. [DOI] [PubMed]
- Rabbitt, R.D., Damiano, E.R., Grant, J.W. 2004. Biomechanics of the semicircular canals and otolith organs. In: Highstein, S., Fay, R.R., Popper, A.N., (Eds.), The vestibular system. Springer, New York. pp. 153–201.
- Ramprashad F, Landolt JP, Money KE, Laufer J. Neuromorphometric features and dimensional analysis of the vestibular end organ in the little brown bat (Myotis lucifugus) J Comp Neurol. 1980;192:883–902. doi: 10.1002/cne.901920415. [DOI] [PubMed] [Google Scholar]
- Ramprashad F, Landolt JP, Money KE, Laufer J. Dimensional analysis and dynamic response characterization of mammalian peripheral vestibular structures. Am J Anat. 1984;169:295–313. doi: 10.1002/aja.1001690306. [DOI] [PubMed] [Google Scholar]
- Reisine H, Simpson JI, Henn V. A geometric analysis of semicircular canals and induced activity in their peripheral afferents in the rhesus monkey. Ann N Y Acad Sci. 1988;545:10–20. doi: 10.1111/j.1749-6632.1988.tb19552.x. [DOI] [PubMed] [Google Scholar]
- Sherwood, N., Timiras, P. 1970. A stereotaxic atlas of the developing rat brain University of California Press, Berkeley, CA.
- Slotnick, B., Leonard, C. 1975. A stereotaxic atlas of the albino mouse forebrain U.S. Dept. of Health, Education, and Welfare, Rockville, MD.
- Spoor F, Zonneveld F. Comparative review of the human bony labyrinth. Am J Phys Anthropol. 1998:211–251. doi: 10.1002/(sici)1096-8644(1998)107:27+<211::aid-ajpa8>3.3.co;2-m. [DOI] [PubMed] [Google Scholar]
- Takagi A, Sando I. Computer-aided three-dimensional reconstruction and measurement of the vestibular end-organs. Otolaryngol Head Neck Surg. 1988;98:195–202. doi: 10.1177/019459988809800303. [DOI] [PubMed] [Google Scholar]
- Takagi A, Sando I, Takahashi H. Computer-aided three-dimensional reconstruction and measurement of semicircular canals and their cristae in man. Acta Otolaryngol. 1989;107:362–5. doi: 10.3109/00016488909127522. [DOI] [PubMed] [Google Scholar]


