Longevity and Metabolism in Drosophila melanogaster

Abstract

We measured age-specific metabolic rates in 2861 individual Drosophila melanogaster adult males to determine how genetic variation in metabolism is related to life span. Using recombinant inbred (RI) lines derived from populations artificially selected for long life, resting metabolic rates were measured at 5, 16, 29, and 47 days posteclosion, while life spans were measured in the same genotypes in mixed-sex population cages and in single-sex vials. We observed much heritable variation between lines in age-specific metabolic rates, evidence for genotype × age interaction, and moderate to large heritabilities at all ages except the youngest. Four traits exhibit evidence of coordinate genetic control: day 16 and day 29 metabolic rates, life span in population cages, and life span in vials. Quantitative trait loci (QTL) for those traits map to the same locations on three major chromosomes, and additive genetic effects are all positively correlated. In contrast, metabolic rates at the youngest and oldest ages are unrelated to metabolic rates at other ages and to survival. We suggest that artificial selection for long life via delayed reproduction also selects for increased metabolism at intermediate ages. Contrary to predictions of the “rate of living” theory, we find no evidence that metabolic rate varies inversely with survival, at the level of either line means or additive effects of QTL.

THERE is long-standing interest in the relationship between longevity and metabolism in experimental animals, dating from the early studies of Rubner (1908) and Pearl (1928). Support for the hypothesis that rate of living controls and is inversely related to life span is mixed. On the positive side, there is substantial evidence that poikilotherms have lower metabolic rates and longer life spans at cooler temperatures (reviewed by Finch 1990; Arking 1998). The general observation that smaller animals have higher mass-specific metabolic rates and shorter life spans has historically been used to support the rate of living theory, but the expected inverse correlation is not observed in birds or bats (Austad 1999), in related species in the genus Drosophila (Promislow and Haselkorn 2002), or in populations of Drosophila melanogaster having different life spans (Arking et al. 1988; Van Voorhies 2001; Van Voorhies et al. 2003, 2004b). Several single-gene mutations in D. melanogaster extend adult life spans without reducing resting metabolic rates (Lin et al. 1998; Tatar et al. 2001; Marden et al. 2003). Many life-extending mutations have been identified in the nematode Caenorhabditis elegans, but their effects on metabolic rate have been a subject of controversy. Van Voorhies and Ward (1999) found that several long-lived mutants had reduced metabolic rates, but Braeckman et al. (2002) reported contradictory results. Current discussion in this area centers on the influence of environmental conditions, especially suboptimal conditions, on organismal physiology (Van Voorhies 2002).

In spite of limited support, interest in the rate of living model persists, in part because of its relationship to the most widely accepted modern mechanistic theory of aging, the oxidative damage model (Harman 1956; Beckman and Ames 1998; Finkel and Holbrook 2000). This model proposes that in the course of normal metabolism, reactive oxygen species (ROS) are produced at low rates in the mitochondria and subsequently cause damage to membranes, proteins, and DNA. The damage, it is proposed, accumulates over time, eventually causing senescence. It has been widely assumed that higher rates of metabolism entail higher rates of ROS production (Beckman and Ames 1998), thus providing a mechanistic link between new and old theories. However, the validity of that assumption is open to question (Brand 2000; St-Pierre et al. 2002; Speakman et al. 2004).

From the point of view of quantitative genetics, metabolism and life span are typical polygenic characters that could show correlations at the phenotypic level for several different reasons (Falconer and Mackay 1996). There can be an environmental component to the phenotypic correlation if an environmental variable affects both traits. There can also be a genetic component of correlation due to pleiotropy or linkage of genes that affect each trait separately. In general, correlation at the phenotypic level is not informative about the correlation of genetic effects. In fact, in well-known cases the genetic and phenotypic correlations have opposite signs (Falconer and Mackay 1996). As far as we are aware, investigation of the relationship between life span and metabolism in experimental animals has proceeded entirely at the phenotypic level; the underlying genetic correlations are unknown.

We recently investigated the relationship between metabolic rate, life span, and body size in laboratory populations of D. melanogaster (Van Voorhies et al. 2003, 2004a,b). Contrary to predictions of the rate of living model, we found that correlations between resting metabolic rate and life span were either near zero or slightly positive. However, those analyses were purely phenotypic; the possibility remains that at the genetic level life span and metabolism could show the kind of negative relationships predicted by the rate of living theory. Here we extend our analysis to genetic causes of correlation, asking whether quantitative trait loci (QTL) that influence metabolism also influence survival. We employ recombinant inbred (RI) lines for our study, which are useful in several respects. In addition to facilitating replicated observations on the same genotypes, the lines are derived from populations artificially selected for long life and therefore exhibit substantial genetic variation in adult life span (Curtsinger and Khazaeli 2002). Further, examination of these lines provides information about the genetic response to direct selection on life histories. Life-span QTL have already been mapped in these lines (Curtsinger et al. 1995; Curtsinger and Khazaeli 2002) and are replicated here. We document statistically significant genetic variations in age-specific metabolic rates and show that there is indeed joint genetic control of age-specific metabolism and life span, although not in the direction predicted by the rate of living theory and only for certain ages.

MATERIALS AND METHODS

Drosophila stocks:

Experimental material consists of 2 parental inbred lines and 51 RI lines derived from an artificial selection experiment for increased longevity. A complete description of stock construction is given elsewhere (Curtsinger and Khazaeli 2002). Briefly, Luckinbill and Clare (1985) selected a genetically heterogeneous population for increased life span via delayed reproduction and, after 50 generations of selection, produced experimental lines with average adult life span approximately twice that of unselected controls. Inbred lines were constructed by sib-mating flies from selected and control lines for 28 generations. Inbred lines derived from the long-lived selected population were found to have significantly longer life span, higher age-specific survival, and lower age-specific mortality than inbreds derived from the control population (Curtsinger and Khazaeli 2002). Following characterization of inbred lines, a single male from control-derived inbred line S9 was mated with a single female from selection-derived inbred line L6, and F₁ and subsequent generations were sib-mated for 28 generations to produce RI lines. Stocks were maintained in 8-dram shell vials with standard cornmeal-molasses-yeast medium (http://flystocks.bio.indiana.edu/media-recipes.htm) at 24° with constant illumination and 60–70% relative humidity in a walk-in incubator. For metabolic measurements, flies were shipped to New Mexico State University and reared there for 2 generations at 24° under continuous illumination (150 lumens) in 25 × 95-mm disposable plastic vials with standard medium (shipped twice weekly from Minnesota).

Survival experiments:

Survival studies were conducted in the Minnesota laboratory at the same time that metabolic rates were measured in New Mexico. Experimental stocks were expanded in half-pint bottles under controlled larval densities (Fukui and Kirscher 1993). Adult flies of both sexes emerging within a 24-hr period were collected under CO₂ anesthesia and numbers were estimated by weight using an electronic balance (Mettler; BB2400). Approximately 160 males and 160 females from each line were transferred into specially designed 1.9-liter population cages (Fukui and Kirscher 1993; Promislow et al. 1996) for survival measurements. The mouth of each cage was covered with a fine mosquito netting and the cages were inverted over an 11-cm-diameter disk of cooked medium, which was replaced every other day. Flies were transferred, without anesthesia, to clean population cages approximately every 10 days. Dead flies were removed by suction, sexed, and recorded every day until the last death. All lines were tested simultaneously in a walk-in incubator to ensure similar environmental conditions. Life spans were also measured at the same time on unmated males in vials, to obtain survival measurements under conditions similar to the metabolic measurements. Unmated males were collected shortly after emergence as described above and then placed in groups of 15 in 8-dram shell vials with standard medium. Two vials were set up for each line. Flies were transferred to fresh vials every other day, and dead flies were counted daily until the last death.

QTL mapping:

We used naturally occurring roo transposable genetic elements as markers for QTL mapping, as previously described (Curtsinger and Khazaeli 2002). The 65 variable marker locations include 12 on the X chromosome, 29 on chromosome II, 24 on chromosome III, and none on chromosome IV, with an average spacing of 5 cM. For data analysis we used interval mapping and composite interval mapping as implemented in Windows QTL Cartographer version 1.20 (Basten et al. 1994, 1999), with Ri2 design, Kosambi mapping function, window size 10 cM, and walking speed 2 cM. Significance thresholds were estimated by permutation tests with 1000 replications per test, which is used for Bonferroni corrections for genome-wise statistical significance. Statistical analyses other than QTL mapping were executed using SYSTAT 10.2 for Windows (Systat Software, Chicago).

Metabolic measurements:

Metabolic rate (as estimated by CO₂ production) and body mass were measured in individual male flies from each line at 5, 16, and 29 days postemergence. For the longest-lived lines we also obtained measurements at 47 days postemergence. Flies were immobilized in a stream of humidified nitrogen gas and then individually placed in 2.2-ml glass measurement chambers. Flies were able to walk, but not fly, inside the chambers. Chambers were sealed with rubber stoppers and then flushed for 15 sec at a flow of 90 ml/min with CO₂-free, water-saturated room air. After 1 hr, a 1.1-ml (standard temperature and pressure) gas sample was removed from the chamber with a Hamilton SampleLock syringe and injected into a Sable System TR-2 carbon dioxide gas respirometry system. The chamber was then reflushed with CO₂-free air and a second sample was taken 1 hr. later. Following the second measurement flies were individually frozen for weighing. A total of 16 flies from each of 53 lines were measured for each sampling period (except day 47, when many lines were extinct), divided between 8 flies measured in the morning and 8 in the afternoon. Each set of experiments also included six chambers without flies to control for background CO₂. The amount of CO₂ produced by each fly was calculated using DATACAN software (Sable Systems, Henderson, NV). Values reported here can be converted to SI units (microwatts) by multiplying microliters of CO₂ per hour by 5.58. The respiratory quotient of 0.95 is used to convert CO₂ production to oxygen consumption. An energy equivalent of 20.1 J/ml oxygen was used for all energy calculations. Weight-adjusted metabolic rates were estimated for each fly from individual measurements of wet weight and CO₂ production. We also estimated total metabolic output for days 5–29 (all lines) and days 5–47 (22 lines) by linear interpolation of line means using estimates on days 5, 16, 29, and 47, followed by integration over the entire time period. However, the total metabolic output estimates were found to be almost perfectly correlated with day 16 and day 29 metabolic rates and are therefore redundant and not considered further.

RESULTS

Summary data on CO₂ production by 2861 flies, each individually measured twice and then weighed, are shown in Table 1 both as CO₂ produced per fly per hour and as CO₂ per milligram of tissue per hour (wet weight). We report both per-fly and weight-adjusted data, because they reflect different biological characters (Hayes 2001) and because there are continuing disagreements about the validity of scaling physiological processes by mass (Packard and Boardman 1999; Van Voorhies et al. 2004a).

TABLE 1.

Line means for metabolic rates measured as CO₂ production at four ages in adult male Drosophila from 51 recombinant inbred lines and two parental inbred lines

		Age (days)
5		16		29		47
Measurement:  First		Second	First	Second	First	Second	First	Second
	No. of lines:  53		53	53	53	53	53	22	22
Per-fly dataa
Min	3.15	2.45	1.81	1.63	1.73	1.81	2.22	2.09
Max	8.39	4.21	3.84	3.20	3.30	3.28	3.17	3.15
Mean	4.68	3.25	2.59	2.35	2.39	2.37	2.67	2.63
SD	1.04	0.41	0.44	0.35	0.35	0.28	0.27	0.31
Weight-adjusted datab
Min	5.56	3.48	2.77	2.46	2.67	2.46	3.25	3.23
Max	19.54	7.62	6.75	5.10	5.48	5.09	4.54	4.64
Mean	9.20	5.33	4.26	3.59	3.70	3.59	3.86	3.82
SD		2.73	0.81	0.71	0.52	0.79	0.52	0.37	0.44

^aMicroliters CO₂ (hr · fly).

^bMicroliters CO₂ (hr · mg).

Metabolic measurements were checked for normality and then subjected to mixed-model multiway analysis of variance (ANOVA), with main effects due to line, age, weight, measurement order (first or second), and time of measurement (AM or PM). First, the full model with five main factors and 10 two-way interaction terms was analyzed and then a reduced model was studied, retaining only those interaction terms that reached statistical significance at the 0.05 level. The reduced model, shown in Table 2, explains 42% of the variance in CO₂ production (P < 0.001). All main factors except weight are statistically significant, although the magnitudes of effects are small in several cases. Age, measurement order, and age × measurement interaction have the largest effects and are discussed below.

TABLE 2.

Analysis of variance for metabolic rate at four adult ages in maleD. melanogaster

Source	SS	d.f.	MS	F	P
Line	257.8	45	5.7	4.8	0.001
Age	1518.6	3	506.2	421.8	0.001
Weight	3.0	1	3.0	2.5	0.110
Time	28.6	1	28.6	23.9	0.001
Measurement	175.5	1	175.5	146.2	0.001
Line × age	469.8	136	3.5	2.9	0.001
Line × weight	266.5	53	5.0	4.2	0.001
Line × time	233.7	53	4.4	3.7	0.001
Age × measurement	431.1	3	143.7	119.7	0.001
Error	6196.9	5164	1.2

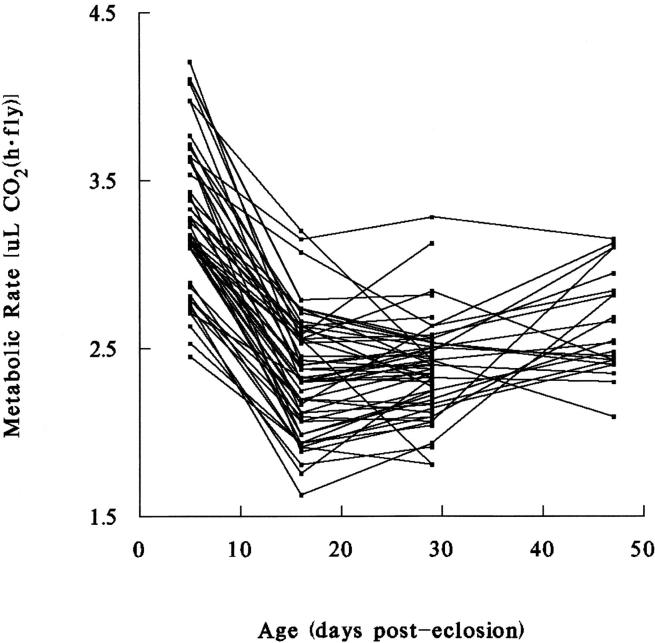
The significant effect of age on CO₂ production has been described previously (Van Voorhies et al. 2003, 2004a,b). Resting metabolic rates decline dramatically in all lines between days 5 and 16 and generally show less age-dependent change after day 16 (Figure 1). It is apparent from Figure 1 and from the statistically significant line × age interaction term of Table 2 that the rank order of lines with respect to metabolic rates changes from age to age. For instance, the lowest-ranking line on day 16 is also low on days 5 and 29, but is among the highest on day 47. The existence of statistically significant interaction means that there is no meaningful categorization of lines into metabolically high or low; metabolic rates are age specific, with the rank order of lines dependent upon both genotype and age.

Figure 1.—

Average age-specific metabolic rate (measured as CO₂ production) in individual male flies from 53 recombinant inbred lines of D. melanogaster. Metabolic rates decline sharply in the first 2 weeks of adult life and generally show less age-related change at older ages. Nonparallel lines indicate significant genotype × age interaction.

The significant measurement and age × measurement terms in Table 2 appear to reflect behavioral factors. First measurements, which were taken 1 hr after flies were placed in measurement chambers, are larger than second measurements, which commenced 1 hr later. On day 5 the mean of first measurements is 44% larger than the mean of second measurements on a per-fly basis (t = 9.2, P < 0.001), and the variance is six times larger. First measurements are 10% larger than second measurements on day 16 (t = 3.2, P < 0.01), but first and second measurements do not differ significantly on days 29 or 47 (t = 0.04 and 0.44, respectively, P > 0.10 in both cases). A similar pattern holds for weight-adjusted data (Table 1). This suggests that young flies are more active when first placed in measurement chambers, but older flies are not as “excitable,” explaining the significant age × measurement interaction term of Table 2. Because of the significant differences at young ages, first and second measurements are treated separately in the following analyses.

When data for all four ages are pooled, lines are a statistically significant source of variance, but the effect is small compared to the age effect (Table 2). However, for particular ages, the line effect is substantial, with line means varying almost twofold at each age (Table 1; Figure 1). To estimate the genetic component of variation at each age, we estimate broad-sense heritabilities of age-specific metabolic rates. CO₂ measurements were subjected to one-way model II ANOVA for each age, partitioning the variance into between-line (genetic) and within-line (error) components. F-statistics and heritability estimates are shown in Table 3. Broad-sense heritabilities are significantly different from zero at all ages, for both first and second measurements and for both per-fly and weight-adjusted data. Heritabilities are small for day 5, in all cases <20%, and moderate to large at later ages, ranging from 24 to 62%.

TABLE 3.

Broad-sense heritability estimates for age-specific metabolic rates in adultD. melanogaster males

	μl CO2 (hr · fly)		μl CO2 (hr · mg)
	F	H2	F	H2
First CO2 measurement
Day 5	2.1***	0.07	2.3***	0.08
Day 16	15.9***	0.48	5.6***	0.24
Day 29	13.1***	0.43	11.6***	0.41
Day 47	6.7***	0.30	6.2***	0.28
Second CO2 measurement
Day 5	3.8***	0.14	3.0***	0.18
Day 16	13.4***	0.45	5.7***	0.28
Day 29	6.6***	0.26	26.6***	0.62
Day 47	6.4***	0.29	5.5***	0.25

^***P < 0.001.

Line means for adult survival vary fourfold in vials and over fivefold in cages and are longer for unmated males in vials than for mated males in mixed-sex population cages (Table 4). Life spans in cages and in vials are significantly and positively correlated across lines (r = 0.63, P < 0.001), suggesting that survival assays provide a robust measure of survival. Broad-sense heritability for life span in population cages is 32%, consistent with previous estimates for these lines (Curtsinger and Khazaeli 2002), while the broad-sense estimate for life span in vials is 34%.

TABLE 4.

Summary statistics for life-span measurements on maleD. melanogaster from 51 RI lines and 2 parental inbred lines

	Cages	Vials
No. of lines	53	53
Minimum line mean (days)	10.8	16.0
Maximum line mean (days)	59.0	65.5
Grand mean (days)	29.4	37.2
SD (days)	11.2	10.3

How is the substantial variation in age-specific metabolic rates related to variation in survival? As shown in Table 5, line means for life span and metabolic rate tend to exhibit zero or slightly positively correlation. There are no statistically significant or marginally significant negative correlations between life span and age-specific metabolic rates in Table 5, but there are seven statistically significant positive correlations and another five that are positive and marginally significant at the P = 0.10 level (r > 0.30, Bonferroni correction with 15 comparisons for each data set). The strongest statistical association is on day 29 (first measurement, both per-fly and weight-adjusted data, r > 0.40). It is also apparent from Table 5 that line means for day 16 and 29 metabolic rates are highly correlated (r > 0.80 for per-fly data, and r > 0.50 for weight-adjusted data). At this level of analysis, we find no evidence for an inverse relationship between life span and metabolic rate, as predicted by the rate of living model, but there is a suggestion of a zero or slight positive relationship, as we previously reported (Van Voorhies et al. 2003).

TABLE 5.

Correlations between survival measures and age-specific metabolic rates

	Life span		CO2
	Cages	Vials	Day 5	Day 16	Day 29	Day 47
Per fly
Life-span cages	—	0.63***	−0.03	0.36	0.43*	0.27
Life-span vials	0.63***	—	−0.11	0.35	0.46**	0.38*
Day 5 CO2	0.11	0.16	—	0.22	0.20	0.33
Day 16 CO2	0.38*	0.32	0.61***	—	0.83***	0.52**
Day 29 CO2	0.29	0.32	0.55***	0.69***	—	0.61**
Day 47 CO2	0.32	0.42*	−0.01	0.07	0.24	—
Per weight
Life-span cages	—	0.63***	−0.20	0.11	0.46*	−0.05
Life-span vials	0.63***	—	−0.20	0.07	0.41*	0.14
Day 5 CO2	−0.15	−0.02	—	0.28	−0.01	0.17
Day 16 CO2	0.06	0.18	0.43*	—	0.50**	0.27
Day 29 CO2	0.26	0.12	0.29	0.51**	—	0.43
Day 47 CO2	−0.22	0.02	0.12	−0.32	0.06	—

Above the diagonal, first CO₂ measurement; below the diagonal, second CO₂ measurement. Bonferroni probabilities, *P < 0.05; **P < 0.01; ***P < 0.001.

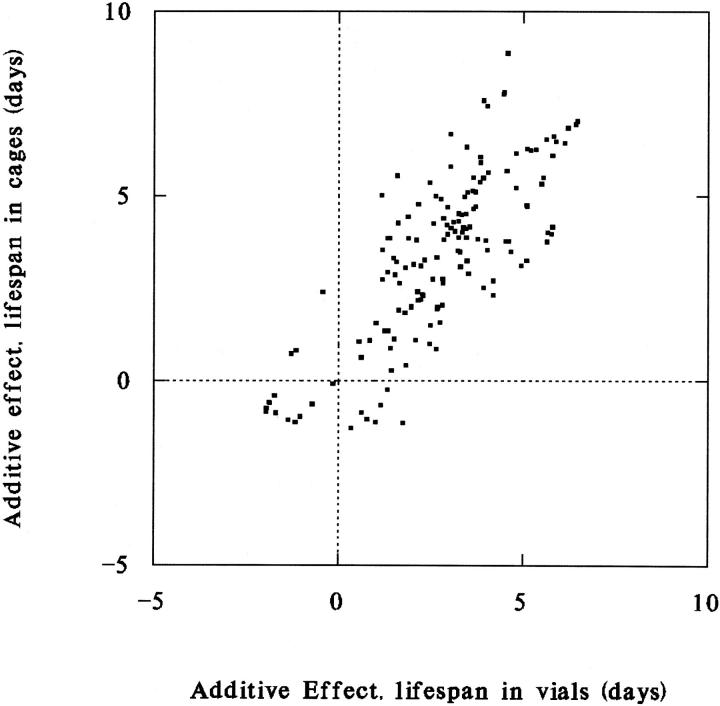
To investigate the genetic basis of correlations, we employ an exploratory graphical method (Curtsinger 2002) based on QTL mapping, as follows. Applying interval mapping as implemented in QTL Cartographer (Basten et al. 1994, 1999) to line means for life span and age-specific metabolic rates, we obtain estimates of additive genetic effects on each trait attributable to each 2-cM segment of chromosomes X, II, and III. We then ask whether any of the small chromosomal segments has additive effects on both traits. Substantial positive or negative effects on both traits attributable to a single segment suggest pleiotropy or close linkage of trait-specific QTL. Here the additive genetic effect is defined as the increment or decrement of the mean phenotype due to an allele derived from the long-lived inbred parent. The additive effect can be positive or negative and is expressed in terms of deviations from the population mean. Figure 2 illustrates the use of the method for two survival traits, life span in population cages and life span in vials. If the two traits were genetically independent, then we would expect to see some data points clustered near the origin, representing chromosomal segments that have little or no effect on either phenotype, and some data points along both major axes, indicating larger effects on one trait or the other, but not both. In Figure 2 most of the data points lie along the main diagonal, suggesting that several chromosomal regions carry pleiotropic or closely linked genes that increase survival in both population cages and vials. Allelic effects are overwhelmingly positive in both environments because the long-lived population used to construct RI lines was subjected to many generations of artificial selection for increased life span. Composite interval mapping produces qualitatively the same result (not shown). It is not appropriate to calculate a correlation coefficient using all of the data points in Figure 2, because estimates of additive effects are not independent for closely linked segments. To minimize this problem we estimate the correlation of additive effects for chromosomal segments that are spaced 10 cM apart, beginning at the left telomere of each major chromosome. For that subset of the data the product moment correlation coefficient is 0.75 (n = 27, P < 0.001). Similar results and significance levels are obtained for spacings of 5 and 15 cM.

Figure 2.—

Additive genetic effects on life spans in population cages and life spans in vials in 53 recombinant inbred lines of D. melanogaster. Estimates are obtained by interval mapping. Each data point represents the estimated effects on both traits attributed to each 2-cM segment of chromosomes X, II, or III. Data points along the main diagonal indicate multiple chromosomal segments with positive effects on both traits.

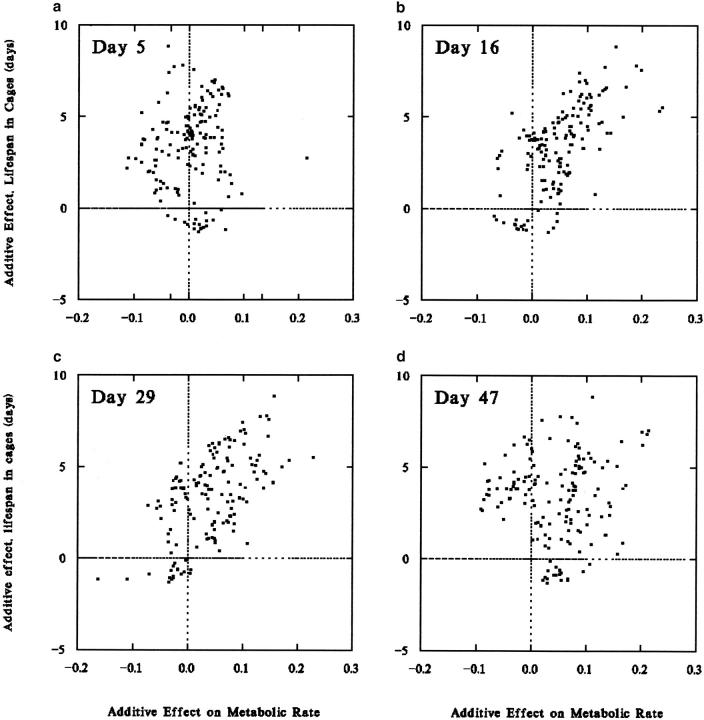
Application of the graphical method to survival and age-specific metabolic rates suggests coordinate genetic control of life span and metabolism, but only for certain ages. In Figure 3a, many chromosome segments are seen to have positive additive effects on life span and little or no effect on metabolic rate on day 5. The largest estimated genetic effects on day 5 metabolic rate are <2% of the mean, and, as noted above, the heritability of metabolic rate at this age is low. Given that there is relatively little heritable variation, it is not surprising that genetic effects on day 5 are not clearly correlated with other phenotypes. In contrast, metabolic rate on day 16 does appear to be genetically closely tied to life span (Figure 3b; with 10-cM spacing, r = 0.63, P < 0.001). A similar strong association is seen for day 29 metabolic rate (Figure 3c; r = 0.50, P < 0.01), but not for day 47 (Figure 3d; r = 0.16, P = 0.43). The pattern of strong associations between life span and metabolic rates on days 16 and 29 and weak associations on days 5 and 47 holds for both first and second measurements, for both cage and vial survival, for both per-fly and weight-adjusted data, and for additive effects estimated by either interval mapping or composite interval mapping methods.

Figure 3.—

Additive genetic effects for adult male life span and metabolic traits in recombinant inbred lines of D. melanogaster. Additive genetic effects on life span in population cages are plotted against additive effects on (a) metabolic rate, day 5; (b) metabolic rate, day 16; (c) metabolic rate, day 29; and (d) metabolic rate, day 47. At the intermediate ages chromosomal segments that increase survival also increase metabolism.

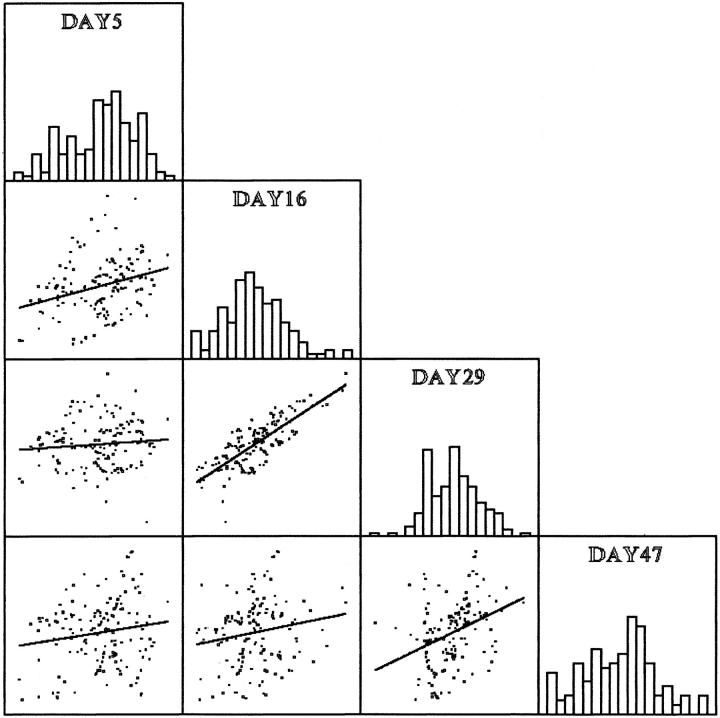
Correlations between additive genetic effects for all pairwise combinations of age-specific metabolic rate measurements are shown in Figure 4. Data are shown in SPLOM (scatter plot matrix) format (Wilkinson 1988), with distributions of additive effects shown on the main diagonal. Most pairwise correlations are nonsignificant (with 10 cM spacing, r < 0.27, P > 0.17), except for days 16 and 29 (r = 0.64, P < 0.001). This suggests that while metabolic rates at the earliest and latest adult ages vary independently, metabolism at the two intermediate ages is subject to coordinate genetic control.

Figure 4.—

SPLOM illustrating correlations of additive genetic effects for each 2-cM region of the genome for metabolic rates measured at four adult ages in a recombinant inbred population of D. melanogaster. Additive genetic effects were estimated by QTL mapping. Distributions of age-specific genetic effects are shown on the main diagonal. Additive effects for day 16 and 29 metabolic rates are significantly and positively correlated; correlations between metabolic rates at other ages are not statistically significant.

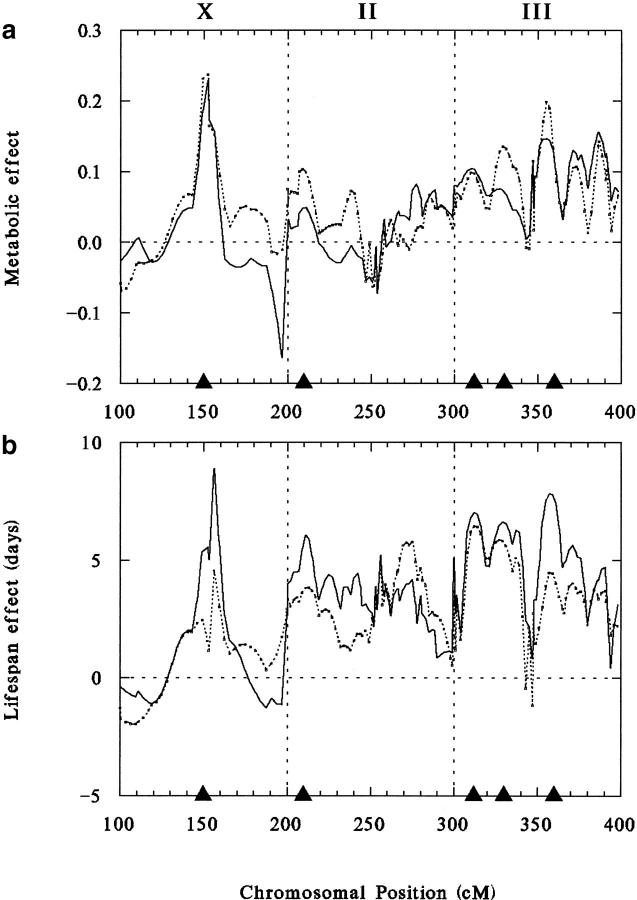
Chromosomal locations of QTL responsible for variations in four positively correlated life span and metabolic traits are shown in Figure 5, where additive effects are plotted as a function of chromosomal position for metabolic rates per fly on days 16 and 29 (Figure 5a) and for survival in cages and vials (Figure 5b). Chromosomal positions are expressed as centimorgans from the left telomere scaled to 100 units for each chromosome and then added to 100, 200, or 300 units for chromosomes X, II, or III, respectively. It is clear that all the maps shown in Figure 5 are quite similar, showing close alignment of major peaks on all three chromosomes. QTL locations and standardized additive effects (estimated additive effect divided by the standard deviation of additive effects for each trait) are listed in Table 6. A major peak near the middle of the X chromosome (chromosomal band 8 based on roo transposable element markers) significantly and positively affects all four traits, increasing each by several standard deviations. There is also close alignment of survival and metabolic peaks at chromosomal positions 210, 312, 330, and 360, in all cases with positive effects on all four traits (Table 6). Approximate cytological locations based on roo elements are chromosomal bands 23, 65, 68, and 91, respectively. The chromosome II location and two of the chromosome III QTL have been detected previously by mapping life-span QTL in these stocks and were found to have similar additive effects (Curtsinger et al. 1998; Resler et al. 1998; Curtsinger and Khazaeli 2002), but the X-linked and centromeric chromosome III locations are new. All five locations correspond to local maxima of the likelihood ratio, which is nearly identical to the additive effects plot (not shown). Results for weight-adjusted CO₂ production are very similar.

Figure 5.—

QTL maps for four positively correlated traits. (a) Metabolic rates on day 16 (solid line) and day 29 (dashed line); (b) mean life span in population cages (solid line) and in vials (dashed line). The abscissa indicates positions on chromosomes X, II, and III, measured in centimorgans and scaled to 100 units for each chromosome. The ordinate indicates additive effects on each trait estimated by interval mapping. Solid triangles show positions of statistically significant QTL peaks detected by interval mapping.

TABLE 6.

QTL affecting life span and age-specific metabolic rates inD. melanogaster

		Standardized additive effect
Chromosome	Locationa	Life-span cages (days)	Life-span vials (days)	CO2 day 16 [μl CO2 (hr · fly)]	CO2 day 29 [μl CO2 (hr · fly)]
X	32	3.9***	2.4***	4.0***	3.5***
II	10	2.7**	1.9*	1.8*	0.8
III	12	3.1***	1.6*	1.8*	1.5*
III	30	2.9***	1.5*	2.3**	1.1
III	60	3.4***	1.8*	3.5***	2.3**

^*P < 0.05;

^**P < 0.01;

^***P < 0.001.

^aCentimorgans from left telomere.

Lin et al. (1995) describe a statistical test for colocation of QTL based on the hypergeometric distribution, which we employ here. The total map length of the three major chromosomes is ∼260 cM, and the average interval over which correspondence of QTL can be assessed is ∼10 cM. This yields n = 26 intervals that can be compared across data sets. A match is declared if a statistically significant QTL is detected in the same 10-cM interval for two different phenotypes. The total number of matches for two phenotypes is m. The probability of observing m matches depends on n, l, and s, where l is the larger total number of QTL detected and s is the smaller number of QTL detected. The exact expression for the probability is given by Lin et al. (1995). For our data, all pairwise comparisons of QTL maps for the traits shown in Figure 5 yield statistically significant colocalizations (P < 0.01 in all cases), while other traits fail to colocalize (P > 0.20 in all cases).

DISCUSSION

Given that RI lines exhibit statistically significant variation in average life spans and in age-specific metabolic rates, the central issue is how survival and metabolism are interrelated. At the phenotypic level, correlations of line means for survival and metabolic traits are close to zero or slightly positive (Table 5), contradicting the predictions of the rate of living theory. At the level of additive effects of QTL, there is a strong correlation between life span and age-specific metabolism at certain ages (Figure 3), but the correlation is positive, again contradicting rate of living predictions.

One could argue that positive correlations arise because some of the inbred lines are “sick,” suffering both impaired metabolism and reduced life expectancy. We reject this explanation, in part because it fails to account for the observed age specificity: QTL that increase life span also increase metabolism, but only at intermediate ages, not at the youngest or oldest ages studied. Further, in the presence of significant line × age interaction (Table 2), it is not clear that there are any sick lines, since none exhibit uniformly low metabolic rates at all ages (Figure 1). Perhaps the most direct way to address the sick line hypothesis is to examine subsets of the data. When we stratify the data by average life spans, we find that for the top 50% of lines the life-span/metabolism correlations remain positive, even though putative sick lines are excluded. For the elite half of lines, average adult life span in cages is 39.0 days (SD = 8.0 days), and correlations between line means for life span and day 16 metabolic rate, life span and day 29 metabolic rate, and day 16 and day 29 metabolic rates are 0.40, 0.39, and 0.74, respectively (P = 0.04, 0.05, and 0.002, respectively). For life spans in vials, the mean of the top 50% of lines is 45.0 days (SD = 7.8 days), and the corresponding correlations are 0.43, 0.42, and 0.78 (P = 0.02, 0.03, and 0.001, respectively). Mean life spans in the elite half of RI lines compare favorably with those observed in typical outbred laboratory populations. A more detailed stratification of the data is presented in Table 7, where lines are classified into quartiles on the basis of mean adult life spans. The last column of Table 7 reports the product-moment correlation coefficient between line mean longevities and metabolic rates for each quartile. None of the correlation coefficients achieves statistical significance at the P = 0.05 level, and only one reaches P = 0.10. The lack of significant correlations at this level of analysis may be due in part to reduced sample sizes inherent in subdividing the data into quartiles. Nevertheless, there is a lack of evidence for a statistically significant inverse relationship between life span and metabolic rate, whether one studies the weakest or strongest lines.

TABLE 7.

Age-specific metabolic rates in populations ofD. melanogaster stratified by average life span

		μl CO2 (hr · fly)
Quartile	Cage life span (days)	Day 5	Day 16	Day 29	Day 47	ra
First measurements
1	16.3	4.97	2.43	2.22	2.52	0.13
2	24.2	4.32	2.49	2.33	2.57	0.03
3	32.0	4.76	2.70	2.33	2.75	−0.13
4	44.0	4.67	2.76	2.63	2.72	−0.12
μl CO2 (hr · fly)
Quartile	Vial life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	25.3	5.02	2.48	2.24	2.43	0.05
2	33.0	4.53	2.48	2.23	2.54	−0.15
3	39.1	4.21	2.48	2.33	2.62	−0.04
4	50.5	4.94	2.93	2.71	2.77	−0.20
μl CO2 (hr · mg)
Quartile	Cage life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	16.3	10.85	4.17	3.19	3.95	0.07
2	24.2	8.06	4.02	3.64	3.77	−0.15
3	32.0	9.39	4.61	3.84	3.95	−0.16
4	44.0	8.55	4.23	4.10	3.79	0.10
μl CO2 (hr · mg)
Quartile	Vial life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	25.3	10.63	4.15	3.29	3.46	−0.02
2	33.0	15.14	4.28	3.39	3.84	−0.15
3	39.1	8.01	4.16	3.81	3.83	−0.01
4	50.5	9.40	4.48	4.28	3.90	0.15
Second measurements
μl CO2 (hr · fly)
Quartile	Cage life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	16.3	3.30	2.24	2.32	2.70	0.13
2	24.2	3.12	2.24	2.32	2.57	0.23
3	32.0	3.28	2.37	2.32	2.59	−0.06
4	44.0	3.32	2.53	2.53	2.71	−0.19
μl CO2 (hr · fly)
Quartile	Vial life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	25.3	3.21	2.26	2.32	2.70	0.18
2	33.0	3.17	2.26	2.26	2.41	−0.13
3	39.1	3.17	2.27	2.35	2.58	0.00
4	50.5	3.44	2.57	2.54	2.76	−0.29
μl CO2 (hr · mg)
Quartile	Cage life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	16.3	5.48	3.87	3.64	4.19	0.06
2	24.2	5.12	3.60	3.73	3.78	−0.09
3	32.0	5.50	4.02	3.99	3.77	−0.13
4	44.0	5.24	3.79	3.99	3.79	−0.13
μl CO2 (hr · mg)
Quartile	Vial life span (days)	Day 5	Day 16	Day 29	Day 47	ra
1	25.3	5.35	3.51	3.78	3.51	0.05
2	33.0	5.19	3.53	3.64	3.62	−0.15
3	39.1	5.20	3.51	3.91	3.86	−0.01
4	50.5	5.57	3.79	4.01	3.91	0.16

^aProduct-moment correlation coefficient between line mean CO₂ production and life span for each quartile.

Our observations suggest that there is a genetic syndrome in these populations that entails high rates of production of CO₂ specifically at intermediate ages and long adult life. In general, genetic correlations can be caused by pleiotropy, close linkage of trait-specific genes, or a combination of those two factors. The extensive overlap of metabolic and life-span QTL peaks reported here (Figure 5) is consistent with a high degree of pleiotropy, which along with epistasis may be a general feature of the genetic architecture of metabolic traits (Montooth et al. 2003). However, the recombinant population studied here is too small to allow us to distinguish between pleiotropy and linkage hypotheses.

Perhaps the most curious aspect of our observations is the age specificity of the survival/metabolism correlation: Why is it observed only for intermediate ages and not at the youngest and oldest ages? There are two possible explanations. The first possibility involves natural selection at the youngest age and loss of statistical power at the oldest age. Metabolic rates are substantially less heritable on day 5 than on later days. The observation that first measurements of young flies are larger on average and more variable than second measurements suggests that young adult flies are more excitable in response to handling, which inflates the phenotypic variance with an added behavioral component. Further, because 5-day-old flies have to feed, fly, walk, and execute mating behaviors to obtain mates in normal lab culture, metabolic rates in young flies might be subject to natural selection in routine lab culture, which reduces additive genetic variance. Both factors tend to reduce the heritability of metabolic rate in young flies. In general, fitness-related traits tend to show lower heritabilities than other traits that are not closely related to Darwinian fitness (Falconer and Mackay 1996). Given the low heritability of day 5 metabolic rates, failure to detect a genetic correlation with life span is not surprising. At the other end of the life history, the heritability of old-age metabolic rate is high. The lack of a statistical relationship between day 47 metabolic rate and life span may be due simply to a loss of statistical power at the oldest ages, when only 22 lines had a sufficient number of individuals still alive for metabolic measurements. In short, the necessary combination of statistical power and adequate genetic variance for age-specific metabolic rate may have existed only at the intermediate ages, on days 16 and 29.

A second possible explanation for the age specificity of genetic correlations concerns the history of the source populations and the manner in which they were artificially selected for long life. Working with genetically heterogeneous populations, Luckinbill and Clare (1985) produced long-lived selection lines by collecting eggs from flies aged 22–26 days in the initial generations of selection, while in control populations eggs were collected from 2–6-day-old flies. Subsequent generations were founded exclusively with eggs collected on the specified days. The only way that a female in the selected population could successfully transmit genes to the next generation was to be alive and fertile at 22–26 days. For males, it is possible to mate at a young age, die shortly thereafter, and still successfully pass genes on to the next generation, because females store sperm. However, multiple mating by females and sperm displacement are common, especially in high-density populations, and the advantage generally goes to the last male (Lefevre and Johnson 1962; Gilchrist and Partridge 1995; Clark and Begun 1998). This argues that males were probably subjected to the same kinds of selective forces as females, a position supported by the observation that males and females have the same life-span QTL in these lines (Curtsinger and Khazaeli 2002). Considering the selection regime, in the selected populations we expect an increase in alleles that promote longer life and also greater ability of males to find females, court them, and mate at ages of 20 days and later. Those behavioral traits involve high mobility and high activity levels and are likely to entail higher metabolic rates. Therefore, we suggest that the Luckinbill selection experiment resulted in the selective increase of alleles that promote improved survival and higher metabolic rates specifically at the selected ages, in the range of 20–30 days postemergence. According to this hypothesis, the relationship between life span and age-specific metabolism at certain ages is special to these particular lines because of their history of artificial selection. We predict a lack of age-specific genetic correlations of the sort reported here in unselected populations. We are presently testing this prediction by measuring life spans and metabolic rates in a new set of RI lines that have not been subjected to artificial selection for increased life span.

Whatever the explanation for patterns of age-specificity, the observed combination of long life and high rates of age-specific CO₂ production is unexpected, considering that both early and recent versions of the rate of living model predict an inverse relationship. We find no support for any kind of rate of living effect in our data; both phenotypic and genetic correlations are all near zero or positive. This result appears to apply to D. melanogaster in general, as we recently observed a similar lack of an inverse relationship between metabolic rate and longevity in an independently derived set of RI lines (Van Voorhies et al. 2004b). While it is likely that there is an oxidative damage component to senescence in D. melanogaster (Arking et al. 1991; Orr and Sohal 1994; Dudas and Arking 1995; Lin et al. 1998; Parkes et al. 1998; Khazaeli and Curtsinger 2000), the observation that life span is not inversely related to metabolic rates suggests either that cellular defenses are sufficient to handle the load of ROS produced over a twofold range of resting metabolic rates or that increased metabolism does not cause greater production of ROS, as has been widely assumed. The latter alternative is consistent with recent studies of mitochondrial uncoupling, which suggest that higher metabolic rates may actually decrease ROS production under some circumstances (Brand 2000; St-Pierre et al. 2002; Speakman et al. 2004).